Multi-Criteria Decision Making Using Preferential Selection Index in Titanium based Die-Sinking PMEDM
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Powder mixed electrical discharge machining (PMEDM) is a new machining technology. The optimization of process parameters in PMEDM is being researched. The determination of the value of the weights of quality indicators in a multi-objective optimization problem is often complex and difficulty. Preferential selection index (PSI) is a new computational technique for solving multi-objective problems. This contributes to the process of solving the multi-objective optimization problems. In this study, material removal rate (MRR) and surface roughness (SR) were optimized with the help of the PSI method. The specimen and tool materials, electrode polarity, current, pulse-on-time, pulse-off-time and powder concentration were considered. The investigation showed that powder concentration can increase MRR with lower SR. The most significant factor was the electrode material. The optimal values were found as SKD11 (workpiece), Gr (tool), + (polarity), 5 μs (ton), 57 μm (toff), 8A (current) and 10 g/l (powder concentration) with a high accuracy of 7.82%. The electrode material and powder concentration could provide strong influence on the performance measures owing to their importance on determining spark energy in the PMEDM. The research results were compared with those of TOPSIS, GRA and MOORA methods. In conclusion, PSI is the method for the highest efficiency.
Keywords:
PMEDM, MRR, SR, PSI1. Introduction
Electrical discharge machining (EDM) is important unconvetnional machining method for making the manufacturing tools and mould (Park et al., 1997; Jeon et al., 2006). Many technological solutions have been introduced to improve the machining process such as optimizing process parameters (Kwon et al., 2012), introducing powders into dielectric fluid (Talla et al., 2016), incorporating the vibration in EDM (Son, 2005; Je et al., 2011). Powder mixed EDM (PMEDM) provides the promising solution to improve productivity and quality in EDM (Vinod et al., 2016; Himadri et al., 2017). Since the number of parameters in PMEDM is high with non-linear nature, the optimization of the technology requires different methods and techniques, especially multi-objective optimization problems.
Taguchi method is well suit and commonly used for experimental design in PMEDM (Mohapatra et al., 2017). This has contributed to the reduction of experimental costs and increased experimental efficiency in the PMEDM. However, Taguchi method has dealt single-response problem only. Several multi criteria making methods were proposed for solving the optimal multi-objective in EDM (Nayak et al., 2017). Vijay et al. (2017) used the Taguchi - Grey Relational Analysis (GRA) to optimize MRR, electrode wear rate (TWR) and overcut (OC) in μ - EDM for machining Titanium alloy. The results show that the use of GRA for multi-objective optimization is appropriate. Durairaj et al. (2013); Rajesh et al. (2017) and Pawan et al. (2018) applied the multi – objective optimization in EDM and WEDM processes tp obtain better quality characteristics such as MRR, SR, wire wear ratio (WWR) and kerf width. The optimal result should provide the high accuracy, fit consistent between theory and experiment. Mahapatra and Sahoo (2018) performed a multi-objective optimization of the process parameters in gear processing by Wire EDM for Inconel 718 using Taguchi - TOPSIS method. The optimal results have shown that the quality of the gears at optimum conditions is better. The comparison of the results of Taguchi-GRA with Taguchi-TOPSIS in multi- objective optimization in EDM (Dastagiri et al., 2017; Gadakh, 2016) and PMEDM (Tripathy et al., 2016) were researched. It has observed that Taguchi-TOPSIS method could be better than Taguchi-GRA method. Sivapirakasam et al. (2011), Tiwary et al. (2014) and Dewangan et al. (2015) also incorporated Taguchi - TOPSIS based multi-objective optimization in EDM process parameter. “Triangular fuzzy” was used to determine the weighted values of the 5 output norms. The combination was also used to optimize three quality indicators simultaneously (SR, MRR and Fractal dimension) in die sinking - EDM by Prabhu et al. (2016). However, the weights of quality indicators are determined by the Analytic Hierarchy Process (AHP). The best quality parameters have been identified with the optimal set of parameters and weighted values have been calculated on a scientific basis even though the method is difficult. Rajesh et al. (2016) simultaneously optimized MRR, TWR, ROC and SR in EDM for Al-18Wt% SiCp MMC by the VIKOR method. The weighted values of indicators can be determined by the method of Entropy weighted measurement. It has been confirmed that this method was suitable for other types of process. Nevertheless the determined the weighting method is quite complex. The literatures proposed the need of multi-objective optimization problem in EDM and PMEDM. In recent times, Dušan et al. (2017) introduced the Performance Selection Index (PSI) methodology for multi-objective optimization in processing methods. The optimization problem is much simpler, since it does not require weighted values of indicators.
From the literature survey, it has been observed that the multi-objective optimization of process parameter in EDM and PMEDM by PSI method had not been researched in a considerable level. Hence, Taguchi - PSI method has been used to enhance the titanium powder mixed EDM process in the present study.
2. Materials and Methods
2.1 Selection of Process Parameters
The selection of process parameters for the present study has been chosen based on previous studies as discussed in the literatures. The process parameters have been chosen as workpiece material (WM), tool material (TM), polarity (TP), peak current (Ip), pulse-on-time (ton), pulse-off-time (toff), titanium powder concentration (PC) with various ranges as shown in Table 1. The various interactions (the electrode material and the workpiece material; the electrode material and the titanium powder concentration; the workpiece material and the titanium powder concentration) have been considered. L27 orthogonal array of Taguchi method with dummy treatment has been used for designing the experiments as shown in Table 2. The MRR has been found by computing the weight difference of workpiece before and after the performance trial using electronic scale AJ203 with an accuracy of 0.001 g. The surface roughness was measured using a strain gauge transducer contact, Mitutoyo SJ-210. The experiments have been performed using AG40L electrical discharge machine (Sodick, Inc. USA) as shown in Fig. 1. The tank was made of CT3 steel with size 330 × 180 × 320 mm. The titanium powder with average size of 45μm was mixed with HD-1 oil dielectric fluid. The tool electrode has been selected with diameter of 23 mm.
2.2. Preference Selection Index (PSI) Method
Maniya and Bhatt (2010) proposed the PSI method to solve the problem multi criteria decision making (MCDM) for material selection. MCDM methods always require accurate identification of the weighted values of the optimized criteria. The determination of the weighted values is quite complex and difficult, especially in the event of a conflict on determining the relative importance of the criteria. The finding of the weights is not needed in such method. The steps of the proposed method to solve the decision making are as follows:
Step 1: Determine the target of the problem and selecting criteria are assessed to ensure the target, select experiment matrix relate to the decision-making problem is being considered. This experimental matrix selection mentions the changes of combinations for different test runs.
Step 2: Construct the first decision matrix from the first selected criteria. Each row of decision matrix is the value of the criteria at one experiment and each column for one criterion. In it, an Xij element of the decision matrix gives the value of a j-th criteria for i-th test run. If the number of experiments is m and the number of criteria is n, the decision matrixes m × n can be performed by Eq. (1).
| (1) |
Step 3: In solving multi-objective problems, it is required to make the value of the criteria non-dimensional. To ensure this purpose, the values of the criteria will be converted into 0 and 1, and this transition is called standardized.
It is better if the criterion is bigger, it will be standardized according to the Eq. (2):
| (2) |
It is better if the criterion is smaller, it will be standardized according to Eq. (3):
| (3) |
Inside, xij is the value of the criteria (i = 1,2,3,… .., m and j = 1,2…., n). The decision matrix is standardized by Eqs. (2) and (3) depending on the objective of the problem.
Step 4: In this step, the Mean of the standardized criteria are calculated by Eq. (4):
| (4) |
Step 5: Optional variation values between the values of each criteria are calculated by using Eq. (5):
| (5) |
Step 6: Evaluate the deviation of the priority level value relate to each criterion by using Eq. (6):
| (6) |
Step 7: The entire priority value is defined for each criteria using the Eq. (7):
| (7) |
Besides, the total priority value of all criteria must satisfy the Eq. (8):
| (8) |
Step 8: Priority index is computed using the Eq. (9):
| (9) |
Step 9: Based on the priority index value to rank. The rankings must be made according to the value of θj. The biggest θj value would be the best solution (optimal solution).
3. Results and Discussion
With target of enhancing the productivity and surface quality, the performance measures have been selected as higher MRR and lower SR. The experimental results of two examined criteriaaccording to Taguchi’s L27 matrix as shown in Table 2. MRR is standardized according to the Eq. (2) and SR is standardized according to the Eq. (3) as shown in Table 3. The computation results have been calculated according to the steps involved in PSI method as shown in Table 4. The priority index of problem with S/N analysis has been also determined as shown in Table 5.
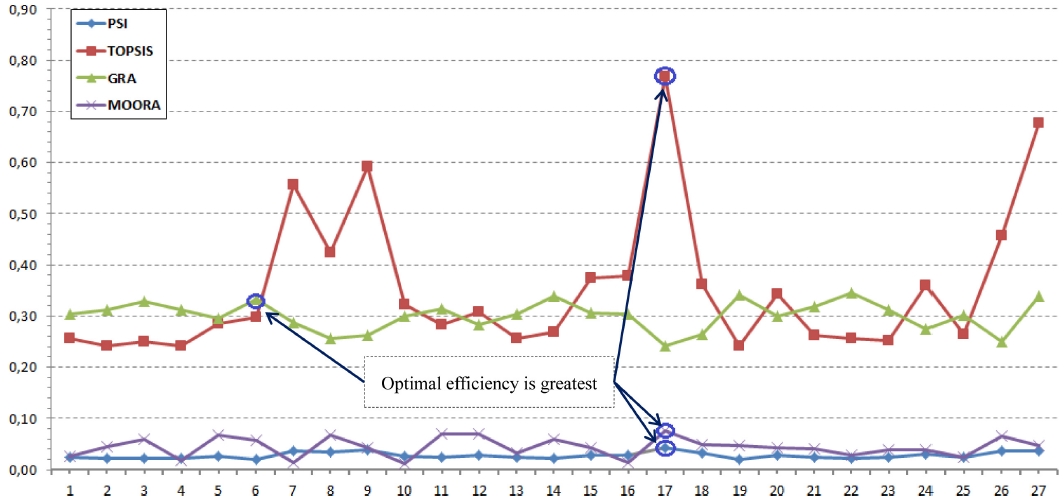
It has been observed that the 17th experiment has provided larger index as shown in Fig. 2. Hence the respective experiment was chosen as the optimal process parameters as SKD11 (WM), Gr (tool), + (polarity), 5 μs (ton), 57 μm (toff), 8 A (Ip) and 10 g/l (PC).
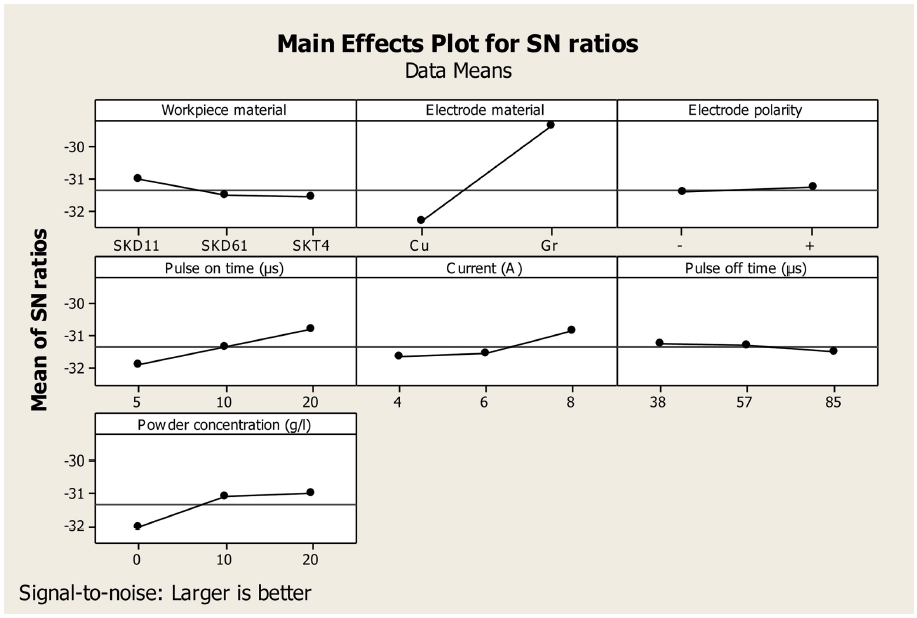
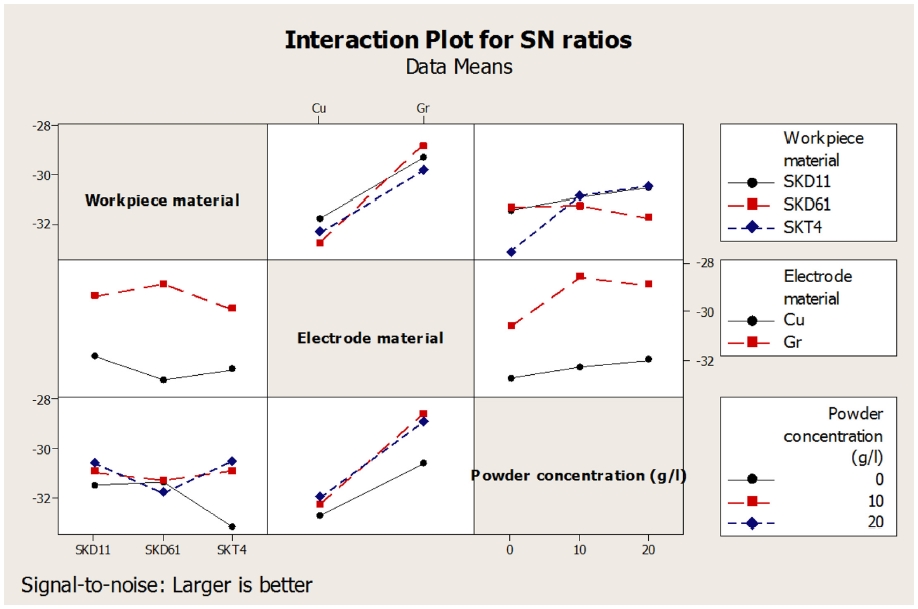
It has observed from experimental analysis that,17th experiment has also provided the maximum value of S/N. The ANOVA analysis of S/N ratio has shown that electrode material and powder concentration could provide strong influence on performance measures owing to their importance on determining spark energy. The polarity of electrode has provided lower influence on determining machining characteristics in PMEDM process. The pulse- on time and current has also given considerable contribution in the machining process. The interactions of the factors could provide significant influence than individual factors on determining the optimal results in PMEDM process as shown in Table 6. The accuracy of the optimum conditions has been evaluated by the Eq. (10) as shown in Table 7. The results have shown that the deviation of the computed values and the empirical values have been lower values only. The PSI method can effectively increase the optimal values as approximately 7.82%. It has proved that PSI based optimization could be completely suitable for PMEDM process with titanium powder. The quality of optimal surface layer was analyzed by Phan et. al., 2018. The analytical results showed that surface layer is good and it contributes advancing the working ability of the steel surface molding.
| (10) |
Evaluate the relevance of the PSI method: The results of multi-objective optimization in PMEDM using titanium powder by PSI method are compared with those of TOPSIS, GRA and MOORA methods, Table 5 and Fig. 2. The results showed that the PSI, TOPSIS and MOORA results were the same. The optimal result by GRA method is obtained at the 6th experiment. In this study, TOPSIS, MOORA and PSI methods are more effective than MOORA method. Compared to PSI method, TOPSIS, MOORA and GRA are more complex methods in solving multi-objective optimization problem because the number of steps to be implemented is more. In addition, It is necessary to determine the priority weights of quality indicators in TOPSIS, MOORA and GRA. And this is often very difficult for new products and machining methods are unclear, and PMEDM is such a machining method. All these have shown that PSI is the simplest and most suitable method in the methods surveyed for PMEDM’s multi-objective optimization using titanium powder.
4. Conclusion
An endeavor was attempted to optimize the process parameters in titanium based PMEDM for machining die steels using Taguchi-PSI. From the trials and investigation, the following decisions were made:
PSI, TOPSIS and MOORA are better than GRA in multi-objective optimization in PMEDM using titanium powder. And PSI is the most suitable method.
PSI method can provide better effective solution to overcome the limitations of TOPSIS, MOORA and GRA methods in PMEDM process.
The optimal values have been found as SKD11 (workpiece), Gr (tool), + (polarity), 5 μs (ton), 57 μm (toff), 8 A (Ip) and 10 g/l (PC) with high accuracy of 7.82%.
The electrode material and powder concentration could provide strong influence on performance measures owing to their importance on determining spark energy.
Acknowledgments
This paper was presented at PRESM 2019
This research is funded by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number “107.01-2017.303”.
REFERENCES
- Park, J. Y., Jeon, E. C., and Jeong, J. H., “Influence on EDM Surface with the Copper and Graphite Electrode According to the Discharge Energy,” Journal of the Korean Society for Precision Engineering, Vol. 14, No. 5, pp. 53-59, 1997.
- Jeon, D.-H., Kim, B. H., and Chu, C. N., “Micro Machining by EDM and ECM,” Journal of the Korean Society for Precision Engineering, Vol. 23, No. 10, pp. 52-59, 2006.
-
Kwon, W.-T. and Kim, Y.-C., “Process Optimization for Productivity Improvement during EDM Machining of a Micro-Hole,” Journal of the Korean Society of Manufacturing Technology Engineers, Vol. 21, No. 4, pp. 556-562, 2012.
[https://doi.org/10.7735/ksmte.2012.21.4.556]

-
Talla, G., Gangopadhayay, S., and Biswas, C., “State of the Art in Powder-Mixed Electric Discharge Machining: A Review,” Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, Vol. 231, No. 14, pp. 2511-2526, 2017.
[https://doi.org/10.1177/0954405416634265]

-
Son, S.-M., “Improvement of Micro-Hole EDM Efficiency Using Vibration Flushing,” Journal of the Korea Academia-Industrial Cooperation Society, Vol. 12, No. 2, pp. 623-628, 2011.
[https://doi.org/10.5762/KAIS.2011.12.2.623]

- Je, S. U., Lee, H. S., Chu, C. N., and Kim, D. W., “Micro EDM with Ultrasonic Work Fluid Vibration for Deep Hole Machining,” Journal of the Korean Society for Precision Engineering, Vol. 22, No. 7, pp. 47-53, 2005.
-
Kumar, V. and Jangra, K., “An Experimental Study on Trim Cutting Operation Using Metal Powder Mixed Dielectric in WEDM of Nimonic-90,” International Journal of Industrial Engineering Computations, Vol. 7, No. 1, pp. 133-146, 2016.
[https://doi.org/10.5267/j.ijiec.2015.7.002]

-
Majumder, H. and Maity, K., “Optimization of Machining Condition in WEDM for Titanium Grade 6 Using MOORA Coupled with PCA—A Multivariate Hybrid Approach,” Journal of Advanced Manufacturing Systems, Vol. 16, No. 2, pp. 81-99, 2017.
[https://doi.org/10.1142/S0219686717500068]

-
Mohapatraa, K. D., Satpathya, M. P., and Sahooa, S. K., “Comparison of Optimization Techniques for MRR and Surface Roughness in Wire EDM Process for Gear Cutting,” International Journal of Industrial Engineering Computations, Vol. 8, No. 2, pp. 251-262, 2017.
[https://doi.org/10.5267/j.ijiec.2016.9.002]

-
Nayak, I., Rana, J., and Parida, A., “Performance Optimization in Electro-Discharge Machining Using a Suitable Multiresponse Optimization Technique,” Decision Science Letters, Vol. 6, No. 3, pp. 283-294, 2017.
[https://doi.org/10.5267/j.dsl.2016.12.002]

-
Meena, V. K., Azad, M. S., Singh, S., and Singh, N., “Micro-EDM Multiple Parameter Optimization for CP Titanium,” The International Journal of Advanced Manufacturing Technology, Vol. 89, Nos. 1-4, pp. 897-904, 2017.
[https://doi.org/10.1007/s00170-016-9130-2]

-
Durairaj, M., Sudharsun, D., and Swamynathan, N., “Analysis of Process Parameters in Wire EDM with Stainless Steel Using Single Objective Taguchi Method and Multi Objective Grey Relational Grade,” Procedia Engineering, Vol. 64, pp. 868-877, 2013.
[https://doi.org/10.1016/j.proeng.2013.09.163]

-
Khanna, R., Kumar, A., Garg, M. P., Singh, A., and Sharma, N., “Multiple Performance Characteristics Optimization for Al7075 on Electric Discharge Drilling by Taguchi Grey Relational Theory,” Journal of Industrial Engineering International, Vol. 11, No. 4, pp. 459-472, 2015.
[https://doi.org/10.1007/s40092-015-0112-z]

-
Kumar, P., Meenu, M., and Kumar, V., “Optimization of Process Parameters for WEDM of Inconel 825 Using Grey Relational Analysis,” Decision Science Letters, Vol. 7, No. 4, pp. 405-416, 2018.
[https://doi.org/10.5267/j.dsl.2018.1.006]

-
Mohapatra, K. D. and Sahoo, S. K., “A Multi Objective Optimization of Gear Cutting in WEDM of Inconel 718 Using TOPSIS Method,” Decision Science Letters, Vol. 7, No. 2, pp. 157-170, 2018.
[https://doi.org/10.5267/j.dsl.2017.6.002]

- Dastagiri, M., Rao, P. S., and Valli, P. M., “TOPSIS, GRA Methods for Parametric Optimization on Wire Electrical Discharge Machining (WEDM) Process,” Proc. of Design and Research Conference (AIMTDR–2016) College of Engineering-India, 2016.
-
Gadakh, V. S., “Parametric Optimization of Wire Electrical Discharge Machining Using TOPSIS Method,” Advances in Production Engineering & Management, Vol. 7, No. 3, pp. 157-164, 2012.
[https://doi.org/10.14743/apem2012.3.138]

-
Tripathy, S. and Tripathy, D. K., “Multi-Attribute Optimization of Machining Process Parameters in Powder Mixed Electro-Discharge Machining Using TOPSIS and Grey Relational Analysis,” Engineering Science and Technology, an International Journal, Vol. 19, No. 1, pp. 62-70, 2016.
[https://doi.org/10.1016/j.jestch.2015.07.010]

-
Sivapirakasam, S. P., Mathew, J., and Surianarayanan, M., “Multi-Attribute Decision Making for Green Electrical Discharge Machining,” Expert Systems with Applications, Vol. 38, No. 7, pp. 8370-8374, 2011.
[https://doi.org/10.1016/j.eswa.2011.01.026]

-
Tiwary, A. P., Pradhan, B. B., and Bhattacharyya, B., “Application of Multi-Criteria Decision Making Methods for Selection of Micro-EDM Process Parameters,” Advances in Manufacturing, Vol. 2, No. 3, pp. 251-258, 2014.
[https://doi.org/10.1007/s40436-013-0050-1]

-
Dewangan, S., Gangopadhyay, S., and Biswas, C. K., “Study of Surface Integrity and Dimensional Accuracy in EDM Using Fuzzy TOPSIS and Sensitivity Analysis,” Measurement, Vol. 63, pp. 364-376, 2015.
[https://doi.org/10.1016/j.measurement.2014.11.025]

-
Prabhu, S. and Vinayagam, B. K., “Multiresponse Optimization of EDM Process with Nanofluids Using TOPSIS Method and Genetic Algorithm,” Archive of Mechanical Engineering, Vol. 63, No. 1, pp. 45-71, 2016.
[https://doi.org/10.1515/meceng-2016-0003]

-
Bhuyan, R. K. and Routara, B. C., “Optimization the Machining Parameters by Using VIKOR and Entropy Weight Method during EDM Process of Al–18% SiCp Metal Matrix Composite,” Decision Science Letters, Vol. 5, No. 2, pp. 269-282, 2016.
[https://doi.org/10.5267/j.dsl.2015.11.001]

-
Petković, D., Madić, M., Radovanović, M., and Gečevska, V., “Application of the Performance Selection Index Method for Solving Machining MCDM Problems,” Facta Universitatis, Series: Mechanical Engineering, Vol. 15, No. 1, pp. 97-106, 2017.
[https://doi.org/10.22190/FUME151120001P]

-
Nguyen, H.-P., Pham, V.-D., and Ngo, N.-V., “Application of TOPSIS to Taguchi Method for Multi-Characteristic Optimization of Electrical Discharge Machining with Titanium Powder Mixed into Dielectric Fluid,” The International Journal of Advanced Manufacturing Technology, Vol. 98, Nos. 5-8, pp. 1179-1198, 2018.
[https://doi.org/10.1007/s00170-018-2321-2]

-
Long, B. T., Phan, N. H., Cuong, N., and Jatti, V. S., “Optimization of PMEDM Process Parameter for Maximizing Material Removal Rate by Taguchi’s Method,” The International Journal of Advanced Manufacturing Technology, Vol. 87, Nos. 5-8, pp. 1929-1939, 2016.
[https://doi.org/10.1007/s00170-016-8586-4]


Doctor in the Faculty of Mechanical Engineering, HaNoi University of Industrial, Vietnam. His research interests are improvement of Electric Discharge Machining, Process Optimization
E-mail: nguyenhuuphan@haui.edu.vn

Professor in the School of Mechanical Engineering, Hanoi University of Science and Technology, Vietnam. His research interests are Metal cutting, industrial instrument, CAD/CAM/CAE
E-mail: long.banhtien@hust.edu.vn

Ph.D candidate in the School of Mechanical Engineering, Hanoi University of Science and Technology, Vietnam. His research interests are PMEDM, Mechatronic and Machining process.
E-mail: ledung202@gmail.com

Associate Professor in the School of Mechanical Engineering, Hanoi University of Science and Technology, Vietnam. His research interests are Plasticity, Machining Process, CAD/CAM/CAE.
E-mail: toan.nguyenduc@hust.edu.vn

Associate Professor in Department of Mechatronics Engineering, School of Mechanical Engineering, SRM Institute of Science and Technology, India. His research interests are Micro machining, Mechatronics, Process Optimization
E-mail: muthu1060@gmail.com