옥외용 이동로봇의 확장 칼만 필터 기반 3차원 위치평가 방법

1. 서론

로봇의 위치평가 기술은 재난지역이나 사고현장에서 인간을 대신하여 작업을 수행하는 로봇, 운전자가 필요 없는 자율주행 자동차 등 다양한 분야에서 그 필요성이 커지고 있다. 이와 같은 분야에서 로봇이 주어진 임무를 정확하게 수행하기 위해서는 로봇 자신의 정밀한 위치평가가 가장 중요한 부분이다.^1,2

이동로봇의 위치평가에 있어서 옥외환경은 실내환경과 달리 구조화되어 있지 않으며 활동범위도 넓기 때문에 사전 환경지도의 제공^3,4이나 위치센서의 사용^5-7이 어렵다. 따라서 옥외환경에서 이동로봇의 위치평가는 위치정보를 쉽게 획득할 수 있는 DGPS (Differential GPS)를 많이 이 용하는데 DGPS의 낮은 위치정밀도를 보정해주기 위해 주행계나 IMU의 정보를 확장 칼만 필터로 융합하는 방법 이 주로 이용된다.^8-11

옥외환경은 일반적으로 실내환경과 다르게 언덕과 같은 지형으로 인해 경사가 존재한다. 즉, 옥외환경은 고도 차가 존재하므로 고도정보를 고려한 3차원 위치평가가 필요하다. 특히 3차원 위치평가를 통한 정밀한 위치추정은 재난지역이나 사고현장에서 인간을 대신하여 생존자 탐색과 같은 임무를 수행하는 재난지역 탐사 로봇, 그리고 산악 지형에서 수색 위치 또는 포격 위치 설정 등의 군사임무를 수행하는 군사용 로봇에게 있어서 임무 성공률과도 연관되므로 매우 중요하다. 그 밖에도 요즘 주목 받고 있는 자율주행 자동차나 건물 및 시설 보수용 로봇, 그리고 골프장 캐디로봇과 같은 서비스용 로봇 등은 평면 위치정보뿐 만 아니라 고도정보가 필수적이다. 따라서 이와 같은 로봇들의 정밀한 임무 수행을 위해서는 3차원 위치평가를 통한 정밀한 위치추정은 매우 중요한 부분이다.

또한 2차원 평면 위치정보만 필요한 경우에도 옥외환경에서 고도정보를 고려하지 않을 경우 로봇이 경사 면을 따라 이동한 로봇의 실제 이동거리와 평면상에서 측정된 이동거리는 차이가 나게 되어 평지에서보다 더 큰 오차가 발생한다. 이와 같은 오차는 경사가 심한 환경 에서 더욱 크게 나타나며 주행거리가 길어질수록 누적 된다. 따라서 옥외환경에서는 고도정보를 포함한 3차원 위치평가가 필요하며 특히 험한 경사가 존재하고 로봇의 활동거리가 길수록 그 중요성이 매우 커진다.

이동로봇의 3차원 위치평가에 대한 연구는 그리 많지 않다. Lai¹²는 이동로봇의 3차원 위치평가를 위해 레이저 거리 측정기와 4개의 인공 반사경으로 구성된 시스템을 제안하였다. Nagatani¹³는 재난지역에서의 생존자 탐색 및 구조를 수행하는 로봇을 위해 3차원 공간에서의 위치 파악과 3차원 매핑을 연구하였다. 이 연구에서는 이동 로봇의 3차원 위치평가를 위해 레이저 거리 측정기를 이용하여 로봇의 위치를 추정한다. 이 방법은 위치 추정 정밀도를 높이기 위해서는 다수의 레이저 거리 측정기를 설치해야 하므로 비용이 늘어나고 이에 따라 구성도 복잡해지게 된다. 특히 옥외환경과 같이 복잡하고 넓은 환경에서 레이저 거리 측정기는 비효율적이다.

본 논문에서는 저가의 DGPS, 디지털컴퍼스 및 경사 센서와 같은 비관성센서를 이용하여 이동로봇의 3차원 위치를 평가하는 방법을 제안한다. 이 방법은 3차원 위치평가를 위해 경위도 방향뿐만 아니라 고도방향에 대해 서도 위치평가를 수행한다. 즉, 주행계로부터 획득한 로봇 의 이동정보와 경사센서의 각도 정보를 이용하여 고도정보를 계산하고, 이 정보와 DGPS로부터 측정된 경위도 및 고도정보를 확장 칼만 필터로 융합함으로써 고도 방향에 대해서도 위치평가를 수행한다. 개발된 3차원 위치 평가 방법의 성능 및 실용 가능성을 평가하기 위해 실제 실험을 수행하고 그 성능을 분석한다.

본 논문의 구성은 다음과 같다. 2장에서는 3차원 위치평가 방법의 시스템 모델과 측정 모델을 제공하고 위치평가 알고리즘을 설명한다. 3장에서는 제안된 방법의 성능검증을 위한 실험방법과 실험결과를 나타냈고 그 결과에 대해 논의한다. 마지막으로 4장에서 결론을 요약 하였다.

2. 이동로봇의 3차원 위치평가 방법

본 연구에서 개발한 옥외용 이동로봇의 3차원 위치평가 방법은 우선 추측항법(Dead-Reckoning, DR)을 이용하여 위치평가를 수행한다. DR에 이용되는 센서는 경사 센서와 로봇의 바퀴에 부착된 두 엔코더를 이용하여 로봇의 3차원 위치와 방향각도, 경사각도를 계산한다. 추측 항법은 바퀴의 미끄러짐이나 불균형, 그리고 바닥의 요철 등으로 인해 시간이 지남에 따라 오차가 누적되어 위치 추정의 신뢰성이 떨어지는 문제가 있다. 본 연구에서는 이와 같은 문제를 해결하기 위해 추가로 DGPS와 디지털 컴퍼스를 이용하며, 확장 칼만 필터(Extended Kalma Filter, EKF)를 통해 오차를 보정한다.

2.1 시스템 모델 및 측정 모델

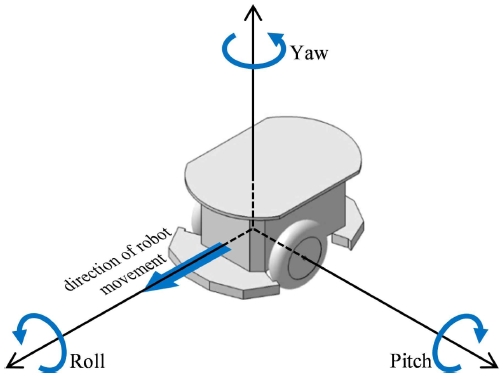
로봇의 회전을 나타내는 각도는 Fig. 1에 나타낸 바와 같이 로봇의 Yaw 방향을 θ, Pitch 방향을 ϕ로 정의할 수 있다. 일반적인 도로는 Roll 방향 각도 변화가 크지 않아 로봇의 위치추정에 별다른 영향이 없으므로 로봇의 상태 변수는 정의된 각도 θ, ϕ와 로봇의 3차원 위치를 나타 내는 x, y, z를 포함하여 다음 식(1)과 같이 정의한다.^14-16

Fig. 1

Angular coordinate system

$\[ X=\left[\begin{array}{c}x\\ y\\ z\\ \theta \\ \varphi \end{array}\right] \]$

(1)

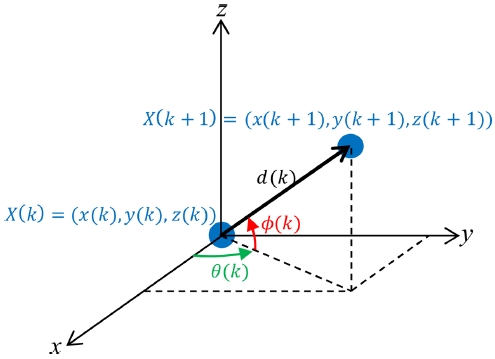
시간 k에서 k+1로 변화할 때 로봇의 위치를 나타내 는 시스템 모델은 Fig. 2와 같은 관계에 의해 다음 식(2)과 같이 표현된다.^15-17

Fig. 2

System modeling

$\[ X\left(k+1\right)=F\left(X\left(k\right),u\left(k\right)\right)+\upsilon \left(k\right) \]$

(2)

여기서 X(k+1)는 시간 k+1에서 로봇의 위치, X(k)는 시간 k에서 로봇의 위치를 나타낸다. F(X(k), u(k))는 상태천이함수이며, v(k)는 평균이 0이고 공분산이 Q(k)인 로봇의 이동과 관련된 가우시안 잡음이다. u(k)는 로봇의 이동거리 d(k)와 방향각 증분 Δθ(k) 및 경사각 증분 Δϕ(k)로 이루어지는 제어입력으로 다음 식(3)과 같다.

$\[ u\left(k\right)=\left[\begin{array}{c}d\left(k\right)\\ \mathrm{\Delta }\theta \left(k\right)\\ \mathrm{\Delta }\varphi \left(k\right)\end{array}\right] \]$

(3)

상태천이함수 F(X(k), u(k))는 시간 k에서 로봇의 위치 X(k)와 제어입력 u(k)를 이용하여 식(4)로 표현된다.

$\[ F\left(X\left(k\right),u\left(k\right)\right)=\left[\begin{array}{c}x\left(k\right)+d\left(k\right)\cos \varphi \left(k\right)\cos \theta \left(k\right)\\ y\left(k\right)+d\left(k\right)\cos \varphi \left(k\right)\sin \theta \left(k\right)\\ z\left(k\right)+d\left(k\right)\mathrm{s}\mathrm{i}\mathrm{n}\varphi \left(k\right)\\ \theta \left(k\right)+\mathrm{\Delta }\theta \\ \varphi \left(k\right)+\mathrm{\Delta }\theta \end{array}\right] \]$

(4)

DGPS와 디지털컴퍼스의 측정값을 로봇의 위치와 연관 시키는 측정 모델은 다음 식(5)과 같이 정의한다.

$\[ Z\left(k+1\right)=H\left(X\left(k+1\right)\right)+\omega \left(k+1\right) \]$

(5)

여기서 ω(k+1)는 평균이 0, 공분산이 R(k+1)인 DGPS와 디지털 컴퍼스의 측정과 관련된 가우시안 잡음 이다. 위치 측정에 사용된 센서인 DGPS와 디지털 컴퍼스는 각각 고유한 측정 메커니즘을 갖고 있으며, 각 센서의 위치정보 발생과정은 로봇의 위치를 제외한 다른 특별한 관계가 존재하지 않는다. 따라서 상태천이함수 H(X(k+1))는 다음 식(6)과 같이 표현된다.

$\[ H\left(X\left(k+1\right)\right)=\left[\begin{array}{c}{x}_{GPS}\left(k+1\right)\\ y_{GPS}\left(k+1\right)\\ z_{GPS}\left(k+1\right)\\ {\theta }_{DC}\left(k+1\right)\\ {\varphi }_C\left(k+1\right)\end{array}\right] \]$

(6)

여기서 x_GPS(k+1), y_GPS(k+1), z_GPS(k+1)은 DGPS의 측정값이고 θ_DC(k+1)은 디지털컴퍼스의 측정값이다. ϕ_C(k+1)은 시간 k에서 k+1까지 DGPS 측정값의 변화량으로부터 계산된 로봇의 Pitch 방향 성분을 나타 내며 다음과 같이 계산된다.

$\[ {\varphi }_C\left(k+1\right)={\sin }^{-1}\left(\frac{\text{Δ}{z}_{GPS}}{\sqrt{{\left(\text{Δ}{x}_{GPS}\right)}^2+{\left(\text{Δ}{y}_{GPS}\right)}^2+{\left(\text{Δ}{z}_{GPS}\right)}^2}}\right) \]$

(7)

여기서 Δx_GPS, Δy_GPS, Δz_GPS은 시간 k에서 k+1까지 DGPS의 x, y, y 방향 변화량을 나타낸다.

3. 위치평가 결과 및 고찰

3.1 실험방법

개발된 3차원 위치평가 방법의 성능을 평가하기 위해 Fig. 3과 같은 환경에서 실험을 수행하였다. 주행거리는 400 m정도이고 고도차가 25 m정도인 내리막길과 오르막길이 존재하는 환경이다. 그림의 X 표시는 기준 경로를 계산하기 위한 기준위치로서 로봇이 주행한 이동 경로 내의 모든 위치에서의 실제 좌표는 측정이 어렵기 때문에 사전에 15 곳의 고도정보를 포함한 실제 좌표를 측정한 후 이것을 연결하여 기준경로로 설정하였다.

Fig. 3

Experimental environment

실험은 리모컨을 이용하여 로봇이 기준경로를 따라 주행시킨 후 기준경로에 대한 DGPS 및 위치평가 결과의 위치오차를 비교 분석하는 방법으로 수행되었다. 로봇은 평균 0.6 m/s의 일정한 속력으로 주행하도록 하였다.

Fig. 4는 실험에 사용된 로봇과 장착된 센서들의 사진으로서 ⓐ는 경사센서, ⓑ는 DGPS, ⓒ는 디지털 컴퍼스를 나타낸다. 로봇 플랫폼은 Adept Technology 사의 Pioneer-3DX이며 그 사양은 Table 1과 같다. 바퀴에는 로봇의 이동정보를 획득할 수 있는 엔코더가 부착되어 있으며, 경사센서는 Level Development 사의 LCH-360-USB, DGPS는 AscenKorea 사의 RCV-3000, 그리고 디지털 컴퍼스는 WithRobot 사의 myAHRS+를 사용하였으며 그 사양은 Table 2와 같다.

Fig. 4

Photo of the robot and sensors(ⓐ: Inclinometer, ⓑ: DGPS, ⓒ: Digital compass)

Table 1

Specifications of the robot

Table 2

Specifications of the sensors

3.2 실험 결과

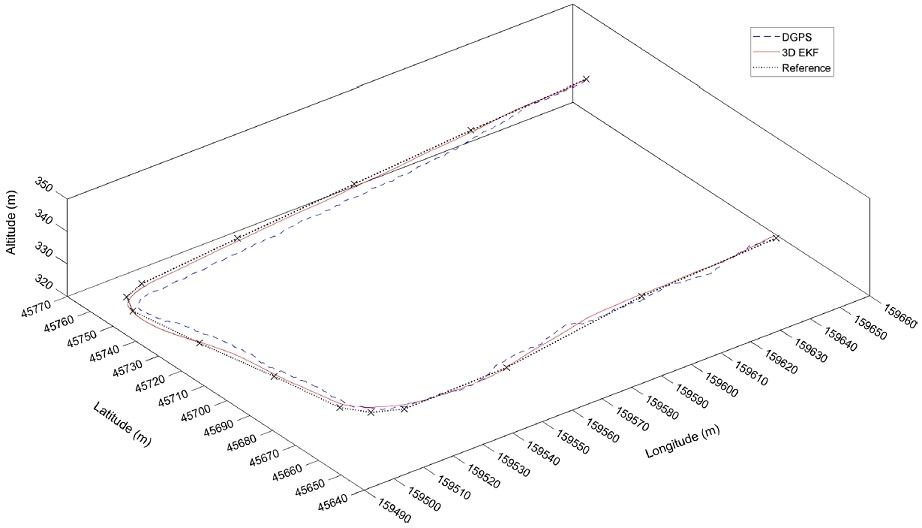
Fig. 5는 DGPS 및 개발된 3차원 위치평가 방법의 결과로서 점선은 DGPS 경로, 실선은 3차원 위치평가 결과, X 표시가 포함된 가는 실선은 기준경로를 나타낸다. 그림에서 알 수 있듯이 DGPS는 기준경로와 비교적 큰 차이를 보이며 로봇이 기준경로를 따라 직선적으로 이동 했음에도 불구하고 평탄하지 못한 결과를 보여주고 있다. 3차원 위치평가 방법은 이와 같은 DGPS의 오차를 보정 하고 이동경로를 어느 정도 평탄하게 하여 기준 경로와 가까운 결과를 보여주고 있다.

Fig. 5

Results of the 3D localization

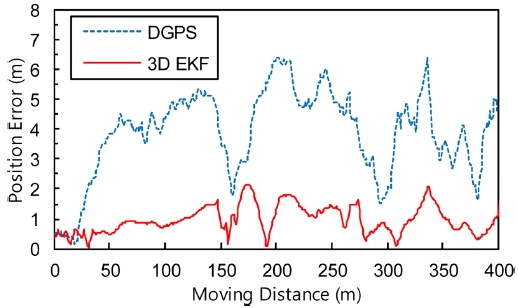
위치평가의 정량적인 성능을 확인하기 위해 각각의 위치오차를 Fig. 6에 나타냈으며, 점선은 DGPS의 위치오차, 실선은 3차원 위치평가의 위치오차이고 이에 대한 위치 오차 특성은 Table 3에 나타냈다. 오차특성을 분석 해보면 DGPS는 최대 6.4 m, 평균 3.9 m의 위치오차를 보이고 있는 반면에 3차원 위치평가는 최대 2.3 m, 평균 0.9 m의 비교적 낮은 위치오차를 보여주고 있다. 따라서 제안된 3차원 위치평가 방법은 DGPS의 위치오차를 크게 개선 해주며 이동경로를 평탄하게 하여 로봇의 실제 이동 경로에 가까운 위치평가 결과를 보여준다고 판단된다.

Fig. 6

Position error (RMS error)

Table 3

Characteristics of the position error (unit : m)

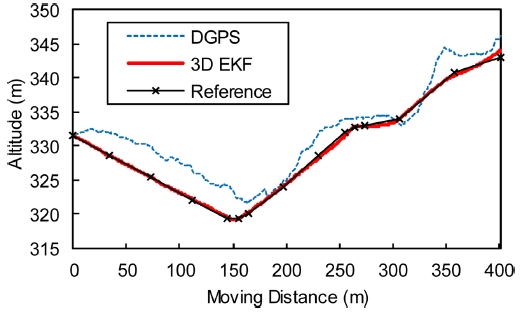
Fig. 5의 결과는 3차원 위치오차로서 고도에 대한 위치오차도 이미 포함되어 있지만 제안된 방법의 고도정보에 대한 성능을 확실히 확인하기 위해 주행거리에 따른 고도에 대한 결과만을 따로 Fig. 7에 나타내었다. 그림에서 점선은 DGPS를 이용하여 획득된 고도이며 실선은 3차원 위치평가의 고도이다. DGPS는 실제고도와는 다소 큰 차이를 보이고 있는 반면에 제안된 방법은 이와 같은 오차를 보정하여 기준경로에 가까운 결과를 제공해주고 있다.

Fig. 7

Results of altitude estimation

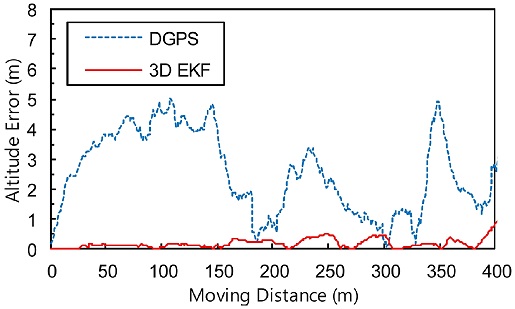
Fig. 8은 고도위치오차를 나타내는데, 점선은 DGPS의 위치 오차, 실선은 3차원 위치평가의 오차이며 이에 대한 위치오차 특성을 Table 4에 나타내었다. DGPS는 최대 5.01 m, 평균 2.53 m의 비교적 큰 오차를 보이는 반면에 3차원 위치평가의 오차는 최대 0.95 m, 평균 0.18 m로써 고도에 대한 오차를 크게 개선해 주고 있다.

Fig. 8

Error for altitude estimation

Table 4

Characteristics of the altitude error (unit : m)

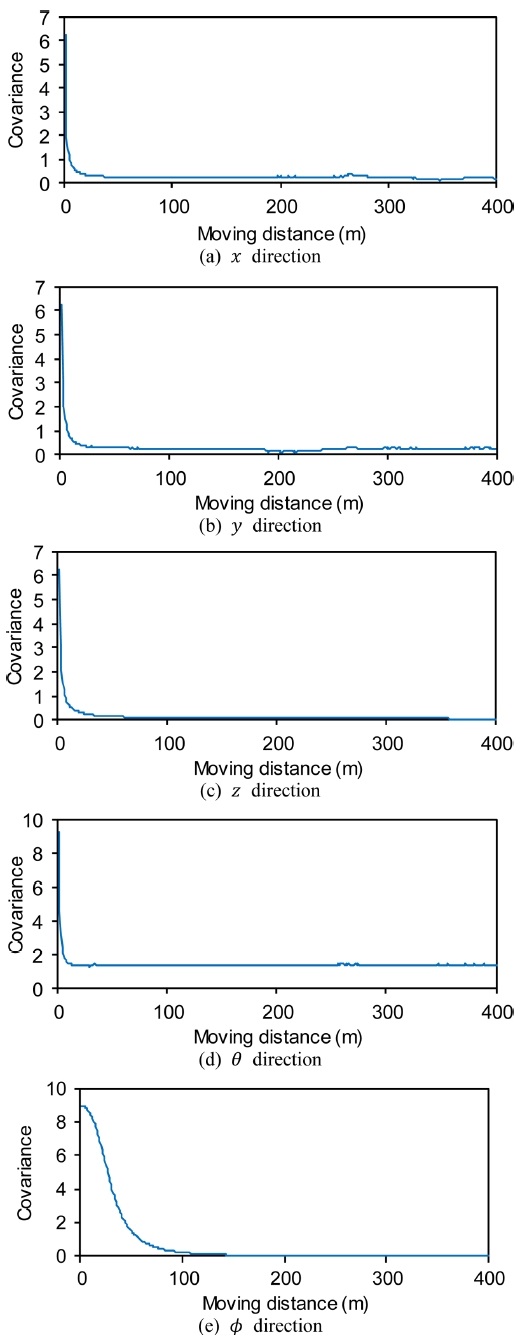
제안된 방법의 오차 수렴성 및 안정성을 확인하기 위해 주행거리에 대한 오차 공분산을 Fig. 9에 나타냈다. Figs. 9(a)는 x 방향, 9(b)는 y 방향, 9(c)는 z 방향, 9(d)는 θ방향, 그리고 Fig. 5(e)는 ϕ 방향으로의 오차공분산을 나타내며, 각 방향의 초기 오차공분산은 로봇의 이동특성 및 Table 2에 나타낸 바와 같은 센서들의 특성을 기준으로 설정 하였다. 결과를 분석해보면 x, y, z, θ 방향의 오차 공분산은 초기에 설정된 오차로부터 이동거리 10 m 내에서 빠르게 감소하여 점차 일정한 값으로 수렴하고 있지만 ϕ 방향 오차공분산은 오차의 수렴속도 측면 에서는 다른 방향에 비해 느리게 수렴하고 있다. 이것은 다른 상태벡터와는 달리 ϕ는 식(7)과 같이 여러 상태 벡터에 연관이 되어 있어 이들 상태 벡터의 수렴성에 영향을 받기 때문이다. 그러나 수렴하는 값의 크기 측면에서 보면 오히려 ϕ 방향의 오차공분산이 다른 방향에 비해 더 낮은 값을 보이고 있으며, 안정성 측면에서도 문제가 없다고 판단된다. 따라서 제안된 방법은 안정적인 성능을 보이고 있는 것으로 사료된다.

Fig. 9

Error covariance

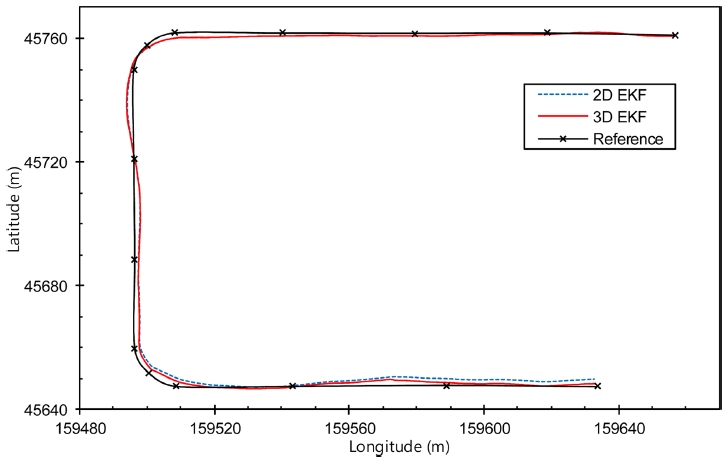
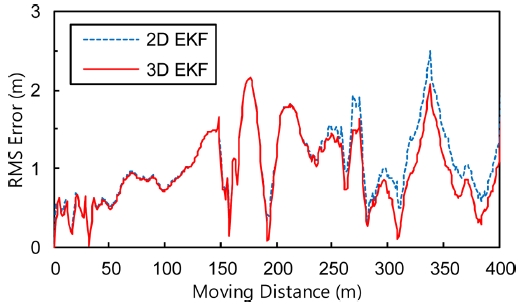
Fig. 10은 제안된 방법과 기존의 2차원 위치평가를 비교한 것이다. 이 실험은 동일한 데이터를 이용하여 2차원 및 3차원으로 위치평가를 하는 방법으로 수행 하였다. 2차원 위치평가는 고도 정보가 없으므로 경위도 평면 위치평가 결과만 비교하였으며 2차원 위치평가 방법은 참고문헌 11과 동일한 방법을 사용하였으며 두 방법의 계산시간은 큰 차가 없었다. 그림 에서 실선은 3차원 위치평가, 점선은 2차원 위치평가, X 표시가 포함된 검은 색 실선은 기준경로를 나타낸다. 실험 결과 Fig. 10과 같이 2차원과 3차원 위치평가의 차이가 거의 없게 보이기 때문에 확실한 비교를 위해 각각의 위치 오차의 통계학적 특성을 Fig. 11에 나타냈다. 전체 적으로 위치 오차의 차이가 작긴 하지만 이동거리가 길어 질수록 3차원 위치평가 결과가 2차원 결과보다 양호함을 알 수 있다.

Fig. 10

Comparison of the 2D and 3D localization results

Fig. 11

Comparison of the 2D and 3D localization error

Table 5

Characteristics of 2-D position error (unit : m)

두 방법의 위치오차가 주행거리가 길어짐에 따라 차이가 발생하고 있는 것은 고도정보를 고려하였는지에 따른 것이다. 예를 들어 로봇이 경사면을 따라 이동한 거리를 d, 경사면의 경사각도를 ϕ라고 하였을 때, 3차원 위치평가에서는 로봇의 수평 이동거리는 dcosϕ가 된다. 그러나 2차원 평가방법에서는 수평이동거리가 d이고 2차원과 3차원 위치평가의 오차는 d(1−cosϕ)가 되므로 경사가 심한 환경일수록 주행 거리가 길어질수록 오차가 더 커진다. 따라서 급격한 경사가 존재하는 환경에서 장시간 임무를 수행하는 경우에 오차는 더욱 커지게 되고 정확한 임무수행에 치명적이다. 결론적으로 고도정보가 필요한 경우에는 2차원 방법은 고도정보를 주지 못하므로 3차원 방법이 필연적이며, 고도정보가 중요하지 아니한 경우에도 급경사가 존재하는 환경이나 장거리 주행이 필요한 경우에는 2차원 방법은 오차가 크게 발생할 수 있으므로 3차원 방법이 더욱 효과적이라고 사료된다.

4. 결론

본 연구에서는 옥외용 이동로봇을 위한 3차원 위치평가 방법을 제안하였다. 이 방법은 로봇바퀴에 장착된 엔코더와 경사센서를 이용하여 예측된 3차원 위치와 DGPS 및 디지털 컴퍼스로부터 획득된 위치 정보를 확장 칼만 필터로 융합하여 로봇의 3차원 위치를 평가하는 방법이다. 본 방법은 기존 2차원 위치평가 방법에서 불가능하였던 고도정보를 포함한 3차원 위치를 평가하는 것으로서, 실험을 통하여 성능을 확인한 결과 제안된 방법은 효과적으로 로봇의 3차원 위치평가가 가능함을 보였다. 또한 본 방법은 경사가 존재하는 환경에서는 고도정보가 필요 없는 평면 위치평가의 경우에도 기존 2차원 위치평가 방법보다 향상된 위치평가 결과를 보였다. 따라서 제안된 방법은 3차원 위치정보가 필요한 다양한 분야에서 활용될 수 있을 것으로 사료된다.

Acknowledgments

이 논문은 2017년도 정부(교육부)의 재원으로 한국연구재단의 공동지원을 받아 수행된 기초연구 사업(No. 2017R1D1A1B03034373)과 2019년도 제주대학교 교원성과지원사업의 공동지원으로 연구되었음.

REFERENCES

• Lim, J. H. and Kim, H. J., “Development of an Autonomous Guide Robot for Campus Tour,” Transactions of the Korean Society of Mechanical Engineers A, Vol. 41, No. 6, pp. 543-551, 2017.
• Lim, J. and Kang, S., “Non-Inertial Sensor-Based Outdoor Localization for Practical Application of Guide Robots,” Journal of the Korean Society for Precision Engineering, Vol. 34, No. 5, pp. 315-321, 2017. [https://doi.org/10.7736/KSPE.2017.34.5.315]
• Lim, J. H. and Kang, S. K., “Localization of a Mobile Robot using Grid Based Sonar Map,” Proc. of the Institute of Control, Robotics and Systems, pp. 461-464, 1999.
• Leonard, J. J. and Durrant-Whyte, H. F., “Directed Sonar Sensing for Mobile Robot Navigation,” Kluwer Academic Publishers, 1992. [https://doi.org/10.1007/978-1-4615-3652-9]
• Choi, B.-S. and Lee, J.-M., “An Efficient Localization of Mobile Robot in RFID Sensor Space,” Journal of Institute of Control, Robotics and Systems, Vol. 12, No. 1, pp. 15-22, 2006. [https://doi.org/10.5302/J.ICROS.2006.12.1.015]
• Lee, H.-S., Song, B.-H., Ham, K.-S., and Youn, H.-Y., “A Method to Reduce Interference in Sensor Network Location Awareness System,” Journal of Internet Computing and Services, Vol. 7, No. 3, pp. 31-39, 2006.
• Mo, S. H., Jeon, Y. P., Park, J. H., and Chong, K. T., “Study of Robust Position Recognition System of a Mobile Robot Using Multiple Cameras and Absolute Space Coordinates,” Transactions of the Korean Society of Mechanical Engineers A, Vol. 41, No. 7, pp. 655-663, 2017.
• Kim, G. W. and Cha, Y. Y., “Efficient Localization of Mobile Robots based on GPS/IMU Sensors in Outdoor Terrain,” Proc. of the Institute of Control, Robotics and Systems Joint Conference, pp. 126-129, 2009.
• Choi, S.-H., Kim, G.-J., Kim, Y.-K., and Lee, J.-M., “Outdoor Positioning Estimation of Multi-GPS/INS Integrated System by EKF/UPF Filter Conversion,” Journal of Institute of Control, Robotics and Systems, Vol. 20, No. 12, pp. 1284-1289, 2014. [https://doi.org/10.5302/J.ICROS.2014.13.0014]
• Lim, J.-H., “A Study on a Localization System for Tour Guide Robot,” Journal of the Korean Society for Precision Engineering, Vol. 29, No. 7, pp. 762-769, 2012. [https://doi.org/10.7736/KSPE.2012.29.7.762]
• Lee, W. S., Cho, I. H., and Lim, J. H., “GPS-Based Human Tracking Methods for Outdoor Robots,” Journal of the Korean Society Precision Engineering, Vol. 35, No. 4, pp. 413-420, 2018. [https://doi.org/10.7736/KSPE.2018.35.4.413]
• Lai, L.-C., Lee, T.-L., Fan, H.-T., and Wu, C.-J., “A Nonlinear Programming Method for 3D Localization of Mobile Robots,” Proc. of the 12th International Conference on Advanced Robotics, pp. 250-255, 2005.
• Nagatani, K., Ishida, H., Yamanaka, S., and Tanaka, Y., “Three-Dimensional Localization and Mapping for Mobile Robot in Disaster Environments,” Proc. of the IEEE International Conference on Intelligent Robots and Systems, pp. 3112-3117, 2003.
• Lim, J.-H., Kang, C.-U., and Kim, S.-K., “A Study on a 3-D Localization of a AUV based on a Mother Ship,” Journal of Ocean Engineering and Technology, Vol. 19, No. 2, pp. 74-81, 2005.
• Bouvet, D. and Garcia, G., “Guaranteed 3-D Mobile Robot Localization Using an Odometer, an Automatic Theodolite and Indistinguishable Landmarks,” Proc. of the IEEE International Conference on Robotics and Automation, pp. 3612-3617, 2001.
• Wang, M., Liu, Y., Su, D., Liao, Y., Shi, L., et al., “Accurate and Real-Time 3-D Tracking for the Following Robots by Fusing Vision and Ultrasonar Information,” IEEE/ASME Transactions on Mechatronics, Vol. 23, No. 3, pp. 997-1006, 2018. [https://doi.org/10.1109/TMECH.2018.2820172]