Application/Comparison Study of a Graphical Method of Forming Limit Curve Estimation for DP590 Steel Sheets

1. Introduction

Today, sheet metal forming methods based on the deformation of materials play an important role in mechanical production and metallurgy. The growing applications of numerical simulations in the field of sheet metal forming have helped engineers solve various problems in improving the formability and reducing the cost and time of products. Accurate simulation results are necessary for mold and product design. Many factors affect the final simulation results, but the most important input data for the ductile fracture prediction of a product is the forming limit curve (FLC) of the sheet material. Several studies have been carried out to predict and evaluate the FLC by using experimental and theoretical methods.^1-3 In addition, this concept has been widely applied in various commercial finite-element software packages for technical studies.

According to the experimental approach, Hecker⁴ and Nakazima⁵ tests are popular methods that have been widely used to clarify the levels of FLCs for sheet metals. However, time-consuming and high-cost computing is the main drawback of this testing method. Therefore, considerable effort has been made to obtain FLCs theoretically. Swift⁶ can be recognized as a pioneering study on predicting FLC. Hill⁷ then proposed a way to improve the accuracy of FLC prediction by adopting necking point criteria. Stören and Rice⁸ developed a solution for FLC prediction by applying a force equilibrium between necking and uniform deformed regions. Banabic⁹ observed and developed a pre-defect in the material and developed a theory of limited deformation based on imperfections of material thickness.

Hora et al.¹⁰ upgraded the Swift diffuse necking criteria and set a modified maximum force criterion (MMFC) by effectively examining the instant deformation state changes until the forming force achieved a maximum value. Some new MMFC models proposed to improve the accuracy of FLC prediction^1,9 based on theoretical models by solving systems of equations. To simplify the determination of a theoretical FLC based on the theory of MMFC for sheet metal, Tuan and Kim¹ discussed a method to predict FLCs based on three special points of the graphical method.

Currently, the finite element (FE) simulation is an indispensable tool to research, evaluate, and discern physical phenomena modeled by various theoretical and experimental equations. To improve the fitting of experimental data with numerical data, Hochholdinger et al.¹¹ upgraded a new FE simulation model by modifying the Hockett–Sherby equation and determining the Zener–Hollomon parameters. To verify the accuracy of FLC prediction compared with corresponding experiments, various previous researchers^12-14 imported forming limit diagram (FLD) curves to FEM software in order to predict fractures and compare them with experimental results.

The current study investigates the press formability of DP590 sheet steel. Various hardening equations were adopted to fit the stress-strain curves of DP590 sheet steel. In addition, FLDs were calculated by a graphical method. The predicted FLCs was then imported to an FEM simulation to observe the fracture occurrence of punch stretching with various notch specimens. The fracture heights of specimens measured by FEM prediction were finally compared with corresponding experimental ones to indicate the predicted accuracy of the hardening equations and FLC calculations by the graphical method.

2. Modified Maximum Force Criterion and Graphical Method

2.2. Application of Graphical Method¹ for DP590

As shown in Eq. (7), the calculation can be obtained by the hardening and yield laws. For special strain modes such as plane strain (β = 0), uniaxial tension (β = -1/2), and equibiaxial tension (β = 1), all terms of Eq. (7) are simply calculated.

To verify FLC prediction by a graphical method, DP590 sheet steel was adopted with a thickness of 1.181 mm. Here, tensile tests were performed at a nominal speed of 20 mm/min. The mechanical properties and chemical composition of DP590 steel are listed in Table 1.

Table 1

Chemical composition and mechanical properties of DP590 material

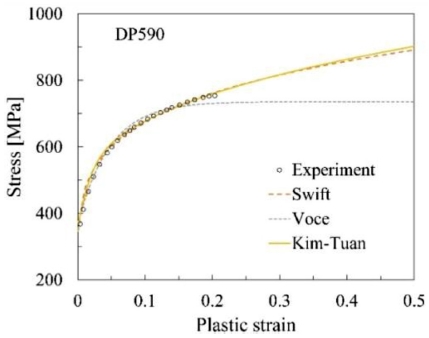
The experimental stress-strain data of a DP590 steel sheet in the 0 direction are used to fit the hardening parameters (Table 2 and Fig. 1) of the constitutive functions of the Swift,⁶ Voce,¹⁷ and Kim-Tuan¹⁸ models as in Eqs. (8)-(10), respectively.

Table 2

Parameters of Swift, Voce and Kim-Tuan equations of DP590

Fig. 1

Flow stress curves of DP340 with various hardening models

$\[ \overline{\sigma }=C{\left({\epsilon }_0+\overline{\epsilon }\right)}^n \]$

(8)

$\[ \overline{\sigma }={\sigma }_Y+P\left(1-exp\left(-Q\overline{\epsilon }\right)\right) \]$

(9)

$\[ \overline{\sigma }={\sigma }_0+K\left(1-exp\left(-t\overline{\epsilon }\right)\right){\left(\overline{\epsilon }+0.002\right)}^h \]$

(10)

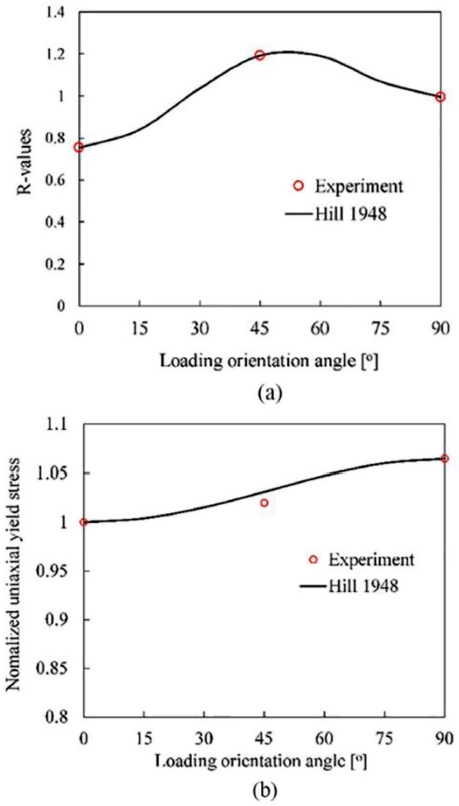
To present the anisotropy of DP590 sheet steel owing to the deference R-value (Table 1), the Hill 1948 yield criterion is used as in Eq. (11) and shows good agreement with the experimental data (Fig. 2).

Fig. 2

Hill anisotropy of DP590 steel sheet prediction for (a) R-value and (b) normalized yield stress

$\[ \overline{\sigma }=\sqrt{G{\sigma }_1^2+F{\sigma }_2^2+H{\left({\sigma }_1-{\sigma }_2\right)}^2} \]$

(11)

where G, F, and H are constants calculated from the R-value as follows:

$\[ \left\{\begin{array}{c}F=\frac{1}{2R_{22}^2}+\frac{1}{2R_{33}^2}-\frac{1}{2R_{11}^2}\hfill \\ G=\frac{1}{2R_{11}^2}+\frac{1}{2R_{33}^2}-\frac{1}{2R_{22}^2}\hfill \\ H=\frac{1}{2R_{11}^2}+\frac{1}{2R_{22}^2}-\frac{1}{2R_{33}^2}\hfill \end{array}\right. \]$

(11-1)

and R₁₁, R₂₂, and R₃₃ are anisotropic yield stress ratios. For the plane stress case, only four yield stress ratios are needed. Here, we assumed that the rolling direction (RD) involves a user-defined reference yield stress. Then, R₁₁ = 1, and R₂₂ and R₃₃ are defined as 1.077 and 0.999, respectively, as in the following Eq. (11-2):

$\[ \left\{\begin{array}{c}{R}_{22}=\sqrt{\frac{r_{90}\left(r_0+1\right)}{r_0\left(r_{90}+1\right)}}\hfill \\ R_{33}=\sqrt{\frac{r_{90}\left(r_0+1\right)}{\left(r_0+r_{90}\right)}}\hfill \end{array}\right. \]$

(11-2)

To review the simple calculation of FLC by a graphical method for DP590 steel, the plane strain stage (β = 0) was first selected and substituted into Eq. (7): $$ \frac{H\text{'}}{H}\ge \frac{1}{g\left(\alpha \right)}$$ at (β = 0). At any strain stage, Eq. (7) can be rewritten as Eq. (12).

$\[ \frac{H\text{'}}{H}\ge A-\frac{B}{\epsilon } \]$

(12)

where A = 1/g(α) and B = (f'/f)*(β/β') are constants.

Thus, A and B can be expressed as a function of α (Eqs. (13) and (14)) when a Von Mises yield function is adopted.

$\[ A\left(\alpha \right)=\frac{2-\alpha }{2\sqrt{1-\alpha +{\alpha }^2}} \]$

(13)

$\[ \text{B}\left(\alpha \right)=\frac{\left(2-\alpha \right){\left(2\alpha -1\right)}^2}{6\left(1-\alpha +{\alpha }^2\right)} \]$

(14)

The calculation for special strain modes such as plane strain (P. S.) (β = 0), uniaxial tension (U. T.) (β = -1/2), and equibiaxial tension (B. T.) (β = 1) can be obtained as listed in Table 3 for A and B in Eqs. (13) and (14). Based on the calculated values and the abovementioned equations, Eq. (12) can be plotted as shown in Fig. 3(a) by adopting the Swift, Voce, and Kim-Tuan models.

Table 3

Calculated constants at plane strain, uniaxial tension, and equibiaxial tension stages

Fig. 3

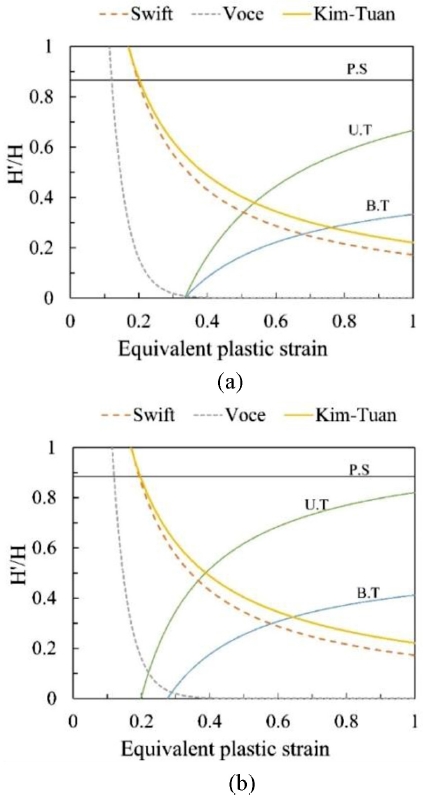
Evaluation of limit strains based on different hardening laws and yield functions of (a) Von Mises and (b) Hill 48

A(α) and B(α) according to the Hill 48 yield function can be obtained by applying Eq. (11) to Eqs. (4)-(6). The results are also presented in Eqs. (15)-(21), Table 3 and Fig. 3(b).

$\[ f\left(\alpha \right)=\sqrt{\left(G+H\right)-2H\alpha +\left(F+H\right){\alpha }^2} \]$

(15)

$\[ f\text{'}\left(\alpha \right)=\frac{\left[-H+\left(F+H\right)\alpha \right]}{\sqrt{\left(G+H\right)-2H\alpha +\left(F+H\right){\alpha }^2}} \]$

(16)

$\[ \beta \left(\alpha \right)=\frac{\left(F+H\right)\alpha -H}{-H\alpha +\left(G+H\right)} \]$

(17)

$\[ \beta \text{'}\left(\alpha \right)=\frac{\left(F+H\right)\left(G+H\right)-H^2}{{\left[-H\alpha +\left(G+H\right)\right]}^2} \]$

(18)

$\[ g\left(\alpha \right)=\frac{\sqrt{\left(G+H\right)-2H\alpha +\left(F+H\right){\alpha }^2}}{-H\alpha +\left(G+H\right)} \]$

(19)

Then:

$\[ A\left(\alpha \right)=\frac{-H\alpha +\left(G+H\right)}{\sqrt{\left(G+H\right)-2H\alpha +\left(F+H\right){\alpha }^2}} \]$

(20)

$\[ B\left(\alpha \right)=\frac{-H+\left(F+H\right)\alpha }{\left(G+H\right)-2H\alpha +\left(F+H\right){\alpha }^2}\times \frac{\left[\left(F+H\right)\alpha -H\right]\times \left[-H\alpha +\left(G+H\right)\right]}{\left(F+H\right){\left(G+H\right)-H}^2} \]$

(21)

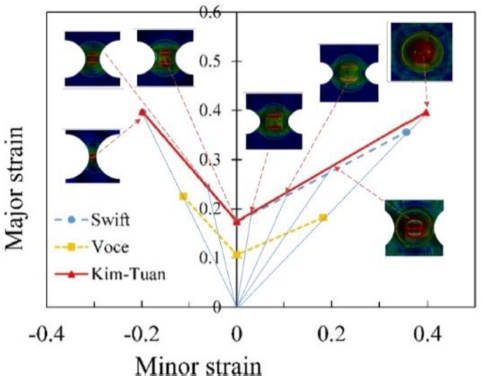
According to the graphical method, the equivalent plastic strains can be determined. To calculate the major and minor strains, Von Mises (Eq. (22)) and Hill 1948 (Eq. (23)) can be adopted. Then, FLC is obtained by drawing three special strain points as shown in Figs. 4(a) and 4(b).

Fig. 4

FLC prediction by graphical method for DP590 steel sheet based on various hardening laws in cases of (a) Von Mises and (b) Hill 48

$\[ {\epsilon }_1=\overline{\epsilon }/\sqrt{\frac{4}{3}\left(1+\beta +{\beta }^2\right)} \]$

(22)

$\[ {\epsilon }_1=\overline{\epsilon }/g\left(\alpha \right) \]$

(23)

where ε₁, ε₂ and β = ε₂/ε₁ are the major and minor strains and the strain ratio, respectively.

3. Experimental and Finite Element Method

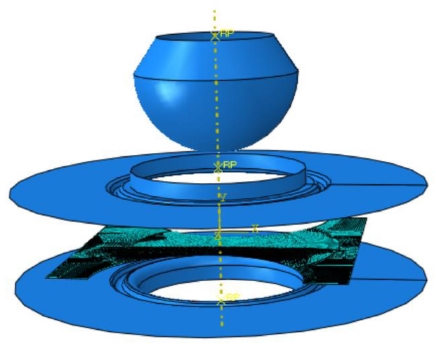
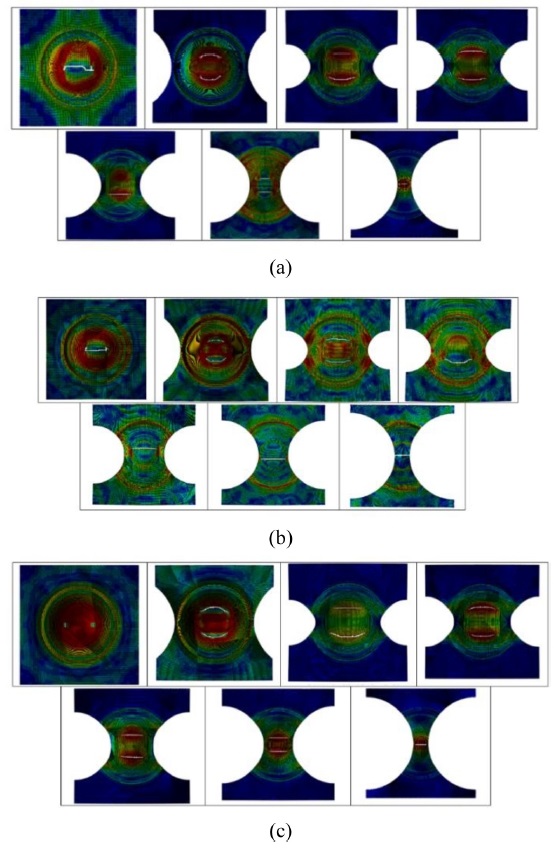
In order to verify the accuracy of the FLD predictions, Hecker punch stretching tests⁴ (Fig. 5(a)) at 15 t of blank holder force and 300 mm/min of punch speed were performed for various specimens (Fig. 5(b)) until the fractures occurred (Fig. 5(c)) in order to measure the fracture heights of the specimens (Fig. 5(d)).

Fig. 5

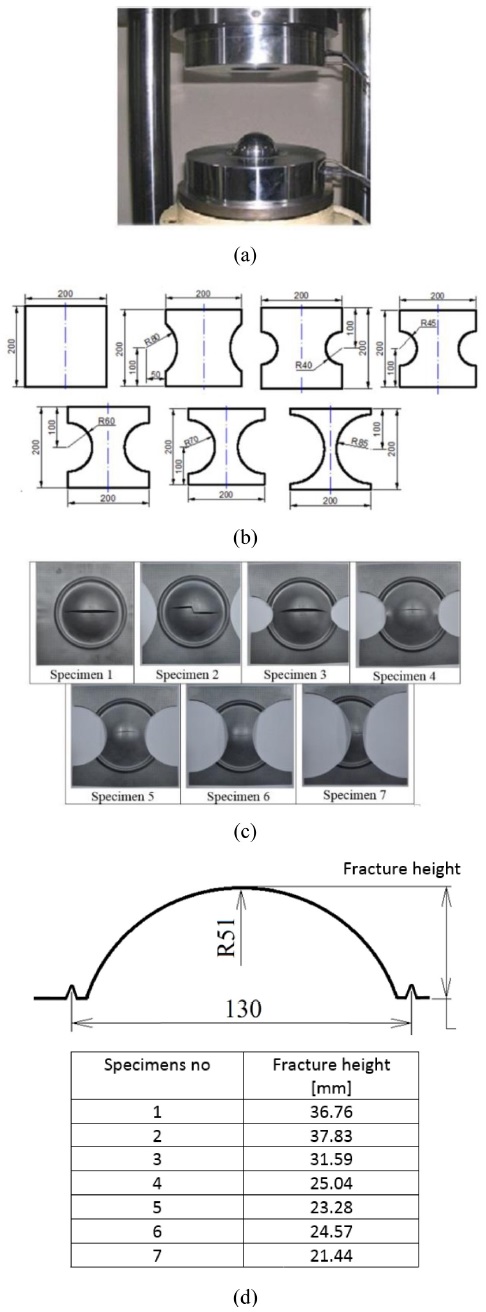
Hecker punch stretching (a) for various specimens, (b) experimental results, and (c) fracture heights of DP590 sheet

To analyze the deformation of Hecker’s punch stretching tests, the commercial software package ABAQUS (6.12)¹⁹ was used. The FE models are depicted in Fig. 6. Specifically, reduced-integration four-node linear shell elements (S4R) are utilized for the blank. The die/tool and clamping parts are assigned as the rigid body. The size of the element for all parts correspond to approximately 1 × 1 mm (length × width).

Fig. 6

FEM model for Hecker punch stretching tests

The mesh density is sufficiently fine to ensure result convergence. The mesh size is also refined by comparing the initial simulations and corresponding experiments. The ENCASTRE condition was assigned for the die. The tool and clamming part are permitted to run in the vertical direction. The blank specimen is held by the concentration force acting on the clamping part. The Coulomb friction law is used in the friction condition.

4. Results and Discussion

When the punch stretching tests are performed by using DP590 steel sheets, fractures tend to occur at high tensile stresses and plastic strains owing to the excessive clamping force. Based on the ductile fracture criterion of FLCs, the equivalent plastic strains/stresses change when the specimen shapes are modified. As a follow-up, the values of FLC prediction were altered. In order to verify the effect of the hardening laws and the FLC prediction on the fracture heights of various specimens, FLC input data from the Voce, Swift, and Kim-Tuan equations following the Hill 48 yield function were implemented in order to predict fracture occurrences in various specimens. This is shown in Fig. 7.

Fig. 7

Deformed shapes of (a) Voce, (b) Swift, and (c) Kim-Tuan’s FLD predictions

In the FE simulation of the forming process, fractures occur when the failure criterion value reaches 1.0, and the element is then deleted. Here, the fracture heights when the fracture elements of deformed shapes occur are verified and compared with the corresponding experiments, as listed in Table 4. To investigate the accuracy of fracture height prediction based on FLC as derived from the Voce, Swift, and Kim-Tuan models, the differences between the fracture heights of the FE method and experimental measurement were estimated as an error of the fracture height Δh(%) = (|h_simulation – h_experiment|) / h_experiment.

Table 4

Comparison of fracture height between experiments and simulation

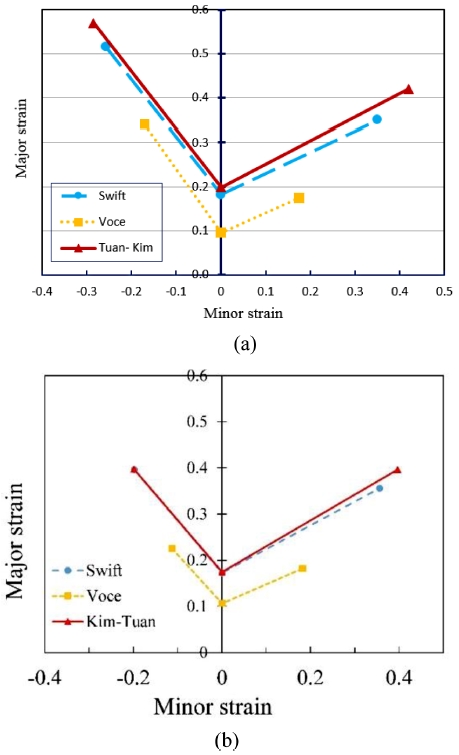
The results show that the Swift model exhibits reasonably good predictions for almost specimens (Fig. 7(a) and Table 4). Otherwise, the Voce model shows incorrect predictions of fracture heights for DP590 sheet steel. Fig. 7(c) and Table 4 also show the results of finite elements from the simulation of punch stretching tests with Kim-Tuan models. The comparison results exhibit additional good agreement between the simulations and experiments with an average error of 2.15(%). The fracture height error of each specimen of the Kim-Tuan model is more uniform than the others.

To determine the accuracy of the FLCs presented in Table 4, the strain path evolution of each specimen is shown in Fig. 8. Both the Swift and Kim-Tuan models exhibit good predictions on the left-hand side for specimens 5-7, while the Kim-Tuan model shows more accurate predictions on the right-hand side of FLC for the DB590 steel sheet (specimens 1-4).

Fig. 8

Strain paths by FEM for each specimen

5. Conclusion

This study applied the graphical method to estimate and predict specific FLDs of DP590 steel sheets. Ductile fracture criteria based on the obtained FLDs were implemented by using an FEM simulation and were compared with the corresponding experimental results of punch stretching tests. The prediction of fracture heights using various FLDs derived by difference hardening laws was compared with that of corresponding experiments. The finite element simulation method results indicated that the Kim-Tuan hardening law predicted more accurate fracture heights of various specimens. Meanwhile, the Voce hardening law showed underestimated predictions. The compared results also indicated that the predicted FLCs can be used to predict the fracture position in a simulation with a smallest estimated average error about 2.15% for the Kim-Tuan model and the largest error of 23.87% for the Voce model.

Acknowledgments

This paper was presented at PRESM 2019

This research is funded by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) under Grant No. “107.02-2016.01”.

REFERENCES

• Pham, Q. T., Nguyen, D. T., Kim, J. J., and Kim, Y. S., “A Graphical Method to Estimate Forming Limit Curve of Sheet Metals,” Key Engineering Materials, Vol. 794, pp. 55-62, 2019. [https://doi.org/10.4028/www.scientific.net/KEM.794.55]
• Mac, T.-B., Do, V.-C., and Nguyen, D.-T., “A Study of Combined Finite Element Method Simulation/Experiment to Predict Forming Limit Curves of Steel DP350 Sheets,” Advances in Mechanical Engineering, Vol. 10, No. 4, pp. 1-9, 2018. [https://doi.org/10.1177/1687814018768148]
• Slota, J. and Spisak, E., “Comparison of the Forming-Limit Diagram (FLD) Models for Drawing Quality (DQ) Steel Sheets,” Metalurgija, Vol. 44, No. 4, pp. 249-253, 2005.
• Hecker, S. S., “Simple Technique for Determining Forming Limit Curves,” Sheet Metal Industries, Vol. 52, No. 11, pp. 671-676, 1975.
• Yue, Z., Badreddine, H., Dang, T., Saanouni, K., and Tekkaya, A., “Formability Prediction of Al7020 with Experimental and Numerical Failure Criteria,” Journal of Materials Processing Technology, Vol. 218, pp. 80-88, 2015. [https://doi.org/10.1016/j.jmatprotec.2014.11.034]
• Swift, H. W., “Plastic Instability under Plane Stress,” Journal of the Mechanics and Physics of Solids, Vol. 1, No. 1, pp. 1-18, 1952. [https://doi.org/10.1016/0022-5096(52)90002-1]
• Hill, R., “On Discontinuous Plastic States, with Special Reference to Localized Necking in Thin Sheets,” Journal of the Mechanics and Physics of Solids, Vol. 1, No. 1, pp. 19-30, 1952. [https://doi.org/10.1016/0022-5096(52)90003-3]
• Stören, S. and Rice, J., “Localized Necking in Thin Sheets,” Journal of the Mechanics and Physics of Solids, Vol. 23, No. 6, pp. 421-441, 1975. [https://doi.org/10.1016/0022-5096(75)90004-6]
• Banabic, D., Aretz, H., Paraianu, L., and Jurco, P., “Application of Various FLD Modelling Approaches,” Modelling and Simulation in Materials Science and Engineering, Vol. 13, No. 5, pp. 759-769, 2005. [https://doi.org/10.1088/0965-0393/13/5/009]
• Hora, P., Tong, L., and Reissner, J., “A Prediction Method for Ductile Sheet Metal Failure in Fe-Simulation,” Proc. of Numisheet, pp. 252-256, 1996.
• Hochholdinger, B., Hora, P., Grass, H., and Lipp, A., “Simulation of the Press Hardening Process and Prediction of the Final Mechanical Material Properties,” Proc. of AIP Conference, pp. 618-625, 2011. [https://doi.org/10.1063/1.3623665]
• Nguyen, D.-T., Dinh, D.-K., Nguyen, H.-M. T., Banh, T.-L., and Kim, Y.-S., “Formability Improvement and Blank Shape Definition for Deep Drawing of Cylindrical Cup with Complex Curve Profile from SPCC Sheets Using FEM,” Journal of Central South University, Vol. 21, No. 1, pp. 27-34, 2014. [https://doi.org/10.1007/s11771-014-1911-x]
• Nguyen, D.-T. and Kim, Y.-S., “A Numerical Study on Establishing the Forming Limit Curve and Indicating the Formability of Complex Shape in Incremental Sheet Forming Process,” International Journal of Precision Engineering and Manufacturing, Vol. 14, No. 12, pp. 2087-2093, 2013. [https://doi.org/10.1007/s12541-013-0283-8]
• Nguyen, D.-T., Kim, Y.-S., and Jung, D.-W., “Coupled Thermomechanical Finite Element Analysis to Improve Press Formability for Camera Shape Using AZ31B Magnesium Alloy Sheet,” Metals and Materials International, Vol. 18, No. 4, pp. 583-595, 2012. [https://doi.org/10.1007/s12540-012-4025-8]
• Paraianu, L., Dragos, G., Bichis, I., Comsa, D. S., and Banabic, D., “A New Formulation of the Modified Maximum Force Criterion (MMFC),” International Journal of Material Forming, Vol. 3, No. 1, pp. 243-246, 2010. [https://doi.org/10.1007/s12289-010-0752-x]
• Pham, Q.-T., Lee, B.-H., Park, K.-C., and Kim, Y.-S., “Influence of the Post-Necking Prediction of Hardening Law on the Theoretical Forming Limit Curve of Aluminium Sheets,” International Journal of Mechanical Sciences, Vol. 140, pp. 521-536, 2018. [https://doi.org/10.1016/j.ijmecsci.2018.02.040]
• Voce, E., “The Relationship between Stress and Strain for Homogeneous Deformation,” Journal of the Institute of Metals, Vol. 74, pp. 537-562, 1948.
• Pham, Q. T. and Kim, Y. S., “Identification of the Plastic Deformation Characteristics of Al5052-O Sheet based on the Non-Associated Flow Rule,” Metals and Materials International, Vol. 23, No. 2, pp. 254-263, 2017. [https://doi.org/10.1007/s12540-017-6378-5]
• Hibbit, D., Karlsson, B., and Sorensen, P., “ABAQUS User’s Manual,” http://dsk.ippt.pan.pl/docs/abaqus/v6.13/books/usb/default.htm, (Accessed 28 AUG 2019)