주파수 영역 피로해석에서 PSD 분석 방식 비교

1. 서론

항공기는 운용 시 다양한 하중에 노출되고 장기간 노출되면 피로파괴가 일어날 가능성이 존재한다. 운용 중 피로파괴가 발생하면 인명피해로 연결될 가능성이 높기 때문에 설계 단계에서 피로파괴를 예측하는 연구가 반드시 필요하다. 항공기는 측정, 추적 등 특수 기능을 담당하는 장비가 항공기 하부에 부착된다. 항공기 하부에 부착되는 장비는 대개 원통형태의 구조를 하고 있으며 POD 구조체라고 한다. POD 구조체도 항공기와 동일한 환경에 노출되어 동일한 반복 하중을 받기 때문에 항공기와 동일한 조건을 적용하여 피로파괴를 예측하여야 한다.

항공기 개발 시 MIL-STD-1530D가 피로파괴에 대한 기준으로 주로 사용된다. MIL-STD-1530D는 항공기의 구조 건전성 프로그램에 대하여 기술한 기준서로 항공기 구조의 건전성을 확보하기 위한 전반적인 요구 사항을 정의하고 이행 방법을 규정하고 있다. 일반적으로 PSD (Power Spectral Density) 데이터를 이용하는 주파수영역 피로해석을 이용하여 피로파괴를 예측한다. 이때, PSD 데이터를 분석하는 방식에 따라 피로해석 결과 간의 차이가 발생한다. 따라서 상황에 맞는 분석 방식을 사용해야 하지만 어떠한 상황에 어떤 방식이 적합한지는 정확하게 규정되어 있지 않다.

이러한 PSD 분석 방식의 특성 상, PSD 분석 방식에 대한 비교 연구는 꾸준히 지속되고 있다. Andrew, H.는 PSD를 이용한 Rainflow Cycle과 기존의 시간 영역 하중을 통한 Rainflow Cycle을 시편을 통해 비교하고 PSD 기법을 배출가스 머플러 설계에 사용한 연구를 수행하였다.¹ Yoon, M.은 시간영역과 주파수영역에서의 등가피로하중을 구하는 이론적 배경 및 과정을 설명하고 외팔보에 단축하중과 다축하중을 적용시켜 피로하중을 구한 것을 비교한 연구를 수행하였다.² Park, J.는 광대역 응답스펙트럼의 피로손상해석에 적용되는 다양한 피로손상모델을 소개하고, 라이져 피로해석에 적합한 피로손상모델 선정을 위한 수치해석적 비교연구를 수행하였다.³ Quigley, J.는 8가지의 PSD 분석 방식을 소개하고 각 방식의 정확도와 오차율을 분석한 연구를 수행하였다.⁴ Jung, H.는 주파수 영역 피로해석에 사용되는 4가지의 PSD 분석방식을 비교하여 그 중 정확도가 높은 Dirlik 방식과 Benasciutti-Tovo 방식을 이용하여 항공기 탑재 장비에 대한 피로 수명을 예측한 연구를 수행하였다.⁵

PSD 분석방식 비교에 관한 연구들이 꾸준히 있었지만 범용적으로 쓰이는 분석방식인 Dirlik, Lalanne, Steinberg 방식을 기체 설계 분야에서 비교한 논문은 없었다. 본 논문에서는 PSD 분석 방식 중 Dirlik, Lalanne, Steinberg 방식을 POD 구조체 피로해석에 적용하고 그 결과를 비교하였다. 피로해석에 적용된 외부진동은 MIL-STD-810G의 규격을 토대로 하였다.

2. 연구배경

2.3 PSD 데이터 분석

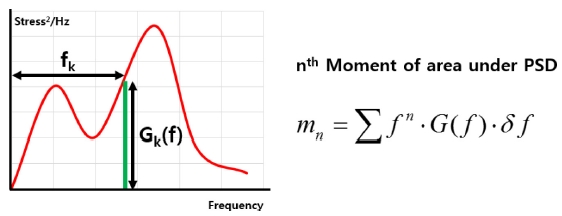
PSD를 분석하는 방법에 따라 PDF의 값이 달라지고 PDF를 이용한 Rainflow 집계 결과 또한 달라지게 된다. PSD 분석은 일반적으로 Fig. 1에 나타낸 것과 같이 PSD 값인 G(f)와 스펙트럼 모멘트(m_n)를 이용해서 계산한다.^5,8

Fig. 1

Moment of area under PSD

예를 들어, 0을 지나는 횟수는 식(2), 피크 점의 개수는 식(3)으로 표현할 수 있고 RMS Stress는 m₀가 된다. 불규칙 계수는 식(4)로 표현할 수 있으며 이때 불규칙 계수는 1에 근접할수록 협대역 파형을 나타내고 0에 가까울수록 광대역 파형을 나타낸다.⁹

$\[ E\left[0\right]=\sqrt{\frac{m_2}{m_0}} \]$

(2)

$\[ E\left[P\right]=\sqrt{\frac{m_4}{m_2}} \]$

(3)

$\[ \gamma =\frac{E\left[0\right]}{E\left[P\right]}=\frac{m_2}{\sqrt{m_0\cdot m_4}} \]$

(4)

PDF를 예측하기 위한 다양한 방법들이 있지만 주로 사용되는 3가지 방식은 Dirlik, Lalanne, Steinberg 방식이다. 대부분의 이론에서 PSD는 정상 상태이고 가우시안 분포를 띄고 있으며 시간 평균과 통계적 평균이 같다고(Ergodic) 가정한다.

2.3.1 Dirlik Method

Dirlik은 PSD의 초기 분석방식인 Narrow Band Method 는 협대역에만 적합하기에 Broad-Band Signal에 알맞은 새로운 N(S)(응력 범위의 확률 밀도 함수, PDF)를 구하는 방식인 Dirlik Method를 제안하였다.^10,11 Dirlik Method는 Monte Carlo 방법과 다양한 시그널을 이용하여 제시한 일종의 경험 기반 해법이다.⁸ 매우 복잡해 보이지만 m₀, m₁, m₂, m₄로 구성되어 있는 식으로 식(5)에 표시하였다.

$\[ N\left(S\right)=E\left[P\right]\cdot p\left(S\right) \]$

(5)

여기서 N(S)는 S N/mm² 범위에 있는 응력의 초당 횟수, E[P]는 피크의 개수이며 p(S)는 식(6)과 같다.

$\[ p\left(S\right)=\frac{\frac{D_1}{Q}\cdot e^{\frac{-Z}{Q}}+\frac{D_2\cdot Z}{R^2}\cdot e^{\frac{-Z^2}{2\cdot R^2}+D_3\cdot Z\cdot e^{\frac{-Z^2}{2}}}}{2\cdot \sqrt{m_0}} \]$

(6)

여기서 매개변수 Z는 S를 정규화한(Normalization) 값이다. Z는 스펙트럼 모멘트로 표현할 수 있으며 이는 식(7)과 같다.

$\[ Z=\frac{S}{2\cdot \sqrt{m_0}} \]$

(7)

나머지 매개변수인 D1, D2, D3, R, Q는 식(8)과 같이 정의한다. 식(8)의 매개변수들은 불규칙 계수인 γ와 mean frequency인 x_m으로 구성되어 있다. 식(4)를 보면 γ는 스펙트럼 모멘트로 구성되어 있는 것을 알 수 있다.

$\[ \begin{array}{c}\begin{array}{cc}{D}_1=\frac{2\cdot \left(x_m-{\gamma }^2\right)}{1+{\gamma }^2}\hfill & D_2=\frac{1-\gamma -D_1+{D_1}^2}{1-R}\end{array}\hfill \\ \begin{array}{cc}{D}_3=1-D_1-D_2\hfill & R=\frac{\gamma -x_m-{D_1}^2}{1-\gamma -D_1-{D_1}^2}\end{array}\hfill \\ Q=\frac{1.25\cdot \left(\gamma -D_3-D_2\cdot R\right)}{D_1}\hfill \end{array} \]$

(8)

여기서 x_m은 식(9)와 같이 스펙트럼 모멘트로 표현할 수 있다. 따라서 식(8)의 모든 매개변수들은 스펙트럼 모멘트에 관한 값이다.

$\[ x_m=\frac{m_1}{m_0}\cdot \sqrt{\frac{m_2}{m_4}} \]$

(9)

따라서 식(6)은 S와 스펙트럼 모멘트(m₀, m₁, m₂, m₄)로 구성된 함수가 된다. Dirlik Method는 Narrow Band 방식보다 우수함이 입증되었고 범용적으로 쓰여왔다.

2.3.2 Lalanne Method

Dirlik과 달리 Lalanne은 충분히 긴 시간 영역에서는 Narrow Band Method도 광대역에 사용할 수 있다는 것을 입증했다. Lalanne 방식 또한 Dirlik과 같이 논리적으로 타당하며 대부분의 상황에서 Dirlik 방식과 비슷한 정확도를 가지지만 Dirlik에 비해 경험식이 덜 들어간 것이 장점이다.^8,12 Dirlik Method와 마찬가지로 식(5)로 표현할 수 있다. 그러나 Dirlik Method와 달리 Lalanne Method의 p(S)는 식(10)과 같다.

$\[ p\left(S\right)=\frac{1}{2RMS}\left\{\begin{array}{c}\frac{\sqrt{1-{\gamma }^2}}{\sqrt{2\pi }}{e}^{\frac{-S^2}{8RM{S}^2\left(1-{\gamma }^2\right)}}\hfill \\ +\frac{S\cdot \gamma }{4RMS}{e}^{\frac{-S^2}{8RM{S}^2}}\left[1+erf\left(\frac{S\cdot \gamma }{2RMS\sqrt{2\left(1-{\gamma }^2\right)}}\right)\right]\end{array}\right\} \]$

(10)

RMS는 RMS Stress로 m₀와 같으며 erf(x)는 다음과 같이 정의한다.

$\[ erf\left(x\right)=\frac{2}{\sqrt{\pi }}{\int }_0^x{e}^{-t^2}dt \]$

(11)

따라서 Lalanne Method는 불규칙 계수와 S에 관한 함수로 Dirlik Method와 마찬가지로 스펙트럼 모멘트로만 표현할 수 있다.

2.3.3 Steinberg Method

Steinberg Method 는 단순성으로 인해 자주 사용되며 주로 전자장비 검증에 사용된다. 주어진 위치에서의 응력 진폭 응답이 1 sigma에서 68.3%의 시간, 2 sigma에서 27.1%의 시간, 3 sigma에서 4.3%의 시간으로 나뉘어진 Gaussian 분포를 갖는다고 가정하여 누적 피로 손상을 계산한다. 이는 식(12)와 같이 표현할 수 있다.¹³

$\[ N\left(S\right)=E\left[P\right]\times \left|\begin{array}{c}0.683 at 2\times RMS\\ 0.271 at 4\times RMS\\ 0.043 at 6\times RMS\end{array}\right. \]$

(12)

RMS는 m₀와 같으며 Steinberg Method는 전체 응력을 3개의 응력으로 분류한다.

3. 주파수영역 피로해석

주파수 영역 피로해석 방법과 유한요소 모델을 사용하고 Ansys Workbench와 Ncode 툴을 이용하여 피로해석을 수행하였다. POD 구조체는 총 1,255,358개의 절점과 733,659개의 요소로 구성되었으며 해석에 사용된 주요 물성치는 Table 1에 표시하였다. PH13-Steel, 17-4PH Steel, AL6061은 MMPDS-01을 참조하였으며 SUS304는 North American Stainless, H-11은 Aircraft Materials를 참조하였다.^14-16

Table 1

Material property

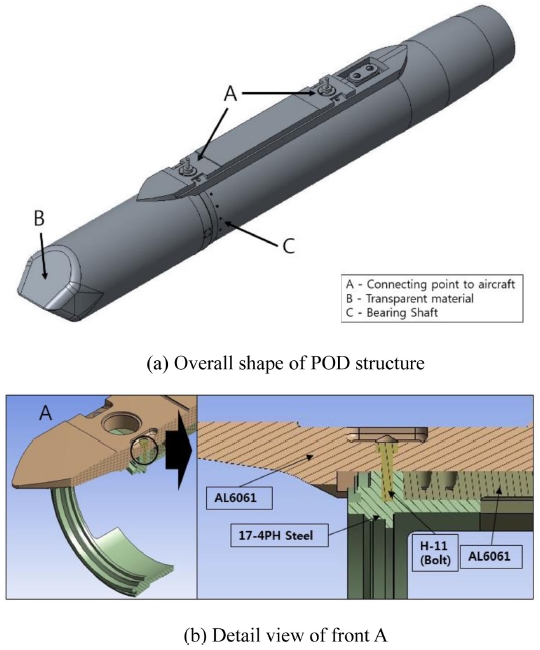
본 연구의 대상이 되는 POD 구조체는 센서가 포함된 원통형 형태로 항공기의 하부에 부착되며 연구에 사용된 POD 구조체를 Fig. 2에 표시하였다. A는 항공기 체결부로 A를 통해 POD 구조체가 항공기에 체결되어 고정된다. B는 사파이어 재질로 목표물의 정보가 B를 통과하여 내부 센서로 입력된다. C는 베어링 샤프트로 POD의 전방 부분이 회전이 가능하도록 하는 기능을 한다. 대부분의 부품들은 AL6061이 소재로 사용되었다. 각 부품들은 A위치에 하나씩 있는 강철로 된 부품에서 서로 체결되며 부품 간의 체결에는 H-11로 만든 볼트가 사용된다. Fig. 2(b)는 전방 체결부 A의 단면도이다. 실제 내부는 센서와 전자장비로 구성되어 있지만 본 연구는 프레임 위주의 피로현상을 분석하기 위한 연구이기에 내부 부품은 Point Mass로 대체하였다. POD 구조체는 각각 파트들의 합으로 구성되어 있으며 이때 각 파트의 연결을 어떤 방식으로 구현하냐에 따라 피로해석의 결과가 달라지게 된다.¹⁷ 솔리드 요소를 사용하는 방식이 가장 정확하지만 가장 많은 해석 시간이 소요된다. 그렇기에 본 연구에서는 프레임 사이의 체결부위는 나사 형태의 솔리드 요소를 이용하여 구현하였으며 프레임 대 케이스나 케이스 대 케이스 연결부위 같은 나머지 체결부위는 Beam 요소를 이용하여 구현하였다.

Fig. 2

POD structure

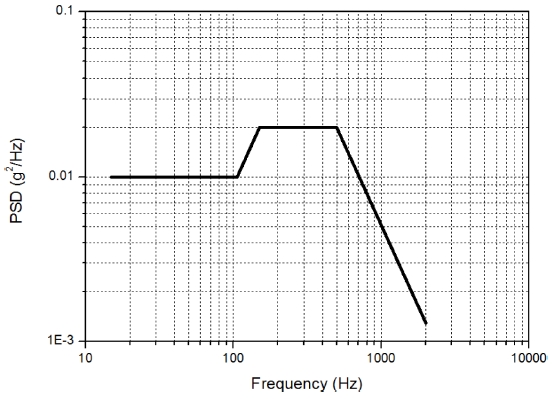
Ansys Workbench에서 Modal Analysis를 이용해 구조체의 고유진동수를 구한 뒤 Harmonic Analysis에서 모드 중첩법을 사용해 POD 구조체의 FRF를 구하였다. 그 후, Ncode Designlife에 FRF와 PSD 데이터를 입력하여 피로해석을 수행하였다. PSD 데이터는 MIL-STD-810G를 참조하였으며 각 축 별로 3시간의 PSD 진동이 가해지는 상황을 구현하였다.¹⁸ 사용된 PSD는 Fig. 3에 표시된 것과 유사하다. 각 축 별로 3시간의 PSD 진동에 피로파괴가 일어나지 않는다면 비행기 수명 동안 피로파괴가 일어나지 않는 것으로 본다. 이 때, PSD 분석방식을 Dirlik, Lalanne, Steinberg 방식으로 하여 총 3번의 피로해석을 수행하였다.

Fig. 3

PSD profile

4. 결과

Ansys Modal Analysis를 통해 얻은 POD 구조체의 Modal 특성을 Table 2에 표시하였다. 실제로는 더 많은 고유진동수가 있지만 그 중 Effective Mass가 5% 이상인 고유진동수치만 표시하였다. 이때, X축은 항공기의 전후방 축, Y축은 좌우 축, Z축은 상하 축이다.

Table 2

Natural frequency of POD structure

Modal Analysis에서 얻은 고유진동수와 Ansys Harmonic Analysis를 통해 얻은 POD 구조체의 축 별 FRF를 Fig. 4에 표시하였다.

Fig. 4

Frequency response function of POD structure

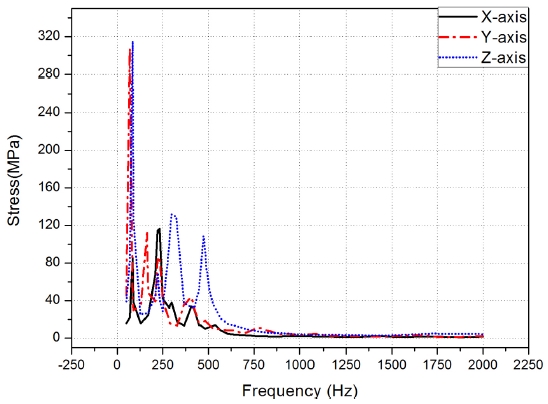
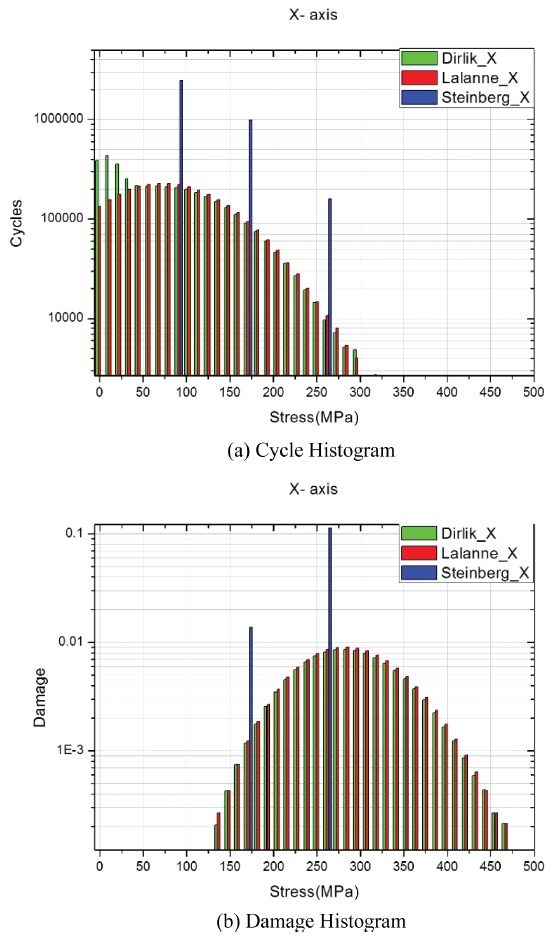
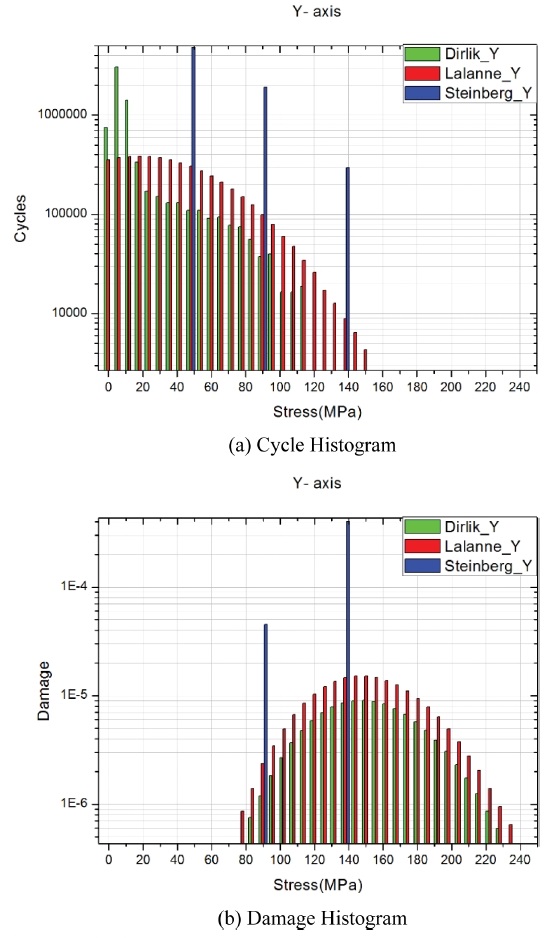
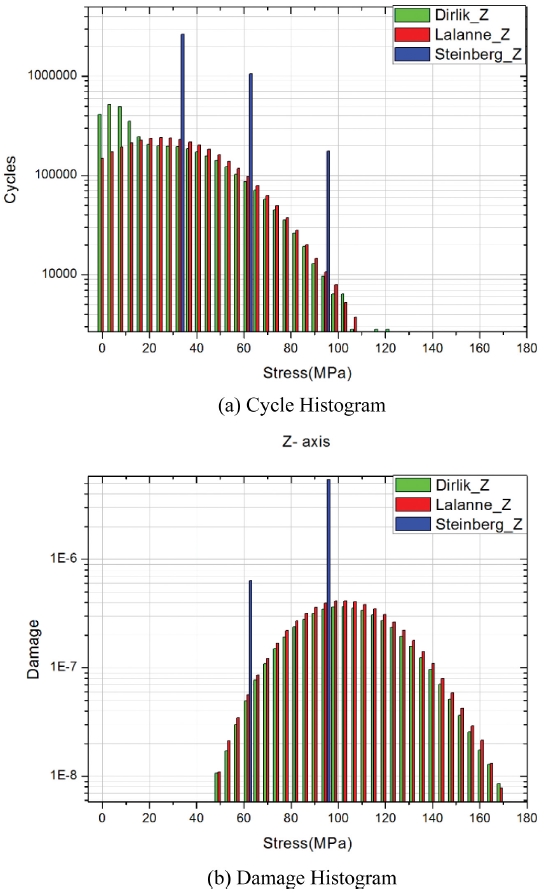
FRF와 PSD를 이용하여 얻은 POD 구조체의 최저 수명을 PSD분석방식 별로 Table 3에 표시하였다. 분석 방식에 상관없이 최저수명 위치는 222,475번 절점으로 모두 동일하였다. 이때, Life는 항공기 수명을 1로 하였을 때의 상대 값이다. 또한 222,475번 절점의 분석 방식 별 Cycle Histogram과 Damage Histogram을 Figs. 5부터 7에 표시하였다.

Table 3

Life of the weakest node in POD structure

Fig. 5

Results of X-axis

Fig. 6

Results of Y-axis

Fig. 7

Results of Z-axis

5. 고찰

먼저 PSD 분석 방식에 관계없이 공통적으로 나타나는 현상이 있다. Cycles Histogram을 분석해보면 X축에서 큰 응력들이 집계되는 것을 볼 수 있고 그 뒤로 Y축, Z축 순이다. 이러한 이유로 인해 Damage Histogram에서 X축의 최대 Damage가 Y축 보다 1,000배 이상, Z축보다 10,000 배 이상 큰 것을 알 수 있다. 즉, X축 진동이 수명에 대부분의 영향을 주는 것을 알 수 있다. 3방식 모두 계산된 수명은 7.901에서 8.737로 방식 별로 최대 10%정도의 차이가 나며 1 이상이기 때문에 수명에는 문제가 없는 것을 알 수 있다.

3가지 분석 방식의 결과는 큰 차이가 없지만 Cycles Histogram을 보면 방식마다 특징이 있는 것을 알 수 있다. Lalanne 방식은 잘려진 정규분포 형태를 띠고 있지만 Dirlik 방식은 Lalanne 방식의 형태에 낮은 응력 범위의 응력이 추가로 집계된 형태다. Steinberg 방식은 식(12)에 나타냈듯이 응력이 3범위로 나누어져 있다. Damage Histogram을 보면 Dirlik 방식이나 Lalanne 방식은 정규분포 형태를 띠고 있으며 Steinberg 방식은 2개의 응력 기둥을 가지고 있다. Lalanne과 Dirlik 방식은 Cycles Histogram에서는 확연히 다른 형태를 띠었지만 Damage Histogram에서는 비슷한 형태를 띠고 있다. 이는 낮은 응력들은 피로 수명에 작은 영향을 주기 때문에 발생한 결과로 Dirlik 방식에서 추가로 집계된 낮은 응력 범위의 응력은 수명에 큰 영향을 주지 않는 것으로 보인다. 마찬가지로, Steinberg 방식의 Cycles Histogram에서 보였던 3 범위 중에서 응력이 낮은 범위는 Damage Histogram에서 보이지 않는다.

상기 결과들을 종합하면 피로한도가 낮은 재료를 사용하거나 더 강한 PSD 진동 데이터를 사용할 경우에는 각 방식마다 유의미한 수명 차이가 나타날 수 있을 것으로 예상한다. 그러나 본 연구에서 사용된 재료와 비슷한 레벨의 PSD를 기준으로 한다면 Dirlik, Lalanne, Steinberg 방식은 비슷한 결과를 보일 것으로 예상한다.

6. 결론

PSD 데이터를 분석하는 3가지 방식(Dirlik, Lalanne, Steinberg)을 사용하여 주파수 영역 피로해석을 수행한 후 결과를 비교하였다.

(1) X축 방향 진동이 수명에 대부분의 영향을 준다.

(2) PSD 분석 방식 별로 최대 10% 정도의 차이가 나며 방식에 관계없이 POD 구조체는 피로파괴로부터 안전하다.

(3) Cycles Histogram에서 Dirlik 방식은 Lalanne 방식에 비해 낮은 응력 범위의 응력 집계량이 많고 Steinberg 방식은 3가지 범위로 나누어서 집계된다.

(4) 대부분의 낮은 응력범위의 응력은 수명에 영향을 미치지 않기 때문에 Dirlik 방식과 Lalanne 방식의 Damage Histogram은 비슷한 형태를 띤다. 마찬가지로 Steinberg 방식의 Cycle Histogram에서 보였던 낮은 응력범위 기둥은 Damage Histogram에서 보이지 않는다.

(5) 본 연구에서 사용된 환경과 유사한 상황에서는 Dirlik, Lalanne, Steinberg 방식에서 큰 차이가 없을 것으로 예상된다. 그러나 피로한도가 낮은 재료를 사용하거나 더 강한 PSD 진동 데이터를 사용한다면 방식에 따라 수명에 차이가 있을 것으로 판단된다.

추후에는 각 방식 별로 차이가 발생하는 조건을 연구 할 예정이다.

Acknowledgments

이 논문은 2018년도 한화시스템㈜의 재원을 지원 받아 수행된 연구이다.

REFERENCES

• Halfpenny, A. and Kihm, F., “Rainflow Cycle Counting and Acoustic Fatigue Analysis Techniques for Random Loading,” Proc. 10th International Conference RASD, pp. 12-14, 2010.
• Yoon, M. Y., Kim, K. H., Park, J. S., Boo, K. S., and Kim, H. S., “The Prediction of Dynamic Fatigue Life of Multi-Axial Loaded Structure,” Journal of the Korean Society for Precision Engineering, Vol. 30, No. 2, pp. 231-235, 2013. [https://doi.org/10.7736/KSPE.2013.30.2.231]
• Park, J. B. and Jeong, S. M., “Fatigue Damage Model Comparison with Tri-Modal Spectrum under Stationary Gaussian Random Processes,” Journal of Ocean Engineering and Technology, Vol. 28, No. 3, pp. 185-192, 2014. [https://doi.org/10.5574/KSOE.2014.28.3.185]
• Quigley, J., Lee, Y.-L., and Wang, L., “Review and Assessment of Frequency-Based Fatigue Damage Models,” SAE International Journal of Materials and Manufacturing, Vol. 9, No. 3, pp. 565-577, 2016. [https://doi.org/10.4271/2016-01-0369]
• Jung, H. S., Kim, K. S., Kim, J. S., and Lee, S. W., “Fatigue Life Evaluation in Frequency Domain of aircraft Equipment Exposed to Random Vibration,” Journal of the Korean Society for Aeronautical and Space Sciences, Vol. 45, No. 8, pp. 627-638, 2017. [https://doi.org/10.5139/JKSAS.2017.45.8.627]
• Palmgren, A., “Durability of Ball Bearings,” VDI-Zeitschrift, Vol. 68, No. 14, pp. 339-341, 1924.
• Miner, M. A., “Cumulative Damage in Fatigue,” Journal of Applied Mechanic, Vol. 67, pp. 159-164, 1945.
• HBM UK Ltd., “DesignLife Theory Guide,” NC-DL-TH 1300001.
• Rice, S. O., “Mathematical Analysis of Random Noise,” Bell System Technical Journal, Vol. 23, No. 3, pp.282-332, 1944. [https://doi.org/10.1002/j.1538-7305.1944.tb00874.x]
• Dirlik, T., “Application of Computers in Fatigue Analysis,” Ph.D. Thesis, University of Warwick, 1985.
• Mrsnik, M., Slavic, J., and Boltezar, M., “Frequency-Domain Methods for a Vibration-Fatigue-Life Estimation – Application to Real Data,” International Journal of Fatigue, Vol. 47, pp. 8-17, 2013. [https://doi.org/10.1016/j.ijfatigue.2012.07.005]
• Lalanne, C., “Mechanical Vibration and Shock Analysis, Fatigue Damage,” John Wiley & Sons, 2010. [https://doi.org/10.1002/9780470611968]
• Steinberg, D. S., “Vibration Analysis for Electronic Equipment,” John Wiley & Sons, 2000.
• Rice, R. C., “Metallic Materials Properties Development and Standardization,” National Technical Information Service, 2003.
• North American Stainless, “Long Products Stainless Steel Grade Sheet,” https://www.northamericanstainless.com/long-products, (Accessed 23 JUL 2019)
• Aircraft Materials, “Alloy Steel H-11 Typical Mechanical Properties,” https://www.aircraftmaterials.com/data/alstst/h11.html, (Accessed 23 JUL 2019)
• Kim, J., Yoon, J. C., and Kang, B. S., “Finite Element Analysis and Modeling of Structure with Bolted Joints,” Applied Mathematical Modeling, Vol. 31, No. 5, pp. 895-911, 2007. [https://doi.org/10.1016/j.apm.2006.03.020]
• Department of Defense Test Method Standard, “MIL-STD-810G,” 2008.