볼트 체결부의 응력장을 고려한 복합재 날개 구조물의 최적 설계

2.1 복합재 구조물의 결합 개념

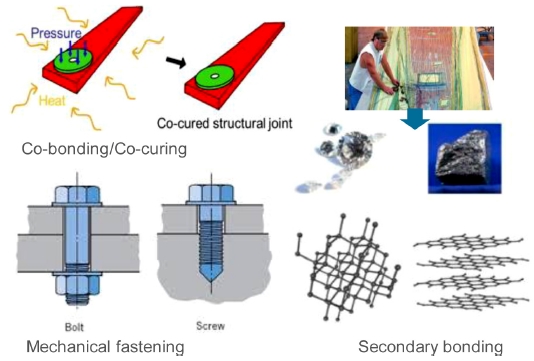
Fig. 1에서와 같이 복합재 구조물을 결합시키는 일반적인 결합개념을 3가지로 구분하여 나타내었다.

Fig. 1

Concept of combining composite structures

기계적 결합은 일반적으로 부품을 결합시킬 때 적용되는 전통적 방법이다. Co-Bonding / Co-Curing은 복합재료 구조물에 많이 사용되는 방법이고, 최근 Secondary Bonding도 점차 사용빈도가 확대되고 있다. 기계적 결합은 기술 성숙도가 높고 결합체의 무게 증가가 필연적이고 구멍이 뚫리기 때문에 결합 부위에서 응력 집중이 일어난다. Co-Curing / Co-Bonding / Secondary Bonding은 무게 감소에 강점이 있지만 기술 성숙도가 낮기 때문에 결함 발생 빈도가 아직까지는 높다.

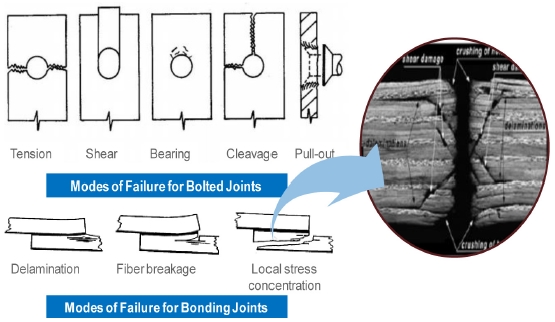
2.2 결합된 구조물의 파괴모드

기계적 또는 본딩으로 접합된 복합재료 구조물은 접합부에는 여러 가지 고장 모드가 발생한다. Fig. 2와 같이 패스너의 손상 5가지와 본딩의 손상 3가지가 대표적인 접합부의 손상이다. Fig. 2와 같이 Tension Failure는 단면에서 파괴되며, Shear-Out Failure는 베어링 고장 도달 전 구멍 간격, 가장자리 거리 또는 Lay-Up 조건에 따라 발생된다. Bearing Failure는 고정 장치 바로 앞의 매트릭스 고장으로 발생되고, 고정 장치 고장 또는 Pull-Out에 의해 고장이 발생된다.

Fig. 2

Modes of failure of mechanical and bonding joints in fiber reinforced polymer composites

2.3 베어링 하중(Bearing Load)

베어링 강도는 일반적으로 구멍의 단면적에서 균일하게 작용하는 평균 응력이다. 식(1)과 같이 표현할 수 있다.

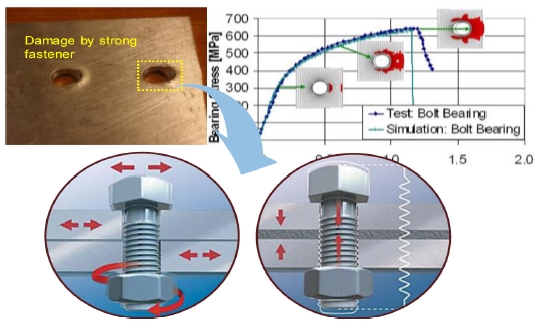
베어링 고장은 고정장치에 의해 적재된 홀의 원주의 절반 부근에 압축 응력으로 인해 발생한다.

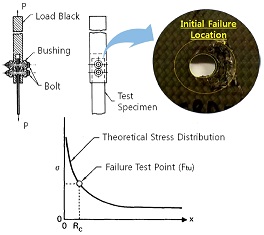
고장 메커니즘은 섬유와 매트릭스를 통해 전단 안에서 발생하며, 최대 스트레스가 발생하는 구멍 가장자리에서 시작된다.¹¹ 베어링 파괴 현상은 강한 재료가 약한 재료를 갈아먹는 현상인데 볼트나 리벳이 복합재 적층 판 구조에 손상을 주는 것을 의미한다. 이로 인한 응력 분포는 하중이 커짐에 따라 Fig. 3과 같이 나타난다.

Fig. 3

Modes of failure of mechanical and bonding joints in fiber reinforced polymer composites

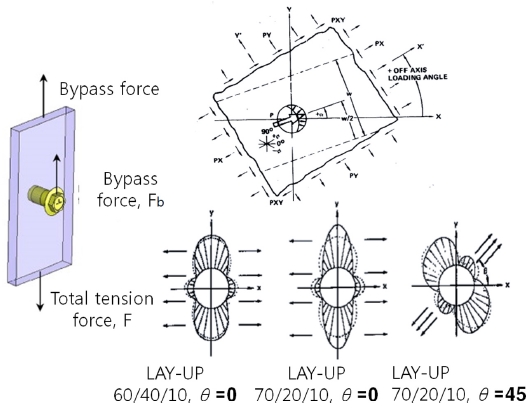
2.4 바이패스 하중(Bypass Load)

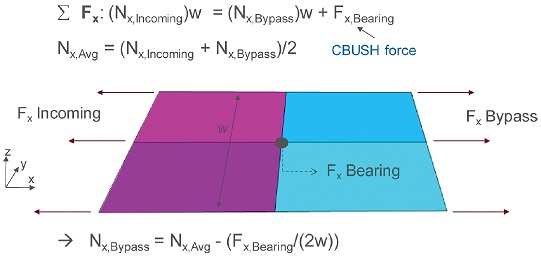
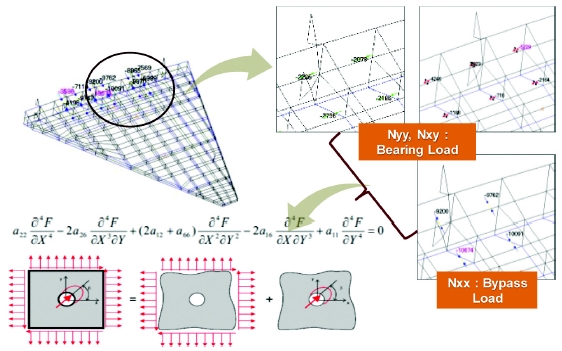
베어링 하중은 볼트에 적용되는 하중이다. Fig. 4과 같이, 하중에 의해 발생된 모멘트가 볼트 구멍 주위에 로컬 응력을 발생된다. 바이패스 하중은 베어링 하중 이외의 하중이 여러 체결부에 이동하는 하중인데, 이 바이패스 하중에 의해서 응력의 구배가 발생된다. 바이패스 하중은 복합재료로 구성된 다중 결합 구조에서 큰 파괴 효과를 일으킬 수 있다. 복합재 구조물이 결합된 영역에서 베어링 하중에 의해 발생된 응력과 바이패스에 의해 발생된 응력을 더해서 체결부 홀 주위의 응력을 평가해야 한다. Fig. 4에서 체결부 주위의 응력의 필드장을 나타내었으며, 바이패스 하중의 크기 및 각도에 의해 패스너 홀 주위의 응력이 달라짐을 알 수 있다.

Fig. 4

Bypass load and bypass load effect in composite structure

2.5 볼트 체결부의 응력 모델

1970년대 후반의 McDonnell社 복합재 시편의 베어링 시험을 했는데 허용 응력과 파괴 위치가 상이하게 나왔다. 하중이 전달되면 복합재 적층판에 장착된 패너스 홀 안쪽에서 파괴되는 현상이 발생되는데 Fig. 5와 같다. 파괴 위치는 특성길이(Characteristic Distance)에 불리우며 볼트 구멍의 안쪽에 해당하는 위치이다. 이는 응력의 구배가 달라져서 예상에서 벗어나는 위치에서 파괴가 진행되기 때문이다. 볼트 체결부의 응력모델의 이론은 1968년에 Leknitskii 미분방정식에서 출발하였으며 식(2)와 같다. 바이패스와 베이링의 응력을 분리하고 미분방정식을 이용해서 계산한다. 이들 결과값을 중첩하여 응력을 산출한다.

Fig. 5

Failure location and characteristic dimension

여기서 S는 복합재의 강성행렬의 역행렬이며 F는 볼트 체결부의 응력장이다.

3.1 체결부의 베어링-바이패스 하중의 해석

다중 볼트 체결 구조는 부정정 구조 시스템이며, 개별 볼트는 일반적으로 탄성 범위에서 동일한 하중을 전달하지 않는다. 재료 및 구조물 선형성의 관계로 두 개의 연속 볼트 하중 R_i 사이의 관계를 얻을 수 있다.

여기서 K_p는 플레이트 상수이고 K_s는 스트랩 상수이다. 중요한 가정은 모든 횡단 행의 볼트가 동일하게 부여된다.¹² 단일 전단 관절의 경우 식(4)와 같다.

한 행의 볼트가 다른 행과 같지 않을 수 있는 이중 전단 접합부의 경우에 식(5)의 상관 계수가 적용된다.

먼저 각 볼트 행의 부하에 대한 초기 추정치를 식(6)과 같이 설정한다.

여기서 nbr은 조인트의 볼트 행 수이다.

체결부에 식(7)을 사용하여 볼트 하중에 대한 예측값을 계산할 수 있다.

이 반복은 모든 볼트의 경우, 한 번 반복에서 다음 번 반복으로의 변경이 상수보다 적거나 ε (여기서 1.0 × 10^-6) 이하이거나 1,000회까지 지속된다. 해당 볼트 행의 바이패스 부하는 적용된 로드와 볼트 행 부하의 차이이다.

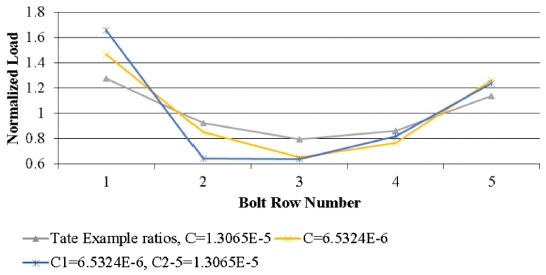
Fig. 6에서 볼 수 있듯이 볼트의 하중 비율은 동일하게 인가되지 않고, 패스너 위치에 따라 다르게 하중이 적용된다. 첫 번째 및 마지막 볼트 행은 더 많은 볼트 유연성으로 인해 많은 하중이 인가된다. 분석의 다음 부분에서 각 조인트 및 볼트 행에 대해 순 섹션 응력과 바이패스 응력이 계산되고 볼트 구멍 둘레의 응력을 확인할 수 있다.

Fig. 6

Normalized joint load vs. Bolt row number

3.2 볼트 체결부의 응력 모델 해석 절차

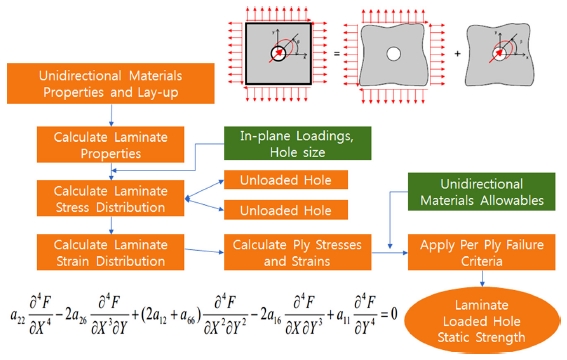
볼트 체결부의 응력 해석 절차는 식(2)의 4차 미분방정식을 푸는 과정이다. 먼저 미분방정식을 풀 수 있는 구조물의 재질, 적층 정보의 입력부터 시작된다. 미분방정식은 Fortran Code로 구성되어 있다. Fig. 7와 같이 복합재료의 재질과 적층정보를 입력하게 되며, 이후 적층판에 대한 강성행렬 계산, 적층판의 응력 분포 계산, 라미네이트 변형률 분포의 순으로 계산할 수 있다. 더불어 적층 Ply 별 응력 및 변형률 계산, 허용치 비교 후 파손 조건 판별 그리고 패스너 홀의 정적 강도 계산순으로 진행된다.

Fig. 7

Analysis procedure for bolted joint stress field model

4.1 Single Lap Joint 모델의 정보

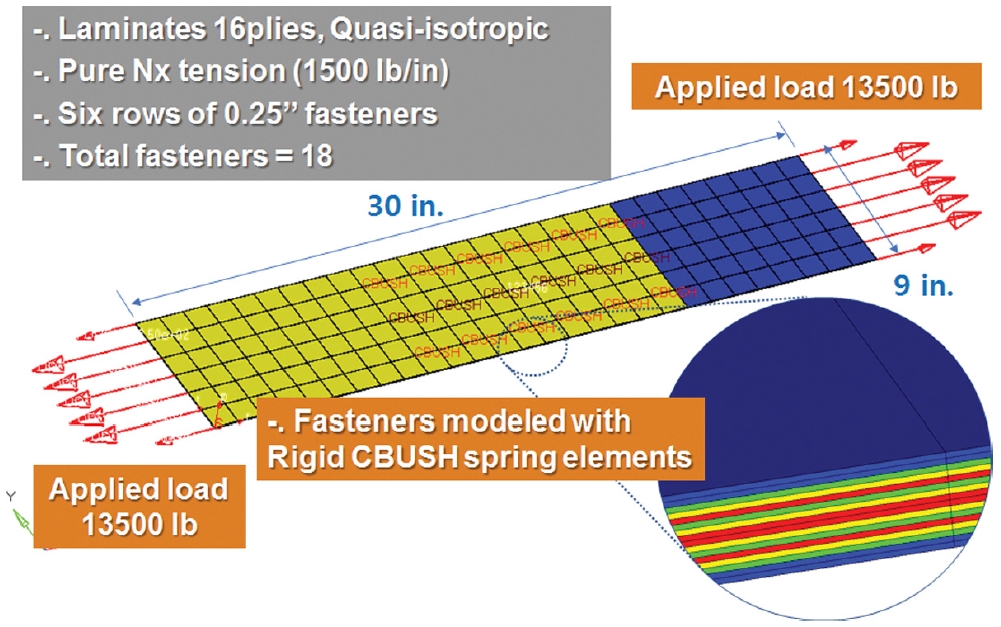
본 절에서 적용된 모델에서 Bearing과 Bypass에 대한 효과가 어느정도 미치는지 안전율을 통하여 계산할 수 있다. 모델의 정보는 Fig. 8과 같다.

Fig. 8

Single lap joint information

복합재료로 구성된 판이 Bolt로 표현할 수 있는 Bushing 요소로 연결되어 있고, 선하중 1500 lbs/in로 하중을 부여하였다. 전체 16 Ply로 (0 / 0 / -45 / 45 / 90 / -45 / 45 / 90)_sym으로 적층된다.

4.2 Single Lap Joint의 체결부 해석 결과

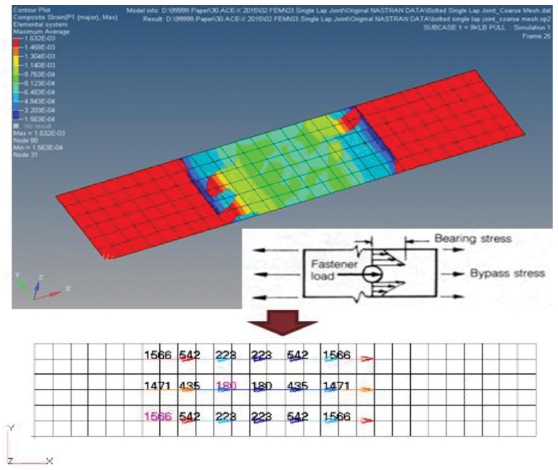
체결부 해석결과는 Single Lap의 연결하는 요소인 Bushing 요소에서의 하중을 추출하여 베어링과 바이패스 하중의 영향성을 계산한다. 베어링과 바이패스의 영향성을 계산하기 위해 식(10)을 이용한다.

베어링 하중을 이용하여 안전율을 계산하면 Fig. 9과 같이 볼트가 장착된 위치에서 전단하중을 추출하고 전단응력을 계산, 그리고 Single Correction Factor, C_f를 0.77을 적용하면 -0.3417이 계산된다.

Fig. 9

X-directional bearing load calculation in single lap joint

베어링과 바이패스 하중을 동시에 고려하기 위해서 유한요소 모델에서 선하중(Load / In)를 추출하고 Fig. 10의 베어링과 바이패스의 관계에서 바이패스 하중을 계산한다. 그리고 볼트 체결부의 응력 모델 미분방정식을 이용하여 여유마진을 산출한다. 베어링과 바이패스 하중을 동시에 고려하면 식(8)에서 계산된 안전율보다 낮은 값이 계산된다. 계산된 베어링-바이패스를 고려한 안전율은 -0.3480이다.

Fig. 10

Bypass load calculation in single lap joint

이는 하중의 전달 효과로 인해 바이패스에 대한 안전율이 추가적으로 1.81% 더해짐을 의미한다. 결합을 위해 많은 패스너가 장착되고, 하중이 매우 큰 구조물에서는 하중의 흐름을 반드시 고려해야 한다.

5.1 날개의 형상 정보

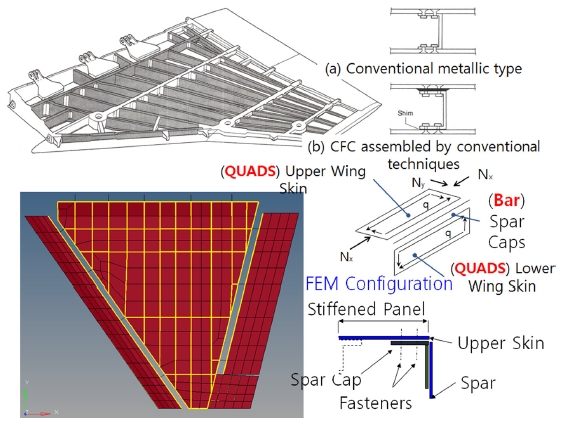
해석 모델은 Fig. 11과 같다. 유로 파이터의 개발 시험 모델을 기본으로 하고, 날개 넓이는 400 ft², 앞전 날개의 각도는 35도, 뒷전 날개의 각도는 -14도를 적용하였다. 날개와 동체가 결합되는 부분은 Lug 형태의 피팅을 적용하였다. Skin과 Spar, Skin과 Rib의 볼트-결합은 Shell Force를 추출할 수 있도록 Bushing 요소를 적용하였다.

Fig. 11

Composite wing structure configuration

5.2 날개 구조의 최적 설계

최적화에 적용된 알고리즘은 전역 반응표면법(Global Response Surface Method)이 적용되었다. GRSM은 적응 반응-표면(Adaptive Response-Surface) 기반의 최적화와 전역 검색의 결합으로 반응표면이 개정되고 알고리즘은 새로운 샘플에서 역시 최적값을 찾아낸다. GRSM은 사용자가 정의한 설계 횟수를 평가할 때까지 이러한 과정을 계속 반복 수행한다.

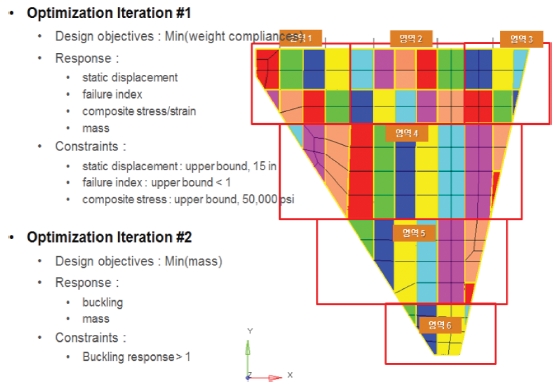
날개 구조의 설계변수를 결정하기 위한 설계 기준은 First Ply Failure Check / Unnotched Laminate Strength Check / Buckling Check / Bearing/Bypass Check를 검토항목으로 선정한다. 설계변수는 Fig. 12와 같이 총 46개의 Skin을 설계변수로 컨포넌트로 구분하였고, 다시 6개의 설계변수로 설정한다. Failure Index는 TSI-Wu로 계산한다.

Fig. 12

Optimization strategy for minimum weight

최적화 단계는 두 단계로 나뉘는데, 첫번째 단계에서는 변위/파괴 지수/응력을 Response로 설정하고 제약조건을 설정한다. 그리고 두번째 단계에서 좌굴모드를 제약조건을 설정하고 질량을 최소화하는 목적함수로 설정하여 최적화가 진행된다.

5.3 날개 구조의 최적 설계 결과

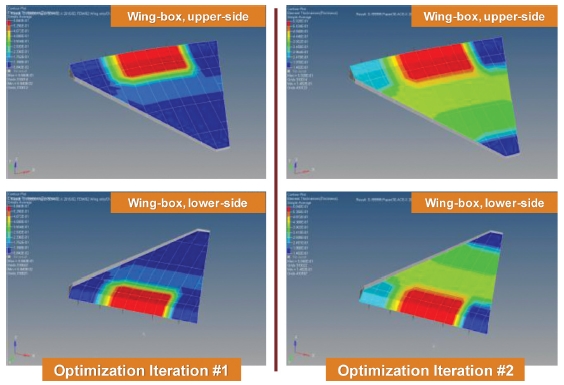
첫번째 단계에서의 최적 설계에서 변위, 파괴 지수, 응력을 만족하는 결과는 Fig. 13의 좌측의 결과이다. Fig. 13의 우측 결과는 두번째 단계의 최적 설계가 진행된 결과이다. 스킨의 두께가 결과로 제시되었다. 첫번째 결과에서 아주 두껍고, 아주 얇은 스킨 형태가 설계 결과물로 제시되었으나 두번째 최적 설계 단계를 거치면서 날개 끝단부로 갈수록 단계별로 스킨의 적층 두께가 줄어든다. 붉은 색은 가장 큰 적층 두께로 78 Ply이고 파란색 부분은 가장 적은 적층 두께는 20 Ply이다. 적층 최적화는 하중 방향에 따라서 적층수가 증감되고, 적층각은 제작사에서 주로 쓰는 0, 45, -45, 90^o가 적절하게 포함된다.

Fig. 13

Optimum design results of wing structure

Fig. 14는 날개와 항공기 동체가 연결되는 Bush 요소에서 하중을 추출하여 볼트 조인트 결합 영역의 응력을 계산하는 단계이다. 다음과 같이 Shell-Force를 먼저 추출하고 식(10)의 미분방정식을 계산하는 해석코드에 복합재 재질 특성과 하중을 입력하여 음의 마진이 계산되면 Fitting을 구성하는 적층 두께를 증가시켜 양의 최소마진이 나올 수 있도록 반복 계산한다.

Fig. 14

Bearing-bypass load check at joint fitting

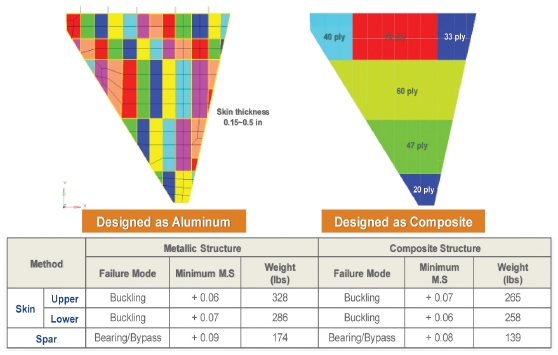
두 단계의 최적 설계 과정을 마치면 최적화 단계가 마무리되고 금속재를 적용할 때와 복합재료를 적용할 때 중량을 비교할 수 있다. Fig. 14의 좌측은 알루미늄을 적용한 날개 모델의 두께이고, 우측의 결과는 복합재료 날개 모델의 두께이다. 대부분은 좌굴에서 최소 안전률이 계산되고 주요 설계인자가 된다. Skin과 Rib가 장착되는 지점에서 Bearing-Bypass 하중이 크고 최소 안전율이 계산된다.

Fig. 15

Result comparison for wing structure

알루미늄이 적용된 설계는 구역 별로 스킨의 두께가 다르고 복합재가 적용된 부위는 제작조건을 고려하여 끝단부 부터 동체에 장착되는 부위까지 하중의 크기 순으로 두께가 순차적으로 증가한다. 복합재의 제작 요건 상 부드러운 설계 두께 증가를 적용해야 응력 집중을 피할 수 있다. 알루미늄 설계 대비 중량의 84% 중량으로 중량 감소의 효과가 있으며, 초기설계 이후 제작 조건, 유지보수 등의 여러 항목을 고려되어야 한다.