Stability Circle을 통한 하지 외골격 로봇의 보행 안정성 판단
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Patients with complete paralysis that only walk with the assistance of exoskeleton robots because they lost their ability to walk. However, robots do not allow the exoskeleton robot to grasp the current state before walking and change the walking pattern. A 'Stability Circle Region' was proposed to determine the current state of the exoskeleton robot. The Stability Circle is an area that can determine the possibility of a fall situation before the next walk using the link parameters of the robot and the current center of gravity of the patients. This study verified the validity of 'stability circle' by simulating the change in the center of mass. Simulation results can be used to determine the stability of walking depending on whether the position of the center of mass before the walking is included in the circle area.
Keywords:
Exoskeleton robot, Gait stability, Rehabilitation robot키워드:
외골격 로봇, 보행 안정성, 재활 로봇1. Introduction
완전마비 환자는 자동차 사고, 낙상 등으로 척수에 강한 외력이 가해지면서 생기는 병태로 운동신경이 마비되어 하지의 보행 능력을 완전히 상실한 환자들이다.1 이러한 환자들의 보행 능력 회복을 위해 많은 외골격 로봇들이 개발되는 중이다. ReWalk Robotics사의 ReWalk2이나 Ekso Bionics사의 Ekso3등 완전마비 환자의 보행 능력을 도와주는 외골격 로봇이 상용화되고 있다. 이러한 로봇들은 대부분 전체 보행 주기에 대해 미리 저장된 보행 Trajectory를 활용하여 착용한 환자들의 보행 능력을 회복시킨다. 하지만 이러한 컨트롤 방법은 로봇이 착용한 환자들의 보행 안정성을 파악하지 않고 움직인다. 때문에 환자가 정상적으로 걷지 못하는 보행 환경에도 대응하지 못하고 결국 낙상과 같은 보행문제를 발생시킨다.
사람의 보행에서 보행의 안정성은 중요한 요소이다. 재활훈련용 하지 외골격 로봇을 입은 대상자는 보행에 장애가 있는 환자들이기 때문에 보행 안정성은 더욱 중요하다. 로봇이 보행 안정성을 판단하지 못하면 환자들이 부상 위험에 노출되기 때문이다. 이러한 문제를 해결하기 위해 휴머노이드 보행 안정성 기술들을 사용하여 해법에 접근하려 하였다.
이족 보행 로봇 보행 안정성 표준에는 다양한 방법들이 있다.4 The Project Center of Mass (GCoM) 방법은 무게중심(CoM)을 지면에 투영시켜 Support Polygon이라는 지면에 닿은 발로 이루어진 영역안에 들어가는지를 파악하여 정적 안정성을 판단하는 방법이다.5 The Zero Moment Point (ZMP)는 로봇의 관성과 중력에 의한 토크의 값이 0이되는 지면의 지점을 나타낸다. 이 ZMP 지점이 Support Polygon 안에 항상 존재하며 벗어날 경우 보행의 불안정성을 판단하는 방법이다.6 The Zero Rate of Angular Momentum (ZRAM) Point 방법은 지면 반력으로 인한 모멘트 변화율을 측정하여 지면반력의 벡터와 평행하고 무게중심을 지나는 벡터의 지면 포인트를 측정하여 안정성을 측정하는 방법이다.7 마지막으로 The Capture Point (CP)가 있다. 이 방법은 이족 보행을 Linear Inverted Pendulum으로 간단하게 모델링하여 시스템을 완전히 멈추게 하기위해 발의 Center of Pressure (CoP)가 어디에 위치해야 하는지를 나타내는 방법이다.8
본 연구에서는 기존 이족 보행 안정성 표준에서 사용하는 힘 센서나 가속도 센서와 같은 센서 시스템을 사용하는 것이 아닌 로봇 조인트에 장착 되어있는 엔코더의 각도 데이터만을 활용한 간단한 보행 안정성 지표를 제안한다. 이를 통하여 기존 보행 안정성 지표화 함께 사용하여 좀더 환자들의 보행 안정성을 확보한다. 하지만 환자들의 보행 의도를 파악하는 것은 매우 어려운 일이다. 또한 사람이 포함된 외골격 로봇의 동역학 모델링은 매우 복잡하기 때문에 환자의 상태를 바로바로 파악하는 것은 매우 어려운 일이다.
우리는 논문에서 ‘Stability Circle Region’을 제안하여 외골격 로봇의 현재 데이터를 활용하여 로봇이 다음 보행 시작 전에 안정성을 미리 판단하여 낙상과 같은 보행 문제를 미리 방지하려 한다. CP 안정성 표준에서 사용된 잘 알려진 Linear Inverted Pendulum Model (LIP)9을 이용하기 위해 외골격 로봇에 적용하기위해 4가지 가정을 하였다. 첫째로 우리는 모든 질량 값을 Center of Mass (CoM)에 집중시켰다고 가정하였다. 둘째 우리는 로봇의 다리 부분의 질량이 없고 바닥과 하나의 Revolute 조인트로 연결되어 있는 시스템으로 가정하였다. 세번째 우리는 Sagittal Plane 상에서의 Forward/Backward 그리고 Up/Down 운동만을 고려하였다. 마지막으로 완전마비 환자용 외골격 로봇 시스템은 환자들의 사용하는 목발 클러치를 사용하기 때문에 Frontal Plane상의 낙상에 대한 안정성보다 Sagittal Plane상의 안정성을 판단하였다. 본 논문에서는 보행 안정성 판별을 위해 다음과 같은 프로세스를 통하여 작동한다.
(1) 하지 외골격 로봇의 LIP 모델을 통하여 CoM의 운동 방정식을 구한다.
(2) 2차 미분 방정식 형태인 CoM의 운동 방정식의 해를 구하여 CoM의 위치를 계산한다.
(3) 각 스텝에서의 CoM의 위치에서 지면까지의 Two-Link Inverse Kinematics 솔루션을 계산한다. 이때 사람의 관절 범위를 고려하여 제한조건을 설정한다.
(4) Inverse Kinematics 솔루션 계산 중 발생하는 역 코사인 함수의 정의역 범위로 인해 발생하는 ‘Stability Circle’을 계산한다.
(5) 로봇의 보행 시작 전 무게중심의 위치와 앞으로의 무게중심 x위치 Trajectory가 ‘Stability Circle’의 Stable한 영역에 존재하는지 판단한다.
(6) 무게중심의 위치가 Stable 한 영역에 있다면 로봇이 보행을 시작한다. 반면에 무게중심 위치가 Unstable 한 영역에 있다면 초기 무게중심 위치를 변경하여 Stable 한 영역에 들어가게 한 후 로봇의 보행을 시작한다.
2장에서는 WAP-2 로봇의 소개와 LIP를 통한 모델링을 이야기 한다. 3장에서는 Inverse Kinematics를 활용한 각 고관절/무릎관절의 각도를 계산하며 4장에서는 ‘Stability Circle Region’을 계산을 유도한다. 마지막으로 5장에서 다양한 초기 조건으로 시뮬레이션 하여 ‘Stability Circle’의 유효성을 검증하였다.
2. LIP Modeling for WAP-2
2.1 WAP-2
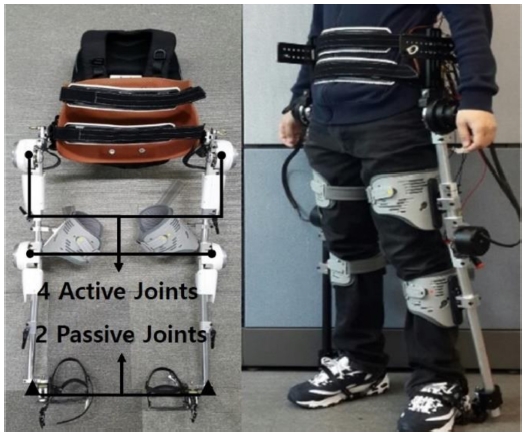
WAP-2는 Walking Assist Robot for Paraplegic Patients의 약자로 Spinal Cord Injury (SCI)로 인한 신체 하지 부분이 마비가 된 완전마비 환자의 하지 보행 능력 회복을 위해 개발된 로봇이다.10 Fig. 1은 WAP-2 로봇의 모습과 착용자가 착용한 후의 사진이다. WAP-2는 총 8개의 조인트를 가지고 있다. Sagittal Plane 안에서 4개의 Active 조인트와 2개의 Passive 조인트를 가지고 있다. 4개의 Active 조인트는 고관절과 무릎관절의 Flexion/Extension 운동을 지원하고 2개의 Passive 조인트는 발목의 Plantar/Dorsi Flexion 모션의 자유도를 가진다. Frontal Plane 안에서는 2개의 Passive 조인트를 가지며 고관절의 Ab/Adduction 모션의 자유도를 제공한다. Active 조인트와 Passvie 조인트의 각도 변화는 Encoder를 통해서 측정하며 상체 등판 IMU 센서의 Roll/Pitch/Yaw와 각속도 데이터를 통하여 상체 움직임 의도를 측정한다.
2.2 LIP Dynamics
Fig. 2에서 보는것과 같이 WAP-2 모델을 LIP로 근사화 시킨다. 여기서 우리는 다리에서 나오는 힘 f의 수직 성분은 중력에 의해 상쇄되지만 수평 성분의 힘이 남아있다는 것을 알 수 있다. 여기서 τ는 로봇 발목 부분에서 토크를 생성하지 않기 때문에 0으로 생각하면 다음과 같은 식(1)을 유도할 수 있다.11
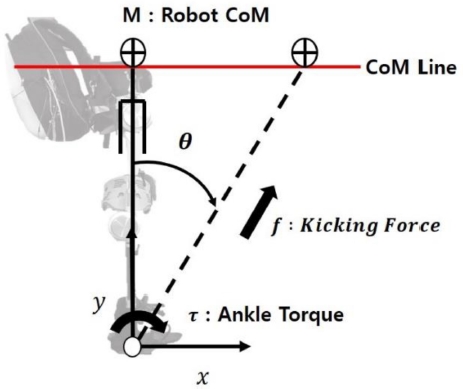
The simplest model for WAP-2 exoskeleton robot. It assume that all mass values are concentrated at the CoM and massless leg
| (1) |
| (2) |
| (3) |
여기서 Kicking Force f는 식(2)로 유도 가능하기 때문에 식(2)를 식(1)에 대입하면 다음과 같이 식(3)이 유도된다. 식(3)을 정리하면 우리는 무게중심의 수평 성분 동역학 미분 방정식을 식(4)와 같이 얻을 수 있다.
| (4) |
우리 모델은 y값이 상수 이기 때문에 우리는 미분 방정식 식(4)를 쉽게 풀면 다음과 같은 결과를 얻을 수 있다.
| (5) |
| (6) |
| (7) |
TC는 CoM의 높이와 중력가속도 값에 의해 변하는 시간 상수이다. x(0)와 는 CoM x 좌표의 초기 위치와 속도 값이다.
3. WAP-2 Inverse Kinematics
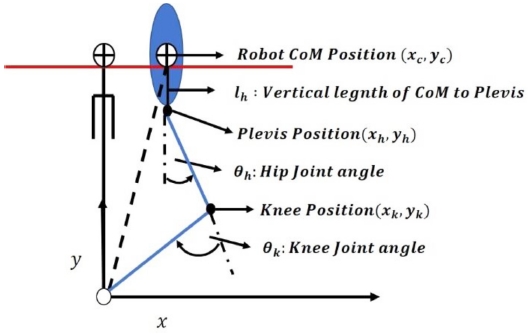
Fig. 3에서 지면에 접촉한 발의 위치를 원점 (0, 0)으로 잡고 고관절과 무릎의 위치를 각각 ph:(xh, yh), pk:(xk, yk)으로 나타낸다. 로봇의 상체가 기울지 않는다고 가정하면 무게중심 위치가 정해지면 고관절의 위치는 무게중심 위치에 y축으로 lh만큼 아래 위치한다고 할 수 있다(식(8)). 무릎위치 pk의 x, y좌표는 각각 식(9)와 식(10)으로 나타낼 수 있다.
| (8) |
| (9) |
| (10) |
이와 같은 방법으로 지면 원점의 위치는 다음과 같이 나타낼 수 있다.
| (11) |
| (12) |
식(11), 식(12)의 xh, yh에 대하여 정리한 후에 각각 제곱하여 더하면 다음과 같이 나타낼 수 있다.
| (13) |
| (14) |
| (15) |
식(15)를 정리하면 식(16)과 같이 나타낼 수 있으며 역 코사인 값 안의 식을 S로 치환하였다(식(17)).
| (16) |
| (17) |
식(11)과 식(12)를 각각 xh − l1sin(θh)과 yh − l1cos(θh)에 대하여 정리한 후에 제곱하여 더하면 식(18)부터 식(20)을 구할 수 있다.
| (18) |
| (19) |
| (20) |
식(20)의 일부를 M으로 치환하여 정리하면 삼각함수에 대한 2차 방정식 형태가 나온다.
| (21) |
| (22) |
| (23) |
2차 방정식을 근의 공식을 이용해 풀면 sinθh은 다음과 같은 해의 형태를 가지며 해에 역사인 함수를 취하면 θh는 식(25)의 값을 가진다.
| (24) |
| (25) |
식(25)값을 식(16)에 대입하면 θk값 또한 구할 수 있다. Inverse Kinematics 해가 고관절과 무릎관절 각도 각각 두 개씩 나오기 때문에 사람의 인체 관절 Range of Motion (ROM)의 값을 제한조건을 두어서 Inverse Kinematics 해가 사람의 관절 범위를 넘어가지 않게 하였다. 구해진 해를 사용하여 로봇을 움직인다.
4. Stability Circle Computation
우리는 챕터3 Inverse Kinematics 해를 구하는 과정에서 ‘Stability Circle’을 유도할 수 있다. 식(16)을 보면 역 코사인 함수가 나온다. 역 코사인 함수의 정의역에 의하면 식(17)의 S값의 범위는 다음과 같이 나타낼 수 있다.
| (26) |
식(26)을 정리하여 나타내면 원 함수의 식으로 나타낼 수 있다.
| (27) |
식(27)의 반지름 r1, r2값은 로봇 링크 길이 l1, l2값이 결정되면 정해지는 상수 값으로 항상 0보다 큰 값을 가지므로 식(27)은 Fig. 4와 같이 원의 영역을 나타낼 수 있다. Fig. 4는 착용자 한 사람의 다리 길이에 로봇링크 길이를 맞춘 후 구한 ‘Stability Circle’의 예이다.
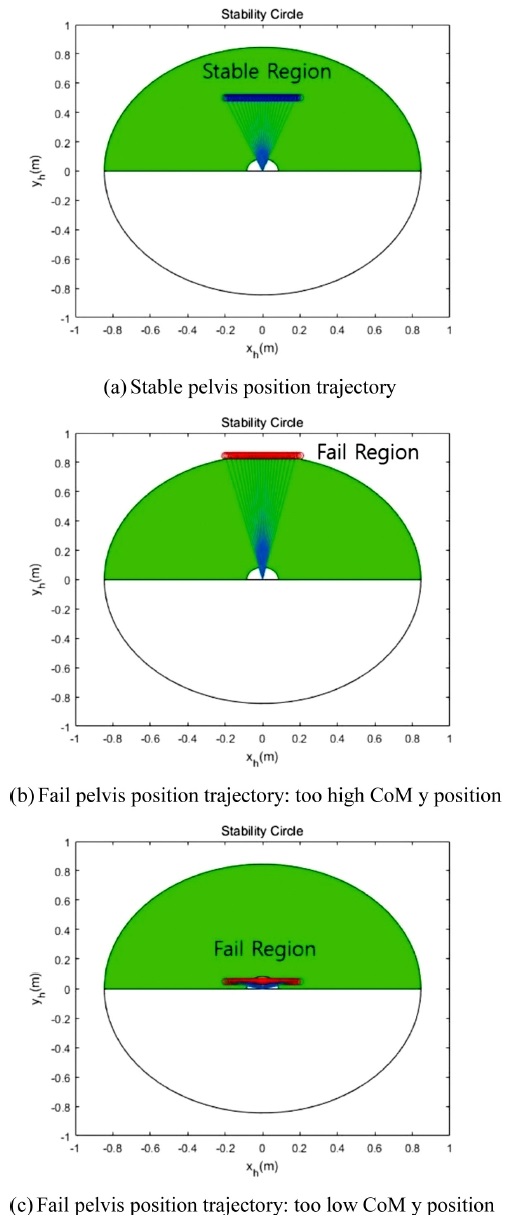
Simulation result (a) is stable pelvis position trajectory(x(0): -0.2 m , yh: 0.5 m) (b) is fail pelvis position trajectory (x(0): -0.2 m, yh: 0.845 m) (c) is also fail pelvis position trajectory (x(0): -0.2 m, yh: 0.2 m)
이 값을 활용하면 무게중심의 위치에서 원점 회전 조인트 까지의 Inverse Kinematics의 해가 존재하는지 알 수 있다. 만약 현재 무게중심의 위치가 원의 영역에 들어가지 않는 경우 Inverse Kinematics 해가 존재하지 않기 때문에 로봇은 불안정한 자세를 가진다.
때문에 원의 영역을 활용하면 보행 전 무게중심의 x, y 위치를 식(27)에 대입한 후 보행 안정성을 판단하여 보행을 시작한다면 외골격 로봇을 입은 환자에게 좀더 안정적인 보행을 제공할 것으로 생각된다.
5. Simulation
5.1 WAP-2 Robot Simulation
2.1절에서 소개한 WAP-2 하지 외골격 로봇의 고관절 링크 길이와 무릎관절 링크 길이 각 링크의 무게 값 그리고 시뮬레이션 환경은 Table 1로 정리 하였다. 로봇의 무게중심 y축 위치를 변화시켜 고관절의 위치의 변화를 그래프로 나타내 ‘Stability Circle’ 내에 있는지 외부에 있는지 시뮬레이션 하였다. Fig. 4는 시뮬레이션 결과를 보여준다. Fig. 4(a)는 무게중심 초기 x(0):-0.2 m, y_h: 0.5 m의 값이며 고관절의 위치 변화 그래프를 보면 모든 Step에서의 값이 원의 영역 안에 들어오기 때문에 역 코사인 함수 정의역 값을 초과하는 값이 없기 때문에 모든 영역에서 Inverse Kinematics의 해를 구할 수 있기 때문에 안정한 영역이라고 할 수 있다. Figs. 4(b)와 4(c)는 각각 다른 Fail 조건을 주었다. Fig. 4(b)의 경우는 무게중심의 초기 y위치를 로봇 링크 길이 l1, l2의 합으로 주었으며 x위치 초기값 x(0)는 Fig. 4(a)와 동일하게 주었다. 결과를 보면 Fig. 4(b)의 고관절 위치 변화 값은 원 영역을 벗어나기 때문에 역코사인 함수의 정의역 값에서 벗어나기 때문에 Inverse Kinematics 해가 실수 영역이 아닌 허수 영역의 값이 나오기 때문에 로봇이 나타낼 수 없는 조인트 값이기 때문에 로봇이 보행 전에 무게중심 y값을 낮춰서 원 영역 안으로 들어갈 필요가 있다. Fig. 4(c)같은 경우는 반대로 보행 시작 전 무게중심의 y위치가 매우 낮은 값을 가질 경우 고관절 위치가 원 영역 안에 들어오다가 작은 원 안의 영역으로 들어가 안정 영역이 아닌 고관절 위치 값을 가지기 때문에 이 영역 또한 Inverse Kinematics 해가 허수의 해가 나오며 불안정한 보행 결과를 초래할 수 있다. 때문에 이런 경우에는 Fig. 4(b)와 반대로 초기 무게중심의 y 위치를 높인 자세를 취한 후 보행을 시작해야 보행에 좀 더 안정성을 가질 수 있다고 볼 수 있다.
6. Conclusion
본 연구에서는 하지 외골격 로봇을 입고 보행 훈련이나 일상생활을 하는 환자들의 보행 안정성을 미리 판단하여 대응하기 위한 방법을 연구하였다. Inverse Kinematics 계산 시 발생하는 역 코사인 함수의 정의역을 사용한 ‘Stability Circle’을 제안하여 영역이 타당한지 시뮬레이션 하였다. 로봇의 보행 시작 전 착용자의 무게중심의 위치를 파악하여 로봇의 파라미터로 구해진 ‘Stability Circle’ 영역 안에 무게중심의 값이 들어오는지 판단하여 로봇이 환자의 무게중심을 조정한 후에 보행을 시작하여 보행의 안정성을 상승시키며 무게중심 x위치의 Trajectory 타당성 또한 판단이 가능하다. 뿐만 아니라 본연구에 사용된 WAP-2 시스템 말고 다른 하지 외골격 로봇 시스템의 파라미터 값이 주어진다면 적용이 가능할 것으로 기대된다.
7. Future Work
후속 연구로는 좀더 자연스러운 사람의 보행을 고려하여 무게중심의 y축 좌표의 값을 상수로 생각하는 것이 아니라 보행 시 발생하는 y축 좌표의 수직 방향의 움직임을 고려한 보행 안정영역을 구할 것이다.
NOMENCLATURE
| M : | Robot Center of Mass |
| f : | Kicking Force |
| g : | Gravity acceleration |
| TC : | Time constant depending the height of the CoM and gravity acceleration |
| ph, pk : | Position of Pelvis and Knee |
| l1 : | Robot pelvis to knee link length |
| l2 : | Robot knee to foot link length |
| θh, θk : | Joint angle of hip and knee |
REFERENCES
- American College of Surgeons, ATLS: Advanced Trauma Life Support for Doctors (Student Course Manual), 8th Ed., Chicago, IL: American College of Surgeons, 2008.
-
Esquenazi, A., Talaty, M., Packel, A., and Saulino, M. “The ReWalk Powered Exoskeleton to Restore Ambulatory Function to Individuals with Thoracic-Level Motor-Complete Spinal Cord Injury,” American Journal of Physical Medicine and Rehabilitation, Vol. 91, No. 11, pp. 911-921, 2012.
[https://doi.org/10.1097/PHM.0b013e318269d9a3]

- Ekso Bionics, “Ekso,” https://ipfs.io/ipfs/QmXoypizjW3WknFiJnKLwHCnL72vedxjQkDDP1mXWo6uco/wiki/Ekso_Bionics.html, (Accessed 24 MAY 2019)
-
Sharbafi, M. A. and Seyfarth, A., “Bioinspired Legged Locomotion: Models, Concepts, Control and Applications,” 1st Ed., pp. 2-698, 2017.
[https://doi.org/10.1016/B978-0-12-803766-9.00001-4]

- Berns, K., Piekenbrock, S., and Dillman, R., “Learning Control of a Six-Legged Walking Machine,” Proc. of the Robotics and Manufacturing International Symposium, ASME, pp. 29-34, 1994.
-
Vukobratović, M. and Borovac, B., “Zero-Moment Point-Thirty Five Years of Its Life,” International Journal of Humanoid Robotics, Vol. 1, No. 1, pp. 157-173, 2004.
[https://doi.org/10.1142/S0219843604000083]

- Goswami, A., Espiau, B., and Keramane, A., “Limit Cycles and Their Stability in a Passive Bipedal Gait,” Proc. of the IEEE International Conference on Robotics and Automation, pp. 246-251, 1996.
-
Pratt, J., Carff, J., Drakunov, S., and Goswami, A., “Capture Point: A Step Toward Humanoid Push Recovery,” Proc. of the 6th IEEE-RAS International Conference on Humanoid Robots, pp. 200-207, 2006.
[https://doi.org/10.1109/ICHR.2006.321385]

- Kajita, S. and Tani, K., “Study of Dynamic Biped Locomotion on Rugged Terrain-Derivation and Application of the Linear Inverted Pendulum Mode,” Proc. of the IEEE International Conference on Robotics and Automation, pp. 1405-1411, 1991.
-
Ji, Y., Yun, D., Jang, H., Lee, D., Khan, A. M., et al., “Study on Efficacy of Gait Training for Hemiplegia Patients Using Lower-Limb Wearable Robot,” Journal of the Korean Society for Precision Engineering, Vol. 32, No. 10, pp. 879-883, 2015.
[https://doi.org/10.7736/KSPE.2015.32.10.879]

-
Kajita, S., Hirukawa, H., Harada, K., and Yokoi, K., “Introduction to Humanoid Robotics,” Springer Berlin Heidelberg, 2014.
[https://doi.org/10.1007/978-3-642-54536-8]


Ph.D. candidate in the Department of Mechatronics Engineering, Hanyang University. His research interest is Wearable & Rehabilitation Robots
E-mail: hshhln@naver.com

Ph.D. candidate in the Department of Mechatronics Engineering, Hanyang University. His research interest is Wearable & Rehabilitation Robots
E-mail: thetiru@naver.com

Ph.D. candidate in the Department of Mechatronics Engineering, Hanyang University. His research interest is Wearable & Rehabilitation Robots
E-mail: sdbin225@gmail.com

M.D. in the Department of Interdisciplinary Engineering Systems, Hanyang University. His research interest is Wearable & Rehabilitation Robots
E-mail: kbskim504@gmail.com

Professor in the Department of Robotics Engineering, Hanyang University. His research interest is medical service robot, future combat robot, field robot, wearable robot, path planning, construction automation robot
E-mail: cshan@hanyang.ac.kr