송전철탑 하중설계를 위한 복수 경간 송전선의 갤로핑 시뮬레이션
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
When wind load acts on the Power Transmission Line (PTL) with asymmetric cross section from icing and snowing, the generated vibration is termed ‘galloping phenomenon’. Since galloping phenomenon triggers short circuits or ground faults of the PTL, various galloping studies are being conducted, at home and abroad. However, galloping analysis is performed for single span in most cases, while actual PTL comprises multiple spans. In this study, PTL is modeled as a mass-spring-damper system, using a multi-body dynamics analysis program, RecurDyn. To analyze dynamic analysis of the PTL, damping coefficient is derived, by using the free vibration experiment of the PTL and Rayleigh damping theory. Through flow analysis, the galloping occurrence condition was identified, and galloping simulation was performed, by modeling the wind load. The effect of galloping on the stress applied to the pylon, was analyzed by flexible modeling the pylon between spans. As a result, approximately 150% of stress is applied to the pylon, so the galloping phenomenon should be considered when designing the pylon.
Keywords:
Power transmission line (PTL), Pylon, Plural span, Galloping, Wind force coefficient, Multi-Body dynamics키워드:
송전선, 송전탑, 복수 경간, 갤로핑, 공력계수, 다물체 동역학1. 서론
송전선로의 경과지가 고산 및 다설지역인 경우 착빙이 예상되며 착빙에 의해 송전선의 단면적이 비대칭을 이루어 공기역학적으로 불안정한 상태가 된다. 이때 착빙된 전선이 강풍을 받게 되면 전선의 자중 및 장력에 의해 과도 진동이 발생하는데 이를 갤로핑이라 한다. 갤로핑에 의한 진동이 발생하면 전선상호간 또는 가공지선과의 사이에 아크가 발생하면서 단락 또는 지락고장을 일으키고 순간 전압강하가 일어나 고장 전류가 생길 수 있다. 이러한 현상이 장시간 지속될 경우 지지부의 피로 파괴로 이어져 송전선 자체가 낙하되거나 송전탑이 무너지는 대형사고로 이어질 수 있다. 2008년 12월 동해시 지흥동 산96에서 갤로핑에 의한 전력선 혼촉 등 국내에서도 갤로핑에 의한 전선 고장이 발생하고 있는 실정이다. 이를 예방하기 위해 난착설링(Difficulty Snow Accretion Ring)을 이용하여 송전선에 착빙설이 부착되는 것을 방지하거나 상간 스페이서(Phase Spacer)를 사용하여 풍하중에 수직한 방향의 전선 이동량을 줄여 갤로핑을 억제하는 등 여러 가지 방법이 이용되고 있으나 이는 근본적인 문제 해결방안이 될 수 없다. 그렇기 때문에 착빙에 따른 전선도약 및 갤로핑 해석에 관한 연구를 통해 원인분석과 방지대책을 세울 필요가 있다.
송전선의 갤로핑 현상은 1900년도 미국에서부터 연구가 시작되었으며1 Davision은 비대칭 형태의 송전선 단면을 이용하여 입사각에 따른 양력의 변화를 풍동실험을 통해 측정하였다.2 Den Hartog는 입사각의 변화에 따라 양력 및 항력이 변하는데, 양력의 기울기 값이 항력보다 클 경우 송전선의 불안정성이 발생한다는 것을 밝혀냈다. 최근 국내에서도 갤로핑 등 착빙설에 의한 송전선로 사고예방을 위해 송전선에 관한 연구가 진행 중이다.3 구재량은 송전선의 양력에 의한 운동과 고유진동수 사이의 상관관계에 대해 연구하였으며 갤로핑 현상이 물리적 특성보다는 자연조건에 영향을 받는다는 결론을 제시하였다.4 정영배는 2D CFD를 이용하여 풍하중에 대한 기초적인 연구와 풍하중에 의한 송전선 케이블의 양력 및 항력계수 값을 제시하였다.5 김지욱은 상용 다물체 동역학 해석 프로그램이 RecurDyn을 이용하여 변동풍속에 대한 갤로핑 시뮬레이션을 수행하였다. 현재까지 갤로핑에 관한 연구는 일반적으로 단수 경간에서 수행되어 왔지만 실제 송전선로는 다중견간으로 이뤄진 경우가 지배적이다.
본 연구에서는 복수 경간으로 송전선로를 모델링하고 각 경간의 운동이 상호간에 미치는 영향과 갤로핑이 송전탑에 가해지는 응력에 미치는 영향을 분석하였다.
2. 송전선 시스템의 동역학적 모델링
2.1 송전선의 다물체 모델링
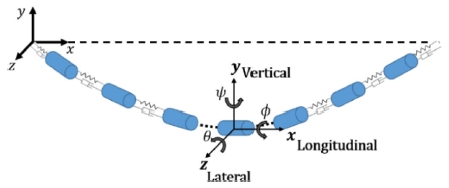
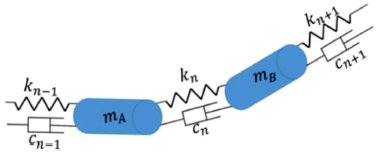
본 연구에서는 상용 다물체 동역학 해석 프로그램인 RecurDyn을 이용하여 송전선을 모델링하였다. 송전선 모델링을 위해 좌표계는 Fig. 1과 같이 정의하였다. 송전선은 Fig. 2와 같이 집중질량과 스프링 및 댐퍼를 이용하여 모델링 하였으며, 500 m 경간의 송전선을 31개의 질량요소와 32개의 스프링 및 댐퍼로 모델링 하였다. Fig. 1에서 송전선의 θ 및 ψ 각에 대한 움직임은 전선도약 및 갤로핑에 대하여 상대적으로 적기 때문에 운동방정식에 고려하지 않았고 송전선의 지지점은 고정이라 가정하였다.
각 집중질량은 4 자유도를 가지며 송전선의 다물체 동역학 모델을 운동방정식으로 표현하면 식(1)과 같다.
| (1) |
여기서 [m]은 124 × 124의 질량 행렬이며, 는 각 질점의 가속도 벡터를 나타내며 식(2)와 같다. Q는 외력항을 나타내며 식(3)과 같다.
| (2) |
| (3) |
식(3)에서 Qg는 중력, Qc는 감쇠력, Qk는 스프링력, QT는 장력을 나타내며 각각 식(4)부터 식(7)과 같이 정의된다.
| (4) |
| (5) |
| (6) |
| (7) |
여기서 g(m/s2)는 중력 가속도이며 [c]는 감쇠 행렬, [k]는 강성 행렬을 나타낸다. (m/s)은 댐퍼길이의 시간변화율, δ(m)는 스프링의 변위이다.
2.2 송전탑의 탄성체 모델링
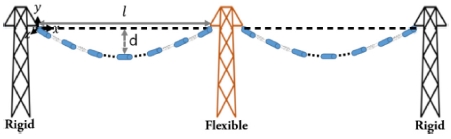
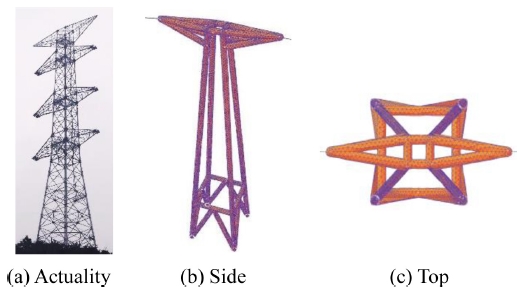
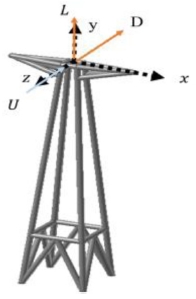
복수 경간 송전선로는 Fig. 3과 같다. 각 경간의 운동이 상호간에 미치는 영향을 분석하기 위해서 경간 사이의 현수철탑은 FEM (Finite Element Method)을 사용하여 유연체로 모델링하였고 Fig. 4와 같다. 송전탑의 외형은 Fig. 4(a)와 같이 일반적인 765 kV송전탑의 형상인 국내 경상남도 밀양시를 지나가는 철탑을 고려하였고 본 연구에서는 관심사항인 저차모드에 영향을 미치는 주요골격만 모델링하였다. 유연체로 모델링한 송전탑의 메쉬타입은 Figs. 4(b)와 4(c)에 보이는 것처럼 견고한 구조의 3D 모델링에 사용되는 Solid 4 (Tetra 4)를 사용하였으며 각 노드에서 3 자유도를 갖고 4개의 기하학 모서리 노드로 정의된다. 해석시간을 고려하여 1초 이내에 정적 평형을 찾는 유연체 송전탑의 최대 요소 크기는 1, 최소 요소 크기는 0.1이다. 노드의 수는 37,837개이고 요소의 수는 11,779개이다. 송전탑 모델링에 사용한 물성치는 ASTM A36 Steel로 Table 1과 같다.
2.3 송전선의 물성치 추출
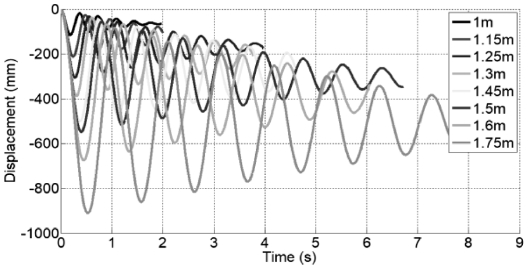
송전선의 동적거동을 해석하기 위해서는 송전선 내부의 감쇠력을 모델링하여 반영하여야 하므로 감쇠력을 결정하는 데에 필요한 감쇠계수가 요구된다. 본 연구에서는 자유진동 실험을 수행하고6,7 Rayleigh 감쇠를 이용하여 송전선의 감쇠계수를 구하였다. 송전선 자유진동 실험은 외팔보 상태에서 자중에 의해 변형이 일어나는 송전선 끝단의 위치변화를 분석하였다. Fig. 5는 송전선 길이에 따른 끝단의 변위를 나타낸다.
자유진동실험을 통해 구한 진폭비를 이용하여 Rayleigh 감쇠계수를 구하였다. Rayleigh 감쇠는 비례감쇠의 한 종류로써 구조물의 강성 행렬과 질량 행렬의 선형조합으로 나타내며 식(8)과 같이 나타낼 수 있다.
| (8) |
여기서 α와 β는 각각 질량비례 및 강성비례 상수이며, 구조물의 주요한 2개의 모드가 i번째 모드와 j번째 모드일 때, 감쇠비를 식(9)와 같다.
| (9) |
감쇠비는 시간영역의 데이터에서 진동 주기와 진폭을 이용하여 계산하며 식(10)과 같다.
| (10) |
여기서 δ1는 대수 감소율이며 식(11)과 같고 A는 진폭을 나타낸다.
| (11) |
실제 송전선은 길이가 매우 길기 때문에 실험을 통하여 진폭을 구하는 것이 매우 어렵다. 그렇기 때문에 멱방정식을 이용하여 진폭비를 곡선 접합하였고 이를 이용하여 Rayleigh 감쇠계수를 추정하였다. 식(12)는 곡선 접합한 멱방정식을 나타낸다. 집중질량의 개수가 31개일 때, 집중질량의 길이는 15.63 m이며 감쇠계수는 57019 Ns/m이다.
| (12) |
여기서 Δ은 진폭비를 나타내며, l은 송전선의 길이를 나타낸다.
2.4 송전선의 모델링 검증
송전선 양 끝 지지점에서의 높이가 같고 처짐 곡선이 포물선 형상을 가진다고 가정하면 케이블 처짐 해석을 통해 송전선의 처짐 곡선은 식(13)과 같이 구할 수 있다.
| (13) |
여기서 m(kg/m)은 단위길이당 질량, l(m)은 경간의 길이, T(N)는 장력을 나타낸다. 적설기간이 1개월 이하인 일반지역의 설계이도인 11.48 m를 송전선 모델에 적용하여 정적 처짐 해석을 수행한 결과 이론상의 처짐 곡선과 송전선 모델의 질점의 위치를 비교하였을 때 오차율은 1% 미만으로 정확성을 검증하였다.8 김지욱은 다설 및 중다설 지역에 대해서도 정확성을 검증하였다.
3. 유동해석을 통한 풍하중계수 추출
3.1 공기력의 정의 및 착빙 단면의 선정
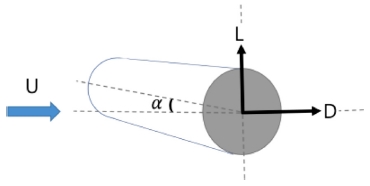
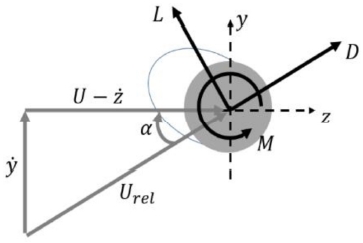
송전선은 자연 상태에서 바람에 노출되어 있고, 바람은 송전선에 풍하중을 가하게 되는데 이를 해석하여 갤로핑 모델링에 적용하기 위해서는 공기력의 모델링이 필요하다. 공기력은 Fig. 6과 같이 정의할 수 있으며 α는 입사각을 나타내고 힘 D를 항력(Drag Force), 힘 L을 양력(Lift Force)이라 한다.
송전선에 가해지는 풍하중을 모델링하여 가진 입력으로 사용하기 위해서는 항력 및 양력 계수가 필요하다. 송전선에 가해지는 풍하중에 저항하는 힘을 항력이라 하며, 수직 방향의 합력, 즉 풍하중이 송전선에 가해지는 하중의 방향에 수직하는 방향으로 생기는 힘을 양력이라 하고 각각 식(14), 식(15)와 같다.
| (14) |
| (15) |
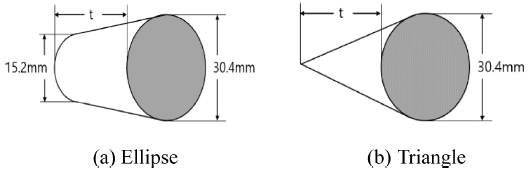
착빙 형상으로는 원통형, D-형상, 타원형, 삼각형 등이 있지만 원통형 착빙은 갤로핑 발생 확률이 낮은 단면이고, D-형상은 자연 상태에서 발생하기 어렵기 때문에 자연 상태에서 발생하기 쉽고 갤로핑의 발생 가능성이 큰 Figs. 7(a) 타원형과 7(b) 삼각형 모양의 착빙 단면을 선정하여 공기력을 모델링하였다. 적설기간과 해발고도에 따라 분류한 일반, 다설 및 중다설 지역의9 착빙 두께는 Table 2와 같다.
3.2 착빙 단면에 따른 공기력계수
타원형 및 삼각형 형상의 착빙 단면에 대하여 0-180°까지 20°간격으로 영각을 증가시키며 유동해석을 수행하였다. 유동해석 시 후류 및 측면의 영향을 받지 않도록 해석 영역을 충분히 크게 설정 하였다.
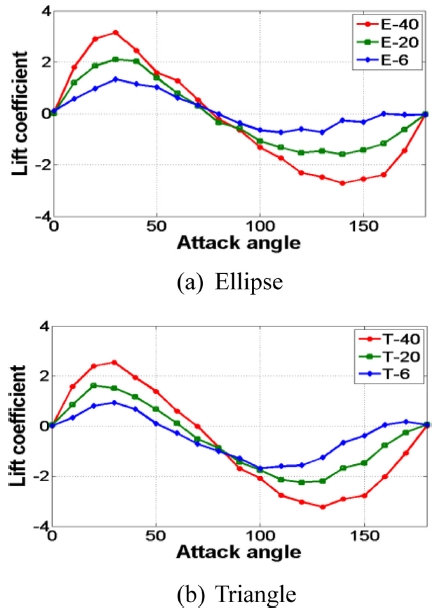
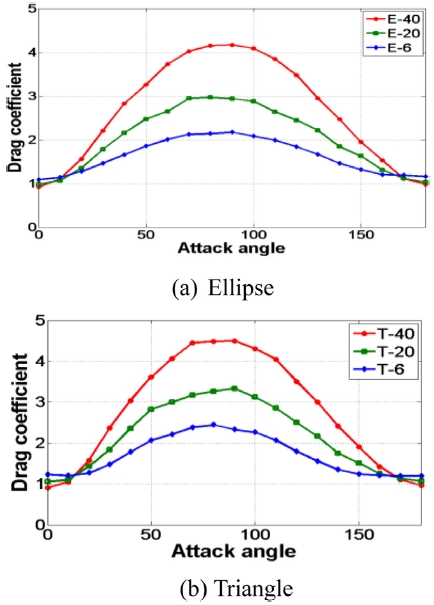
Figs. 8(a)와 8(b)는 각각 타원형 및 삼각형 착빙 단면의 양력 계수(Lift Coefficient)를 나타낸다. 일반, 다설 및 중다설 지역 착빙 두께를 고려하였으며, 영각(Attack Angle)에 따른 양력 계수를 유동해석 프로그램인 ANSYS Fluent를 이용하여 도출하였다. 양력은 영각의 변화에 따른 단면의 비대칭성으로 인하여 발생하기 때문에 영각이 0°와 180°에서는 단면의 대칭성으로 인하여 양력 계수가 0에 가까운 값이 나오며 20° 근처에서 최대값을 갖는다. 양력은 풍하중 방향에 수직하는 방향으로 생기므로 영각이 90-180°에서 양력이 반대 방향으로 작용하기 때문에 양력 계수도 음의 값을 가진다. Figs. 9(a)와 9(b)는 각각 타원형 및 삼각형 착빙 단면에서 일반, 다설 및 중다설 지역에 대한 항력계수를 나타낸다. 착빙 두께가 증가함에 따라 수풍면적이 증가하기 때문에 항력 계수는 커진다. 삼각형 단면이 타원형 단면에 비해 더 큰 항력계수 값을 가지며 항력은 수풍면적이 가장 작은 0°에서 최소값, 수풍면적이 가장 큰 90°에서 최대값을 갖는다.
4. 갤로핑 시뮬레이션을 통한 송전철탑 하중 설계
4.1 갤로핑 시뮬레이션 조건
갤로핑(Galloping)은 착빙설에 의해 전선단면이 비대칭성을 가질 때 송전선 주위를 흐르는 공기에 의하여 생성된 양력과 항력에 의한 불안정한 진동으로 인해 발생한다. 갤로핑 시뮬레이션을 위해서 송전선에 작용하는 힘에 대하여 정의하면 Fig. 10과 같다. 착빙된 송전선에 풍력이 가해지면 풍력의 속도와 송전선의 수직속도로 인해 송전선에 상대 속도가 작용하게 된다. 여기서 U는 풍속을 나타내며, 와 은 각각 송전선의 수직(Vertical), 수평(Lateral) 속도, Urel은 상대 풍속을 나타낸다. 입사각 α는 식(16)과 같고 풍력에 의한 송전선의 항력, 양력은 각각 식(17), 식(18)과 같다.
| (16) |
| (17) |
| (18) |
영각을 고려하면 수직 방향 및 수평 방향 힘은 각각 식(19), 식(20)와 같다.
| (19) |
| (20) |
갤로핑 시뮬레이션 수행 시 Variable Equation을 사용하여 송전선로의 운동에 따라 변화하는 영각(α)을 업데이트하며 풍하중을 적용하였다. 송전탑에 작용하는 풍하중 모델링은 Fig. 11과 같다. 송전탑의 경우 수직 이동량이 거의 없으므로 영각은 일정하다.
갤로핑 시뮬레이션은 풍속은 점진적으로 증가하며 이후에는 풍속은 일정하다 가정한다. 각각의 집중질량과 송전탑에 RecurDyn의 병진 힘(Translational Force)을 이용하여 수직 방향(Fy) 및 수평 방향 힘(Fz)을 적용하였다.
4.2 갤로핑 발생 가능성 분석
물체가 움직일 때 어느 한 순간에 작용하는 공기력은 정적인 상태에서 작용하는 힘과 바람, 물체의 상대 속도에 의해 발생하는 영각으로 작용하는 힘의 합으로 볼 수 있으며 이를 준정상이론(Quasi-Steady Theory)이라 한다. 갤로핑 현상은 준정상 상태라 할 수 있으며 송전선의 갤로핑 현상을 1 자유도 운동방정식으로 나타내면 식(21)과 같다.
| (21) |
식(21)을 물체의 속도에 대한 항에 대하여 정리하면 등가의 감쇠는 식(22)와 같게 되며 감쇠가 음으로 변하면 진폭이 감소하는 것이 아니라 증가함으로 갤로핑이 발생하게 된다.
| (22) |
식(22)가 음수가 되기 위해서는 괄호 안이 음수가 되어야 한다. 식(23)을 Den Hartog Criterion이라 하며, 갤로핑 발생의 필요조건이다.
| (23) |
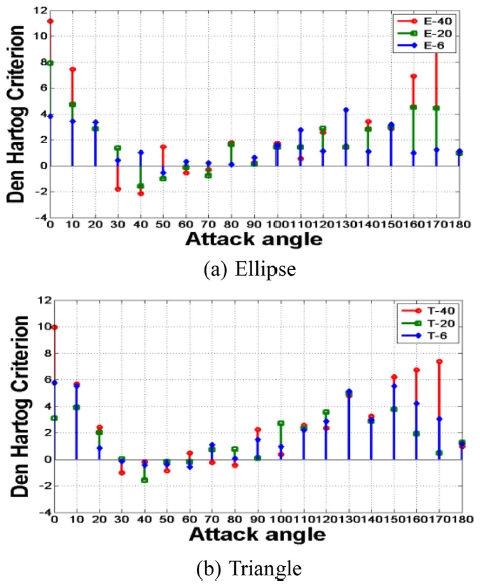
Figs. 12(a)와 12(b)는 착빙 형상별 공기력계수로 Den Hartog Criterion을 적용한 결과이다. 타원형 단면에서 30-70°에서 삼각형 단면에서 40 mm일 때 30-80°에서 송전선의 불안정성을 야기할 수 있다. 90-180°의 영각에 대해서 두 착빙 형상 모두 갤로핑 발생 가능성은 낮을 것으로 보인다.
4.3 시뮬레이션 결과
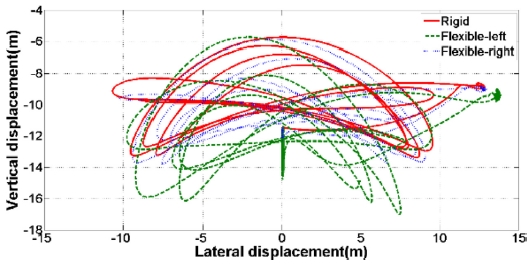
갤로핑 발생 가능 케이스 중 수풍면적과 송전선의 불안전성을 고려하여 변위가 가장 클 것이라 예상되는 삼각형 착빙 단면의 착빙 두께 40 mm, 영각 80°일 때의 갤로핑 시뮬레이션을 수행하였고 송전선의 궤적을 Fig. 13에 나타내었다. 경간 사이 송전탑이 강체일때는 경간 사이의 운동이 상호영향을 끼치지 못하기 때문에 단수 경간일때와 같은 운동을 한다. 그러나 송전탑의 유연체 모델링시 각 경간의 운동은 상호 영향을 미쳐 운동방향이 같을 때는 진폭이 더 커졌지만 반대일 때는 상쇄되는 경향을 보인다. 복수 경간 송전선로의 갤로핑 시뮬레이션시 단수 경간에 비해 전체적인 송전선로의 운동범위가 확장되는 것을 Fig. 13을 통해 확인할 수 있다.
송전탑의 경우 풍하중만 작용할 때에는 최대응력과 변위가 80 MPa에 2 mm이지만 갤로핑 발생시에는 120 MPa에 4 mm로 최대응력과 변위가 약 50% 증가하였다.
5. 결론
본 연구에서 송전선을 다수의 집중질량과 스프링 및 댐퍼로, 경간 사이 송전탑은 유연체로 모델링하였다. 송전선의 자유진동실험을 수행하고 진폭비와 고유진동수를 이용하여 Rayleigh 감쇠 계수를 추정하였고 실제 일반지역의 설계이도와 비교 검토하여 송전선로 모델링에 적용하였다. 유동해석을 통해 갤로핑 발생 조건을 파악하고 풍하중을 모델링하여 갤로핑 시뮬레이션을 수행하였다. 복수 경간에서 갤로핑이 발생했을 때 각 경간의 운동이 상호간에 미치는 영향과 송전탑에 가해지는 응력에 미치는 영향을 분석한 결과 송전탑 설계 시에는 갤로핑 현상을 고려하여야 한다.
Acknowledgments
이 논문은 부경대학교 자율창의학술연구비(2017)에 의하여 연구되었음.
REFERENCES
-
Davision, A. E., “Dancing Conductors,” Transactions of the American Institute of Electrical Engineers, Vol. 49, No. 4, pp. 1444-1449, 1930.
[https://doi.org/10.1109/T-AIEE.1930.5055685]

-
Den Hartog, J. P., “Transmission Line Vibration Due to Sleet,” Transactions of the American Institute of Electrical Engineers, Vol. 51, No. 4, 1932.
[https://doi.org/10.1109/T-AIEE.1932.5056223]

- Koo, J. R., Bae, Y. C., Lee, D. Y., Kim, H. S., Son, S. M., et al., “Protection Method of Ice and Snow Failure at the Power Transmission Line,” Proc. of the Korean Society for Noise and Vibration Engineering Spring Conference, pp. 735-738, 2015.
- Chung Y. B., “A Basic Study of Wind Load for a Cable Using Two-Dimension Computational Fluent Dynamics,” Journal of the Wind Engineering Institute of Korea, Vol. 13, No. 2, pp. 83-89, 2009.
- Kim, J. W., “Sleet Jump and Galloping Simulation for Power Transmission Line by Using RecurDyn,” M.Sc Thesis, Pukyong National University, 2018
- Lee, J. H., “Experimental Study of Beam and Plate Large Deformation,” M.Sc. Thesis, Pusan University, 2003.
- Alipour, A. and Zareian, F., “Study Rayleigh Damping in Structures Unceratinities and Treatments,” Proc. of 14th World Conference on Earthquake Engineering, Beijing, China, 2008.
- Kim, J. W. and Sohn, J. H., “Sleet Jump Simulation of Power Transmission Line by Using Multi-Body Dynamics,” Journal of the Korean Society of Industry Convergence, Vol. 20, No. 5, pp. 431-439, 2017.
- Lilien, J. L., “State of the Art of Conductor Galloping,” CIGRE, 2007.

Graduate Student of Department of Mechanical Engineering at Pukyong National University. Her research interests are optimum design and dynamic analysis of multibody system.
E-mail: yj1124@pukyong.ac.kr

Researcher of Research Institute of Industrial Science & Technology at Pukyong National University. His research interests are parallel computing, particle dynamics and multibody system dynamics.
E-mail: kangsia@live.co.kr

Professor of Department of Mechanical Design Engineering at Pukyong National University. His research interests are mechanism design and multibody system dynamics.
E-mail: jhsohn@pknu.ac.kr

Professor of Department of Control and Inst. Engineering at Pukyong National University. His research interest is control and signal processing.
E-mail: gsbyun@pknu.ac.kr