조인트 구속조건 결합형 관성센서기반 수직변위 추정


Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Displacement estimation based on inertial sensor signals is usually performed in aid of global positioning systems or barometers. However, due to low accuracy estimation capabilities of such aiding sensors, inertial sensor-based displacement estimation is difficult to achieve high accuracy. This paper will show that it is possible to determine the vertical displacement of a link connected by a joint with higher accuracy while only using the inertial sensor. The proposed method utilizes a predetermined position vector from the joint center to the sensor and link orientation. By combining the joint constraint, accuracy of the orientation estimation is ensured even in highly dynamic conditions, and thus, the vertical displacement estimation with high accuracy can be achieved. Experimental results show that the proposed method outperformed the method by fusing inertial sensor and barometer signals as well as the method using inertial sensor signals only without constraint combination.
Keywords:
Joint constraint, Inertial sensor, Vertical displacement, Kalman filter키워드:
조인트 구속조건, 관성센서, 수직변위, 칼만필터1. 서론
본 논문은 로봇 및 인체 모델을 포함하여 조인트로 연결된 다링크(Multi-Link) 시스템에 있어, 관성센서를 이용하여 센서 부착 지점의 링크 수직변위를 추정하는 방법에 대한 것이다. 링크의 변위 추정은 다양한 목적을 위해 요구되어지는데, 예를 들어 머니퓰레이터의 변위는 역기구학 해석에 활용되며, 인체역학 모델에서는 이를 통해 전신 모션캡처가 이루어진다.1,2
최근 로봇공학, 운동역학, 재활공학과 같은 다양한 분야에서 관성센서를 이용한 변위 추정이 활발히 연구되고 있다.3-7 관성센서가 각광을 받는 근본적인 이유는 이 센서가 일반적인 변위 센서와 달리 송신과 수신의 관계가 없다는 점이다. 즉, 일반적인 변위 센서는 송신기 또는 수신기중 한 가지가 고정지점에 위치하여, 이 지점에 상대적인 운동체의 변위를 감지하는 방식으로 작동한다. 예를 들어, 광학식 카메라 시스템은 카메라가 고정지점에 위치하고, 추정 대상체에 부착된 마커를 카메라에 노출시키므로서, 카메라와 함께 고정된 좌표계에서 관측된 마커의 위치를 제공하는 방식이다. 따라서, 일반적인 변위 추정 센서에 있어 제한적인 작동범위는 불가피하다. 따라서 이동체를 대상으로 한 변위추정에 있어, 공간제약성이 없는 관성센서의 적용이 필요한 것이다.8,9
하지만, 관성센서는 가속도계를 통한 선형가속도 및 자이로스코프를 통한 각속도를 제공할 뿐 변위를 직접적으로 제공하지 않는다. 따라서, 관성센서 신호를 통한 변위 추정은 칼만필터 등을 통한 복잡한 신호처리 과정을 거쳐야 한다. 또한, 구속이 없는 단일 이동체의 변위 추정에 있어, 관성센서 단독으로는 적분에 따른 표류오차를 피할 수 없으므로 GPS (Global Positioning System)나10,11 바로미터(Barometer)12-14 등과 융합을 통해 변위를 추정하고 있다. 이때 GPS나 바로미터는 표류하지 않는 변위값을 제공하며, 관성센서는 고샘플링률을 제공하므로, 두 센서의 융합을 통해 고샘플링률과 고정확도의 변위추정을 도모하는 것이다. 하지만, GPS나 바로미터 신호는 표류오차를 방지하는 동시에 궁극적으로 추정값의 결정에 가장 크게 기여한다. 다시 말해, 표류오차 방지를 위해 GPS나 바로미터 신호에 의존하는 이상 이들 신호에 오차가 증가하면 추정값도 심각하게 영향을 받는 것은 불가피하다.14,15 이와 같이 관성센서 기반 변위추정은 관성센서 단독이 아닌 이종 센서와의 융합을 기반으로 하는 경우가 많으며, 이 경우에도 정확도를 확보하는 것이 매우 어렵다.
본 논문이 대상으로 하는 조인트로 연결된 링크의 변위 추정에 있어서는 조인트에 의해 변위의 자유도가 제약을 받으므로, 관성센서만을 이용하면서도 보다 높은 정확도로 변위 결정이 가능하다. 이는 기본적으로 ‘자세경유 변위추정(Displacement Estimation Via Orientation)’라고 할 수 있다. 이 접근법은 다음의 두 단계를 거친다. 첫째, 조인트중심에서 센서로의 위치벡터(Position Vector from Joint Center to Sensor, 이하 J2S 벡터)를 사전 캘리브레이션을 통해 결정한다. 이때 J2S 벡터는 센서좌표계에서 관찰되므로, 상수(Constant)이다. 둘째, 고정좌표계에 대한 센서의 자세를 추정한다. 그렇다면 앞서 구한 J2S벡터를 고정좌표계에서 관찰되는 벡터로 좌표계 변환을 하므로써 센서의 변위를 추정하는 것이다. 이때 자세는 고정좌표계에 대한 자세로서 일반적으로 조인트에 부착되는 엔코더를 통한 각도와는 다르다.
하지만 이러한 자세경유 변위추정 역시 추정정확도 개선에 많은 여지가 있다. 사전 캘리브레이션을 통한 J2S 벡터와 관성센서를 통한 자세를 이용하는 만큼, 이 둘의 정확도를 향상시키므로써 추정 성능 향상이 가능하다. 하지만, 자세경유 변위추정과 관련한 대부분의 문헌은 J2S 벡터를 구하는 방법에 대한 것이다.16-18 반면, 자세 추정 알고리즘에 대해서는 조인트로 구속된 링크라는 점을 이용하지 않고, 일반적인 비구속 강체에 대한 범용 자세 결정 알고리즘을 적용하고 있다. 그러나 동적조건에서는 가속도로 인해 자세 결정에 이용되는 가속도계신호 관련 참조벡터의 신뢰성이 훼손되고 결과적으로 자세 추정 성능이 크게 감소할 수 있다.9,19
이에 대한 대응으로 가속도 보상 메커니즘이 적용된 자세추정 칼만필터가 개발되고 있다. 그럼에도 불구하고, 동적조건이 지속되는 로봇시스템이나, 고속 가동조건이 빈번히 발생하는 기계시스템의 경우 기존의 가속도 보상 메커니즘으로는 추정 정확성 향상에 한계가 있다.19,20 조인트로 연결된 링크는 해당 조인트의 종류에 따라 허용된 형태의 상대운동을 하고 다른 움직임은 구속되어진다. 이러한 조인트 구속조건은 자세추정의 정확성을 향상시키기 위해 활용될 수 있으며, 앞서 설명하였듯이 이는 변위 추정정확도 향상으로 이어질 수 있다.
본 논문은 조인트 구속조건 결합형 관성센서기반 수직변위 추정 방법을 제안한다. 특히 3방향 회전조인트인 볼조인트의 구속 조건에 대하여, 제안 방법의 성능을 구속조건이 아닌 가속도 보상 메커니즘 적용을 통한 변위추정방법과 바로미터 융합형 변위 추정방법의 성능과 비교 분석하였다.
2. 수직변위 추정 방법
본 논문에서 제안하는 수직변위추정 구속 칼만필터는 참고문헌21에서 제안된 비구속 자세추정 칼만필터를 기반으로 전개된다.
고정된 항법좌표계(Navigation Frame, n)에 상대적인 이동하는 센서좌표계(Sensor Frame, s)의 3차원 자세를 의미하는 방향코사인행렬 Rns는 식(1)과 같이 표현가능하다.
| (1) |
여기서, Xs, Ys, Zs는 각각 n좌표계의 X, Y, Z축 단위벡터를 s좌표계에서 관찰한 것이다. 이처럼 우측 윗첨자를 통해 벡터의 관측 좌표계를 표기한다. 가장 일반적인 좌표축 설정이 그러하듯 n좌표계의 Z축이 상향중력방향으로 설정되는 경우, Zs는 수직축에 대한 센서의 기울기를 의미하는 틸트(Tilt)벡터이며, 이를 통해 롤, 피치와 같은 자세 정보를 얻을 수 있다.21 따라서, 이후 기술되는 칼만필터에서는 Zs를 추정한다.
6축 관성센서를 구성하는 자이로스코프와 가속도계의 신호는 각각 식(2)와 식(3)과 같이 모델링되었다.
| (2) |
| (3) |
여기서, ωs는 각속도, nG는 자이로스코프 신호잡음, gs는 중력가속도, as는 센서가속도, nA는 가속도계 신호잡음이다. 또한, 식(3)의 센서가속도는 식(4)와 같은 마르코프 연쇄식 기반식이 적용되었다.
| (4) |
칼만필터의 진행모델은 스트랩다운 적분식으로부터 이산시간 k에 대하여 식(5)와 같이 모델링된다.
| (5) |
여기서 I는 단위행렬, Ts는 샘플링 간격이며, ‘×’는 해당 벡터의 외적(Cross Product) 행렬을 의미한다. 또한, 칼만필터의 측정모델은 식(6)과 같다.
| (6) |
여기서, g는 중력가속도의 크기이며, 이산시간 k에 대하여, k|k−1는 예측값(a priori), k|k는 보정값(a posteriori)을 의미한다.21
식(5)와 식(6)을 통해 도출되는 비구속 자세추정 칼만필터식은 식(7)과 식(8)과 같다.
| (7) |
| (8) |
여기서 식(5)로부터 식(7)의 상태벡터 xk는 틸트벡터 , 천이행렬 Φk-1은 I−Ts[sG,k−1×], 진행 잡음 wk-1은 이며 공분산 행렬 을 갖는다. 식(6)으로부터 식(8)의 측정벡터 zk는 , 관측행렬 Hk은 gI, 측정 잡음 vk는 이며 공분산 행렬 을 갖는다.21 이때 ΣG와 ΣA는 각각 nG와 nA에 대한 공분산 행렬로서 와 로 설정되었다(여기서, σG와 σA는 신호잡음에 대한 표준편차).
식(4)의 센서가속도 모델은, 생체역학적 응용관점에서 ‘관성센서가 많은 시간 정적조건을 유지한다’는 가정을 바탕으로 한다. 따라서, 기계시스템에서 동적조건이 장시간 지속되는 경우 가정이 위배되어 모델링의 불확실성이 증가하고 오류를 발생시킬 수 있다.19 다음은 조인트 구속조건을 통해 불확실성이 제거된 센서가속도 모델을 칼만필터에 결합하는 과정이다.
바닥에 소켓부분이 고정된 볼조인트에 연결된 링크에 있어, 조인트중심에서 센서로의 J2S (Joint to Sensor) 위치벡터를 S좌표계 관점에서 표현한 벡터를 ps라 하면, 센서가속도 as는 식(9)와 같다.
| (9) |
이때, J2S벡터는 ps는 캘리브레이션을 통해 결정된 값으로 가정한다 (본 논문에서는 참고문헌16 이용). 식(9)에 ωs = sG − nG과 [nG×][nG×] = 0를 적용하여 정리하면, 식(10)과 같이 측정모델로 사용가능한 가속도단계의 조인트 구속조건식이 된다.19
| (10) |
여기서 구속조건 오차 εa는 식(11)과 같다.
| (11) |
식(11) 우변의 각항에 있어, 와 nG를 오른쪽에 위치시키기 위하여 −이를 통해 에 대한 공분산행렬 도출이 가능하게 하기 위하여 [[a×]b×] = [a×][b×] - [b×][a×]와 [a×]b = -[b×]a 등의 행렬 규칙이 적용되었다.19
식(10)과 식(11)을 통해, 조인트 구속조건을 통한 2차 측정모델이 식(12)와 같이 정리된다.
| (12) |
따라서, 식(6)을 통한 비구속 칼만필터에서의 보정값은, 식(12)를 통한 구속조건 결합형 칼만필터에서 추가적인 보정과정을 거치게 된다. 즉, 비구속된 보정 상태벡터 xk|k와 오차 공분산 행렬 Pk|k은, 각각 구속된 보정 상태벡터 cxk|k와 구속된 오차 공분산행렬 cPk|k로 각각 식(13)과 식(14)와 같이 갱신된다.
| (13) |
| (14) |
여기서, 구속 측정벡터 czk는 , 구속 칼만이득 cKk는 gPk|k (g2Pk|k + cBk)-1, cBk는 εc + nA의 공분산 행렬이다. 식(13)을 통해 구속된 상태벡터 가 구해지면, 본 논문의 추정대상인 수직변위 dzn는 식(15)와 같이 구해진다. 여기서 dzn는 dn의 Z방향 성분, 즉, .
| (15) |
여기서, 는 구속조건 결합을 통해 불확실성이 제거된 자세정보이므로, 이를 통해 구한 dzn 역시 불확실성이 제거된 고정확도의 수직변위이다.
3. 실험
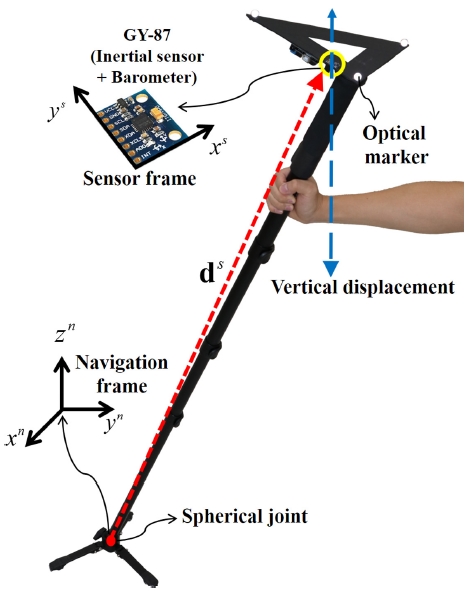
제안하는 수직변위 추정 기법의 성능을 검증하기 위하여 GY-87 모듈 시스템이 Arduino사 UNO보드에 연결되어 사용되었다. GY-87은(가속도계와 자이로스코프를 포함하는) 6축 InvenSense MPU-6050 관성센서와 3축 Honeywell HMC5883L 지자기센서, 그리고 Bosch BMP180 바로미터로 구성된다. 이 중 관성센서는 제안기법을 위해 사용되고, 바로미터는 비교기법을 위해 사용되며, 지자기센서는 사용되지 않았다. 또한, 성능비교를 위한 참조값을 얻기 위해 OptiTrack사의 Flex13 광학식 모션캡쳐 시스템을 사용하였다(마커위치 절대오차 < 0.1 mm). 샘플링 주기는 모든 시스템에서 100 Hz로 설정하였다.
관성센서가 부착된 삼각자에 세 개의 마커를 부착하므로써 마커 위치정보를 이용하여 Zs의 참조값을 구하고, 이를 통해 수직변위 참조값을 구한다. 하단에 볼조인트가 있는 링크에 관성센서 및 마커가 부착된 삼각자를 고정시키고, 볼조인트의 소켓부분을 바닥에 고정함으로써 식(9)가 성립하도록 하였다. 여기서 J2S벡터 ds는 [−9 −4 165]T cm였다(Fig. 1 참조).
링크를 손으로 붙잡고 임의로 움직여 가며 실험이 진행되었다. 본 논문의 주제는 수직변위 추정이므로 수직변위가 발생하도록(즉, n좌표계의 Z축방향) 움직였으나, 전후/좌우 방향으로도 임의의 움직임을 가하며 실험이 진행되었다. 조인트 구속조건 결합에 따른 추정 성능개선 효과를 확인하기 위하여 다음과 같이 일정크기 이상의 센서가속도가 존재하는 실험조건을 설정하였으며, 모두 65초간 진행되었다.
• Test 1: 참조값 ∥aS∥의 평균 6.8 m/s2
• Test 2: 참조값 ∥aS∥의 평균 10.7 m/s2
• Test 3: 참조값 ∥aS∥의 평균 12.5 m/s2
제안하는 수직변위 추정기법(Method A)과 아래의 비교기법들(Methods B - D)의 성능이, 참조값에 따른 RMSE (Root Mean Square Error)를 통해 비교 분석되었다.
• Method B: 참고문헌21의 자세칼만필터를 통해 추정한 경우. 즉, 조인트 구속조건 결합형이 아닌 비구속 자세칼만필터를 사용한 경우.
• Method C: 참고문헌14의 수직변위 추정 기법. 즉, 자세경유 변위추정기법이 아닌, 관성센서−바로미터 융합을 통해 추정한 경우.
• Method D: 바로미터만을 사용하여 수직변위를 추정한 경우.
4. 결과 및 고찰
Table 1은 각각의 경우에 대한 수직변위 추정 RMSE를, Fig. 2는 그에 해당하는 결과그래프를 보여준다. Fig. 2(c)는 Test 3 전구간(65초간)을 보여주고 있는 반면, Figs. 2(a)와 2(b)는 각각 Test 1과 Test 2 일부 구간 (5초간)만 보여주고 있는데, 이는 Test 1과 Test 2에서 Method A와 Method B의 차이를 보여주기 위함이다.
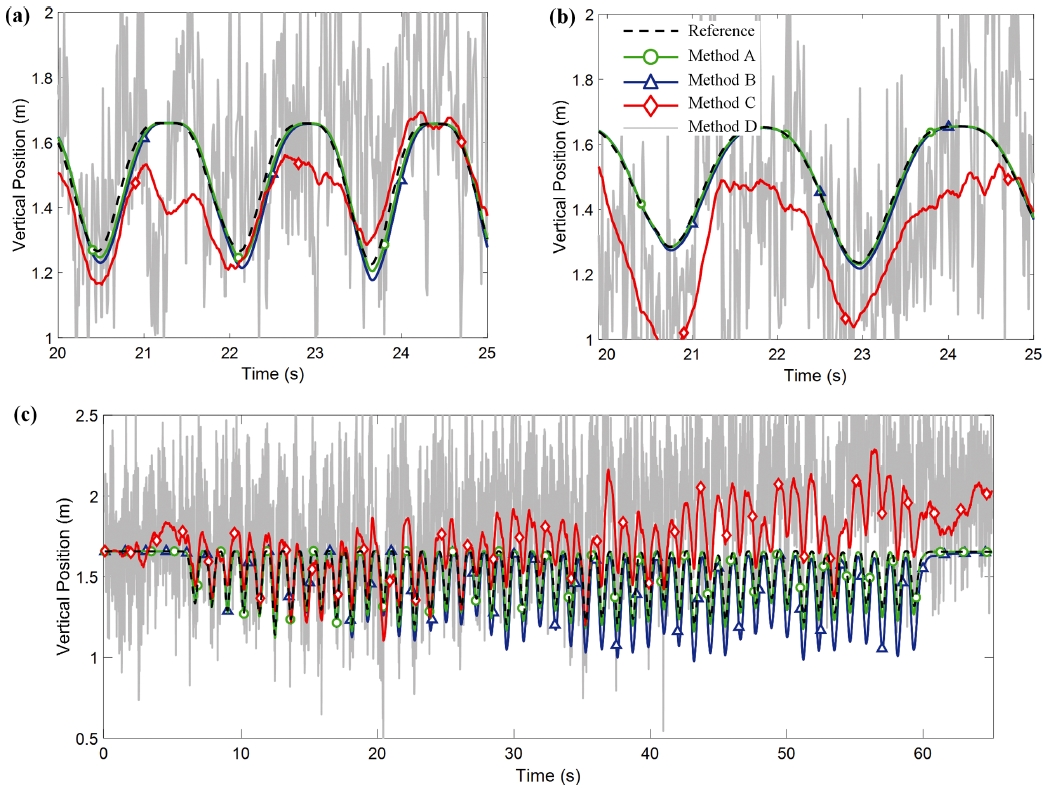
Estimation results of (a) Test 1, (b) Test 2, and (c) Test 3, from Method A (green line with circle markers), Method B (blue with triangles), Method C (red with diamonds), and Method D (gray)
모든 경우에서 자세경유 변위 추정기법인 Method A와 Method B가 관성센서-바로미터융합 기법인 Method C에 비해 월등히 우수한 추정성능을 보였다. Method C는 바로미터 신호인 Method D에 비해 평균 19.4 cm의 성능향상을 보였으나, 큰 오차를 보이는 바로미터 신호를 추종하는 모습을 보였다.
Method A와 Method B의 비교에 있어서, 모든 실험에서 제안방법인 Method A가 우세하였다. 하지만, 우세폭은 Test 1에서 0.35 cm, Test 2에서 0.94 cm, Test 3에서 7.65 cm로 상이하였으며, 이는 각 테스트의 센서가속도 조건과 관련성이 있다. 즉, Method B에서는 센서가속도가 증가할수록 가속도계신호 관련 참조벡터의 신뢰성이 훼손되고 자세 추정 성능이 감소하였고, 결과적으로 수직변위 추정 성능 저하되는 모습을 보였다(Table 2참조). 즉, 상대적으로 센서가속도가 크지 않은 Test 1에서는 Method B에 적용된 참고문헌21의 자세 칼만필터가 지니고 있는 가속도 보상 메커니즘으로 인해 Method A와 큰 차이가 없이 정확한 추정을 하고 있는 반면(Fig. 2(a) 참조), Test 3에서는 Fig. 2(c)에서 보이듯 동적조건의 시간이 경과함에 따라 오차가 증가하여, 동작이 멈추기 전까지 오차를 회복하지 못하는 모습이 관찰되었다. 이 경우 Table 2에서 보이듯 자세추정 오차 역시 Method A와 큰 폭의 차이를 보였다.
반면, 제안방법인 Method A에서는 비록 센서가속도가 증가하면서 추정오차가 다소 증가하는 모습을 보였으나, 모든 테스트에서 3 cm 이내의 우수한 성능을 보였다. 제안방법의 경우 조인트 구속조건을 결합하므로서 센서가속도에 의한 자세추정의 불확실성이 제거되었으므로, 이론적으로 센서가속도에 무관한 추정성능을 보여야 한다. 하지만, Table 1에서 보여지는 약간의 관련성은, 가속조건에서 링크의 미세한 휨, 관성센서 계측값의 부정확성, 고정조인트의 미세 움직임 등에 기인한 것으로 판단된다.
본 논문은 링크의 수직변위 추정을 주제로 하고 있다. 만약 수직변위가 아닌, 전후좌우를 포함한 3차원 변위 추정을 대상으로 한다면, 제안 기법이 사용하는 관성센서(자이로스코프 + 가속도계)에 더하여 지자기 센서가 필요하다. 지자기 센서를 추가하므로써 식(1)에서 Zs가 아닌 Rns 전체를 추정할 수 있고, 이를 통해 식(15)의 대신 대신 dn = Rns ds가 가능하다. 하지만, 가속도계가 센서가속도라고 하는 불확실성 요소를 갖는 것처럼, 지자기센서는 자기교란이라고 하는 불확실성 요소를 갖고 있다. 본 논문에서의 조인트 구속조건은 센서가속도라는 불확실성을 제거할 수 있지만, 자기교란과는 물리적 연관성이 없다. 따라서, 자세경유 3차원 변위추정에 있어, 전후좌우 방향의 정확도 향상을 위해서는 별도의 고려가 필요할 수 있다.
5. 결론
본 논문은 조인트로 연결된 링크에 대하여, 조인트 구속조건 결합형 관성센서기반 수직변위 추정 방법을 제안하고 있다. 자세경유 변위추정 방식을 통해 관성센서만을 이용하여 매우 높은 정확도로 수직변위를 추정하는 방법을 제안하고 있다. 특히, 조인트 구속조건을 결합하여 자세추정에 있어서의 불확실성을 제거하고 이를 통해 수직변위 추정의 정확도를 향상시켰다. 조인트 구속조건을 결합하지 않은 기존의 비구속형 자세결정 기법을 경유한 경우에 비하여, 모든 경우에서 우세한 수직변위 추정성능을 보였다. 특히, 센서가속도가 크고 오랫동안 지속된 경우에도 비구속형과 달리 성능이 유지되는 것을 확인하였다.
제안 방법은 다관절 머니퓰레이터나 말단효과장치의 고정 관성좌표계 관점에서의 절대 위치 추적 등을 위하여 적용될 수 있다. 본 논문을 통해 응용분야가 다소 제한적일 수는 있으나, 관성센서만으로 수직변위를 추정할 수 있는 예시를 보여주고 있다. 특히 구속조건 결합을 통해 추정성능의 향상을 확보할 수 있다는 점을 보여주고 있다.
Acknowledgments
이 논문은 2018년도 정부(교육부)의 재원으로 한국연구재단기초연구사업(No. 2018R1D1A1B07042791)의 지원을 받아 수행됨.
REFERENCES
-
Giansanti, D., Maccioni, G., and Macellari, V., “The Development and Test of a Device for the Reconstruction of 3-D Position and Orientation by Means of a Kinematic Sensor Assembly with Rate Gyroscopes and Accelerometers,” IEEE Transactions on Biomedical Engineering, Vol. 52, No. 7, pp. 1271-1277, 2005.
[https://doi.org/10.1109/TBME.2005.847404]

-
Lee, D.-H., Baek, S. Y., and Cho, N. G., “Six-Degree-of-Freedom Manipulator Displacement Measurement Using Stereo Vision,” Journal of the Korean Society for Precision Engineering, Vol. 32, No. 2, pp. 191-198, 2015.
[https://doi.org/10.7736/KSPE.2015.32.2.191]

-
Meng, X., Zhang, Z.-Q., Wu, J.-K., and Wong, W.-C., “Hierarchical Information Fusion for Global Displacement Estimation in Microsensor Motion Capture,” IEEE Transactions on Biomedical Engineering, Vol. 60, No. 7, pp. 2052-2063, 2013.
[https://doi.org/10.1109/TBME.2013.2248085]

-
Ruffaldi, E., Peppoloni, L., and Filippeschi, A., “Sensor Fusion for Complex Articulated Body Tracking Applied in Rowing,” Proc. of the Institution of Mechanical Engineers, Part P: Journal of Sports Engineering and Technology, Vol. 229, No. 2, pp. 92-102, 2015.
[https://doi.org/10.1177/1754337115583199]

-
Zhou, H. and Hu, H., “Reducing Drifts in the Inertial Measurements of Wrist and Elbow Positions,” IEEE Transactions on Instrumentation and Measurement, Vol. 59, No. 3, pp. 575-585, 2010.
[https://doi.org/10.1109/TIM.2009.2025065]

-
Schepers, H. M., Roetenberg, D., and Veltink, P. H., “Ambulatory Human Motion Tracking by Fusion of Inertial and Magnetic Sensing with Adaptive Actuation,” Medical & Biological Engineering & Computing, Vol. 48, No. 1, pp. 27-37, 2010.
[https://doi.org/10.1007/s11517-009-0562-9]

-
Filippeschi, A., Schmitz, N., Miezal, M., Bleser, G., Ruffaldi, E., et al., “Survey of Motion Tracking Methods Based on Inertial Sensors: A Focus on Upper Limb Human Motion,” Sensors, Vol. 17, No. 6, p. 1257, 2017.
[https://doi.org/10.3390/s17061257]

-
Lee, J. K. and Park, E. J., “Quasi Real-Time Gait Event Detection Using Shank-Attached Gyroscopes,” Medical & Biological Engineering & Computing, Vol. 49, No. 6, pp. 707-712, 2011.
[https://doi.org/10.1007/s11517-011-0736-0]

-
Lee, J. K. and Park, E. J., “Minimum-Order Kalman Filter with Vector Selector for Accurate Estimation of Human Body Orientation,” IEEE Transactions on Robotics, Vol. 25, No. 5, pp. 1196-1201, 2009.
[https://doi.org/10.1109/TRO.2009.2017146]

-
Waegli, A. and Skaloud, J., “Optimization of Two GPS/MEMS-IMU Integration Strategies with Application to Sports,” GPS Solutions, Vol. 13, No. 4, pp. 315-326, 2009.
[https://doi.org/10.1007/s10291-009-0124-5]

-
Sadi, F. and Klukas, R., “New Jump Trajectory Determination Method Using Low-Cost MEMS Sensor Fusion and Augmented Observations for GPS/INS Integration,” GPS Solutions, Vol. 17, No. 2, pp. 139-152, 2013.
[https://doi.org/10.1007/s10291-012-0267-7]

-
Sabatini, A. M. and Genovese, V., “A Sensor Fusion Method for Tracking Vertical Velocity and Height Based on Inertial and Barometric Altimeter Measurements,” Sensors, Vol. 14, No. 8, pp. 13324-13347, 2014.
[https://doi.org/10.3390/s140813324]

-
Zihajehzadeh, S., Lee, T. J., Lee, J.-K., Hoskinson, R., and Park, E. J., “Integration of MEMS Inertial and Pressure Sensors for Vertical Trajectory Determination,” IEEE Transactions Instrumentation and Measurement, Vol. 64, No. 3, pp. 804-814, 2015.
[https://doi.org/10.1109/TIM.2014.2359813]

-
Lee, J. K., “A Two-Step Kalman/Complementary Filter for Estimation of Vertical Position Using an IMU-Barometer System,” Journal of Sensor Science and Technology, Vol. 25, No. 3, pp. 202-207, 2016.
[https://doi.org/10.5369/JSST.2016.25.3.202]

-
Lim, J. and Kang, S., “Non-Inertial Sensor-Based Outdoor Localization for Practical Application of Guide Robots,” Journal of the Korean Society for Precision Engineering, Vol. 34, No. 5, pp. 315-321, 2017.
[https://doi.org/10.7736/KSPE.2017.34.5.315]

-
Seel, T., Schauer, T., and Raisch, J., “Joint Axis and Position Estimation from Inertial Measurement Data by Exploiting Kinematic Constraints,” Proc. of Control Applications International Conference, pp. 45-49, 2012.
[https://doi.org/10.1109/CCA.2012.6402423]

-
Olsson, F. and Halvorsen, K., “Experimental Evaluation of Joint Position Estimation Using Inertial Sensors,” Proc. Information Fusion 20th International Conference, pp. 1-8, 2017.
[https://doi.org/10.23919/ICIF.2017.8009669]

-
Vargas-Valencia, L. S., Elias, A., Rocon, E., Bastos-Filho, T., and Frizera, A., “An IMU-to-Body Alignment Method Applied to Human Gait Analysis,” Sensors, Vol. 16, No. 12, pp. 2090, 2016.
[https://doi.org/10.3390/s16122090]

-
Choi, M. and Lee, J., “Inertial Sensor-Based Attitude Estimation Combining a Kinematic Constraint for Elimination of Acceleration-Induced Inaccuracy,” Transactions of the Korean Society of Mechanical Engineers. A, Vol. 42, No. 3, pp. 263-269, 2018.
[https://doi.org/10.3795/KSME-A.2018.42.3.263]

-
Choi, M. J. and Lee, J. K., “IMU-Based Attitude Estimation Kalman Filter with Kinematic Constraint Projection,” Journal of Institute of Control, Robotics and Systems, Vol. 24, No. 2, pp. 175-181, 2018.
[https://doi.org/10.5302/J.ICROS.2018.17.0204]

-
Lee, J. K., Park, E. J., and Robinovitch, S. N., “Estimation of Attitude and External Acceleration Using Inertial Sensor Measurement During Various Dynamic Conditions,” IEEE Transactions on Instrumentation and Measurement, Vol. 61, No. 8, pp. 2262-2273, 2012.
[https://doi.org/10.1109/TIM.2012.2187245]


Professor in the Department of Mechanical Engineering, Hankyong National University. His research interests include inertial-sensing-based human motion tracking, biomechatronics, wearable sensor applications, and system dynamics and control.
E-mail: jklee@hknu.ac.kr