절삭력 비교를 통한 고경도 금형강 가공용 엔드밀 형상 설계에 관한 연구

1. 서론

자동차 산업, 금형 산업 등 여러 분야에서 내구성과 내마멸성이 우수한 고경도 재료를 사용하는 경우가 증가하고 있다. 열처리된 금형강은 우수한 기계적, 물리적 성질을 가지는 반면 고속 가공시 급격한 절삭 온도의 상승 및 극심한 공구 마멸이 발생하여 공구의 수명이 나쁘다는 단점이 있다.^1,2 이러한 고경도 금형강의 엔드밀 가공에 있어 가공 성능의 고능률화를 위해 적절한 공구의 형상 설계가 필요하다. 선행 연구를 살펴보면, Wang^3,4등은 코팅 종류 변화를 통해 엔드밀의 마모를 비교하였고, 절삭속도 변화에 따른 절삭력, 절삭온도, 응력분포를 비교하여 공구 성능을 평가하였다. Kim⁵등은 런아웃 타입에 따른 절삭력 분포를 분석하여 높낮이가 각각 달리 발생하는 원인을 이론적으로 규명하였으며 이론적으로 절삭력을 예측하고 실험을 통해 검증하였다. Jung⁶등은 엔드밀 가공 시 절삭력 예측을 위해 칩 하중을 계산하였고, Cho⁷ 등은 엔드밀의 절삭 날 형상이 가공면 거칠기에 미치는 영향을 분석하였다. Sheu⁸등은 절삭조건 및 Helix Angle에 따른 절삭력의 이론값과 실험값을 비교하였다. 현재까지의 연구를 살펴보면 HRC50 - 60 수준의 고경도 금형강에 대한 고속가공 성능 향상을 위해 절삭공구의 개발, 공구의 코팅, 가공조건 개선 등의 연구가 진행되었으나 엔드밀의 형상 최적화에 대한 연구 결과는 명확하지 않으며 특히 최적 설계에 있어 연구의 필요성이 있는 상황이다. 일반적으로 절삭가공 시 공구가 갖는 힘을 정량화하여 나타내는 절삭력이 실험에 많이 이용되고 있으며 공구마멸과 가공물의 상태를 파악하는 데 유용하게 이용되고 있다.⁹ 그러나 엔드밀 가공에서는 공구 회전마다 각 절삭 날의 진출입이 반복되는 복잡한 메커니즘을 가지고 있기 때문에 정확한 절삭력 예측이 어렵다. 절삭력을 분석함에 있어서 엔드밀의 1회전 절삭 시 발생하는 절삭력을 비교하거나 절삭구간의 최대값 및 평균값으로 비교해야 한다. 최근에는 이론적인 모델을 이용해 절삭력을 예측하고 검증하는 단계까지 이르렀으나 그 방법도 많은 제약이 존재한다.⁵

따라서 본 연구에서는 해석프로그램과 실험계획법을 이용하여 엔드밀 형상 설계 요소 중 절삭력 변화에 영향을 미치는 유의인자를 발굴하며, 절삭실험을 통해 유의인자의 변화에 따른 절삭력 특성을 분석함으로써 엔드밀의 형상 설계에 대한 기초자료 및 최적 형상을 제시하고자 한다.

2. 엔드밀 형상의 특성

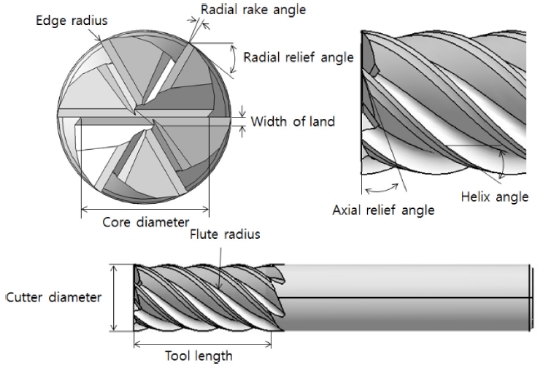
엔드밀의 형상은 Fig. 1과 같이 공구직경에 비하여 공구길이의 비가 큰 세장형 공구로서 다양한 곡면형상을 포함한 윤곽가공과 키웨이와 같은 미소량의 축방향의 가공과 반경방향의 가공을 동시에 수행하기 위한 형상적인 특징을 갖추고 있다.¹⁰

Fig. 1

Shape variables of end mill cutter

엔드밀은 다양한 형상을 가지고 있기 때문에 피삭재의 특성과 절삭조건 등을 고려하여 적합한 형상의 엔드밀을 선택해야 한다. 고경도 금형강 가공용 엔드밀의 경우 높은 경도로 인하여 절삭날의 마모 및 파손이 쉽게 일어나기 때문에 엔드밀의 형상 변화에 대하여 더욱 민감한 결과가 발생할 수 있다. 따라서 일반적인 엔드밀에 비하여 Number of Flutes가 많고, Core Diameter가 커서 강성이 매우 강하며, Rake Angle과 Relief Angle의 크기 및 절삭 날 끝의 형상은 인선강성을 고려하여 제작된다.

Rake Angle은 공구 경사각으로써 절삭 시 전단각을 결정하는 인자이다. 고경도 소재에 고속 가공을 할 경우 충격으로 인한 절삭 날의 크랙이나 치핑이 발생하기 쉽다. 이를 견디기 위하여 공구는 음의 경사각을 가지도록 제작된다. 경사각이 작을수록 충격에 강하지만 전단저항이 증가하여 절삭력과 진동 및 가공오차를 증가시킨다. Relief Angle은 공구 여유각으로 불리며 소재와 날이 접촉하는 면적을 결정하는 요소이다. 여유각의 감소는 공구 여유면과 피삭재의 마찰 면적을 증가시키고 절삭저항이 증가한다. 공구여유각의 증가는 여유면의 마찰 면적을 감소시켜 절삭저항을 감소시키지만 인선부의 안정성이 악화된다.

Edge Radius는 공구 날 끝의 형상을 결정하며 절삭성을 영향을 미치는 요소이다. Edge Radius가 작을수록 절삭성은 커지지만 파손 및 치핑이 일어날 가능성이 높다. 클 경우 공구 날 끝의 강성이 증가하여 파손의 확률이 낮아지지만 소재와의 접촉면적이 커지므로 공구마모의 확률은 더 커지게 된다. Flute Radius는 포켓홈 사이의 곡면을 나타내고 Width of Land는 절삭 날의 폭을 나타낸다. Helix Angle은 공구의 비틀림 정도를 결정하는 인자로 크기가 커지면 절삭 날이 더 많은 시간 동안 절삭에 참여함으로써 긴 칩을 배출하게 되고 그 만큼 절삭 날에 수직인 방향의 절삭력을 감소시키는 역할을 하게 된다. 주로 15^o 근방의 작은 Helix Angle은 키, 홈 가공 등에 쓰이고, 고경도재를 가공할 경우 50^o 근방의 큰 Helix Angle이 사용된다. Number of Flutes는 엔드밀의 칩포켓의 크기를 결정하는 인자이다. 칩 배출이 문제시 되는 저속의 홈 가공 등에는 칩 포켓의 크기를 증가시키기 위해서 적은 날수의 공구를 사용하고 칩 배출보다는 공구의 강성이 중요한 고경재 가공의 경우에는 날이 많은 공구로 가공하게 된다.¹¹

3. 엔드밀 형상의 유의인자 선정

3.1 해석프로그램의 적용 및 신뢰성 확인

엔드밀 형상을 변화시키고자 할 때 많은 형상 변수들이 존재하기 때문에 모든 형상에 대해서 실험을 하는 것은 비용적, 시간적 어려움이 따른다. 따라서 엔드밀 가공에 영향을 미치는 형상의 유의인자 선정을 위하여 해석적인 방법을 적용하였으며 적용한 해석프로그램은 Third Wave System社의 AdvantEdge이다.

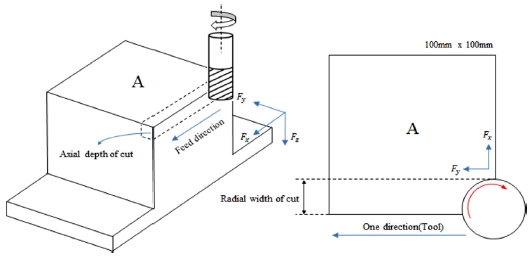
해석의 절삭 모델은 Fig. 2와 같이 플랫형 6날 Ø10 엔드밀의 하향절삭 및 건식절삭을 적용하였다. 해석에서 사용한 엔드밀의 형상은 Table 1과 같이 나타내었으며 Tool Length의 길이는 해석 시간을 고려하여 절삭에 참여하지 않는 길이만큼 축소를 하여 적용하였다. 해석 절삭 조건은 Table 2와 같이 M 社의 추천 절삭조건을 기준으로 하고 Axial Depth of Cut만 최대값으로 설정하였다. 공구의 재료는 Carbide이며, 피삭재는 SKD11(HRC60)을 사용하였다.

Fig. 2

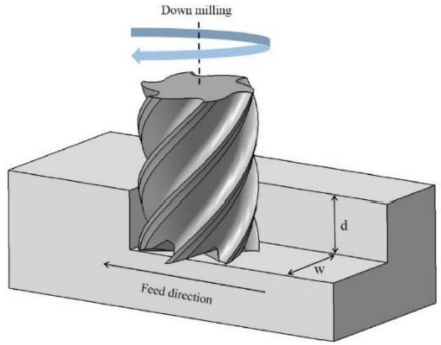
Analytical model in simulation software (AdvantEdge); d is axial depth of cut, w is radial width and down milling is applied

Table 1

End mill shape value used for analysis

Table 2

Cutting conditions

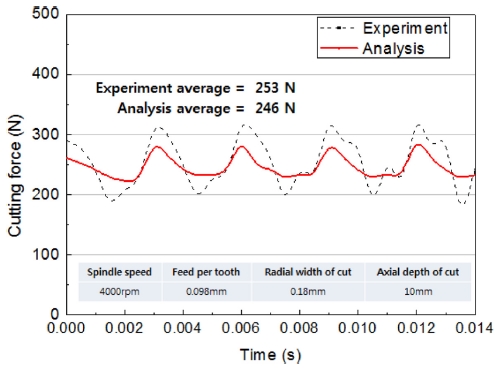
절삭력 예측을 위해 해석프로그램을 사용하는 것은 결과값에 대한 신뢰성 확인이 필수적이다. 신뢰성 확인을 위해 해석에 사용된 절삭조건과 동일한 절삭조건으로 실험을 진행하였으며, 실험에 사용된 엔드밀은 M 社의 고경도 강 가공용 엔드밀의 형상과 유사하게 제작하여 사용하였다. 실험 장비는 화천기계의 SIRIUS-2이고, 절삭력 측정을 위해 Kistler社의 Multi Component Dynamometer 9257B를 사용하였다.

Fig. 3과 같이 엔드밀의 약 1회전에 대한 실험 결과값과 해석 결과값을 비교하면, 공구 날의 절삭시간은 실제 절삭시간과 일치하고 날의 진출입 시 절삭력의 증감이 명확하며 절삭 날의 진입 후 접촉면적이 최대가 될 때 절삭력이 최대가 됨을 확인하였다. 실험 값의 진폭이 해석 값의 진폭보다 크지만 평균 절삭력을 비교했을 때 실험 평균값은 253 N이고 해석 평균값은 246 N으로 유사한 값을 가진다. 절대값의 차이는 있지만 절삭력 파형에서 증감의 경향이 유사하고 평균 절삭력의 차이가 작기 때문에 평균 절삭력을 이용하여 유의인자 선정을 하는 것에 대한 신뢰성이 있다고 판단하였다.

Fig. 3

Comparison of cutting force between experimental and analytical results

3.2 실험계획법을 이용한 유의인자 선정

실험계획법은 일정한 조건을 정하여 최소의 실험으로 신뢰성 높은 정보를 얻는 방법이다.¹² 본 연구에서는 엔드밀 형상 인자의 최적화를 위해 체계적인 방법인 다구찌 실험계획법을 적용하여 해석을 실시하고 ANOVA (분산분석)를 통해 유의인자를 선정하였다. ANOVA는 데이터 전체의 분산 중 몇 개의 요인 효과에 대응하는 분산과 나머지 오차 분산으로 나누어 검정이나 추정을 실시하는 것으로 유의 수준을 0.05로 설정하여 유의수준과 확률 P-Value를 비교하여 유의인자를 선정한다.¹³ 앞서 엔드밀 형상에 대해 8가지 인자를 선정하였고 각 인자에 대해 Table 3과 같이 2수준으로 정하여 직교배열표에 따라 총 12번의 해석을 진행하였다.

Table 3

Selection of control factors and determination of each levels

Table 4는 통계 소프트웨어 Minitab을 이용한 ANOVA의 결과이며, 1st Pooling의 분석 결과로는 5개 인자의 값이 확인되었다. Helix Angle과 Flute Radius는 0.238, 0.246으로 낮은 유의확률을 나타내지만 Radial Relief Angle, Axial Relief Angle, Edge Radius의 P-Value 값은 0.05이하이므로 절삭력에 대해 유효한 인자임을 확인하였다. Edge Radius는 1st Pooling에서 0.001, 2nd Pooling에서 0의 P-Value를 가지므로 유의인자 중 유의도가 1순위임을 알 수 있다.

Table 4

Results of ANOVA for effective factors on cutting force

4. 엔드밀 형상과 절삭력 관계

유의인자에 대해 자세히 분석하기 위해 Table 5와 같이 기존 형상에서 최소로 변화 시킬 수 있는 3수준으로 변화시켰다.

Table 5

Setting range of effective factors for detailed analysis

Fig. 4와 같이 1 Pass당 100 mm의 단속절삭으로 4 m를 가공하였으며 각 Pass에 대한 절삭력 추출구간은 절삭 날이 완전히 절입된 시점부터 공구의 중심축이 소재의 끝과 일치하는 시점까지이다. 각 형상에 대하여 정량적 비교를 위해 절삭력의 평균값을 취하였으며, 절삭력 파형의 변화를 확인하기 위해 100 mm(1 Pass) 가공과 4000 mm(40 Pass) 가공의 절삭력 편차를 비교하였다. 절삭력의 진폭은 절삭시간에 따른 각 절삭 날의 절삭력 분포와 안정성을 확인 할 수 있고 최대값을 정의할 수 있다. 절삭력의 편차 및 진폭의 비교를 통해 절삭 날의 마모와 파손을 예상할 수 있다.

Fig. 4

Schematic diagram of end mill experiment

4.1 Edge Radius에 따른 절삭력 변화

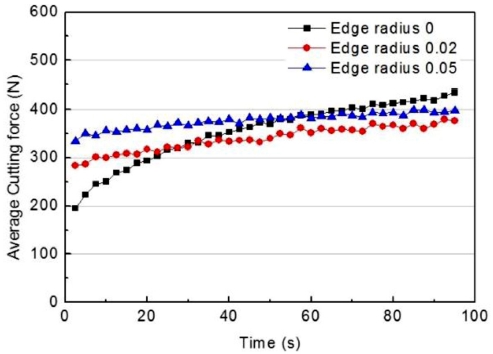
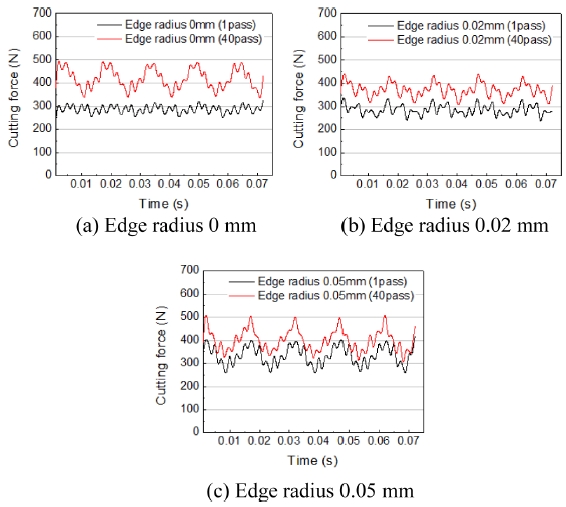
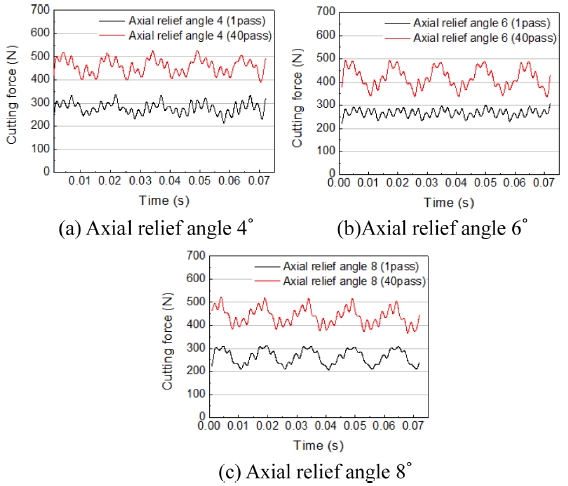
Fig. 5는 Edge Radius를 변화시켜 Table 2의 절삭 조건으로 실험한 결과이다. Edge Radius의 크기가 클수록 초기 평균 절삭력이 크지만 종료 시점에서는 Edge Radius 0 mm가 최대값이며 Edge Radius 0.02 mm 보다 14%, Edge Radius 0.05 mm보다 9% 더 크다. Edge Radius 0.02 mm, 0.05 mm의 절삭력 증가율은 전체 절삭 구간에 대하여 비슷한 경향을 보였지만 Edge Radius 0 mm 경우 초기에 큰 증가율을 가지며 급격하게 절삭력이 상승하였다. 평균 절삭력의 급격한 상승은 날 끝에 미세 치핑으로 인해 발생하였으며 Edge Radius 0 mm의 절삭 날이 예리하고 강성이 작기 때문에 절삭 날이 진입할 때의 충격으로 인해 발생했다고 판단하였다. Figs. 6(a)에서 6(c)는 각 형상에 대해 1 Pass와 40 Pass에서 각각 5회전 절삭 후의 파형을 나타내었다. Fig. 6(a)에서 Edge Radius 0 mm의 40 Pass 평균 절삭력은 1 Pass에 비해 57% 증가하였고 편차는 24 N 증가하였다. Fig. 6(b)에서 Edge Radius 0.02 mm의 40 Pass 평균 절삭력은 30% 증가하였고 편차는 14% 증가하였다. Fig. 6(c)에서 Edge Radius 0.05 mm의 40 Pass 평균 절삭력은 19% 증가하였고 편차는 5% 증가하였다.

Fig. 5

Experiment results of cutting force according to edge radius

Fig. 6

Cutting force waveforms according to edge radius

절삭력 파형의 결과로는 Edge Radius가 클수록 1 Pass의 절삭력 편차의 절대값이 크지만 1 Pass와 40 Pass의 절삭력 편차 차이는 작아져 절삭력 파형의 변화가 작다. Edge Radius 0 mm만 다른 수준들에 비해 편차의 차이가 크고 파형의 형태도 크게 바뀌었다. Edge Radius 0 mm에서 절삭력 특이점을 보였듯이 공구마모와 표면 거칠기가 크게 상승한 것을 확인하였다. Edge Radius 0.02 mm를 기준으로 0 mm의 마모량은 최대 15 μm, 표면 거칠기는 0.1 μm의 차이를 보였으며 Edge Radius 0.05 mm의 공구마모와 표면 거칠기도 상승한 결과를 보였다.

4.3 Radial Relief Angle에 따른 절삭력 변화

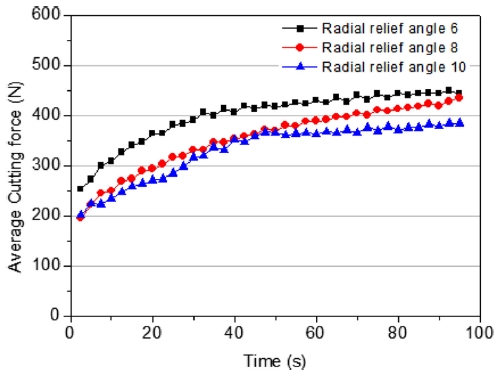
Fig. 7은 Radial Relief Angle 변화에 따른 실험결과이며, Radial Relief Angle이 클수록 절삭력의 크기가 작은 것을 확인할 수 있고 Radial Relief Angle 10^o은 전체 구간에서 절삭력이 최소이다. 그러나 Radial Relief Angle이 클수록 절삭력은 작지만 실제 절삭의 접촉 면적이 증가하기 때문에 공구의 마모량이 커질 가능성이 있다.¹⁴ 절삭력을 통해 충분히 예측을 할 수 있을 것이라고 판단되지만 Radial Relief Angle의 형상에 대해 더 정밀한 설계를 할 경우 절삭력 뿐만 아니라 공구 마모량도 확인해야 한다.

Fig. 7

Experiment results of cutting force according to radial relief angle

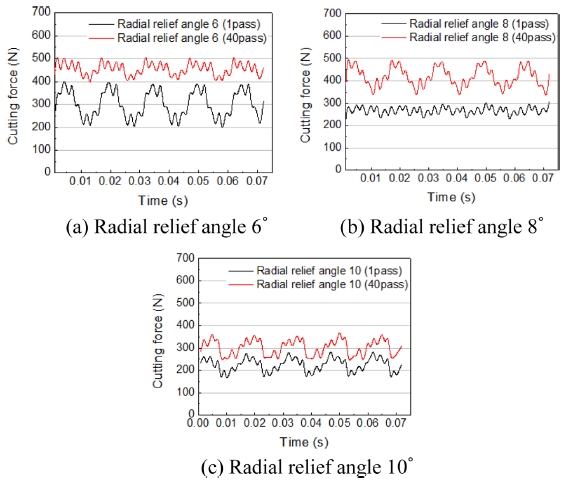
Figs. 8(a)에서 8(c)는 Radial Relief Angle의 형상에 따른 1 Pass와 40 Pass 절삭력 파형을 나타내었다. Radial Relief Angle이 커질수록 편차의 차이는 줄어들고 Radial Relief Angle 10^o는 평균 절삭력이 35% 증가하고 편차 변화는 6% 증가하여 3개의 형상중 최소값을 가진다. 파형의 형태 또한 유사하였다. Radial Relief Angle 6^o에서 1 Pass의 편차가 높아 불안정한 절삭의 형태를 나타냈지만 40 Pass에서는 상대적으로 크게 낮아져 절삭 날의 균형적인 절삭력 분포로 판단할 수 있지만 40 Pass의 평균 절삭력은 455 N으로 51% 증가하여 3개의 형상 중 최대값이다. Radial Relief Angle 10^o에서 마모량이 최대이지만 6^o와 8^o의 마모량과 비교를 하면 3 μm 이하이므로 본 연구에서 선정된 Radial Relief Angle에 따른 공구마모의 차이는 없으며 표면 거칠기도 차이가 없는 것으로 확인하였다. 따라서 평균 절삭력과 편차의 결과를 비교하면 Radial Relief Angle 10^o의 형상이 가장 우수하다.

Fig. 8

Cutting force waveforms according to radial relief angle

4.4 Axial Relief Angle에 따른 절삭력 변화

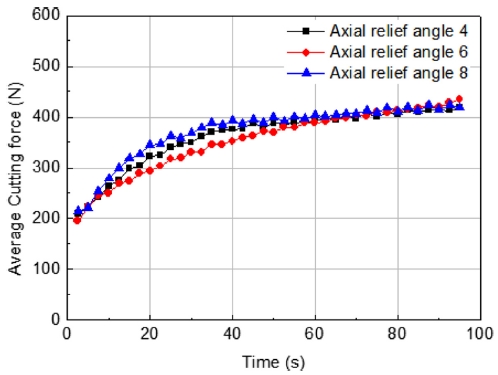
Axial Relief Angle의 절삭력 실험결과는 Fig. 9와 같으며 절삭 초기 구간에서는 형상에 따라 평균 절삭력과 증가율의 차이가 있지만 종료시점에서는 3개의 형상 모두 비슷한 평균 절삭력을 나타내고 있다. Axial Relief Angle 6^o는 초기 구간에서 절삭력과 증가율이 최소이고 종료 시점에서는 절삭력이 435 N으로 최대이다. Figs. 10(a)와 10(c) 에서 1 Pass의 절삭력 파형을 비교하면 Axial Relief Angle 4^o에서 평균 절삭력이 최대이며 절삭력 편차가 다른 수준들에 비해 상대적으로 크다. 그러나 1 Pass와 40 Pass의 편차 차이를 비교했을 경우에는 증가율이 4%로 가장 낮은 것을 확인하였다. Axial Relief Angle 4^o의 파형은 다른 수준들에 비해 1 Pass와 40 Pass에서 유사하여 마모가 상대적으로 작게 발생하였다고 분석할 수 있다. Axial Relief Angle 6^o의 파형에서 절삭력 증가율이 57%이고 40 Pass에서 평균 절삭력이 가장 낮았다. Axial Relief Angle에 따른 평균 절삭력의 변화에 대해 명확한 경향이 없지만 공구 마모는Axial Relief Angle 8^o에서 최대이며 상대적으로 큰 차이를 보인다. 표면 거칠기는 4^o에서 최대값이지만 공구마모의 영향이 더 크다고 판단이 되며 Axial Relief Angle 4^o를 형상 설계에 적용하면 절삭력 편차에 대해 개선이 될 것이라고 판단된다.

Fig. 9

Experiment results of cutting force according to axial relief angle

Fig. 10

Cutting force waveforms according to axial relief angle

5. 결론

본 연구에서는 고경도 금형강의 절삭 가공 시 엔드밀 형상 변화에 따른 절삭력 특성을 분석하였으며, 절삭력 관점에서 다음과 같은 결론을 도출하였다.

1. 해석프로그램으로 계산한 절삭력은 실험을 통해 측정한 절삭력 값과 비교하였을 때 형상에 따른 절삭력 크기의 경향은 잘 일치함을 보였다.

2. Edge Radius가 감소하면 날 끝의 접촉면적이 작아져 절삭력이 감소하지만 강성이 작아지기 때문에 파손의 가능성이 크다. 증가할 경우 편차 차이는 감소하지만 절삭력이 증가하여 마모율이 커진다.

3. Radial Relief Angle의 증가는 여유면의 접촉면적의 감소로 절삭력을 감소시키고 편차와 파형의 변화가 감소한다.

4. Axial Relief Angle의 변화에 따른 절삭 종료 시점의 평균 절삭력은 차이가 크지 않지만 Axial Relief Angle 4^o에서 절삭력 편차의 차이가 가장 작다.

5. Radial Relief Angle 10^o, Edge Radius 0.02 mm, Axial Relief Angle 4^o를 적용하면 엔드밀 절삭 시 개선된 절삭력 특성을 얻을 수 있을 것이라고 기대된다.

Acknowledgments

“본 연구는 과학기술정보통신부 및 정보통신기술진흥센터의 Grand ICT 연구센터지원사업의 연구결과로 수행되었음” (IITP-2018-2016-0-00318).

REFERENCES

• Kim, H., Yoon, S., and Kim, T., “A Study on the Cutting Characteristics in the Machining of SKD11 by Face Milling,” Proc. of the KSPE Autumn Conference, Vol. 95, pp. 73-78, 1995.
• Kim, S. W., Lee, D. W., and Kim, J. S., “Evaluation of Machining Characteristics for Difficulty-to-Cut Material (Heat-Resistant Alloy),” Proc. of KSPE Autumn Conference, pp. 135-138, 1997.
• Wang, C., Xie, Y., Qin, Z., Lin, H., Yuan, Y., et al., “Wear and Breakage of TiAlN-and TiSiN-Coated Carbide Tools During High-Speed Milling of Hardened Steel,” Wear, Vols. 336-337, pp. 29-42, 2015. [https://doi.org/10.1016/j.wear.2015.04.018]
• Wang, C., Ding, F., Tang, D., Zheng, L., Li, S., et al., “Modeling and Simulation of the High-Speed Milling of Hardened Steel SKD11 (62 HRC) Based on SHPB Technology,” International Journal of Machine Tools and Manufacture, Vol. 108, pp. 13-26, 2016. [https://doi.org/10.1016/j.ijmachtools.2016.05.005]
• Kim, J.-D., Yoon, M.-C., and Kim, B.-T., “An Analysis of the Cutting Force for Peripheral End-Milling Considering Run-Out,” Journal of the Korean Society of Manufacturing Process Engineers, Vol. 11, No. 4, pp. 7-12, 2012.
• Jung, Y.-H., Kim, J.-S., and Hwang, S.-M., “Chip Load Prediction in Ball-End Milling,” Journal of Materials Processing Technology, Vol. 111, Nos. 1-3, pp. 250-255, 2001. [https://doi.org/10.1016/S0924-0136(01)00528-3]
• Cho, C. Y. and Ryu, S. H., “Analysis of Cutting Edge Geometry Effect on Surface Roughness in Ball-End Milling Using the Taguchi Method,” Journal of The Korean Society of Manufacturing Technology Engineers, Vol. 23, No. 6, pp. 569-575, 2014. [https://doi.org/10.7735/ksmte.2014.23.6.569]
• Sheu, J. J., Xu, D. M., and Liu, C. W., “Cutting Force and Tool Deflection Predictions for High Speed Machining of Hard to Cut Material,” Advanced Materials Research, Vols. 154-155, pp. 1157-1164, 2011. [https://doi.org/10.4028/www.scientific.net/AMR.154-155.1157]
• Kim, J., Kim, K., Kang, M., Kim, J., and Kim, K., “Monitoring and Machinability Evaluation in High-Speed Machining of High Hardness Steel (SKD11),” Proc. of KSPE Spring Conference, pp. 987-990, 2000.
• Ko, SL., “Development of Software for Determining Grinding Wheel Geometry and Setting Condition in End Mill Manufacturing,” Journal of the Korean Society for Precision Engineering, Vol. 13, No. 8, pp. 164-174, 1996.
• Kang, M.-C., Kim, J.-S., Lee, D.-W., Kim, K.-H., and Ha, D.-G., “Machinability Evaluation According to Variation of Endmill Shape for High Speed Machining,” Journal of the Korean Society for Precision Engineering, Vol. 19, No. 5, pp. 133-138, 2002.
• Bae, H. and Park, H., “Analysis of Working Factors for Improvement of Surface Roughness on High Speed End-Milling,” Journal of the Korean Society of Precision Engineering, Vol. 21, No. 6, pp. 52-59, 2004.
• Lee, S.-J., Choi, S.-H., Cho, Y.-T., Jung, Y.-G., and Jung, J.-Y., “Selection of the Efficient Superfinishing Condition on an Anodized Al7075 Surface in Experimental Design,” Journal of the Korean Society of Precision Engineering, Vol. 33, No. 12, pp. 993-998, 2016. [https://doi.org/10.7736/KSPE.2016.33.12.993]
• Park, J. and Ko, S., “Machining Characteristics in High Speed Endmill Operation Considering Clearance Angle,” Journal of the Korean Society of Precision Engineering, Vol. 21, No. 8, pp. 43-49, 2004.