CMP 연마패드의 동적 점탄성에 관한 유한요소해석

1. 서론

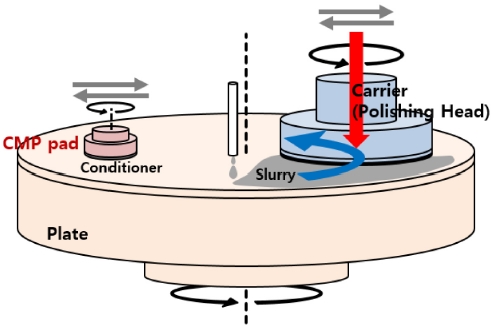
CMP (Chemical Mechanical Planarization) 공정은 반도체 공정에서 다층구조형성을 위한 기판의 평탄화 기술로써, 연마 슬러리(Polishing Slurry)의 화학적 성분에 의한 화학 반응 하에서의 웨이퍼 표면, 연마패드, 연마 슬러리 내 연마 입자간 마찰에 의해 재료 제거가 발생한다.¹ CMP 공정에서 연마패드는 중요한 소모품 중 하나로 하부의 정반에 부착되어 회전운동을 한다. 그와 동시에 웨이퍼가 부착된 상단의 연마헤드가 회전하고, 이 때 발생하는 일정한 상대속도와 가해지는 압력에 의해 연마가 진행된다. 여기서 재료제거율은 웨이퍼와 연마헤드 간의 상대속도와 압력의 곱에 비례하는 프레스톤 방정식(Preston Equation)에 지배적인 영향을 받는다. CMP 공정에서 웨이퍼 내 균일한 재료 제거를 위해서는 접촉 면 전체가 균일한 압력을 받도록 하는 것이 이상적이나, 연마패드의 동적 특성의 영향으로 인해 실제로는 웨이퍼와 패드의 접촉 영역에서의 불균일한 압력분포가 발생하고 특히 웨이퍼 가장자리 영역에서의 비정상적인 재료제거율이 발생한다.²

선행 연구자들은 이러한 웨이퍼의 압력 불균형 문제를 개선하기 위해 유한요소해석을 통한 공정 조건의 최적화를 위한 연구를 진행하였다.³ 대부분의 연구는 정적 유한요소해석을 통한 웨이퍼 압력분포의 최적화 측면에서 연구를 진행하였으며, 실제 패드에서 나타나는 동적 특성을 고려하지 않았다. 기존 연구에서 유한요소해석을 위한 물성의 설정을 위해 여러 방법을 통해 얻어진 DMA (Dynamic Material Analysis)를 이용하여 연마패드의 저장탄성계수와 손실탄성계수를 측정하거나,^4,5 인장실험 및 압축실험을 통해 연마패드의 탄성계수를 측정하는 방법을 사용하였다.^6,7 그러나 이러한 방법에 의한 재료 물성 정의 시, 유한요소해석에서의 연마패드의 하중에 대한 실제 변형률과 시간에 따른 동적 거동을 나타내기 힘들다. CMP 공정에서 대부분의 연마 균일도 문제는 패드의 동적 점탄성 특성에 의한 것으로 알려져 있다. 실제 CMP의 환경은 슬러리와 마찰입자가 존재하는 습식 상태에서의 동적 마찰 환경이나, 본 실험에서는 이외의 인자들을 무시하고 건식환경에서의 패드의 동적 특성만을 확인하였다. 이러한 동적 특성을 고려한 유한요소해석을 통해서 추후 CMP 공정을 명확히 이해할 수 있다.

본 연구에서는 점탄성 측정기를 이용하여 연마패드의 주기적인 압축-회복 실험을 실시하고 추출된 변형률 곡선을 분석하여 점탄성 파라미터를 얻었다. 연마패드의 압축-회복 실험에서의 변형과 유한요소해석에서 나타나는 변형을 서로 비교하여 이를 통해 연마패드의 동적 점탄성 물성을 정의하는 방법을 제안하였다.

2. 점탄성

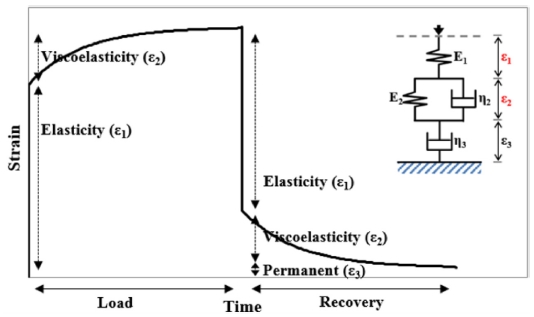
폼(Form) 또는 펠트(Felt) 구조의 고분자 재료는 그 구조로 인하여 하중에 의해 순간적으로 변형하는 탄성거동과 시간에 따라 서서히 변형하는 점성거동이 동시에 나타난다. 이러한 재료의 성질을 점탄성(Viscoelasticity)이라고 하는데 이는 시간 의존적인 동적 재료물성이다. CMP 연마패드 또한 다공성의 폴리우레탄 또는 폴리우레탄 함침 펠트로 만들어지므로 그와 유사한 점탄성 거동이 나타난다. 이러한 CMP 연마패드의 점탄성은 4-Element Burger’s Model을 통해 표현할 수 있다. 4-Element Burger’s Model은 하중에 대해 즉시 변형하며 즉시 회복하는 탄성 거동을 나타내는 스프링(Spring) 요소와 시간에 따라 서서히 변형하고 서서히 회복하는 점탄성 거동을 나타내는 포크트(Voigt) 요소, 하중에 제거된 후에도 회복되지 않는 영구적인 변형을 나타내는 대쉬폿(Dashpot) 요소를 가지고 있다. 이 모델의 구성과 하중에 대한 거동의 개략도는 Fig. 2에 나타나 있다.

Fig. 1

Schematics of viscoelasticity measurement system in FEA

Fig. 2

Viscoelastic behavior of CMP polishing pad schematic

3. 실험 방법

3.1 점탄성 측정 실험

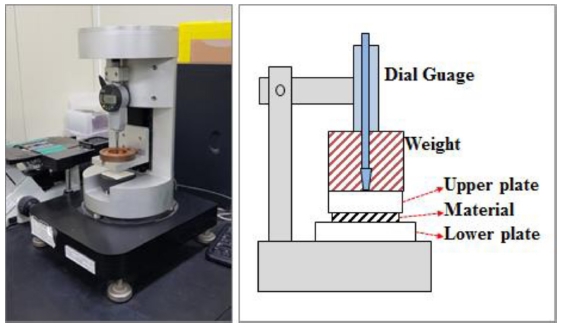
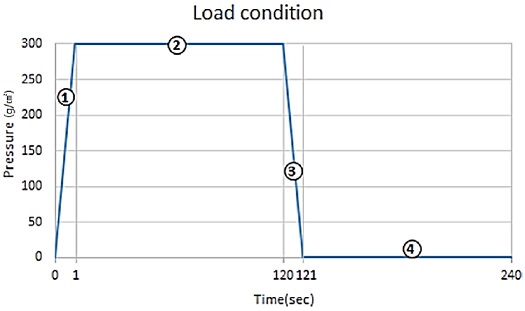
CMP 연마패드의 점탄성 거동을 측정하기 위하여 점탄성 측정기(Viscoelasticity Measurement System; G&P Technology)를 사용하였다. Fig. 3에 나타나 있는 점탄성 측정기는 측정 시편에 주기적으로 일정한 하중을 가하여 시편의 반복적인 압축 및 회복에 의해 발생하는 두께 변화를 측정한다. 이 때 발생하는 연마패드의 두께 변형량을 1 μm의 측정 최소단위를 갖는 다이얼 게이지를 이용하여 실시간으로 측정하였다. 연마패드는 상용패드인 SUBA 400, SUBA 600, SUBA 800 패드를 사용하였다. 본 실험에서는 14.4 N(300 g/cm²)의 하중조건을 부여하였고 1 주기 당 압축 120초, 회복 120 초의 시간을 두고 15회 반복하였다.

Fig. 3

Viscoelasticity measurement system

3.2 유한요소해석

3.2.1 해석 모델 제작

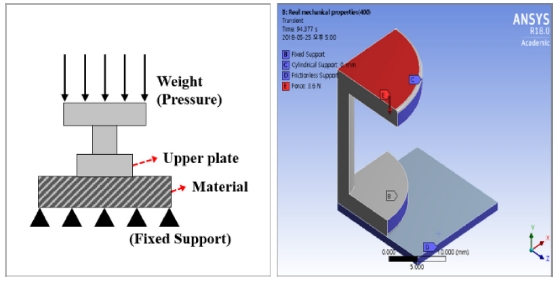
유한요소해석에서의 동적 물성에 의한 연마패드의 점탄성 거동을 확인하기 위해 해석 모델을 제작하였다. Fig. 4에 나타난 것과 같이 점탄성 측정기와 동일한 치수를 갖는 3D 모델을 제작하였다. 연마패드의 하부에는 고정 구속을 부여하였으며 가압 영역은 하중조건으로 대체하였다. 또한 해석시간을 줄이기 위하여 전체 모델의 1/4을 모델링 하고 단면에 대칭 조건을 부여하였다. 해석을 위해 상용 소프트웨어인 ANSYS Workbench 18.0을 사용하였으며 시간에 따른 변형을 나타내기 위하여 프로그램 내 동적 구조해석 방법인 과도 구조 해석(Transient Structure Analysis)을 이용하였다.

Fig. 4

Schematics of viscoelasticity measurement system in FEA

Fig. 5

Load condition for finite element analysis model

3.2.2 재료 물성 정의

유한요소해석을 위해 모델의 부속품인 상부 플레이트와 연마패드의 재료물성을 정의하였다. 상부 플레이트의 물성에는 알려져 있는 알루미늄의 물성치를 부여하였다. 연마패드의 물성을 정의하기 위해 ANSYS Workbench의 Engineering Data에서 Isotropic Elasticity와 Prony Volumetric Relaxation을 이용하였다. Isotropic Elasticity는 하중에 대한 연마패드의 등방성 탄성변형을 나타내기 위한 재료물성 정의 방법이며, Prony Volumetric Relaxation은 응력이완으로 인한 탄성계수의 감소를 감소율과 완화시간을 변수로 갖는 지수함수 형태로 점탄성을 나타내기 위한 재료물성 정의 방법이다. 연마패드의 물성은 일반적으로 알려져 있지 않으므로 본 연구에서는 실험을 통해 측정된 연마패드의 점탄성 데이터를 바탕으로 이를 정의하였다.

3.2.3 하중 조건

유한요소해석에서의 시간에 따른 연마패드의 점탄성 변형을 확인하기 위해 점탄성 측정 실험과 동일한 하중조건을 부여하였다. Fig. 4와 같이 전체 과정을 각각 Loading, Load Creep, Unloading, Recovery Creep의 4개의 단계로 나누어 해석을 진행하였다. 0 - 1 초의 Loading 단계에서 14.4 N(300 g/cm²)의 하중을 부여하였고 1 - 120 초의 Load Creep 단계에서 앞서 부여된 하중을 유지하였다. 120 - 121 초의 Unloading 단계에서 하중을 제거하고 121 - 240 초의 Recovery Creep 단계에서 하중이 제거된 상태를 유지하였다. 이를 통해 하중에 대한 연마패드의 실제 거동과 시뮬레이션에서의 거동을 비교하였다.

4. 실험결과 및 토의

4.1 점탄성 측정 결과

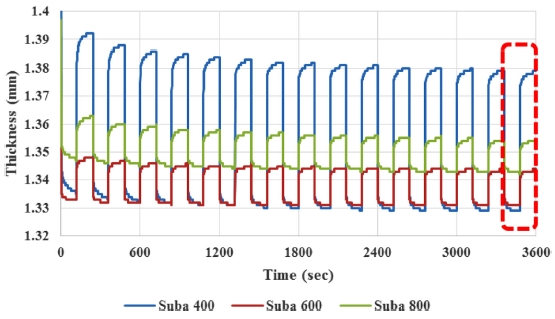
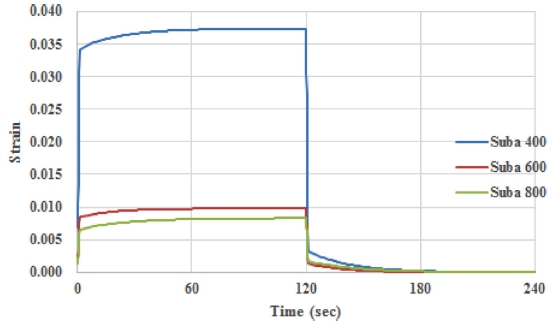
Fig. 6은 점탄성 측정기의 반복 하중에 의해 발생하는 연마패드의 두께 변화를 나타낸 것이다. 연마패드의 두께는 초기 하중에 대해 큰 변화를 보이는데 실험이 진행됨에 따라 압축과 회복이 반복되면서 패드 내부 구조 또는 표면의 돌기 구조의 영구변형으로 인해 변형률의 폭이 일정하게 수렴하는 것을 확인할 수 있다. 본 실험에서는 반복적 압축/회복의 15 번 째 주기에서 나타나는 연마패드의 두께 변형 데이터에서 시간에 따라 변하는 초기 두께에 대한 변형률 데이터를 얻었다. 이 데이터를 하중에 대한 탄성 변형과 점탄성 변형을 표현할 수 있는 식(1)에 피팅하면 Fig. 7과 같은 그래프를 얻을 수 있으며 탄성 변형률 ε₁과 점탄성 변형률 ε₂, 지연시간(Relaxation Time, τ)을 얻을 수 있다. 또한 식(2), (3)에 따라 탄성 변형률과 점탄성 변형률을 이용해 각각 1차 탄성계수(Primary Elastic Modulus, E₁)와 2차 탄성계수(Secondary Elastic Modulus, E₂)를 얻을 수 있다. 위 과정을 통해 얻어진 각 패드에 대한 물성은 Table 1에 정리하였다.

Fig. 6

Polishing pad thickness during 15 cycles of loading-recovery test

Fig. 7

Strain-time graph of 15th cycle of loading-recovery test of polishing pads

Table 1

Mechanical property data of polishing pad at 15th cycle of loading-recovery test

$\[ \epsilon ={\epsilon }_1+{\epsilon }_2\left(1-e^{\left(-t/\tau \right)}\right) \]$

(1)

$\[ E_1=\frac{P}{{\epsilon }_1} \]$

(2)

$\[ E_2=\frac{P}{{\epsilon }_2} \]$

(3)

4.2 유한요소해석 결과

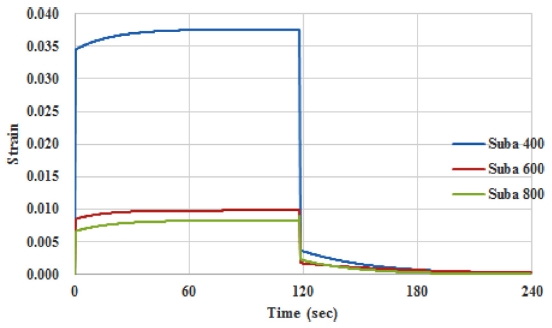
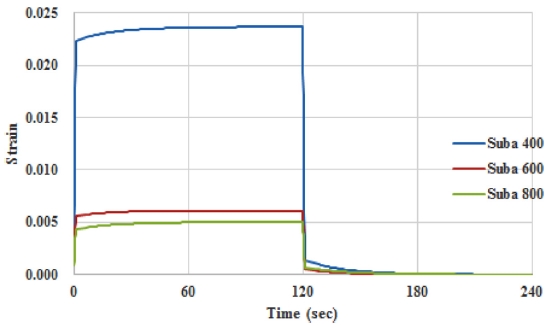
연마패드의 물성을 정의하기 위하여 점탄성 측정 결과를 통해 얻어진 파라미터를 바탕으로 Table 2와 같이 가정하였다. Isotropic Elasticity를 정의하기 위해 영 률(Young’s Modulus)은 1차 탄성 계수를 사용하였고 프와송 비(Poisson’s Ratio)는 0.35로 모두 동일하게 하였다. Prony Volumetric Relaxation을 정의하기 위한 값으로 상대 탄성률(Relative Moduli)은 탄성계수의 감소율을 나타내는 E₁/(E₁+ E₂) 값을 사용하였고 지연시간(Relaxation Time)에는 지수형태의 식에 피팅된 지연시간(τ) 값을 사용하였다. 앞서 정의된 점탄성 측정 실험과 동일한 하중조건에 따라 유한요소해석을 진행하였고 하중에 의해 발생하는 시간에 따른 연마패드의 두께 변형의 거동을 확인하였다. 유한요소 해석을 통해 나타난 연마패드의 두께변화는 Fig. 8에 나타나 있다. 이 때의 두께 변형률은 실험에서 얻어진 두께 변화 그래프인 Fig. 7과 비교했을 때 상대적으로 작은 변형이 발생하는 것을 확인할 수 있다. 여기서 정의한 재료물성은 하중에 대한 두께 변형만을 고려하여 가정한 탄성계수이므로 3-D 모델에서 프와송 비에 따른 단면 변화의 영향을 고려해야 한다. 이 때문에 동일한 변형률을 나타내기 위해 연마패드의 재료물성을 수정해야 하며 수정된 물성은 Table 3에 나타나 있다. 수정된 물성을 적용하여 다시 유한요소해석을 실시 하였을 때 Fig. 8과 같은 변형률이 나타나며 이는 실험에서 나타나는 하중에 대한 실제 패드의 변형률과 동일한 거동을 보인다. 해석을 통해 수정된 물성을 통해 나타난 연마패드의 변형과 실제 압축 실험에서 나타나는 연마패드의 변형의 거동이 일치하므로 이 때의 재료물성이 해석상에서 실제 거동과 동일한 변형을 나타내며 유한요소해석에 적용할 연마패드의 기계적 물성으로 사용될 수 있다.

Table 2

Material properties of polishing pad for FEA

Fig. 8

Strain-time graph of finite element analysis model by assumed material properties of polishing pad

Fig. 9

Strain-time graph of finite element analysis model by modified material properties of polishing pad

Table 3

Modified material properties of polishing pad for FEA

5. 결론

점탄성 측정기를 통해 얻은 CMP 연마패드의 변형률을 바탕으로 유한요소해석에서의 동적 점탄성 물성을 정의하였다. 연마패드의 하중에 대한 변형률로부터 1차 탄성계수, 2차탄성계수, 완화시간 데이터를 얻었다. 이를 바탕으로 연마패드의 탄성 재료물성정의 방법인 Isotropic Elasticity과 점탄성 재료물성 정의 방법인 Prony Volumetric Relaxation을 사용하였고 실험과 동일한 하중 조건에서의 유한요소해석을 실시하였다. 유한요소해석에서 하중에 따른 연마패드의 점탄성 거동을 확인하였으나 실제에 비해 나타난 두께 변형률이 작게 나타났다. 이를 보완하기 위해 실제 변형률과 해석에서 나타난 변형률을 비교하여 물성을 수정하였다. 다시 진행한 유한요소해석을 통해 이 때 정의된 물성이 실제 변형과 잘 일치하는 것을 확인하였다.

정의된 동적 점탄성 물성을 통해 유한요소해석에서 나타나는 연마패드 동적 거동을 나타낼 수 있으며 얻어진 동적 점탄성 물성이 추후 CMP 공정의 동적 해석에 활용될 수 있을 것으로 생각된다

Acknowledgments

이 논문은 부산대학교 기본연구지원사업(2년)에 의하여 연구되었음.

REFERENCES

• Bae, J.-H., Lee, H.-S., Park, J.-H., Nishizawa, H., Kinoshita, M., et al., “Effect of Pad Thickness on Removal Rate and Within Wafer Non-Uniformity in Oxide CMP,” Journal of the Korean Institute of Electrical and Electronic Material Engineers, Vol. 23, No. 5, pp. 358-363, 2010. [https://doi.org/10.4313/JKEM.2010.23.5.358]
• Chen, K.-S., Yeh, H.-M., Yan, J.-L., and Chen, Y.-T., “Finite-Element Analysis on Wafer-Level CMP Contact Stress: Reinvestigated Issues and the Effects of Selected Process Parameters,” The International Journal of Advanced Manufacturing Technology, Vol. 42, Nos. 11-12, pp. 1118-1130, 2009. [https://doi.org/10.1007/s00170-008-1672-5]
• Li, I., Forsthoefel, K. M., Richardson, K. A., Obeng, Y. S., Easter, W. G., et al., “Dynamic Mechanical Analysis (DMA) of CMP Pad Materials,” MRS Online Proceedings Library Archive, Vol. 613, 2000. [https://doi.org/10.1557/PROC-613-E7.3.1]
• Lu, H., Obeng, Y., and Richardson, K., “Applicability of Dynamic Mechanical Analysis for CMP Polyurethane Pad Studies,” Materials Characterization, Vol. 49, No. 2, pp. 177-186, 2002. [https://doi.org/10.1016/S1044-5803(03)00004-4]
• Kim, B. S., Tucker, M. H., Kelchner, J. D., and Beaudoin, S. P., “Study on the Mechanical Properties of CMP Pads,” IEEE Transactions on Semiconductor Manufacturing, Vol. 21, No. 3, pp. 454-463, 2008. [https://doi.org/10.1109/TSM.2008.2001223]
• Lee, D. and Lee, H., “Estimating the Mechanical Properties of Polyurethane-Impregnated Felt Pads,” Journal of Mechanical Science and Technology, Vol. 31, No. 12, pp. 5705-5710, 2017. [https://doi.org/10.1007/s12206-017-1111-3]