10 kWh급 플라이휠 에너지 저장 시스템의 로터 설계에 관한 연구

1. 서론

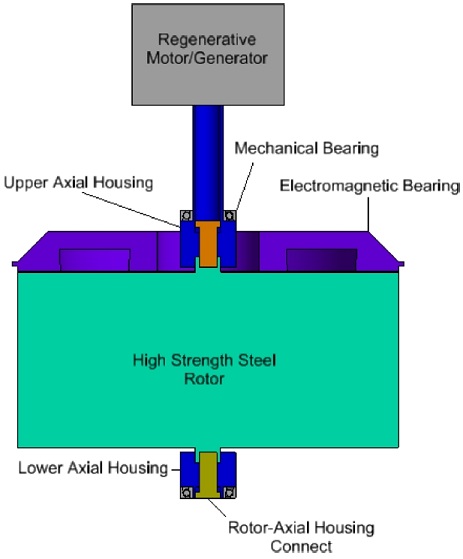
근래 친환경 에너지 생산에 관하여 세계적으로 그 중요성이 대두되고 있으며 이에 따라 풍력 발전, 태양광 발전, 조력 발전 등 다양한 친환경 에너지 생산에 대한 연구와 개발이 활발히 이루어지고 있다. 이러한 연구와 함께, 생산된 에너지를 안정적, 지속적으로 소비자들에게 공급하기 위해 에너지 저장 기술에 대한 연구 역시 진행되고 있다. 이러한 에너지 저장 기술은 저장 기술의 성질에 따라 물리적, 전기화학적, 전기적 방법으로 나눌 수 있다. 물리적 에너지 저장 기술의 일종인 플라이휠 에너지 저장 시스템(FESS, Flywheel Energy Storage System)은 Fig. 1과 같은 형태로 다음과 같이 작동하게 된다. 먼저, 외부로부터 공급된 전기에너지는 시스템의 상부에 위치한 회생식(Regenerative) 모터/발전기에 의해 회전력으로 전환된다. 그리고 전환된 회전력은 로터-축 하우징 연결체(Rotor-Axial Housing Connect)에 의해 연결된 로터(Rotor)를 회전시킴으로써 공급된 전기에너지를 로터의 회전에너지로 변환 시켜 에너지를 저장한다. 본 연구에서 설계된 로터는 약 1200 kg에 가까운 질량을 가지며, 로터는 공중에 부양(Levitation)된 채로 회전하게 된다. 따라서 부양력을 만들기 위한 마그네틱 베어링(Magnetic Bearing)이 로터의 상부에 위치하여 부양용 자기력을 생성한다. 한 편, 시스템을 보호하는 하우징의 내부는 펌프를 통해 진공 또는 매우 낮은 압력으로 유지되어 회전 간 마찰에 의한 손실을 최소화한다.

Fig. 1

System design configuration

FESS는 타 에너지 저장기술에 비해 에너지의 저장 및 방출 효율이 높고 수명이 긴 장점을 갖고 있다.¹ 그러나 일반적으로 설비를 구축하는데 드는 비용이 크고 20000 RPM 이상의 속도로 회전하는 로터는 결함에 취약하여, 회전 중 사고 발생 시, 타 에너지 저장기술에 비해 상당히 높은 위험성을 지니고 있기 때문에, 주로 대용량의 에너지 저장을 필요로 하는 대규모 시설에서 전문적으로 사용되었으며, 아직 기술의 상용화 초기 단계로서 더 높은 기술적 성숙도가 요구되는 상황이다.² 이를 극복하기 위해 고강도강(High Strength Steel) 로터, 복합재 로터(Composite Rotor), 초전도 베어링(Superconducting Bearing), 자기 베어링(Electro Magnetic Bearing) 등을 이용하여 FESS에 대한 다양한 연구가 이루어 지고 있으며, 미국을 중심으로 상업적으로 이용되고 있다.^3-15

Table 1에 정리된 다양한 FESS 중 국내에서 제작된 FESS의 경우^3,6-8, 공통적으로 최대 회전 속도가 18000 RPM 이상이며, 로터 재료로 탄소섬유 복합재(Composite Carbon Fiber)를 사용하였다. 이는 탄소섬유 복합재의 높은 경량성과 내구성을 이용하여 고속 회전을 보다 낮은 수준의 회전력으로 구현함과 동시에 고속의 회전 속도 하에서 발생하는 로터 내부의 응력을 충분히 지지하기 위함이다. 그러나 탄소섬유 복합재의 경우, 일반적으로 고강도 강에 비해 고가이고, 재사용이 불가능하며, 제작, 가공 및 폐기 처리에 큰 비용이 발생한다.¹⁶ 그리고 이러한 고비용, 친환경적이지 못한 문제가 일반적으로 FESS의 상용화의 어려움을 야기하는 가장 큰 요인으로 지적되었다.

Table 1

State of the art of FESS

이에 따라 Xiaojun Li et al,⁴ Active Power,¹² AMBER¹³에서는 합금강을 이용하여 로터를 제작함으로써 더 저렴하고 재사용이 가능한 형태의 FESS를 제작하기도 하였다.¹⁶ 본 논문에서는 이러한 연구 흐름에 맞추어 비용이 상대적으로 저렴하고, 가공성이 높으며, 재사용이 가능하여 친환경적인 고강도 강(High Strength Steel)을 로터 재료로 선정하여 연구를 수행하였다.

FESS에서 고속으로 회전하는 원통 형태의 로터에서는 반경 방향(Radial Direction), 원주 방향(Circumferential Direction)으로 응력이 발생하며, 이 응력은 원의 중심에 도달할수록, 로터의 회전속도가 빨라질수록 커진다. 이에 따라 고속 회전 시 발생하는 응력에 의해 로터가 변형되지 않고, 안정적으로 운용되기 위해 회전체는 고강도의 재료로 구성하고 회전체 주변에 마그네틱 베어링을 사용함으로써 축 방향, 반경 방향 변위를 제어하기도 한다. 뿐만 아니라 에너지 충전 및 방전을 위해 PCS (Power Conversion System), 모터, 발전기, 압력 제어용 펌프, 하우징 등의 요소들을 복합적으로 사용하여 플라이휠 에너지 저장 시스템을 제작한다.¹ 이 중 로터의 경우, 직접적으로 에너지를 저장하는 본체이며 에너지 저장 용량 및 로터 형상을 결정하기 위해 식(1) - (3)을 고려하여 설계한다.

식(1)은 로터에 저장되는 에너지를 결정하며, 저장 에너지는 회전에 의한 각속도(ω)의 제곱, 극관성모멘트(I_P)에 비례하며, 극관성모멘트는 식(2)로서 회전체의 질량(m)과 반경(r)의 제곱에 각각 비례한다. 따라서 회전체에 저장되는 에너지를 증가시키기 위해서는 높은 회전속도를 구현하거나 질량과 반경이 큰 물체를 회전시켜야 한다. 그리고 식(2)와 식(3)에 해당하는 극관성모멘트와 횡관성모멘트의 비(I_P/I_T)를 정함으로써 로터의 형상을 설계하는데, 이 관성모멘트의 비가 약 0.85를 기준으로 이 값보다 작을 때, 직경보다 높이가 긴 실린더 형상의 로터가 설계되며, 이 값 보다 클 때 직경이 높이보다 긴 디스크 형상의 로터가 설계될 수 있다. 그리고 로터의 형상은 회전체의 동적 안정성에 영향을 미친다. 디스크 형상 로터의 경우, 고속 회전 시 자이로스코픽 효과(Gyroscopic Effect)와 진동의 영향이 실린더 형상의 로터에 비해 크기 때문에 일반적으로 시스템 전반의 안정성 확보를 위한 제어에 어려움이 따른다. 이로 인해 현재 상용화 된 대다수의 FESS용 로터는 실린더 형태로서, 낮은 극관성모멘트를 높은 각속도로 보상하여 에너지 저장 용량을 확보하고, 높은 각속도로 인해 발생하는 높은 수준의 응력에 대응하기 위해 탄소섬유 복합재(Carbon Fiber Reinforced Composite)를 사용함으로써 구조적 안정성을 확보한다. 그러나 본 연구에 적용된 고강도 강 로터의 경우, 강괴를 단조, 열처리, 절삭하여 로터를 제작하며 열처리 과정 중, 냉각과정을 거치는데, 냉각과정에서의 냉각속도가 높을수록 강의 강도가 높아진다. 이는 높은 냉각속도에서 마르텐사이트 조직의 성장 비율이 높고, 마르텐사이트 조직이 강의 강도에 큰 영향을 주기 때문이다. 이러한 특성으로 인해 고강도 강 로터의 경우, 로터의 표면적이 크게 제작하는 것이 냉각속도를 높여 강도를 증대시키기에 유리하다. 또한 로터 재료의 강도가 높을수록 더 높은 회전속도에서 많은 양의 에너지를 안정적으로 저장할 수 있으므로 로터의 높은 강도는 로터의 에너지 저장 밀도를 증가시킨다. 따라서 고강도 강 로터는 표면적이 큰 디스크 형상으로 제작될 때 높은 에너지 저장밀도를 나타내어 에너지 충전 및 방전 효율을 극대화시킬 수 있다.

한 편, 탄소섬유 복합재로 구성된 로터에 비해 강철로 구성된 로터는 같은 에너지 용량을 가질 때, 직경과 밀도가 더 크기 때문에 극관성모멘트가 상대적으로 커지게 되고, 이에 따라 낮은 회전속도로 시스템을 운용할 수 있어 제어에 용이하다. 또한, 상대적으로 낮은 회전 속도의 로터를 사용함에 따라 마그네틱 베어링뿐만 아니라 볼 베어링과 같은 기계식 베어링을 로터의 회전을 지지하기 위해 사용할 수 있다. 그러므로 본 논문에서는 10 kWh용 고강도 강(AISI 4340) 디스크형 로터에서 최대 회전속도 10000 RPM 회전 시의 자이로스코픽 효과를 고려하여 로터, 엥귤러 컨텍트 볼 베어링의 설계를 진행하였으며, 이를 기반으로 설계 최대 회전속도 10000 RPM 하의 로터에서 발생하는 응력 수준을 파악하고, 설계 본에 대해 모드, 고유진동수, 위험 속도 해석을 수행하여 안전성을 확인하였다. 위험 속도 해석의 경우, 미국 회전체 안전기준 API (American Petroleum Institute) Standard 617¹⁷을 참조함으로써 안정적 운용이 가능할 수 있도록 하였다.

2. 로터-베어링 설계

2.1 설계 조건

Table 2와 같이 에너지 저장용량과 최대 로터 회전속도를 각각 10 kWh, 10000 RPM으로 정하고, 이를 식(1)에 대입하여 극관성 모멘트를 계산하면, 극관성 모멘트는 65.72 kg·m²의 고정된 값으로 나타난다. 그리고 형상을 결정하기 위해 관성모멘트 비를 변화시키며 형상에 따라 달라지는 로터의 동역학적 특성에 대해 다음 절에서 다루었다.

Table 2

Rotor design properties

2.2 로터-베어링 동역학

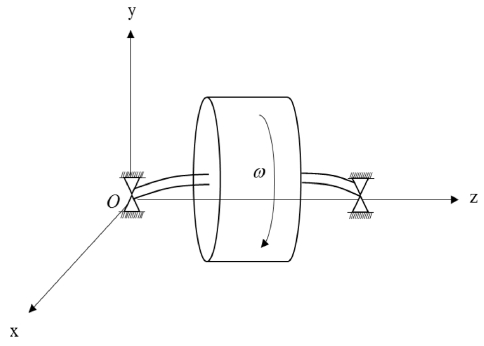
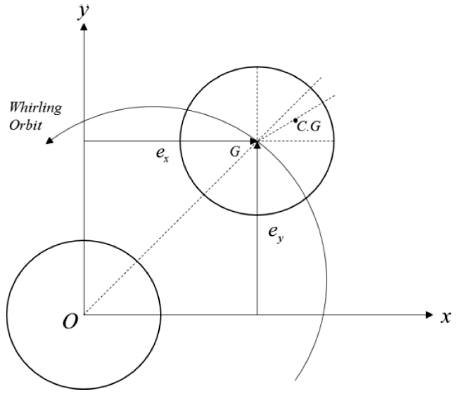
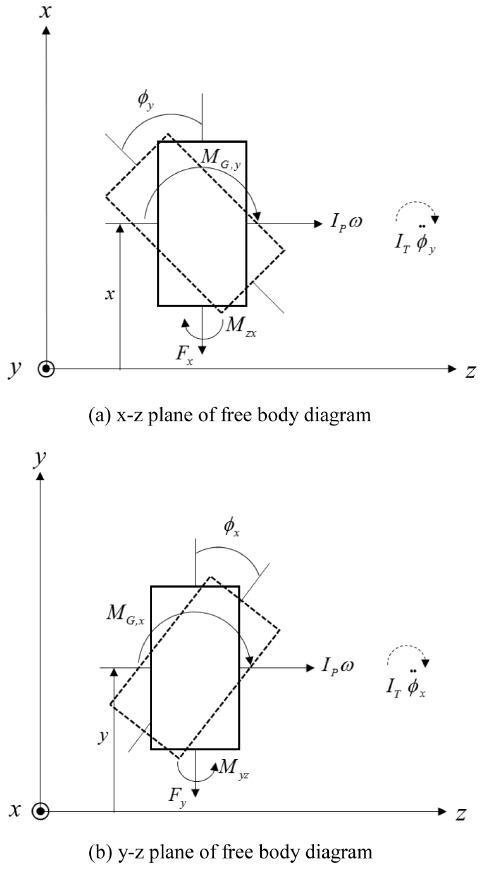
Fig. 2와 같이 축이 양단 고정 베어링에 의해 지지되며, 로터가 축과 함께 연결되어 각속도 ω로 z축을 중심으로 회전하고 있는 Jeffcott Rotor Model로서 회전체를 고려하였다.¹⁸ 이 경우, 로터가 축 전체 길이의 중앙에 위치하고, 로터의 기하학적 중심(Geometric Center)과 무게중심(Center of Gravity)이 완전히 일치하여 있을 경우, 이론적으로 축과 로터의 휘돌림(Whirling)이 없기 때문에 자이로스코픽 효과에 의한 모멘트를 무시할 수 있다. 그러나 디스크 형상으로 제작된 높은 밀도를 가진 고강도 강 로터는 제작 시 무게중심의 편심이 발생할 수 있으므로 이를 고려하여 설계하여야 한다. 그러므로 Fig. 3과 같이 로터 중심으로부터 x, y 방향으로의 편심 e_x, e_y가 존재하며, 기하학적 중심과 무게중심이 점 G와 점 C. G로 나타날 때, 축의 연성을 고려하여 Fig. 2의 자유물체도를 그리면 Fig. 4와 같다.

Fig. 2

Fixed rotating disk with flexible axis and eccentricity

Fig. 3

Fixed rotating disk with flexible axis and eccentricity

Fig. 4

Free body diagram of fixed rotating disk y-z plane

먼저, Fig. 4에서 각운동량 I_pω가 z축 방향으로 로터 일체의 회전에 의해 나타난다. 동시에, 자이로스코픽 모멘트 M_G,x, M_G,y가 로터에 작용하고 있으며, 편심에 의한 직교 변위와 각 변위 x, y, ϕ_x, ϕ_y가 존재한다. 이에 따라 변위에 대한 반력 F_x, F_y, M_yz, M_zx를 고려하면 로터의 회전 운동에 의한 힘과 모멘트의 평형을 식(4)로 나타낼 수 있다.

$\[ -F_x=m\ddot{x} \]$

(4-a)

$\[ -F_y=m\ddot{y} \]$

(4-b)

$\[ -M_{zx}-M_{G,y}=I_T{\ddot{\varphi }}_y \]$

(4-c)

$\[ M_{yz}-M_{G,x}=I_T{\ddot{\varphi }}_x \]$

(4-d)

식(4-c)와 식(4-d)의 자이로스코픽 효과에 의한 모멘트 항은 식(5-a), 식(5-2)와 같이 각각 나타낼 수 있다. 이를 식(4-c)와 식(4-d)에 대입하면 식(6)과 같이 4개의 방정식으로 평형방정식을 세울 수 있다.

$\[ M_{G,x}={-I}_P{\omega \ddot{\varphi }}_y \]$

(5-a)

$\[ M_{G,y}={-I}_P{\omega \dot{\varphi }}_x \]$

(5-b)

$\[ \begin{array}{c}m\ddot{x}+F_x=0\\ m\ddot{y}+F_y=0\\ I_T{\ddot{\varphi }}_y-I_P\omega {\dot{\varphi }}_x+M_{zx}=0\\ I_T{\ddot{\varphi }}_x-I_P\omega {\dot{\varphi }}_y+M_{yz}=0\end{array} \]$

(6)

식(4), 식(5)에서 나타나는 4개의 반력 항들은 다시 직교 변위, 각 변위에 대한 강성의 곱으로 식(7)과 같이 표현할 수 있으며, k_ll, k_aa, k_la는 각각 선형 강성, 회전 강성, 복합 강성으로서 회전체 재료의 탄성계수 E, 축 부 단면 이차 관성모멘트 I, 축 길이 l로 계산할 수 있다.¹⁹ 이를 다시 식(6)에 대입하고 정리하면 식(8)로서 운동방정식을 표현할 수 있다.

식(8)은 식(9)와 같이 행렬로 구성된 4자유도계 운동방정식으로 나타낼 수 있으며, 각 항은 식(10)으로 구성되어 있다.

식(10)에서 M 행렬은 시스템의 질량행렬, G 행렬은 자이로스코픽 행렬, K 행렬은 강성행렬, x 행렬은 변위 행렬이며, 식(9)의 해(변위행렬)를 구하는 과정에서 관성모멘트의 비를 변화시키며 계산을 수행하였고, 이를 바탕으로 다음 절에서 로터에서 발생하는 반경 방향과 축 방향 하중을 계산하여 베어링을 선정하고 수명을 계산하였다.

$\[ \left[\begin{array}{c}{F}_x\\ F_y\\ M_{yz}\\ M_{zx}\end{array}\right]=\left[\begin{array}{cccc}{k}_{ll}& 0& k_{la}& 0\\ 0& k_{ll}& 0& k_{la}\\ k_{la}& 0& k_{aa}& 0\\ 0& k_{la}& 0& k_{aa}\end{array}\right]\left[\begin{array}{c}x\\ y\\ {\varphi }_y\\ {\varphi }_x\end{array}\right] \]$

(7)

$\[ \begin{array}{c}m\ddot{x}+k_{ll}x+k_{la}{\varphi }_y=0\\ m\ddot{y}+k_{ll}y+k_{la}{\varphi }_x=0\\ I_T{\ddot{\varphi }}_y-I_P\omega {\dot{\varphi }}_x+k_{la}x+k_{aa}{\varphi }_y=0\\ I_T{\ddot{\varphi }}_x-I_P\omega {\dot{\varphi }}_y+k_{la}y+k_{aa}{\varphi }_x=0\end{array} \]$

(8)

$\[ \mathbf{\text{M}}\ddot{\mathbf{\text{x}}}\text{-}\omega \mathbf{\text{G}}\dot{\mathbf{\text{x}}}+\mathbf{\text{Kx}}=0 \]$

(9)

$\[ \begin{array}{c}\mathbf{\text{M}}=\left[\begin{array}{cccc}m& 0& 0& 0\\ 0& m& 0& 0\\ 0& 0& I_T& 0\\ 0& 0& 0& I_T\end{array}\right]\\ \mathbf{\text{G}}=\left[\begin{array}{cccc}0& 0& 0& 0\\ 0& 0& 0& 0\\ 0& 0& 0& I_P\\ 0& 0& -I_P& 0\end{array}\right]\\ \mathbf{\text{K}}=\left[\begin{array}{cccc}{k}_{ll}& 0& k_{la}& 0\\ 0& k_{ll}& 0& k_{la}\\ k_{la}& 0& k_{aa}& 0\\ 0& k_{la}& 0& k_{aa}\end{array}\right]\\ \mathbf{\text{x}}=\left[\begin{array}{c}x\\ y\\ {\varphi }_y\\ {\varphi }_x\end{array}\right]\end{array} \]$

(10)

2.3 로터-베어링

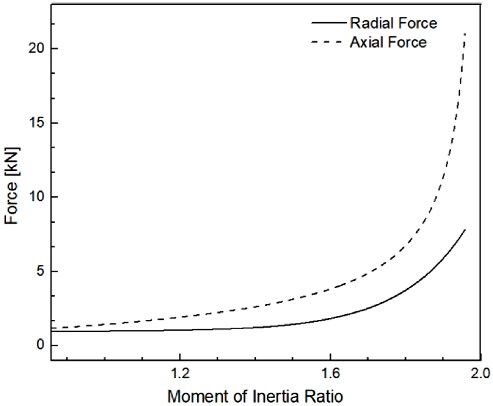
베어링에 적용되는 반경 방향 하중의 경우 관성모멘트 비를 변화시키며 변위행렬의 변화에 식(7)과 같이 강성행렬을 곱하여 반력을 계산함으로써 F_x와 F_y에 해당하는 반력 항의 평균을 반경 방향 힘으로 계산하였다. 축 방향 하중의 경우, 관성모멘트 비의 변화에 따라 로터의 질량이 증가하는데, 로터의 하중을 지탱하기 위해 로터 하부에는 베어링뿐만 아니라 케이싱이 함께 장착되어 로터의 무게를 지지한다. 또한 로터의 직상부에 전자석을 배치하여 로터를 부양시키므로 베어링에 적용되는 축 방향 하중은 로터 하중의 30%를 지지하도록 하였다. 이는 전류 차단과 같은 긴급상황 시 전자석의 미작동으로 인하여 시스템에 적용되는 로터 무게에 의한 하중이 발생시킬 수 있는 손상을 케이싱과 베어링을 통하여 지지하기 위함이며, 이에 따른 계산 결과를 Fig. 5에 나타내었다. Fig. 5에서 축 방향 하중은 반경 방향 하중과 함께 나타나며, 축 방향 하중이 반경 방향 하중보다 항상 높은 수준으로 발생함을 알 수 있다. 따라서 반경 방향 하중을 지탱함과 동시에 축방향 하중을 지탱할 수 있는 베어링이 선정되어야 하며, 본 연구에서는 내륜 상용 엥귤러 볼베어링 NSK, Co. 7212 C Single로 채택하여 베어링 세부 사항을 Table 3에 나타내었다. Table 3에서, NSK, Co. 7212 C Single 베어링은 동적부하용량(Basic Dynamic Load), 정적부하용량(Basic Static Load)으로 각각 64 kN, 49 kN을 지닌다. 그리고 베어링 재료의 항복응력 1370 MPa, 최대 회전 가능 속도가 그리스 윤활, 오일 윤활 시 각각 9500 RPM, 13000 RPM을 가져 오일 윤활 시 로터의 최대 회전속도와 앞서 고려된 관성모멘트 비의 범위 내에서 계산된 반경 방향, 축 방향 하중을 충분히 안정적으로 지지할 수 있다. 앞서 계산된 반경 방향 및 축 방향 하중을 기반으로 ISO 베어링 내구수명 계산식 식(11)과 NSK, Co. Rolling Bearing 규격²⁰에 따라 관성모멘트 비의 변화에 의한 베어링 내구수명을 계산하였다.

Fig. 5

Axial and radial force distribution of rotor versus increasing moment of inertia ratio

Table 3

Angular ball bearing NSK, Co. 7212 C single specification

$\[ L_h=500\times \frac{33.3}{N}\times {\left(\frac{C}{P}\right)}^3 \]$

(11)

$\[ P={XF}_R+Y{F}_A \]$

(11-2)

식(11-a)에서 L_h는 구하고자 하는 베어링의 수명 시간(hr), N은 베어링에 적용되는 회전수(RPM), C는 동적 부하 용량(kN) 그리고 P는 베어링에 적용되는 하중(kN)에 해당한다.

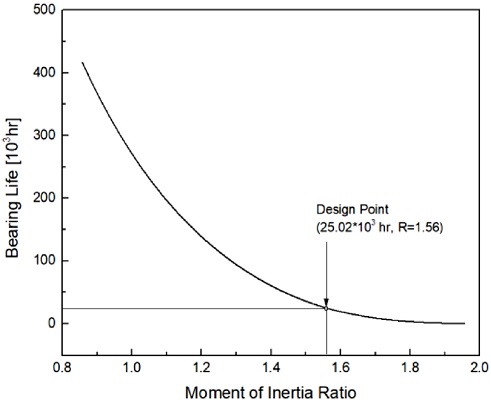
여기서 회전수 N은 10000 RPM이며, 동적 부하 용량 C는 64 kN으로서 NSK, Co. Rolling 베어링 규격에 의해 주어지는 값이다. 그리고 베어링에 적용되는 하중 P의 계산은 식(11-b)로 구할 수 있는데, X와 Y는 각각 반경 방향 하중 계수, 축 방향 하중 계수이며, 이 또한 베어링 규격에서 주어지는 값에 해당한다. 그리고 F_R과 F_A는 각각 반경 방향, 축 방향 하중이며, 앞서 계산하였던 반경 방향, 축 방향 하중을 대입하여 계산함으로써 관성모멘트 비에 따라 변화하는 수명시간을 Fig. 6에 나타내었다.

Fig. 6

Bearing life design point

앞서 Fig. 5에서 관성모멘트 비가 증가할수록 반경 방향, 축 방향 하중이 증가하므로, Fig. 6에서 또한 증가하는 베어링 하중에 의해 관성모멘트 비가 증가할수록 베어링 수명이 감소함을 알 수 있으며, 본 연구에서는 베어링 수명 25000시간을 주는 관성모멘트 비 1.56을 설계점으로 채택하였다. 고강도 강 로터 FESS의 경우, 에너지 저장 밀도를 증가시키기 위해 극관성모멘트를 가능한 높게 설계하여 최대한 디스크 형상의 로터를 구현함과 동시에 축 방향, 반경 방향 하중을 최대한 낮은 수준으로 유지하여 베어링 수명을 높이는 것이 중요하다. 그러나 베어링이 로터 하우징 내의 진공에 가까운 매우 낮은 압력에서 운용되기 때문에 베어링 윤활유가 정밀하게 베어링 씰(Bearing Seal)을 통해 밀봉되어야 하고, 진공 내에서 고속 회전하는 로터를 지지하는 베어링은 회전 마찰에 의해 발생하는 열이 소산되기 어려워 열 변형에 취약하게 되므로 베어링 허용 수명을 25000시간으로 제한하였다. 이에 따라 관성모멘트 비 1.56으로 로터를 설계하고 이에 따른 로터 특성을 Table 4에 정리하였다.

Table 4

Rotor specification

Table 4에서 알 수 있듯, 로터는 질량이 1200 kg에 달하며, 반경이 0.38 m, 높이가 0.34 m이므로 디스크 형상을 가지는 회전체로 제작될 수 있으며, 구조의 표면적이 실린더 형상의 로터에 비해 넓어 냉각 효율을 증대시켜 높은 에너지 밀도를 나타낼 수 있다. 이에 따라 추후 설계될 마그네틱 베어링 시스템은 1200 kg(11.76 kN)의 무게를 부양시킬 수 있는 자기력을 생성할 수 있도록 제작되어야 한다.

3. 로터 안정성 검증

본 장에서는 앞서 설계된 로터의 회전 시 구조적 특성과 회전 동역학적 특성을 파악하여 실제 가동 시 안정적으로 작동할 수 있는지 검증하였다.

FESS에서 로터는 파손, 결함 등의 문제가 생겼을 때 대형 사고로 이어질 수 있는 가장 큰 위험성을 갖고 있으므로 본 연구에서는 로터를 핵심 위험인자로 파악하여 시뮬레이션을 진행하였으며, 10000 RPM 회전 시 로터의 응력 상태, 로터의 공진 가능성 그리고 로터-베어링 시스템의 동적 안정성 검증으로 구성되어 있다.

3.1 로터 구조 안정성

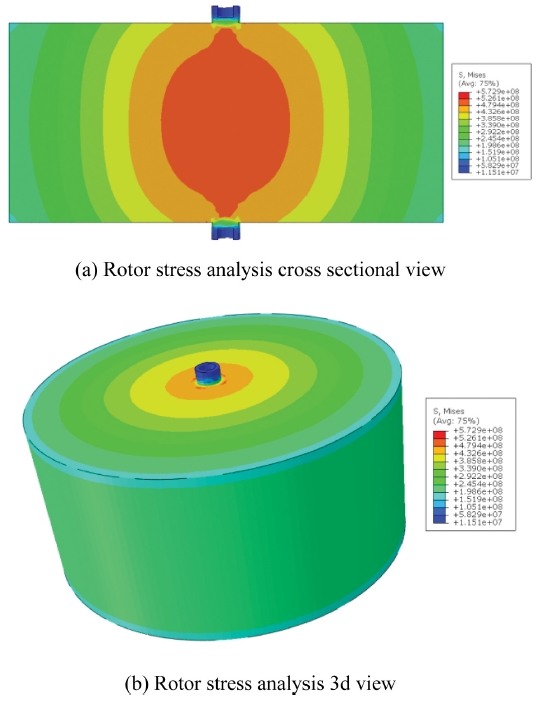
일반적으로 로터는 회전 시 구조의 중심부에 가까울 수록, 그리고 회전 속도가 높을수록 로터 내부에서 발생하는 응력이 커지게 된다. 이에 따라 발생하는 높은 수준의 응력이 로터 재료의 항복 응력(Yield Stress)을 초과할 때 소성변형이 시작되어 극한 인장 강도(Ultimate Tensile Stress)에 도달하면 봉재의 경우 네킹(Necking)이 발생하여 재료의 두드러지는 변형을 일으킨다. 그러므로 앞서 설계된 로터가 최대 10000 RPM의 회전속도에서 회전체의 변형을 일으킬 지에 대한 검증이 필요하다. 따라서 본 연구에서는 Fig. 1의 로터 상 하부 끝 단 연결부에 로터-축 연결체(Rotor-Axial Housing Connect)가 체결되고, 이를 상, 하 축 부 하우징(Upper, Lower Axial Housing)이 감싸는 형태의 로터를 10000 RPM 회전속도에서 응력 해석을 수행하여 발생하는 응력을 파악하여 이를 Fig. 7에 나타내었다.

Fig. 7

Rotor stress analysis

해석은 상용 프로그램 Abaqus를 통해 앞서 설계한 로터 형상 전체에 10000 RPM(1046.67 rad/s)의 회전 체적력(Rotational Body Force)을 로터의 중심을 기준으로 적용시켰으며, 로터 전체가 회전하기 때문에 구속(Constraint) 조건과 경계 조건(Boundary Condition) 없이 수행되었다.

Fig. 7에서 로터는 중심부에서 가장 높은 응력을 나타내어 최대 572.9 MPa가 나타나며, 상, 하 끝단의 체결 부에서 가장 낮은 유효 응력이 나타나 최소 11.51 MPa의 유효 응력이 나타났다. 그리고 로터 내부에서 발생한 응력이 로터의 중심선을 기준으로 서서히 로터 외부쪽으로 이동함을 알 수 있다.

따라서 로터 내부에서 가장 먼저 변형이 일어나 외부로 결함이 번질 수 있음을 확인하였다. 또한 로터 내부에서 발생한 최대 572.9 MPa의 유효응력은 로터 재료의 항복응력 1400 MPa의 약 40%에 달하는 응력이므로 재료의 탄성영역 내에서 두드러지는 변형 없이 안정적으로 운용할 수 있다고 판단하였다.

3.2 로터 진동 안정성

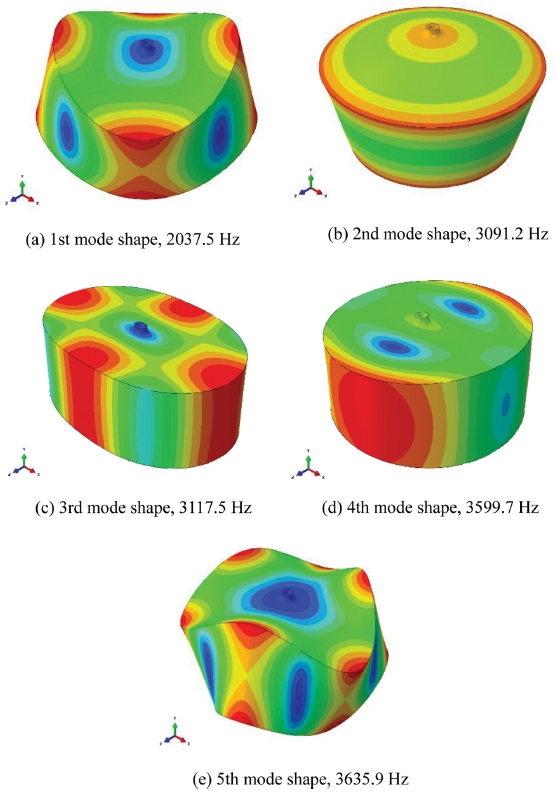
FESS에서 로터는 모터에 의해 가동되는 시간 하에서 항상 회전 가진력을 외부로부터 받고 있다. 뿐만 아니라 설계된 로터는 반경 0.38 m, 10000 RPM(1046.67 rad/s, 166.67 Hz)의 속도로 회전하므로 로터 끝 단 회전 속도는 397.7 m/s에 달한다. 따라서, 비록 로터 내부의 압력이 진공에 가깝도록 유지될 지라도 로터의 회전 속도에 기인하여 잔존 공기에 의한 충격파가 발생하여 추가적인 가진력에 노출될 수밖에 없다. 따라서 로터는 회전에 의해, 그리고 충격파에 의한 가진력으로 공진이 발생하지 않도록 로터의 회전 주파수보다 최소 200% 이상의 고유진동수 또는 이하의 고유진동수를 가져야 한다. 이에 따라 본 연구에서는 고유진동수와 모드를 파악하기 위한 해석을 수행하였으며, 이를 Fig. 8에 나타내었다.

Fig. 8

Rotor modal analysis

Fig. 8에 나타난 로터의 1 - 5차 모드 형상에서 로터는 굽힘과 비틀림이 현상이 발생함을 알 수 있으며, 1차 모드가 발생하는 고유진동수가 2037.5 Hz 이므로 로터의 최대 운전 속도 166.67 Hz(10000 RPM)와 12배 이상의 차이가 난다. 따라서 회전 시 공진에 의한 로터의 변형은 고려하지 않아도 무방할 정도로 안전함을 알 수 있다.

3.3 로터-베어링 시스템 동적안정성

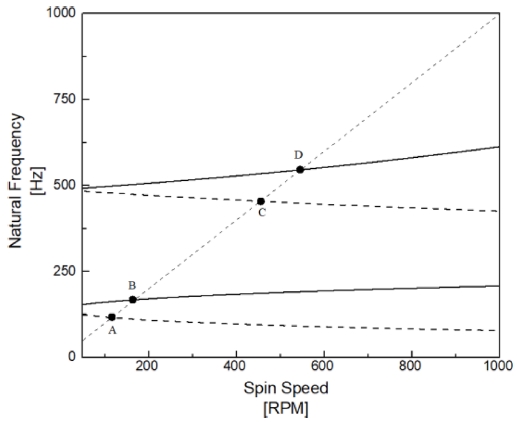
설계된 로터와 베어링 시스템은 가동 시 특정 회전 속도에 도달하면 로터 자체의 회전과 로터의 회전축을 기준으로 회전체 시스템의 휘돌림(Whirling) 운동을 동반한다. 이에 따라 로터의 회전축은 로터의 회전 방향과 같은 방향으로 휘돌림 운동이 나타나는 전방 휘돌림(Forward Whirling) 운동 또는 로터의 회전 방향과 반대 방향으로 휘돌림 운동이 나타나는 후방 휘돌림(Backward Whirling)이 발생한다. 그리고 일반적으로 전, 후방 휘돌림 운동이 나타나는 운전 속도를 위험 속도로 판단한다. 뿐만 아니라 휘돌림 운동은 일반적으로 회전체 운동 안정성에 큰 영향을 미쳐 API Standard617에서는 전체 위험 속도가 운전 속도 범위 20% 이상의 상, 하 분리 여유를 가지도록 설계함을 원칙으로 하고 있다. 따라서 설계된 로터-베어링 시스템에서의 위험 속도를 판단하기 위해 Campbell Diagram을 작성하여 이를 Fig. 9에 나타내었다.

Fig. 9

Campbell diagram

본 연구에서 수행된 위험속도 분석은 베어링의 감쇠를 고려하지 않고 계산되었으며, 이는 본 연구에서 설계된 베어링의 경우, 일반적 상용 구름 베어링으로, 로터 양 끝에 결합되었을 때 베어링 질량이 약 2 kg에 달한다. 따라서 베어링 질량이 로터에 비해 매우 작을뿐더러 구름 베어링 특성상 실질적으로 감쇠(Damping) 효과가 매우 작아 비감쇠 모델과 유사하기 때문이다.²¹

먼저, Fig. 9에서 1차 전, 후방 위험 속도의 경우 각각 B점과 A점으로 표시되어 있으며, B점의 경우, 167.24 RPM, A점의 경우 117.24 RPM 로서 후방 휘돌림 운동을 먼저 개시한 후 전방 휘돌림 운동으로 전개된다. 또한 2차 전, 후방 위험 속도는 각각 D, C점으로 표시되어 있으며, C점의 경우 454.09 RPM, D점의 경우, 545.69 RPM으로 나타난다. 위의 1차, 2차 위험 속도는 운전 속도 범위(2500 - 10000 RPM)에서 하(Downward) 20% 범위(2000 RPM) 이하에 존재하므로 API Standard 617에 부합하여 로터-베어링 시스템은 동적으로 안전하다고 판단할 수 있다.

한 편, 위와 같이 운전 속도 범위보다 매우 낮은 영역에서 1, 2차 위험 속도가 나타나는 원인을 본 연구에서는 로터의 높은 극관성모멘트로 판단하였다. 일반적인 로터-베어링 시스템에서의 경우, 운전영역의 20% 범위 이하 또는 이상의 영역에서 위험속도가 존재하기 위해 40 - 50%의 분리여유를 갖도록 설계된다. 그러나 본 연구에서 설계된 로터의 경우, 매우 높은 극관성모멘트와 질량을 가진 회전체이므로 회전을 시작한 시점 부근에서 위험 속도가 상대적으로 일찍 발생하고, 회전체가 일정 수준 이상의 회전운동을 개시하면 극관성모멘트가 매우 높기 때문에 외부 가진에 대한 저항이 높아 오히려 로터의 불안정적인 운동이 발생하기가 어려워지는 상황이 나타나는 것이라 판단하였다.

4. 결론

본 연구에서는 10 kWh급 플라이휠 에너지 저장장치의 구성요소 중 직접적으로 에너지를 저장하는 부품인 로터와 로터의 운동을 지지하는 베어링을 중심으로 설계를 수행하였다. 로터는 AISI4340 합금강을 재료로 채택하여 복합재 플라이휠 로터에 비해 친환경적이고 저렴한 비용으로 제작할 수 있도록 하였으며, 로터의 형상에 따라 달라지는 축 방향, 반경 방향 하중을 파악하여 하중에 대응하기 위해 엥귤러 볼 베어링을 선정하고 베어링 수명을 기준으로 로터의 형상을 설계하였다. 그리고 설계된 로터에 대해 회전 시 구조적으로 안정적인지 판단하기 위한 구조해석을 진행하였고, 회전 주파수에 의한 공진가능성을 조사하기 위해 모드 해석을 수행하였다. 그리고 설계된 로터-베어링 시스템의 동적 안정성을 판단하기 위해 시스템의 위험속도를 파악하였다. 이러한 과정에 의해 결론적으로 본 연구에서 설계된 로터-베어링 시스템은 응력에 의한 로터의 변형, 회전 시 공진, 위험속도의 측면에서 안정적으로 작동할 것이라고 판단하였다. 그러나 전체 시스템을 보호할 하우징과 하우징 내부에서 진공을 유지하기 위한 펌프, 마그네틱 베어링 제어 시스템, 베어링 실, 베어링 냉각 시스템 등 부수적인 부품의 설계가 완료되지 않은 상태이며, 마그네틱 베어링의 경우, 1200 kg을 부양시킬 수 있는, 11.76 kN 이상의 자기력을 생성하여 로터를 부양시키므로 위험성이 매우 높은 부품으로 판단되어 안정성에 대한 검증이 반드시 필요하다. 뿐만 아니라 모터/발전기의 경우 FESS의 에너지 저장 효율에 직접적인 영향을 미치므로 이에 대한 연구와 검증 또한 필요하다. 따라서 추후 앞서 언급한 부품들에 대한 추가적인 설계와 해석, 그리고 실제로 제작함으로써 안정성과 효율성을 재확인할 필요가 있으며, 이에 대한 연구를 수행할 계획이다.

Acknowledgments

이 논문은 2015년도 정부(미래창조과학부)의 재원으로 한국연구재단의 선도연구센터지원사업(No. 2012R1A5A1048294)과 2017년도 정부(산업통상자원부)의 재원으로 한국산업기술진흥원-산업용 무인비행장치 전문이력양성사업(No. G02N05660000601)의 지원을 받아 수행된 연구임. 이에 관계자 여러분께 감사드립니다.

REFERENCES

• Bolund, B., Bernhoff, H., and Leijon, M., “Flywheel Energy and Power Storage Systems,” Renewable and Sustainable Energy Reviews, Vol. 11, No. 2, pp. 235-258, 2007. [https://doi.org/10.1016/j.rser.2005.01.004]
• Luo, X., Wang, J., Dooner, M., and Clarke, J., “Overview of Current Development in Electrical Energy Storage Technologies and the Application Potential in Power System Operation,” Applied Energy, Vol. 137, pp. 511-536, 2015. [https://doi.org/10.1016/j.apenergy.2014.09.081]
• Lee, J.-H., Park, C.-B., and Lee, B.-S., “A Study on the Design of the Flywheel Energy Storage Device to Store the Regenerative Energy,” The Transactions of the Korean Institute of Electrical Engineers, Vol. 62, No. 7, pp. 1045-1052, 2013. [https://doi.org/10.5370/KIEE.2013.62.7.1045]
• Li, X., Anvari, B., Palazzolo, A., Wang, Z., and Toliyat, H., “A Utility-Scale Flywheel Energy Storage System with a Shaftless, Hubless, High-Strength Steel Rotor,” IEEE Transactions on Industrial Electronics, Vol. 65, No. 8, pp. 6667-6675, 2018. [https://doi.org/10.1109/TIE.2017.2772205]
• Koshizuka, N., “R&D of Superconducting Bearing Technologies for Flywheel Energy Storage Systems,” Physica C: Superconductivity and its Applications, Vols. 445-448, pp. 1103-1108, 2006. [https://doi.org/10.1016/j.physc.2006.05.045]
• Kim, Y. C., Kyung, J. H., Choi S. K., “Experimental Study on the Dynamic Behavior of a 500 Wh Flywheel Energy Storage Device,” Proc. of The Korean Society for Noise and Vibration Engineering Autumn Conference, pp. 36-42, 1997.
• Lee, J.-P., Han, S.-C., Park, B.-C., Han, Y.-H., Park, B.-J., et al., “Vibration Control of Flywheel Energy Storage System,” The Transactions of the Korean Institute of Electrical Engineers, Vol. 58, No. 9, pp. 1750-1756, 2009.
• Jeoung, H.-M., Jeoung, J.-W., Choi, J.-H., and Koh, C.-S., “Development of a Flywheel Energy Storage System using Superconducting Magnetic Bearing,” The Korean Institute of Power Electronics, Vol. 4, No. 5, pp. 433-441, 1999.
• Piller Power Systems, “UBT+ Rotary UPS Brochure,” http://www.piller.com/en-GB/documents/516/ubt-rotary-ups-brochureen.pdf, (Accessed 21 DEC 2018)
• Townley, D., “Introducing Pentadyne Power Flywheel Energy Storage System,” Proc. of Electrical Energy Storage Systems Applications and Technologies Conference, 2002.
• Beacon Power, “Beacon Power 400 Performance Specifications,” http://beaconpower.com/wp-content/themes/beaconpower/inc/beaconpower_400_ds_081414, (Accessed 25 Jan 2019)
• Active Power, “CleanSource XT UPS Single Module Systems,” http://www.activepower.com/en-US/documents/3974/cleansourcext250-ups-en.pdf, (Accessed 21 DEC 2018)
• Sanders, S., Senesky, M., He, M., and Chiao, E., “Low-Cost Flywheel Energy Storage Demonstration,” Energy Research and Development Division Final Project Report, 2015.
• Energiestro, “VOSS, Volant de Stockage Solaire, Solar Storage Flywheel,” http://www.energiestro.fr/pdf/EnergiestroVOSS.pdf, (Accessed 21 DEC 2018)
• Strasik, M., Johnson, P., Day, A., Mittleider, J., Higgins, M., et al., “Design, Fabrication, and Test of a 5-kwh/100-kw Flywheel Energy Storage Utilizing a High-Temperature Superconducting Bearing,” IEEE Transactions on Applied Superconductivity, Vol. 17, No. 2, pp. 2133-2137, 2007. [https://doi.org/10.1109/TASC.2007.898065]
• Arani, A. K., Karami, H., Gharehpetian, G., and Hejazi, M., “Review of Flywheel Energy Storage Systems Structures and Applications in Power Systems and Microgrids,” Renewable and Sustainable Energy Reviews, Vol. 69, pp. 9-18, 2017. [https://doi.org/10.1016/j.rser.2016.11.166]
• American Petroleum Institute, “Axial and Centrifugal Compressors and Expander-compressors,” American Petroleum Institute 8th Edition, 2014.
• Jeffcott, H. H., “XXVII. The Lateral Vibration of Loaded Shafts in the Neighbourhood of a Whirling Speed - the Effect of Want of Balance,” The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, Vol. 37, No. 219, pp. 304-314, 2009. [https://doi.org/10.1080/14786440308635889]
• Timoshenko, S. P., Young, D. H., “Elements of Strength of Materials,” New York Van Nostrand Company, 5th Edition, 1968.
• NSK, “Rolling Bearings,” NSK Ltd., 1996.
• Lee, A. S., Kim, Y. C., and Park, J. K., “Rotordynamics of a Centrifuge Rotor-Bearing System for 100,000 rpm Operation,” Korean Society of Mechanical Engineers Vibration Conference, pp. 818-823, 1997.