금형 수명을 고려한 자동차 엔진 마운트용 어댑터의 냉간 단조 금형 설계에 관한 연구
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Process and die design of cold forging for the asymmetric part, engine mount adapter has been studied. Forging of the asymmetric part frequently causes die failure because of the high forging load and local stress concentration of the die. Thus, performing process design of cold forging to minimize forging load is required. Preform for the engine mount adapter was chosen based on the forging load and filling rate of forgings by the finite element analysis. In the die design, number of stress rings, interface radius, and relative interference were investigated in several cases with maximum principle stress by the finite element method. The shape of the die was determined by comparing the load changing the radius of the flange area. Also, the life of the designed die was calculated using the Goodman theory by cyclic fatigue loading. As a result, it was confirmed that the calculation life and results of the test were identical. In this study, it is verified that stress concentration and fatigue life should be considered simultaneously in the design of cold forging die for the asymmetric part.
Keywords:
Cold forging, Shrink fitting, Die life, Fatigue analysis, Finite element analysis키워드:
냉간 단조, 금형 박음, 금형 수명, 피로해석, 유한요소해석1. 서론
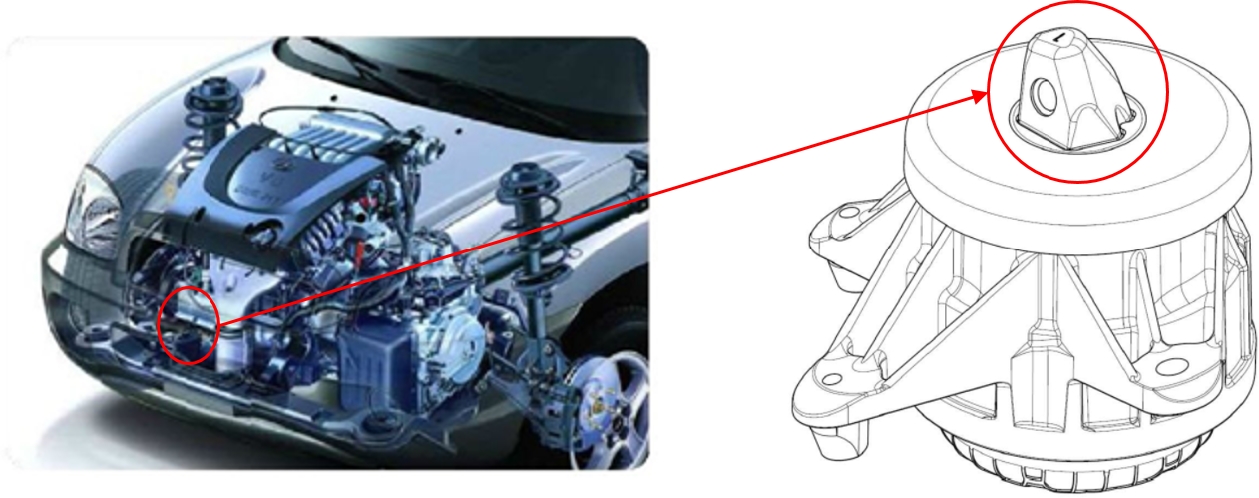
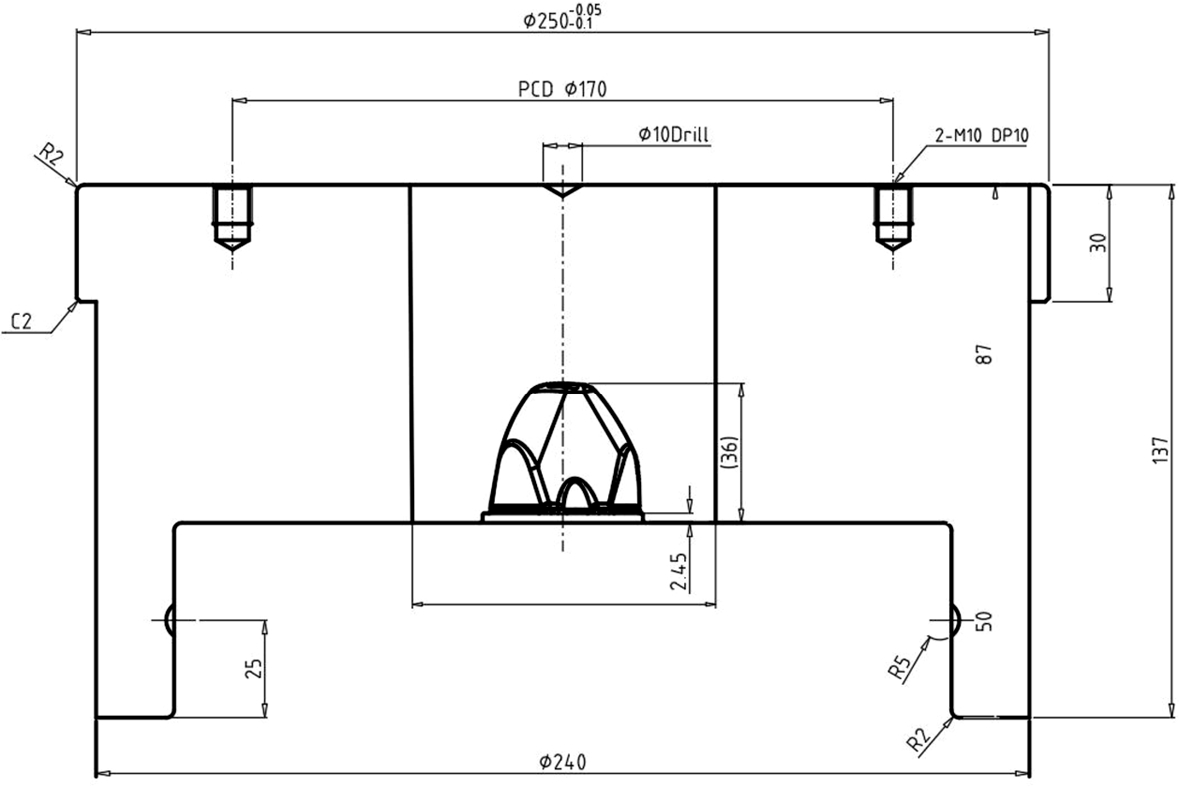
자동차에서 엔진 마운트는 엔진의 진동을 감쇠시키는 부품으로서 유압 마운트와 어댑터로 구성되어 있으며 엔진을 차체에 고정하는 역할을 한다. 엔진 마운트에 사용되는 어댑터는 일종의 체결부품으로서 기능에 따라 다양한 형상을 가진다. Fig. 1과 같은 엔진 마운트용 어댑터는 원통 부 중심축을 기준으로 비대칭인 사각뿔 모양의 특수한 구조를 가지고 있으며 단조 공정 설계 시 체적분할이 어려움으로 열간 단조 후 절삭 가공을 거쳐 생산되어 왔다. 이러한 공법은 생산성이 낮고 제조 공정이 복잡하여 대량 생산 및 원가 절감을 위해 냉간 단조 공법을 이용한 공정 설계가 요구된다. 본 연구에서는 유한요소해석을 이용하여 단조품의 충진도요구를 만족시키면서 대량생산에 적합한 단조공정을 설계하였다.
밀폐단조 공법(Closed Die Forging)으로 비대칭 형상의 제품을 성형할 경우, 공정 설계 시 예비성형체(Preform)의 형상에 따라 성형 하중이 큰 차이가 발생할 수 있다. 성형하중의 크기에 따라 단조 금형의 수명에도 직접적인 영향을 미치므로 냉간 및 열간 단조 공정 설계에서 예비성형체 설계에 대한 연구가 활발히 수행되어 왔다.1-5 냉간 단조는 상온에서 진행됨으로 소재의 유동응력이 열간 보다 훨씬 높다. 따라서 금형에 걸리는 응력 또한 높아짐으로 쉽게 파손이 발생할 수 있다. 이를 방지하기 위하여 일반적으로 금형 분할과 박음(Shrink Fitting) 설계를 적용하고 있다 금형 분할과 박음에 대한 이론은 단조 성형 시 발생되는 내압(Internal Pressure)으로 인해 금형에 인장 원주방향응력(Hoop Stress)이 작용함으로 보강링을 이용하여 인서트에 압축응력을 부과하여 인장응력을 상쇄시키는 것이다. 적절한 분할 직경과 박음량(Relative Interference)에 따라 금형 수명연장에 큰 영향을 미친다. 일반적으로 분할경에 대해서는 Lamé의 수식이 대표적이며, 분할 수와 박음량은 작용하는 내압의 크기에 따라 설계된다.6-9 하지만 축에 대하여 비대칭인 형상인 경우 성형 과정에서 비대칭 단면의 모서리부분에서 응력 집중이 발생되어 금형이 쉽게 파손될 수 있다. 따라서 비대칭 형상의 금형을 설계할 경우는 응력집중에 따른 응력 상승효과 뿐만 아니라 금형 분할과 박음에 의해 평균응력과 단조작업에 의한 교차응력에 따른 피로수명 해석을 함께 검토할 필요가 있다.10-12
본 연구에서는 비대칭 형상의 엔진 마운트 어댑터에 대한 냉간 단조 공정을 설계하였고 예비성형체의 형상, 금형 분할경, 박음량 및 보강링 개수에 따른 금형의 응력 변화를 비교하였으며 유한요소해석을 통하여 플랜지 부의 곡률변화에 따른 단조품의 성형성과 금형 응력을 해석하였다. 금형 응력이 가장 낮은 설계조건으로 양산이 이루어질 경우, 응력집중에 따른 금형 파손이 예상되는 지점의 금형 피로 수명을 Goodman 이론을 이용하여 예측함으로써 제안된 설계의 수명을 예측할 수 있는 방안을 제시하였다.
설계한 금형으로 단조실험을 실시하였고 실제 금형 수명을 비교함으로써 비대칭 형상을 가진 제품의 금형 설계에서 금형의 응력해석과 피로 수명해석이 동시에 필요함을 확인하였다.
2. 엔진용 어댑터의 예비성형체 형상 설계
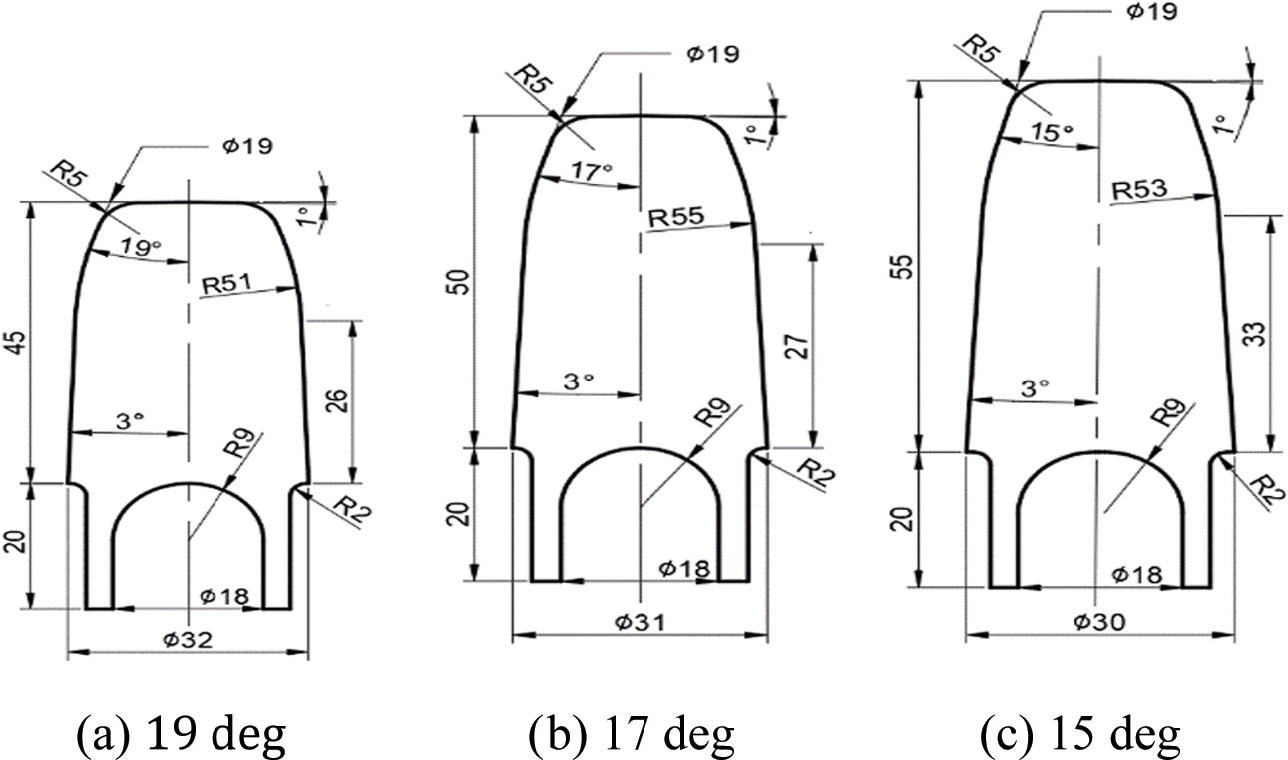
단조 공정 설계에서 예비성형체는 다단 단조 공정으로 성형 후 열처리(Annealing)와 인산염 피막(Phosphating) 공정을 거쳐 냉간 프레스에서 단일 공정으로 최종 성형된다. 예비성형체의 형상에 따라 냉간 프레스 공정에서의 성형하중과 금형 응력에 직접적인 영향을 줄 수 있다. 다단공정으로 생산하기 위하여 Fig. 2와 같이 직경과 길이에 따른 예비성형체 3종류를 설계하였고 끝단의 각도는 각각 19 deg, 17 deg, 15 deg를 적용하였다.
설계한 형상에 따른 성형 하중과 성형성을 예측하기 위하여 DEFORM-3D를 이용한 강소성 성형 시뮬레이션을 하였다. 경계조건은 성형 속도 100 mm/sec, 유동응력은 소재 재질 S10C에 상당하는 DEFORM-3D의 기계적성질을 사용하였고, 금형과 소재 간의 마찰 상수는 0.12를 적용하였다.
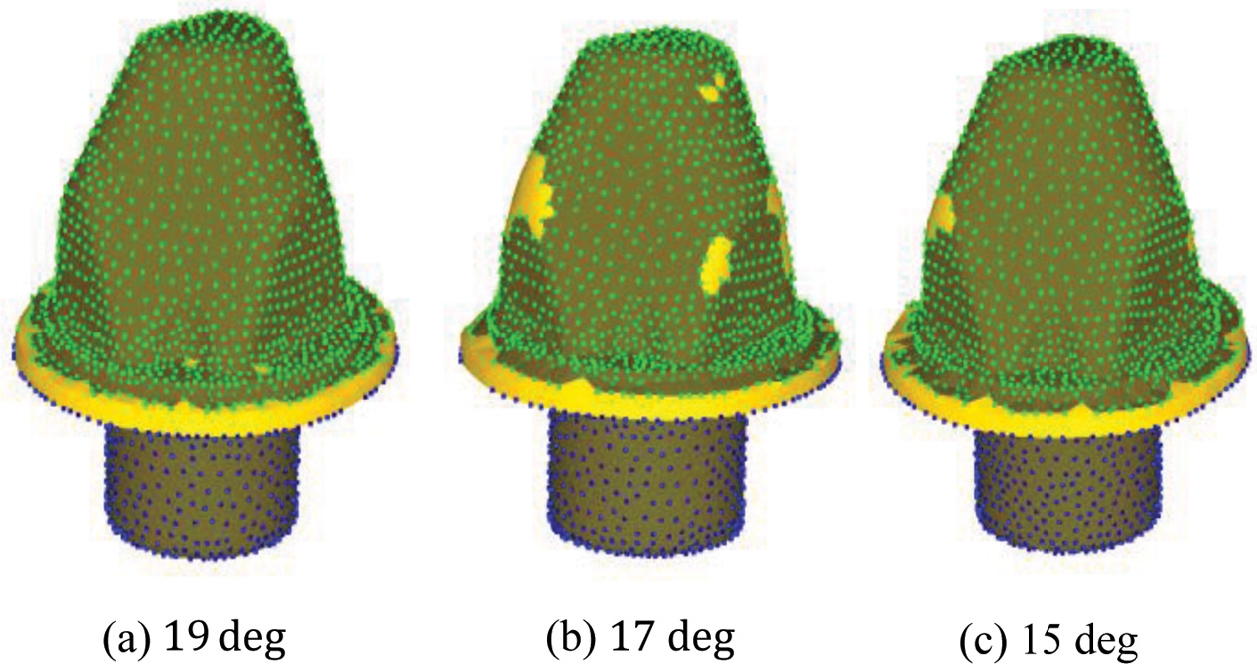
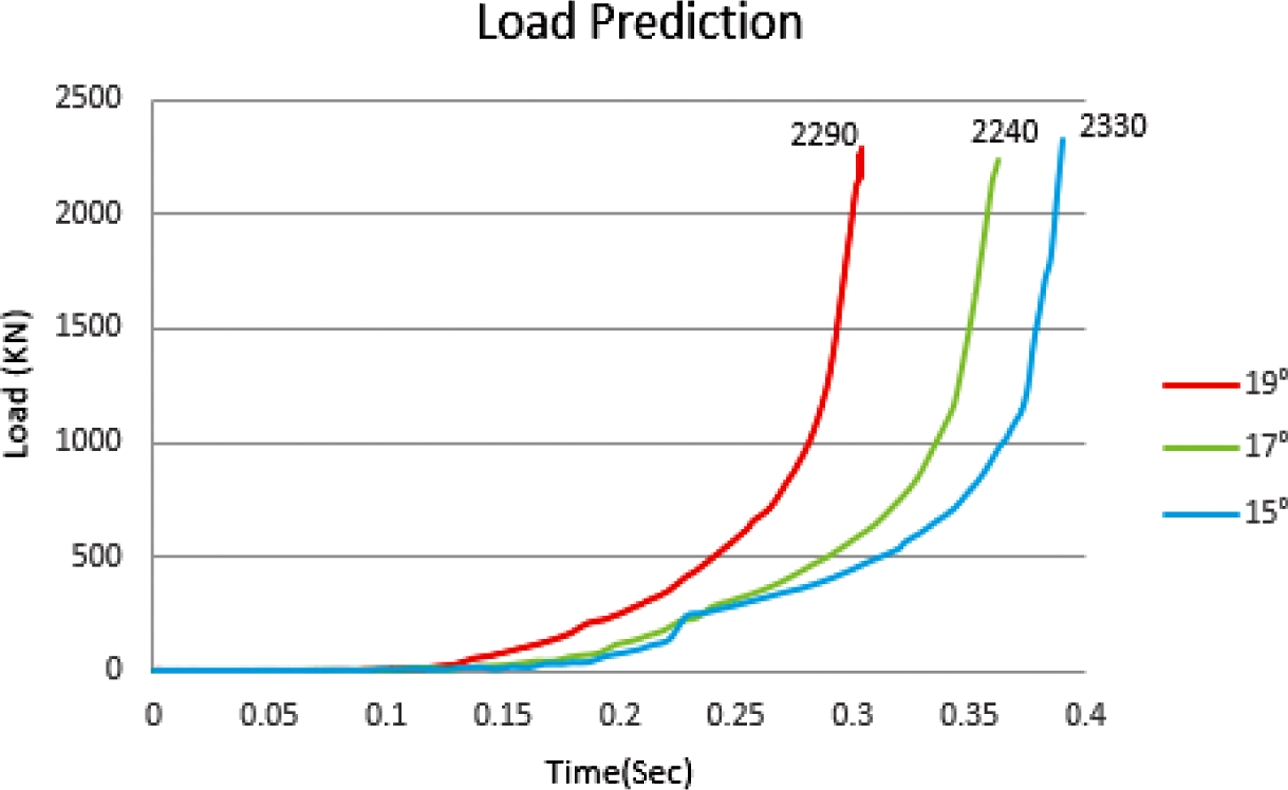
유한요소해석 결과로서 예비성형체 치수에 따른 제품의 충진도를 Fig. 3에 나타내었고, 성형 하중은 Fig. 4와 같이 그래프로 정리하였다. 19 deg, 17 deg, 15 deg에 대하여 각각 약 2,290 kN, 2,240 kN, 2,330 kN으로 예측되었다. 성형하중은 15 deg, 19 deg, 17 deg 순으로 하중이 낮아 졌으며, 충진도 관점에서는 동일 스트로크(Stroke)에서 금형과의 접촉 형상이 예비성형체 각도가 19 deg일 때가 가장 높게 나타났다.
냉간 단조 공정은 낮은 성형하중, 높은 금형 수명과 제품의 충진도가 요구됨으로 본 연구에서는 충진도가 가장 좋고 성형하중 또한 2,290 kN으로 적절한 값을 나타내는 19 deg, 45 mm 의 예비성형체를 선정하였다.
3. 금형 구조 및 형상 설계
Fig. 5는 개발 초기 단계에서 현장 경험에 의한 1중 박음 단조 금형의 도면을 나타낸 것이다. 도면에서 상부 금형의 형상으로 인서트 외경의 크기가 ø 95 mm, 분할 외경의 크기가 ø 210 mm로 금형을 1중 박음으로 제작하였으나 약 600회 단조 성형 후 금형에 파손이 발생하였다. 이는 성형과정 초기 개발에서 설계된 공정에서 금형 응력이 과도 하게 발생되어 나타난 현상으로 판단된다. 이러한 금형 응력에 의한 파손을 방지하기 위하여 금형을 1중, 2중 박음에 대한 분할경과 박음량의 변화 및 플랜지 부위의 곡률 크기에 따른 성형 충진도와 응력 변화를 유한요소 해석을 통하여 분석하여 금형 응력을 최소화하는 조건을 도출하였다.
3.1 1중 박음 조건의 금형 응력 해석
냉간 단조 금형에서 단조 공정에 의한 성형력이 원통형 내경을 가진 금형에 작용할 때 인서트에 원주방향 응력과 반경방향 응력이 발생하게 되며 이러한 응력분포를 계산하는 수식이 Lamé의 식이다. 하지만 비대칭 형상으로 인해 금형에 응력집중이 발생하는 경우에 Lamé의 수식으로 정확한 분할경과 박음량을 계산할 수 없다. 따라서 본 연구에서는 금형 분할의 일반식인 Morgan 수식인 식(1)과 식(2)를 이용하여 분할경을 계산하였다.13
| (1) |
| (2) |
분할경을 금형의 외경(D2)은 ø 210 mm, 플랜지 부 끝단의 직경(d0)이 ø 43mm일 경우 분할경(D1)은 ø 95mm로 계산된다. 계산 값은 내경에 균일한 면압이 작용할 경우에 대하여 계산된 값으로 응력 집중에 의한 응력 변화를 예측하기 위하여 인서트 외경을 ø 95mm, ø 85mm, ø 75mm의 3가지로 선정하여 유한 요소해석을 하였다.
금형 박음량은 인서트 외경의 0.4%, 0.6%, 0.8%로 3가지 조건으로 선정하였으며, 인서트 소재는 SKH51, 보강링 소재는 STD61을 적용하였다. 금형 응력 해석은 비대칭 형상으로 인해 분할모델을 사용하지 않고 전체 금형으로 1차 박음 해석한 후 단조성형이 완료된 상태에서 접촉 노드의 하중을 경계조건으로 입력하였다.
금형에 과도하게 높은 응력이 작용하여 파단이 발생하는 것은 대표적인 취성파괴현상으로 최대 주응력(Maximum Principle Stress)이 최대강도를 초과하게 되면 파단이 발생된다. 냉간 단조용 금형은 단조작업에 의해 발생되는 금형의 인장응력을 줄이기 위하여 금형박음이 적용되고, 금형파손은 단조작업에 따른 인장응력에 의해 발생됨으로 압축과 인장 응력이 구분되는 주응력을 기준으로 판단하게 된다.7,14,15 각 조건의 유한요소해석 결과 중 분할경 ø 75와 박음량 0.8%에 대한 최대 주응력의 변화를 대표적으로 도시하면 Fig. 6과 같다. 해석결과에서 보강링으로 인한 압축응력은 약 343 MPa, 단조성형 과정에서 최대 인장응력은 약 763 MPa로 예측 되었다. 이는 가장 쉽게 파손이 발생할 것으로 예상되는 모서리 부분을 기준으로 측정하였다. 기타 각 조건별 박음 후, 단조과정에서의 응력변화를 Fig. 7과 같이 그래프로 나타내었다.
Principal stress distribution of die with 1 stress ring at the diameter ø 73 and 0.8% shrinkage fitting
Maximum principal stress distribution of die with 1 stress ring for finite element analysis conditions
인서트의 재료는 SKH51 소재로 허용강도는 2400 MPa이며, 보강링은 STD61 소재로 허용강도는 1600 MPa이다. Fig. 7에 나타낸 바와 같이 분할경 3가지 조건과 박음량 0.4%, 0.6%, 0.8% 조건에서 파단강도 이하로 유지되어야 한다.
Table 1에 각 조건별 박음 후 응력과 단조하중이 부과된 후의 응력을 정리하였다. 1중 박음으로 금형을 제작할 경우 분할경과 박음량에 관계없이 보강링의 주응력은 허용치는 1,600 MPa 미만임을 알 수 있다. 하지만 Insert의 경우 0.4% 박음량일 경우 분할경과 관계없이 단조 성형 후 주응력이 2,400 MPa을 초과 또는 근접하여 금형의 파괴가 일어날 것으로 예상되며, 0.6% 박음량일 경우도 인서트 금형에 2400 MPa에 가까운 응력이 작용하여 금형 수명에 문제가 생길 것으로 예상된다.
0.6%의 박음량에서 분할경이 ø 85mm에서 가장 적은 1630 MPa의 주응력이 예측되었다. 3가지 조건에서 가장 큰 박음량인 0.8%의 경우 분할경 ø 75mm, ø 85mm, ø 95 mm에 대하여 각각 1290 MPa, 1060 MPa, 1330 MPa의 주응력이 인서트에 작용하고 있어 인서트만을 고려할 경우 0.8% 박음량이 적합한 것으로 생각된다. 하지만 실제 열박음 공정에서 보강링의 강도한계 범위에서 진행할 수 있는 열박음 최대 박음량은 약 0.6% 수준이므로 제작상의 문제로 인서트 응력을 더 줄이기 위해 보강링의 개수를 추가할 필요가 있다.
유한요소해석에서 1중 박음 금형을 0.6% 박음량으로 제작할 경우 분할경 ø 75mm, ø 85mm, ø 95mm중에서 ø 85mm가 가장 낮은 1630 MPa 응력이 나타났다. 따라서 1중 박음으로 금형을 설계할 경우 박음량을 0.6% 이상으로 적용하는 것이 유리하다.
3.2 2중 박음에 따른 금형 응력 해석
2중 박음 해석을 위한 Morgan 수식은 식(3)부터 식(5)와 같이 표현된다. 소재와 접하는 내경(d0)을 ø 43mm, 2차 보강링의 외경(D2)을 ø 210 mm로 입력하여 계산하였다.
| (3) |
| (4) |
| (5) |
식(3)부터 식(5)로 계산된 인서트 분할경(D1)은 ø 73mm이고 1차 보강링의 외경(D2)은 ø 128 mm로 계산되었다.
2중 박음은 인서트의 크기는 ø 73mm로 선정하여 각각 1차 박음의 박음량을 0.4%, 0.5%, 0.6%, 2차 박음 박음량은 동일하게 0.4%로 설계하고 3가지 조건에 대한 해석을 진행하였다.
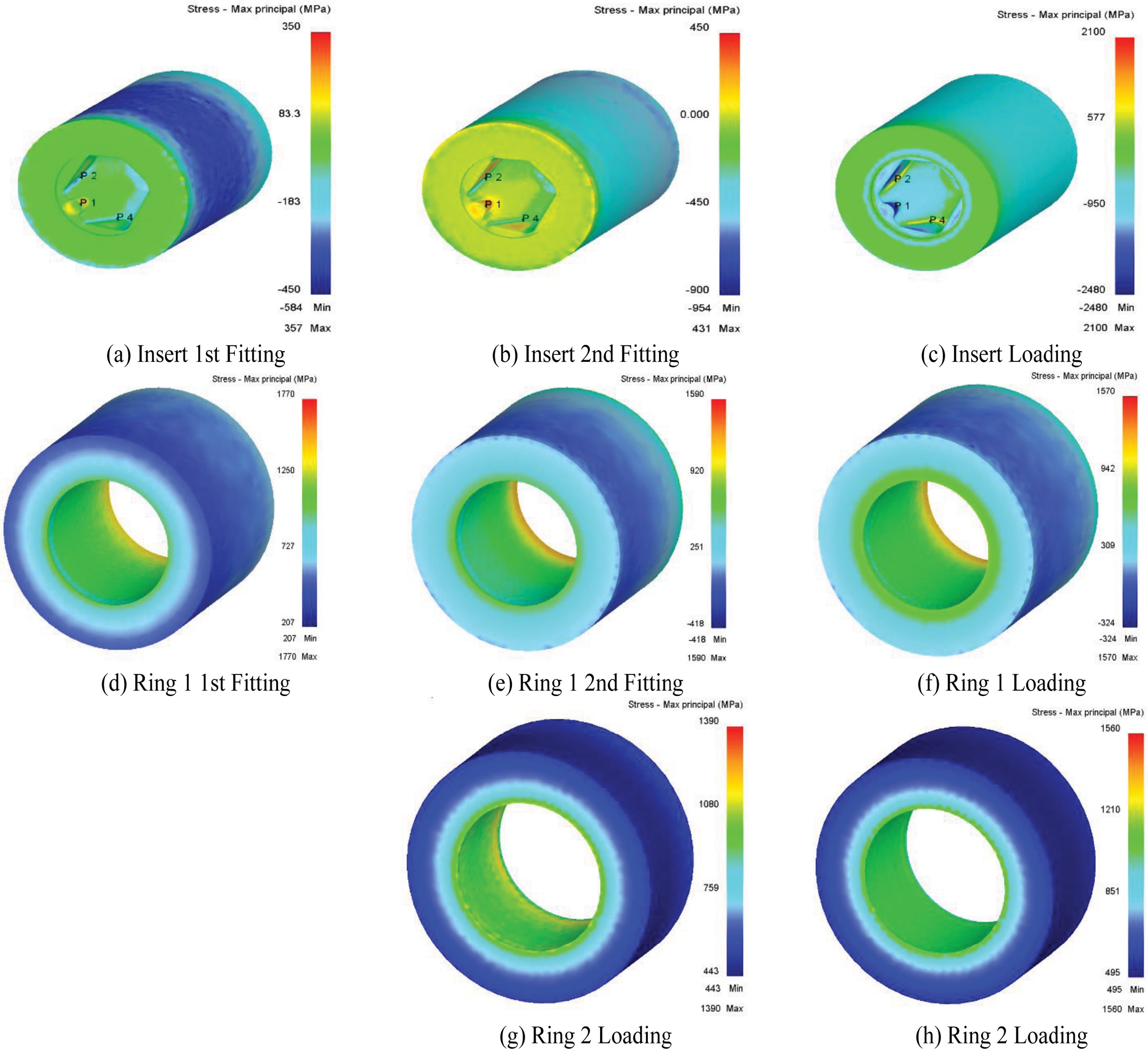
2중 박음의 해석결과는 Figs. 8(a)부터 8(c)는 Insert의 응력분포, Figs. 8(d)부터 8(f)는 1차 보강링의 응력 분포, Figs. 8(g)부터 8(h)는 2차 보강링의 응력 분포를 각각 나타낸 것이다. Table 2에는 조건별 박음 후 응력과 단조하중이 부과된 후의 응력을 정리하여 나타내었다. Table 2에서 1차 보강링과 2차 보강링 모두 보강링의 주응력 허용치인 1,600 MPa을 초과하지 않는 것으로 예측되었다. 인서트의 경우 단조 성형 후 주응력 허용치인 2,400 MPa을 초과하지 않았으나 1차 박음량 0.4%, 2차 박음량 0.4%인 Table 2 Case 1의 경우 1,930 MPa의 주응력이 작용하고 있는 것을 볼 수 있었으며 주응력이 높게 나타나므로 금형 수명의 문제가 발생할 것으로 예상된다.
1차 박음량 0.5%, 2차 박음량 0.4%인 Case 2의 경우와 1차 박음량 0.6%, 2차 박음량 0.4%인 Case 3의 경우 각각 인서트에 작용하는 응력이 1,130 MPa, 558 MPa로 보강링을 추가하지 않았을 때의 응력보다 낮은 주응력을 보이고 있는 것을 알 수 있었다.
가장 낮은 주응력을 보이는 해석 조건은 1차 박음량 0.6%, 2차 박음량 0.4%으로 보강링을 늘리는 것을 통하여 금형 응력을 낮출 수 있을 것이다.
3.3 플랜지 곡률에 따른 응력 해석
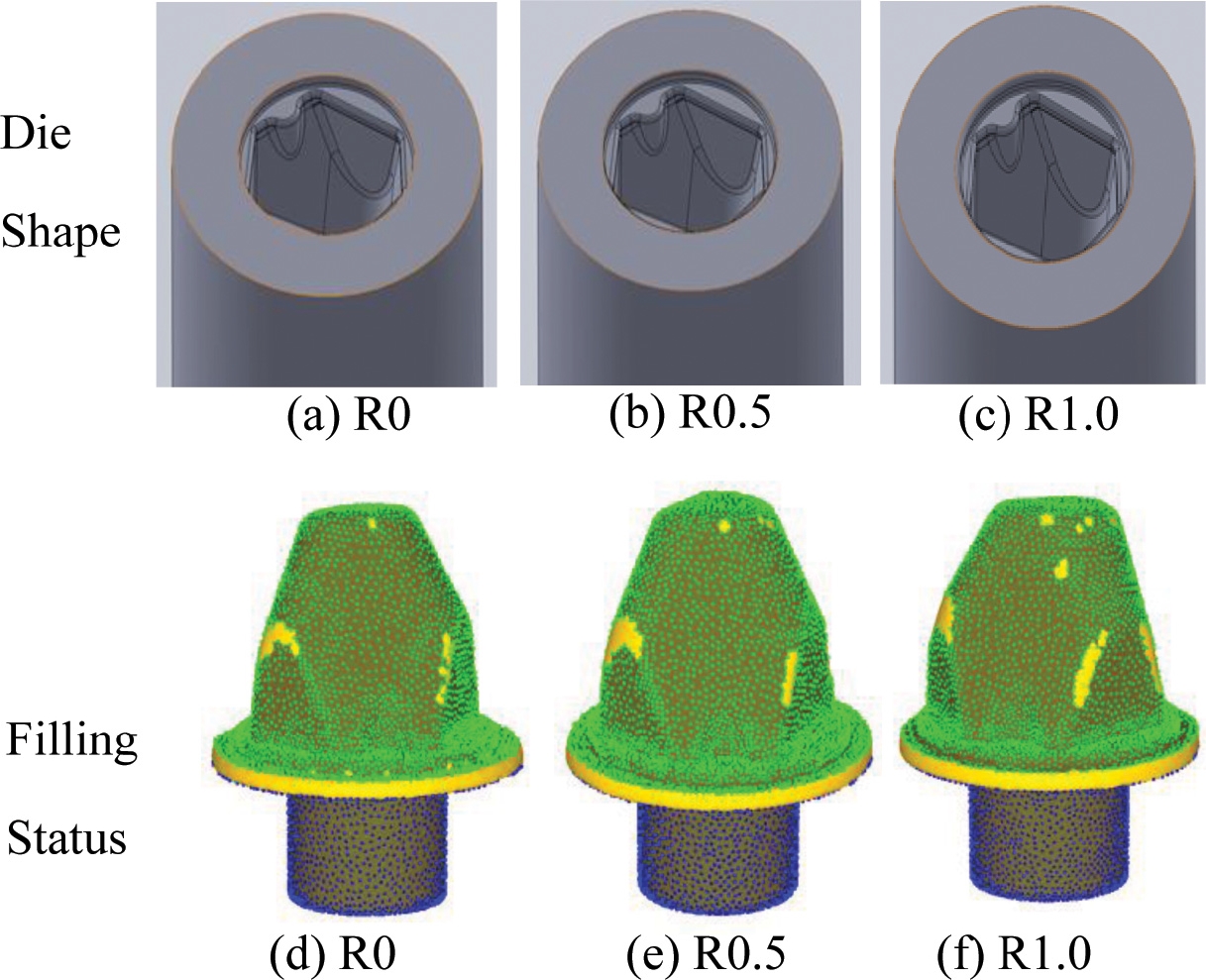
마운트 어댑터를 냉간 단조 공법으로 성형할 경우 머리부 충진 시 플랜지 부와 연결되는 부위에 금형 응력이 집중되어 금형 파손이 일어날 수 있으므로 금형에 곡률을 부여하여 금형 면압을 저감하고자 하였다. 플랜지 부의 곡률은 충진도와 응력에 영향을 미침으로 곡률의 크기에 따른 변화를 유한요소해석을 통하여 분석하였다. 곡률은 R0, R0.5, R1.0으로 3가지 경우에 관하여 해석을 진행하였으며, Figs. 9(a)부터 9(c)는 Insert 금형 응력 집중부에 곡률 R값의 형상을 나타내었다.
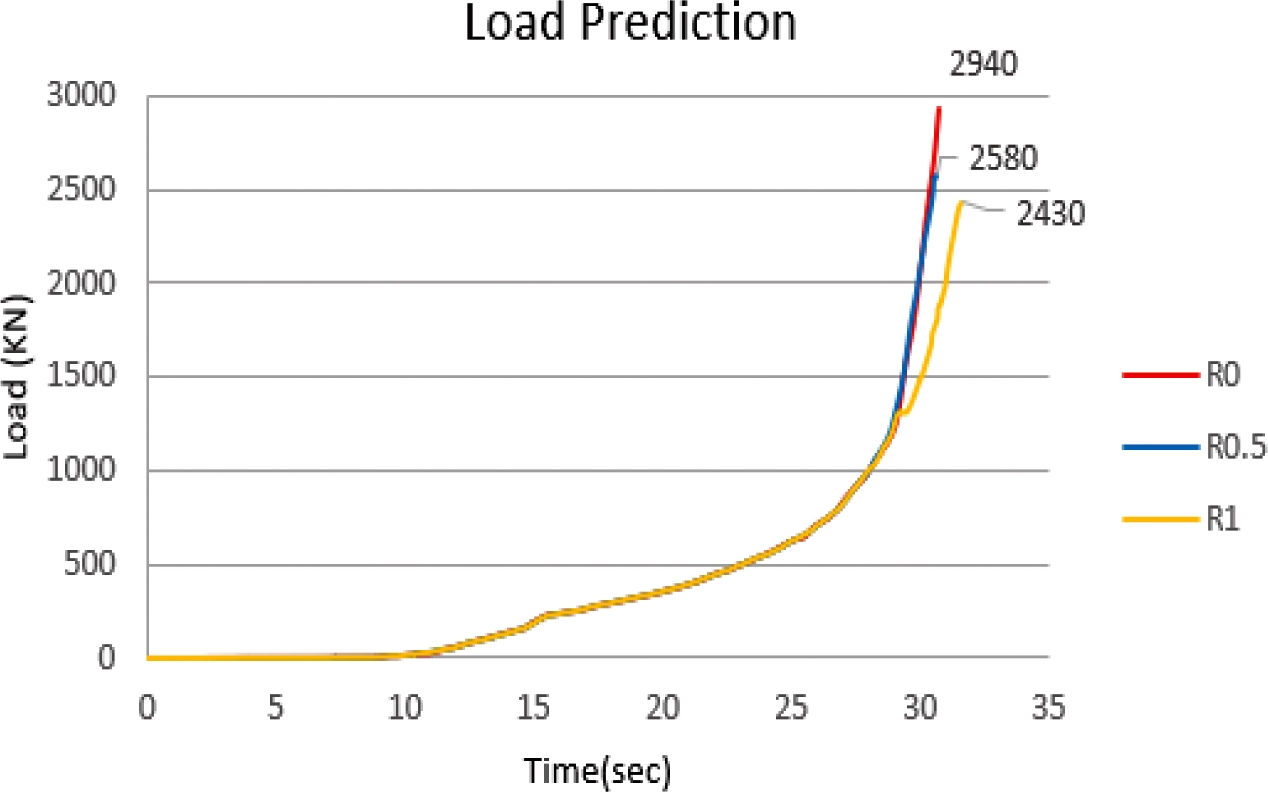
해석결과 Fig. 9(a)는 곡률이 R0인 경우로 하중이 2940 kN으로 가장 높게 예측되었고, Fig. 9(a)는 곡률 R0.5일 때 하중을 2580 kN, Fig. 9(a)는 곡률 R1.0에서 2430 kN의 가장 낮은 하중이 계산되었다. 하지만 Figs. 9(f)와 같이 9(c)가 충진도가 가장 낮은 것으로 볼 수 있으며 하중과 성형성을 종합적으로 고려했을 때 R0.5이 적절한 것으로 판단하였다. Fig. 10은 곡률에 따른 하중 분포를 나타낸 것이며 금형의 곡률이 증가하면 소재의 속도장의 연속성이 보장되고, 국부적인 비유동영역(Dead Metal Zone)이 사라져 소재 유동이 용이하게 됨에 따라 성형하중이 감소하는 것을 알 수 있다.
4. 금형의 금형 수명 계산
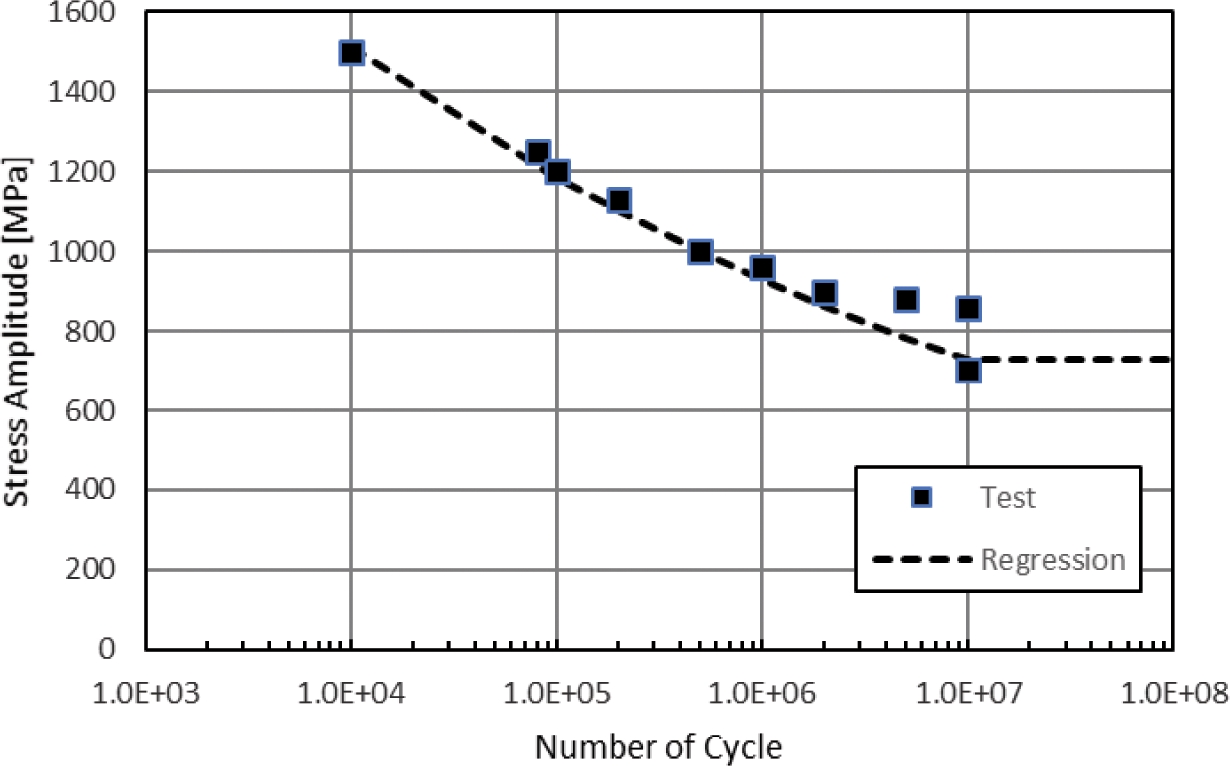
금형의 수명에 영향을 주는 요소에는 금형 재료, 열처리, 금형 조립공차, 윤활, 마모 등 다양한 인자들이 있다. 본 연구에서는 금형에 대하여 금형 응력에 따른 피로의 관점으로 접근하고자 하였다. 냉간 단조용 금형은 수만에서 수십만개의 제품이 생산 가능해야 가격경쟁력을 가질 수 있음으로 본 연구에서는 고싸이클 피로(High Cycle Fatigue)방법에 근거하여 금형 수명을 계산하였다. 피로해석은 금형에서 주로 파손이 발생되는 인서트에 대하여 분석되어야 함으로 Fig. 11와 같이 선행 연구에서 제시된 SKH51 소재의 응력-수명 선도(S-N Curve)를 사용하였다.16
일반적인 S-N 곡선은 교번하중에 대한 평균응력의 영향이 고려되지 않는다. 반면 단조 공정 중 금형에 작용하는 응력은 교번하중의 중심값인 평균응력이 금형의 위치별로 다르기 때문에 이를 고려한 피로수명 해석이 요구된다. 평균응력 효과를 고려하기 위해 일반적으로 널리 적용되고 있는 선도로는 Goodman과 Geber가 있다.11 Geber 선도가 실험 수명과 예측 수명이 일치하기는 하지만 수식이 복잡하고 피로수명 예측의 안정성 때문에 Goodman 선도가 보수적인 설계에 널리 사용된다.17
선행연구의 실험결과를 이용하여 허용 응력범위(S)와 수명(N)과의 관계식을 구하면 식(6)와 같다.
| (6) |
이를 피로강도(Sf)를 이용한 일반적인 금형 수명 식의 형태로 나타내면 a, b의 재료상수가 a = 4017.03, b = -0.106055로 식(7)과 같이 계산할 수 있다.
| (7) |
한편 Goodman 이론과 a, b 수식과의 관계를 이용하여 평균응력(σm), 교차응력(σa), 최대강도(Sut)를 고려한 금형 수명은 식(8)과 같이 나타낼 수 있다.18
| (8) |
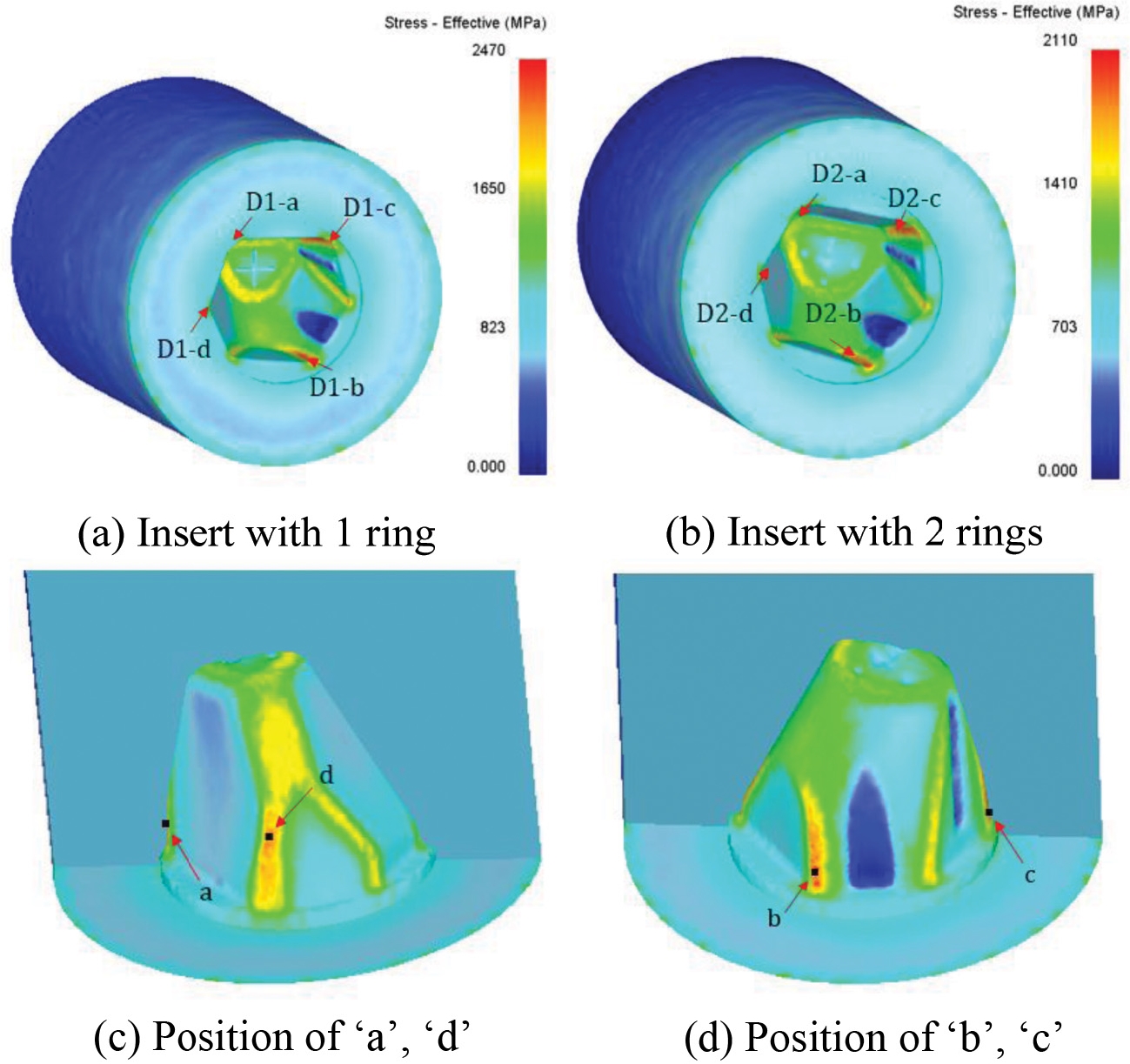
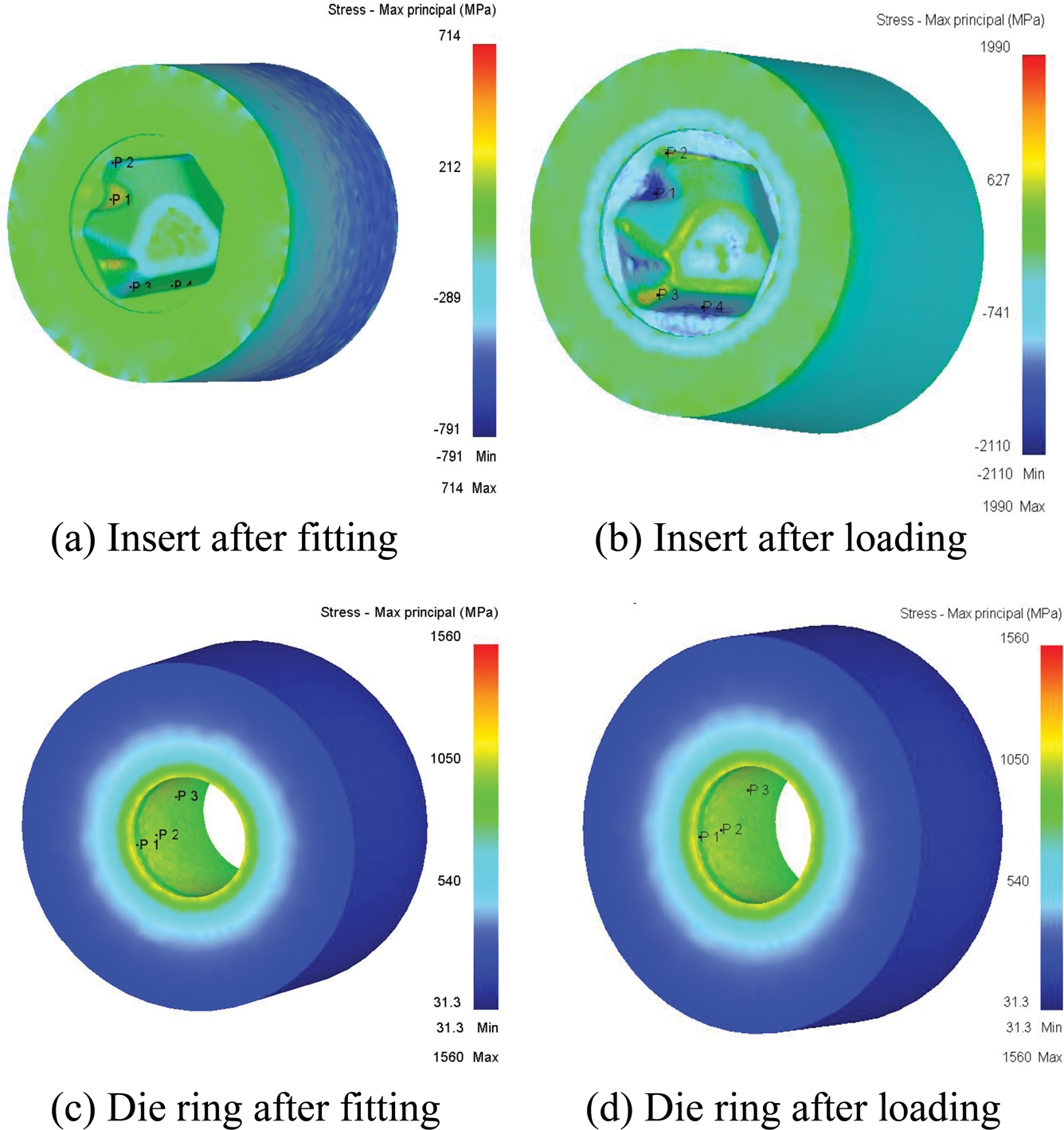
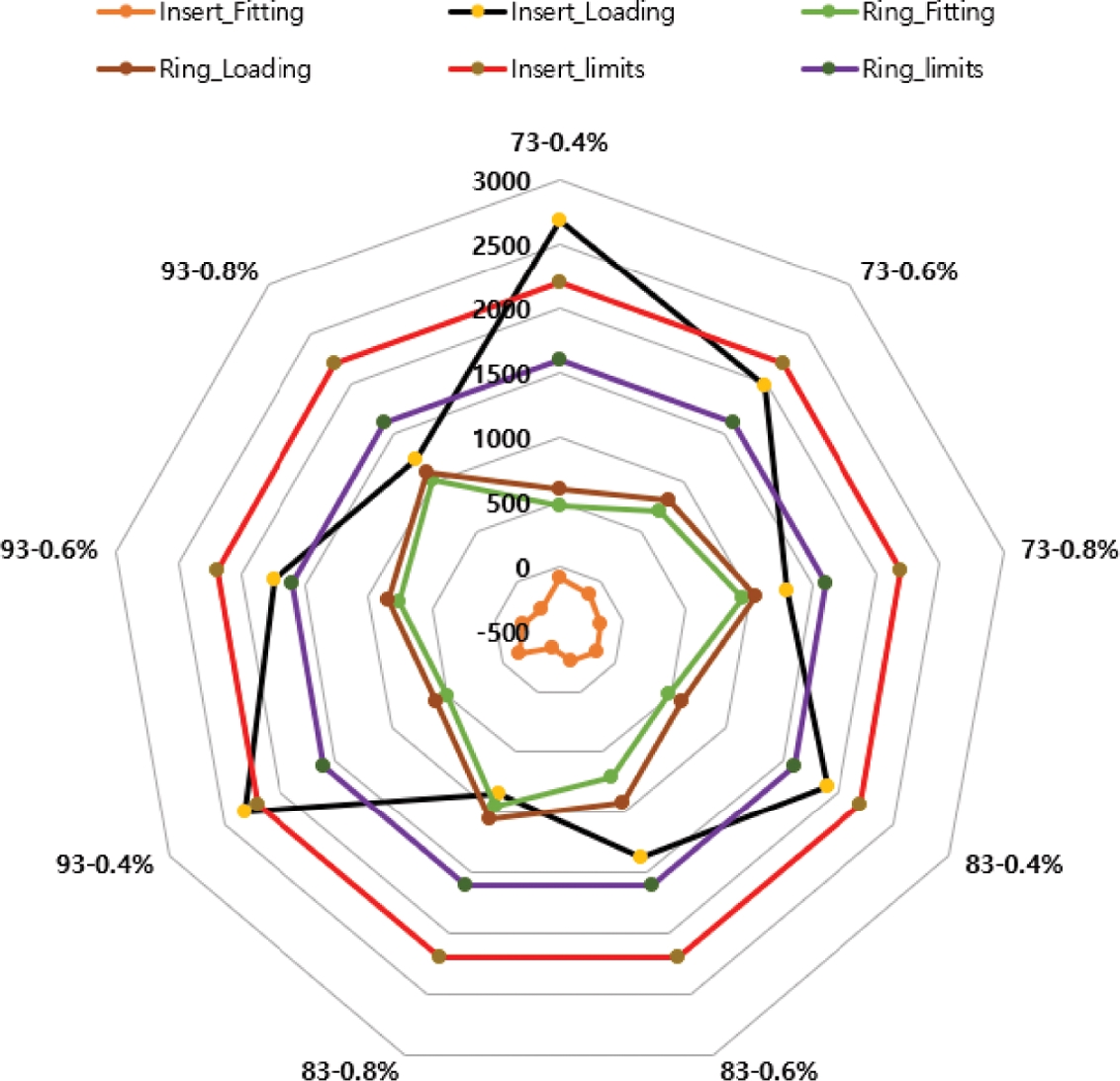
Table 3은 1중 박음에서 가장 낮은 응력을 보인 분할경 ø 85 mm의 박음량 0.6% 조건과 2중 박음에서 가장 낮은 응력을 보인 ø 73 mm의 1차 박음량 0.6% 2차 박음량 0.4%의 상당 응력이 높게 나오는 부위 4지점을 선정하여 나타낸 것이다. 상당응력분포 비교를 위한 위치와 최종 단조후의 응력 값을 1중 박음(D1)과 2중 박음(D2)에 대하여 Fig. 12에 나타냈다.
1중 박음 시 가장 높은 상당응력은 D1-a 부분의 1,330 MPa로 예측되었다. 2중 박음의 1차 Fitting시 D2-b 부분에서 1,500 MPa이 가장 높은 것으로 나타났고, 2차 Fitting시 같은 부위인 D2-b에서 2,760 MPa로 가장 높게 예측되었다. 1중 박음과 2중 박음 후 성형하중을 금형에 입력하여 해석한 상당응력은 1중 박음시 D1-a 부분에서 2,470 MPa로 가장 높게 나타났고, 2중 박음 시 D2-b 부분에서 2,110 MPa로 나타났다.
인서트의 열처리 후 경도가 HrC64일 경우 SKH51 금형강의 인장강도는 약 2,400 MPa이며, 이를 식(8)에 대입하여 계산하면 Table 3와 같이 금형 수명을 계산할 수 있다. 금형 수명은 평균응력과 교차응력에 따라 달라짐으로 2중 박음의 경우 최대응력이 나타나는 D2-b 지점에서 D2-a, D2-d보다 금형 수명이 높을 것으로 예상된다.
금형의 금형 수명 예측결과에 대한 타당성을 검증하기 위하여 1중 박음과 2중 박음으로 제작된 금형의 실제 작업수량을 비교하였을 때 1중 박음은 300개, 2중 박음은 120,000개 작업 후 파손되었다. 1중 박음과 2중 박음 금형의 파손 형상 및 단조품을 Fig. 13에 나타내었다.
금형의 파손 부위를 관찰하여 볼 때 금형응력해석 결과에서 응력집중이 발생한 위치와 동일한 지점에서 발생한 것을 알 수 있다.
5. 결론
본 연구에서는 자동차 엔진용 마운트 어댑터를 냉간 단조공법으로 성형하기 위하여 예비성형체의 형상, 금형구조, 곡률크기에 따른 응력변화와 응력상태를 고려한 금형 금형수명을 계산하고 설계된 공정과 금형으로 시작업을 진행하여 다음과 같은 결론을 얻었다.
(1) 비대칭 형상의 냉간 제품 성형시 발생되는 금형의 인장응력을 줄이기 위해 Morgan 수식을 이용한 금형 분할 설계를 하였고, 유한요소해석을 통하여 1중 박음 조건에서는 ø 83 mm 분할경, 0.6% 박음량에서 1630 MPa의 응력을 보였으나 0.6% 이하의 다른 조건에서는 대부분 1900 MPa 이상의 높은 응력범위를 나타내었다. 따라서 1중 박음의 경우 보강링은 0.6% 이상을 적용하는 것이 좋다.
(2) 2중 박음의 경우 Insert와 1차 보강링을 0.6%, 1차 보강링과 2차 보강링을 0.4%로 설계하였을 때 Insert에서 가장 낮은 885 MPa의 응력이 나타났으며, 2차 보강링에서 988 MPa의 최대응력이 예측되었다. 보강링에서는 응력이 증가하였으나 금형 수명을 고려하 2중 박음 0.6% / 0.4% 조건으로 금형을 제작하는 것이 유리하다.
(3) 어댑터 머리부의 최종단계 성형시 플랜지부에 응력이 집중되어 금형 파손이 일어날 수 있으므로 금형 곡률에 따른 하중변화를 비교한 결과 2940 kN에서 2430 kN으로 17.3% 감소하였다. 따라서 금형 곡률크기는 설계범위 내에서 가능한 크게 설계하는 것이 바람직하다.
(4) Goodman 수식을 이용하여 금형 수명을 계산한 결과 금형수명은 2중 박음의 경우 138,982회, 1중 박음의 경우 40회로 계산되었다. 단조실험에서는 1중 박음의 경우 300개, 2중 박음의 경우 120,000개의 제품을 성형한 후 파손되어 금형 수명 계산의 타당성을 확인하였다. 따라서 금형 응력 예측과 이에 따른 금형 수명 계산방법은 타당하며 단조 공정 설계 시 매우 유용할 것으로 판단된다.
NOMENCLATURE
| d0 : | Inner diameter of insert die |
| D1 : | Outer diameter of insert die |
| D2 : | Outer diameter of 1st stress ring |
| D3 : | Outer diameter of 2nd stress ring |
| S : | Stress Amplitude of forging die |
| N : | Number of cycle |
| a,b : | Material constants |
| Sf : | Fatigue strength |
| Sut : | Ultimate strength |
| σm : | mean stress |
| σa : | Alternative stress |
Acknowledgments
이 논문은 중원대학교 교내학술연구비 지원에 의한 것임(No. : 2017-037).
REFERENCES
-
Yang, C. and Ngaile, G., “Preform Design for Forging and Extrusion Processes based on Geometrical Resemblance,” Proceedings of the Institution of Mechanical Engineers, Part B: Journal of Engineering Manufacture, Vol. 224, No. 9, pp. 1409-1423, 2010.
[https://doi.org/10.1243/09544054JEM1799]

- Han, S. Y., Jeong, Y. D., and Kim, D. H., “Preform Design for the Warm Forging of the Precision Bevel Gear,” Proc. of the 11th International Scientific Conference, pp. 231-234, 2002.
-
Ozturk, M., Kocaoglan, S., and Sonmez, F. O., “Concurrent Design and Process Optimization of Forging,” Computers and Structures, Vol. 167, pp. 24-36, 2016.
[https://doi.org/10.1016/j.compstruc.2016.01.016]

- Cho, N. C., Lee, S. H., Hong, S. S., and Lee, J. S., “Forming of Axisymmetric Heavy Forgings by Preform Design,” Transactions of Materials Processing, Vol. 2, No. 3, pp. 15-26, 1993.
- Jung, H. C., Lee, Y. S., and Kim, S. W., “A Study on the Effect of Preform Shape and Residual Stress on Die Stress,” Proc. of the Spring Conference on Korean Society for Technology of Plasticity, pp. 451-454, 2012.
-
Wang, C., Kam, H., and Wang, X., “Determination of Optimal Shrink Fitting Ratio for 2-Layer Compound Forging Die by Improving Fatigue Life in Backward Extrusion,” Procedia Engineering, Vol. 207, pp. 2215-2220, 2017.
[https://doi.org/10.1016/j.proeng.2017.10.984]

-
Kang, J., Bae, J., On, H., and Kwon, Y., “Tapered Joint Design for Power Transmission of MW-Grade Wind Turbine,” Transactions of the Korean Society of Mechanical Engineers A, Vol. 39, No. 11, pp. 1183-1189, 2015.
[https://doi.org/10.3795/KSME-A.2015.39.11.1183]

- Lee, K. S., Kim, G. Y., and Ahn, Y. S., “Study on the Optimum Design of the Insert Ring and Shrunk Ring of the Cold Forging Die for an Automotive Wheel Nut,” Transactions of Materials Processing, Vol. 27, No. 3, pp. 165-170, 2018.
- Li, Q., Kim, M. C., Jung, D. C., Son, Y. H., and Joun, M. S., “Quantitative Analysis of Effect of Shrink Fit in Cold Forging,” Journal of the Korean Society for Precision Engineering, Vol. 28, No. 3, pp. 301-307, 2011.
-
Lee, H. C., Saroosh, M., Song, J., and Im, Y. T., “The Effect of Shrink Fitting Ratios on Tool Life in Bolt Forming Processes,” Journal of Materials Processing Technology, Vol. 209, No. 8, pp. 3766-3775, 2009.
[https://doi.org/10.1016/j.jmatprotec.2008.08.032]

-
Lee, I., Lee, S., Lee, S., Jeong, M., Seo, P., et al., “Prediction of Shearing Die Life for Producing a Retainer Using FE Analysis,” Transactions of Materials Processing, Vol. 24, No. 4, pp. 264-271, 2015.
[https://doi.org/10.5228/KSTP.24.4.264]

-
Saroosh, M., Lee, H. C., Im, Y. T., Choi, S. W., and Lee, D. L., “High Cycle Fatigue Life Prediction of Cold Forging Tools based on Workpiece Material Property,” Journal of Materials Processing Technology, Vol. 191, Nos. 1-3, pp. 178-181, 2007.
[https://doi.org/10.1016/j.jmatprotec.2007.03.015]

- Yamamoto H., “Compressive Machining Tool,” Japan Machinist, pp. 102-117, 1971. (in Japanese)
-
Vazquez, V., Hannan, D., and Altan, T., “Tool Life in Cold Forging – An Example of Design Improvement to Increase Service Life,” Journal of Materials Processing Technology, Vol. 98, No. 1, pp. 90-96, 2000.
[https://doi.org/10.1016/S0924-0136(99)00309-X]

- Yurtdaş, S., İnce, U., Kılıçaslan, C., and Yıldız, H., “A Case Study for Improving Tool Life in Cold Forging: Carbon Fiber Composite Reinforced Dies,” Research on Engineering Structures and Materials, Vol. 3, pp. 65-75, 2017.
-
Lu, L., Shiozawa, K., and Morii, Y., “Gigacycle Fatigue Behavior and Fracture Morphology of High Speed Tool Steel, JIS SKH 51,” The Japan Society of Mechanical Engineers, Vol. 69, No. 679, pp. 662-670, 2003.
[https://doi.org/10.1299/kikaia.69.662]

- Zorowski, C. F., “Design for Strength and Endurance–Chapter9: Fluctuating Load Analysis,” http://designforstrength.com/chapter-09.pdf, (Accessed 11 NOV 2019)
- Dehghani, K. and Jafari, A., “Finite Element Stress Analysis of Forging Dies to Improve their Fatigue Life,” Materials Science-Poland, Vol. 28, No. 1, pp. 139-152, 2010.

Director of R&D Center in Taejung Technical Mfg Co., LTD. His research interest are forging process and die design optimization
E-mail: kh.ann@itaejung.com

Professor in the Department of Mechanical Engineering, Chungbuk National University. His research interest are machine design optimization by structural analysis and forging process design
E-mail: hycho@chungbuk.ac.kr

M.Sc. candidate in the Department of Convergence Engineering, Jungwon University. Her research interest are forging process and machine design by finite element analysis
E-mail: 213ska@naver.com

Professor in the Department of Aeromechanical Engineering, Jungwon University. His research interest is the design optimization of forging process and machine components by finite element analysis
E-mail: jhkang@jwu.ac.kr