Delay-Time Adjustable Input Shaping Method for Positioning Systems Subject to Repetitive Motion
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Most positioning systems experience residual vibration during operation. Such residual vibration can be eliminated or reduced to an acceptable level by using the input shaping method. However, adopting the input shaping methods typically introduces a certain amount of time-delay into a system. This study focused on the development of a delay-time adjustable input shaping method to eliminate vibration caused by repetitive motion in positioning systems. The proposed input shaping method, called the virtual mode (VM) input shaper, uses a virtual frequency parameter that adjusts delay-time and cancels residual vibration. Unlike most previous input shaping studies, this study investigated VM input shaping performance to eliminate the steady-state vibration induced by repetitive motion in positioning systems. To this end, an analytical formulation was derived and used for simulating the input shaping performance with varying dominant parameters involved in a system. Experiments were also performed to validate the proposed method.
Keywords:
Positioning system, Delay-time, Residual vibration, Input shaping, Virtual mode키워드:
위치결정 장치, 지연시간, 잔류진동, 입력 성형기, 가상 모드1. Introduction
The use of positioning systems has become widespread in numerous types of machines, including machine tools, manufacturing machines for liquid crystal displays and semiconductors, and cranes. To maintain high productivity, these machines are operated at high speeds, which often lead to operation with a significant level of residual vibration. The input shaping method has been acknowledged as an effective technique for reducing such residual vibration.1,2 However, adopting an input shaping method introduces a time-delay into control systems, which slows the control processes of positioning systems.
Many input shaping studies have been conducted with the goal of eliminating residual vibrations in flexible positioning systems while minimizing time-delay. Singhose and Pao demonstrated how effective input shaping can be compared to other time-optimal control methods in terms of eliminating the vibration in flexible systems.3 Singhose and Singh focused on the time-delay phenomenon considering reference commands.4 The main concept of their study was time-delay filtering and control while regulating flexible systems.
Singhose and Pao compared various methods of input shaping in terms of command speed.5 Their comparison revealed that input shapers with negative impulses provide faster maneuvering compared to input shaping methods using only positive impulses. Several studies6-8 have focused on negative impulse shapers as main tools for reducing the rise time of a system. However, this strategy degrades the insensitive nature of the command shaper regarding natural frequency errors.
Singh and Vadali proposed a time-delay controller for the attenuation of residual vibration in flexible structures.9 Their intention was to identify an optimal time-delay or minimize time-delay using special time-delay elements. In the reference,10 the authors discussed time-efficient input shaping control techniques for container crane systems. The main idea was to compensate for the maneuvering time of input shaping with a lower level of residual vibration. An adaptive time-delay command-shaping filter was studied by Rhim and Book.11 They derived a formulation in which time-delay is not considered to be a function of system parameters and can be adjusted freely for multi-mode elastic systems. Baumgart and Pao derived shorter shapers that could perform the command generation process with less delay-time for multi-input-multi-output systems.12
Singhose described the relationship between the insensitivity and command duration of various input shapers.13 He emphasized that achieving greater robustness of input shaping typically results in a longer rise time. Among a number of input shaping methods, so-called the specified insensitivity shaper manifested its ability to reduce rise time. Hong et al. developed a novel command shaping method using artificial mode constraints.14 Their objective was to reduce both residual vibration and command shaping duration for a single-mode system. Pai proposed an observer-based discrete-time neuro-sliding mode control scheme combined with input shaping.15 The goal was to improve the robustness of the control scheme in the presence of modeling uncertainties while maintaining a duration of the impulse sequence. The drawback of this technique is that it operates based on feedback control, which makes the system complicated and expensive. The zero-time-delay input shaping scheme was introduced by Zhao and Tomizuka, who modified reference commands to compensate for the delay-time expected from command shaping, then applied command shaping to the modified unshaped commands.16
Masoud and Alhazza outlined a smooth multi-mode command shaping method.17 The goal of their study was to smooth command profiles to remove vibrations and jerks while providing an optionally changeable maneuvering time. The main downside of this method is a degradation in robustness when reducing maneuvering time. It has been widely acknowledged that the greater the maneuvering speed a command shaper employs, the more sensitive it becomes to modeling errors.
Many studies have been and are being carried out in the field of input shaping because input shaping is a very efficient method for coping with rapidly developing technologies requiring smoother, faster, and more efficient positioning systems. However, most researchers have focused on input shaping methods that are confined to transient vibrations. Very few studies have addressed input shaping methods for the elimination of forced steady-state vibration. Regarding the difference between transient and steady-state vibrations, transient vibration is oscillation that is induced after one-time motion, whereas steady-state vibrations are oscillations that occur during repetitive motions after a sufficient time has elapsed for transient vibrations to decay. Kwon and Hong investigated input shaping performance for the forced motion of positioning systems.18 They applied the zero-vibration (ZV) input shaping method to eliminate residual vibrations during repetitive motions. However, they did not extend their research to other input shaping schemes. Because the conditions of forced vibration differ from those of transient vibration, the shaping results for forced vibration are also different from those for transient vibration.
This paper introduces the command generation method called virtual mode (VM) input shaping that enables an input shaper to adjust delay-time while expeditiously reducing steady-state vibrations. This paper rigorously deals with a delay-time adjustable function for the VM input shaping method on steady-state vibration. The delay-time is adjusted by simply changing a virtual frequency parameter. This paper also describes the robustness of the VM input shaper when altering the virtual frequency value based on both simulations and experiments. Additionally, to interpret the characteristics of the input shaping more accurately, the effects of several important parameters of VM input shaping, including maximum velocity, moving distance, and acceleration time, are analyzed with respect to residual vibration in steady-state vibration. This analysis is performed using the analytically derived equations and responses or easily handling the steady-state vibration with the VM command shaper. Experimental results are also provided to validate the proposed VM input shaper.
2. Concepts of VM Input Shaping
The VM input shaping method has been detailed in Refs. 19-21. Here, the VM input shaping method is briefly summarized. The VM input shaping method is based on a special type of multi-mode input shaping. Unlike conventional multi-mode input shaping that is basically performed by convoluting individual single-mode input shapers, this multi-mode input shaping method designs shapers with the lowest possible number of impulses based on the pole-zero cancellation concept. With marginal loss of insensitivity, the proposed multi-mode shaper can reduce delay-time compared to a conventional, convolved multi-mode shaper. In general, the number of impulses in this multi-mode shaper is equal to the number of modes plus one.19
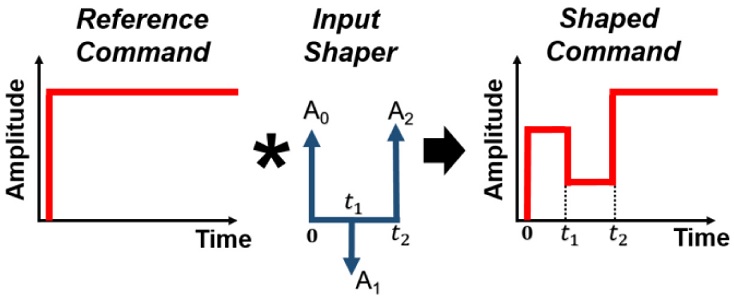
The VM input shaping method utilizes a two-mode input shaper with three impulses A0, A1, and A2 with consideration for one extra mode in addition to the target mode that should be suppressed. This extra mode is defined as the VM. The VM frequency is a design parameter for adjusting the delay-time. To generate a command shaper, the impulse amplitudes and their application timings must be derived. A VM command shaper can be represented as Eq. (1).2
| (1) |
where δ(t) is a unit impulse function. Assuming that the natural frequency (ωn) and damping ratio (ζ) of the vibration system are known, and that the first impulse is applied at a time of zero, the second and third impulse locations, t1 and t2, are calculated as Eqs. (2) and (3).2
| (2) |
| (3) |
where ων is the VM frequency. The impulse amplitudes are obtained using the following Eqs. (4)-(6).2
| (4) |
| (5) |
| (6) |
Here, are the non-dimensional natural frequency and non-dimensional damped natural frequency, respectively, which are defined as Eqs. (7) and (8).2
| (7) |
| (8) |
As shown in Eqs. (4)-(8), the impulse amplitudes and their timings depend on the system natural frequency and damping ratio.
By simply changing the virtual frequency, the system robustness and the duration of command generation can be adjusted. The relationships between the virtual frequency, system robustness, and command generation delay-time will be detailed later.
Fig. 1 presents an illustration of the VM input shaping process. If the system parameters are known precisely, then most or all of the residual vibration can be eliminated after the time of the last impulse.21
3. VM Input Shaping for Steady-State Vibration
3.1 System Modeling
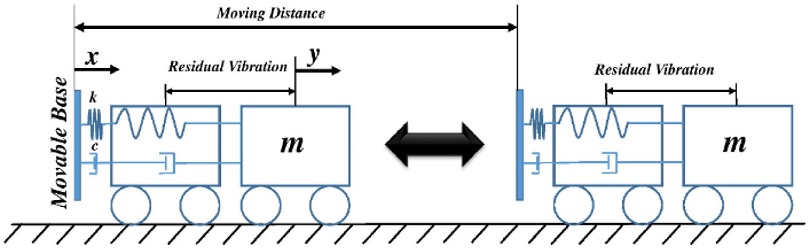
Fig. 2 presents an illustration of a single-degree-of-freedom system moving forward and backward repetitively along a horizontal plane.18
In this model, a mass m is attached to a moving base by a spring k and damper c. The equation of motion for the system is expressed as Eq. (9).
| (9) |
The transfer function can be represented as Eq. (10)
| (10) |
The displacement of the mass, which is defined as y, is analyzed when an input motion x is applied to the moving base. As illustrated in Fig. 2, residual vibration may be induced at the starting and stopping points of each forward and backward motion of the moving base.
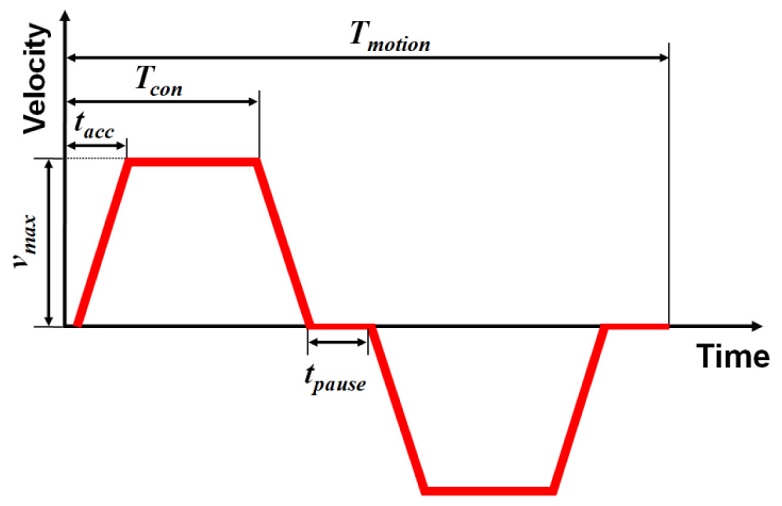
A velocity profile of a reference command is presented in Fig. 3. According to this velocity profile, the moving base experiences acceleration during the acceleration time tacc until it reaches its maximum velocity νmax. After the elapsed time Tcon (Constant Time), the base begins decelerating. At the ending part of the forward motion, the moving base stops for a period of tpause. Next, the same motion is repeated in the opposite direction. In this manner, the moving base repeats forward and backward movements.
3.2 Analytically Derived Shaped Command and Response
To analyze a VM input shaped command and its response accurately for steady-state vibration, analytical formulations for the governing equations and responses were derived and employed in our simulations.
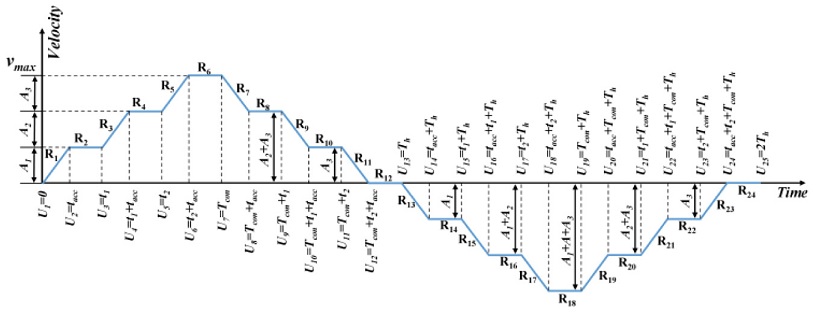
One set of forward and backward motions of a VM input shaped command profile is presented in Fig. 4. Considering the velocity command with piecewise commands Ri, the shaped command can be represented as Eq. (11)
| (11) |
where Ak , k = 1,2,3 represents impulse values for the shaper.
| (12) |
In Eq. (11), Ak is selected from A1, A2, or A3 depending on the ending point of each velocity Ri command. The “±” sign is chosen based on whether the velocity changes from positive to negative or vice versa. Th represents the half period of a command for one forward and backward motion.
After defining all separate velocity commands Ri, the sum of individual commands is calculated as Eq. (13).
| (13) |
To obtain the response equation, the derived input velocity command equation is multiplied for the target system using a Laplace transform formula as Eq. (14).
| (14) |
The time-domain response y(t) can be obtained by simply performing the inverse Laplace transform of Y(s). Then, the R(t) and y(t) formulas are readily available analytically for a command shaped by the VM input shaper.
| (15) |
where
| (16) |
4. Simulations
4.1 Application of the Proposed Input Shaper to Steady State Vibration
To demonstrate the effectiveness of the proposed input shaping method, simulations are performed. The simulation condition of parameters is provided in Table 1.
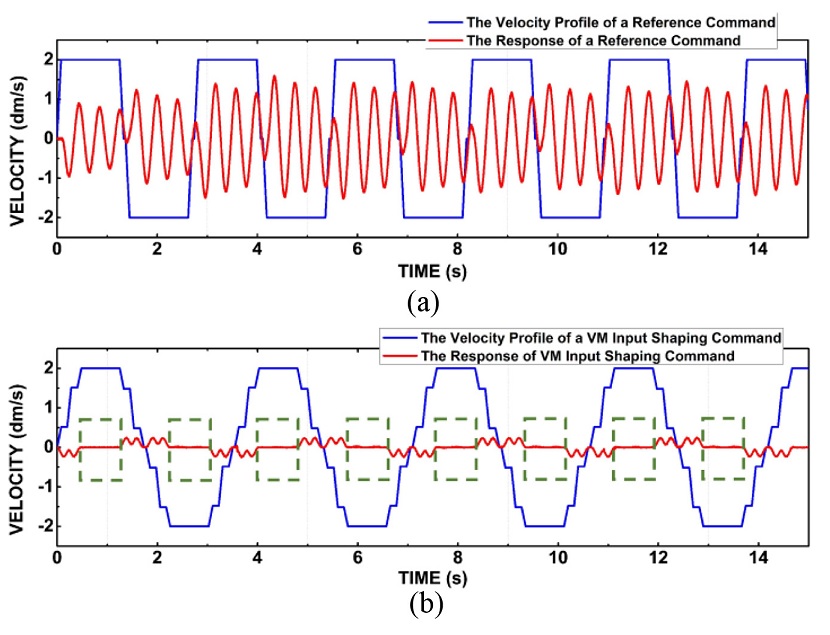
Fig. 5(a) presents the response during the motion of ten forward and backward movements based on the reference command. Significant residual vibration occurs during the motion. Over time, the vibration pattern converges to a steady-state response. In this figure, the response becomes sufficiently steady after the sixth or seventh forward motion.
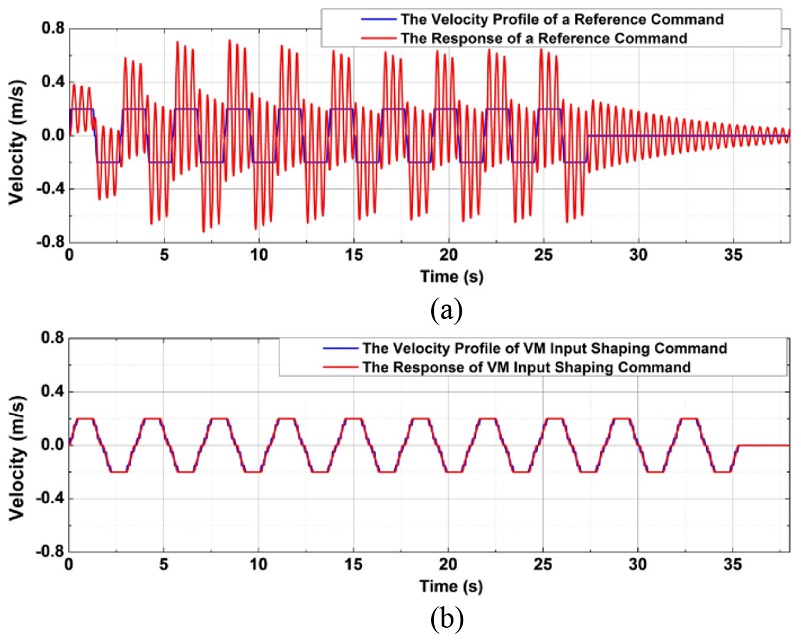
Time domain responses of a reference command and VM input shaped command: (a) Reference command and its response and (b) VM input shaped command and its response
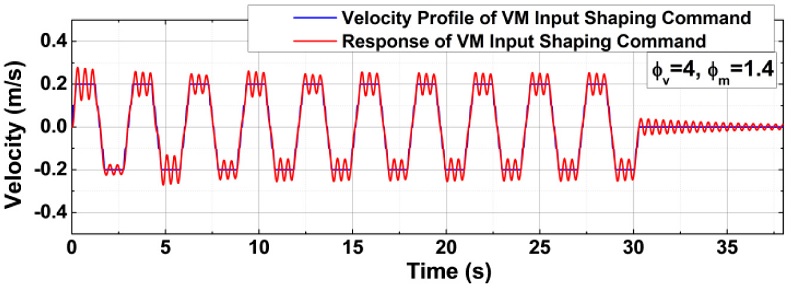
Fig. 5(b) illustrates a VM input shaped command that results in zero residual vibration. This response is obtained when the normalized modeling frequency (NMF, ϕm = ωm/ωn) is equal to one (i.e., No Modeling Frequency Error). Fig. 5 also reveals that there is a delay-time when applying an input shaped command. The duration difference for ten forward and backward motions between the VM input shaped command and a conventional command is approximately 8 s. The advantage of the VM input shaping method is that the delay-time can be adjusted by changing the virtual frequency.
Fig. 6 presents time-domain responses obtained with varying normalized virtual frequency (NVF) values (ϕν = ων/ωn). This simulation was implemented under the condition of 5% NVF (ϕν = 1.05). The simulation results demonstrate that increasing the NVF reduces the duration of input shaping. Specifically, the command duration is reduced from 35.13 s to 29.59 s by increasing the NVF from one to six. As a result, a reduction in the input shaping duration can be accomplished by increasing the NVF. However, it should be noted that the impulse amplitudes of the shaper also increase as the NVF increases.
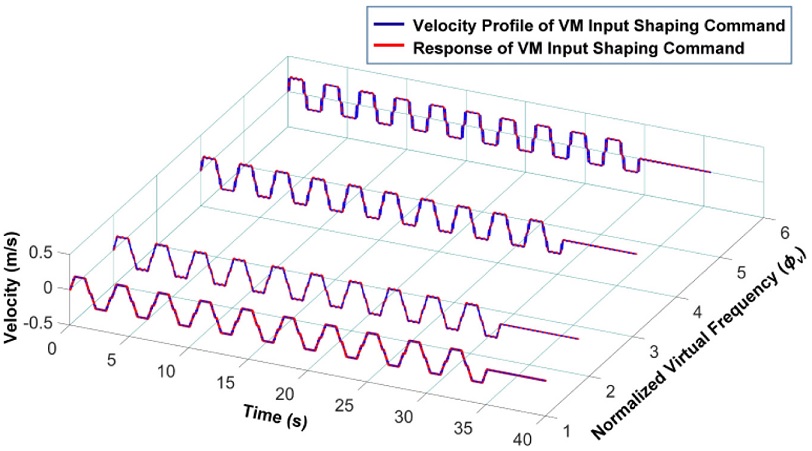
Time-delay variation with changing virtual frequency in the time-domain response of VM input shaping
Because a large impulse magnitude results in high acceleration and velocity, the actuator capacity must be carefully considered to apply the command shaper with impulses of large magnitudes. By altering the virtual frequency, the delay-time of VM input shaping can be adjusted to an acceptable value while effectively eliminating the residual vibration component of forced vibration. However, Fig. 7 reveals that modeling errors in the system characteristics can also lead to residual vibration.
4.2 Performance of the Proposed Input Shaper
To analyze the relationship between the VM input shaping parameters and vibration response, an analysis for a VM shaped command and its response is performed.
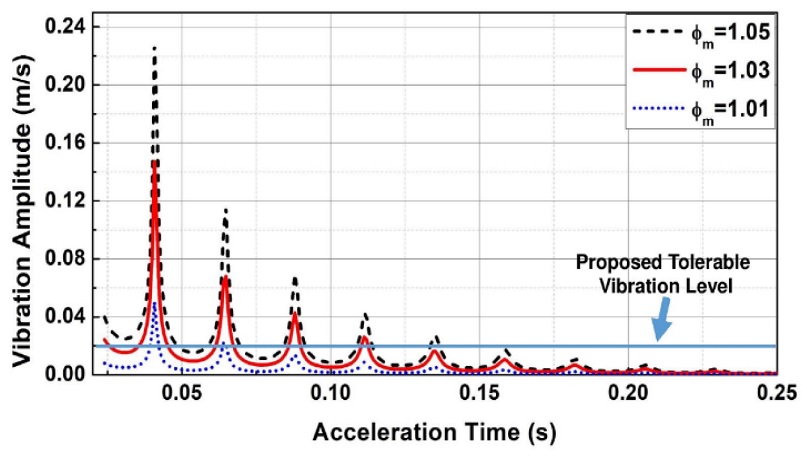
Fig. 8 presents the sensitivity curves with respect to different NVFs. Fig. 8(a) shows the sensitivity for 1.2-2.5 of NVF, while Fig. 8(b) depicts the sensitivity for 2.5-9 of NVF. These sensitivity curves illustrate how robust the system is against modeling errors for different virtual frequencies. The width of the sensitivity curve for a given level of vibration amplitude defines the insensitivity that represents the robustness of the system quantitatively. The width is determined at the tolerable vibration level of 0.02 m/s, which is equivalent to a 5% vibration response to the given reference command.
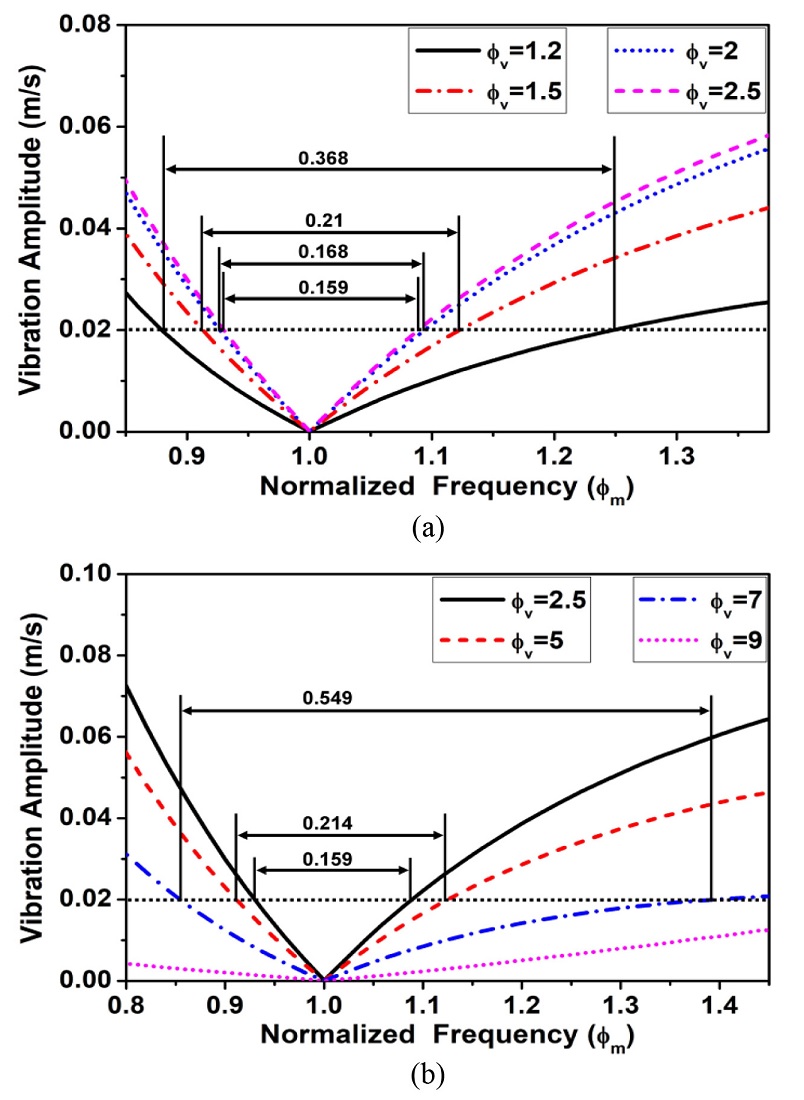
Sensitivities for different NVFs (ϕν): (a) Sensitivity for an NVF of ϕν=1.2-2.5 and (b) Sensitivity for an NVF of ϕν = 2.5-9
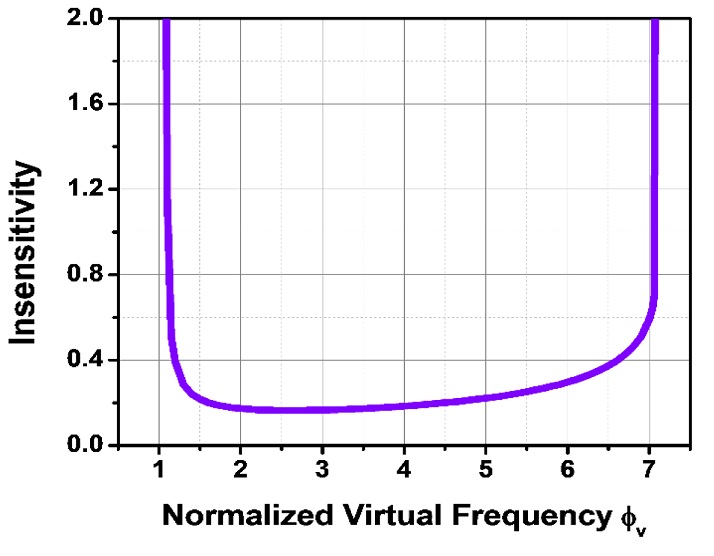
The simulation results demonstrate that robustness decreases as the NVF increases from 1 to 2.5. However, above 2.5, the robustness increases with the NVF up to a value of seven. It should be noted that increasing the NVF makes the motion faster.
Fig. 9 presents insensitivity values as a function of NVF. Here, the insensitivity values represent the robustness of the system against errors, which are represented as bars in Fig. 8. At an NVF of one, the insensitivity becomes infinite. However, because there is always a difference between the theoretical and actual frequencies, the NVF should also be considered for a uncertain error. As already shown in Fig. 9, robustness decreases as the NVF increases from 1 to 2.5. After ϕν = 2.5, system insensitivity begins to shift to the stronger side. It should be noted that increasing the NVF value decreases the maneuvering time of commands. However, as the maneuvering time decreases, the amplitudes of command impulses increase. Therefore, the value of the NVF parameter should be intelligently selected such that VM input commands maneuver the system in a reasonably short time while allowing high amplitudes of impulses.
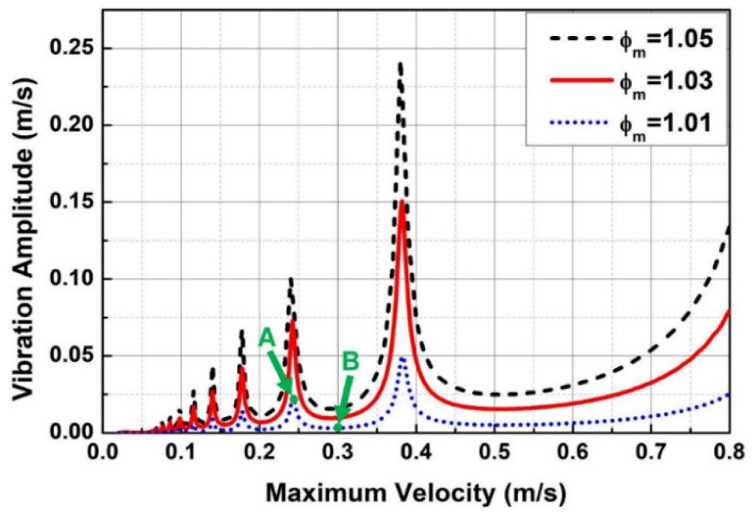
Fig. 10 presents the maximum velocity and vibration response characteristics under three different NMF conditions for VM input shaping. If the NMF is close to its exact value (ϕm = 1), the VM shaper becomes less sensitive to changes in maximum velocity. However, it can be observed that an increase in motion speed with a greater NMF error leads to a greater vibration response. Fig. 10 indicates a new opportunity to reduce residual vibrations to an arbitrarily low level by increasing or decreasing the maximum velocity. For example, assuming that a positioning system is moving according to a VM command under the conditions of νmax = 0.24 m/s (Maximum Velocity) and ϕm = 1.01 (Normalized Frequency), which is illustrated by an “A” arrow in Fig. 10, the system vibration magnitude becomes 0.0183 m/s. However, if the maximum velocity is increased to νmax= 0.29 m/s, then the vibration amplitude is reduced to 0.0032 m/s, which is represented by the “B” arrow. This approach enables the command designer to find an optimal maximum velocity when employing VM input shaping.
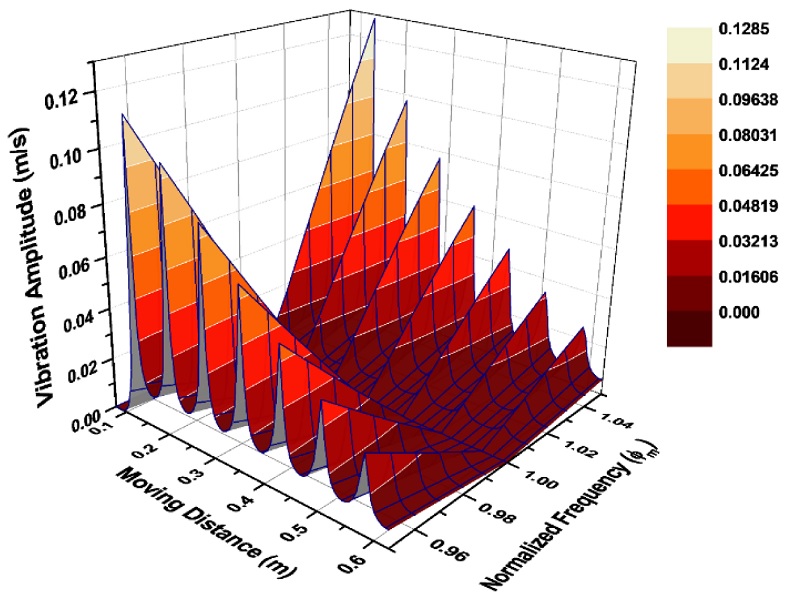
The vibration responses to changes in moving distance of a VM input shaper are presented in Fig. 11. As the normalized frequency moves closer to one, the system robustness increases against variations in moving distance. Additionally, this simulation result indicates that the greater the moving distance used for the VM input shaper, the smaller the residual vibration in the system. It should also be noted that the vibration amplitude changes with periodic fluctuations when increasing the moving distance (the period is equal to 0.075 m). By carefully analyzing these lines, an optimal moving distance can be estimated. This result can be used when adjusting the distance to avoid any additional residual vibration.
A visual representation of the dependency of vibration responses on acceleration time is presented in Fig. 12. The graph indicates that if the system reaches its maximum velocity with a longer acceleration time, system oscillations become smaller. In this case, it should be noted that variations in acceleration time alter the maximum velocity in the following manner, Eq. (17)
| (17) |
where νmax is the maximum velocity, L is the moving distance, tacc is the acceleration time, and Tcon is the time assigned for the constant velocity. As the acceleration time increases, the maximum velocity of the motion decreases and the delay-time of VM input shaping increases. However, adopting a shorter acceleration time may lead to decreased robustness of system control. Similar to the moving distance parameter discussed above, acceleration time characteristics should be analyzed carefully to find the optimally applicable values of acceleration time for system control.
5. Experiments
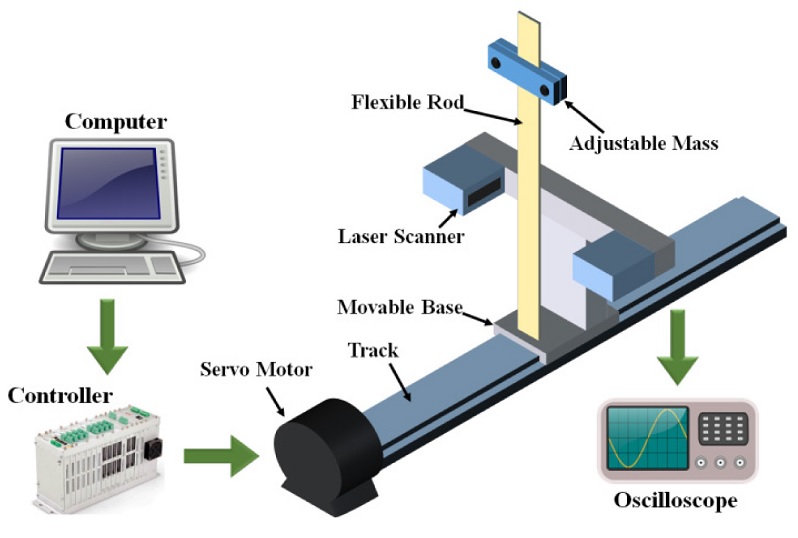
To experimentally validate the proposed VM input shaping method, a series of experiments were carried out using a single-degree-of-freedom positioning system. The experimental setup is presented in Fig. 13.
First, a motion command is sent to the positioning system from the computer through a PMAC motion controller. The servo motor drives the base moving forward and backward along the track. When applying a motion command, the flexible rod experiences residual vibration, which is measured by a laser scanning micrometer attached to the base. An adjustable mass on the flexible rod can be clamped at any position to adjust the natural frequency.
Initially, a reference command was tested on the experimental equipment to obtain the system characteristics, including the natural frequency (ωn) and damping ratio (ζ). The system characteristics and design conditions are listed in Table 2.
Based on the parameters listed in Table 2, a precise VM input shaped profile was developed and inputted into the system. The time-domain responses of the system were obtained as shown in Fig. 14. Figs. 14(a) and 14(b) present the vibrations when a reference command or VM input shaped command is applied to the system. As shown in Fig. 14(b), residual vibration is reduced dramatically when using a VM input shaped command. A small amount of vibration (outside the dashed boxes) occurs due to the presence of the system inertial force during acceleration and deceleration. Such vibration is observed because we measure the relative vibration between the base and the flexible rod. However, no vibration is observed during moving at maximum velocity.
Experimental time domain responses (a) Reference command and its vibration response and (b) VM input shaped command and its response
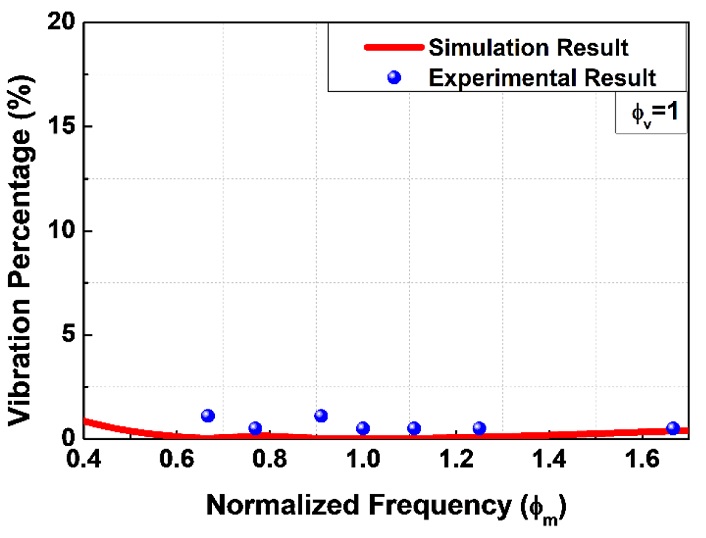
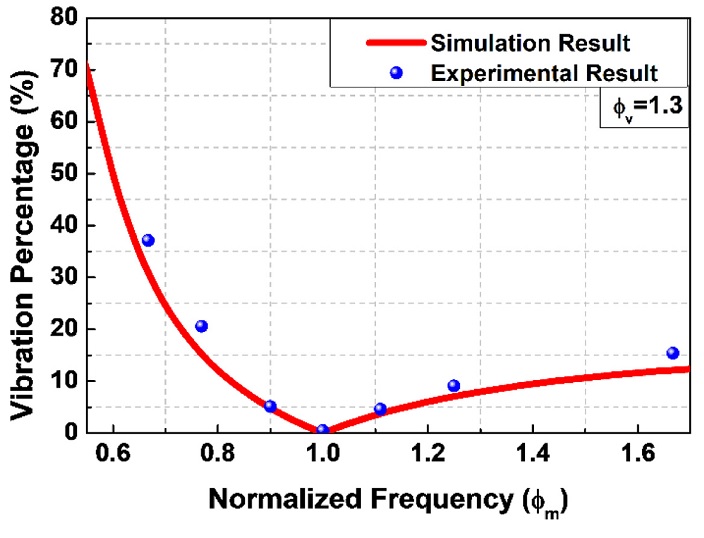
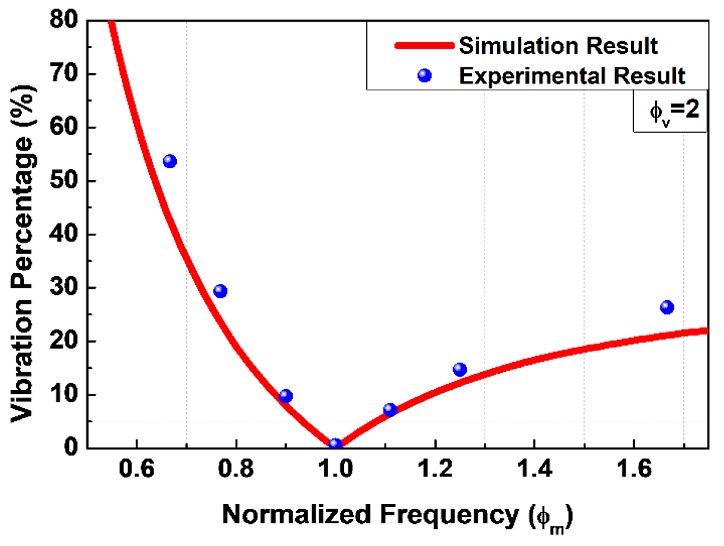
By repeating the same experiment several times with different NVFs and NMFs, VM shaper sensitivity curves were generated, as shown in Figs. 15-17. These figures present the sensitivity curves for NVFs of 1, 1.3 and 2, respectively. These figures also compare experimental results (points) to simulation results (curves).
Good agreement between the experimental results and simulation results indicate that a reasonable VM input shaped profile was generated. As already discussed in the simulation with Fig. 9, the sensitivity is extremely low at the NVF of 1 and is getting bigger as the NVF increases. It should be also noted that the modeling error sensitivity is asymmetric with respect to the NMF of 1. The proposed VM input shaping method is less sensitive to the modeling errors for higher modeling errors.
6. Conclusions
This paper presented a delay-time adjustable input shaping method called the VM input shaping method for steady-state vibration reduction. The robustness of the proposed VM input shaping method was demonstrated based on the sensitivity curves for various normalized virtual frequencies. The effects of important command parameters for the VM input shaping method on vibration reduction performance were analyzed through various simulations. The findings of this study were verified experimentally using a flexible single-degree-of-freedom positioning system. Adjusting the duration of input shaping commands and increasing robustness by altering the virtual frequency demonstrated the effectiveness of the proposed input shaping method for steady-state vibration reduction.
Acknowledgments
This research was financially supported by the Ministry of SMEs and Startups of Korea.
REFERENCES
- Singhose, W. E. and Seering W. P., “Command Generation for Dynamic System,” Lulu, 1st Ed., 2011.
- Hong, S. W., “Input Shaping Method for Mechanical Vibration Control,” Chaosbook, 2014.
- Singhose, W. E. and Pao, L. Y., “Comparison of Input Shaping Techniques for Speed-Critical Multi-Mode Flexible Systems,” Proc. of the IEEE International Conference on Control Applications and IEEE International Symposium on Intelligent Contro, pp. 379-384, 1996.
-
Singh, T. and Singhose, W., “Input Shaping/Time Delay Control of Maneuvering Flexible Structures,” Proc. of the American Control Conference, pp. 1717-1731, 2002.
[https://doi.org/10.1109/ACC.2002.1023813]

-
Singhose, W. and Pao, L., “A Comparison of Input Shaping and Time-Optimal Flexible-Body Control,” Control Engineering Practice, Vol. 5, No. 4, pp. 459-467, 1997.
[https://doi.org/10.1016/S0967-0661(97)00025-7]

- Singhose, W., Singer, N. C., and Seering, W. P., “Design and Implementation of Time-Optimal Negative Input Shapers,” Proc. of the International Mechanical Engineering Congress and Exposition, pp. 151-157, 1994.
-
Singhose, W., Seering, W. P., and Singer, N. C., “Time-Optimal Negative Input Shapers,” Journal of Dynamic Systems, Measurement, and Control, Vol. 119, No. 2, pp. 198-205, 1997.
[https://doi.org/10.1115/1.2801233]

-
Singhose, W., Biediger, E. O., Chen, Y. H., and Mills, B., “Reference Command Shaping Using Specified-Negative-Amplitude Input Shapers for Vibration Reduction,” Transactions of the American Society of Mechanical Engineers Journal of Dynamic Systems Measurement and Control, Vol. 126, No. 1, pp. 210-214, 2004.
[https://doi.org/10.1115/1.1650385]

- Singh, T. and Vadali, S., “Robust Time-Delay Control of Multimode Systems,” Proc. of the American Control Conference, Vol. 3, pp. 681-685, 1994.
- Park, B. J., Hong, K. S., and Huh, C. D., “Time-Efficient Input Shaping Control of Container Crane Systems,” Proc. of the IEEE International Conference on Control Applications, pp. 80-85, 2000.
-
Rhim, S. and Book, W. J., “Adaptive Time-Delay Command Shaping Filter for Flexible Manipulator Control,” IEEE/ASME Transactions on Mechatronics, Vol. 9, No. 4, pp. 619-626, 2004.
[https://doi.org/10.1109/TMECH.2004.839046]

-
Baumgart, M. D. and Pao, L. Y., “Discrete Time-Optimal Command Shaping,” Automatica, Vol. 43, No. 8, pp. 1403-1409, 2007.
[https://doi.org/10.1016/j.automatica.2007.01.003]

-
Singhose, W., “Command Shaping for Flexible Systems: A Review of the First 50 Years,” International Journal of Precision Engineering and Manufacturing, Vol. 10, No. 4, pp. 153-168, 2009.
[https://doi.org/10.1007/s12541-009-0084-2]

-
Hong, S. W., Seo, Y. K., and Singhose, W., “A New Command Shaper Design for Residual Vibration Reduction in Flexible Systems Using Artificial Mode Constraints,” International Journal of Engineering and Technology, Vol. 5, No. 2, pp. 210-213, 2013.
[https://doi.org/10.7763/IJET.2013.V5.544]

-
Pai, M. C., “Discrete-Time Dynamic Output Feedback Input Shaping Control of Vibration in Uncertain Time-Delay Flexible Structures,” Applied Mathematics and Computation, Vol. 250, pp. 675-688, 2015.
[https://doi.org/10.1016/j.amc.2014.11.038]

-
Zhao, Y., Chen, W., Tang, T., and Tomizuka, M., “Zero Time Delay Input Shaping for Smooth Settling of Industrial Robots,” Proc. of the International Conference on Automation Science and Engineering, pp. 620-625, 2016.
[https://doi.org/10.1109/COASE.2016.7743459]

-
Masoud, Z. N. and Alhazza, K. A., “A Smooth Multimode Waveform Command Shaping Control with Selectable Command Length,” Journal of Sound and Vibration, Vol. 397, pp. 1-16, 2017.
[https://doi.org/10.1016/j.jsv.2017.02.049]

- Christopher, J., Hong, S. W., and Kwon, S. W., “Input Shaping Performance on Reduction of Steadystate Vibration due to Repeated Motion of Positioning Device,” Proc. of the International Conference on Civil, Structural and Mechanical Engineering, 2015.
- Park, S. W., Hong, S. W., and Danielson, J., “A New Design Method for Multi-Mode Input Shapers to Eliminate Residual Vibration in Dynamic Systems,” Journal of the Korean Society for Precision Engineering, Vol. 26, No. 4, pp. 100-106, 2009.
- Hong, S. W., Choi, H. S., Seo, Y. G., and Park, S. W., “A Method of Input Shaper Design Using Virtual Mode for Undamped Vibration Systems,” Journal of the Korean Society of Manufacturing Technology Engineers, Vol. 17, No. 6, pp. 83-90, 2008.
- Seo, Y. G., Jang, J. W., and Hong, S. W., “Residual Vibration Reduction of Precise Positioning Stage Using Virtual-Mode Based Input Shapers,” Journal of the Korean Society of Manufacturing Technology Engineers, Vol. 18, No. 3, pp. 255-260, 2009.

Master degree student at the Mechanical System Engineering Department of the Kumoh National Institute of Technology. His research focus is vibration control.
E-mail: azizjonks@gmail.com

Professor in the Department of Mechanical System Engineering of the Kumoh National Institute of Technology. His current research interests include the modeling and analysis of spindles and bearings, command shaping for positioning systems, and structural vibration analysis for mechanical systems.
E-mail: swhong@kumoh.ac.kr