매질의 종류와 공기 항력 계수를 고려한 도비된 파편의 이동 거리 연구
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
When a building explodes, debris generated bounces after hitting the ground with high energy. It is called the ricochet phenomenon. Ricochet phenomena increase the risk of damage by increasing the moving distance of the debris. The ricochet of debris is impacted by the type of medium. In this paper, the behavior and travel distance of debris after ricocheting are studied according to the type of medium. For various initial conditions, the ricochet of the debris was studied through FEM, and the resulting values were fitted to the 3D curved surface, to predict the speed and angle after the ricochet. The trajectory of the sphere was calculated with the flight formula, considering drag force by using the MATLAB. The ricochet of debris is impacted by the contact area with the medium. As the contact area increases, the reflection angle increases due to the increase of the repulsive force. As the size of the debris increases, the contact area increases and the energy loss increases, but it moves further because of the increase of the weight and kinetic energy. The type of media around the building can be used as an appropriate means of controlling the travel distance of the debris.
Keywords:
Ricochet, Spherical debris, Sand, Concrete, Moving distance, Drag coefficient키워드:
도비, 구 파편, 모래, 콘크리트, 이동 거리, 항력 계수1. 서론
탄약고 또는 건물이 폭파하면 무수히 많은 파편이 생성되어 비산된다. 파편은 지면과 충돌한 뒤 운동이 정지되기도하고, 구르거나 다시 튀어 오른다. 튀어 오른 파편은 파편의 이동 거리와 파편의 위험성을 증가시킨다. 물체가 매질과 충돌한 뒤 다시 튀어 오르는 현상을 도비(Ricochet)라고 한다. 도비된 건물의 파편은 큰 운동에너지를 가지고 있기 때문에 다른 물체에 충돌 시 매우 위험하다. 그러므로 파편의 도비 현상에 대한 정확한 이해가 있어야 파편의 이동 거리와 안전거리를 정확히 설정할 수 있다.
처음으로 도비 현상을 연구하고 이용했던 국가는 영국이다. 16, 17세기의 해상전투에서 포탄의 사정거리를 증가시키는데 도비 현상을 이용하였다. 제2차 세계대전에서는 근접하기 어려웠던 댐을 도비 현상을 이용해 폭파한 기록이 있다.1,2 그 후 물에서의 도비 연구가 본격적으로 진행되었다. 발사체의 임계 각도(Critical Angle)를 측정하는 실험과 이를 이용해 발사체의 다양한 초기 조건에 따른 임계 각도를 예측하는 실험식들이 만들어졌다.3,4 고체 매질에서의 도비는 물에서의 도비보다 더 복잡하다. 균질한 매질인 물에서의 도비는 대체로 비슷한 경향성의 결과를 나타낸다. 하지만 모래, 진흙같이 작은 알갱이로 이루어져 다공성과 유동성이 있는 고체들은 균질하지 않기 때문에 물에서의 도비와는 다른 경향성을 보인다.5,6 건물 폭파로 인한 파편의 연구는 실험과 다양한 시뮬레이션을 통해 연구되고 있다. 폭파 연구가 진행됨에 따라서 도비의 중요성이 대두되고 있다. 파편의 도비는 파편의 초기 조건, 매질의 종류와 특징에 다라 다양하게 변화한다.7-9 하지만 파편 연구에서 사용되는 도비 수식은 많은 요인들을 고려하지 못하고 단순한 수식으로 표현되어있다. 그러므로 다양한 조건에서 연구된 도비 후의 파편 거동은 안전거리 또는 이동 거리를 계산할 때 오차를 줄일 수 있다.
본 연구에서는 매질과 종류에 따른 콘크리트 구의 이동 거리를 연구하였다. 파편의 비행에는 계속 변화하는 레이놀즈 수에 따른 항력 계수를 적용하여 보다 정확한 파편의 비행 궤도를 계산하였다. 파편의 이동 거리 연구는 유한요소해석을 통해 계산된 파편의 도비 후 속력, 각도를 3차원 곡면으로 피팅한 결과와 항력 계수를 고려한 비행 수식을 가지고 MATLAB으로 계산하였다. 이 과정을 통해 다양한 초기 조건과 모래, 콘크리트 매질에서의 파편의 발사각에 따른 반사각과 이동 거리를 계산하고 비교하였다.
2. 도비와 항력 계수에 따른 비행 궤적 수식
2.1 도비 수식
물체가 매질에 충돌하면 반발력(FL)이 발생하는데 식(1)과 같이 나타낼 수 있다.10,11
| (1) |
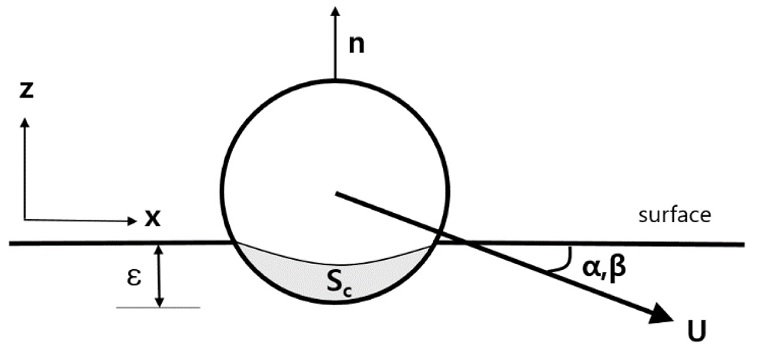
여기서 CL은 양력계수, ρw는 매질의 밀도, U는 물체의 속도, Sc는 물체와 매질의 접촉 면적, f (α, β)는 반발력의 각도 의존성을 포함하는 무차원 함수이다. 여기서 α는 받음각(Attack Angle), β는 물체와 매질의 충돌각(Impact Angle)이다. ε은 물체의 관입 깊이이다. Fig. 1은 물체가 매질에 충돌할 때의 과정을 나타낸 그림이다. 물체의 도비 발생 유무에 가장 관련 있는 것은 매질 표면에 수직인 방향으로의 반발력이다. 식(2)는 물체의 z축 방향으로의 반발력을 나타낸 식이다. 식(2)를 간단히 표현하면 식(3)과 같이 표현할 수 있다. 식(3)은 식(4)와 식(5)로 나타낼 수 있다.10,11
| (2) |
| (3) |
| (4) |
| (5) |
식(4)는 반발력이고, 식(5)는 유효마찰계수의 역할을 한다. 즉, 물체가 도비가 되려면 매질과의 마찰로 인한 에너지 손실보다 z축 방향으로의 반발력이 더 크면 도비가 되는 것이다. 물체의 관입 깊이와 매질과의 접촉 면적은 반발력과 에너지 손실에 모두 영향을 주기 때문에 도비 과정에서 매우 중요한 요소이다.
2.2 공기 항력에 따른 물체의 비행 궤적 수식
본 연구에서는 계속 변화하는 파편의 레이놀즈 수에 따른 정확한 항력 계수를 고려하여 정확한 파편의 궤적 공식을 사용하였다. 항력(D), 레이놀즈 수(Re), 시간 상수(Time Constant)는 다음 식(6)부터 식(8)과 같이 표현할 수 있다.12,13
| (6) |
| (7) |
| (8) |
여기서 CD는 항력 계수이고, ρa는 공기 밀도, A는 공기 흐름에 수직으로 투영되는 물체의 면적, U는 파편의 속도, d는 파편의 반지름, μ는 공기의 점도, m은 파편의 질량이다. 식(6)을 뉴턴의 제 2법칙에 적용하면 식(9)와 같이 레이놀즈 수와 시간 상수에 관련되게 가속도를 정의할 수 있다.
| (9) |
식(8)을 식(9)에 대입하면 x, z축에 대하여 물체의 가속도를 식(10)과 같이 간단히 구할 수 있다.
| (10) |
변형된 중앙차분법을 사용하면 레이놀즈 수와 항력 계수를 고려한 물체의 속도는 식(11)과 식(12)와 같이 나타낼 수 있다.
| (11) |
| (12) |
식(13)과 식(14)는 시간과 속도에 따라서 파편의 위치를 나타낸 식이다.
| (13) |
| (14) |
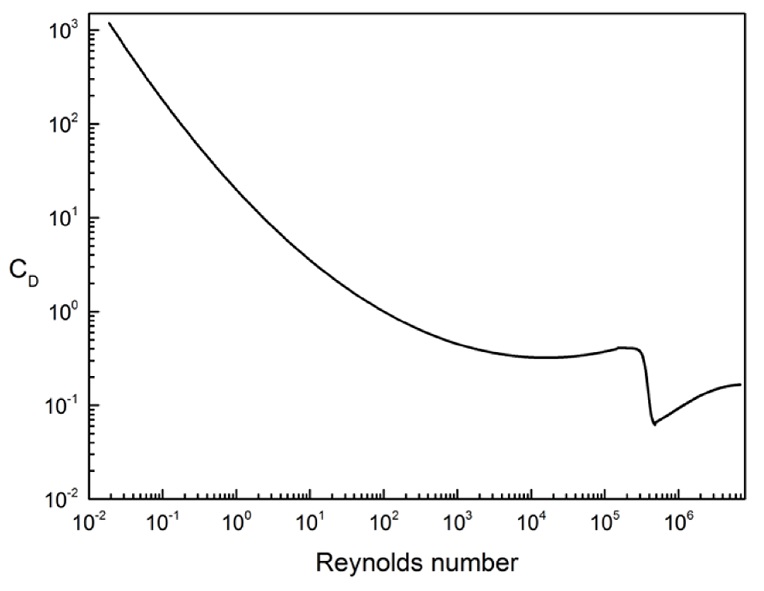
본 논문에서 구의 레이놀즈 수가 사용되었고, Fig. 2는 구의 레이놀즈 수에 따른 항력 계수를 나타낸 그림이다.
3. 도비 실험과 해석
콘크리트 구가 매질에 충돌하고 도비하는 과정은 유한요소해석을 이용해 연구하였다. 유한요소해석 프로그램은 충돌 해석전문 프로그램인 ANSYS Explicit Dynamics을 이용하였다. 해석에서 가장 중요한 점은 모델의 물성치를 실제와 가장 비슷하게 설정하는 것이다. 하지만 본 연구에서 사용되는 모래는 종류와 주위 환경에 따라서 물성치의 범위가 매우 넓기 때문에 해석에서 사용할 물성치를 명확히 선택해야 할 필요가 있다. 본 연구에서는 모래의 물성치 설정의 신뢰성을 높이기 위해 고속에서의 타 도비 연구 실험과 저속에서의 도비 실험을 직접 수행하여 해석 결과와 비교하였다. 해석과 실험의 오차율이 감소하여 해석의 신뢰도가 높아졌을 때 모래의 물성치를 확정하고 다양한 초기 조건에서의 구 파편의 해석을 수행하였다.
3.1 선행 해석과 도비 실험
타 연구에서 진행된 실험은 25 mm 구경 탄환의 고속 도비실험이다. 실험에서 사용된 모래는 밀도 외에 다른 물성은 정확히 명시하지 않았다. 밀도는 1670 kg/m3이다. 25 mm 탄환의 초기 조건은 입사각 12.5, 25°이고 초기 속도는 589 m/s이다.14
본 해석에서 사용된 모래의 해석 모델은 모래, 흙, 암석에 주로 사용되는 Drucker-Prager 모델이다. 식(15)는 Drucker-Prager모델의 간단한 수식이다.15
| (15) |
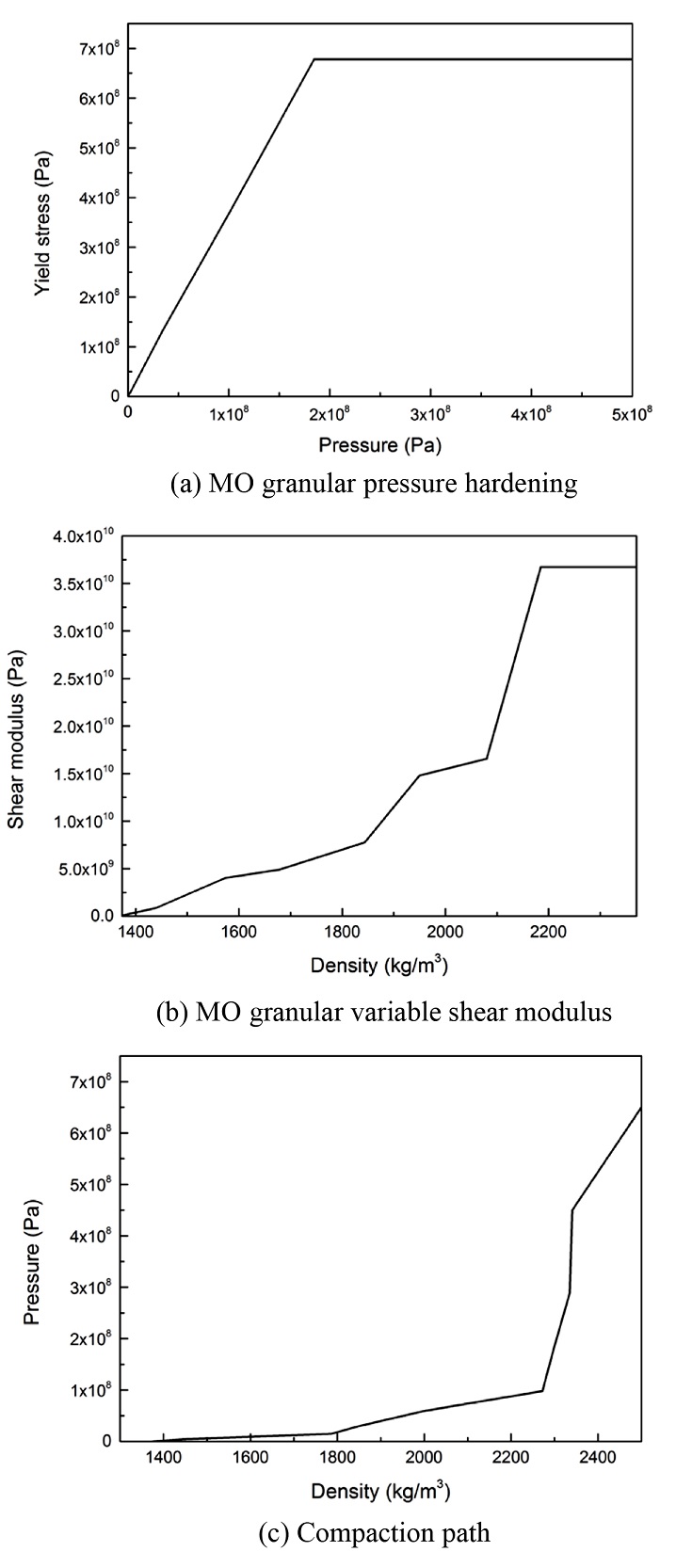
여기서 σY는 총 항복 응력(Total Yield Stress), σp는 압력 항복 응력(Pressure Yield Stress), σρ는 밀도 항복 응력(Density Yield Stress)이다. 본 해석에서는 Drucker-Prager Strength 모델에서 파편의 도비에 영향을 주는 MO Granular Pressure Hardening, MO Granular Variable Shear Modulus, Compaction Path를 변경하여 해석을 진행하였다. 본 해석에서 사용된 세 개의 물성치는 Fig. 3에 나타나있다.
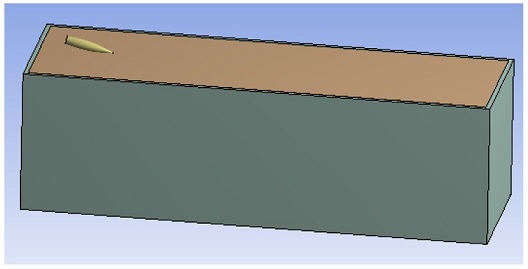
본 해석에서는 모래를 작은 알갱이 구성되어 있고, 흐름이 있는 연속체라고 가정하였다. 모래가 사용되는 해석에는 모래를 알갱이 자체로 모델링하는 SPH (Smooth Particle Hydrodynamics)기법을 사용하는 것이 적합하다. 하지만 해석 소요 시간이 너무 길기 때문에 본 해석에서는 모래를 유체인 오일러(Euler)로, 콘크리트 구를 고체인 라그랑지(Lagrangian) 모델로 설정하는 Arbitrary Lagrangian-Eulerian 해석을 이용하였다. Fig. 4는 25 mm 탄환과 모래를 모델링한 그림이다. 모래의 크기는 1000 mm × 300 mm × 300 mm(가로×세로×높이)이다.
고속에서의 탄환 발사 실험은 많은 제약으로 인해 실제로 수행하기 쉽지 않다. 그러므로 타 연구를 참조할 수밖에 없지만 저속에서의 발사 실험은 수행 가능하다. 본 연구에서는 에어타카를 이용해 모래에서의 철구 파편의 도비 현상 실험을 수행하였다. Fig. 5는 모래에서의 철구 도비 실험 개략도이다. 에어컴프레셔의 압력 변환을 통해 철구의 초기 속도를 다양하게 변화시킬 수 있다. 철구의 지름은 10mm이다. 철의 밀도는 7500 kg/m3이다. 철구의 입사각은 15, 20°이고 철구의 초기 속도는 28, 32 m/s이다. 실험은 동일한 조건에서 3번 반복 실험하였다. 실험에서 사용된 모래의 밀도는 1500 kg/m3이다.
3.2 콘크리트 구 도비 해석과 피팅
본 연구에서는 콘크리트 구의 다양한 지름, 입사 속력, 입사 각도에 따른 도비 후의 반사 속력, 각도가 해석을 통해 연구되었다. 건물의 폭파된 파편을 수집할 때 파편의 무게, 크기에 따라서 분류가 이루어진다. Table 1은 콘크리트 파편의 무게와 크기에 따라 분류된 것을 나타낸다. 폭파 실험 후 파편 수집 시 가장 많이 생성되는 파편은 Mass Bin 8, 9, 10이다. Ref. 16의 폭파 실험에서 생성된 파편에서 Mass Bin 8, 9, 10은 전체 파편 중에 81.98%를 차지한다.16 그러므로 본 해석에서는 Mass Bin 8, 9, 10 크기 범위 안에서 지름을 선정하였다. 선정된 지름은 20, 30, 40 mm이다. 구의 재질은 콘크리트이다. Ref. 16에서 수집된 파편이 콘크리트 파편이기 때문이다. 구의 초기 속도는 10, 50, 100, 150, 200 m/s가 선정되었다. 초기 입사 각도는 매질이 모래의 경우 1, 5, 10, 15, 20, 30, 40, 50°이고, 콘크리트의 경우 60°를 추가로 해석하였다. 매질은 모래와 콘크리트를 선정하였다. 선행 해석과 마찬가지로 ANSYS Explicit Dynamics가 사용되었고, 모래의 물성은 선행 해석에서의 모래와 동일하다. 콘크리트의 밀도는 2440 kg/m3이고, 전단 탄성률은 7.88 × 109 Pa이다. 해석된 결과값을 가지고 동일한 지름의 구와 매질에 관하여 입사 속력, 각도에 따른 반사 속력, 각도를 예측하기 위해 MATLAB의 Curve Fitting Tool을 이용하여 3차원 곡면으로 피팅하였다.
3.3 콘크리트 구 이동 거리 계산
도비되는 콘크리트 구의 계산을 위해서 본 연구에서는 MATLAB을 사용하였다. 구의 궤적 계산을 위해서는 2.1절의 식(6)부터 식(8), 식(11)부터 식(14)를 사용하였다. 구의 정확한 비행 궤적 계산을 위해서 0.01초의 시간 간격으로 변하는 레이놀즈 수에 따른 항력 계수를 고려하여 비행 궤적 수식에 대입하였다.
구가 지면에 충돌한 뒤 발생하는 구의 다음 궤적은 도비되기 직전의 구의 입사 속력, 각도를 가지고 유한요소해석의 결과값의 피팅으로 얻어낸 3차원 곡면에서 구의 도비 후 속력과 각도의 값을 초기 조건으로 추출하여 계산하였다. 그리하여 반사각이 1° 이하로 감소하거나 속도가 0이 되면 구의 운동이 정지되도록 설정하였다. 1° 이하에서 계산을 멈추는 이유는 입사각이 1° 이하이면 도비가 아닌 구의 구름 현상으로 간주하였기 때문이다. 그리하여 운동이 멈추는 지점까지의 수평거리가 구의 최종 이동 거리다. 콘크리트 구의 초기 속도는 실제 폭파 실험의 조건들을 따라 계산하였다. 식(16)은 파편의 초기 속도(Debris Launch Velocity)를 구하는 공식이다.17
| (16) |
여기서 NEQ (Net Explosive Quantity)는 포장재, 총알 등을 제외한 폭발 물질의 총 질량, Vw는 건물 또는 탄약고 내부 용적, ρw는 벽의 밀도, tw는 벽 두께이다. 실제 폭파 실험 보고서에서 사용된 건물의 용적은 252.57 m3, 벽의 밀도는 2400 kg/m3, 벽의 두께는 0.19 m이다. NEQ는 1000 kg이다.16
그러므로 파편의 초기 속도는 122.99 m/s이다. 본 연구에서는 파편의 초기 속도로 120 m/s를 선정하였다. 콘크리트 구의 초기 발사각은 1°부터 1°씩 증가하여 10°까지이다. 폭파가 이루어진 장소의 매질은 명확히 나와 있지 않지만 사진으로 참고했을 때 모래로 뒤덮인 지면이다.
4. FEM 해석 결과
4.1 선행 해석 결과와 도비 실험 비교
Table 2는 25 mm 구경 탄환의 고속 도비 실험과 FEM을 비교한 결과이다. 입사각이 12.5°일 때는 속력이 불과 8 m/s밖에 차이나지 않으며, 25°일 때도 많은 차이가 발생하지 않았다. Table 3 은 10 mm 철구의 저속 도비 실험과 FEM 결과를 비교한 표이다. 실험의 결과 값들은 3번 실험의 평균값이다. 25 mm 구경 탄환의 도비 실험과 마찬가지로 오차가 매우 작은 것을 확인할 수 있다. 고속과 저속에서 모두 FEM 결과와 실제 실험의 오차가 크지 않기 때문에 모래의 물성치가 해석에 사용되기에 적절하다고 판단할 수 있다.
4.2 콘크리트 구 도비 해석 결과와 피팅
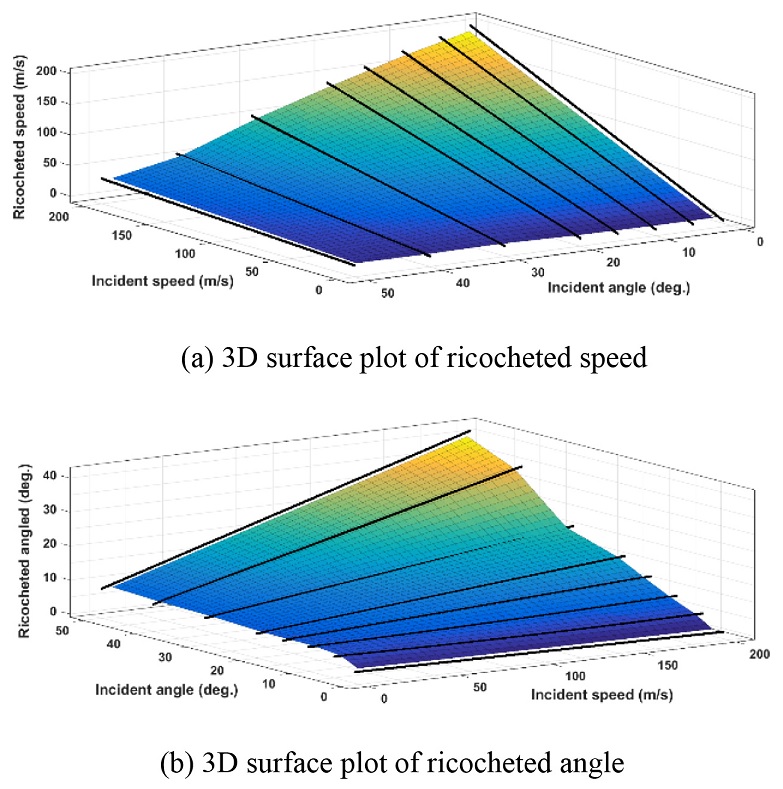
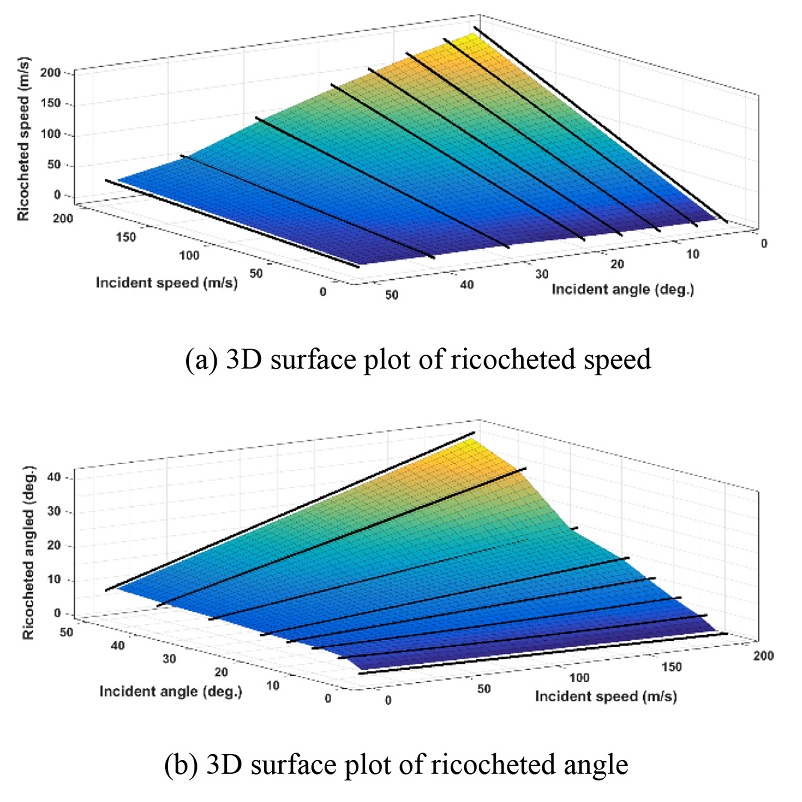
각 조건에서 해석된 결과들은 동일한 지름에 따른 도비 후의 반사 속도와 각도로 각 상황에 알맞은 선형 또는 곡선 피팅이 이루어졌다. 그리고 여러 입사 각도와 속도로 피팅된 곡선들을 가지고 MATLAB의 Curve Fitting Tool을 이용해 3차원 곡면을 구성하였다. 본 절에서는 Mass Bin 7에 해당하는 40 mm 콘크리트 구에 대한 피팅 결과값만 나타내었다. Figs. 6과 7은 매질이 모래와 콘크리트일 때의 다양한 입사 속력과 각도에서 도비된 파편의 속력과 각도로 피팅된 3차원 피팅 곡면이다. 매질이 모래일 때와 콘크리트일 때 모두 입사각이 증가할수록 도비되는 구의 속력은 감소한다. 다만 감소되는 비율의 차이는 구의 크기에 따라 다르다. 도비된 구의 반사 각도를 보면 두 매질에서의 경향성이 다르게 나타난다. 모래에서는 입사 속력이 증가할수록 반사되는 각도가 증가한다. 하지만 콘크리트에서는 입사각과 입사 속력이 증가할수록 반사되는 각도가 감소한다. 이는 모든 크기의 구에서 동일하게 나타난다.
5. 구 파편의 최종 이동 거리와 발사각에 따른 도비각
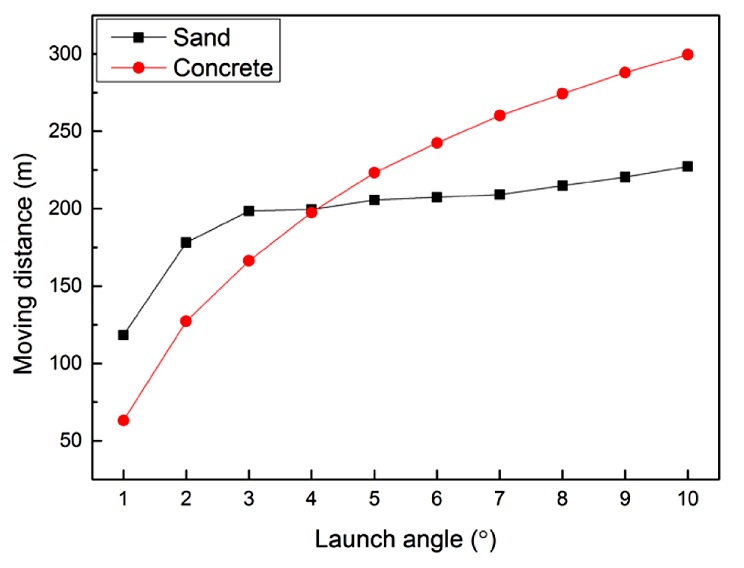
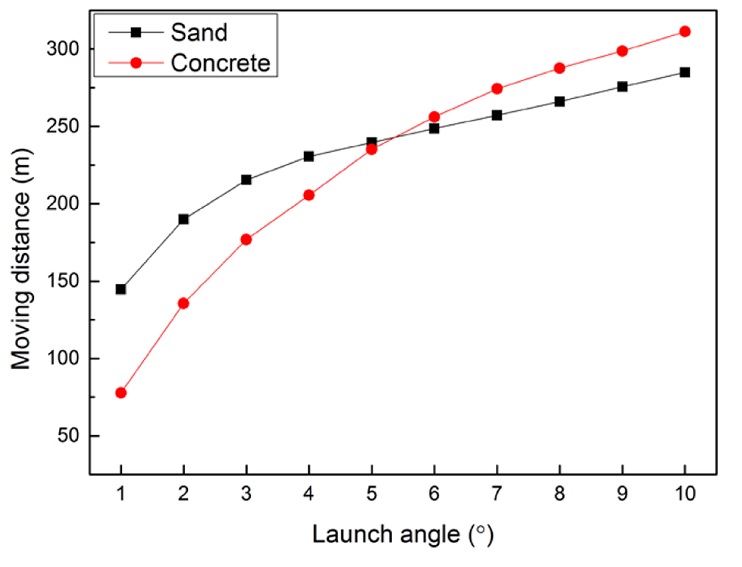
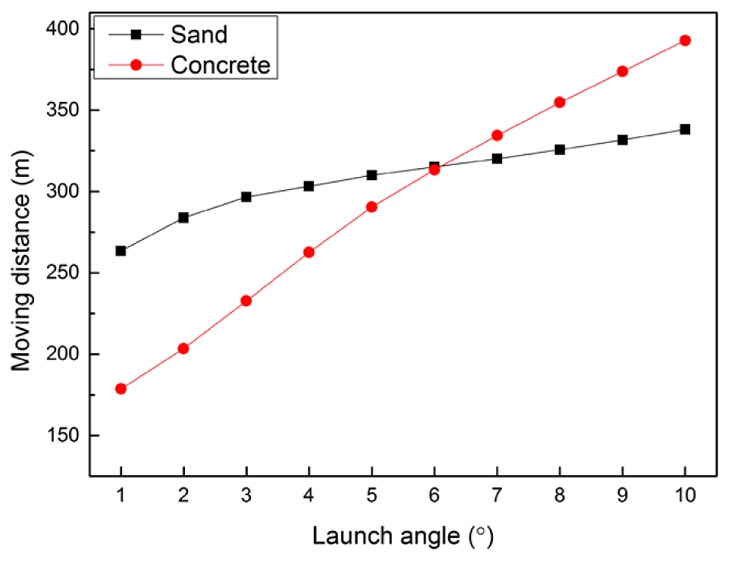
도비되는 콘크리트 구의 최종 거리는 2.1절에서 언급된 공기 항력 계수에 따른 물체의 비행 궤적 식과 다양한 조건에서 해석되어 3차원 곡면으로 피팅된 결과들을 가지고 MATLAB을 이용해 계산하였다. Fig. 8은 20 mm 콘크리트 구가 모래와 콘크리트에서 도비될 때의 이동 거리를 나타낸 그래프이다. Fig. 9는 30 mm 콘크리트 구가 모래와 콘크리트에서 도비될 때의 이동 거리를 나타낸 그래프이다. Fig. 10은 40 mm 콘크리트 구가 모래와 콘크리트에서 도비될 때의 이동 거리를 나타낸 그래프이다. 입사각이 작을 때는 모래에서의 구 이동 거리가 더 크지만 입사각이 증가하면서 콘크리트에서의 이동 거리가 더 크게 된다. 파편의 최대 이동 거리는 392.86 m로 발사각 10°, 40 mm 구 일 때이다. 최소 이동 거리는 63.14 m로 발사각 1°, 20 mm 구일 때이다. 두 경우 모두 매질은 콘크리트이다.
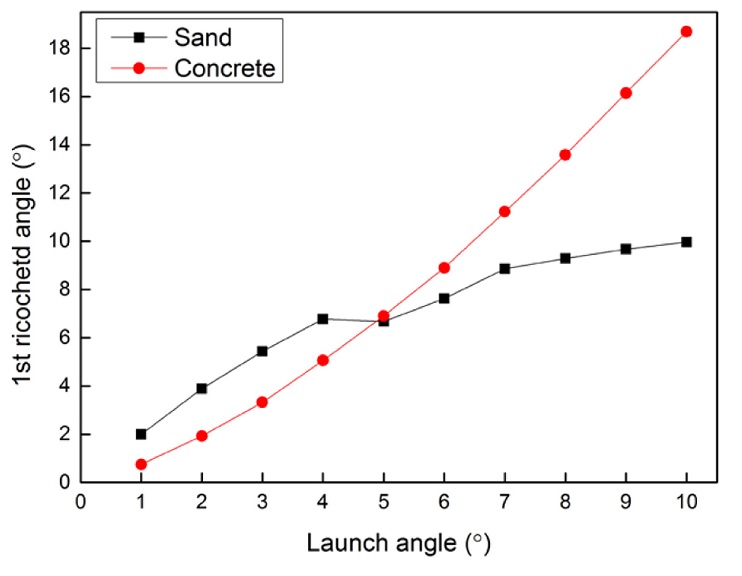
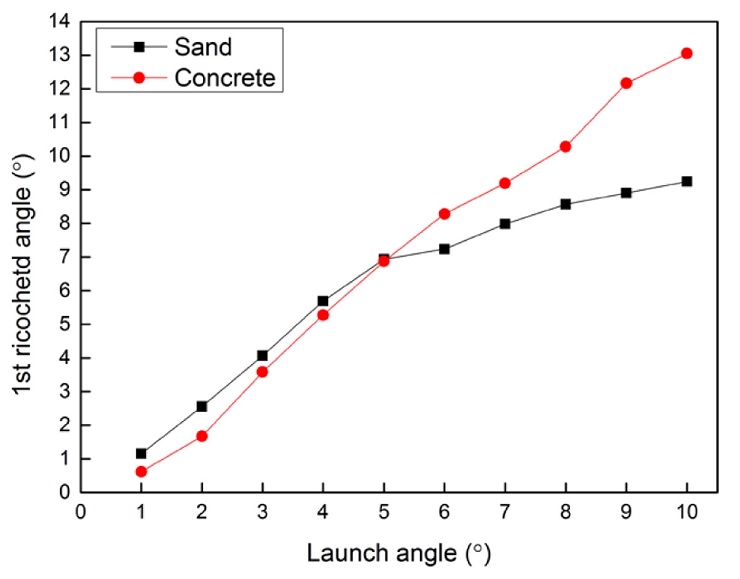
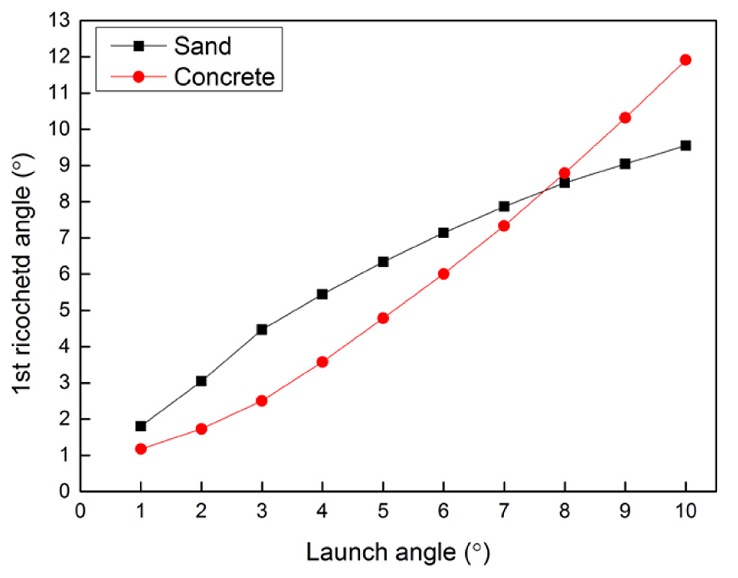
구 파편의 발사각에 따른 도비각 또한 이동 거리와 비슷한 경향성을 가지고 나타난다. Fig. 11은 20 mm 콘크리트 구의 발사각에 따른 도비각을 나타낸 그림이다. Fig. 12는 30 mm 콘크리트 구의 발사각에 따른 도비각을 나타낸 그림이다. Fig. 13은 40 mm 콘크리트 구의 발사각에 따른 도비각을 나타낸 그림이다. 발사각이 작을 때는 모래에서의 도비각이 크지만 발사각이 증가하면서 콘크리트에서의 발사각이 더 커지게 된다. 20 mm 구에서는 발사각이 5° 이상부터 콘크리트에서의 도비각이 증가하였고, 40 mm 구에서는 8° 이상부터 콘크리트에서의 도비각이 증가하였다.
6. 고찰
본 논문에서는 두 매질에서 레이놀즈 수에 따른 항력 계수를 고려한 도비된 콘크리트 구 파편의 이동 거리를 연구하였다. 발사각이 낮을 때는 모래에서의 이동 거리가 더 길다가 발사각이 높아지면 콘크리트에서의 이동 거리가 더 길어진다.
그 이유는 발사각에 따른 구 파편의 첫번째 도비각을 보면 알 수 있다. 저 발사각에서는 모래에서의 도비각이 더 큰 것을 Figs. 11부터 13을 통해 확인할 수 있다. 콘크리트에서의 도비각이 낮은 이유는 파편과 매질의 충돌 시 접촉면적과 관계가 있다. 콘크리트와 충돌하는 구 파편의 접촉면적은 모래보다 극히 작다. 접촉면적이 작기 때문에 수직 방향으로의 반발력이 작고 이는 모래에서보다 작은 도비각으로 나타나게 된다. 반면에 발사각이 증가하면 콘크리트에서의 도비각이 증가하게 된다. 발사각과 입사각은 비례 관계이므로 발사각이 증가하면 입사각 또한 증가하게 된다. 그러므로 매질이 모래인 경우 모래와의 접촉면적 증가로 인해 반발력이 증가하지만 도비 시 더 많은 마찰로 인해 에너지 손실도 증가하게 된다. 그러므로 발사각이 증가하면 모래에서는 콘크리에서보다 더욱 낮은 도비각이 나타나게 된다. 이는 파편의 도비와 비행에 영향을 주어 고 발사각에서는 콘크리에서의 파편이 더 멀리 이동하게 된다.
마지막으로 본 연구의 결과와 실제 폭파 실험의 결과를 비교해 보면 실제 파편의 이동 거리 분포도는 대게 100-400 m에 위치한다. 최고로 멀리 날아간 파편은 572 m에 위치하지만 주변에 다른 파편들은 거의 존재하지 않는다.16 보고서에서는 파편의 모양, 크기에 따른 파편의 이동 거리, 정확한 매질의 물성에 대해서는 명시하지 않았기 때문에 본 연구의 결과와 정확한 비교는 어렵다. 하지만 본 연구의 결과들의 범위가 실제 실험의 범위 안에 위치하므로 본 연구 결과값들은 신뢰할 수 있다고 판단된다.
7. 결론
본 논문에서는 매질이 모래와 콘크리트일 때 도비되는 콘크리트 구의 이동 거리를 연구하였다. 이 연구의 결론은 다음과 같다.
매질이 모래인 경우 저 발사각에서는 매질과의 접촉으로 손실되는 에너지보다 수직 방향으로 발생하는 반발력이 더 크므로 충돌 시 접촉 면적이 작은 콘크리트에서보다 반사각이 더 크다. 하지만 발사각이 증가하면 파편의 관입 깊이 또한 더 깊어져 모래와 마찰로 인하여 손실되는 에너지가 더 증가한다. 그러므로 운동에너지 손실이 거의 없는 콘크리트에서 보다 반사각이 감소하게 된다. 이는 도비되는 파편 이동에 영향을 주어 두 매질에서의 이동 거리의 차이를 만들게 되는 주된 요인이 된다.
이 연구의 결과들은 건물 폭발 시 주변의 매질에 따라 좀 더 정확한 안전거리를 연구하는데 유용하다. 그리고 건물 주변의 매질 종류는 파편의 이동 거리를 제어하는 적절한 수단으로 이용될 수 있다.
NOMENCLATURE
| A : | Area of the debris normal to the air flow |
| α : | Attack angle |
| β : | Impact angle |
| CD : | Drag coefficient |
| CL : | Lift coefficient |
| d : | Debris diameter |
| D : | Drag force |
| DLV : | Debris launch velocity |
| ε : | Penetration depth |
| F : | Force |
| FL : | Repulsive force |
| FLz : | Repulsive force to z-direction |
| g : | Gravity acceleration |
| m : | Debris mass |
| NEQ : | Net explosive quantity |
| μ : | Air viscosity |
| ρa : | Air density |
| ρm : | Medium density |
| ρw : | Wall density |
| Re : | Reynolds number |
| Sc : | Contact area with medium |
| σd : | Density yield stress |
| σp : | Pressure yield stress |
| σY : | Total yield stress |
| τ : | Time constant |
| tw : | Wall thickness |
| U : | Debris speed |
| V : | Volume of building |
Acknowledgments
본 연구는 국방과학연구소의 순수기초과제(No. UD170027GD)인 “매질에 따른 건물 파편의 도비 현상 연구” 지원으로 수행되었음.
REFERENCES
-
Johnson, W., “Ricochet of Non-Spinning Projectiles, Mainly from Water Part I: Some Historical Contributions,” International Journal of Impact Engineering, Vol. 21, Nos. 1-2, pp. 15-24, 1998.
[https://doi.org/10.1016/S0734-743X(97)00032-8]

-
Johnson, W., “The Ricochet of Spinning and Non-Spinning Spherical Projectiles, Mainly from Water. Part II: An Outline of Theory and Warlike Applications,” International Journal of Impact Engineering, Vol. 21, Nos. 1-2, pp. 25-34, 1998.
[https://doi.org/10.1016/S0734-743X(97)00033-X]

-
Johnson, W. and Reid, S. R., “Ricochet of Spheres Off Water,” Journal of Mechanical Engineering Science, Vol. 17, No. 2, pp. 71-81, 1975.
[https://doi.org/10.1243/JMES_JOUR_1975_017_013_02]

-
Hutchings, I., “The Ricochet of Spheres and Cylinders from the Surface of Water,” International Journal of Mechanical Sciences, Vol. 18, No. 5, pp. 243-247, 1976.
[https://doi.org/10.1016/0020-7403(76)90006-0]

-
Baif, Y. and Johnson, W., “The Effects of Projectile Speed and Medium Resistance in Ricochet Off Sand,” Journal of Mechanical Engineering Science, Vol. 23, No. 2, pp. 69-75, 1981.
[https://doi.org/10.1243/JMES_JOUR_1981_023_015_02]

-
Daneshi, G. and Johnson, W., “The Ricochet of Spherical Projectiles Off Sand,” International Journal of Mechanical Sciences, Vol. 19, No. 8, pp. 491-497, 1977.
[https://doi.org/10.1016/0020-7403(77)90022-4]

-
Knock, C., Horsfall, I., Champion, S. M., and Harrod, I. C., “The Bounce and Roll of Masonry Debris,” International Journal of Impact Engineering, Vol. 30, No. 1, pp. 1-16, 2004.
[https://doi.org/10.1016/S0734-743X(03)00057-5]

-
Kim, Y. K. and Choi, W. C., “Ricochet of Spheres on Sand of Various Temperature,” Defence Science Journal, Vol. 68, No. 2, pp. 150-158, 2018.
[https://doi.org/10.14429/dsj.68.11846]

-
Xu, J., Lee, C., and Fan, S., “A Study on the Ricochet of Concrete Debris Against Soil,” International Journal of Computational Methods, Vol. 12, No. 4, Paper No. 1540009, 2015.
[https://doi.org/10.1142/S0219876215400095]

-
Rosellini, L., Hersen, F., Clanet, C., and Bocquet, L., “Skipping Stones,” Journal of Fluid Mechanics, Vol. 543, pp. 137-146, 2005.
[https://doi.org/10.1017/S0022112005006373]

-
Clanet, C., Hersen, F., and Bocquet, L., “Secrets of Successful Stone-Skipping,” Nature, Vol. 427, p. 29, 2004.
[https://doi.org/10.1038/427029a]

- Bassett, N., Brower, M., Michel, S., and Shinew, M., “Golf Ball Projectile Motion,” SCRIBD, https://www.scribd.com/document/405278359, (Accessed 11 DEC 2019)
- Katsunori, S., “Golf Ball Trajectory Simulation Method,” US Patent, 8452577, 2013.
-
Moxnes, J. F., Frøyland, Ø., Skriudalen, S., Prytz, A. K., Teland, J. A., et al., “On the Study of Ricochet and Penetration in Sand, Water and Gelatin by Spheres, 7.62 mm APM2, and 25 mm Projectiles,” Defence Technology, Vol. 12, No. 2, pp. 159-170, 2016.
[https://doi.org/10.1016/j.dt.2015.12.004]

- Kim, J. Y., “ANSYS Workbench Training Manual,” Taesung Software and Engineering, pp. 9-28, 2010.
- Conway, R. T., Tatom, J. W., and Swisdak J, M. M., “SciPan 4: Program Description and Test Results,” https://apps.dtic.mil/dtic/tr/fulltext/u2/a532254.pdf, (Accessed 11 DEC 2019)
-
Van Der Voort, M. and Weerheijm, J., “A Statistical Description of Explosion Produced Debris Dispersion,” International Journal of Impact Engineering, Vol. 59, pp. 29-37, 2013.
[https://doi.org/10.1016/j.ijimpeng.2013.03.002]


Ph.D. candidate in the Department of Mechanical Engineering, Korea University. His research interest is ricochet, collision and penetration.
E-mail: gokkolove@korea.ac.kr

Professor in the Department of Mechanical Engineering, Korea University. His research interest is manufacturing system and ricochet.
E-mail: wcchoi@korea.ac.kr