IMU-Based Joint Angle Estimation Under Various Walking and Running Conditions
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Previous studies on joint angle estimation have been restricted to slow-speed level walking conditions, even though slope walking and running elicit unique biomechanical characteristics. Measurements were mostly based on an optical motion capture system despite in-the-lab limitation of measurement technique. The contribution of this study is twofold: (i) to propose a joint angle estimation method by applying a state-of-the-art parallel Kalman filter based on an inertial measurement unit (IMU) that can overcome in-the-lab limitation, and (ii) to demonstrate its application to level walking condition as well as slope walking and running conditions to fill a gap in joint kinematics literature. In particular, this study focuses on knee flexion/extension and ankle dorsiflexion/plantarflexion angles at various speed variations. The parallel Kalman filter applied in the proposed method can compensate external acceleration through Markov-chain-based acceleration modeling, that may enhance joint estimation performance in high speed walking conditions. To validate the proposed estimation method, an optical motion capture system was used as reference. In addition, patterns for each condition were investigated to identify and evaluate presence of classifying features.
Keywords:
IMU, Joint angle estimation, Level walking, Slope walking, Running키워드:
관성센서, 관절각 추정, 평지 보행, 경사로 보행, 달리기1. Introduction
Lower limb angular kinematics, such as the joint angle, is required to characterize and assess gait abnormalities.1-3 Optical motion capture systems constitute the most common measurement systems used for quantifying lower limb kinematics. To estimate the joint angle that constitutes our main interest in this study, reflective markers are attached to the anatomical landmarks and anatomical frames of each body segment are determined based on the positions of the markers. The joint angle is estimated from the orientation of the two body segments that are adjacent to the joint.4,5 However, the camera-based optical systems can only work within a limited space where the camera can see the markers, which is referred to as “in-the-lab limitation.” This inherent limitation of the camera-based systems makes it difficult to use them outdoors and for daily life measurements, despite their capability in achieving high precision measurement.
For this reason, the use of the lightweight and the low-cost inertial measurement unit (IMU) in estimating joint angles has been receiving increased attention from researchers. A typical IMU consists of a triaxial gyroscope, a triaxial accelerometer, and a triaxial magnetometer and can estimate the three dimensional (3D) orientation. As none of the sensors requires any fixed external source, such as a transmitter or receiver, the IMU works as a wearable sensor that overcomes the in-the-lab limitation. In literature, Takeda et al.6 used translational acceleration calculated from the angular velocity during gait. The estimated translational acceleration was then subtracted from the measured data to obtain the gravitational acceleration to attain a higher accuracy in the estimations of orientation. Alonge et al.7 proposed a new method to estimate the hip and knee angles based on the use of a complementary filter instead of the Kalman filter which is more popular. Seel et al.8 and Cooper et al.9 proposed estimation methods of knee flexion/extension using IMUs subject to biomechanical constraints. In both methods, the knee joint was modeled as a hinge joint. However, in reality, the human knee joint may violate hinge joint constraints as it is not a mechanical joint. This may degrade the accuracy of the joint angle estimation. Bonnet et al.10 used Fourier series to represent 3D hip and knee joint angles based on a four-degree-of-freedom serial chain model of the leg. Dejnabadi et al.11 proposed the joint angle estimation method that does not need to integrate the angular velocity when this model is used, but instead uses anatomical models personalized for each subject prior to measurements.
While the aforementioned approaches successfully demonstrated the feasibility of the IMU-based joint angle estimation, they have been restricted to the level walking condition, even though slope walking and running exhibit unique biomechanical characteristics. In addition, walking speeds in previous experiments were low in general. Note that one of the critical factors affecting the estimation accuracy in IMU-based orientation estimation is the object’s acceleration. This is because accelerometer signals under accelerated motion conditions cannot work as reference vectors along the vertical axis any more. Accordingly, the estimation accuracy of the joint angle in fast motion conditions can be significantly reduced by the external acceleration and fast walking and running conditions in such cases. However, joint angles during running and slope walking at different speeds have not been explicitly investigated.
In this regard, the contribution of this study is twofold: (i) to propose a joint angle estimation method by applying a state-of-the-art parallel Kalman filter based on IMU that can overcome the in-the-lab limitation, and (ii) to demonstrate its application to not only level walking condition but also slope walking and running conditions to fill a gap in joint kinematics literature. In particular, this study focuses on knee flexion/extension and ankle dorsiflexion/plantarflexion angles at various speed variations. The parallel Kalman filter applied in the proposed method has a capability of compensating the external acceleration through Markov-chain-based acceleration modeling, which may enhance the joint estimation performance in high speed walking conditions. The patterns of the knee and ankle joint angles that depend on various walking and running conditions are also discussed.
The second section presents the proposed joint angle estimation method based on an existing parallel Kalman filter.12 The experimental setup and test results are presented in the third section. Conclusions are outlined in the fourth section.
2. Method
2.1 Parallel Orientation Kalman Filter
The proposed method uses three reference frames: the navigation or absolute frame {n}, sensor frame {s}, and anatomical body frame {b}. The rotation matrix of the frame {s} with respect to frame {n} is denoted as where , , and , are the x-, y-, and z- directional column vectors, respectively, and the Kalman filter estimates are denoted by Rns.
The accelerometer or magnetometer signals can be modeled as
| (1) |
where is the sensor measurement at the kth sampling time, is the component obtained by projecting a reference vector, such as gravity and the local magnetic field, is the disturbance component, such as the external acceleration and magnetic disturbance, and vk is white Gaussian noise. The gyroscope signal is modeled as where is the gyroscopic signal at the kth sampling time, is the true angular velocity, and gwk is white Gaussian noise.
The state and measurement equations for the Kalman filter are respectively,
| (2.a) |
| (2.b) |
where
| (3) |
Here, Δt is the sampling time, and ca and cb are the parameters of the first-order Gauss–Markov-chain-based disturbance model.
The process noise covariance matrix Qk and measurement noise covariance matrix M are respectively
| (4) |
The variance of the gyroscope gσ2 and the variance of the accelerometer or magnetometer yσ2 are estimated when the sensors are static.12
Once the state vectors in Eq. (2.a) are estimated, corresponding to the accelerometer, which denotes gravity, can be used to obtain and that correspond to the magnetometer that denotes the local magnetic field, and can be used to obtain . The matrix is then estimated by orthogonalizing the unit vectors, i.e., .
2.2 Joint Angle Estimation
Anatomical reference frames for the body segments are defined using the optical camera system.13 As IMUs are arbitrarily attached to each body segment, a calibration procedure should be performed to convert the sensor frame to the anatomical frame. Assuming that the body segment is a rigid body, the transformation matrix between the sensor and anatomical frames is constant, and it can be obtained using initial static posture data, i.e., . Thus, the body segment orientation with respect to the navigation frame is obtained using the following equation: .
The joint angle can be extracted from the rotation matrices of the two adjacent segments.14 When the rotation matrices of the thigh and shank are represented by Rthigh and Rshank respectively, the formulas used to calculate the knee flexion/extension angle are as follows:
| (5.a) |
| (5b) |
| (5c) |
| (5d) |
where α is the knee flexion/extension angle. The x-axis lies in the frontal plane with its positive direction from left to right. The z-axis also lies in the frontal plane and its positive direction is proximal. The ankle dorsiflexion/plantarflexion angle is calculated using the shank and foot rotation matrices in the same manner.
3. Results and Discussion
3.1 Test Setup
For the verification of the proposed method, three wireless MTw IMU sensors (Xsens Technologies B.V., Netherlands) were attached to the right foot, right lower leg, and right upper leg, as shown in Fig. 1. An OptiTrack Flex13 optical motion capture system (NaturalPoint, Inc. USA) was used to obtain the reference orientation.

Test setup in which three IMUs and optical markers are placed on the right foot, lower leg, and upper leg parts of the test participant. A plastic right triangle ruler was mounted on top of each MTw IMU, and three reflective markers from the OptiTrack motion capture system were attached to each of the vertices of the ruler using adhesive tape
As a proof-of-concept, one healthy male subject (age = 24 years; height = 177 cm; weight = 72 kg) participated in the validation study. To verify the proposed method, the participant performed the following tests on a treadmill:
• Test 1: Level walking at a speed of 0.75 m/s
• Test 2: Level walking at a speed of 1.5 m/s
• Test 3: 15° slope walking at a speed of 0.75 m/s
• Test 4: 15° slope walking at a speed of 1.5 m/s
• Test 5: Level running at a speed of 2.0 m/s
• Test 6: Level running at a speed of 2.5 m/s
Note that to identify the pattern of the joint angle at various conditions, we performed level and slope walking and running at different speeds.
3.2 Results and Discussion
The angular variation of the knee joint increased in the stance phase as the walking speed increased. During slope walking, the flexion angle of the knee joint at the moment of the toe-off decreases more than that during level walking. In Figs. 2(e) and 2(f) which are the running test results, it was found that the flexion of the knee joint increases overall as compared with that during the walking test. From these results, it can be seen that the maximum value of the flexion of the knee joint increases in proportion to the walking speed.
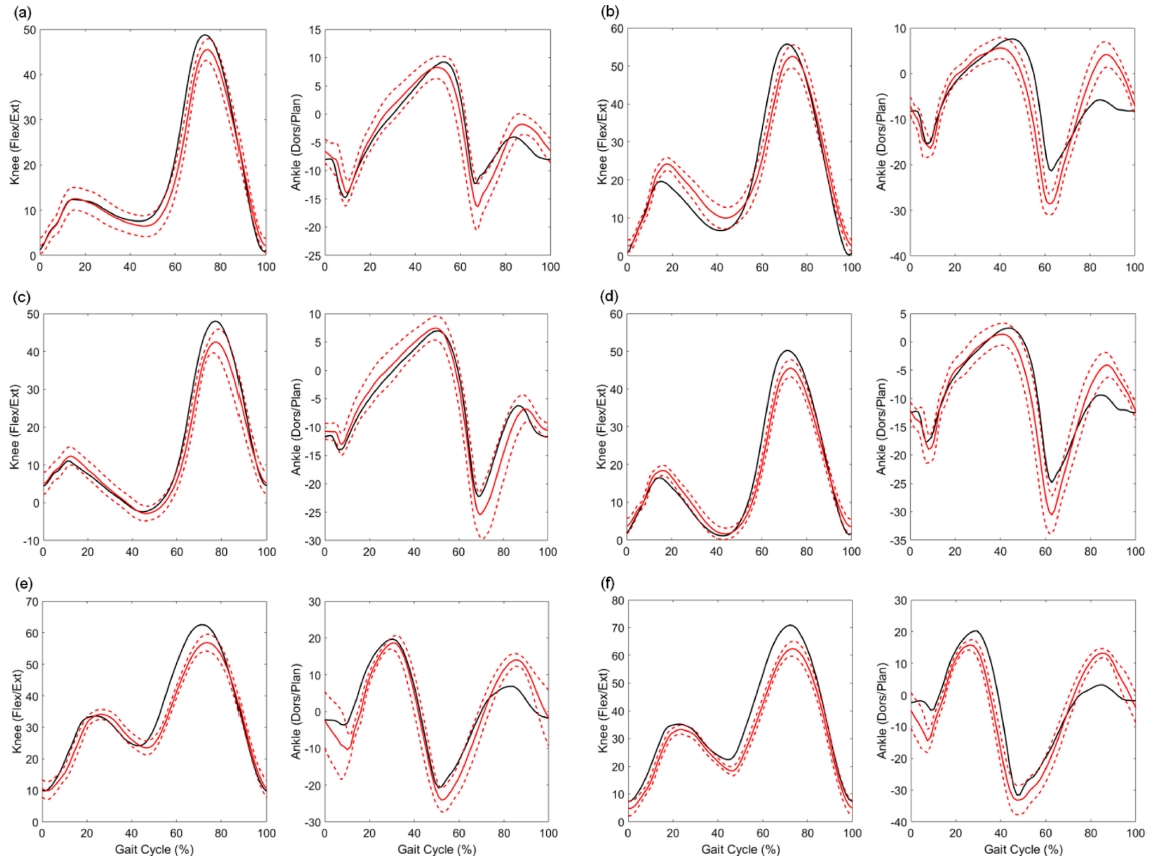
Comparison of the joint angles estimated based on the proposed IMU-based method and the optical motion capture system. The thick red solid and dotted lines represent the means and one standard deviation bands of the IMU-based angle estimation method, and the black lines are the means estimated with the use of the optical system. A colour version of this figure is available online. (a) – (f) correspond to tests 1 – 6.
In regard to the ankle joint, the results of level walking and slope walking did not elicit any significant differences. However, the range of motion during running was larger than that during level and slope walking. Additionally, the results of tests 5 and 6 showed that the maximum point of the ankle joint during plantarflexion during running was earlier than that during walking. In all the tests, errors during the swing phases were larger than those during the stance phases. This is because of the rapid increase in the external acceleration in the swing phases. Additionally, in tests 5 and 6, which are running tests, the results for the ankle joint show that the increase in the external acceleration affects the beginning of the next stance phase. The reason for this is that the magnitude of the external acceleration generated by the foot is larger than those of the shank and thigh, i.e., the magnitudes of the external accelerations follow the order foot > shank > thigh.
Table 1 gives the root-mean-squared error (RMSE) results of the joint angles over time estimated using the proposed method in comparison to the truth reference. The RMSEs of tests 1 and 3, which were associated with the slowest walking speeds, were smaller than those of other tests. The results of tests 1 - 4 show that the inclination of the walkway does not have a significant effect on the estimation accuracy. The mean error range was between 2.44o and 6.23o, thus demonstrating the feasibility of the proposed joint angle estimation method.
From the above results, it may be seen that the estimation errors generally increase in proportion to the magnitudes of the external acceleration. This implies that, although the Kalman filter applied in the proposed method has an acceleration compensation mechanism based on a Markov chain model, the effect of the acceleration on the estimation accuracy cannot be thoroughly vanished by the mechanism. Note that, in the proposed method, the joint angle is obtained through orientation estimation of unconstrained body segments. In fact, however, the segments are connected by the joint. The joint provides a kinematic constraint equation that can be utilized for the joint angle estimation and improve the estimation accuracy.
4. Conclusion
This study presented a new joint angle estimation method based on IMU signals by utilizing a parallel Kalman filter to compensate for the effects of external acceleration during fast motion. The experimental results demonstrated the feasibility of the proposed method. The interdependencies of the knee and ankle joint angles at various walking and running conditions were investigated. As the proposed approach has no restriction regarding the measurement space, it can be applied to accurately measure joint angles in real-life settings to provide clinicians and biomedical engineers with valuable data during rehabilitation.
In our future work, biomechanical constraints will be augmented with the orientation estimation Kalman filter to improve the joint angle estimation performance. Furthermore, magnetic disturbances generated around a treadmill will be investigated to eliminate any potential issue causing distortions in orientation and to the joint angle.
Acknowledgments
This research was supported by Basic Science Research Program through the National Research Foundation of Korea(NRF) funded by the Ministry of Education(grant number: 2018R1D1A1B07042791).
REFERENCES
-
Muro-De-La-Herran, A., Garcia-Zapirain, B., and Mendez-Zorrilla, A., “Gait Analysis Methods: An Overview of Wearable and Non-Wearable Systems, Highlighting Clinical Applications,” Sensors, Vol. 14, No. 2, pp. 3362-3394, 2014.
[https://doi.org/10.3390/s140203362]

-
Lee, J. K., Desmoulin, G. T., Khan, A. H., and Park, E. J., “Comparison of 3D Spinal Motions During Stair-Climbing Between Individuals with and Without Low Back Pain,” Gait & Posture, Vol. 34, No. 2, pp. 222-226, 2011.
[https://doi.org/10.1016/j.gaitpost.2011.05.002]

-
Klucken, J., Barth, J., Kugler, P., Schlachetzki, J., Henze, T., et al., “Unbiased and Mobile Gait Analysis Detects Motor Impairment in Parkinson's Disease,” PloS One, Vol. 8, No. 2, pp. 56956, 2013.
[https://doi.org/10.1371/journal.pone.0056956]

- Pietraszewski, B., Winiarski, S., and Jaroszczuk, S., “Threedimensional Human Gait Pattern–Reference Data for Normal Men,” Acta of Bioengineering and Biomechanics, Vol. 14, No. 3, pp. 9-16, 2012.
-
Leardini, A., Sawacha, Z., Paolini, G., Ingrosso, S., Nativo, R., et al., “A New Anatomically Based Protocol for Gait Analysis in Children,” Gait & Posture, Vol. 26, No. 4, pp. 560-571, 2007.
[https://doi.org/10.1016/j.gaitpost.2006.12.018]

-
Takeda, R., Tadano, S., Natorigawa, A., Todoh, M., and Yoshinari, S., “Gait Posture Estimation Using Wearable Acceleration and Gyro Sensors,” Journal of Biomechanics, Vol. 42, No. 15, pp. 2486-2494, 2009.
[https://doi.org/10.1016/j.jbiomech.2009.07.016]

-
Alonge, F., Cucco, E., D'Ippolito, F., and Pulizzotto, A., “The Use of Accelerometers and Gyroscopes to Estimate Hip and Knee Angles on Gait Analysis,” Sensors, Vol. 14, No. 5, pp. 8430-8446, 2014.
[https://doi.org/10.3390/s140508430]

-
Seel, T., Raisch, J., and Schauer, T., “IMU-Based Joint Angle Measurement for Gait Analysis,” Sensors, Vol. 14, No. 4, pp. 6891-6909, 2014.
[https://doi.org/10.3390/s140406891]

-
Cooper, G., Sheret, I., McMillian, L., Siliverdis, K., Sha, N., et al., “Inertial Sensor-Based Knee Flexion/Extension Angle Estimation,” Journal of Biomechanics, Vol. 42, No. 16, pp. 2678-2685, 2009.
[https://doi.org/10.1016/j.jbiomech.2009.08.004]

-
Bonnet, V., Joukov, V., Kulic, D., Fraisse, P., Ramdani, N., et al., “Monitoring of Hip and Knee Joint Angles Using a Single Inertial Measurement Unit During Lower-Limb Rehabilitation,” IEEE Sensors Journal, Vol. 16, No. 6, pp. 1557-1564, 2016.
[https://doi.org/10.1109/JSEN.2015.2503765]

-
Dejnabadi, H., Jolles, B. M., and Aminian, K., “A New Approach to Accurate Measurement of Uniaxial Joint Angles Based on a Combination of Accelerometers and Gyroscopes,” IEEE Transactions on Biomedical Engineering, Vol. 52, No. 8, pp. 1478-1484, 2005.
[https://doi.org/10.1109/TBME.2005.851475]

-
Ligorio, G. and Sabatini, A. M., “A Linear Kalman Filtering-Based Approach for 3D Orientation Estimation from Magnetic/Inertial Sensors,” Proc. of Multisensor Fusion and Integration for Intelligent Systems International Conference, pp. 77-82, 2015.
[https://doi.org/10.1109/MFI.2015.7295749]

-
Cappozzo, A., Catani, F., Della Croce, U., and Leardini, A., “Position and Orientation in Space of Bones During Movement: Anatomical Frame Definition and Determination,” Clinical Biomechanics, Vol. 10, No. 4, pp. 171-178, 1995.
[https://doi.org/10.1016/0268-0033(95)91394-T]

-
Grood, E. S. and Suntay, W. J., “A Joint Coordinate System for the Clinical Description of Three-Dimensional Motions: Application to the Knee,” Journal of Biomechanical Engineering, Vol. 105, No. 2, pp. 136-144, 1983.
[https://doi.org/10.1115/1.3138397]


M.Sc. candidate in the Department of Mechanical Engineering, Hankyong National University. His research interests include sensor calibration and inertial-sensing-based human motion tracking.
E-mail: yxaw12@hknu.ac.kr

Professor in the Department of Mechanical Engineering, Hankyong National University. His research interests include inertial-sensing-based human motion tracking, biomechatronics, wearable sensor applications, and system dynamics and control.
E-mail: jklee@hknu.ac.kr