정현파 외삽 예측필터에 의한 시스템 거동 예측

1. 서론

산업용 생산설비와 같은 시스템의 제어에서 그 성능을 제한하는 요소는 다양한 원인에서 발생한다. 예를 들어 정밀 스테이지의 위치제어시 발생하는 에러의 요인을 살펴보면, 시스템 구성요소인 Digital Analog Converter(디지털 아날로그 변환기), 센서 등에서 발생하는 시간지연, 모델링 되지 않은 다이나믹스, 미리 알 수 없는 외란 등 미리 수치화되지 못하는 많은 요소들이 영향을 주어 순간순간 위치 에러를 발생시킨다. 이렇게 순간적으로 발생하는 에러신호를 미리 모델링 할 수는 없지만 시간적으로 조금이라도 미리 알 수 있다면, 제어성능을 높이는데 큰 도움이 될 것이다.

순수하게 신호의 관점에서 볼 때, 우리가 전송하는 디지털 문자 데이터 등은 다음 순간 어떤 문자가 나올지 예측하는 것이 매우 어렵지만, 시스템에서 발생하는 물리적인 신호는 한정된 밴드폭과 주요 주파수로 구성된 아날로그 신호이므로 주파수 분석을 통하여 짧은 미래의 다음 신호의 예측이 가능하다. 예를 들면 위치 제어 시스템에서 시스템의 거동이 느리고, 상대적으로 예측 알고리즘의 동작 주파수가 굉장히 빠른 경우 여러 개의 과거 데이터를 가지고 몇 Step 앞을 예측하는 것은 높은 신뢰성으로 예측이 가능하다. 즉 과거 데이터를 바탕으로 주파수 분석의 관점에서 예측하는 것이다.

신호예측기법은 푸리에 급수가 발견된 이후로 여러 가지 방법으로 다양한 분야에 적용되어 오고 있다.^1,2 Vargas 와 McLaughlin는 음성 신호에서 음성신호의 공진을 예측하는데 주파수를 이용한 신호예측기법을 사용했으며³ Matsumoto는 주파수 분석을 사용하지는 않았지만 시간영역에서의 신호예측 기법을 사용하여 서보모터의 속도 제어기의 성능을 개선하였다.⁴ 뿐만 아니라 공학의 여러 분야에서 널리 쓰이는 칼만필터의 경우에도 시스템 업데이트 시 비록 한 Step이긴 하지만 모델링에 의존한 예측을 수행한다. 이러한 방법을 응용하여 의학의 분야에서도 뇌파를 예측하는데 칼만 필터가 사용되며,⁵ 신호의 모델이 존재하지 않는 상태에서도 칼만필터의 시스템 노이즈값을 증가시켜 신호를 한 Step 예측하여 추종할 수 있게 한다.⁶

이러한 외삽을 기반으로 한 예측기법을 Finite Impulse Response Filter(유한 임펄스 응답 필터)의 형태로 설계하면 정현파 등의 파형을 예측하는 데 매우 신뢰성 있게 예측할 수 있다.^7,8

Butler는 FIR필터 방식을 기반으로 정현파 주파수 분석을 이용하여 복합 구조의 스테이지 제어에서 이를 피드포워드 제어기에 응용하였으며,⁹ 하드디스크의 제어나 위치추적 시스템에서 폐루프 제어기의 게인이 크고 튼튼한 모델의 반복 제어시 피드포워드에 활용하는 연구도 찾아볼 수 있다.^10-12

본 연구에서 제안된 예측필터는 단순한 기존 정현파 외삽구조에서 더 나아가, 핵심 주파수들을 선별 및 가중치 적용하고 예측 시 발생하는 예측오차를 보상해주는 피드백 알고리즘을 통하여, 보다 먼 예측시간을 가질 수 있고 상당히 신뢰성 있는 예측값을 얻을 수 있는 예측 필터를 개발하였다. 제안된 다중 주파수를 활용한 예측필터 및 보상 알고리즘은 상대적으로 긴 예측시간 하에서도 신뢰성 있는 데이터를 얻을 수 있으며, 저주파로 입력되는 외란 아래에서도 상당히 강인하게 실시간 예측이 가능하다.

2. 외삽 기반의 예측법

2.1 정현파 외삽 기반의 신호 예측

물리적인 신호의 시간 영역에서의 외삽 기반의 예측법은 크게 두 가지로 나눌 수 있다. 식(1)과 같이 과거 데이터들을 시간영역에서 다항식으로 모델링한 외삽법과 식(2)와 같이 과거데이터들의 주파수 성분을 분석하여 사용하는 정현파 외삽이다.¹

$\[ {y\left(k\right)= a}_{n-1}{t}^{n-1}+...+a_{1}t+a_0 \]$

(1)

$\[ y\left(t\right)= {\sum }_{i=1,...,m}\left(a_i\mathrm{s}\mathrm{i}\mathrm{n}\left({\omega }_{i}t\right)+b_i\mathrm{c}\mathrm{o}\mathrm{s}\left({\omega }_{i}t\right)\right) \]$

(2)

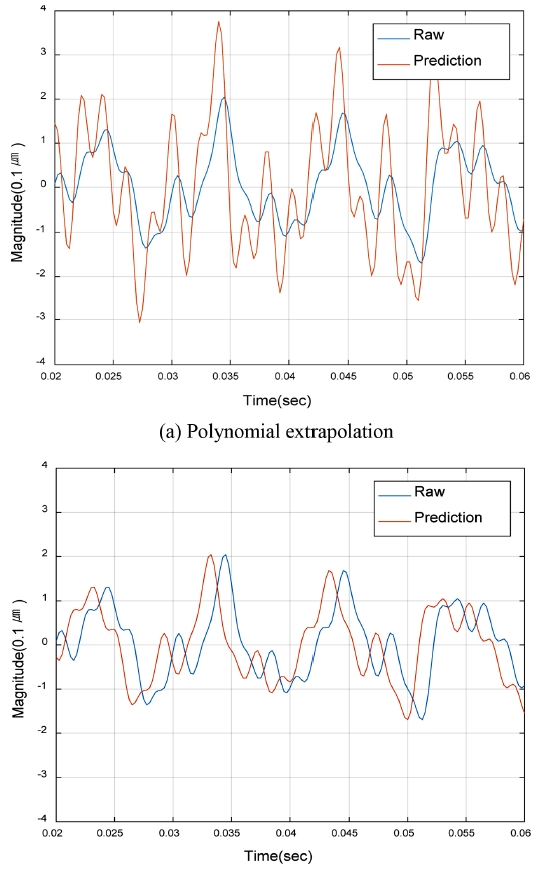
한정된 밴드폭을 가지는 산업용 기기에서 발생하는 신호는 해당 밴드폭 내의 여러 개의 주요 주파수 성분으로 구성된 신호이므로 푸리에 급수를 통한 주파수 분석 및 예측이 가능하다. 상기한 두 가지 외삽 방법의 비교를 위하여, 주파수 4개로 구성된 가상의 신호를 바탕으로 시뮬레이션을 수행하였다.

Fig. 1(a)은 1차 식의 다항식을 사용한 외삽법을 도시하였고, Fig. 1(b)는 95 Hz, 210 Hz, 270 Hz, 500 Hz의 4가지 주파수를 활용하여 각각 1.25 ms 앞의 값을 예측한 결과의 그래프이다. 일반적으로 주파수 성분을 반영하여 예측을 하는 것이 선행 예측 시점에 관계없이 정확히 예측을 하는 것을 확인할 수 있으며, 본 연구에서는 이러한 정현파 기반의 신호예측기법을 기반으로 제어시스템의 신호 예측기를 개발하였다.

Fig. 1

Comparison of two prediction filters

3. 예측 필터의 설계 및 예측오차 보상 알고리즘

3.1 실험 시스템

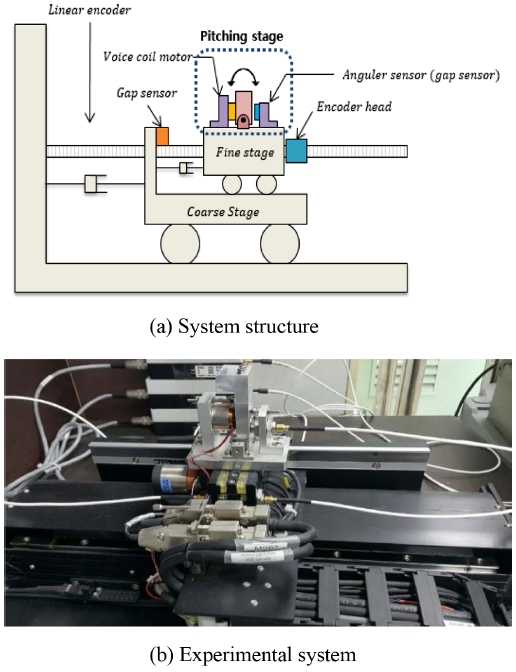
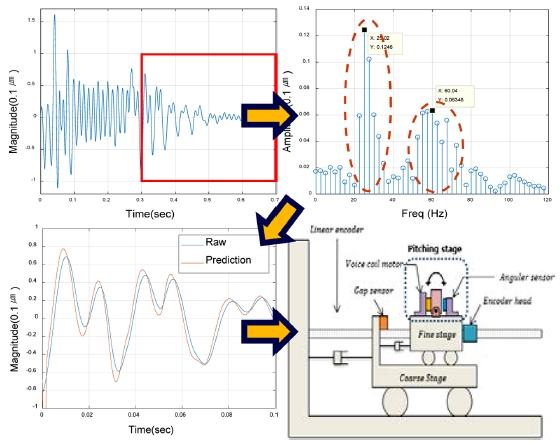
본 연구의 목적은 상기한 정현파를 이용한 신호예측기법을 활용하여 제어시스템에서의 시스템 거동을 예측하는 것이다. Fig. 2는 본 논문의 실험에서 사용한 듀얼 스테이지인데 조·미동 스테이지가 마스터-슬레이브로 구동하는 듀얼 스테이지와 상단에 피치 축 스테이지가 결합된 복합 스테이지이다.

Fig. 2

Precision dual state for experiment

제안된 예측필터의 성능을 평가하기 위해 피치 축을 제외한 조미동 스테이지를 사용하였고, 인터럽트 주파수는 4 kHz를 사용하였다. 제어 밴드폭은 미동, 조동이 각각 50 Hz, 70 Hz이고, 최대가속도 1.5 g, 최대속도 0.35 m/s에서 7차식 프로파일로 구동하였고, 해당 시스템의 위치에러 신호를 예측하는 시뮬레이션과 실험을 진행하였다.

3.2 정현파 외삽 예측필터의 다중 주파수 확장

식(3)에서 나타난 바와 같이 예측하려고 하는 신호는 여러 개의 주요 주파수로 구성되어 있으므로, 예측필터 설계의 핵심 파라메터는, 예측에 사용할 주요 주파수의 개수 및 선정, 사용할 과거 데이터의 개수 그리고 예측시점(Step)이다.

3.2.1 주요 주파수의 선별 적용

예측필터의 설계 예시를 위하여 식(11)과 같은 4개의 주파수로 구성된 가상의 신호를 고려하자.

$\[ y\left(t\right)=\mathrm{ sin}\left(2\pi 95t\right)+\frac{1}{2}\sin \left(2\pi 210t\right)+\frac{1}{3}\sin \left(2\pi 270t\right)+\frac{1}{4}\mathrm{s}\mathrm{i}\mathrm{n}\left(2\pi 500t\right) \]$

(11)

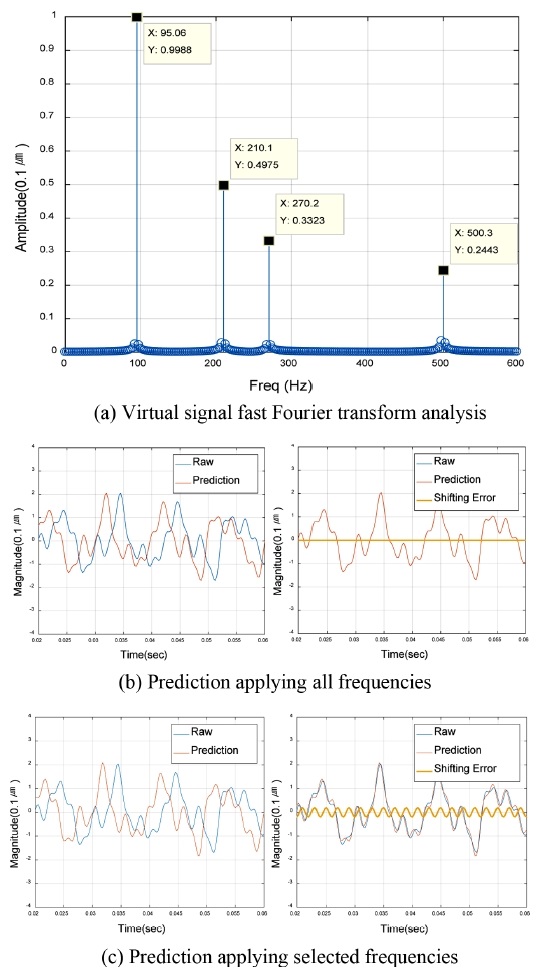
따라서 이 신호를 Fast Fourier Transform Analysis(고속 푸리에 변환 분석)하였을 때 Fig. 3(a)와 같이 4개의 해당 주파수의 성분 크기를 확인할 수 있다. Fig. 3(b)는 4개의 주파수 성분을 모두 적용해서 10Step 앞의 값을 예측한 결과이며, Fig. 3(c)는 그중 하나의 주파수 성분을 생략하고 3개의 주파수만을 적용하여 예측한 결과이다.

Fig. 3

FFT analysis and prediction errors

Figs. 3(b)와 3(c)의 우측그래프는 예측값을 기존 데이터와 동일시점으로 이동시켜서 예측오차와 함께 도시한 그래프이다. 모든 주파수 성분을 적용하였을 때는 예측오차가 거의 존재하지 않으며 정확히 예측하는 것을 확인할 수 있다. Fig. 3(c)과 같이 3개의 주파수 성분만을 적용하여 예측하면 우측의 그래프처럼 어느 정도의 예측오차가 발생하는 것을 확인할 수 있다.

Fig. 4는 실제 듀얼 스테이지의 제어시 발생하는 위치 에러신호를 FFT 분석한 것으로, 상당히 다양한 주파수로 구성된 정현파들의 합으로 이루어져 있는 것을 확인할 수 있다. 하지만 현실적으로 예측필터 설계시 모든 주파수를 고려할 수는 없으므로 주요한 주파수 성분을 선정하여 예측에 활용하여야 한다.

Fig. 4

FFT analysis of the position error signal

3.2.2 핵심 주파수 선별 및 다중 주파수 예측필터

위에서 설명한 바와 같이 실제 제어시스템에서의 신호 성분은 다양한 주파수로 구성되어 있지만, 현실적으로 신호처리 구조에서는 한정된 개수의 주파수를 사용해서 신호를 예측해야 하므로, 핵심 주파수의 선별과 각 주파수의 기여량을 반영하는 효율적인 예측필터의 개발이 필요하다.

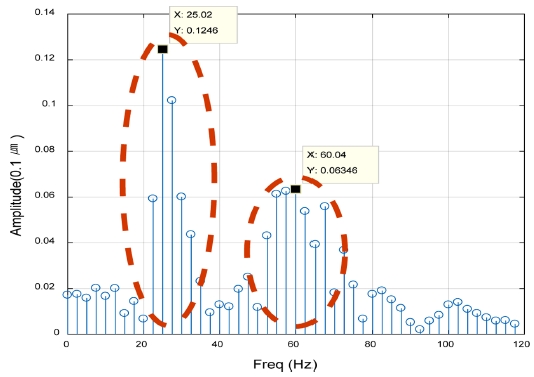
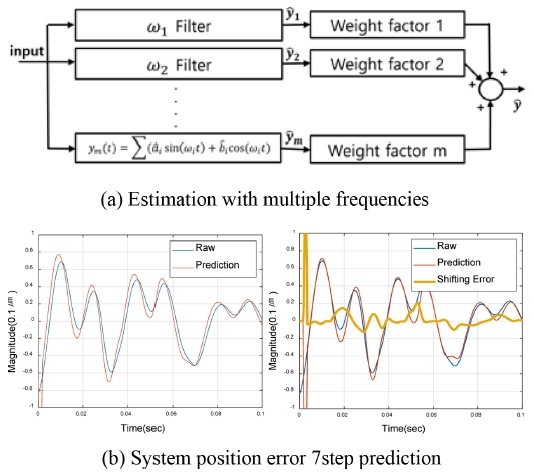
본 연구에서는 그러한 필요성을 충족시키기 위해 병렬 구조의 신호처리 기법을 사용한 가중치 예측기법을 개발하였다. 우선 Fig. 5(a)와 같은 구조에서, 상대적으로 높은 스펙트럼을 선정하고 그 크기를 사용하여 가중치 값을 선정하였다. Fig. 5(a)의 경우를 보면 상대적으로 높은 스펙트럼의 주파수 개수는 2개이고, 그 주파수의 중심값은 각각 대략 25 Hz와 60 Hz가 됨을 확인할 수 있다. 핵심주파수가 2개 이상일 때는 Fig. 5(b)와 같이 해당 주파수들을 가지고 가중치를 반영한 병렬필터 각각의 예측치를 더해서 최종 예측치를 구하는 가중치 예측 알고리즘을 개발하였다.

Fig. 5

Estimation with weighted multiple frequencies

Fig. 5(a)는 다중 주파수를 이용한 예측필터의 블록선도이며, Fig. 5(b)는 Fig. 4에서 분석한 신호를 7Step 앞서서 예측한 신호의 결과 그래프이다.

3.3 예측 필터의 오차 보상 알고리즘(EET 알고리즘)

본 연구에서 제안된 구조의 다중 주파수를 활용한 예측필터는 계산주기가 빠른 경우 상당히 정확한 성능을 보여주지만, 한정된 개수의 주파수 사용으로 인한 오차가 발생한다. 그래서 본 연구에서는 추가로 상기한 구조로 제안된 다중 주파수 예측필터의 성능을 더욱 더 개선하기 위하여, 예측치의 오차를 트랙킹하여 필터의 출력에 실시간으로 반영해주는 새로운 예측에러 보상 알고리즘을 개발하였다.

제안된 다중주파수 예측필터가 2 ms후의 값을 예측하는 경우, 실제 2 ms 이후에는 실제값을 알 수 있게 된다. 이러한 오차는 대부분 외란을 포함한 모델링되지 않은 주파수대역의 오차인데, 이 과거 예측치의 오차를 사용하면 현재 시점에서 예측하는 예측치에 해당 에러를 보정해 줄 수 있다.

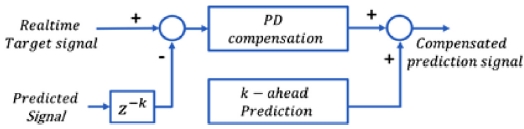
본 연구에서는 과거에 예측한 값과 현재의 실측치를 비교하여 해당 오차를 비례 게인(P)과 미분게인(D)을 통하여 앞으로의 예측치 계산에 활용하는 Fig. 6과 같은 구조의 EET (Estimation Error Tracking) 보상 알고리즘을 개발하였다.

Fig. 6

Estimation error compensation with PD compensator

이러한 보정 동작은 마치 피드백 제어시스템에서 PD 트랙킹제어와 유사한 구조로 예측에 대한 에러를 보정하며, 저주파로 변화하는 오차에 대해서는 상당한 보정효과를 거둘 수 있고, 간단한 계산량으로 효율적인 보정이 가능하다.

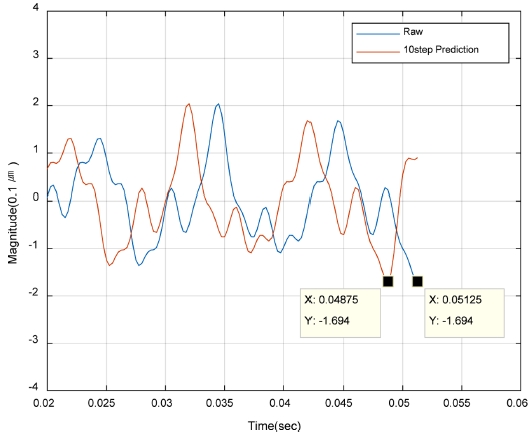
Fig. 7은 제안된 EET알고리즘의 입력값인 실시간 예측오차를 구하는 방법을 위해 식(11)과 같은 가상의 신호를 바탕으로 실시간으로 10Step(2.5 ms) 선행하여 예측하고 있는 모습을 도시한 그래프이다. X축은 시간이며, Y축이 발생한 위치 오차라고 할 때 우측의 마킹시점인 현재의 위치에러와 비교 가능한 데이터는 좌측의 마킹시점인 예측데이터의 10Step(2.5 ms)전의 데이터이다. 신호가 구성하는 모든 주파수를 사용해서 신호를 예측했기 때문에 그림 내부의 표시된 2개의 마킹시점 중 Y값들을 비교해보면 10Step 전에 예측한 Y값과 실제 10Step 후에 실제 발생한 Y값이 동일한 것을 확인할 수 있다. 하지만 주파수를 선별 적용하였을 때는 두 값이 동일하지 않으므로 이러한 입력값을 바탕으로 보정을 해주어야 한다. 이러한 예측치의 보정은 현재 시점에서 예측시점만큼의 이전 예측값을 토대로 지속적으로 이루어지며, EET 알고리즘의 설계시 PD제어기를 튜닝하듯이 어느 정도 보상기의 비례 및 미분 보정계수를 조정해 주어야 한다.

Fig. 7

Estimation result with EET compensation algorithm

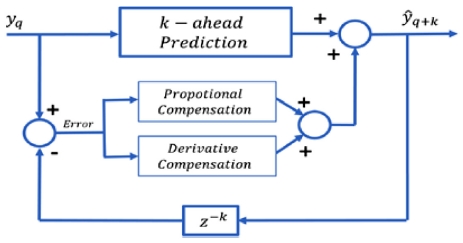
Fig. 8은 상기한 다중주파수 신호예측 알고리즘과 에러보정 EET 알고리즘을 모두 포함한 최적 예측치를 구하는 전체 블록선도이다. 예측하고 싶은 시스템 거동 오차를 핵심 파라메터들의 규칙성과 주파수 분석을 바탕으로 구한 예측치를 가중치 알고리즘에 PD보상 알고리즘을 적용하여 K Step 앞의 최선의 예측값을 구한다.

Fig. 8

Suggested signal estimation algorithm with EET compensation feedback structure

4. 예측 필터의 스테이지 관측기 적용

4.1 트랙킹 제어기에서의 구간별 위치에러 예측

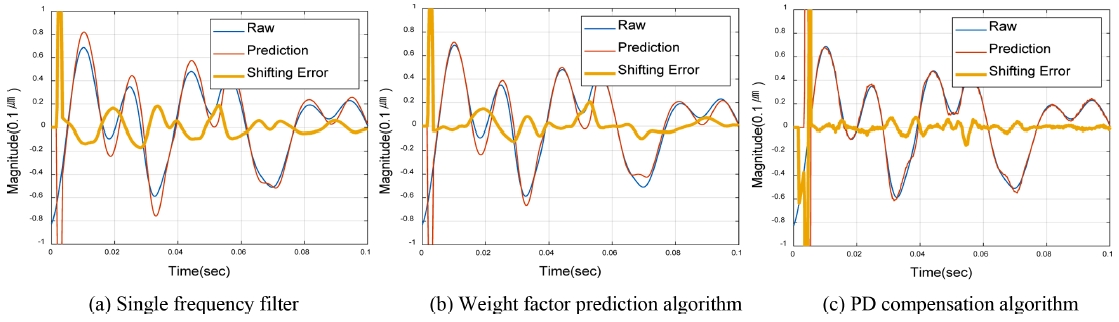
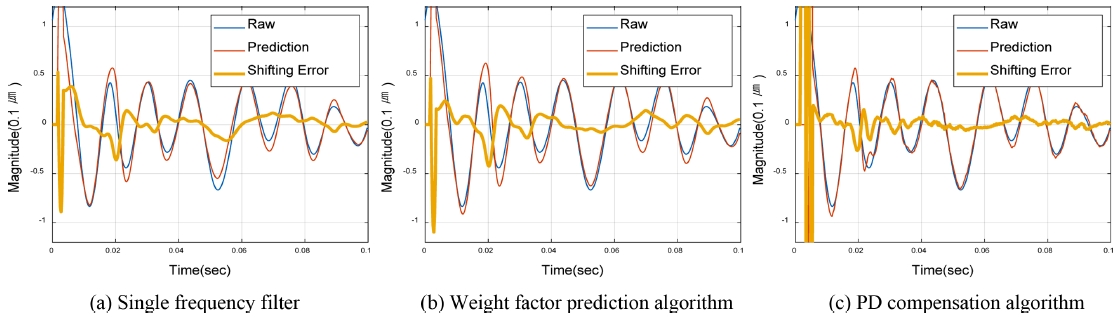
Fig. 9는 제안된 다중 주파수를 이용한 EET 예측필터를 사용하여 실제 정밀 스테이지를 구동하면서 실시간으로 발생하는 위치오차에 대한 예측을 수행하였다. 정밀스테이지의 구동 관련 구간은 크게 가속구간, 등속구간, 감속구간 그리고 정착구간 네 가지로 나눌 수 있는데, 이 중 구동 프로파일의 종류에 영향을 받지 않는 등속구간과 정착구간에 대한 위치 에러에 대한 신호 예측을 수행하였다.

Fig. 9

General application of the prediction filter algorithm

예측 알고리즘을 적용하기 위해서 우선 예측하고자 하는 신호를 수집하여 FFT분석을 통해 핵심주파수와 주파수의 개수를 먼저 선정하고 논문에 상기한 순서대로 설계하였다. 본 연구의 목표는 신호 예측기의 구체적인 설계 및 성능 확인이기 때문에, 본 논문에서는 예측한 결과치를 위치 제어에 활용하지는 않았다.

4.2 실제 시스템에서의 예측결과

해당 알고리즘들의 성능과 실제 구동시 실시간 예측을 잘 하는지, 제어기에 적용이 가능한지 확인하기 위해 세가지 조건을 가지고 각각 비교 실험을 진행하였다. Fig. 10과 Fig. 11은 각각 정착 구간과 등속구간의 데이터를 바탕으로 세가지 조건을 변화시켜가며 실험한 결과의 그래프이고 Table 1과 Table 2는 각 구간의 데이터의 예측 오차를 이동표준편차값을 구한 표이다.

Fig. 10

7step precedence prediction result of one frequency filter and two algorithms in settlement section

Fig. 11

7step precedence prediction result of one frequency filter and two algorithms in constant velocity section

Table 1

Comparison of moving standard deviation of prediction error in settlement section

Table 2

Comparison of moving standard deviation of prediction error in constant velocity section

Fig. 10(a)와 Fig. 11(a)는 핵심주파수 1개만 적용하여 7step 선행 예측한 예측치를 기존 위치에러와 동일시점에서 예측오차를 비교분석한 그래프이며, Fig. 10(b)와 Fig. 11(b)는 가중치 예측 알고리즘을 적용하여 같은 조건에서의 비교분석 그래프이고, Fig. 10(c)와 Fig. 11(c)는 PD 보상 알고리즘을 추가로 적용하여 같은 조건에서 수행한 비교 결과이다.

결과적으로 핵심주파수 1개만을 선별 적용한 예측값과 보상알고리즘까지 적용한 최적의 예측치를 예측시점을 선행해가며 이동표준편차값을 구해본 결과는 Table 1과 Table 2와 같이 각각 약 54%, 37%이상 큰 폭으로 예측오차가 감소한 것을 확인할 수 있었다.

5. 결론

본 연구에서는 정현파 주파수 분석을 이용하여 산업용 기기의 제어시스템에 사용될 수 있는 신뢰성 있는 신호 예측필터를 설계하였다. 제안된 예측필터는 예측하고자 하는 신호의 핵심주파수들의 주파수 특성과 가중치를 이용하고, 예측값의 오차를 추출하여 이를 추적 보정하는 피드백 구조를 가지고 있어서 제한된 개수의 주요 주파수 성분만을 사용하는 한계에서 오는 오차를 보정할 수 있는 EET 보정 알고리즘 구조를 포함한다.

제안된 예측필터는 비교적 짧은 미래의 신호를 높은 정확도로 예측해주므로, 이는 제어시스템의 성능향상에 필요한 다양한 신호의 제어에 사용될 수 있으며, 본 연구에서는 모션 스테이지의 트랙킹 구동에 따른 위치 에러의 추적에 적용하여 성능을 검증하였다.

제안된 알고리즘은 산업용 장비에서, 센서 신호 혹은 제어에서 발생하는 에러 등을 예측하여 제어에 직접적으로 활용할 수도 있고, 특히 센서의 시간지연이 커서 관측기의 성능이 낮은 경우에도 이의 개선에 아주 유용하게 사용될 수 있다. 이러한 방법이 실제 현장에서 큰 효력을 가지는 이유는 트랙킹 제어의 경우 제어 시스템의 구성 요소별로 발생하는 시간지연이 시스템의 성능에 큰 영향을 주기 때문이다.

랜덤이나 정보전송 신호가 아닌 물리적인 시스템으로부터 생성되는 신호들은 한정된 밴드폭을 가지므로, 제시한 예측필터를 활용하면 상당한 정확도로 해당 신호를 예측할 수 있으며, 다양한 시스템에 대하여 시간지연과 관련된 여러 가지 성능향상의 용도로 사용 가능하다.

Acknowledgments

본 연구는 2017년도 산업통상자원부의 재원으로 한국산업기술평가관리원의 지원을 받아 수행된 연구임(No.10050532).

REFERENCES

• Lee, C. H., “Signigicantly Visible Signals and Systems,” Hanbit Academy, pp. 248-281, 2015.
• Seo, J. W. and Park, H. W., “Prediction of the Chatter during the Milling Process of the Machine Tool,” Journal of the Korean Society for Precision Engineering, Vol. 32, No. 5, pp. 441-446, 2015. [https://doi.org/10.7736/KSPE.2015.32.5.441]
• Vargas, J. and McLaughlin, S., “Cascade Prediction Filters with Adaptive Zeros to Track the Time-Varying Resonances of the Vocal Tract,” IEEE Transactions on Audio, Speech, and Language Processing, Vol. 16, No. 1, pp. 1-7, 2008. [https://doi.org/10.1109/TASL.2007.907573]
• Matsumoto, Y., “Evaluation of the Digital Prediction Filter Applied to Control a Class of Servomotor by Microcomputers,” IEEE Transactions on Industrial Electronics and Control Instrumentation, Vol. 23, No. 4, pp. 359-363, 1976. [https://doi.org/10.1109/TIECI.1976.351408]
• Banerjee, A., Basu, K., and Chakraborty, A., “Prediction of EEG Signal by Digital Filtering,” Proc of the Intelligent Systems & Networks International Conference, pp. 1-6, 2007.
• Kim, J. H., “Controlling the Linear Motor with DSP,” Dong-Il, pp. 77-174, 2003.
• Handel, P., “Predictive Digital Filtering of Sinusoidal Signals,” IEEE Transactions on Signal Processing, Vol. 46, No. 2, pp. 364-374, 1998. [https://doi.org/10.1109/78.655422]
• Harju, P. T., “Polynomial Prediction using Incomplete Data,” IEEE Transactions on Signal Processing, Vol. 45, No. 3, pp. 768-770, 1997. [https://doi.org/10.1109/78.558500]
• Butler, H., “Feedforward Signal Prediction for Accurate Motion Systems using Digital Filters,” Mechatronics, Vol. 22, No. 6, pp. 827-835, 2012. [https://doi.org/10.1016/j.mechatronics.2012.05.002]
• Chew, K. K. and Tomizuka, M., “Digital Control of Repetitive Errors in Disk Drive Systems,” Proc. of American Control Conference, 1989, pp. 540-548, IEEE, 1989. [https://doi.org/10.23919/ACC.1989.4790250]
• Kempf, C., Messner, W., Tomizuka, M., and Horowitz, R., “Comparison of Four Discrete-Time Repetitive Control Algorithms,” IEEE Control Systems, Vol. 13, No. 6, pp. 48-54, 1993. [https://doi.org/10.1109/37.248004]
• Tomizuka, M., “Model Based Prediction, Preview and Robust Controls in Motion Control Systems,” Proc. of Advanced Motion Control 4th International Conference, pp. 1-6, 1996.