무기효과분석에 근거한 초소형 자연형 파편탄두 설계
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The design of subminiaturized natural fragment warhead is based on the analysis of its effectiveness against target personnel. Toward this end, the personnel incapacitation probability suggested by Sperrazza and Kokinakis was used. The effectiveness of various natural fragment warhead designs was analyzed by altering the fragment mass, velocity, number, and the target distance. A preliminary optimal design value of the natural fragment warhead in a subminiaturized missile was suggested, which was greater than the threshold value of the fragment mass to cope with air resistance. We also determined that the appropriate fragment mass was about 2.1204 × 10-4 kg (3.3 grain) in case of a subminiature warhead. This work facilitates the development of final optimal design stage of the natural fragment warhead in a subminiaturized missile and can also be utilized for the analysis and design of different types of fragment warhead.
Keywords:
Natural fragment warhead, Personnel incapacitation probability, Sperrazza and kokinakis, Fragment mass, Fragment impact velocity키워드:
자연형 파편탄두, 대인무력화확률, 스페라자 & 코키나키스, 파편질량, 파편충돌속도1. 서론
최근 전세계적으로 미래병사의 전투력 향상 및 생존성 향상을 위해 미래병사의 몸에 첨단 전자/통신장비, 센서, 방호장비 및 화기 등을 장착하는 미래병사체계(Future Soldier System)에 대한 연구가 활발히 진행 되고 있다.1,2 이 가운데 미래 병사의 전투력 향상을 위한 화기 중 하나인 병사 휴대 초소형 유도탄 기술에 관한 연구도 수행되고 있으며3,4 이의 일환으로 본 연구에서도 병사 휴대 초소형 유도탄에 탑재되는 탄두(Warhead) 설계방법을 다루고자 한다. 유도탄 개발기술의 경우 각 국의 국방기술 보안정책에 의해 기술자료 확보에 어려움이 많으며 특히 미래병사 화기로 사용할 초소형 유도탄의 경우 아직까지 전세계적으로 배치/운용되고 있지 않아 관련 연구자료 수집에 어려움이 많은 상황이다.
또한, 유도탄 내 탑재되는 탄두의 경우 유도탄 무기효과를 결정하는 중요한 구성품이라 관련된 기술자료 확보는 더욱 용이하지 않다. 따라서, 본 연구에서는 미래병사체계용 초소형 유도탄에 탑재되어 운용될 수 있는 초소형 탄두설계에 방법을 다루고자 하며, 대인무기효과를 고려한 파편형 탄두를 설계하는 방법을 다루고자 한다. 이를 위해 대인무력화효과(Personnel Incapacitation Effectiveness) 분석방법을 소개하고 무력화확률과 자연형 파편탄두 설계와 연계하여 미래병사 체계용 초소형 유도탄의 체계운용개념이 결정되었을 때 무기효과관점에서 적합한 탄두를 설계하는 방법을 제시하고자 한다. 본 연구에서 고려한 탄두는 저가로 제작 가능한 자연형 파편탄두를 고려하였으며, 대인무기효과분석을 위해 사용한 대인 무력화효과 분석은 스페라자와 코키나키스(Sperrazza and Kokinakis)가 제시한 대인무력화 확률식을 활용하였다.5
2. 본론
2.1 대인무력화확률
초소형 유도탄의 대인무기효과분석에 근거한 탄두설계를 위해서는 먼저 탄두 폭발 시 발생하는 파편이 대인표적에 주는 피해 수준을 평가할 수 있어야 한다. 이를 위해 스페라자와 코키나키스는 총알이나 파편들이 신체에 주는 피해수준을 유사 실험과 분석을 통해 대인무력화확률을 예측할 수 있는 방법을 제안하였다.
스페라지 & 코키나키스 대인무력화확률 PI/H은 다음 식(1-a)과 같으며, 식(2-b)의 스페라자 에너지(Sperrazza Energy) ESP의 함수로 표현된다.5
| (1-a) |
| (1-b) |
여기서, m은 파편 질량(Grain), V는 대인 신체 충돌 시 파편의 충돌속도(ft/sec), a, b, n는 무력화기준(Casualty Criterion)과 신체피격위치 및 병사 착용복장에 따라 결정되는 실험적 계수(Coefficient), ESP는 V의 충돌속도와 m의 질량을 갖는 파편의 스페라자 에너지(grain(ft/sec)3/2)이다. 참고로 그레인(Grain)은 질량 단위로 7000분의 1 lb 즉, 0.0648989 gram을 의미한다.
식(1-a)의 계수(Coefficient) 중 b는 한계 스페라자 에너지(Threshold Sperrazza Energy)라 불리며 주어진 파편질량과 충돌 속도에 의해 계산된 스페라자 에너지 ESP 값이 한계 스페라자에너지인 b 값 이하인 경우 파편은 신체 내로 침투하지 못해 부상을 입히지 못하며 식(1-a)에 의해 대인무력화확률, PI/H는 0이 된다.
또한, 임의 파편 질량에 대해 한계 스페라자에너지 b에 도달하는 파편 충돌속도를 한계충돌속도(Threshold Impact Velocity) Vth라 정의하며 이것을 식으로 표현하면 다음 식(1-c), 식(1-d)와 같다.
| (1-c) |
| (1-d) |
식(1)의 계수 a, b, n은 야드-파운드 단위계로 수행된 실험에 의해 결정된 값이므로 기존에 제시된 실험계수 값을 계속해서 사용하며, SI 단위계(MKS 단위계)로 표현된 수식 전개를 위해서는 식(1)의 파편 질량과 속도만 SI 단위계(MKS 단위계)로 변환하여 식(1)을 표현하면 식(2)와 같다.
| (2-a) |
| (2-b) |
| (2-c) |
| (2-d) |
여기서, mmks는 파편 질량(kg), Vmks는 파편의 충돌속도(m/sec), a, b, n은 무력화기준(Casualty Criterion)과 신체 피격위치 및 병사 착용복장에 따라 실험적으로 결정된 계수(Coefficient)로 식(1-a)에 표현된 수치와 동일한 값, ESP는 Vmks의 충돌속도와 mmks의 질량을 갖는 파편이 갖는 야드-파운드 단위로 변환된 스페라자 에너지(grain(ft/sec)3/2), Vth_mks는 한계충돌속도(m/sec)이다.
병사에게 가해진 피해수준 분류는 병사가 부상을 입은 시점으로부터 더 이상 임무를 수행할 수 없는 시간 간격(Time Interval)에 따라 달라지며, 병사가 파편이나 총알 등에 피격되어 부상을 입게 되면 부상위치에 따른 피해수준도 달라지게 된다.
결론적으로 식(2)의 대인무력화확률 계산 시 사용되는 실험계수 값은 부상위치와 임무수행이 불가한 시간간격에 따라 달라지게 된다.6
그러나, 본 연구에서는 초소형 유도탄용 탄두설계에 있어서 탄두의 직경과 무게 요구조건 외에는 다른 설계요구조건이 정해지지 않은 유도탄 개발 초기상태에서 탄두의 대인 무력화 효과분석에 근거한 탄두설계 방법을 다루고자 한다. 따라서, 분석의 편의를 위해 각 신체위치 면적 당 무력화 확률을 전신 면적으로 나눈 전신(Whole Body) 실험계수 값을 사용하였으며, 사용한 전신 실험계수 값은 다음과 같다.5
a = 7.47 × 10-3, b = 21,200, n = 0.3629
참고로 실험계수 값은 병사가 헬멧과 두꺼운 동복을 착용하고 있더라도 피격 시 5분 내 병사의 공격능력이 상실되는 무력화 기준(Casualty Criterion) 시 적용하는 실험계수 값으로 미 육군연구소(ARL: Army Research Laboratory)가 제시한 값이다.5
2.2 표적거리에 따른 파편속도
식(2)로부터 대인무력화확률은 파편질량과 충돌속도를 높이면 증가하게 되나 파편의 충돌속도는 공기저항에 의해 탄두가 폭발하는 위치에서 발생하는 파편 초기속도 보다 감소하게 된다.
탄두폭발 지점에서 발생한 파편의 초기속도 V0와 거리 x 만큼 떨어진 표적에서의 파편 충돌속도는 다음 식과 같다.7
| (3) |
여기서, x는 탄두 폭발 위치에서 떨어진 거리(m), Vx(x)는 x 만큼 떨어진 표적에 충돌하는 파편속도(m/sec), V0는 탄두 폭발 시 파편의 초기속도(m/sec), ρair는 공기밀도(kg/m3), CD는 파편 형상에 따른 항력계수, Afrag는 파편 진행방향에 수직한 면에 투영된 파편의 단면적(m2), mmks는 파편 질량(kg)이다.
식(3)의 파편 단면적 Afrag의 경우 파편의 밀도와 파편 형상 추정을 통해 식(4)와 같이 구할 수 있다.
이때 각 파편은 정육면체, 구, 원기둥 (길이/직경=1) 중의 한 형태를 갖는다고 가정하였으며, 보수적인 탄두 효과분석을 위해 파편은 회전운동에 의해 진행방향 중 가장 큰 투영단면적을 갖고 공기 중을 이동한다고 가정하고 파편 단면적을 구하였다.
또한, 식(4)에서 각 파편에 대한 파편 단면형상계수를 정리하면 다음 식(5)와 같다.
| (4-a) |
| (4-b) |
| (4-c) |
| (5-a) |
| (5-b) |
| (5-c) |
여기서 Sf_cubic는 정육면체 파편의 단면형상계수(m2/kg2/3), Sf_sphere는 구형 파편의 단면형상계수(m2/kg2/3), Sf_cylinder는 길이/직경 비가 1인 원기둥 파편의 단면형상계수(m2/kg2/3)이다.
결론적으로 식(4)와 식(5)를 이용하여 거리에 따른 파편속도 식(3)을 재정리하면 식(6)과 같이 거리에 따른 파편속도, Vx(x)는 파편의 재질과 파편의 초기속도가 결정되면 구할 수 있게 된다. 또한, 탄두효과분석에 있어서 파편의 비행시간은 상대적으로 매우 짧기 때문에 본 연구에서는 중력에 의한 파편 속도변화 및 방향변화는 고려하지 않았다.
| (6) |
여기서, Sf는 파편의 재질과 형상에 따른 파편의 단면 형상계수(m2/kg2/3)이다.
2.3 자연형 파편탄두 폭발 시 파편 초기속도
파편형 탄두에는 자연형 파편(Natural Fragment), 조절형 파편(Controlled Fragment) 및 성형 파편(Preformed Fragment) 등이 있으나 가장 저렴하고 손쉽게 제작 가능한 자연형 파편탄두를 고려하였다.
원기둥 형태의 자연형 파편탄두가 폭발 시 파편의 초기속도, V0는 거니(Gurney) 방정식을 이용해 다음 식(7)과 같이 구할 수 있다.8
| (7) |
여기서, V0는 탄두 폭발 시 발생하는 파편의 초기속도(m/sec), 는 화약종류에 따라 실험적으로 결정된 거니(Gurney) 상수(m/sec), E는 화약의 단위질량 당 에너지를 에너지 변환 손실을 고려하여 실험적으로 구한 단위질량 당 운동에너지() (m/sec)2, Cexp는 탄두 내 화약의 질량(kg), Mcase은 파편이 되는 탄두의 금속케이스 질량(kg), Cexp/Mcase은 탄두의 단위 길이 단면적 당 금속케이스 질량과 화약량의 비율이다.
식(7)은 무한대의 길이를 갖는 원기둥 형태의 자연형 파편탄두(Natural Fragment Warhead)가 폭발할 때 발생하는 파편의 초기 속도에 대한 방정식으로 탄두의 길이에 대한 영향이 배제된 식이나 탄두의 직경과 무게 만 주어진 상태에서 탄두의 대인무력화 효과를 분석하는 설계 초기에는 설계될 탄두의 길이를 변수로 설정해야 하고 설계 초기에는 설계될 탄두길이를 알 수 없으므로 탄두 길이 효과를 고려한 수정된 거니방정식(Modifed Gurney Equation)이 아닌 일반 거니 방정식을 사용하였다.
결론적으로 식(7)로부터 자연형 파편탄두 내 화약량과 금속케이스 질량이 주어지면 탄두 폭발 시 파편의 초기속도를 구할 수 있다.
2.4 파편의 평균질량 및 파편갯수
자연형 파편탄두가 폭발할 때 발생하는 파편은 다양한 크기를 갖게 되며 평균 파편질량을 중심으로 산포하는 형태를 갖게 된다. 모트(Mott)는 자연형 파편탄두가 폭발할 때 발생하는 파편들의 평균질량을 실험적으로 구하였으며,8 파편의 평균질량 μmks를 MKS 단위계로 변환하여 나타내면 식(8)과 같다.
| (8) |
여기서, μmks는 발생하는 파편의 평균 질량(kg), B는 실험으로 결정된 화약상수(Explosive Constant) ((oz)1/2/(in)7/6), t는 탄두의 금속케이스 두께(m), Di는 화약의 직경이자 금속케이스 내경(m) 이다.
식(8)로부터 파편의 평균질량을 구하기 위해서는 탄두 금속케이스 두께와 화약의 직경을 알아야 하며 탄두 금속케이스 두께는 다음 식(9)과 같이 표현될 수 있다.
| (9) |
여기서, t는 탄두의 금속케이스 두께(m), Do는 탄두 외부 금속케이스 직경으로 유도탄 체계로부터 주어지는 값(m), Di는 화약의 직경이자 금속케이스 내경(m)이다.
탄두의 외경, 금속케이스 재질, 화약의 종류 및 폭발 시 요구되는 파편의 초기속도로부터 화약의 직경이자 금속케이스 내경 Di는 거니 방정식을 이용하여 식(10)과 같이 구할 수 있다.
| (10) |
여기서, Di는 탄두 금속케이스 내부직경이자 화약직경(m), Do는 탄두 외부직경으로 금속케이스 외부직경(m), ρm는 금속케이스 재질의 밀도(kg/m3), ρe는 충전화약의 밀도(kg/m3), 는 거니(Gurney) 상수(m/sec), V0는 탄두 폭발 시 파편의 원하는 초기속도 (m/sec) 이다.
또한, 유효 탄두길이 Lwh는 탄두의 전체 질량과 부피와의 관계로부터 다음 식과 같이 구할 수 있으며 이때 고려한 탄두 내 화약 형태는 내부에 빈 공간(Void)이 없다고 가정하였다.
| (11) |
그리고, 탄두의 금속케이스 질량과 화약의 질량은 각각 다음과 같다.
| (12-a) |
| (12-b) |
일반적으로 탄두의 총 질량은 유도탄 체계설계로부터 주어지므로 알고 있는 값으로 최대허용탄두질량은 다음 식과 같이 표현되며 일정한 값을 갖게 된다.
| (13) |
여기서, Mtotal_wh는 탄두의 총 질량(kg), Mtotal_wh_effect는 유효 탄두 총 질량(kg), Cexp는 화약 질량(kg), Mcase는 파편이 되는 탄두 금속케이스 질량(kg), Mdead는 탄두 앞뒤 마개 등의 각종 기계적 인터페이스용 구성품의 질량으로 파편효과가 미미한 구성품의 질량이다.
모트(Mott)는 파편의 평균질량을 기준으로 탄두 폭발 시 발생하는 파편 총 개수 Ntotal_frag를 다음 식(14)과 같이 제시하였다.8
| (14) |
여기서, Ntotal_frag는 파편의 총 개수, Mtotal_wh_effect는 유효 탄두 총 질량(kg), Cexp는 화약 질량(kg), Mcase는 파편이 되는 탄두 금속케이스 질량(kg)이다.
3. 시뮬레이션
탄두의 유효 총 질량, Mtotal_wh_effect, 탄두의 직경, Do, 탄두의 금속케이스 재질, 화약의 종류 및 요구되는 파편 초기속도 등이 주어지면 식(6)으로부터 거리에 따른 파편속도 Vx(x)와 식(8)로부터 파편의 평균질량, μmks을 구할 수 있게 된다. 또한, 식(2-a)를 통해 1개의 파편에 의한 대인무력화확률 PI/H를 구할 수 있게 된다.
본 연구에서는 대인무력화효과 분석방법을 소개하고 대인무력 화확률과 자연형 파편탄두 설계를 연계하여 파편형 탄두를 설계하는 방법을 제시하는데 주된 연구목적이 있고, 또한, 미래병사체계의 경우 현재 운용개념이 수립 중에 있으므로 본 연구에서는 초소형 유도탄의 비행속도, 폭발고도 및 지면과의 충돌각도 등의 유도탄 운용개념을 고려한 대인무력화효과분석은 수행하지 않았다.
따라서, 탄두는 곡사포 형태로 낙하하여 대인공격을 위한 적정 높이에서 폭발한다고 가정하였으며, 파편 진행방향은 탄두 폭심으로부터 방사형으로 균일하게 퍼진다고 가정하였다. 또한, 파편의 속도 역시 탄두 폭발 시 발생하는 파편의 초기 속도에 의해서만 결정된다고 가정하였으며 탄두 폭발 시 양끝단에서 발생하는 파편의 비산각과 병사의 자세(Posture) 등의 영향은 고려하지 않았다.
식(2)를 이용하여 탄두의 대인무력화확률을 계산하기 위해서는 표적과 임의 거리 x에서 떨어진 위치에서 폭발한 탄두의 파편이 표적과 충돌하는 속도와 파편질량을 구해야 한다. 본 연구에서 고려한 자연형 파편탄두의 요구사양 및 설계규격은 Table 1과 같으며 탄두의 무게와 탄두 외경 외에 나머지는 설계자에 의해 결정될 수 있다고 가정하였다.
3.1 파편 초기속도 V0와 파편 평균질량 μmks관계
식(2)을 살펴보면 대인무력화확률은 파편의 대인충돌속도와 파편 질량이 커질수록 커지게 됨을 알 수 있다. 또한, 식(2-b)의 식으로부터 스페라자 에너지 ESP는 질량 mmks보다 대인충돌속도 Vmks에 영향을 더 받을 것이므로 탄두 폭발 시 파편 초기속도가 높은 탄두설계가 대인표적에 효과적일 것이라 생각할 수 있다.
그러나, 탄두의 외경과 중량이 제한되어 파편의 초기속도를 높이기 위해 화약을 증가시키면 그만큼 파편이 될 금속케이스 질량은 줄어들 뿐 만 아니라 과도한 폭발력에 의해 파편의 평균질량은 감소하게 될 것이라는 것을 식(7), 식(8), 식(12)를 통해 예상할 수 있다.
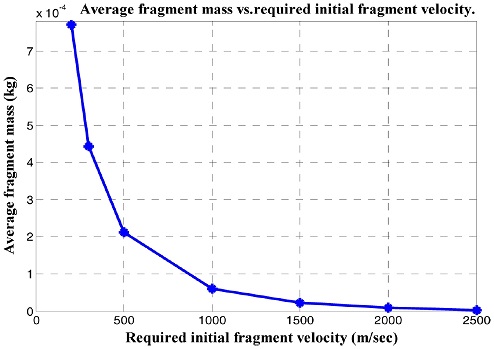
파편 초기속도 변화에 따른 파편의 평균질량 변화를 구해보면 다음 Fig. 1과 같다. Fig. 1은 요구되는 파편의 초기속도가 커질수록 발생하는 파편의 평균질량은 작아짐을 보여주며 대인무력화효과를 높이기 위해 파편이 높은 초기속도를 갖도록 탄두를 설계하더라도 폭발 시 발생하는 파편의 평균질량이 작아져 식(2-b)의 스페라자 에너지에 근거한 대인무력화효과는 달라지게 된다.
3.2 파편의 스페라자 에너지(Sperrazz Energy)
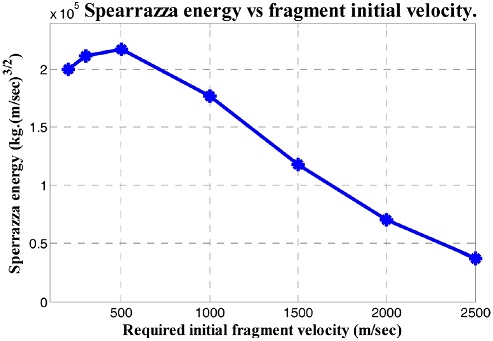
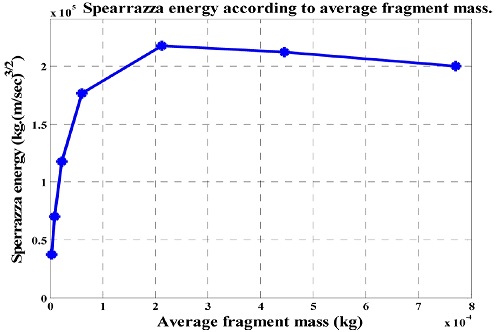
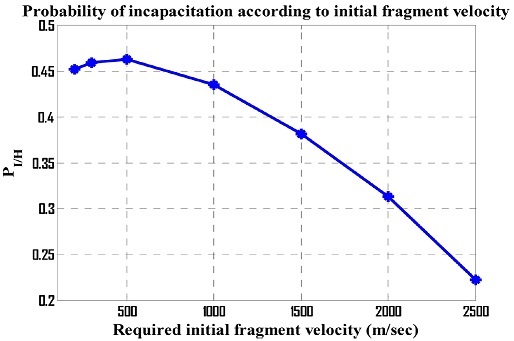
Fig. 1에 나타낸 파편 초기속도와 평균질량에 대해 1개 파편이 갖는 스페라자 에너지 변화를 Figs. 2와 3에 나타내었으며 대인무력화확률은 Fig. 4에 나타내었다.
Fig. 2을 보면 파편의 초기속도가 500 m/sec일 때 스페라자 에너지가 최대가 됨을 볼 수 있으며 이때의 파편의 평균질량은 Fig. 3으로 부터 2.1204 × 10-4 kg (3.3 grain)임을 알 수 있다.
Fig. 4역시 초기속도 변화에 따라 스페라자 & 코키나키스 대인무력화확률 PI/H을 나타낸 것으로 초기속도 500 m/sec에서 대인무력화확률이 최대가 됨을 볼 수 있다.
3.3 표적과의 거리에 따른 파편속도 변화
3.2절에서 대인무력화확률 및 스페라자 에너지 계산에 있어 파편의 대인충돌속도를 탄두 폭발 시 초기속도로 가정하였다. 그러나, 파편의 속도는 공기저항에 의해 표적과의 거리에 따라 감소하게 되며 표적과 충돌하게 된다.
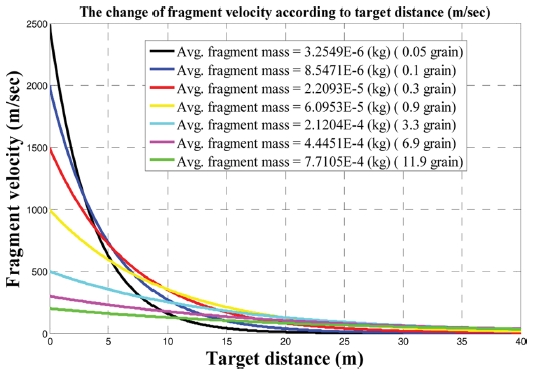
따라서, 본 절에서는 앞에서 제시한 Table 1의 탄두설계 요구사양을 만족하는 여러가지 형태로 설계된 자연형 파편탄두가 폭발할 때 표적거리에 따른 파편의 충돌속도 변화를 Fig. 5에 나타내었다. 이때 식(6)에 파편의 단면형상계수는 보수적인 탄두 효과분석을 위해 가장 큰 값을 사용하였으며 표적과의 최대 거리는 40 m로 가정하였다.
Fig. 5을 살펴보면 가장 작은 파편 질량을 갖고 파편의 초기속도가 가장 높은 자연형 파편탄두 설계안(Avg. Fragment Mass = 3.2549 × 10-6 kg (0.05 grain))의 경우, 표적 거리가 늘어 남에 따라 파편속도가 급격히 감소하여 다른 설계 안들과 비교했을 때 1 m 이상에서는 좀 더 큰 파편 질량과 작은 초기속도를 갖는 파편이 표적거리가 늘어남에 따라 더 큰 표적충돌속도를 가짐을 볼 수 있다.
이 이유로는 파편 초기속도가 큰 경우는 탄두 폭발 시 발생하는 파편의 평균질량이 상대적으로 작게 되어 식(6)로부터 표적 거리가 늘어남에 따른 속도감소가 더 커지기 때문이다.
3.4 표적거리에 따른 1개 파편의 대인무력화확률
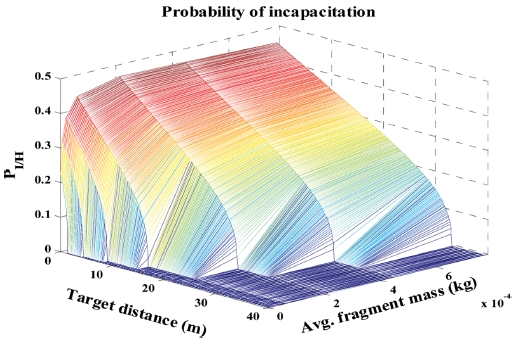
본 절에서는 초기속도가 다른 자연형 파편탄두 설계 안에 대해서 표적거리가 늘어남에 따른 대인무력화확률 변화를 관찰하고자 한다. 이때 고려된 파편의 수는 1개이다. 각 탄두 설계 경우에 대한 거리에 따른 대인무력화확률의 변화를 Figs. 6에서 8에 나타내었다. 세계적으로 가장 많이 사용되는 M67 수류탄의 경우 무게가 390 g이며, 유효무력화반경은 15 m, 위험반경은 50 m이다. 반면에 본 연구에서 고려한 유도탄은 전체무게가 200 g이고 탄두유효질량은 50 g으로 M67보다 작으므로 최대 40 m이내의 표적거리에 대한 대인무력화확률을 관찰하였다.
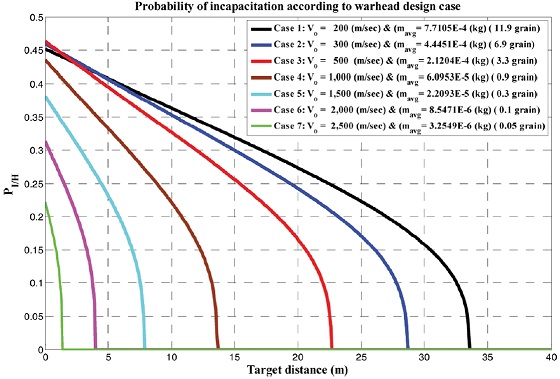
Probability of incapacitation with respect to the target distance according to various warhead design cases
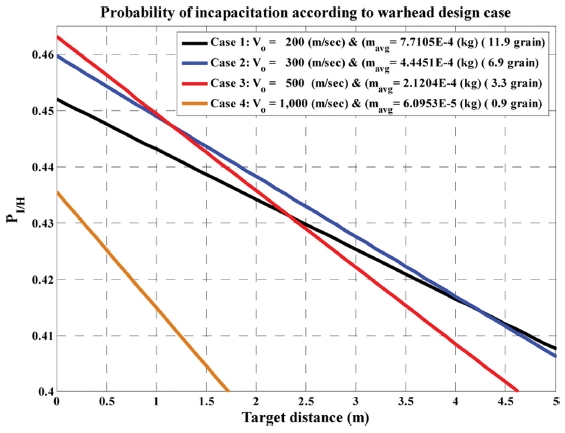
Figs. 6에서 8로부터 Table 2의 7가지 탄두설계안 모두 공기저항으로 인한 파편속도 감소로 인해 33.6 m 이상의 표적거리에서는 무력화효과를 갖지 못 함을 볼 수 있다.
이 중 Case 1의 탄두 설계가 33.6 m의 가장 넓은 대인무력화반경을 갖는 반면에 4.2 m 이내의 거리에서는 Case 2의 탄두 설계가 Case 1 보다 높은 무력화효과를 가진다. 또한, 1.6 m 이내에서는 Case 3가 가장 높은 무력화효과를 가짐을 볼 수 있다.
결국, 최적 탄두설계는 표적거리 등의 체계운용 개념에 따라 선정되어야 함을 다시 한번 알 수 있으며 사용된 각 탄두 설계안별 설계제원은 Table 2에 나타내었다.
3.5 파편 개수를 고려한 대인무력화확률
3.4절에서는 1개의 파편에 대한 대인무력화확률을 다루었다. 그러나, 탄두는 폭발 시 탄두 금속케이스가 식(14)에 따라 많은 파편조각으로 나눠져 방사되게 된다. 따라서, 본 절에서는 거리에 따른 대인무력화확률 계산에 각 탄두 설계안 별 파편 개수 효과를 고려하여 대인무력화 확률을 분석하고자 한다.
먼저 앞 절에서 설정한 가정에 의해 각 탄두 폭발 시 발생하는 파편은 방위각 방향으로 균일하게 방사되며 탄두 양끝단 마개 부근에서 발생하는 파편의 비산각은 고려하지 않았다.
또한, 탄두 길이방향의 파편 역시 평행하게 방사되고, 병사의 전신투영면적을 정사각형이라 가정하면 다음 식(15)과 같이 파편개수를 고려한 대인무력화확률을 구할 수 있다.
| (15-a) |
| (15-b) |
여기서, PI/H_soldier는 표적거리 x에 위치한 병사의 전신 평균투영면적에 충돌하는 파편 개수와 공기저항에 의한 충돌속도 감소를 고려한 대인무력화확률, PI/H,i(x)는 i번째 파편이 폭심(Explosive Center)에서 거리 x만큼 떨어진 곳에서 갖는 파편속도에 의한 대인무력화확률, ASoldier는 병사가 서 있을 때 노출되는 전신평균투영면적(0.5572 m2), nx는 거리 x 위치에 서 있는 병사에게 충돌하는 파편 개수이다.
Table 2의 각 탄두 설계 별 파편개수를 고려하여 얻은 거리 x에 서 있는 병사에 대한 대인무력화확률 PI/H_soldier는 Fig. 9와 같으며 Fig. 9(b)는 Fig. 9(a) 대인무력화확률을 10 m 이내 표적거리에 대해 자세히 나타낸 그림이다.
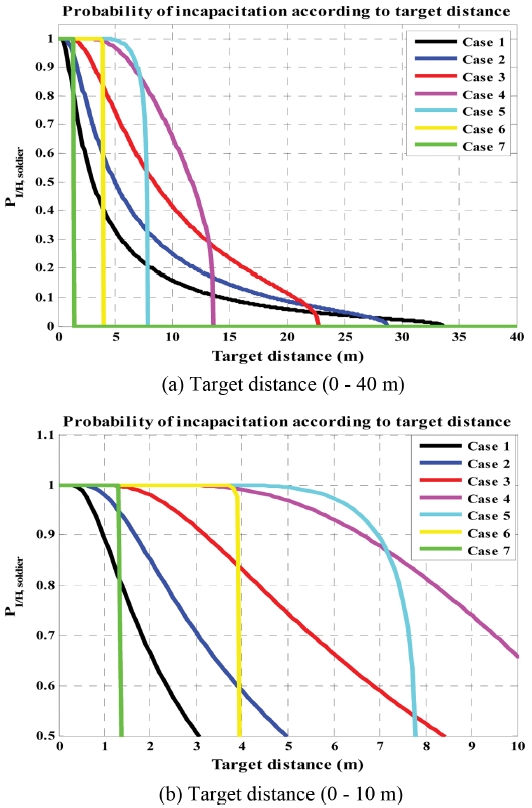
Probability of incapacitation considering the number of total fragment and soldier’s presented area according to target distance
각 탄두설계 별 유효무력화거리(Effective Incapacitation Distance), dI/H_effective와 최대무력화거리(Maximum Incapacitation Distance), dI/H_max는 Table 3에 나타내었으며 유효무력화거리는 다음 식(16)과 같다.5 또한, 최대무력화거리는 대인무력화확률 값이 0이 되는 거리로 정의하였다.
| (16) |
Fig. 9와 Table 3을 살펴보면 파편개수가 가장 많은 Case 7 탄두설계안은 유효무력화거리와 최대무력화거리가 1.4 m로 가장 작으며, 파편개수가 가장 적은 Case 1의 탄두설계안의 경우 최대 무력화거리는 33.6 m로 가장 크고 유효무력화거리는 8.92 m로 작음을 알 수 있다.
Case 7탄두설계안이 작은 무력화거리를 갖는 이유는 파편 질량이 너무 작아 공기저항에 의한 큰 속도감소 때문이며, Case 1 탄두설계의 경우 파편질량이 커 큰 최대무력화거리를 갖지만 파편개수가 작아 유효무력화 거리는 작아짐을 알 수 있다.
따라서, 초소형 탄두의 경우 충분한 대인무력화효과를 갖기 위해서는 일정크기 이상의 파편질량과 파편개수를 가져야 하며 Table 2의 탄두설계 안 중 가장 큰 유효무력화거리를 갖는 최적 탄두설계안은 Case 3 탄두설계안이다.
그러나, 체계운용개념에 따라 유효무력화거리가 10 m 이상이며, 가능한 큰 최대무력화거리를 갖는 탄두효과 요구조건이 주어진다면 유효무력화거리 요구조건을 만족하는 설계안 중 가장 큰 최대무력화 거리를 갖는 Case 2 탄두설계안이 최적 설계안이 될 수 있다.
결론적으로 대인무기효과분석에 근거한 초소형 탄두 설계는 유효무력화거리 및 최대무력화거리 등의 체계운용 개념 및 요구조건에 따라 설계되어야 하며 특별한 체계요구조건이 없이 단순히 제한된 탄두무게 및 직경을 만족하는 초소형 탄두설계를 선택해야 한다면 Case 3를 선택하는 것이 유효무력화거리 측면에서 최적의 탄두설계안이라 판단된다. 이때 Case 3 탄두설계안의 파편질량은 2.1204 × 10-4 kg (3.3 grain)이다
4. 결론
본 연구에서 대인표적 피해효과를 분석할 수 있는 스페라자와 코키나키스 대인무력화확률식에 근거하여 초소형 유도탄용 자연형 파편탄두 설계방법을 제시하였고, 파편질량, 파편속도, 표적거리, 파편개수에 따라 여러가지 탄두설계에 대한 대인무력화확률을 분석하였다. 또한, 유효무력화거리 등의 무기효과 관점에서 초소형 자연형 파판탄두 최적설계안을 제시하였으며 제시된 탄두설계의 경우 파편질량은 2.1204 × 10-4 kg (3.3 grain)임을 알 수 있었다. 본 연구는 향후 미래병사체계 내 초소형 유도탄의 체계운용개념이 설정되면 무기효과분석관점에서 유도탄의 비행조건과 파편 비산각 등을 고려한 자연형 파편탄두 최적설계에 활용가능하며, 각종 파편형 탄두의 파편 최적설계에도 활용 가능하다고 생각된다.
또한, 본 연구는 향후 대인무기용 탄두에 의한 피해를 최소화 할 수 있는 대인 보호용 방탄장비 및 보호복 개발을 위한 기초자료로 활용될 수도 있을 것이다.
REFERENCES
- Kim, S., “Trend of Technology Development on Future Soldier System,” Defense and Technology, Vol. 382, No.12, pp.76-87, 2010.
- Wikipedia, “Future Integrated Soldier Technology,” https://en.wikipedia.org/wiki/Future_integrated_Solider_Technology, (Accessed 5 SEP 2018)
- Agency for Defense Development, “A Guided Missile launching Machanism for a Soldier,” KOR Patent, No. 1013434200000, 2013.
- Tech Holic, “Developing Subminiature Guided Missile with 64 cm Length,” http://www.techholic.co.kr/news/articleView.html?idxno=13562, (Accessed 20 SEP 2018)
-
Driels, M. R., "Weaponeering : Conventional Weapon System Effectiveness,” AIAA Educational Series 2nd Edition, pp. 703-734, 2013.
[https://doi.org/10.2514/4.869259]

- Couldrick, C. A., “A Systems Approach to the Design of Personal Armour for Explosive Ordnance Disposal,” Ph.D. Thesis, College of Defense Technology Engineering Systems Department of Cranfield University, pp. 143-146, 2005.
-
Carleone, J., “Tactical Missile Warheads,” American Institute of Aeronautics & Astronautics, Vol. 155, pp. 461-464, 1993.
[https://doi.org/10.2514/4.470677]

-
Lloyd, R., “Conventional Warhead Systems Physics and Engineering Design,” American Institute of Aeronautics and Astronautics Reston, Vol. 179, pp. 19-77, 1998.
[https://doi.org/10.2514/4.472558]


Ph.D./chief research engineer in LIG Nex1 Co., Ltd. His research interest is dynamics of nonlinear systems, fault diagnostics, and biomimetic robot.
E-mail: drbaek100@naver.com

Chief research engineer in LIG Nex1 Co., Ltd. His research interest is avionics, flight control computer and precision guidance missile.
E-mail: sefeel00@hanmail.net

Ph.D./research director in LIG Nex1 Co., Ltd. His research interest is weapon effectiveness.
E-mail: yongelee@daum.net

System Engineer in LIG Nex1 Co., Ltd. His research interest is system design of a precision guided munition.
E-mail: kimsungun@hanmail.net