A Study on a Single Continuous Deformable Mirror for Correction of Atmospheric Disturbance
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The deformable mirror is the main component of the adaptive optical imaging system, which removes the atmospheric disturbance and acquires the target image without any loss and the beam transmission system, which transmits the laser beam to a long distance. The mirror transforms the optical wavefront distortion caused by atmospheric disturbance into the opposite wavefront shape thereby correcting the distorted wavefront. In order to develop the deformable mirror, it is necessary to analyze the adaptive optics system and the usage environment where the application is required. In the present work, a prototype of a deformable mirror with a single continuous mirror was developed. In order to design the deformable mirror, the main factors of the adaptive optics system and the large diameter telescope were analyzed. Subsequently, the mirror material and the actuator were selected by confirming the amount of deformation through the finite element analysis. Based on the data collected, we designed and fabricated the prototype of the deformable mirror, and the Gaussian model was derived by analyzing the influence function of the deformable mirror through the design data. It was observed that the derived Gaussian model matched with the Zernike polynomial. Apparently, the fitting ability of the deformable mirror was confirmed.
Keywords:
Deformable mirror, Wavefront distortion, Requirement analysis, Finite element analysis, Influence function, Zernike polynomial키워드:
변형거울, 파면 왜곡, 요구사항 분석, 유한요소해석, 영향 함수, 제르니케 다항식1. Introduction
The deformable mirror is the main component of the adaptive optical imaging system which removes the atmospheric disturbance and acquires the target image without loss and the beam transmission system which transmits the laser beam to a long distance.1-2 It transforms the optical wavefront distortion caused by atmospheric disturbance into the opposite wavefront shape thereby correcting the distorted wavefront.
The adaptive optics system consists of a wavefront sensor, a wavefront compensator and a signal processor. With the tip-tilt mirror, the deformable mirror compensates the wavefront distortion measured by the wavefront sensor. In general, the tip-tilt mirror compensates for the lower order term of the third order or lower, and the deformable mirror compensates for the higher order term of the higher order than the fourth order. To compensate for the high order term of the wavefront distortion, the deformable mirror is designed in many cases by deforming the reflecting mirror surface by several μm.
Since Babcock proposed the use of a deformable optical element driven by a wavefront sensor to compensate for the atmospheric effects affecting the image of the telescope, much research has been done on the development of a deformable mirror in parallel with the development of science and technology.3 Deformable mirrors are classified into divided a segmented deformable mirror,4 a bimorph deformable mirror,5 a membrane deformable mirror6 and single continuous deformable mirrors according to their actuating method and shape. In the early days, a split mirror was developed to change the position and tip-tilt of a small flat mirror, but there was a problem that light was lost due to a gap between the mirror and the mirror. Therefore, a bimorph deformable mirror, a membrane deformable mirror and a single continuous deformable mirror was developed to obtain a clearer image. The bimorph deformable mirror is a type in which actuators arranged parallel to the reflecting mirror surface locally compresses and expands to deform the reflecting mirror. And the membrane deformable mirror is a type in which the thin film moves by magnetic force. The bimorph mirror is suitable to correct low order wavefront distortion and can have a large deformation displacement, but it is difficult to correct the wavefront distortion of the high frequency component and to make it in a form having many channels. The membrane mirror has a large deformation displacement and is advantageous in that it can be mass-produced easily, but it is physically weak and can be easily broken. For this reason, both the bimorph deformable mirror and the membrane mirror are unsuitable for beam transmission systems. A single continuous deformable mirror operates in such a way that an actuator positioned orthogonally to the reflecting mirror pushes and pulls the reflecting mirror. However, unlike the segmented mirror, there is no problem of light loss.
This research focuses on the design and development of a single continuous deformable mirror that compensates for wavefront distortion of high order terms in adaptive optics system. The specifications of the reflecting mirror and the actuators were determined through the requirements analysis considering the atmospheric characteristics and the application system, and the influence functions were derived through the finite element analysis. In addition, we designed and developed the deformable mirror prototype and the control software that can compensate for the atmospheric disturbance by eliminating high order aberrations. The deformable mirror prototype was developed to deform the reflecting mirrors by arranging the piezoelectric actuators vertically below the reflecting mirror. The correction performance of atmospheric disturbance is predicted through the influence function derived from the design data.
This paper is composed as follows. In section 2, the main specifications of the deformable mirror and determined through the requirements analysis. In section 3, the design and fabrication of the deformable mirror prototype are discussed. In section 4, the correction performance of atmospheric disturbance is predicted by the influence function analysis and comparative analysis with the Zernike polynomial. Finally, section 5 concludes.
2. Requirements Analysis
In order to design a deformable mirror for correction of atmospheric disturbance, an analysis of an adaptive optics system including a deformable mirror and a large diameter telescope system employing an adaptive optics system should preceded. In this study, for the design of deformable mirror prototype, the deformation displacement specification is presented considering the atmospheric characteristics, and the reflecting mirror material and actuator are determined.
2.1 Analysis of the Deformation Displacement
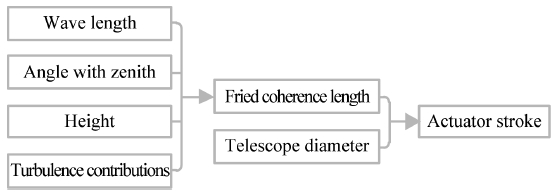
In the design of the deformable mirror, the main characteristic of the atmosphere is the Fried coherence length.7 The Fried coherence length is calculated by the wave length, the angle with zenith, the height (altitude) and the turbulence contributions. The deformation displacement and the actuator stroke are derived from the Fried coherence length and the telescope diameter as shown in Fig. 1.
The Fried coherence length is the range in which the same atmospheric effect is exhibited as 0.1219 m by Hardy’s Eq. (1) The main factors for deriving above result are wave length and height. The wave length range of 550 nm - 850 nm, which is the visible light region, should be considered, and the large telescope should be located at a high altitude in consideration of light pollution and viewing angle. As a result, the Fried coherence length was calculated assuming that the wavelength was 500 nm and the height was 1000 m, and other parameters are shown in Table 1.
| (1) |
In the ideal case, the deformation displacement is the same as the wavefront distortion derived from Fried coherence length and the telescope diameter as shown in eq. (2) Since the wavefront distortion is a deviation, for the adaptive optics system the RMS and PTV values are often related via a scaling factor 5.8 Therefore, it was analyzed that the deformation displacement should be more than ±1.64 μm.
| (2) |
2.2 Schematic Design
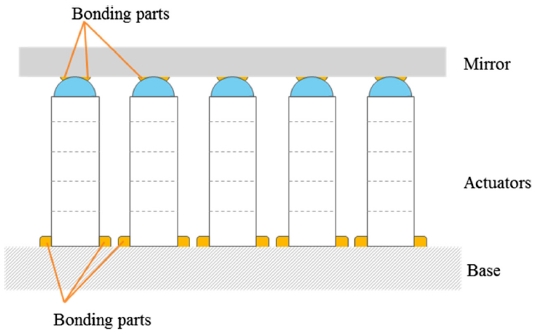
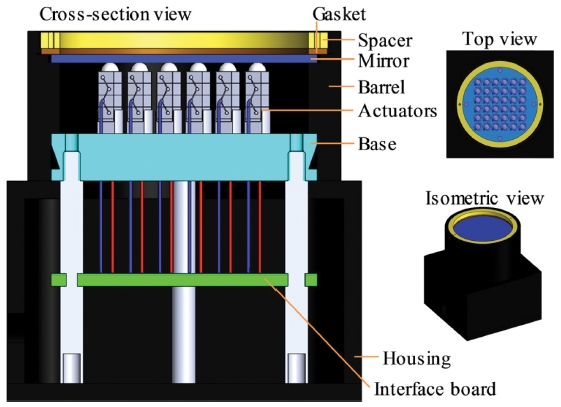
In this study, we have developed a single continuous mirror, which has a reflecting mirror and the actuators are under the mirror and the actuators pushes or pulls the mirror as shown in Fig. 2. The thickness of the reflecting mirror was set to 1 mm in consideration of the beam transmission system. In addition, the base has a sufficient rigidity to minimize the effect of the actuator being acted upon by the reaction. The actuator is bonded to the reflecting mirror using an adhesive and is also bonded to the base. For bonding, 353NDPK (Thorlabs) and TS10 (Thorlabs) are used as an adhesive, and a guide hole for fixing the position is provided on the base, so that the actuator can be fixed in place and adhered.
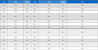
The reflecting mirror must have optically and mechanically stable properties. It should also be possible to polish the surface and to coat the required reflection coefficient with the spun material. Table 2 summarizes the materials that can be used as a material for reflecting mirrors according to theses design requirements.
The reflecting mirror must be displaced with respect to the actuation of the actuator. In addition, the deformation displacements must be deformable beyond the total required displacement analyzed in section 2.1. As a result, the reflecting mirror material is selected as the ULE which is the smallest in Young’s modulus and suitable for the reflecting mirror.
2.3 Finite Element Analysis
In order to confirm whether the reflecting mirror can be deformed more than the standard which already derived in section 2.1, the deformable mirror to be developed in modeled in a simplified form composed of the reflecting mirror and the actuator, and the finite element analysis is performed. The model shape including the design element is shown in Fig. 3, and the elastic modulus of the actuator is 50 GPa assuming that the piezoelectric ceramic actuator will be used.
In the finite element analysis, 9 actuators were placed under the reflecting mirror. Among them, only the central actuator was driven. The bottom parts of the actuators were analyzed under fixed conditions and the damping of the ceramic can be neglected because it was very low. Also, the part fixed by bonding was assumed to be 1 mm in diameter. In order to confirm whether deformation exceeding the standard occurs, deformation of the reflecting mirror according to the generated force of the actuator is checked and summarized as shown in Table 3.
Based on the finite element analysis, it was confirmed that the actuator should generate a force of 240 N or more in order to satisfy the deformation standard of the reflecting mirror. Accordingly, the actuator was determined as PK4JMP1 (Thorlabs) by comparing the specifications of the actuators that can be purchased. This actuator has a maximum displacement of 8.8 μm at 150 V and a blocking force of 360 N at 150 V. The size of this actuator is 3.4 × 4.8 × 10.0 mm.
3. Development of the Deformable Mirror
3.1 Design
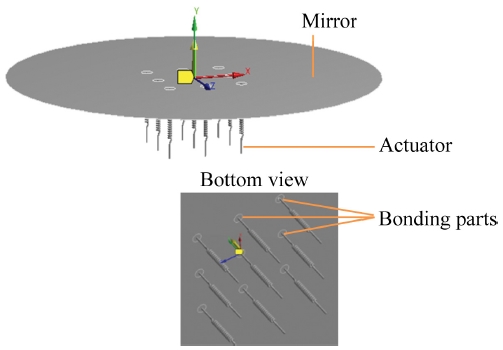
The deformable mirror designed by using the previously determined reflecting mirror and actuator is shown in Fig. 4. There is a spacer for fixing the reflecting mirror, and the reflecting mirror is pressed with a gasket. The base is designed to have sufficient rigidity, and actuators are bonded to the reflecting mirror and base. Each actuator is arranged at 5 mm distance and all the actuators are located inside the barrel. The actuator receives driving signals from the outside, thus each cable of the actuator is connected to an interface board inside the housing to receive an external signal.
3.2 Equipment Setup
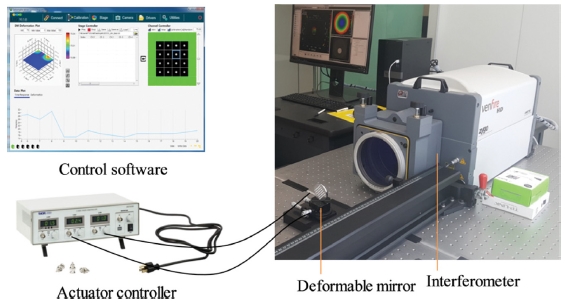
The deformable mirror consists of control software, actuator controller and deformable mirror prototype as shown in Fig. 5. The control software was developed in this study so that the driving signal can be input to the deformable mirror and the amount of change can be confirmed immediately. The actuator controller, purchased from Thorlabs, supplies voltage up to 150 V at a speed of 50 - 60 Hz to each actuator through the interface board so that the deformable mirror can be deformed. With this configuration, the surface of the deformable mirror can be deformed, and the amount of the deformation can be confirmed by using an interferometer.
4. Simulation and Measurement
The influence function is the shape of the reflecting mirror surface when a unit voltage is applied to the actuator. Since the reconstructed wavefront is made up of a linear combination of each influence function, the influence function is a measure of how well the deformable mirror can correct the wavefront error.9-10 In this section, the influence function is derived from the finite element analysis data of the deformable mirror designed and fabricated in section 3, and the influence is analyzed to establish the Gaussian model to confirm the fitting ability.
4.1 Analysis of the Influence Function
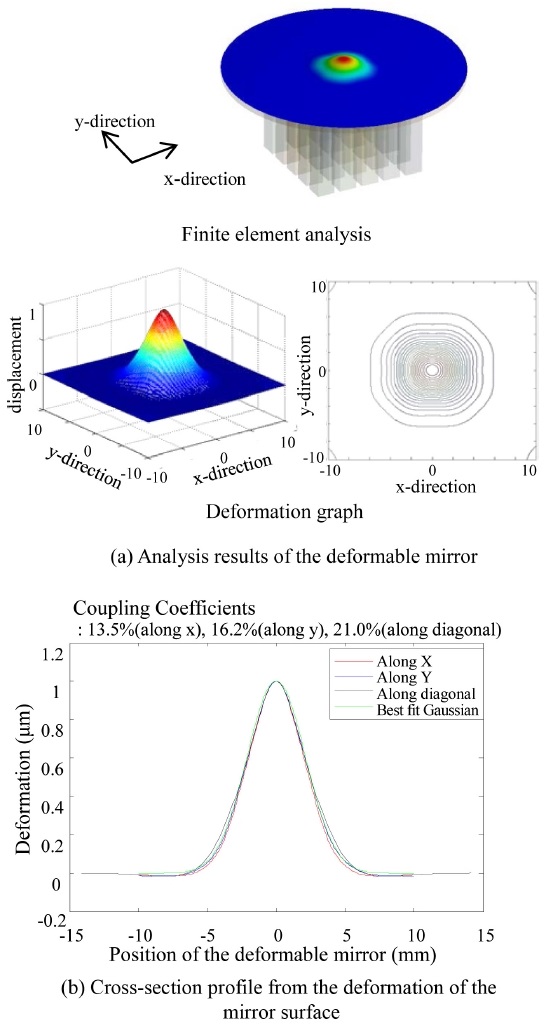
The surface phase data values of the reflecting mirror plane derived from the finite element analysis are shown in Fig. 6(a). when 1 μm deformation is generated on the surface of the deformable mirror, the deformation around the center of the actuator is expressed as shown in Fig 6(a).
The surface phase data values derived from the finite element analysis can be represented by the cross-section profiles as shown in Fig. 6(b). According to the cross-section profiles, the coupling coefficient in each direction can be calculated. The deformable mirror has a coupling coefficient of 13.6% in the x-direction, 16.2% in the y-direction and 21.0% in the diagonal direction. The coupling coefficient can be changed the Gaussian model by linear fitting method as eq. (3).
| (3) |
In eq. (3), ω represents the coupling coefficient, d represents the actuator spacing, and α represents the Gaussian coefficient. The result of the analysis of the influence function is that each coefficient of eq. (3) is approximated by ω = 0.17, α = 2.
4.2 Analysis of Zernike Polynomial and Gaussian Model
A Zernike polynomial is a set of polynomials defined on a unit circle. Each polynomial is expressed as the product of a radial polynomial and a circumferential trigonometric function. The radial polynomial represents how the representation changes from the center of the circular aperture to the edge. It is normalized as a special case of the Jacobi polynomial and is orthogonal on a unit circle. In this study, Zernike polynomials using the orthogonalization Noll’s method were used.11,12
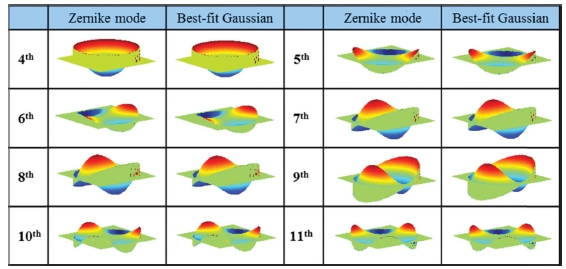
The performance analysis of the Zernike polynomial from the 4th to 11th terms of the polynomial was conducted using the design parameters of the deformable mirror prototype. The result is the same as the Zernike column in Fig. 7. In addition, the performance analysis is performed using the Gaussian model of the influence function derived in section 4.1. The result is the same as the Gaussian column in Fig. 7. When we compare the two indicators, we ca n see that they are almost similar from the 4th to 11th terms. This means that the correction performance is close to 1.
4.3 Measurement
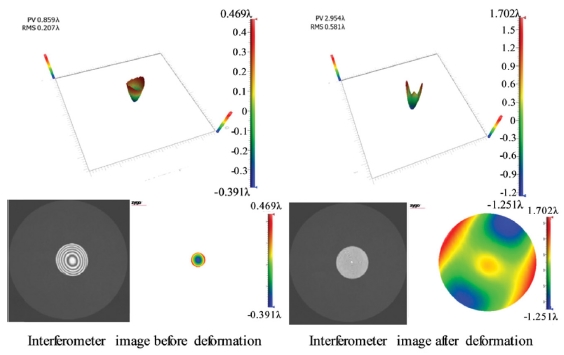
Using the ZYGO interferometer, the deformation of the deformable mirror prototype was measure as shown in Fig. 8. After the deformation, it is confirmed that the shape is deformed based on the center of the deformable mirror. Before deformation, the surface was 0.859 λ (P-V), 0.207 λ (RMS), but after deformation it was confirmed to be 2.954 λ (P-V), 0.591 λ (RMS).
5. Conclusion
In this study, we developed a single continuous deformable mirror that can be applied to adaptive optical imaging system and beam transmission system and analyzed the influence function by deformation. The conclusion is summarized as follows.
(1) The required deformation displacement of the deformable mirror was derived from the major parameters of the atmosphere and the large telescope. The required deformation displacement is ±1.64 μm.
(2) Using the deformable mirror prototype, control software and actuator controller, deformation was measured.
(3) The best-fit Gaussian model was derived through the analysis of the influence function. The derived Gaussian model can implement the Zernike mode from 4th to 11th order.
NOMENCLATURE
| r0 : | Fried coherence length |
| σ2 : | Wavefront distortion |
| λ : | Wave length |
| ζ : | Angle with zenith |
| E : | Young’s modulus |
| ρ : | Material density |
| v : | Poisson’s ratio |
| I(r) : | Gaussian influence function (Gaussian IF) |
REFERENCES
-
Polejaev, V. I. and Vorontsov, M. A., “Adaptive Active Imaging System Based on Radiation Focusing for Extended Targets,” Adaptive Optics and Applications, Vol. 3126, pp. 216-221, 1997.
[https://doi.org/10.1117/12.290150]

-
Billman, K. W., Breakwell, J. A., Holmes, R. B., Dutta, K., Granger, Z. A., et al., “ABL Beam Control Laboratory Demonstrator,” Airborne Laser Advanced Technology II, Vol. 3706, pp. 172-180, 1999.
[https://doi.org/10.1117/12.356954]

-
Babcock, H. W., “The Possibility of Compensating Astronomical Seeing,” Publications of the Astronomical Society of the Pacific, Vol. 65, No. 386, pp. 229-236, 1953.
[https://doi.org/10.1086/126606]

-
Acton, D. and Smithson, R., “Solar Imaging with a Segmented Adaptive Mirror,” Applied Optics, Vol. 31, No. 16, pp. 3161-3169, 1992.
[https://doi.org/10.1364/AO.31.003161]

- Safronov, A., “Controllable Bimorph Optics Based on Piezoelectric Structures,” Ph. D. Thesis, General Physics Institute of Russian Academy of Sciences, 1995.
-
Yellin, M., “Using Membrane Mirrors in Adaptive Optics,” in Imaging Through the Atmosphere, Vol. 75, pp. 97-103, 1976.
[https://doi.org/10.1117/12.954743]

- Hardy, J. W., “Adaptive Optics for Astronomical Telescopes,” Oxford University Press, 1998.
- Hamelinck, R., “Adaptive Deformable Mirror: Based on Electromagnetic Actuators,” Ph. D. Thesis, Department of Mechanical Engineering, Technische Universiteit Eindhoven, 2010.
-
Chu, M. T., Pauca, V. P., Plemmons, R. J., and Sun, X., “A Mathematical Framework for the Linear Reconstructor Problem in Adaptive Optics,” Linear Algebra and Its Applications, Vol. 316, Nos. 1-3, pp. 113-135, 2000.
[https://doi.org/10.1016/S0024-3795(00)00019-7]

- Weston, J., Paul, H., Giet, S., and Marcus, A., “A Method of Forming an Optical Device,” https://patentscope.wipo.int/search/en/detail.jsf?docId=WO2012038707, (Accessed 6 SEP 2018)
-
Noll, R. J., “Zernike Polynomials and Atmospheric Turbulence,” Journal of the Optical Society of America, Vol. 66, No. 3, pp. 207-211, 1976.
[https://doi.org/10.1364/JOSA.66.000207]

-
Huang, L., Rao, C., and Jiang, W., “Modified Gaussian Influence Function of Deformable Mirror Actuators,” Optics Express, Vol. 16, No. 1, pp. 108-114, 2008.
[https://doi.org/10.1364/OE.16.000108]


Research engineer in the Department of ISR Mechanical R&D Lab, LIG Nex1 Co., Ltd. His research interests are system design and mechanical engineering.
E-mail: hyuncheol.cho@lignex1.com

Research engineer in the Department of ISR Mechanical R&D Lab, LIG Nex1 Co., Ltd. His research interests are mechanical engineering and structural analysis.
E-mail: seongjin.kim@lignex1.com

Research engineer in the Department of ISR Mechanical R&D Lab, LIG Nex1 Co., Ltd. His research interests are mechanical engineering and structural analysis.
E-mail: jeongmin.kang@lignex1.com

Research engineer in the Department of ISR Mechanical R&D Lab, LIG Nex1 Co., Ltd. His research interests are mechanical engineering and structural analysis.
E-mail: hyunsu.jung@lignex1.com