고정밀 3축 UVW 스테이지의 기구학 및 정확도 비교분석
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
UVW Stage is widely used in manufacturing processes of PCB, LCD, OLED, and semiconductor industries. The precision of UVW Stage is closely associated with the quality of products. Two approaches for kinematics of UVW Stage are proposed for comparative analysis. Program of proposed kinematics algorithm is developed for motion control and applied to UVW Stage driving. The position of the stage for each algorithm is sequentially measured by laser interferometer. Both virtual stage and real stage are used for accuracy analysis. The performance of each algorithm is evaluated based on this accuracy analysis.
Keywords:
UVW Stage, Kinematics, Accuracy, Motion control키워드:
UVW 스테이지, 기구학, 정확도, 모션 제어1. 서론
평면상에서 X, Y, θ축의 고정밀 이송을 수행하는 스테이지는 PCB, 반도체, LCD, OLED 등의 제조장비에 필수적으로 사용되고 있다.1 XY 스테이지에 θ축을 직렬로 연결한 기존의 XYθ 스테이지는 만들기에는 쉬운 구조로 되어 있어 있으나, 스테이지의 두께 및 무게가 커져서, 최근에는 3개의 구동축을 병렬로 연결하여 스테이지의 두께를 얇게 구성한 UVW 스테이지가 많이 사용되고 있다.2,3
이러한 3축 UVW 스테이지는 평면상에 3개의 구동축을 배치하여 구동축의 직선운동을 통하여 X, Y, θ 모션을 구현할 수 있는 병렬구조의 기구로 큰 하중의 물체를 높은 정밀도로 위치결정을 할 수 있다. 고정밀 UVW 스테이지는 견고한 구조, 유연한 이동, 고정밀 등의 장점으로 인하여 그 이용 범위를 계속 넓혀 가고 있다.
X, Y, θ 이송하는 병렬구조의 스테이지는 구동부의 구조를 다양하게 구성하는 방법으로 연구되었다. 루카스 피벗(Lucas Free-Flex Flexural Pivot)을 이용한 병렬링크 구조의 스테이지4와 리소그라피장비에 사용한 θ 미세구동기5에 대한 연구가 진행되었다. 또한 Flexure 구조의 유연한 구동부를 이용하여 정밀 X, Y, θ 운동을 구현하는 연구도 진행되었다.6,7
UVW 스테이지에 대한 연구로는, 박형의 컴팩트한 구조로 고정밀도, 고강성을 가지면서, 정렬 작업시 인가되는 정하중 및 편하중에 대한 변형을 최소화하는 연구가 있다.8 Wang은 UVW 스테이지 자유도 계산 및 기구학적 정기구학, 역기구학을 분석하고 다물체동역학 소프트웨어와 MATALB을 이용하여 기구학적 수식을 검증하는 연구를 진행하였다.9
UVW 스테이지의 정확도는 반도체 등의 생산제품의 품질을 결정하는 매우 중요한 요소이다. 그러나 기존의 연구들은 주로 스테이지의 구현 및 응용에 집중하였고, 스테이지의 정확도에 대한 측정 및 분석에는 미흡하였다. 이에 본 연구에서는 UVW 스테이지의 기구학적 해석과 정밀도 측정 및 분석을 하고자 한다. 이를 위하여 기구학 해석 방법을 두가지로 접근하여 각각에 대한 정밀도 측정 및 분석을 행하여 각각의 방법에 대한 성능을 평가한다.
본 논문은 다음과 같이 구성된다. 2장에서는 UVW 스테이지 기구 구조와 모션구동원리에 대하여 설명한다. 3장에서는 UVW 스테이지에 대한 두가지 기구학적 해석방법을 제시하고 각각의 차이점에 대하여 설명한다. 4장에서는 두가지 기구학적 방법의 정확도를 평가하기 위하여 다물체동역학 소프트웨어를 이용한 가상 스테이지와 서보모터가 장착된 실제 스테이지를 이용한다. 실제 스테이지의 구동을 위하여 기구학 알고리듬이 적용된 모션프로그램을 개발하고 실제 스테이지를 구동하여 결과값을 레이저간섭계를 이용하여 측정한다. 이 측정값은 RecurDyn 시뮬레이션과의 결과와 비교분석한다.
2. UVW 스테이지의 구조 및 모션형태
2.1 스테이지의 링크와 조인트 및 자유도
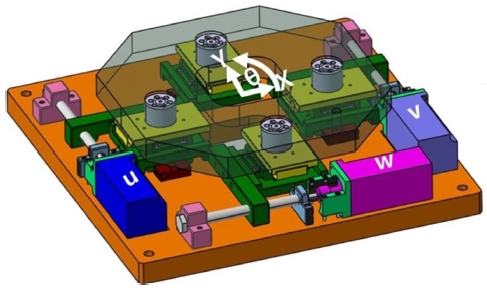
UVW 스테이지는 Fig. 1과 같이 바닥부와, X, Y, θ로 움직이는 상판부, 그리고 U, V, W 모터로 구동되는 가이드 레일부로 구성된다. 가이드레일부는 고정밀도의 서보모터(Servo-Motor)와 연결된 스크류, 너트, 레일부로 구성되고, 레일부는 상하좌우의 대칭된 구조로 배치되어 있다.
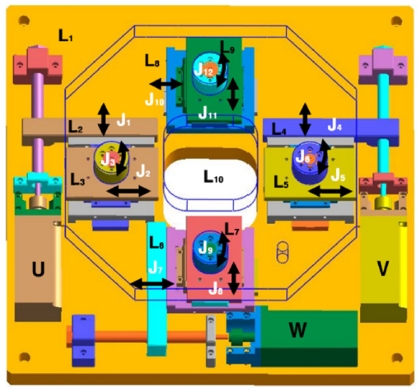
Fig. 2에는 UVW스테이지의 링크와 조인트를 표시하였다. 여기서 Li는 각 링크를 나타내며 링크의 총 개수는 10개이다. Ji는 각 조인트를 의미하고 조인트의 수는 12개이다. L1은 고정링크이고, L10은 상판 링크이다. J1, J2, J4, J5, J7, J8, J10, J11은 직진조인트이고, J6, J9, J12는 회전조인트이다.
가령 U축의 상하구동부를 살펴보면, 링크 L2는 직진조인트 J1에서 상하로 움직이는 가이드링크이며, 링크 L3은 직진조인트 J2에서 좌우로 움직이는 가이드링크이다. 이러한 링크 L3에 J3 회전조인트가 결합되면 상하/좌우/회전이 되는 레일부를 구성하게 된다. 즉, 실제로 U축은 상하로 구동하지만 최종적으로 레일부와 연결되는 상판부는 상하/좌우/회전까지 가능하게 된다. 나머지 V, W축도 U축도 유사하게 구성되어 움직이게 된다. 단 링크 L8, L9와 조인트 J10, J11, J12로 구성된 상부의 레일부는 구동모터가 장착되어 있지 않다. 이는 W축 움직임의 견고성을 더하기 위하여 추가된 부분이다.
스테이지의 링크와 조인트 정보를 이용하여 UVW 스테이지의 자유도(Degree of Freedom, DOF)를 계산하면 DOF = 3 × (10 − 1) − 2 × 12 = 3이다. 즉, UVW 모터 3개를 가지고 상판부는 X, Y, θ의 3개 자유도의 운동을 할 수 있게 된다.
2.2 스테이지의 모션형태
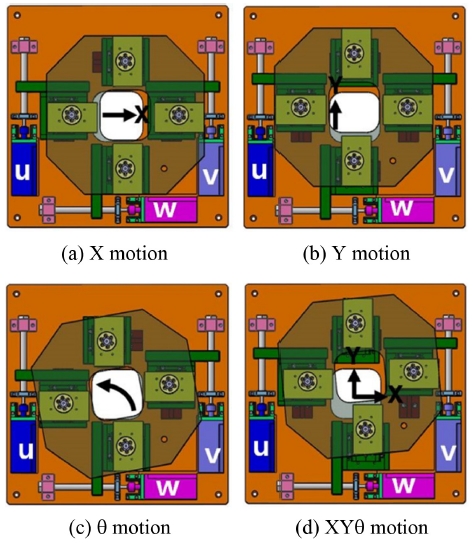
Fig. 3은 U, V. W축의 구동을 통하여 스테이지의 다양한 형태의 운동을 구현할 수 있는 경우를 보여주고 있다.
W축만을 움직이면 Fig. 3(a)와 같이 X축 방향의 운동을 구현할 수 있다. U, V축을 같은 방향으로 동일한 양을 움직이면 Fig. 3(b)와 같이Y축 방향의 운동을 구현할 수 있다. 반면 U, V축을 다른 방향으로 동일한 양을 움직이면 Fig. 3(c)와 같이 θ 방향의 운동을 구현할 수 있다. 만약에 U, V, W축을 임의로 움직이면 Fig. 3(d)와 같이 X, Y, θ 방향으로 움직이는 복합운동을 구현할 수 있다. X, Y, θ 축의 이동을 하기 위해서는 스테이지의 기구학 해석을 통하여 역기구학 식을 세워야 한다.
3. UVW 스테이지의 두가지 기구학 방법
본 장에서는 UVW 스테이지의 상판부가 X, Y, θ 축상에서 x, y, θ 만큼의 변위량을 움직이기 위해서 U, V, W축의 구동량 u, v, w을 구하는 과정인 역기구학식과 반대의 경우인 정기구학식을 세운다. 본 연구에서는 UVW 스테이지의 기구학적 접근방법을 2가지로 제시하여 각각의 방법에 대하여 식을 구축한다.
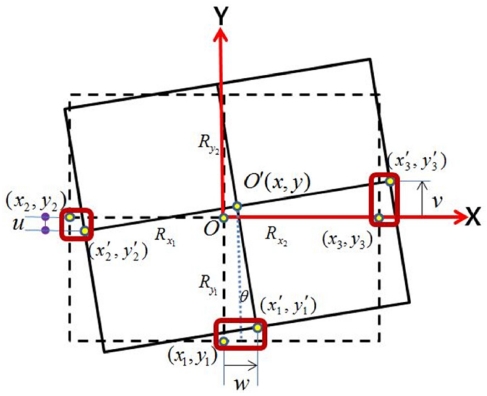
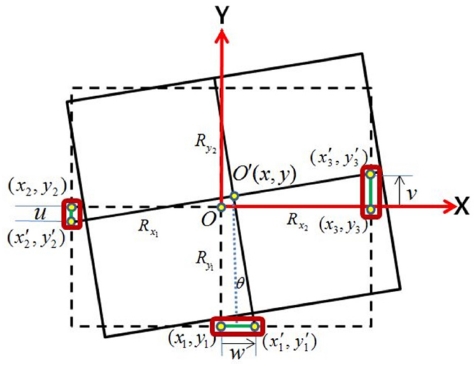
스테이지의 주요 기하학적 특징을 Figs. 4와 5에 도시하였다. 점선의 사각형이 스테이지의 초기상태이고 실선의 사각형이 스테이지의 움직인 상태이다. 스테이지의 X방향 반지름은 Rx이고 이에는 좌측의 Rx1, 우측의Rx2 의 2종류가 있다, 동일하게 Y방향 반지름 Ry에도 하측의 Ry1, 상측의 Ry2의 2종류가 있다. 원래 이러한 반지름 값들은 서로 다르게 설계하여도 무방하나, 본 연구의 스테이지는 모든 반지름 값이 동일한 85 mm로 되어 있는 대칭구조이다.
3.1 첫 번째 기구학 방법
Fig. 4을 보면, 초기상태의 스테이지가 x, y, θ의 이동을 하게 되면, 상판부의 중심점 O가 O'로 이동하게 된다. 이때, Fig. 2의 J3, J6, J9 조인트의 위치 (x1, y1), (x2, y2), (x3, y3)은 (x1', y1'), (x2', y2'), (x3', y3')로 이동하게 된다.
여기서, 이러한 위치들의 좌표값의 변화량을 관찰함으로써 구동량 u, v, w을 다음과 같이 구할 수 있다.
| (1) |
| (2) |
| (3) |
상기의 식은 스테이지의 역기구학식이며, 이를 통하여 x, y, θ로부터 u, v, w의 값을 계산할 수 있다.
식(1)부터 식(3)을 이용하면, 스테이지의 정기구학식을 유도할 수 있다. 식(1)과 식(2)를 더하면 다음과 같이 y를 구할 수 있다.
| (4) |
이어서, 식(4)를 식(1)에 대입하면 θ을 구할 수 있다.
| (5) |
식(4)와 식(5)를 식(1)에 대입하면 x를 구할 수 있다.
| (6) |
3.2 두 번째 기구학 방법
Fig. 5을 보면, 초기상태의 스테이지가 x, y, θ의 이동을 하게 되면, 상판의 중심점 O가 O'로 이동하게 된다. 이때, 첫번째 기구학 방법과 다른점은 조인트의 위치 (x1, y1), (x2, y2), (x3, y3)이 수직 또는 수평이동 중에 한 방향만으로 이동하여 (x1', y1'), (x2', y2'), (x3', y3') 로 이동한다고 간주하는 것이다.3
각 위치의 좌표값의 변화량을 통하여 구동량을 구해보면, 다음과 같은 역기구학 수식을 구할 수 있다.
| (7) |
| (8) |
| (9) |
식(7)부터 식(9)를 이용하면, 다음과 같은 스테이지의 정기구학식을 구할 수 있다.
| (10) |
| (11) |
| (12) |
4. 스테이지의 정확도 분석 방법의 체계
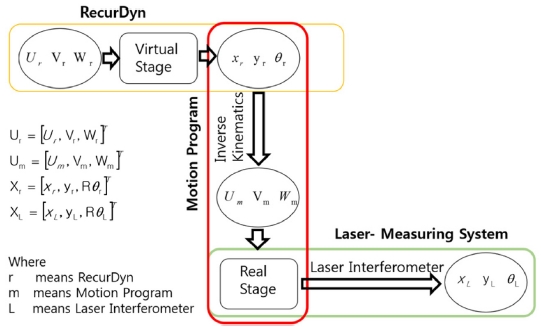
두 가지 기구학 방법에 대한 정확도 비교분석을 시뮬레이션과 정확도 측정실험을 통하여 시행하고자 한다. 이를 위하여 Fig. 6의 순서도에 의하여 체계적으로 분석을 행하고자 한다.
Fig. 6에서 보면 가상 스테이지(Virtual Stage)와 실제 스테이지(Real Stage)의 2개의 구성요소가 있다. 다물체동역학 소프트웨어인 RecurDyn을 이용하여 스테이지의 모델링을 하고, 이를 가상 스테이지(Virtaul Stage)라 칭한다. 가상스테이지에 구동입력 Ur = [ur, vr, wr]을 입력하면 시뮬레이션을 통해 스테이지의 x, y, θ이 출력된다. 이러한 출력을 Xr= [xr, yr, Rθ r]로 정의한다. θr에 반지름 R을 곱한 이유는 단위를 mm로 변환하여 x, y와 동일하게 정밀도 분석시 일관성을 유지하기 위함이다. 이러한 동역학 소프트웨어를 통해 구한 Ur과 Xr은 가장 정확한 값이 되므로 정밀도 분석을 위한 기준값이 된다.
가상 스테이지를 통하여 기준값을 설정한 이유는 2장에서 언급한 바와 같이, 본 연구의 UVW 스테이지는 10개의 링크와 12개의 조인트로 구성된 복잡한 병렬기구인 관계로, 3장에서 설립한 단순한 기구학식의 결과로는 기준을 세우기가 곤란함이다. 이에 정확한 수치연산이 가능한 다물체동역학 소프트웨어를 이용하여 가상스테이지에 u, v, w의 구동입력을 가하여 이로부터 출력 x, y, θ를 구하고 이를 기준값으로 이용한 것이다.
실제 스테이지는 모션제어기와 서보모터, 서보드라이브가 장착되어 실제로 구동되는 스테이지이다. 모션제어기는 3장에서 구한 역기구학식을 이용한 C++ 기반의 모션프로그램을 포함한다. 이러한 모션프로그램에 앞에서 구한 Xr을 입력하면 역기구학식 계산을 통하여 Um= [um, vm, wm]이 계산되어진다. 이 Um은 실제 스테이지의 서보모터의 구동량이 되어 실제로 스테이지를 움직이게 한다.
Um에 의하여 실제 스테이지가 구동하게 되면 스테이지의 상판부는 원하는 x, y, θ만큼 움직이게 된다. 실제로 상판부의 움직임 x, y, θ은 측정을 통하여 알 수 있다. 본 연구에서는 정밀한 측정을 위하여 레이저 간섭기를 이용하여 이러한 x, y, θ값을 측정하였다. 레이저 간섭계를 이용하여 측정한 값을 Xr = [xr, yr, Rθ r] 이라고 정의한다.
기준값인 Xr과 실제 측정값인XL의 차이를 계산하면 결국 스테이지의 이동량의 정확도를 계산할 수 있게 되고, 이를 통하여 2가지 기구학 방법의 정확도를 비교분석 할 수 있게 된다.
4.1 레이저간섭계를 이용한 위치 측정
Fig. 7(a)은 UVW 스테이지와 모션제어기, 서보드라이브, 서보모터 등의 모션제어시스템과 레이저 간섭계를 설치한 그림이다. 모션제어기는 PC상에 설치되어 있고, 모션프로그램의 역기구학식에서 계산된 스테이지 구동량 u, v, w가 모션제어기를 통하여 펄스로 3개의 서보드라이브로 전송이 된다. 서보드라이브는 지정된 구동량을 움직이도록 각각의 서보모터를 피드백제어한다.
Fig. 7(b)는 레이저간섭계를 이용하여 y방향의 운동량을 측정하는 경우의 광학계설치 사진이다. 광학계를 통하여 조사 및 반사되는 레이저의 간섭측정은 연결된 PC를 통하여 계산된다(x, θ 방향은 지면관계상 생략한다).
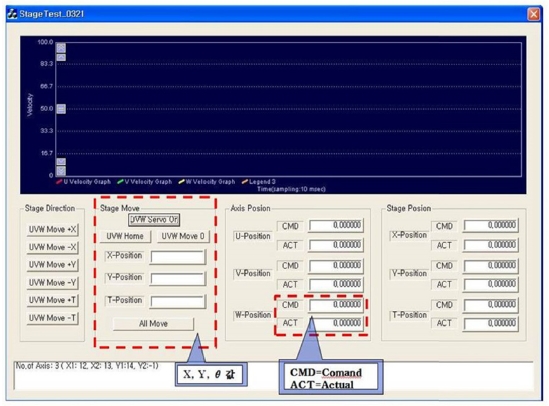
Fig. 8은 역기구학 알고리즘을 적용한 모션 프로그램으로 C++ 작성된 윈도우 기반 프로그램이다. 그림상에서 좌측의 점선으로 테두리된 부분에서 원하는 x, y, θ 량을 입력하게 된다. 프로그램상에 입력된 역기구학 식을 통해서 계산된 u, v, w 구동량은 CMD (Command) 부분에 표시된다. 실제 서보모터가 움직이는 양은 ACT (Actual)량으로 표시되면, 이는 상부의 그래프상에서도 확인할 수 있도록 하였다.
일단, 레이저간섭계를 이용하여 측정한 x, y, θ량이 보장받기 위해서는 실제 스테이지에 대하여 반복정밀도가 확보되어야 한다. 이러한 정밀도를 검증하기 위하여 x, y, θ 모두에 대하여 0.1 mm부터 1 mm까지 5번 반복 구동하고 레이저 간섭계로 측정하여 정밀도를 계산하였다. 단, θ를 구동할 때는 반지름 R을 곱하여 단위를 mm로 변환하였고, 그 범위가 0.1 mm에서 1 mm가 되도록 하였다. 정밀도는 x, y, θ에 대한 u, v, w을 구하는 기구학 방법론과는 상관없는 문제인 관계로, 첫번째 방법을 적용하였다.
Table 1은 X 방향으로 0.1 mm부터 1 mm까지 실험값을 정하고 구동한다. 실험값 한 개는 5번 구동 및 측정한다. AVE를 평균값이고 STD는 표준편차값이다. Table 1에서 보면 STD에 근거한 X축의 정밀도는 0.3 m이라고 말할 수 있다.
Table 2은 Y 방향으로 0.1 mm부터 1 mm까지 실험값을 정하고 구동한다. 실험값 한 개는 5번 구동 및 측정한다. AVE를 평균값이고 STD는 표준편차값이다. Table 2에서 보면 STD에 근거한 Y축의 정밀도는 0.4 mm이라고 말할 수 있다.
Table 3은 θ 방향으로 Rθ를 0.1 mm부터 1 mm까지 실험값을 정하고 구동한다. 이때 실제 θ구동량은 길이를 반지름 R = 8 mm로 나눈 값이다. 실험값 한 개는 5번 구동 및 측정한다. AVE를 평균값이고 STD는 표준편차값이다. Table 3에서 보면 STD에 근거한 θ축의 정밀도는 0.2 mm이라고 말할 수 있다.
결국, x, y, θ의 정밀도를 평균해서 구해 보면 본 실험에서 사용한 스테이지의 구동정밀도는 0.1 mm부터 1 mm의 구동범위 내에서 0.3 mm이라고 말할 수 있으며, 이 정도의 정밀도는 이후 시행할 정확도의 평가에 타당한 근거가 될 것으로 사료된다.
4.2 두가지 기구학 방법의 정확도 측정
이번 실험에서는 두가지 기구학적 방법에 모션정확도를 측정한다. 이를 위하여 두가지 기구학 방법에 대하여 Fig. 6의 가상 스테이지의 출력 Xr을 구하고, 실제 스테이지의 출력 XL을 레이저간섭계로 측정한 후에 두 출력의 값의 오차를 구한다. 오차의 유클리디안 평균인 |EX|은 (xr − x'L)2 − (yr − y'L)2 − (Rθr − Rθ'L)2의 제곱근으로 구한다.
정확도 평가를 위하여 움직인 길이가 1,000 mm 이내로 움직이는 소변위 사례와 1,000 mm 이상으로 움직이는 대변위 사례의 2가지로 구분하여 실험하였다.
각각의 사례에는 x와 y만 움직이는 경우, x, y, θ가 같이 움직이는 경우로 구분하여 묶어서 실험하였다.
Table 4는 소변위사례의 첫번째 방법의 경우의 정확도를 측정한 결과이고, Table 5는 소변위사례의 두번째 방법의 경우의 정확도를 측정한 결과이다.
Table 4의 오차평균은 5.8 μm이고 Table 5의 오차평균은 6.3 mm로 측정되었다. 이를 통하여, 첫번째 방법이 두번째 방법보다 정확도면에서 우수한 것으로 나타났다.
Table 6는 대변위사례의 첫번째 방법의 경우의 정확도를 측정한 결과이고, Table 7는 대변위사례의 두번째 방법의 경우의 정확도를 측정한 결과이다.
Table 6의 오차평균은 20.0m이고 Table 7의 오차평균은 37.1mm로 측정되었다. 이를 통하여 첫번째 방법이 두번째 방법보다 정확도면에서 우수한 것으로 나타났다.
정확도 측정결과, 소변위, 대변위 모두의 경우에서 첫번째 방법이 두번째 방법보다 좋은 정확도를 보여주고 있다. 이는 첫 번째 기구학에서는 조인트의 좌표변화가 x, y방향 모두에서 발생한다는 전제하에서 역기구학식이 설립되었고, 두번째 기구학에서는 조인트의 좌표변화가 한 방향만으로만 발생한다는 전제하에서 역기구학식이 설립되, 첫번째 방법이 좀더 스테이지 운동의 운동범위를 유연하게 적용함으로써 나타난 것으로 사료된다.
5. 결론
본 논문은 UVW 스테이지의 정확도 분석을 위하여 두가지 기구학적 해석방법을 세우고, 두가지 기구학적 방법의 정확도를 평가하기 위하여 다물체동역학 소프트웨어를 이용한 가상 스테이지와 서보모터가 장착된 실제 UVW 스테이지를 이용하였다. 가상 스테이지는 다물체동역학 소프트웨어를 통하여 구축하였고 이를 이용한 시뮬레이션을 통하여 정확도의 기준값을 구하였다. 서보모터가 장착된 실제 스테이지의 모션구동을 위하여 기구학 알고리듬이 포함된 모션프로그램을 개발하고 실제 스테이지을 구동하였다. 구동된 스테이지의 위치를 레이저 간섭계를 통하여 측정하여 측정값을 구하였고, 반복정밀도를 측정함으로써 측정값의 근거를 마련하였다.
마지막으로, 두가지 기구학 방법에 대하여 이론적으로 구한 기준값과 실험을 통하여 구한 측정값의 오차를 구함으로써, 정확도를 구하였다. 결국 두가지 기구학 방법에 대한 정확도를 비교분석함으로써 각각의 방법에 대한 성능을 비교평가할 수 있었고, UVW 스테이지의 효율적인 모션구동방법에 대한 근거를 마련하였다.
NOMENCLATURE
| u : | Displacement amount of u axis driving |
| v : | Displacement amount of v axis driving |
| w : | Displacement amount of w axis driving |
| x : | x position of workbench of UVW stage |
| y : | y position of workbench of UVW stage |
| θ : | θ position of workbench of UVW stage |
Acknowledgments
본 연구는 금오공과대학교 학술연구비의 연구수행으로 인한 결과임을 밝힙니다.
REFERENCES
- Shin, D., “Measurement and Correction of PCB Alignment Error for Screen Printer Using Machine Vision (1),” Journal of the Korean Society of Precision Engineering, Vol. 20, No. 6, pp. 88-95, 2003.
- Park, J.-Y., Han, S.-Y., Lee, N.-H., Choi, J.-O., and Shin, H.-S., “Alignment System Development for Producing OLED Using Fourth-Generation Substrate,” Proc. of Korean International Display Society Conference, pp. 873-878, 2008.
- Kim, J. S., Hwang, J. D., Kim, M. S., Yoo, J. C., and Ahn, J. H., “Development of the Thin - Alignment Stage for Fine Positioning,” Proc. of KSPE Autumn Conference, pp. 305-306, 2006.
- Han, S.-J., Park, J.-H., and Park, H.-J., “Development of Three DOF Alignment Stage for Vacuum Environment,” Journal of the Korean Society for Precision Engineering, Vol. 18, No. 11, pp. 138-147, 2001.
- Kim, D. M., Kim, K. H., Lee, S. Q., and Gweon, D. G., “Optimal Design and Control of xyθ Fine Stage in Lithography System,” Journal of the Korean Society of Precision Engineering, Vol. 19 No. 12, pp. 163-170, 2002.
-
Kang, D., Kim, K., Choi, Y., Gweon, D., Lee, S., et al., “Design and Control of Flexure Based XY θz Stage,” Korean Society of Mechanical Engineers, Vol. 19, No. 11, pp. 2157-2164, 2005.
[https://doi.org/10.1007/BF02916513]

- Kang, J.-O., Seo, M.-H., Han, C.-S., and Hong, S.-W., “Development of 3-Axis Fine Positioning Stage: Part 1. Analysis and Design,” Journal Korean Society of Precision Engineering, Vol. 21, No. 3, pp. 147-154, 2004.
-
Kang, D.-B., Ahn, J.-H., and Son, S.-M., “Development of Thin and Parallel XYθ Alignment Stage,” Journal of the Korea Academia-Industrial Cooperation Society, Vol. 12, No. 1, pp. 74-79, 2011.
[https://doi.org/10.5762/KAIS.2011.12.1.074]

- Wang, Weijun., “A New Type of Composite Group Institutions and Drift in the Use of the Simulation of the Ship,” M.Sc. Thesis, Shanghai University, https://max.book118.com/html/2015/1204/30823743.shtm, (Accessed 3 AUG 2018)