외부가속도와 바이어스 효과를 고려한 칼만필터 기반 자세추정 방법 비교

1. 서론

본 연구에서는 IMU (Inertial Measurement Unit) 센서를 활용한 기존 칼만필터 기반 자세(Attitude: Roll, Pitch) 추정 알고리즘들을 다양한 외부 가속도 시나리오에 적용하고 그 성능에 대해 조사한다. IMU 센서는 일상생활활동 모니터링,¹ 생체의 역학적 분석,^2,3 신경질환 검진,⁴ 증강현실⁵ 등 다양한 분야에 빈번하게 활용되고 있다. 이러한 이유로 IMU 기반 자세 추정 방법에 대한 많은 연구들^6-8이 수행되어 왔다. 또한 많은 연구들에서 향상된 자세 추정을 위하여 가속도 센서와 자이로 센서의 측정값을 칼만필터를 기반으로 융합하였다. 칼만필터는 1960년에 R. E. Kalman에 의해 개발된 상태 추정 알고리즘⁹으로 관성항법장치를 포함한 많은 분야에서 적용되어왔다.

하지만 칼만필터로 가속도 센서와 자이로 센서를 융합하여 자세를 추정할 경우 자이로 센서의 바이어스와 외부가속도 효과에 의한 가속도 센서 오차 등에 의해 추정 에러가 발생하게 된다. 이에 바이어스와 외부가속도를 고려하여 자세 추정의 정확성을 높이기 위한 방법^10-13들이 다음과 같이 연구되었다. 우선 자이로 센서의 바이어스를 보정하기 위해 센서의 특성을 이용한 보정방법,^14,15 칼만필터를 이용한 방법,⁸ 역전파 신경망을 이용한 방법¹⁶등이 소개되었다. 가속도 센서의 외부 가속도 보정을 위해 칼만필터의 레지듀얼을 이용한 보정방법¹¹과 가속도 모델 기반의 보정방법¹² 등이 또한 제안되었다.

그러나 이러한 연구들에서 제안된 방법들은 비교적 가속도가 작은 환경¹¹ 또는 회전변위가 ±5^o 정도로 매우 제한된 테스트 환경에서 적용되었다.⁸ 그리고 일부 연구에서는 단일 축 즉, Roll과 Pitch 중 한 축에 대해서만 알고리즘을 적용하였다.¹⁷ 따라서 이러한 기존 연구 결과들을 비교적 큰 외부 가속도가 작용하는 동적 시스템들, 예를 들어 험지와 같은 비정형 환경에서 빠르게 주행하는 모바일 로봇, 왜풍 속에서 비행하는 쿼드롭터, 고속 반복 작업을 수행하는 로봇팔 등의 자세를 추정하는데 바로 적용하기에는 어려움이 있다. 특히 Roll과 Pitch가 동시에, 크고 빠르게 진동하는 환경에서는 IMU 센서의 측정값 오차가 크게 증가할 수 있으며¹⁷ 이러한 오차는 정밀하고 정확한 자세 정보 수집 및 모션 제어를 어렵게 만든다. 그러므로 본 연구에서는 실제 다양한 동적 시스템들에서 발생할 수 있는 외부 가속도 시나리오를 Roll과 Pitch 방향으로 동시에 적용하여 선행연구에서 제안된 자세추정 방법들이 외부가속도와 바이어스 효과를 얼마나 잘 고려할 수 있는지 실험을 통하여 각각의 특성 및 성능을 비교하여 조사한다. 참고로 본 연구에서 언급된 외부가속도는 가속도 센서에 작용하는 가속도 중에 중력가속도를 제외한 모든 가속도를 의미하며 본 연구에서는 회전가속도 운동을 통해 센서모듈에 외부가속도를 발생시켰다.

본 논문의 구성은 다음과 같다. 2장에서는 바이어스와 외부가 속도 효과를 고려한 칼만필터 기반 센서융합 자세추정 방법들을 설명한다. 3장에서는 이들 방법들을 Roll과 Pitch 방향으로 동시에 다양한 외부 가속도 효과를 제공하는 동적 환경에 적용하여 실험하고 각각의 특성과 성능을 조사한다. 4장에서는 실험결과를 논의한다.

2. 칼만필터 기반 센서융합 자세추정 방법

본 절에서는 바이어스와 외부가속도를 고려한 칼만필터 기반 센서융합 자세추정 방법들을 설명한다. 참고로 본 연구에서는 가속도 센서과 자이로 센서를 칼만필터로 융합하여 자세를 추정하였다. 본 연구에서는 외부가속 보정 여부와 방법에 따라 다음 세 가지 자세추정 알고리즘(Algorithms 1, 2, 3)을 연구하였다. 먼저 모든 자세추정 알고리즘에 자이로 센서의 바이어스 보정방법을 적용하였다. 그리고 Algorithm 1에서는 외부가속도 효과를 보정하지 않는다. 이에 반해 가속도 센서에서 외부가속도 효과를 보정하기 위해 Algorithm 2에서는 칼만필터의 레지듀얼을 이용한 보정방법을 그리고 Algorithm 3에서는 단순화된 가속도 모델 기반 보정방법을 적용하여 각 알고리즘의 성능과 특성을 조사하였다.

2.1 Algorithm 1

본 연구에서 사용한 첫 번째 알고리즘은 외부가속도는 보정하지 않고 자이로 센서의 바이어스만 보정한 칼만필터이다.⁸ 이 칼만필터는 가속도 센서에서 계산된 자세(Roll: ϕ, Pitch: θ)와 자이로 센서로부터 계산된 자세 회전속도($$ \dot{\varphi }$$, $$ \dot{\theta }$$)를 융합하여 정확한 자세값을 계산한다. 첫 번째 알고리즘에서 사용한 칼만필터는 다음의 상태방정식으로부터 유도된다.

$\[ \begin{array}{c}{\mathit{X}}^k=\mathit{A}{\mathit{X}}^{k-1}+\mathit{B}\mathit{u}\hfill \\ {\mathit{y}}^k=\mathit{H}{\mathit{X}}^k\hfill \end{array} \]$

(1)

여기서,

$\[ \begin{array}{c}\begin{array}{cc}\mathit{X}={\left[\varphi ,{\beta }_{\varphi },\theta ,{\beta }_{\theta }\right]}^{\text{T}}& \mathit{u}={\left[\dot{\varphi },\dot{\theta }\right]}^{\text{T}}\end{array}\\ \begin{array}{ccc}\mathit{A}=\left[\begin{array}{cccc}1& -dt& 0& 0\\ 0& 1& 0& 0\\ 0& 0& 1& -dt\\ 0& 0& 2& 1\end{array}\right]& \mathit{B}=\left[\begin{array}{cc}dt& 0\\ 0& 0\\ 0& dt\\ 0& 0\end{array}\right]& \mathit{H}={\left[\begin{array}{cc}1& 0\\ 0& 0\\ 0& 1\\ 0& 0\end{array}\right]}^{\text{T}}\end{array}\end{array} \]$

위 상태방정식에서 $$ {\beta }_{\dot{\varphi }}$$, $$ {\beta }_{\dot{\theta }}$$는 각각 $$ \dot{\varphi }$$, $$ \dot{\theta }$$의 바이어스이다. 자이로 센서에서 측정된 회전속도로부터 자세를 계산할 때, 바이어스에 의해 발생하는 적분오차를 제거해주기 위해 상태변수에 바이어스를 추가하였다.

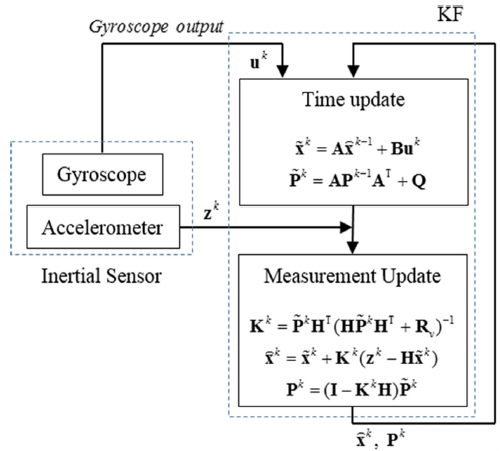
위 상태방정식을 사용한 칼만필터의 구조는 Fig. 1과 같다. Fig. 1에서 Time Update는 예측부이며 Measurement Update는 측정보상부이다. 우선, 예측부에서 $$ {\tilde{\mathbf{x}}}^k$$은 상태 추정벡터이며 식(1)의 상태벡터와 같다. $$ {\stackrel{\mathrm{~}}{\mathbf{\text{P}}}}^k$$은 예측된 에러 공분산 벡터이며 A, B 행렬은 식(1)의 A, B행렬과 같다. u^k는 입력값이며 여기서는 자이로 센서로부터 계산된 자세 회전속도이다. Q는 공정잡음 공분산 행렬이며 제어 입력 노이즈(또는 측정 노이즈 공분산 행렬) R_v에 의해 발생한다고 가정하면 식(2)와 같다.

Fig. 1

Overview of normal kalman filter

$\[ \mathit{Q}={\mathit{B}\mathit{R}}_v{\mathit{B}}^{\text{T}} \]$

(2)

Fig. 1의 예측부에서 입력으로 사용되는 자세 회전속도는 글로벌 좌표에서 표현되는 값이다. 그러나 자이로 센서에서 측정되는 회전속도값은 센서 좌표에서 측정되는 값이므로 좌표변환이 필요하다. 자이로 센서값을 자세 회전속도 값으로 변환하기 위해 식(5)의 좌표 변환 행렬 $$ {}_S{}^G\mathit{R}$$을 사용한다.^7,18

$\[ {}_S{}^{G}R=\left[\begin{array}{ccc}\cos \left(\gamma \right)\cos \left(\theta \right)& \sin \left(\gamma \right)& 0\\ -\sin \left(\gamma \right)\cos \left(\theta \right)& \cos \left(\gamma \right)& 0\\ \sin \left(\theta \right)& 0& 1\end{array}\right] \]$

(3)

식(3)의 $$ {}_S{}^G\mathit{R}$$ 행렬은 센서값을 센서좌표계에서 글로벌좌표계로 변환해주는 행렬이며 이 행렬의 오일러 회전 순서는 X-Y-Z이다. 위 행렬에서 γ는 오일러각 yaw이며 본 연구에서는 yaw각을 고려하지 않으므로 γ는 0이다.

다음으로 Fig. 1의 측정보상부에서 K^k, $$ {\stackrel{\mathrm{⁀}}{\text{x}}}^k$$, H는 각각 칼만 이득(Gain), 추정 벡터, 관측 행렬이며 관측행렬은 식(1)의 관측행렬과 같다. R_v는 측정 노이즈 공분산 행렬이며 z^k 값의 분산을 사용한다. z^k는 관측벡터이며 가속도 센서로부터 계산된 Roll, Pitch 값을 사용한다. 가속도 센서로부터 Roll, Pitch는 각각 다음과 같이 계산한다.¹⁹

$\[ \begin{array}{c}\varphi ={\tan }^{-1}\left(ay/az\right)\mathrm{ }\hfill \\ \theta ={\tan }^{-1}\left(-ax/\sqrt{a{y}^2+a{z}^2}\right)\mathrm{ }\hfill \end{array} \]$

(4)

위 식에서 ax, ay, az는 각각 가속도 센서의 x, y, z축 방향으로 측정된 가속도값이다.

2.3 Algorithm 3

본 연구에서 비교하는 세 번째 알고리즘은 모델기반 외부가속도 보정 칼만필터¹²이다. 모델기반 외부가속도 보정 칼만필터는 식(8)처럼 가속도 센서에 작용하는 외부가속도를 가속도 센서 모델에 추가하여 외부가속도를 추정하고 자세 계산 시 제거해주는 방식이다.

$\[ {\mathit{y}}_A={}^S\mathit{g}+{}^S\mathit{a}+{\mathit{n}}_A \]$

(8)

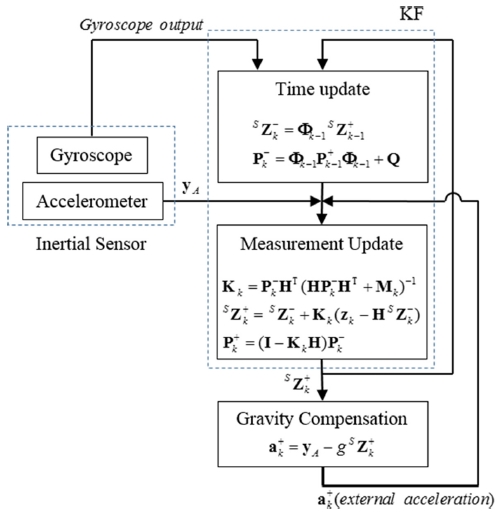
식(8)에서 y_A는 가속도 센서의 측정값이며 ^Sg, ^Sa는 각각 센서에서 측정된 중력가속도와 외부가속도, n_A는 측정 노이즈이다. 본 연구에서 사용한 모델기반 외부가속도 보정 칼만필터의 구조는 Fig. 2 와 같다.

Fig. 2

Overview of external acceleration model-based Kalman filter

여기서 $$ {{}^S\mathbf{\text{Z}}}_k^{-}$$은 z축 회전행렬이며 $$ {\mathbf{\text{Φ}}}_{k\text{-1}}\mathbf{\text{, }}{\mathbf{\text{P}}}_k^{\mathbf{\text{-}}}\mathbf{\text{, Q}}$$는 각각 변환행렬, 예측에러 공분산 행렬, 공정잡음 공분산 백터이다. K_k, H, M_k는 각각 칼만 이득, 추정 벡터, 측정잡음 공분산 벡터이며 z_k는 측정벡터이다. y_A, g, $$ a_k^{+}$$는 각각 가속도 센서값, 중력가속도, 외부가속도이다. 본 알고리즘에서 외부 가속도를 보정하는 방법은 다음과 같다. 우선, 가속도 센서에서 측정된 가속도 값 y_A에서 칼만필터로부터 추정된 중력가속도 $$ g^S{\mathbf{\text{Z}}}_k^{+}$$를 제거해주어 외부가속도 $$ {\mathbf{\text{a}}}_k^{+}$$를 추정한다. 그리고 추정된 그 외부가속도값을 가속도 센서의 측정값에서 제거해주어 외부가속도를 보정한다. 외부가속도 모델 칼만필터의 각 변수들에 대한 좀 더 자세한 정보는 참조문헌¹²을 참고한다.

3. 알고리즘 실험

3.1 실험 방법

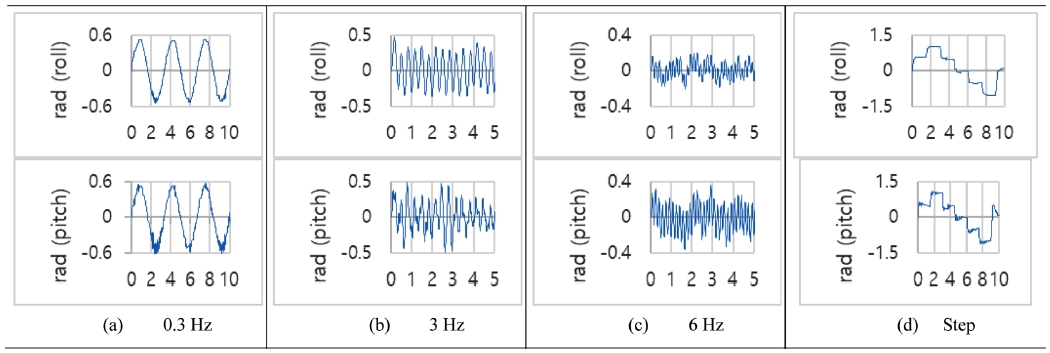
본 절에서는 2절에서 설명한 세가지 칼만필터 기반 자세추정 방법의 특성과 성능을 실험을 통하여 조사한다. 먼저, 실험을 위하여 테스트 베드를 Fig. 3와 같이 제작하였다. 실험 방법은 IMU 센서를 테스트 베드에 부착하여 원하는 입력에 따라 Roll(ϕ), Pitch(θ) 방향으로 회전시키다. 이때 IMU 센서로부터 추정된 Roll, Pitch 회전각도와 엔코더로부터 측정된 Roll, Pitch 회전각도를 비교하여 IMU 기반 자세 추정 알고리즘들의 추정 에러를 계산한다. 테스트 베드에서 상대적으로 낮은, 중간, 높은 외부 가속도 효과를 발생시키기 위하여 세가지 서로 다른 회전 주파수(0.3, 3, 6 Hz)를 입력으로 사용하여 Roll, Pitch를 회전시키며 실험하였다. 추가적으로 Roll과 Pitch 방향으로 크기가 변하는 직각파 입력을 사용하여 각 알고리즘의 자세 추정 에러를 비교하였다.

Fig. 3

Attitude test equipment

3.2 실험 결과

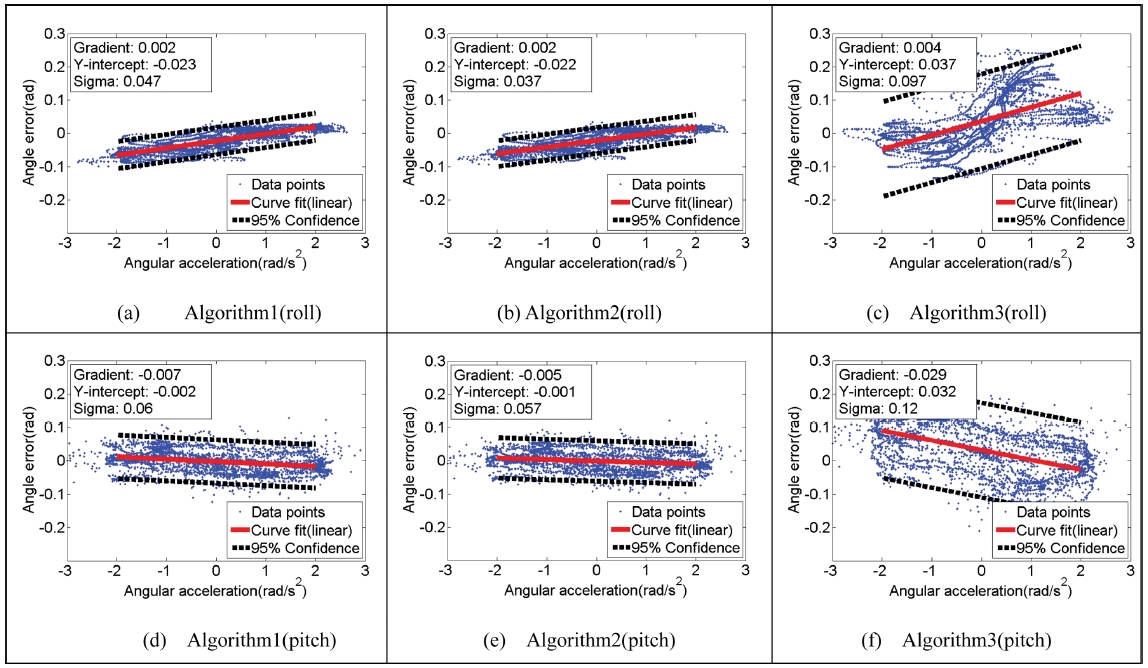
IMU 센서를 Roll과 Pitch 방향으로 0.3, 3, 6 Hz 사인파 및 크기가 변하는 직각파를 입력으로 사용하여 회전시켰을 때, 엔코더에서 측정한 실제 회전각을 Fig. 4에서 보여준다. 이 때 Algorithms 1-3의 추정에러를 Figs. 5부터 8에 요약하였다. Figs. 5부터 8은 4개의 서로 다른 외부가속도 입력에 대해 각각의 Roll과 Pitch 방향 추정 에러를 외부가속도의 함수로 보여준다. Figs. 5부터 8에 표시된 에러 기울기(Gradient)와 y절편 (y-Intercept)은 Curve Fitting을 통해 결정되었다. 이 기울기를 통해 각가속도와 추정 에러가 비례관계에 있음을 확인할 수 있으며 y절편을 통해 추정 에러의 편차를 알 수 있다. 그리고 각 그림에 표시된 Sigma 값은 실험 데이터값의 표준편차이다.

Fig. 4

Actual orientation angles measured by encoders

Fig. 5

Experimental results: orientation errors as a function of external acceleration (0.3 Hz)

Fig. 6

Experimental results: orientation errors as a function of external acceleration (3 Hz)

Fig. 7

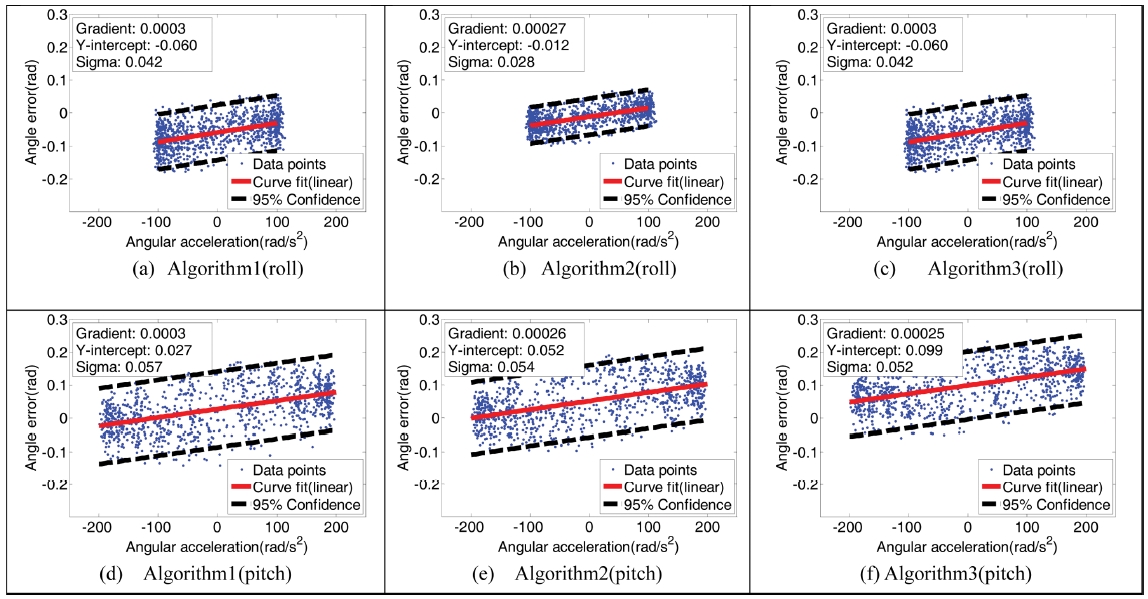
Experimental results: orientation errors as a function of external acceleration with a sinusoidal input of 6 Hz

Fig. 8

Experimental results: orientation errors as a function of external acceleration (step input)

우선 센서를 비교적 낮은 가속도인 0.3 Hz의 주파수를 갖는 사인파 입력으로 회전시킨 경우, Fig. 5, Roll 방향에서는 Curve Fitting의 기울기가 Algorithm 3이 Algorithm 1, 2보다 2배 컸다. Curve Fitting의 y절편과 실험값의 표준편차는 Algorithm 2가 가장 작았다.

Pitch 방향에서는, 기울기, y절편, 표준편차 모두 Algorithm 2가 가장 작았으며 Algorithm 3이 가장 컸다. Algorithm 3은 Algorithm 2보다 기울기, y절편, 표준편차가 각각 580%, 3200%, 210% 컸다.

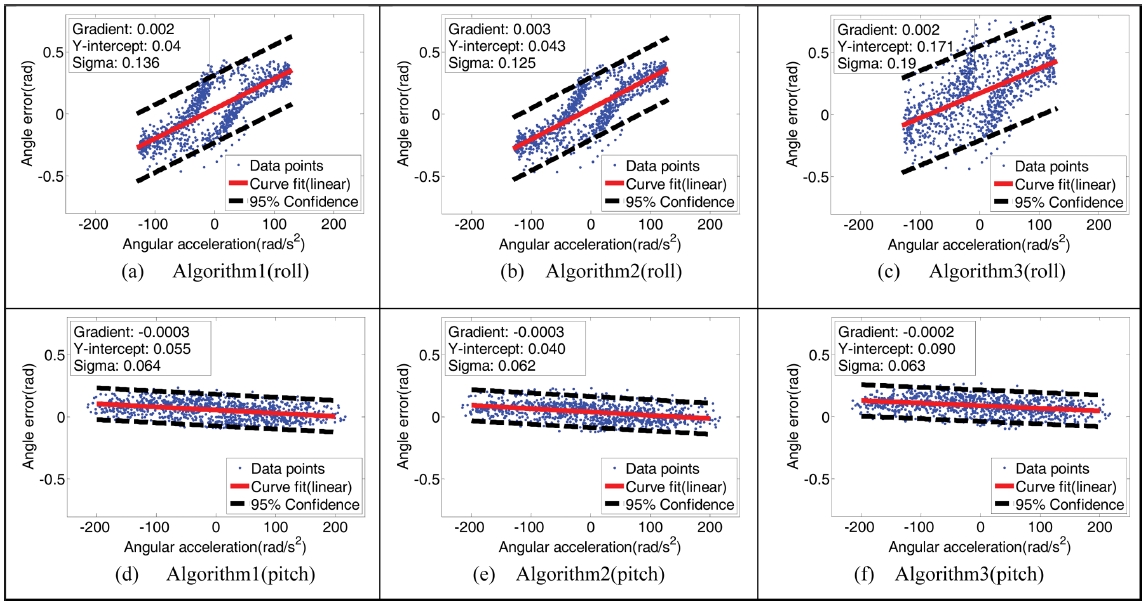
다음으로 3 Hz 주파수의 사인파 궤적으로 회전시킨 결과, Fig. 6를 보면, Roll 방향에서는 기울기가 Algorithm 2의 경우 Algorithm 1과 3에서 보다 0.001 컸다. y절편은 Algorithm 1의 경우 0.04로 가장 작았으며 Algorithm 3의 절편이 0.171로 가장 컸다. 표준편차는 Algorithm 2에서 0.125로 가장 작았으며 Algorithm 3의 표준편차가 0.19로 가장 컸다. Pitch 방향의 경우는 Algorithm 3의 기울기가 Algorithm 1과 2의 경우보다 0.0001 작았으며 y절편의 경우는 Algorithm 2가 0.04로 가장 작고 Algorithm 3이 0.09로 가장 컸다. 표준편차는 Algorithm 2에서 0.062로 가장 작았다.

다음으로 6 Hz 주파수의 사인파 궤적으로 회전하였을 때의 결과, Fig. 7을 보면, Roll 방향에서는 기울기, y절편, 표준편차 모두 Algorithm 2가 가장 작았으며 Algorithm 1, 3보다 각각 10%, 80%, 35% 작았다. Pitch 방향에서는 기울기가 Algorithm 3에서 0.00025로 가장 작았으며 Algorithm 1의 경우 0.0003으로 가장 컸다. y절편은 Algorithm 1에서 0.027로 가장 작았으며 Algorithm 3에서 0.099로 가장 컸다. 표준편차의 경우는 Algorithm 3이 0.052로 가장 작았다.

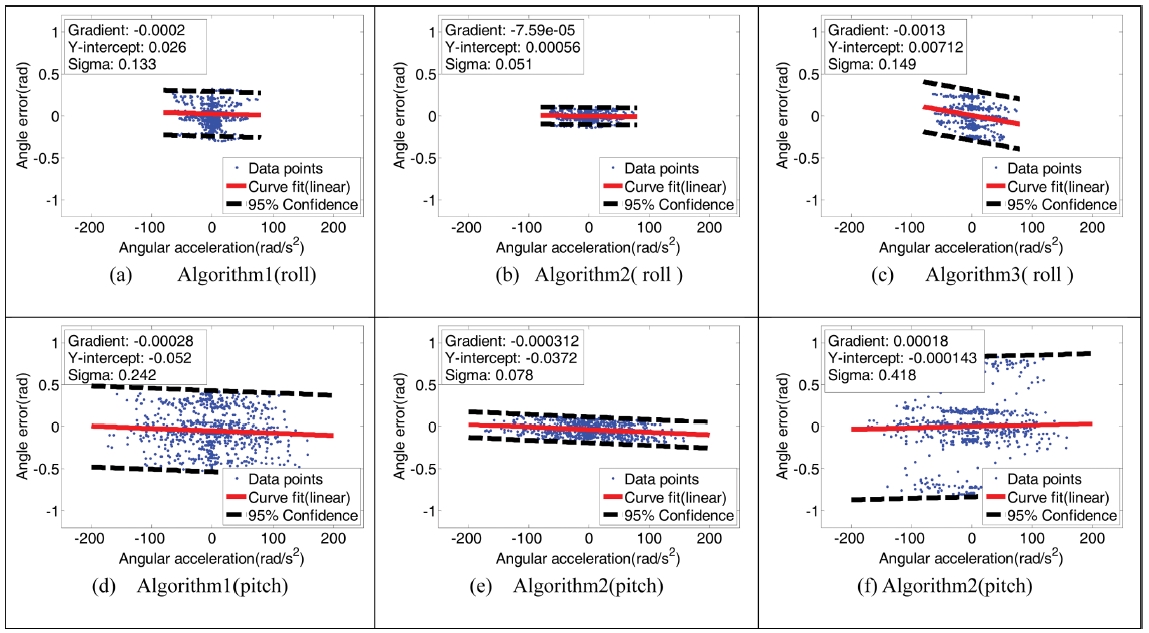
다음으로 직각파 궤적으로 회전시켰을 때의 실험 결과, Fig. 8를 보면, Roll 방향에서는 기울기, y절편, 표준편차 모두 Algorithm 2가 가장 작았다. 기울기와 표준편차는 Algorithm 3이 가장 컸으며 Algorithm 2와의 차이는 각각 1712%, 292%이다. y절편은 Algorithm 1이 가장 컸으며 Algorithm 2와의 차이는 4642%이다. Pitch 방향에서는 기울기가 Algorithm 3의 0.00018이 가장 작았으며 Algorithm 2의 0.000312가 가장 컸다. y절편은 Algorithm 3의 -0.000143이 가장 작았으며 표준편차는 Algorithm 2의 0.078이 가장 작았다.

네 가지 서로 다른 외부가속도 시나리오를 적용한 실험 결과로부터 Curve Fitting의 기울기는 Roll 방향에서 1번, Pitch 방향에서는 2번을 제외하고 Algorithm 2가 가장 작았다. 참고로 직각파 형태의 외부가속도 시나리오를 적용한 경우 Pitch 방향에서 Algorithm 3의 기울기가 Algorithm 2보다 작았지만 표준편차가 4배 이상 차이가나 이 결과를 제외하였다. y절편은 Roll, Pitch 방향에서 각각 1번씩을 제외하고는 Algorithm 2가 가장 작았다. 표준편차도 Roll, Pitch 방향에서 각각 1번씩을 제외하고는 Algorithm 2가 가장 작았다.

4. 결론

본 논문에서는 가속도의 변화가 큰 동적 환경을 고려하기 위하여 바이어스와 외부가속도 보정 방법을 적용한 자세 추정 알고리즘을 조사하였다. 이를 위해 세가지 알고리즘(Algorithms 1, 2, 3)의 추정 성능을 실험하고 그 결과를 분석하였다. 실험을 통해 자세추정 오차가 외부가속도의 크기에 선형적으로 비례함을 확인하였다. 따라서 자세추정 오차를 외부가속도에 대하여 선형적으로 Curve Fitting하였다. 그리고 기울기와 y절편 그리고 표준편차를 판별기준으로 사용하여 각 알고리즘을 비교하였다. 여기서 기울기는 외부가속도 보정 성능을 나타내며 기울기가 작을수록 추정성능이 좋다. Y 절편은 센서 마운팅 등 하드웨어 오차로 인해 발생하는 자세추정의 오프셋을 나타내다. 그리고 알고리즘의 추정성능이 정밀할수록 표준편차가 작아진다.

실험 결과로부터 외부가속도가 클 경우와 중간일 경우, Algorithm 2의 추정성능이 가장 우수하며 외부가속도가 작을 경우에는 Algorithm 1과 2의 추정성능이 비슷하였다. 특히 적용된 대부분의 외부가속도 효과에 대하여 Algorithm 2의 기울기, y절편, 표준편차가 가장 작아 비교적 균일하고 정밀한 추정성능을 보여주었다. 따라서 서론에서 언급했던 동적 시스템들, 즉 큰 가속도가 작용하거나 고속에서 높은 주파수로 회전하는 동적 시스템들의 자세추정에 Algorithm 2를 활용할 경우 Algorithm 1, 3보다 우수한 추정결과를 얻을 수 있을 것으로 예상된다.

Acknowledgments

본 연구는 2017년도 한밭대학교 교내학술연구비의 지원을 받았음.

REFERENCES

• Mathie, M., Coster, A., Lovell, N., and Celler, B., “Detection of Daily Physical Activities Using a Triaxial Accelerometer,” Medical and Biological Engineering and Computing, Vol. 41, No. 3, pp. 296-301, 2003. [https://doi.org/10.1007/BF02348434]
• Uiterwaal, M., Glerum, E., Busser, H., and Van Lummel, R., “Ambulatory Monitoring of Physical Activity in Working Situations, a Validation Study,” Journal of Medical Engineering & Technology, Vol. 22, No. 4, pp. 168-172, 1998. [https://doi.org/10.3109/03091909809032535]
• Yun, X., Calusdian, J., Bachmann, E. R., and McGhee, R. B., “Estimation of Human Foot Motion During Normal Walking Using Inertial and Magnetic Sensor Measurements,” IEEE Transactions on Instrumentation and Measurement, Vol. 61, No. 7, pp. 2059-2072, 2012. [https://doi.org/10.1109/TIM.2011.2179830]
• Williamson, R. and Andrews, B., “Detecting Absolute Human Knee Angle and Angular Velocity Using Accelerometers and Rate Gyroscopes,” Medical and Biological Engineering and Computing, Vol. 39, No. 3, pp. 294-302, 2001. [https://doi.org/10.1007/BF02345283]
• Bachmann, E. R., “Inertial and Magnetic Tracking of Limb Segment Orientation for Inserting Humans into Synthetic Environments,” Ph.D. Thesis, School of Naval Postgraduate Monterey CA, 2000.
• Park, M.-S. and Hong, S.-K., “Indirect Kalman Filter Based Sensor Fusion for Error Compensation of Low-Cost Inertial Sensors and Its Application to Attitude and Position Determination of Small Flying Robot,” Journal of Institute of Control, Robotics and Systems, Vol. 13, No. 7, pp. 637-648, 2007. [https://doi.org/10.5302/J.ICROS.2007.13.7.637]
• Park, Y.-G. and Park, C. G., “EKF Based Attitude Estimation Algorithm with Considering Innovation Covariance for ARS,” The Korean Society for Aeronautical and Space Sciences, No. 4, pp. 406-409, 2015.
• Sanz, R., Rodenas, L., Garcia, P., and Castillo, P., “Improving Attitude Estimation Using Inertial Sensors for Quadrotor Control Systems,” Proc. of the International Conference on Unmanned Aircraft Systems, pp. 895-901, 2014. [https://doi.org/10.1109/ICUAS.2014.6842338]
• Kalman, R. E., “A New Approach to Linear Filtering and Prediction Problems,” Journal of Basic Engineering, Vol. 82, No. 1, pp. 35-45, 1960. [https://doi.org/10.1115/1.3662552]
• Lee, J. K., “Kalman Filter for Estimation of Sensor Acceleration Using Six-Axis Inertial Sensor,” Transactions of the Korean Society of Mechanical Engineers A, Vol. 39, No. 2, pp. 179-185, 2015. [https://doi.org/10.3795/KSME-A.2015.39.2.179]
• Suh, Y. S., “Orientation Estimation Using a Quaternion-Based Indirect Kalman Filter with Adaptive Estimation of External Acceleration,” Transactions on Instrumentation and Measurement, Vol. 59, No. 12, pp. 3296-3305, 2010. [https://doi.org/10.1109/TIM.2010.2047157]
• Lee, J. K., Park, E. J., and Robinovitch, S. N., “Estimation of Attitude and External Acceleration Using Inertial Sensor Measurement During Various Dynamic Conditions,” Transactions on Instrumentation and Measurement, Vol. 61, No. 8, pp. 2262-2273, 2012. [https://doi.org/10.1109/TIM.2012.2187245]
• Roetenberg, D., Luinge, H. J., Baten, C. T., and Veltink, P. H., “Compensation of Magnetic Disturbances Improves Inertial and Magnetic Sensing of Human Body Segment Orientation,” Transactions on Neural Systems and Rehabilitation Engineering, Vol. 13, No. 3, pp. 395-405, 2005. [https://doi.org/10.1109/TNSRE.2005.847353]
• Artese, G. and Trecroci, A., “Calibration of a Low Cost MEMS INS Sensor for an Integrated Navigation System,” The International Archives of the Photogrammertry, Remote Sensingand Sparial Informarion Sciences, Vol. 37, pp. 877-882, 2008.
• Lee, S. C., Yoo, T. S., and Hong, S. K., “Calibration of Deterministic Error for MEMS IMU Using Least Squares Method,” The Korean Society for Aeronautical and Space Sciences, Vol. 2011, No. 11, pp. 1094-1097, 2011.
• Fontanella, R., Accardo, D., Caricati, E., Cimmino, S., and De Simone, D., “An Extensive Analysis for the Use of Back Propagation Neural Networks to Perform the Calibration of MEMS Gyro Bias Thermal Drift,” Location and Navigation Symposium, pp. 672-680, 2016. [https://doi.org/10.1109/PLANS.2016.7479760]
• Cutti, A. G., Giovanardi, A., Rocchi, L., and Davalli, A., “A Simple Test to Assess the Static and Dynamic Accuracy of an Inertial Sensors System for Human Movement Analysis,” Proc. of Engineering in 28th Medicine and Biology Society International Conference, pp. 5912-5915, 2006. [https://doi.org/10.1109/IEMBS.2006.260705]
• Farrell, J., “Aided Navigation: GPS with High Rate Sensors,” McGraw-Hill, pp. 56-58, 2008.
• Pedley, M., “Tilt Sensing Using a Three-Axis Accelerometer,” Freescale Semiconductor Application Note, Vol. 1, pp. 2012-2013, 2013.