2.5 톤 저상형 고소작업차량 붐 조인트의 최적설계

2.1 붐 조인트 모델

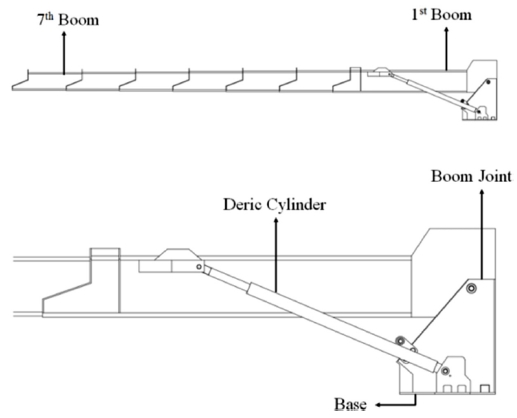
일반적인 고소작업차량의 실제 모습은 Fig. 1과 같다. 본 논문에서 다루는 2.5 ton저상형 고소작업차량의 전고는 2,300 mm이며, 붐의 각도 0^o일 때 최대 인출 11 m, 붐의 각도 18^o일 때 최대 인출 17 m의 텔레스코픽 붐이 탑재되어 있다.

Fig. 1

Photo of aerial lift truck

붐 조인트의 안정성을 확인하기 위해 Fig. 2와 같이 베이스(Base), 붐 조인트(Boom Joint), 1st - 7th 붐(Boom), 데릭 실린더(Deric Cylinder)로 구성된 3D 모델을 작성하였다. FEM 해석을 위한 모델의 형상은 붐 조인트에 최대 모멘트가 가해지는 붐의 각도 0^o일 때의 형상으로 하였다.

Fig. 2

Part name

2.2 Mesh 및 경계조건

Mesh 작업을 위해 3D 형상의 단순화를 위해 붐 조인트(Boom Joint)에 부착되어 있는 불필요한 용접 구조물을 제거한 뒤 Mesh 작업을 실시하였다. 붐 조인트 부분의 모든 축(Shaft)과 부싱(Bushing)의 요소는 원통 형상에 적합한 Hexagonal Mesh이고, 요소의 크기는 10 mm이다. 그 외 붐과 프레임의 요소는 Tetra Mesh이고, 요소의 크기는 20 mm이다. Mesh 결과 요소 개수(Elements)는 237,162개이고, 절점 개수(Nodes)는 541,141개로 분할되었다.

붐 조인트의 축의 재질은 SM45C이고, 부싱과 베이스의 재질은 SS41, 그 외 붐과 프레임의 재질은 ATOS80이다. 안전율은 국제표준 ‘크레인-하중 및 조합 하중에 관한 설계원리’ (ISO8686-2⁸)에 따라 1.48을 적용하였다.

구조해석의 경계조건은 Fig. 3과 같다. 붐 조인트의 베이스 하단 면에 고정조건(Fixed Support)을 부여하였고, 7th 붐의 끝단면에 -z 방향으로 작업하중 3 kN의 힘을 가하였으며, 자중을 고려하였다. 설계목표인 300 kgf 하중을 견디도록 설계 되었기 때문에 작업하중 3 kN을 적용하였다. 각각의 붐은 Bonding 경계조건을 부여하였으며, 각 조인트 및 핀은 회전 자유도를 허용하는 경계조건을 부여하였다.

Fig. 3

Boundary conditions

2.3 구조해석 결과

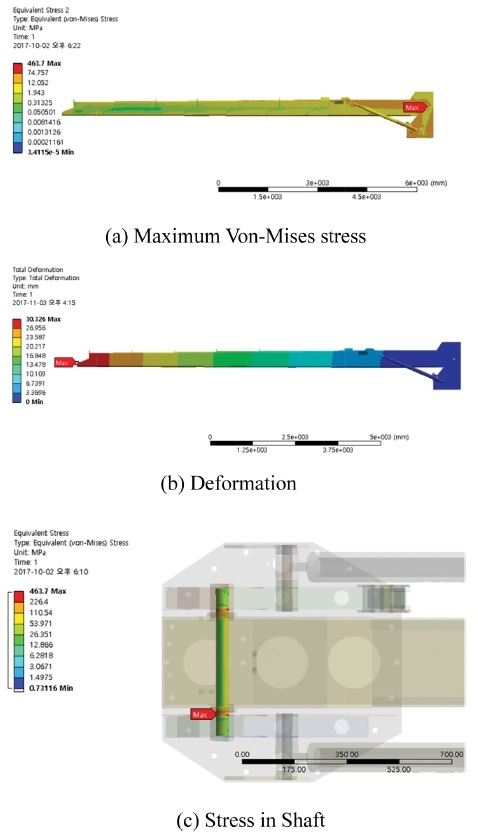
구조해석의 결과 Figs. 4(a)와 4(b)와 같이 최대등가응력(Maximum Von-Mises Stress)이 463.7 MPa, 처짐이 30.3 mm 발생하였다. 최대등가응력이 발생한 지점은 Fig. 4(c)를 보면 붐 조인트의 축 부분에서 나타나는 것을 알 수 있다. 축의 재질은 SM45C이며 안전율 1.48이 적용된 허용응력은 Table 1에 따라 331 MPa이므로 파괴의 위험이 있다.

Fig. 4

Stress and deformation results (initial)

Table 1

List of materials used in structure analysis

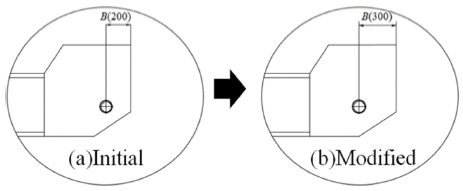
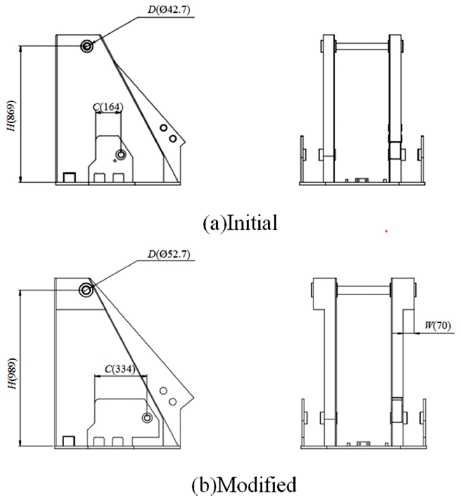
파손될 것이라 예측되는 붐 조인트의 축에 걸리는 응력을 완화시키기 위해 Fig. 5와 같이 B의 값을 200 mm에서 300 mm로 변경하였고, Fig. 6과 같이 D의 값을 42.7 mm에서 52.7 mm로, H의 값을 869 mm에서 989 mm로, C의 값을 164 mm에서 334 mm로, W의 값을 0 mm에서 70 mm로 보강 설계하여 구조해석을 수행하였다. 위의 인자 범위는 고소작업차량 작동에 무리가 없는 범위 내에서의 최대한도이다.

Fig. 5

Modified 1st boom

Fig. 6

Modified boom joint

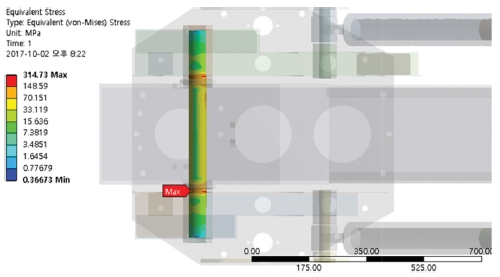
보강된 모델의 구조해석 결과 Fig. 7과 같이 붐 조인트 축에서의 최대등가응력이 314.73 MPa 발생하였다. 이는 축의 재질인 SM45C의 허용응력 331 MPa보다 낮으므로 파손의 우려가 없다고 판단할 수 있다.

Fig. 7

Stress of modified model

3.1 직교배열법

5개의 인자(D, H, C, B, W)에 대해 직교배열을 실시하기 위해 L₁₆(2¹⁵) 직교배열표를 이용하여 직교배열을 실시하였다.

L₁₆(2¹⁵) 직교배열은 4개의 요소를 사용한 배치이다. 이때 4개의 요소를 a, b, c, d라고 하면, 중복을 제외하여 각 요소를 1개, 2개, 3개, 4개 조합하여 a, b, c, d, ab, ac, ad, bc, bd, cd, abc, abd, acd, bcd, abcd 15개의 항이 생성된다. 실험자는 생성된 15개의 항에 대해 최대 15개의 인자를 배치하여 실험을 수행할 수 있으며, 인자가 15개 미만일 경우 남는 항은 통계적 Error항으로 취급한다. 실험의 수는 4개의 요소에 대해 2개 수준이므로 2⁴회이며 각 항의 높고 낮은 수준을 랜덤하게 배열하여 각기 다른 16회의 실험 조건을 생성할 수 있다.⁹

본 논문에서는 5개의 인자를 다루므로 5개의 항을 15개의 항들 중에서 임의로 선정한다. 이때 나머지 10개의 항은 통계적 Error 항으로 취급한다. Table 2는 상용 통계프로그램인 MINITAB을 이용해 5개의 인자에 대해 프로그램 내에서 자동으로 직교배열항의 배치를 수행한 결과이다.⁹

Table 2

L16(215) Orthogonal array of 5 factors

Table 3는 상용 통계 프로그램인 MINITAB을 이용하여 직교배열법을 실시한 5개의 인자에 대해 분산분석을 수행한 결과이다.

Table 3

Analysis of variance (orthogonal array)

표에서 DF는 인자의 자유도를 뜻한다. Adj SS는 Sum of Square 즉, 높은 인자 수준일 때의 반응 값들 합과 낮은 인자 수준일 때의 반응 값들 합의 차를 제곱하여 실험의 개수로 나눈 값을 의미한다. 해당 항이 높은 수준일 때의 각각의 반응값 Y를 합친 값을 T₁, 해당 항이 낮은 수준일 때의 각각의 반응값 Y를 합친 값을 T₀이라고 하고, 실험의 개수를 N이라고 하면 Adj SS는 식(1)과 같다.⁹

5개의 인자에 대한 Adj SS (SS_D, SS_H, SS_C, SS_B, SS_W)는 위의 식(1)을 사용하여 D, H, C, B, W 각항에 대한 Adj SS 값을 구한다. 에러 항에 대한 Adj SS (SS_Error)는 동일한 방법으로 10개의 Error 항들에 대한 각각의 Adj SS 값을 구한 뒤 모두 합친 값이다. Error항의 Adj SS는 전체적인 실험값에 대한 변동 중 5개의 인자로 설명되지 않는 변동의 크기를 의미한다.⁹

Adj MS는 Mean Square 즉, Adj SS를 DF로 나눈 값이다. F-Value의 값은 각 인자의 Adj MS를 Error의 Adj MS로 나눈 값으로 클수록 해당 인자가 반응값 Y에 큰 영향을 끼치는 것을 의미한다. P-Value는 F-Value가 커질수록 작아지며 0.05 이하일 때 해당 인자가 유의성을 갖는다고 판단한다.⁹

P-Value 값을 보면 D, H, C 인자들이 0.05 이하이므로 이 3개의 인자는 반응값에 상당히 유의한 인자이다.

3.2 완전요인배치법

직교배열을 통해 유의성을 확인한 3개의 인자(D, H, C)에 대해 완전요인배치법을 실시하여 3개의 인자만으로 응력을 최소화시킬 수 있는 수준을 탐색하였다.

실험은 3인자 2수준으로 계획하였으며 곡면성을 확인하기 위해 중앙점을 포함하여 진행하였다. 각 실험의 결과는 Table 4에 명시되어 있다.

Table 4

Design of 2-level 3-factor with center point

Table 5는 MINITAB을 이용하여 3개의 인자에 대해 분산분석을 실시한 뒤 P-Value가 0.05 이상인 인자들을 제외시켜 Error 항으로 치환하는 풀링(Pooling) 작업을 거친 결과이다.

Table 5

Analysis of variance (2-level 3-factor) - after pooling

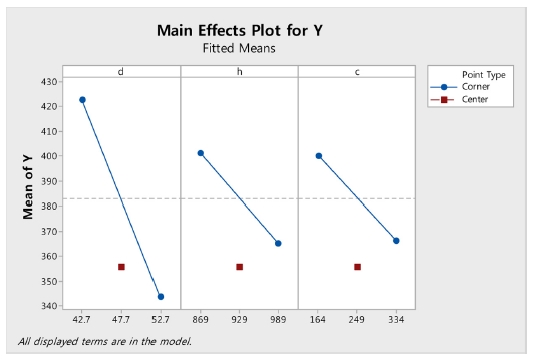
3개의 인자(D, H, C)의 P-Value 값이 0.05 이하이므로 유의한 것을 알 수 있다. Fig. 8을 보면 주효과도에 중앙점이 포함된 것을 알 수 있다. 중앙점이 주효과도의 직선상에서 벗어난 것은 곡면성이 있다는 것을 의미한다. Table 5 상에서도 Curvature의 P-Value값이 0.003이므로 곡면성의 유의성을 확인할 수 있다. 이는 좀 더 고차의 실험계획이 필요하며 반응표면분석법의 추가적인 수행이 요구된다.

Fig. 8

Main effects plot

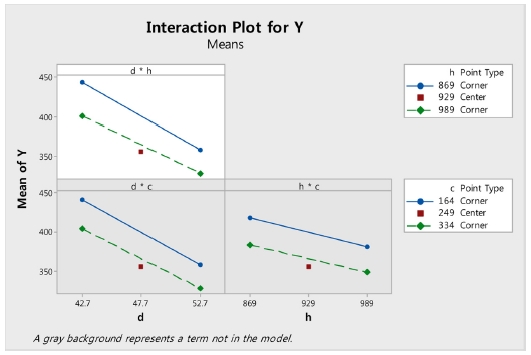
Fig. 9은 인자 간의 교호작용을 나타낸다. 각 인자의 수준에 따른 반응값 Y 값이 나타나있으며 기울기가 엇갈리는 형태를띄면 교호작용이 있다는 의미이다. 3인자 2수준의 실험에서는 D*H항이 유의성을 나타내고 있으나 P-Value 값이 0.046이고, 엇갈림이 크지 않기 때문에 유의성의 정도가 크지 않다.⁹

Fig. 9

Interaction plot

3.3 반응표면분석법

완전요인배치법을 통해 곡면성이 확인됨에 따라 고차의 실험인 반응표면분석법을 실시하였다. 인자의 수준 범위를 초과해서는 안되기 때문에 면중심의 중심합성법을 통해 실험을 계획하였다. 각 실험의 결과는 Table 6에 명시되어 있다.

Table 6

Design of central composite

Table 7은 MINITAB을 이용하여 3개의 인자에 대한 반응표면 분석의 분산분석을 실시한 뒤 P-Value에 따라 풀링 작업을 거친 결과이다.

Table 7

Analysis of variance (central composite) - after pooling

완전요인배치법에서는 D*H항을 다소 유의하다고 판단되었으나 반응표면분석 결과 유의하지 않음이 판단되었으며, 2차 항인 D*D항이 높은 유의성을 보였다.

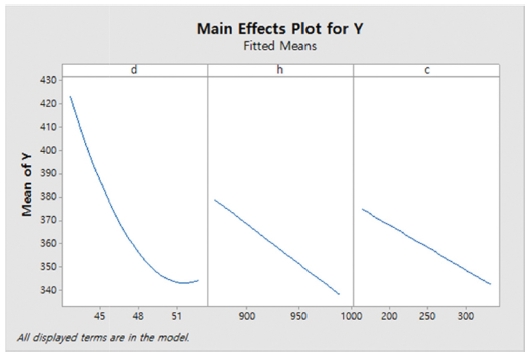
인자 간의 교호작용이 유의하지 않으므로 D, H, C 3개인자는 독립적이며 수준이 올라갈수록 반응값 Y값이 떨어지는 것을 알 수 있다. D*D항이 유의한 것으로 보아 D인자는 2차함수꼴의 곡면 거동을 취할 것으로 예상되며 이는 Fig. 10의 주효과도를 보면 확연히 알 수 있다.

Fig. 10

Main effects plot (central composite)

분산분석을 통해 검증된 유의한 인자 D, H, C, D*D와 반응값Y에 대한 회귀방정식은 식(2)와 같다.

3.4 반응최적화

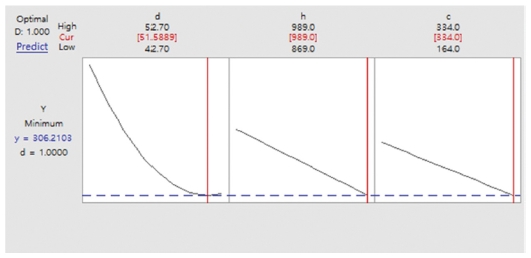
반응표면분석법을 통해 도출된 회귀식(2)를 통해 MINITAB의 반응최적화를 실시한 결과 인자 수준 범위 내 최저 응력 값의 위치는 Table 8과 같다.

Table 8

Optimal design

반응최적화를 수행한 결과 Fig. 11에서와 같이 D인자의 최적화 수준이 51.5889 mm로 계산되었으나, 실제 제품의 수치로 사용하기에 부적절하므로 최적화 수준을 51.6 mm으로 수정하고 최적화된 수준으로 3D 모델을 수정하였다.

Fig. 11

Optimization plot

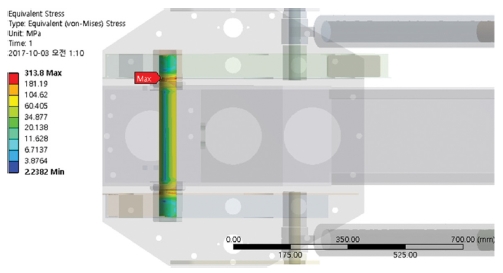
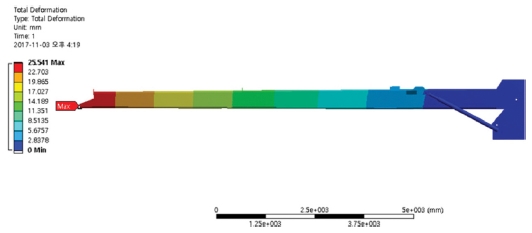
최적화 모델에 대한 구조해석 결과는 Figs. 12와 13과 같다. 구조해석 결과 붐 조인트의 축 부분에서 최대등가응력 313.80 MPa이 발생하였다. 이는 반응최적화 결과 306.21 MPa과 97.58% 일치한다.

Fig. 12

Stress of optimized model

Fig. 13

Deformation of optimized model

초기 모델의 최대등가응력과 처짐량은 463.70MPa, 30.326 mm이다. 최적화 모델의 최대등가응력과 처짐량은 313.80 MPa, 25.541 mm이므로 최적화를 통해 최대등가응력의 32.33% 감소, 처짐량의 15.78% 감소를 얻을 수 있었다.