리스트라이킹이 고강도강 스탬핑에서의 형상정밀도에 미치는 영향에 관한 연구

2.1 인장시험

본 연구에서 사용된 강판 소재는 이중조직강인 두께 1.0 mm의 SPFC780DP으로, 인장시험을 실시하여 Table 1과 같이 등방성 가공경화모델에 필요한 물성치를 도출하였다.

Table 1

Material properties of SPFC780

Yoshida-Uemori 모델(이하 Y-U모델)을 적용한 유한요소 해석을 수행하기 위해서는 반복인장-압축시험을 통해 결정되는 10개의 파라메터,⁸ 즉 Y, B, C, R_sat, m, b, h, E₀, E_a, ζ이 필요하다. 그런데 반복 인장-압축시험은 단축인장 시험과는 달리 시험을 직접 수행하기 어려워, 규격명칭이 동일한 SPFC780DP강의 이전 연구에서 사용한 반복인장-압축시험 결과를 해석에 이용하였다. 그렇지만 규격명칭이 동일한 소재이더라도 재료시험의 결과는 약간씩 차이가 날 수 있다. 가급적 실험에 사용하는 소재로 측정한 물성치를 사용하는 것이 해석의 정확도 향상에 도움을 주기 때문에, 드로우벤딩 실험에 사용하는 소재로 단축인장시험은 실시하였으며, 이 시험결과를 반복인장-압축시험 결과¹와 적절한 방법으로 조합하여 Y-U 파라메터를 구했다.

2.2 Y-U Parameter의 결정

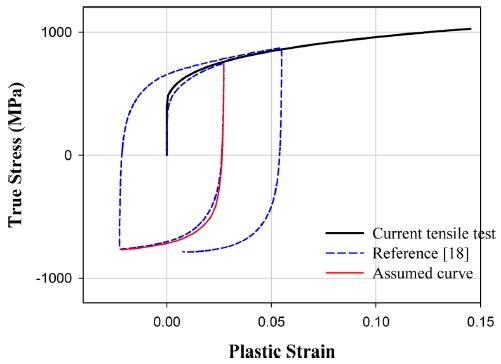
Fig. 1은 SPFC780DP재료에 대하여 이번 연구에서 사용하는 판재에서 채취한 인장시험편으로 측정한 단축인장시험결과를 동일한 규격명칭의 반복인장-압축시험 결과를 함께 표현한 그래프인데, 동일한 강종이라면 단축인장시험 곡선의 모양은 인장-압축시험의 최초구간인 인장영역에서는 동일해야 하지만, 대체로 비슷하지만 인장항복점 부근에서는 곡선의 모양에 약간의 차이가 나타났다.

Fig. 1

Assumption of stress-strain curve in compressive region (SPFC780DP)

그런데 항복점 부근은 탄소성 천이영역이기 때문에 특히 이 부근에서의 거동은 스프링백의 해석결과에 크게 영향을 미칠 수 있기 때문에 스프링백 해석정확도 향상을 위해서는 실제 성형에 사용되는 재료의 물성을 최대한 반영하는 것이 좋다.

한편 반복인장-압축시험 곡선의 모양은 인장항복점 부근과 압축항복점 부근의 형태가 서로 유사한 것을 알 수 있다.

이러한 관찰을 토대로 따라서 인장-압축곡선을 인장영역에서는 실험에 사용하는 재료로 인장시험한 결과를 사용하고, 압축영역에서는 압축항복점 부근의 곡선 모양을 인장항복점 부근과 유사하게 수정하여 만들었다. 이 방법으로 생성된 곡선으로부터 10개의 Y-U 파라메터를 결정하였다.

이 방법을 채택한 이유는 바우싱거효과의 측정에 필요한 인장-압축시험은 직접 실시할 수 없었지만, 등방경화에 비해 이동경화의 크기가 비교적 작다는 점과, 항복점부근의 곡선형태가 스프링백에 큰 영향을 미칠 수 있다는 점, 인장항복점 부근의 곡선 형태가 압축항복점 부근과 서로 유사하다는 점, 그리고 실제 실험재료의 등방경화 거동은 예측의 정확도 향상을 위해 반드시 반영되어야 한다는 점을 모두 고려했기 때문이다.

Table 2는 이 방법으로 도출된 인장-압축 곡선으로부터 결정된 SPPFC780DP강의 Y-U 파라미터들을 정리한 것이다.

Table 2

Yoshida-Uemori parameters of SPFC780DP

3.1 실험장치의 설계

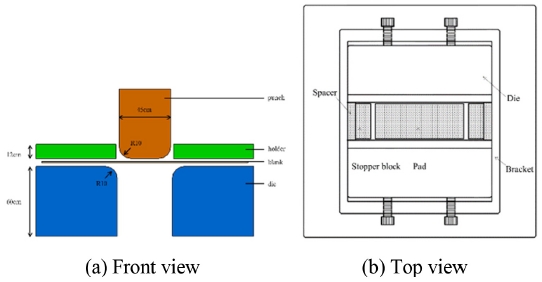
Fig. 2는 평면변형 U 드로우벤딩 실험에 사용한 금형의 형상을 나타내었다. 펀치너비는 45 mm, 펀치라운드 반경과 다이라운드 반경은 모두 10 mm로 설계하였다. 금형설계시 다이간격을 조절할 수 있도록 설계하여 판재두께와 틈새크기에 맞추어 다이 금형 간의 간격을 설정할 수 있도록 하였다. 즉 다이 금형간의 간격은 미리 가공된 스페이서(Spacer)로, 펀치스트로크는 바닥면에 설치된 패드(Pad)로, 리스트라이킹 깊이는 패드(Pad)와 스토퍼블록(Stopper Block)의 높이 차이로 조절할 수 있도록 하였다.

Fig. 2

Design of U-draw bending die

바인더력(Binder Force)의 조절을 위해 Fig. 3과 같이 가스스프링을 채택하였는데, 가스스프링은 가스 압력으로 가압력을 비교적 쉽게 조절할 수 있고, 또 압축이 되더라도 압축력의 증가가 비교적 작아 실험조건을 일정하게 유지하기 쉽기 때문이다.

Fig. 3

Experimental setup for U-shape draw bending

3.2 실험 및 유한요소 해석

본 연구에서는 바인더력, 플랜지길이, 다이-펀치 간의 틈새, 성형깊이 등의 드로우벤딩 공정변수가 그리고, 리스트라이킹이 스프링백에 미치는 영향을 조사하려고 한다.

Fig. 4

Deformed shape after U-draw bending

바인더력은 가스스프링의 압력으로, 플랜지 길이는 블랭크의 크기로 자유롭게 조절할 수 있으며, 틈새, 성형깊이, 리스트라이킹 깊이는 각각 미리 여러 단계로 가공된 스페이서블록의 길이, 패드의 높이, 스토퍼블록의 높이로 단계별로 조절된다. 모든 실험에서 테프론 윤활유인 WD-40를 사용하여 윤활하였다.

기본 실험조건은 블랭크 크기를 178 mm × 80 mm, 바인더력을 10 kN, 펀치스트로크을 50 mm, 펀치와 다이의 틈새를 1.1 mm로 설정하였고, 각 공정변수를 3 수준으로 변경하면서 각 공정변수의 영향을 조사하였다.

리스트라이킹 공정은 형상 정밀도 개선을 위해 드로우벤딩한 뒤 펀치를 재차 가압하는 공정으로 기본실험 조건으로 드로우벤딩한 뒤, 바닥에 패드를 설치한 후 스토퍼블록을 두어 펀치의 진행을 정지시킨다. 즉 원래 성형깊이보다 0.2 mm, 0.4 mm 더 진행할 수 있도록 판재두께와 리스트라이킹 깊이, 그리고 패드두께를 고려하여 미리 가공한 스토퍼블록으로 펀치의 진입깊이를 조절하였다.

스프링백에 미치는 바우싱거효과의 영향을 조사하기 위하여 상용성형해석 S/W인 Hyperform⁹에서 등방경화모델과 Y-U 복합경화모델을 각각 적용하여 해석한 결과를 비교하였다.

등방경화모델로 해석할 때는 Table 1에 나타낸 물성치를 사용하였고 복합경화경화모델로 해석할 때는 Table 2에 제시된 파라미터값을 사용하였다. 해석시 마찰계수는 모두 0.125로 설정하였고 성형 해석 결과를 이용하여 스프링백 해석을 진행하였다.

3.3 성형후 형상의 측정 및 정량적 분석

각종 공정변수가 스프링백에 미치는 영향을 조사하기 위해 실험결과와 유한요소해석 결과를 정량적으로 비교 분석할 필요가 있다.

스프링백의 크기를 정량적으로 분석하기 위해 Fig. 5와 같이 광학식 3D 스캐너(SmartSCAN, 3D Systems, ACION)을 이용하여 성형후 형상을 측정하였고, 측정된 점군 데이터(Data Cloud)를 다시 면데이터로 변환하였다(GeomagicDesignX S/W 이용). 스프링백을 정량적으로 분석하기 위해 Fig. 6에 도시한 것과 같이 측정된 형상데이터에서 시편의 길이방향으로 중심단면에 대한 2차원 형상데이터를 추출하였다.

Fig. 5

Deformed shape measurement with 3D scanner

Fig. 6

Quantification of deformed shape

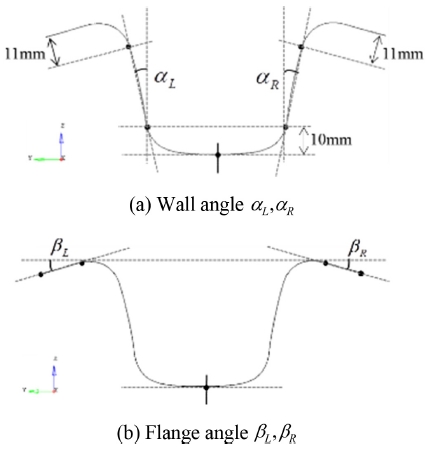
이렇게 추출된 형상정보로부터 단면의 형상과 측면부분의 벌어짐, 플랜지 부위의 처짐, 측면부위의 휨, 바닥면의 휨등을 확인할 수 있다. 측정된 단면형상을 정량화하기 위해 Fig. 6에 도시한 방법으로 단면 형상을 처리한 후 벽면의 좌우측 각도 α_L과 α_R, 플랜지면의 좌우측 각도 β_L과 β_R를 구하였다. 해석결과도 마찬가지 방법으로 정량화하였다.

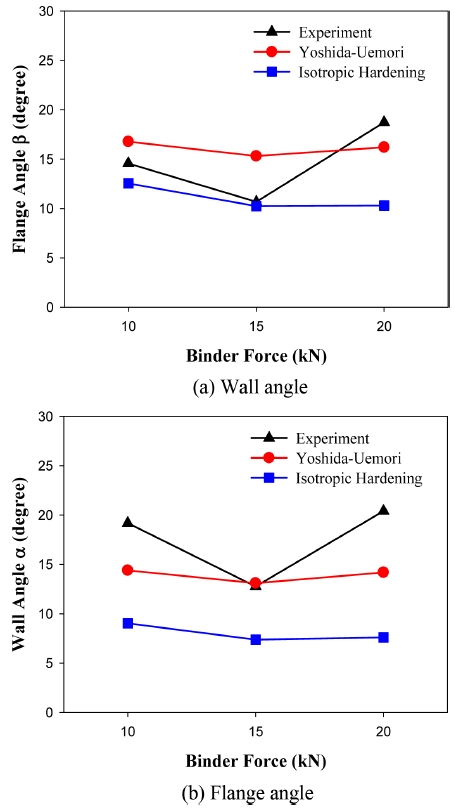
U-드로우벤딩은 대칭조건으로 실험하였기 때문에, 실험과 해석결과 모두 좌우측이 거의 비슷하게 나타나, 양쪽에서 측정된 각도를 평균하여 나타내었다. Figs. 7부터 10은 벽면각도 α와 플랜지 각도 β에 공정변수가 미치는 영향을 조사하기 위해 실험결과를 등방경화모델의 해석결과, Y-U의 복합경화 모델의 해석결과와 비교하고 있다.

Fig. 7

Change of angles to show the effect of binder force

Fig. 8

Change of angles to show the effect of blank size

Fig. 9

Change of angles to show the effect of stroke length

Fig. 10

Change of angles to show the effect of clearance

Figs. 7(a)와 7(b)는 바인더력이 성형후 영상에 미치는 영향을 보여주고 있다. 바인더력이 증가함에 따라 실험결과에서는 벽면과 플랜지면이 벌어지는 각도가 모두 감소 후 증가하는 경향을 보이고 있으나, 해석에서는 바인더력의 영향이 크지 않았으며, Y-U모델의 예측결과가 등방경화모델보다 실제 실험결과와 더 가깝게 나타났다.

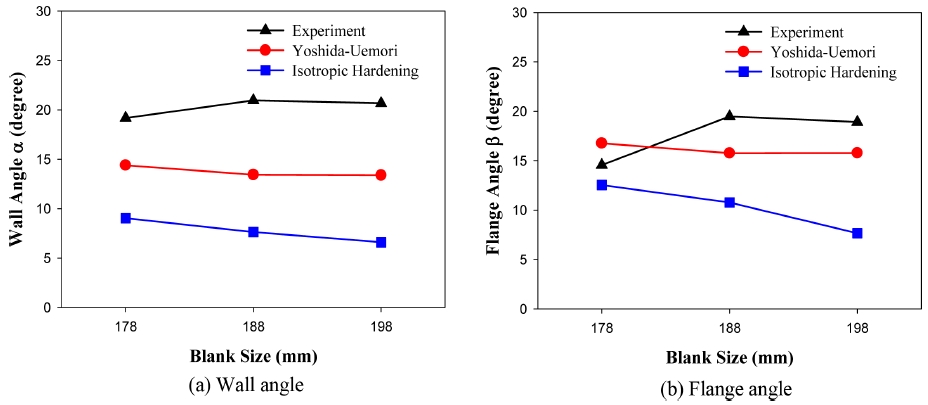
Figs. 8(a)와 8(b)는 블랭크 크기, 즉 플랜지 길이가 성형후 형상에 미치는 영향을 보여주고 있다. 블랭크 크기가 178 mm에서 198 mm까지 증가하는 동안 벽면각도와 플랜지 각도가 모두 실험결과는 거의 일정 또는 미세하게 증가하는 추세를 보이는데 반하여, 해석결과는 등방경화, Y-U모델 모두 약간 감소하는 추세이며, Y-U모델의 해석결과가 등방경화에 비해 실험결과와 더 가깝게 나타났다.

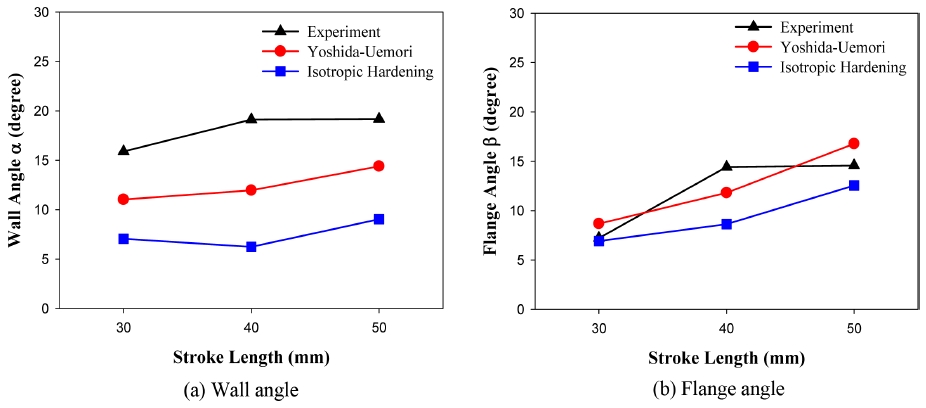
Figs. 9(a)와 9(b)는 성형깊이가 성형후 형상에 미치는 영향을 나타낸 것이다. 성형깊이가 증가함에 따라 벽면각도와 플랜지각도 모두 증가하고 있으며, 벽면각도는 두 경화모델 모두 해석결과가 실험과는 큰 차이를 보이지만, Y-U모델의 해석결과가 등방 경화모델보다 실험과의 오차가 작았다. 플랜지 각도도 Y-U모델이 등방경화 모델보다 실험과의 오차가 작았다.

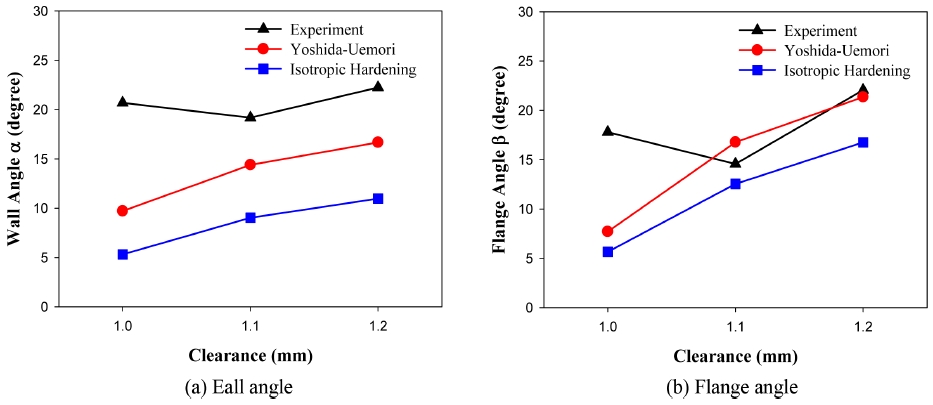
Figs. 10(a)와 10(b)는 다이와 펀치간의 틈새의 영향을 보여주고 있다. 해석에서는 틈새가 증가할수록 벽면각도가 증가하고 있으나, 실험에서는 각도변화가 크지 않았고, Y-U모델의 해석결과가 등방경화 모델보다 실험과 가깝게 나타났다. 플랜지각도도 해석에서는 틈새가 증가할수록 크게 커지는 경향을 나타내고 있으나 실험에서는 그 경향이 일정하지 않았다. 즉 기준조건인 틈새 1.1 mm보다 클 경우, 실험과 해석 모드 각도가 증가하였으나, 틈새 1.0 mm의 경우, 해석에서는 각도가 작게 나타났으나 실험에서는 오히려 크게 나타났다.

실험결과와 해석과의 차이가 크게 나타난 이유는 금형에 작용하는 힘 때문에 금형이 변형되었기 때문으로 판단된다. 즉 성형동안 금형을 밀어내는 힘이 작용하는데, 틈새가 작을수록 이 힘의 크기가 커진다. 그런데 Fig. 1과 같이 실험에 사용한 금형은 다이의 폭을 조절할 수 있도록 설계되었고, 이 간극을 볼트로 지탱하게 되어 있는데, 큰 힘이 작용하면 볼트와 이를 지지하는 브라켓을 변형시킬 수 있고, 이로 인해 다이 간격을 벌어졌기 때문에, 당초 설정한 틈새를 유지할 수 없게 된 것이 주요 원인으로 추정된다. 따라서 가변형 금형에서는 틈새를 지나치게 작게 설정하면 틈새 변화를 유발할 수 있기 때문에 금형설계시 고정볼트나 브라켓 등과 같은 금형의 치수조절장치의 변형 가능성을 미리 고려할 필요가 있다.

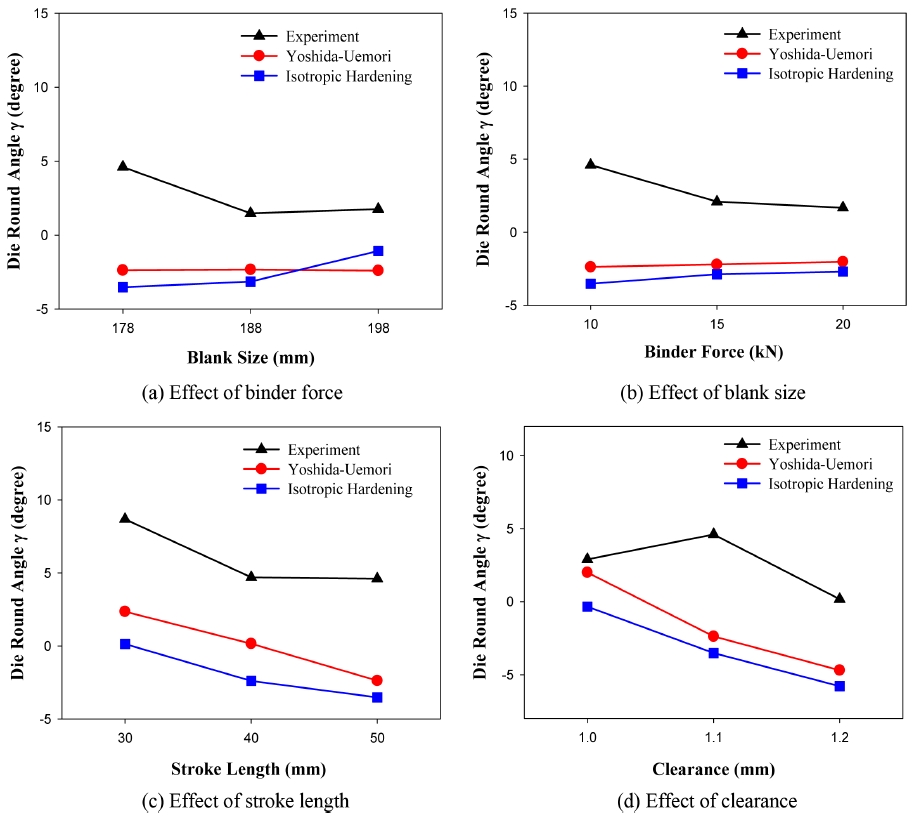
지금까지 스프링백후의 단면형상과 금형형상의 차이를 검토하였다. 그런데 벽면각도는 펀치 라운드에서의 스프링백이 원인인데, 플랜지부의 각도는 펀치라운드와 다이라운드의 스프링백이 모두 작용한 결과이다. 따라서 플랜지에서의 스프링백각도보다는 펀치라운드에서의 스프링백과 다이라운드에서의 스프링백을 분리하여 조사할 필요가 있다. 펀치라운드에서의 스프링백은 벽면 각도로 표현되었기 때문에 다이라운드에서의 스프링백의 크기는 벽면각도와 플랜지각도의 차이로 판단하면 된다. Figs. 7부터 10의 결과를 다시 정리하여 다이라운드에서의 스프링백 각도 γ를 도출하여 Fig. 11에 나타내었다.

Fig. 11

Change of die round angle due to springback

스프링백 각도가 양수일 경우는 스프링백에 의해 다이라운드에서 벽면과 플랜지가 이루는 각도가 증가하는 상황이고, 반대로 음일 경우 벽면과 플랜지가 이루는 각도가 감소되는 상황을 의미한다. 이러한 노력에도 불구하고 Fig. 11의 다이라운드에서의 각도변화는 여전히 실험과 해석결과와는 상당한 차이를 보이고 있다. 그렇지만 대체적으로 바우싱거효과를 고려하는 Y-U모델의 해석결과가 등방경화모델보다 실험에 가깝게 나타났다.

리스트라이킹 공정이 스프링백에 미치는 영향을 조사하기 위하여 기본실험조건, 즉 펀치변위 50 mm로 드로우벤딩한 시편을 다시 리스트라이킹을 실시하였다. 이때 1차 드로우벤딩 공정보다 펀치변위를 각각 0.2 mm, 0.4 mm 더 진행시킨 후 변형후 형상을 조사하였다.

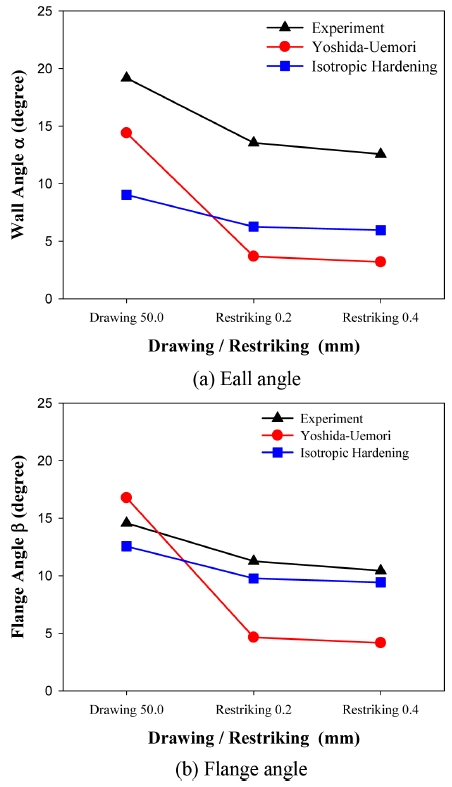
Figs. 12(a)와 12(b)는 리스트라이킹을 거친 시편과 드로우벤딩만 한 시편의 형상비교를 통해 리스트라이킹 동안 발생한 벽면과 플랜지부의 각도 변화를 각각 나타낸 것이다. 대체로 리스트라이킹을 거치면서 시편의 형상정밀도가 향상, 즉 벽면각도와 플랜지 각도가 모두 감소되었다. 그런데 리스트라이킹 변위 0.2 mm와 0.4 mm의 결과는 실험과 해석모델 모두 서로 비슷하게 나타났는데, 그 이유는 실제 실험에서는 패드 때문에 펀치가 일정한 깊이 이상으로 진입하지 못했기 때문으로 판단된다. 즉 리스트라이킹 깊이의 영향을 조사하기 위한 실험을 계획할 때 리스트라이킹 깊이단계의 간격을 지나치게 넓게 설정하였기 때문으로 판단된다. 지금까지와는 달리 리스트라이킹에서는 등방경화 모델이 복합경화 모델보다 실험결과와 더 가깝게 나타났다.

Fig.12

Changes of angles to show the effect of restriking with comparison of analysis

Table 3은 리스트라이킹의 형상개선효과를 정리한 것으로 리스트라이킹 실험전후의 벽면각도, 플랜지 각도, 그리고 각도개선 비율을 나타내었다. 리스트라이킹 깊이 0.2 mm일때는 벽면각도는 29.4%, 정도, 플랜지각도는 22.7% 정도 감소하였다. 리스트라이킹 깊이 0.4 mm에서는 벽면각도는 34.5%, 플랜지각도는 28.4% 정도 감소하였다. 리스트라이킹 깊이를 증가시키면 형상개선효과가 좋아지지만, 깊이가 증가함에 따라 개선효과는 감소하였다. 그 이유로는 앞에서 설명한 바와 같이 실험을 계획할 때 리스크라이킹 깊이를 지나치게 크게 설정하였기 때문으로 판단된다.

Table 3

Result of restriking experiment to show the effect of restriking depth