지뢰방호구조 설계인자가 지뢰폭압충격 특성에 미치는 효과

1. 서론

일반적으로 군용 지상무기 플랫폼 소재로 사용되는 판재는 특수 재질의 고강도, 고경도의 장갑판재를 사용하고 있으며 차량 방호뿐 아니라 탑승 승무원들의 생존성을 높이기 위해서 철갑탄 및 지뢰, 급조 폭발물(Improvised Explosive Device, IED)과 같은 발사체 충격 및 폭약 폭발시 발생압력에 대한 방호설계를 수행하고 있다. 최근 중동지역의 분쟁과 전 세계적인 테러 발생으로 인하여 선진국을 중심으로 신규개발 전투용 차량의 방호성능을 점점 높여 설계하고 있고, 또한, 기 개발 차량의 방호성능을 개량하는 사업을 통해서 방호성능을 향상시키는 추세이다. 특히, 급조 폭발물이나 지뢰폭압 등의 위협체는 한번에 여러 승무원에 상해를 주기 때문에 확보해야 할 방호성능 중 가장 우선순위에 있다고 말할 수 있다. 그러나, 지뢰방호성능을 높이기 위해서는 장갑판재가 두꺼워져야 하며, 이에 따라 차량 중량이 증가하므로 고 비용 및 저 기동성의 문제가 발생한다. 방호성능 개선에 따라 동반되는 비용 상승과 저 기동성 문제를 해소하기 위해서 장갑차 차체 설계시 초기부터 방호 및 구조설계를 동시에 만족하는 최적화 설계가 요구되며, 최적화 설계를 위해서는 지뢰 기폭시 지뢰방호 설계인자들의 지뢰폭압충격 특성과 지뢰방호구조 특성연구가 필요로 된다. 이와 같은 지뢰방호 설계인자의 특성연구로써 Yuen¹은 V-hull 구조의 지뢰폭압구조 형상 연구를 위해서 실제 장갑차 축소 모델을 대상으로 시험을 수행하였고, 바닥판 각도, 지상고, 폭약량 등의 설계인자와 처짐량과 충격량 등의 반응인자의 상관관계를 확인하였다. Suhaimi²는 장갑차 차체 지뢰방호 설계인자 특성 연구를 해석적 방법으로 수행하였는데, 지상고와 지뢰기폭위치 그리고, 승무원 의자 높이 등을 설계인자로 하여 차체구조와 인체 더미가 포함된 해석을 통해서 설계인자들과 충격응답 가속도와의 상관관계를 분석하였다. 또, Jiang³은 지뢰 기폭시 장갑차 차체의 폭압충격저감 최적화 설계를 해석적 방법으로 수행하였고, 내부 특정위치의 충격에너지 저감 설계를 제시하였다.

지뢰방호 설계는 차체 방호뿐 아니라, 승무원 상해치 안전이 동시에 요구되어지는데, 지뢰폭압시험은 고 비용과 고 위험성을 동시에 갖고 있으므로 이러한 위험성을 최소화하기 위해서 시험에 앞서 해석을 통한 인체 상해치 예측이 필요하다. Denefeld⁴는 지뢰폭발압력에 대한 장갑차 방호와 차량 탑승 승무원 상해치를 동시에 만족하는 장갑차 차체 설계를 위해서 차량과 인체를 모델링하여 해석적 방법으로 평가하였다. 또한, 방호 연구분야에 통계적 분석방법들이 활용되고 있는데, Bobbili⁵는 철갑탄 충격시 장갑판재 두께 및 형상에 따른 관통특성연구를 위해서 충격해석을 수행하였고, 철갑탄의 충돌속도, 형상 및 두께에 대한 분산분석을 수행하여 설계인자들의 영향성 분석을 수행하였다. 이와 같이 효과적인 지뢰방호 설계를 위해서 설계인자 선정과 초기 설계 적용 유무가 매우 중요한데, 국내에서는 지뢰방호설계를 위한 설계인자 분석 및 적용에 대한 연구가 미비 하다고 말할 수 있다. 따라서, 본 연구에서는 효율적인 장갑차 지뢰방호 설계를 위해서 실제 장갑차를 기초로 한 해석모델 형상과 주요 설계인자 및 지뢰 폭발시 방호성능을 나타내는 반응인자를 정의하였고, 실험계획법(DOE)에 의해서 주요 설계인자들의 조합들로 구성된 조건들을 형상화하여 지뢰폭압환경에서의 주요 설계요소들과 폭압충격특성인 반응인자들에 상관관계에 대한 수치해석을 수행하여 지뢰폭압충격 특성을 평가하였다. 폭발충격해석은 상용 프로그램인 LS-DYNA를 사용하였으며, 해석결과는 일반 데이터 분석과 통계적인 방법인 주효과 분석(Main Effect Analysis) 및 분산분석(ANOVA)⁶을 병행하여 분석하였다.

2. 수치해석

2.1 해석 방법

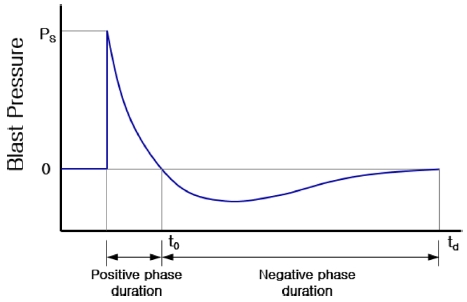
폭발현상은 대표적인 유체-구조 연성 문제이며, 이런 현상을 계산하는 방법은 라그랑지 방법 및 ALE (Arbitrary Lagrange and Euler) 방법이 있다.^7,8 LS-DYNA의 CONWEP (Conventional Weapons Effects)^9,10은 대표적인 라그랑지 방법으로써, 폭약이 공기중에서 폭발할 때 폭발파에 의해 전달되는 압력을 실험적으로 분석하여 폭압지점으로 부터의 거리와 피폭되는 각도에 의해 폭발압력이 구조물에 전달되는 현상을 모사하는 식으로 부터 구조물의 손상을 계산하는 방식이다. Kingery¹¹에 의해서 제안되었으며, 미국 육군연구소(ARL)에서 개발하여 폭발충격해석 방법으로 현재 세계적으로 가장 많이 사용되고 있다. CONWEP은 광범위한 폭발 시험결과를 이격 거리에 따른 작용압력으로 정의하여 사용함으로써 계산시간을 단축할 수 있다. 따라서, 본 연구에서는 폭발시 충격파 거동 보다는 폭발압력에 의한 구조물의 반응 및 손상 거동이 중요하므로 CONWEP을 사용하였다. CONWEP에서 사용되는 압력파는 식(1)의 Friedlander 식¹²으로 표현할 수 있으며, Fig. 1의 그래프는 식(1)의 시간변화에 따른 압력 프로파일의 크기를 보여주고 있다.

Fig. 1

Pressure-time profile for a blast wave

$\[ P\left(t\right)=P_s{e}^{-\left(\frac{t}{t_0}\right)}\cdot \left(1-\frac{t}{t_0}\right) \]$

(1)

여기서, P_s: 최대 폭발압력, t₀: 기폭시 폭발압력의 진행방향 지속시간을 나타낸다.

2.2 고속충격해석 모델

일반적으로 고속충격해석에는 소성운동 모델(Plastic-Kinematic Model)과 존슨-쿡 모델(Johnson-Cook Model)¹³이 사용되는데, 이 모델들은 재료의 물성 변화 및 파손 등의 거동을 모사하는 방법상 차이가 발생하므로, 해석 목적에 따라서 해석모델이 결정되어 사용된다. 본 연구의 폭발충격해석은 폭약 폭발시 폭발압력 접촉에 의한 요소간의 요소소실(Failure of Element)이 매우 중요하므로 존슨-쿡 모델을 사용하였고, 변동 응력식은 식(2)로 나타낼 수 있다.

$\[ {\sigma }_Y=\left(A+B_{\epsilon }^n\right)\left(1+C\cdot \text{ln}{\dot{\epsilon }}^{*}\right)\left(1-T^{*m}\right) \]$

(2)

여기서, σ_Y: 유효응력, ε: 유효 소성 변형률, $$ {\dot{\epsilon }}^{*}$$: 표준화된 유효 소성 변형률 속도, A, B, C, m, n: 재료상수이며, 온도 성분 T^*는 식(3)으로 정의할 수 있다.

$\[ T^{*}=\frac{T-T_{room}}{T_{melt}-T_{room}} \]$

(3)

여기서, T: 절대 온도, T_room: 상온, T_melt: 녹는점이다. 존슨-쿡 모델에서 요소소실은 식(4)의 누적손상법칙⁹에 따라서 발생하며 다음과 같다.

$\[ D=\sum \frac{{\mathrm{\Delta }}_{\epsilon }}{{\epsilon }_f} \]$

(4)

여기서,

$\[ {\epsilon }_f=\left[D_1+D_2\exp \left(D_3{\sigma }^{*}\right)\right]\left[1+D_4\ln {\dot{\epsilon }}^{*}\right]\left[1+D_5{T}^{*}\right] \]$

(5)

이며, Δ_ε: 하중 증가 동안의 유효소성변형 증가분, σ^*: 유효응력에 의해 일반화된 평균응력, D₁, D₂, D₃, D₄, D₅는 파괴상수 이며, 요소소실은 식(4)에서 D = 1일 때 발생한다.

파괴변형, ε_f과 손상누적, D는 평균응력, 변형률, 온도의 함수로 나타낼 수 있고, 폭압충격해석에 필요한 장갑판재 재료물성 및 존슨-쿡 모델 상수^1,15는 Tables 1-3에 나타내었다.

Table 1

Material properties of armor plate

Table 2

Johnson-Cook model constants of armor plate

Table 3

Temperature constants and Johnson-Cook fracture constants of material

또, 재료의 내부에너지와 압력 및 체적과의 상관관계는 상태방정식으로 정의 할 수 있으며, Zukas¹⁶는 폭발압력 속도 500-2000 m/s 범위에서 솔리드-솔리드 충격시 일정한 압력이 발생하고, 발생압력이 재료의 강도에 영향을 준다고 했다. 따라서, 상태방정식은 폭발충격 해석시 폭발압력에 접촉되는 재료의 파손발생에 중요하며 주로 비선형 상태방정식^17,18을 사용한다. 본 연구에서는 Mie-Gruneisen 상태방정식^17,19이 사용되었으며 압축된 재료의 압력은 식(6)으로 나타낼 수 있다.

$\[ P=\frac{{\rho }_0{C}_{sp}^2\mu \left(1+\left(1-\gamma /2\right)\mu -\left(\alpha /2\right){\mu }^2\right)}{\left[1-\left(S_1-1\right)\mu -S_2{\mu }^2/\left(\mu +1\right)-S_3{\mu }^3/{\left(1+\mu \right)}^2\right]}+\left(\gamma +\alpha \mu \right)E_0 \]$

(6)

여기서, E₀: 단위 체적당 내부에너지, C_sp: 충격 및 입자속도 그래프의 인터셉트, S₁, S₂, S₃: 충격 및 입자속도 그래프의 기울기 계수, γ: Gruneisen 계수, α: 체적누적 인자이며, 압축 인자인 μ = ρ/ρ₀−1로 나타낼 수 있다. 장갑판재의 상태방정식 상수는 Espinosa,¹⁷ Gailly,¹⁸ Flores-Johnson²⁰로부터 인용하였으며, Table 4에 나타내었다.

Table 4

Mie-Gruneisen EOS constants

3. 폭발충격해석 모델의 검증

3.1 충격시험

본 연구에서 확인하고자 하는 장갑판재의 고속충격 특성의 신뢰성 있는 측정 데이터를 확보하기 위해서는 폭발충격해석 모델의 신뢰성이 중요하므로, 기 수행했던 장갑판재 평판(1.5 m × 1.5 m)의 폭발충격시험과 동일조건의 해석수행 결과를 비교하여 본 연구에서 사용할 폭발충격해석 모델의 신뢰성을 검증하고자 하였다.

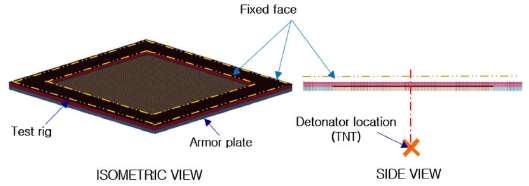
Fig. 2는 DSM Dyneema사에서 기 수행했던 폭발충격시험의 형상을 나타낸 그림으로써, 시험방법 및 조건은 NATO 시험규격인 STANAG4569²¹에 따라서 수행하였으며, 폭약량 및 설치 높이 그리고, 판재 두께 등은 군사보안 등의 이유로 표시하지 않았다.

Fig. 2

Mine blast test for armor plate (courtesy of DSM Dyneema)

Fig. 3은 폭발충격시험 결과로써 폭약 폭발시 폭발압력에 의해 발생한 판재의 측면 방향에서의 소성변형 형상을 나타낸 것이다.

Fig. 3

Test result of armor plate (courtesy of DSM Dyneema)

3.2 충격해석

폭발충격해석 모델의 신뢰성을 검증하기 위해서 시험과 동일한 조건의 충격해석을 수행하였으며, Fig. 4는 충격해석 모델의 형상 및 경계조건을 나타낸 것이다.

Fig. 4

Finite element model for mine blast simulation and boundary condition

대상 장갑판재는 동일한 크기 및 두께 모델링을 하였으며, 요소는 폭압 접촉시 판재의 변형과 접촉에 의한 요소소실을 모사하기 위해서 솔리드 요소를 사용하였다. 장갑판재 윗면에는 판재를 구속하기 위한 ‘ㅁ’ 형태의 시험지그를 모델링 하여 상부면은 구속하였고, 시험지그와 장갑판재 접촉면은 폭약 폭발시 접촉이 발생하므로 접촉조건을 적용하여 높이 방향의 자유도만 구속 하였다. 폭약의 종류와 크기, 폭발위치 및 높이 등도 시험조건과 동일하게 하였다.

Fig. 5는 폭발충격해석 결과로써 장갑판재의 측면방향의 변형형상이며, Fig. 3의 시험결과의 변형형상과 비교를 통해서 유사한 변형 경향성을 확인 할 수 있다. 또, Fig. 6은 시험과 해석결과로써 장갑판 센터부에서의 시간에 따른 수직 방향의 변위를 비율(Rate)로 나타낸 그래프이며, 시험과 해석결과의 시간에 따른 변위값의 유사한 경향성을 확인할 수 있다.

Fig. 5

Simulation result of armor plate (plastic deformation)

Fig. 6

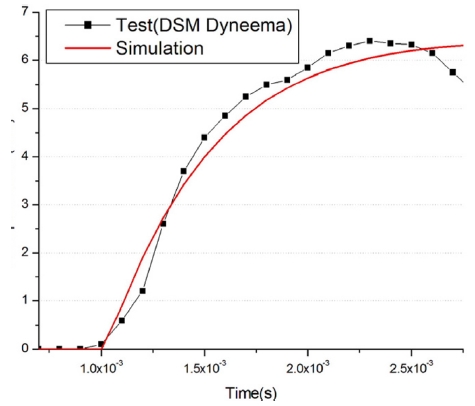
Vertical displacement results of test and simulation at the center point (courtesy of DSM Dyneema in test result)

Table 5는 시험과 해석결과의 수직방향 최대 변위값 비율을 비교한 것이고, 오차율은 실제 최대 변위값을 비교하여 나타낸 것이다. 시험값 기준 해석결과의 오차율은 약 0.6% 수준으로 발생하였다. 따라서, 동일 조건의 변형거동과 수직방향의 변위 그래프 및 최대 변위값 비교를 통해서 시험과 해석결과의 유사 경향성을 확인할 수 있었다.

Table 5

Maximum displacement results of test and simulation

4. 폭발충격해석

4.1 폭발충격해석 모델

3장에서 단일 장갑판재를 대상으로 폭발충격시험 및 동일 조건의 해석수행을 통해서 해석모델의 신뢰성을 확인하였고, 이 충격해석모델을 사용하여 NATO 군사규격인 STANAG (Standization Agreement) 4569 Level 2 (TNT 6 kg) 수준의 폭약 폭발시 각 해석모델의 변형형상과 반응인자들에 대한 각 설계인자들의 영향성을 확인 하고자 하였다.

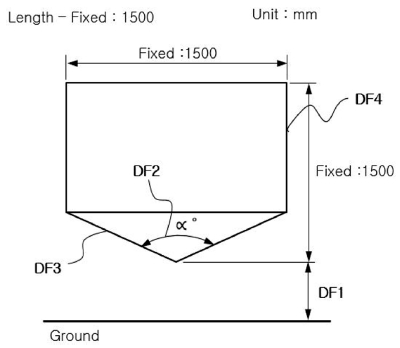
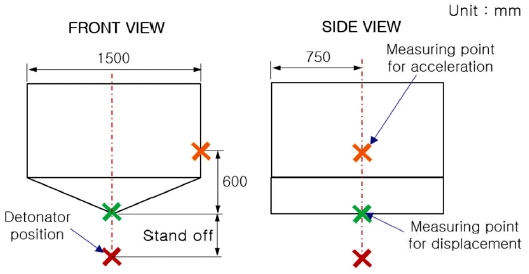
Fig. 7은 장갑차의 지뢰방호 설계시 고려해야할 주요 설계인자들의 위치를 나타낸 설계모델 형상으로써, 크기는 실제 운용중인 해외 차량의 크기를 참고로 형상을 단순화 하였다. 주요 설계인자로써 지상고(DF1), 바닥판 각도(DF2), 바닥판 두께(DF3), 측면판 두께(DF4)의 총 4개의 설계인자를 선정하였는데, 폭은 실제 차량과 유사하게 하였고, 길이는 폭약 폭발시 변형을 고려하여 폭과 동일하게 하였으며, Table 6에 4개의 주요 설계인자와 수준을 나타내었다.

Fig. 7

Configuration of simulation model with design parameters

Table 6

Main design parameters and levels for simulation model

Fig. 7의 선정 되어진 주요 설계인자는 장갑차 차체 기본 설계 시 방호 및 구조성능을 만족시키기 위해서 일반적으로 초기 설계인자로 정의하는 것으로써, 정의된 설계인자로부터 결정된 치수가 차량의 방호성능 뿐 아니라, 차체 중량 증감에 의한 따른 차량의 기동성능에 매우 중요한 영향을 미친다.

Table 6의 주요 설계인자 선정은 장갑차 구조 및 방호설계시 고려하는 설계인자들로 구성하였다. 또, 각 수준 선정인 경우 지상고(DF1)와 바닥판 각도(DF2)는 장갑차로써 운용이 가능한 범위를 임의로 선정하였고, 특히, 장갑판 두께수준 선정은 현재 운용하고 있는 해외 장갑차인 Stryker(미국), LAV3(캐나다), Pandur II(체코), Piranha(스위스), BTR-80A(러시아) 등의 크기 평균값(6.7 × 2.8 × 2.4m)을 기준으로 중량 범위(14.2-22.0 톤)를 만족할 수 있는 두께범위를 선정한 후 미국군사규격²²에 정의되어 있는 정확한 두께 범위를 최종 선정하였다.

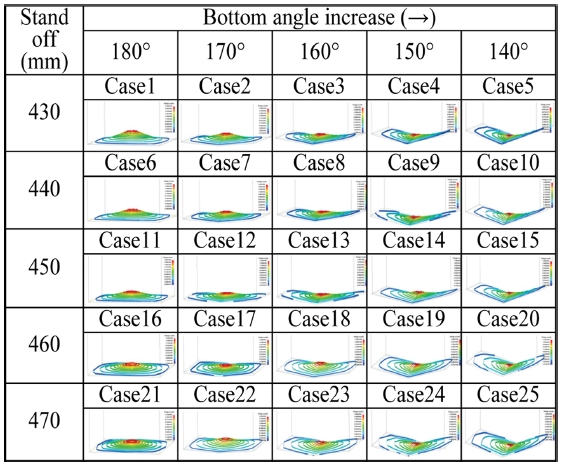
Tables 7은 6의 주요 설계인자와 수준들의 조합에 의한 폭발충격해석 실험점을 결정하기 위해서 실험계획법 중의 하나인 Taguchi Design 방법을 사용하여 총 25가지 실험점을 설계하여 나타낸 것으로써, 해석모델의 순서는 지상고(DF1) 증가에 따라서 분류하였다.

Table 7

Defining of simulation cases by DOE

Table 8은 폭발충격해석 결과의 반응인자를 나타낸 것으로써, 총 4가지를 정의하였다. 지뢰방호 설계시 장갑차의 주요 성능 중 하부방호성능 외에 차량 내부에 탑승 승무원의 인체 상해치가 매우 중요하므로 인체 상해에 영향을 미치는 내부 특정위치의 응답가속도와 바닥면의 수직 동적변위 그리고, 최초 설계시 차량의 기동성능을 좌우하는 경량화 설계 등을 반응인자로 선정하였다.

Table 8

Responses for design parameters

4.2 유한요소모델 및 경계조건

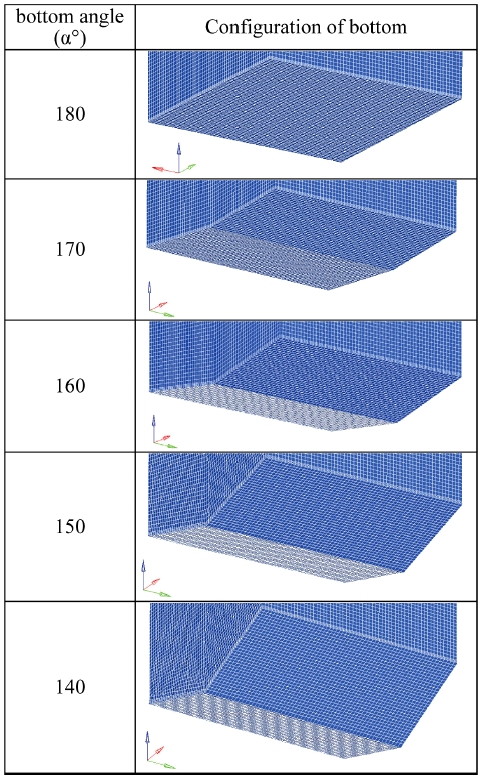
Fig. 8은 폭발충격해석에 사용한 유한요소해석 모델로써, 바닥판 각도 5가지(180^o, 170^o, 160^o, 150^o, 140^o)의 대표적인 유한요소모델 형상을 나타낸 것이다. 폭약 폭발시 발생하는 폭발압력에 의한 변형 및 거동을 구현하기 위해서 바닥판은 10,800개의 솔리드 요소를 사용하였고, 측면 및 상부는 29,520개의 쉘 요소를 사용하였다. 특히 모델의 바닥면은 전체가 폭발압력 영향을 받기 때문에 바닥면의 요소 크기는 균일하게 10으로 구성하였다. 구속조건으로는 해석모델의 상부면을 X, Y, Z축 방향으로 고정하였고, 폭약 기폭위치 및 지상고는 각각 NATO 규격과 Table 7의 각 해석모델별 지상고(DF1)를 적용하였다. 충격해석 방법은 대표적인 실험식 기반 라그랑지 방법인 CONWEP을 사용하였고, 해석시간은 바닥판의 충분한 변형을 고려하여 0.03초로 정하였다.

Fig. 8

Finite element model for mine blast analysis by DOE

Fig. 9는 해석결과의 반응인자 중 수직 동적변위, 충격응답가속도 측정위치를 나타낸 것이며, 충격응답가속도 측정위치는 실제 승무원 의자 높이를 고려한 바닥판 끝에서 수직방향 600 mm 떨어진 측면판 위치로 정하였고, 수직 동적변위 측정위치는 폭약 폭발시 가장 압력의 영향이 큰 바닥판 중심부로 정하였다.

Fig. 9

Measuring points for response data

5. 결과 및 고찰

5.1 폭발충격해석 결과분석

Table 8의 지뢰방호 설계인자가 고려해야 할 반응인자 중에서 수직변위는 장갑차 탑승 승무원의 발과 접촉이 일어나지 않도록 최소 변위 설계가 되어야 하고, 최대 충격응답가속도 또한 승무원의 상해치에 영향을 미치기 때문에 승무원의자 조립위치의 차체에서 측정된 충격응답가속도가 최소값이 되도록 설계해야 한다.

Fig. 10은 Table 7의 총 25개 실험점에 대한 폭발충격해석 결과로써 수직변위 형상을 나타낸 것이다. 바닥판 각도와 지상고에 의해서 분류하였으며, 해석결과로부터 폭발충격 영향은 거의 바닥판에 집중되어 있음을 확인할 수 있다.

Fig. 10

Vertical deformation configuration of simulation results

Fig. 11은 폭발충격해석을 수행한 총 25개 중 바닥판에 요소소실 즉, 균열이 발생한 8개의 바닥판 형상에 대한 등가응력 분포를 나타낸 것으로써, 바닥판 센터부에 균열이 집중되어 있음을 확인할 수 있는데, 균열 발생은 곧 방호성능을 나타낸다. Fig. 11의 결과를 Fig. 10의 그림과 비교해서 볼 때, 총 8개의 모델 중에서 7개(Case 1, 2, 6, 7, 11, 16, 22)가 바닥판 각도 180^o, 170^o에서 발생하였으므로, 해석결과로 부터 바닥판 각도를 160^o 이하로 작게 하는 것이 바닥판 균열발생을 억제하고 방호성능을 높이는데 효과적임을 알 수 있다.

Fig. 11

Bottom element eroding configuration of simulation results (details)

Table 9는 총 25개 실험점에 대해서 4가지 반응인자에 대한 해석결과를 나타낸 것으로써, 앞서 Fig. 10, 11의 변위 및 응력결과분석을 통해서 반응인자인 균열발생에 바닥판 각도가 주요 설계인자임을 확인하였고, 나머지 3개의 주요설계인자의 영향성은 통계적인 분석을 통해서 확인하고자 한다.

Table 9

Simulation results for 25 cases

5.2 폭발충격해석 결과 통계적 분석

Table 6의 4개의 주요 설계인자들이 Table 8의 반응인자들에 미치는 효과를 좀 더 정확하게 분석하기 위해서 통계적인 방법인 주 효과 분석(Main Effect Analysis)과 분산분석(AVONA)을 사용하여 설계인자들의 영향성을 분석하였다. 분산분석을 수행하기 전에 확인 사항으로 본 연구에서 정의한 각 설계인자들은 실제 군용장갑차 지뢰방호 설계시 독립적인 인자로써 사용되고 있으며, 또한, 각 설계인자들의 수준 증감에 따른 각각의 반응인자들의 성능은 정규분포성과 분산의 동질성을 나타냄을 평판을 대상으로 한 지뢰폭압시험을 통해서 확인하였다.

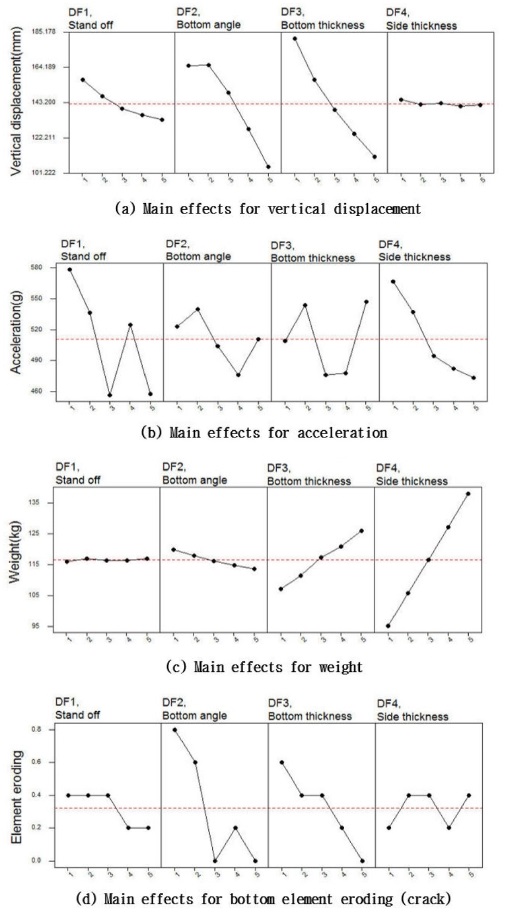
Fig. 12는 4가지 반응인자들에 대한 4가지 설계인자들의 주 효과 분석결과를 나타낸 그래프로써, 그래프의 경사가 클수록 반응인자에 큰 영향을 주는 설계인자임을 의미한다. 또, Table 10은 4가지 설계인자들의 주 효과 분석을 위한 분산분석을 수행한 결과로써, 주 효과 영향성을 F-Value 비교를 통해서 확인 할 수 있으며, F-Value가 상대적으로 큰 값이 다른 설계인자에 비해서 반응인자에 더 큰 영향을 주는 것을 의미한다. 따라서, Fig. 12의 주효과 그래프와 Table 10의 분산분석의 F-Value값을 동시에 비교하여 분석할 수 있다.

Fig. 12

Main effects analysis of 4 design parameters

Table 10

ANOVA results of 4 design parameters

Fig. 12(a)는 수직 동적변위에 대한 4가지 설계인자들의 영향성을 분석한 결과로써, 바닥판 각도(DF2)와 바닥판 두께(DF3) 그래프 경사가 가장 크고, Table 10(a)의 F-Value 결과 비교를 통해서 바닥판 두께(DF3)가 수직 동적변위에 가장 큰 영향을 주는 주효과 설계인자임을 확인할 수 있다.

Fig. 12(b)는 충격응답가속도 크기에 대한 4가지 설계인자들의 영향성을 분석한 결과로써, 지상고(DF1)와 측면판 두께(DF4) 그래프 경사가 가장 크고, Table 10(b)의 F-Value 결과 비교를 통해서 지상고(DF1)이 상대적으로 충격응답가속도에 큰 영향을 주는 설계인자임을 알 수 있다. 그러나, 충격응답가속도의 경우에는 F-Value 결과에서 보는 바와 같이 4가지 설계인자들의 영향성이 명확히 구분되지 않음을 알 수 있는데, 이것은 모든 설계인자들의 특성 보다는 설계인자들 간의 상호작용에 의한 효과가 반응인자에 더 큰 영향을 주는 것을 의미한다.

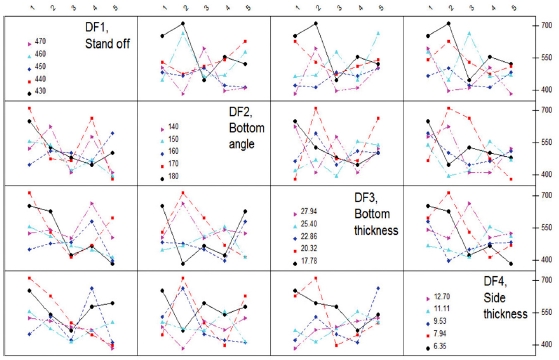
Fig. 13은 충격응답가속도에 대한 설계인자들의 교호작용(Interaction)을 분석한 결과로써, 4가지 설계인자들이 각 수준에서 대부분 서로 교차됨을 확인할 수 있는데, 결과 그래프가 서로 평행하지 않고 교차 되는 형상은 설계인자들 간의 교호작용이 발생하였음을 나타낸다. 즉, 충격응답가속도에 대한 지상고의 영향성은 바닥판 각도, 바닥판 두께, 측면판 두께 변화에 따라서 차이가 크게 발생할 수 있음을 의미한다.

Fig. 13

Interaction plot for acceleration

Fig. 12(c)는 중량에 대한 4가지 설계인자들의 영향성을 분석한 결과로써, 바닥판 두께(DF3)와 측면판 두께(DF4) 그래프 경사가 가장 크며, Table 10(c)의 F-Value 결과 비교를 통해서 측면판 두께(DF4)가 중량에 가장 큰 영향을 주는 주 효과 설계인자임을 확인 할 수 있다.

Fig. 12(d)는 방호성능 기준인 바닥판의 균열발생에 대한 4가지 설계인자들의 영향성 분석결과로써, 바닥판 각도(DF2)와 바닥판 두께(DF3) 그래프 경사가 가장 크며, Table 10(d)의 F-Value 결과비교를 통해서 바닥판 각도(DF2)가 지뢰방호성능에 가장 큰 영향을 주는 주 효과 설계인자임을 확인할 수 있다.

6. 결론

군용 장갑차 플랫폼의 지뢰방호설계에 필요한 주요 설계인자들의 폭압충격특성 연구를 위해서 TNT 6 kg 폭약을 폭발원으로 하는 폭발충격해석을 수행하였다. 폭발충격해석 수행을 위해서 해석 대상 모델과 주요 설계인자 및 수준을 선정하고, 실험계획법에 의한 실험점을 결정한 후, 총 25개의 폭발충격해석을 수행하여 지상고, 바닥판 각도, 바닥판 및 측면판 두께 등의 주요 설계인자가 수직 동적변위, 충격응답가속도, 중량 및 방호성능 등의 반응인자에 미치는 영향을 해석결과 비교 및 통계적인 분석을 통해서 다음과 같은 결론을 얻을 수 있었다.

(1) 군용 차량 차체로 사용되는 장갑판재를 대상으로 한 동일 폭발환경조건의 시험 및 해석결과 비교를 통해서 최대 수직 동적 변위의 오차율이 0.6% 수준으로써 폭발충격해석 모델의 신뢰성을 확인하였다.

(2) 반응인자인 수직 동적변위에 영향을 주는 주요 설계인자는 바닥판 두께(DF3)임을 확인할 수 있었고, 최소 변위설계를 위해서는 바닥판 두께를 증가시키는 것이 효과적임을 확인하였다.

(3) 반응인자인 충격응답가속도에 영향을 주는 주요 설계인자는 지상고(DF1)임을 확인 할 수 있었고, 최소 충격응답가속도 설계를 위해서는 지상고를 높이는 것이 효과적이나, 다른 설계인자들의 조건에 따라서 영향성이 차이가 발생할 수 있음을 확인하였다.

(4) 반응인자인 중량에 영향을 주는 주요 설계인자는 측면판 두께(DF4)임을 확인 할 수 있었고, 경량화 설계를 위해서는 측면판 두께를 조절하는 것이 더 효과적임을 확인하였다.

(5) 반응인자인 방호성능 즉, 균열발생에 영향을 주는 주요 설계인자는 바닥판 각도(DF2)임을 확인 할 수 있었고, 균열발생을 최소화 하기 위해서는 바닥판 각도를 160^o 이하로 최소화 하는 것이 효과적임을 확인하였다.

군용 장갑차 차체구조 설계시 주요 설계인자인 지상고, 바닥판 각도, 바닥판 및 측면판 두께 선정에 대한 설계기준설정은 완성차의 방호 및 기동성능을 좌우 하므로, 본 연구결과는 미래에 개발하고자 하는 지상무기 플랫폼 설계시 설계기준 설정 또는 설계 절차에 활용이 가능할 것으로 판단된다.

REFERENCES

• Yuen, S. C. K., Langdon, G. S., Nurick, G. N., Pickering, E. G., and Balden, V. H., “Response of V-Shape Plates to Localised Blast Load: Experiments and Numerical Simulation,” International Journal of Impact Engineering, Vol. 46, pp. 97-109, 2012. [https://doi.org/10.1016/j.ijimpeng.2012.02.007]
• Suhaimi, K., Risby, M. S., Tan, K. S., and Knight, V. F., “Simulation on the Shock Response of Vehicle Occupant Subjected to Underbelly Blast Loading,” Procedia Computer Science, Vol. 80, pp. 1223-1231, 2016. [https://doi.org/10.1016/j.procs.2016.05.488]
• Jiang, W., Vlahopoulos, N., Castanier, M. P., Thyagarajan, R., and Mohammad, S., “Tuning Material and Component Properties to Reduce Weight and Increase Blastworthiness of a Notional V-Hull Structure,” Case Studies in Mechanical Systems and Signal Processing, Vol. 2, pp. 19-28, 2015. [https://doi.org/10.1016/j.csmssp.2015.10.001]
• Denefeld, V., Heider, N., Holzwarth, A., Sättler, A., and Salk, M., “Reduction of Global Effects on Vehicles after IED Detonations,” Defence Technology, Vol. 10, No. 2, pp. 219-225, 2014. [https://doi.org/10.1016/j.dt.2014.05.005]
• Bobbili, R., Paman, A., Madhu, V., and Gogia, A., “The Effect of Impact Velocity and Target Thickness on Ballistic Performance of Layered Plates Using Taguchi Method,” Materials & Design, Vol. 53, pp. 719-726, 2014. [https://doi.org/10.1016/j.matdes.2013.06.005]
• Chua, M. S., Rahman, M., Wong, Y. S., and Loh, H. T., “Determination of Optimal Cutting Conditions Using Design of Experiments and Optimization Techniques,” International Journal of Machine Tools and Manufacture, Vol. 33, No. 2, pp. 297-305, 1993. [https://doi.org/10.1016/0890-6955(93)90081-5]
• Chafi, M. S., Karami, G., and Ziejewski, M., “Numerical Analysis of Blast-Induced Wave Propagation Using FSI and Alemulti-Material Formulations,” International Journal of Impact Engineering, Vol. 36, Nos. 10-11, pp. 1269-1275, 2009. [https://doi.org/10.1016/j.ijimpeng.2009.03.007]
• Neuberger, A., Peles, S., and Rittel, D., “Scaling the Response of Circular Plates Subjected to Large and Close-Range Spherical Explosions. Part I: Air-Blast Loading,” International Journal of Impact Engineering, Vol. 34, No. 5, pp. 859-873, 2007. [https://doi.org/10.1016/j.ijimpeng.2006.04.001]
• Soutis, C., Mohamed, G., and Hodzic, A., “Modelling the Structural Response of GLARE Panels to Blast Load,” Composite Structures, Vol. 94, No. 1, pp. 267-276, 2011. [https://doi.org/10.1016/j.compstruct.2011.06.014]
• Lu, Y. and Wang, Z., “Characterization of Structural Effects from Above-Ground Explosion Using Coupled Numerical Simulation,” Computers & Structures, Vol. 84, No. 28, pp. 1729-1742, 2006. [https://doi.org/10.1016/j.compstruc.2006.05.002]
• Kingery, C. N. and Bulmash, G., “Airblast Parameters from TNT Spherical Air Burst and Hemispherical Surface Burst,” US Army Armament and Development Center, Ballistic Research Laboratory, 1984.
• Baker, W. E., “Explosions in Air,” University of Texas Press, 1973.
• Johnson, G. R. and Cook, W. H., “A Constitutive Model and Data for Metals Subjected to Large Strains, High Strain Rates and High Temperatures,” Proc. of the 7th International Symposium on Ballistics, 1983.
• Vo, T. P., Guan, Z., Cantwell, W., and Schleyer, G., “Modelling of the Low-Impulse Blast Behaviour of Fibre–Metal Laminates Based on Different Aluminium Alloys,” Composites Part B: Engineering, Vol. 44, No. 1, pp. 141-151, 2013. [https://doi.org/10.1016/j.compositesb.2012.06.013]
• Kılıç, N. and Ekici, B., “Ballistic Resistance of High Hardness Armor Steels Against 7.62 mm Armor Piercing Ammunition,” Materials & Design, Vol. 44, pp. 35-48, 2013. [https://doi.org/10.1016/j.matdes.2012.07.045]
• Zukas, J. A., Nicholas, T., Swift, H. F., Greszczuk, L. B., Curran, D. R., et al., “Impact Dynamics,” Journal of Applied Mechanics, Vol. 50, No. 3, pp. 702-703, 1983. [https://doi.org/10.1115/1.3167125]
• Espinosa, H. D., Dwivedi, S., Zavattieri, P. D., and Yuan, G., “A Numerical Investigation of Penetration in Multilayered Material/Structure Systems,” International Journal of Solids and Structures, Vol. 35, No. 22, pp. 2975-3001, 1998. [https://doi.org/10.1016/S0020-7683(97)60353-4]
• Gailly, B. A. and Espinosa, H. D., “Modelling of Failure Mode Transition in Ballistic Penetration with a Continuum Model Describing Microcracking and Flow of Pulverized Media,” International Journal for Numerical Methods in Engineering, Vol. 54, No. 3, pp. 365-398, 2002. [https://doi.org/10.1002/nme.427]
• Jiang, L., Guan, M., Li, X., and Liao, H., “High Rotating Speed Projectile Penetrating into Moving Vehicle Door at Different Incident Angle,” Theoretical and Applied Fracture Mechanics, Vol. 55, No. 2, pp. 113-117, 2011. [https://doi.org/10.1016/j.tafmec.2011.04.002]
• Flores-Johnson, E., Saleh, M., and Edwards, L., “Ballistic Performance of Multi-Layered Metallic Plates Impacted by a 7.62-mm APM2 Projectile,” International Journal of Impact Engineering, Vol. 38, No. 12, pp. 1022-1032, 2011. [https://doi.org/10.1016/j.ijimpeng.2011.08.005]
• Nato Standard, “Procedures for Evaluating the Protection Level of Armored Vehicle,” AEP-55, Vol. 2, 2011.
• MIL-DTL-46100E, “Detail Specification: Armor Plate, Steel, Wrought, High-Hardness,” 2008.