다축 공작기계의 기구학 및 루프강성 해석

1. 서론

금형부품의 발달로 인해 빠른 시간 내에 다양한 재질을 가진 가공물을 가공할 필요성이 증대되고 있다. 빠른 시간 내에 복잡한 형상을 가공을 위해서는 셋업의 변화 없이 한 번에 가공이 가능한, 다축의 공작기계가 필요하게 되었다. 또한, 강도가 높은 재질의 정밀한 가공을 위해서는 기구적으로 고강성이 필요하게 되는 등 기구의 정역학적 해석의 필요성이 증대되고 있다. 예전의 직선 운동으로 구성되어 있는 공작기계의 경우 베이스에서 툴끝단까지의 관계를 나타에서 기구학 식이 단순하고, 직관적으로 구할 수 있는 경우가 많았다. 하지만, 회전축이 포함된 4축 이상의 공작기계는 수학적인 방법을 이용하여, 일반적인 기구학 및 운동학적 성능 해석을 진행하여 왔다.¹ So 등²은 수직으로 배치되는 5축 공작기계의 정기구학과 역기구학을 계산하는 알고리즘을 개발하였다. 그렇지만, 2개의 회전 운동과 3개의 직선 운동을 가지는 수직인 5축 공작기계에 대한 일반화된 역기구학 방정식을 유도한 한계를 가진다. Moon 등³은 Screw 이론을 이용하여 직렬 구조의 가변형 공작기계(RMTs)의 기구학을 계산하고, 계산 예시를 보였다. 그렇지만, 연구가 기구학 해석으로 끝났고, 강성을 포함한 동역학적 해석 등의 계산은 포함되지 않았다. Hsu 등⁴은 주어진 5축 공작기계의 포스트 프로세서를 만들기 위해, 정기구학과 역기구학 식을 계산하였다. 계산된 기구학을 바탕으로 5축 에러 모델을 만들고 보정을 통해서 에러를 줄이는 연구를 진행하였다. 이는 기구학 계산이 일반화하는데 한계를 가지며, 에러 모델 관련해서만 연구를 진행하였다. She와 Chang,⁵ Tutunea-Fatan과 Feng⁶은 3가지 대표적인 타입의 5축 가공기를 분석하는 방법을 제시하였다.

또한 기계의 성능을 평가하는 방법에 대해서도 몇몇 연구가 진행되었다. Choi 등⁷은 루프강성을 고려하여 5축 복합 가공기 구조물의 성능을 강성 측면에서 향상시켰다. 그렇지만 FEM 방식을 사용하여 모델 구성의 시간이 많이 소요되고, 주어진 모델에만 적용가능하다. Kim 등⁸은 라그랑지안 방정식을 이용하여 기구를 5개의 요소(베드, 테이블, X, Y, Z축 이송계)들로 나누고, 각각의 요소를 포함하여 루프강성 및 루프강성에 미치는 영향도를 보였다. 또한 Lee와 Ha⁹는 강체기반의 수평형 타입의 머시닝센터 3D모델을 바탕으로 구성을 최적화할 수 있는 프로그램을 개발하였다. 이들 논문에서는 정강성 등의 지표를 사용하여 모델을 해석하였지만, 주어진 모델에만 적용할 수 있는 한계를 가진다.

본 연구에서는 동차변환행렬(Homogeneous Transformation Matrix, HTM)를 활용한 정기구학 해석을 바탕으로 다양한 형상에 대한 공작기계의 기구학을 구한 후, 루프강성을 수학적 모델로 계산하였다. 상용 프로그램의 루프강성을 계산하는 방식을 사용하여, 루프강성의 수학적 모델을 검증하였다. 수학적 모델이 기존의 상용 프로그램과 1% 이하의 오차를 보임을 확인함으로써, 수학적 모델의 검증을 완료하였다.

2. 일반적인 로봇에 대한 정기구학 해석

2.1 DH 파라미터를 활용한 정기구학 해석

일반적인 로봇의 기구학 해석에는 주로 DH 파라미터 방법에 의해 구할 수 있다.¹⁰ 공작기계 내에서 공작물에서 공구에 이르는 좌표변환 행렬을 구하기 위해서는 각각의 링크에 대한 단위 좌표변환을 먼저 구한다. 이 각각의 링크 간의 좌표 변환은 식(1)과 같이 구할 수 있다.

$\[ {}_i{}^{i-1}T=Rot\left(X_{i-1},{\alpha }_{i-1}\right)Trans\left(X_{i-1},a_{i-1}\right)Rot\left(Z_i,{\theta }_i\right)Trans\left(Z_i,d_i\right) \]$

(1)

여기서, Rot(X,a)는 X축에 대한 각도 a만큼의 회전 변환 행렬, Trans(X,a)는 X축에 대한 거리 a만큼의 직선 이송 변환 행렬, α_i-1는 X_i-1축에 대한 Z_i-1축과 Z_i축 사이의 각도, a_i-1는 X_i-1축을 따라 측정한 Z_i-1축과 Z_i축 사이의 거리, θ_i는 Z_i-1축에 대한 X_i-1축과 X_i축 사이의 각도, d_i는 Z_i-1축을 따라 측정한 X_i-1축과 X_i축 사이의 거리를 각각 나타낸다.

공작물에서 공구에 이르는 전체 변환 행렬은 각각의 링크 간의 좌표변환 행렬의 순차적인 곱으로 표현이 가능하다.

$\[ {}_n{}^{0}T={}_1{}^{0}T{}_2{}^{1}T\cdots {}_n{}^{n-1}T \]$

(2)

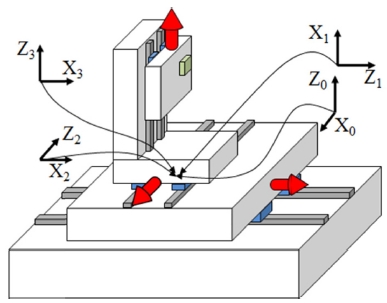
그렇지만, 공작기계에서 DH 파라미터 방법을 사용하기 위해서는 축을 잘 선택해야 하는 번거로운 점이 있다. DH 파라미터에서 축의 이송방향을 Z축으로 고려하고, Z_i-1축과 Z_i축 사이의 관계를 이용하여, X_i-1축을 정의하는 과정을 거쳐야 한다. 일반적으로 X_i-1축은 Z_i-1축과 Z_i축에 각각 수직이 되는 직선으로 선택되며, Z_i-1축과 Z_i축이 교차하는 경우에는 Z_i-1축과 Z_i축이 이루는 면에 수직하게 선택된다. 이로 인해 Fig. 1에서 보는 바와 같이 Z축이 변함에 따라 X축이 다양하게 변한다. 또한 Table 1에서 보는 바와 같이 90도 각으로 좌표축 변환이 많이 필요함을 확인할 수 있다.

Fig. 1

Axis definition for three axis machine (XYZ)

Table 1

DH parameter for three axis machine (XYZ)

로봇과는 달리 공작기계는 주로 직교 좌표형태로 움직이고 평행한 축이 거의 없다. 움직임 축을 Z방향으로 선정하는 DH 파라미터 방법은 X축 선정 및 축변환 과정에 있어서 직관적으로 선택하기 힘들다. 또한 직관적이지 못하기 때문에 사용자가 축을 선택하는데 있어 주의를 요하는 단점이 있다. 특별한 경우(X₀', Y₀', Z₀')을 기준 축으로 설정하는 경우 기구학을 풀지 못하는 한계점을 지닌다. 이를 위해서 직관적으로 축 설정이 가능하고, 직교 좌표형태의 구조를 표현하기 쉬운 HTM 방식을 좌표 변환에 활용하고자 한다.

2.2 HTM을 활용한 정기구학 해석 정리

HTM을 활용한 정기구학 해석 방법론에 대해서 제안하고자 한다. 먼저 T_i-1 좌표계와 T_i 좌표계의 두 좌표계 간 상대거리를 구한 후, T_i 좌표계 내에서의 기구 운동을 표현함으로써 두 좌표계 사이의 좌표변환을 계산한다. T_i-1 좌표계와 T_i 좌표계 사이의 상대값을 표현하는 방법은 다음과 같다. 두 좌표간의 원점의 상대거리를 X_i-1, Y_i-1, Z_i-1 방향에 대해서 각각 dx_i-1, dy_i-1, dz_i-1로, X_i-1, Y_i-1, Z_i-1 방향에 대한 각도 변화를 각각 dA_i-1, dB_i-1, dC_i-1로 나타내면 상대 거리 HTM은 다음 식(3)과 같다.

$\[ \begin{array}{c}{}_i{}^{i-1}T=\left[\begin{array}{cccc}1& 0& 0& d{x}_{i-1}\\ 0& 1& 0& d{y}_{i-1}\\ 0& 0& 1& d{z}_{i-1}\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}cd{A}_{i-1}& -sd{A}_{i-1}& 0& 0\\ sd{A}_{i-1}& cd{A}_{i-1}& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\\ \left[\begin{array}{cccc}cd{B}_{i-1}& 0& sd{B}_{i-1}& 0\\ 0& 1& 0& 0\\ -sd{B}_{i-1}& 0& cd{B}_{i-1}& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& cd{C}_{i-1}& -sd{C}_{i-1}& 0\\ 0& sd{C}_{i-1}& cd{C}_{i-1}& 0\\ 0& 0& 0& 1\end{array}\right]\end{array} \]$

(3)

T_i좌표계 내에서의 기구 운동은 다음과 같이 표현된다. X_i, Y_i, Z_i 방향의 직선 이송을 각각 x_i, y_i, z_i로, X_i, Y_i, Z_i 방향에 대한 각도 변화를 각각 A_i, B_i, C_i로 나타내면 운동 관련 HTM은 다음 식(4)와 같다.

$\[ T_{im}=\left[\begin{array}{cccc}1& 0& 0& x_i\\ 0& 1& 0& y_i\\ 0& 0& 1& z_i\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& c{A}_i& -s{A}_i& 0\\ 0& s{A}_i& c{A}_i& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}c{B}_i& 0& s{B}_i& 0\\ 0& 1& 0& 0\\ -s{B}_i& 0& c{B}_i& 0\\ 0& 0& 0& 1\end{array}\right]\left[\begin{array}{cccc}c{C}_i& -s{C}_i& 0& 0\\ s{C}_i& c{C}_i& 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right] \]$

(4)

일반적인 기구 운동의 경우, 6축의 운동이 아닌 1축의 운동으로 표현되고, 나머지 변수는 0으로 된다.

운동을 포함한 T_i-1 좌표계와 T_i 좌표계의 두 좌표계 간 상대 변환은 다음 식(5)와 같다.

$\[ {{}_i{}^{i-1}T}_m={}_i{}^{i-1}T\times T_{im} \]$

(5)

이 관계를 이용해 베이스에서 끝단까지의 관계는 행렬을 순차적으로 곱함으로써 구할 수 있다.

$\[ {{}_n{}^{0}T}_m={{}_1{}^{0}T}_m{{}_2{}^{1}T}_m\cdots {{}_n{}^{n-1}T}_m \]$

(6)

Fig. 1에 나타난 공작기계를 HTM 방식으로 나타내면 다음과 같다(Table 2). 이 때는 각 축간의 좌표계를 맞추기 위해 불필요하게 계산했던 다수의 90도의 회전을 사용하지 않고도 축 표현이 가능하다.

Table 2

HTM parameter for three axis machine (XYZ)

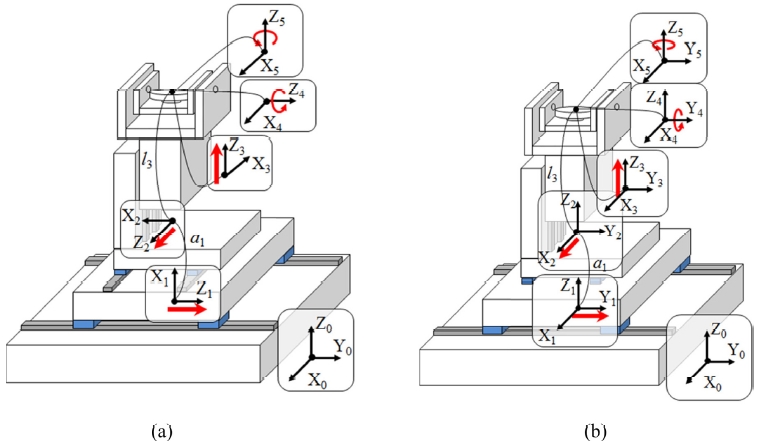
다른 예로, Fig. 2에서와 같이 회전을 포함한 5축의 시리얼 조합(Y-X-Z-B-C)에 대해서 HTM 방식을 활용하여 정기구학을 계산한 결과는 다음과 같다.

Fig. 2

Axis assignment by using DH parameter (a) and HTM (b)

두 관계식은 같은 결과를 나타내지만, 축 선정에 있어서도 DH 파라미터를 이용하면 복잡한 규칙에 의거하여 Z축 및 X축을 유의하여 설정해야 한다. 반면에 HTM 방식을 사용할 때에는 직관적으로 회전 축과 직선 축을 정의해줄 수 있다. 축설정이 복잡하기 때문에, Table 3에서와 같이 DH 파라미터를 이용한 관계식에는 단순한 좌표 변환을 위해 많은 회전이 포함되어야 하지만, HTM 방식을 사용할 때에는 불필요한 회전 부분을 생략할 수 있다(Table 4). 이로 인해 HTM 방식을 사용하는 경우 축 선정의 편의성을 가질 수 있고, 일관성 있는 축 선정도 가능하다.

Table 3

DH parameter for three axis machine (YXZBC)

Table 4

HTM parameter for three axis machine (YXZBC)s

3. 루프강성 계산

3.2 루프강성 물리적 검증 모델

앞장에서 제시한 수학적 모델을 검증하기 위해 MATLAB의 Simmechanics를 이용하여 물리적 모델링을 구성하였다. Simmechanics는 3D 기계 시스템에 대한 다물체동역학 시뮬레이션을 구현할 수 있는 모델링 툴이다. 강체 바디와 조인트 구속조건, 힘 요소에 대한 블록을 활용하여 멀티 바디 시스템을 구현하고, Simmechanics 내의 수식을 바탕으로 기계시스템의 모션 방정식을 풀 수 있다.

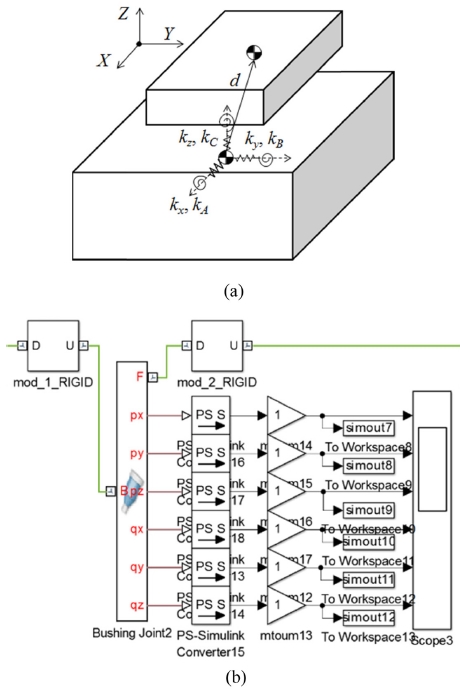
먼저 운동을 하는 각각의 강체를 스프링으로 연결하고, 이렇게 연결된 모듈을 적층함으로써 전체 기구 구성을 완성한다. 2개의 유니트 강체를 연결하기 위한 입력 조건은 다음과 같다. 먼저 X, Y, Z 각 선형 강성을 k_x, k_y, k_z로 정의하고, 회전 강성을 k_A, k_B, k_C로 정의했다. 그리고 각 유니트별 무게 중심 간의 거리를 d로 표현하였다. 이를 두 유니트간의 관계를 물리적 모델로 표현하면 다음과 같다. 물리적 모델링은 각 유니트 강체 사이에 6자유도 조인트 블록을 연결하고, 각각의 6자유도 강성 및 유니트 강체간의 무게중심 거리를 입력하면 물리적 모델을 완성할 수 있다. 추가적으로 각각의 강성에 해당하는 변위를 보기 위해 추가적인 결과 뷰어를 연결할 수 있다(Fig. 3).

Fig. 3

Stiffness configuration (a) and physical unit and joint modeling (b) of two rigid bodies

전체 기구구성을 위해서는 각각의 유니트 강체를 적층해야 한다. 2개의 유니트 강체를 연결하는 방법으로 나머지 운동하는 강체를 연결하여 전체 기구 구성을 완성하였다. 기구부의 베이스와 툴 끝단에는 외력을 입력하는 블록과 변위를 측정하는 모듈을 추가하여, 외력에 대한 변위를 측정할 수 있다.

3.3 루프강성 시뮬레이션

이 장에서는 앞장에서 만든 물리적 모델을 활용하여 수학적 모델의 타당성을 검증하고자 한다. 수학적 모델의 타당성을 검증하기 위해서 Y축 이송 스테이지 위에 Z축 및 Y축으로 회전하는 3축의 모델을 활용하였다. 물리적 모델은 유니트와 조인트의 적층된 형태의 모듈로 구성하였다. Table 5에는 각각의 조인트에 대해서 입력된 6자유도 강성과 각각의 유니트간의 상대 거리를 표시하였다. 또한, 외력을 입력으로 가할 수 있게 하였고, 결과로 변위를 확인할 수 있는 시스템으로 시뮬레이션을 구현하였다. 변위를 비교한 결과 본 논문에서 제시한 수학적 모델과 비교를 위한 물리적 모델의 최대 차이는 0.69%로 나타남을 확인할 수 있었다(Table 6). 이는 선형화 과정에 있어서 오차로 보이며, 수학적 모델을 활용해도 정확한 결과를 얻을 수 있음을 확인할 수 있었다.

Table 5

Input parameters for the simulation of physical model

Table 6

Simulation result of physical modeling

4. 루프강성 해석 적용 예

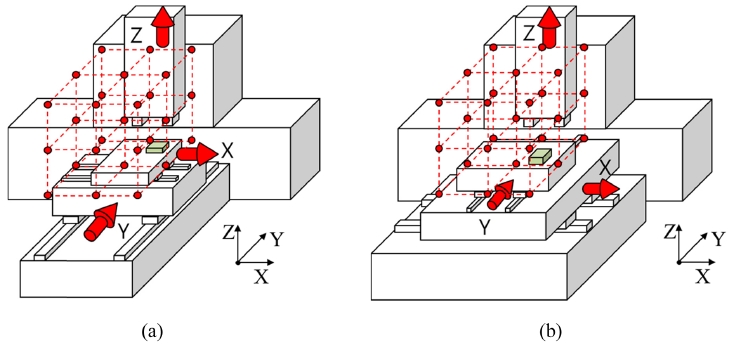
루프강성 계산을 활용하면 개념설계 단계에서 더 좋은 강성의 공작기계 구성을 선정할 수 있다. 본 논문에서 개발한 강성해석 방법론을 바탕으로 작업영역이 같지만 축 구성이 다른 두 개의 공작기계의 루프강성을 비교해 보고자 한다. 베이스를 중심으로 수평으로 XY축을 움직이는 공작물부분과 Z축을 움직이는 툴부분으로 구성된 2개의 수직형 공작기계를 비교하였다. 베이스를 기준으로 Y축 위에 X축을 적층한 구조를 모델 1, 베이스를 기준으로 X축 위에 Y축을 적층한 구조를 모델 2라고 정의한다(Fig. 4). 즉 모델2는 모델1의 XY 스테이지를 Z축을 중심으로 90도 회전한 형태이다.

Fig. 4

Schematics of test model 1(a) and model 2(b)

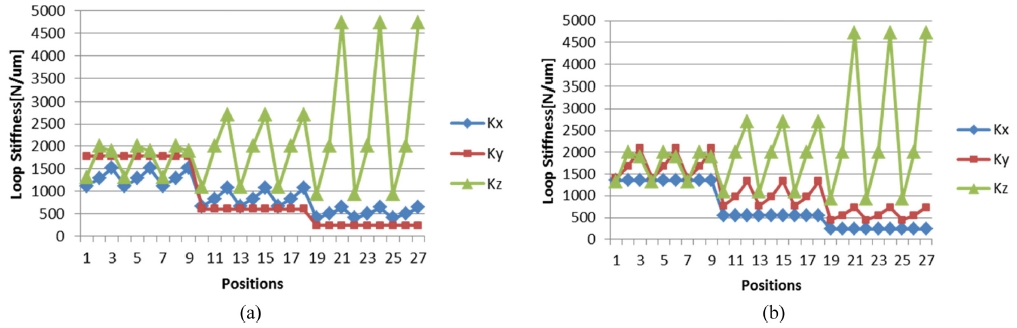
각각 공작기계의 구체적인 파라미터는 Table 7-10에 표시하였다. 두 개의 모델은 동일한 스트로크, 유니트 강성 값을 가지게 했다. 작업영역은 X, Y, Z축 각각 홈 위치와 양쪽 스트로크 끝 부분을 고려하여 총 27개의 위치로 정의하였다. 특히 XY 스테이지 위의 오프셋된 점들에서의 하중도 고려할 수 있기 때문에, Z축의 이송에 대한 작용점 변화도 고려된 것이다. 각각의 점에 대해서 X, Y, Z 방향으로 강성을 계산하였고, 강성이 최소가 되는 점을 각각 비교하였다.

Table 7

Stiffness and stroke of each unit

Table 8

HTM parameter for YX axis (Model 1) [mm]

Table 9

HTM parameter for XY axis (Model 2)[mm]

Table 10

HTM parameter for Z axis (Model 1, Model 2)[mm]

그 결과 모델 1의 최소 루프강성은 246 N/um, 모델 2는 최소 루프강성이 236 N/um로 나타남을 확인하였다(Fig. 5). 동일한 파라미터 값을 넣었을 때, YX 스테이지 위에 공작물을 올려놓은 경우가 XY 스테이지 위에 공작물을 올려 놓은 경우보다 최소 루프강성이 4% 증가되어 나타남을 확인할 수 있다.

Fig. 5

Loop stiffness results of model 1(a) and model 2(b)

5. 결론

HTM 방식을 이용하여, 일반화된 공작기계에 적용할 수 있는 정기구학을 구하는 방법을 제시하였다. 루프 강성에 대해서 수학적 모델을 완성하고, 물리적 모델로 검증한 결과 1% 미만의 정확도를 가지는 것을 확인하였다. 각각의 유니트 강성들의 조합으로 전체 루프 강성을 구현하는 기구 모델을 설계함으로써, 루프강성을 수학적 모델로 구현할 수 있음을 보였다. 또한 관계식을 활용하여, XYZ 3축으로 구성된 공작기계의 루프강성을 비교하여, YX 스테이지를 활용한 경우가 4% 정도의 루프강성 증대 효과가 나타남을 확인하였다. 추후 역으로 전체 강성에 대해 각 유니트별 필요 강성을 구하는 역설계 모델을 제작할 예정이다. 루프 강성 분배 모듈을 활용하여 기준 모델을 바탕으로 사용자가 정의한 전체 루프 강성을 구현하기 위해 필요한 각각의 유니트 강성을 분배하는 기술을 구현할 예정이다.

REFERENCES

• Park, C.-H., Hwang, J.-H., Lee, C.-H., and Song, C.-G., “Development of an Accuracy Simulation Technology for Mechanical Machines,” Journal of the Korean Society for Precision Engineering, Vol. 28, No. 3, pp. 259-264, 2011.
• So, B.-S. and Jung, Y.-H., “Inverse Kinematics for Five-Axis Machines Using Orthogonal Kinematics Chain,” Korean Journal of Computational Design and Engineering, Vol. 13, No. 2, pp. 153-161, 2008.
• Moon, Y. and Kota, S., “Generalized Kinematic Modeling Method for Reconfigurable Machine Tools,” ASME Journal of Mechanical Design, Vol. 124, No. 1, pp. 47-51, 2002. [https://doi.org/10.1115/1.1424892]
• Hsu, Y. Y. and Wang, S. S., “A New Compensation Method for Geometry Errors of Five-Axis Machine Tools,” International Journal of Machine Tools and Manufacture, Vol. 47, No. 2, pp. 352-360, 2007. [https://doi.org/10.1016/j.ijmachtools.2006.03.008]
• She, C.-H. and Chang, C.-C., “Design of a Generic Five-Axis Postprocessor Based on Generalized Kinematics Model of Machine Tool,” International Journal of Machine Tools and Manufacture, Vol. 47, Nos. 3-4, pp. 537-545, 2007. [https://doi.org/10.1016/j.ijmachtools.2006.06.002]
• Tutunea-Fatan, O. R. and Feng, H.-Y., “Configuration Analysis of Five-Axis Machine Tools Using a Generic Kinematic Model,” International Journal of Machine Tools and Manufacture, Vol. 44, No. 11, pp. 1235-1243, 2004. [https://doi.org/10.1016/j.ijmachtools.2004.03.009]
• Choi, Y. H., Jang, S. H., Kim, I. S., Cho, Y. J., and Oh, C. W., “Structural Layout Design Alternative of a 5-Axes Multi-Tasking Machine Considering Loop Stiffness,” Proc. of the Korean Society of Manufacturing Technology Engineers Spring Conference, pp. 226-231, 2006.
• Kim, S. U., Jeon, K. M., Kim, J. Y., and Yang, M. Y., “Study on the Evaluation of Machine Tools Design by Lagrangian,” Proc. of the Korean Society of Manufacturing Technology Engineers Spring Conference, pp. 9. 2010.
• Lee, C. H. and Ha, J. Y., “Development of Simulator for Optimal Machine Tools Configuration,” Proc. of the KSPE Autumn Conference, 307-308, 2010.
• Craig, J., “Introduction to Robotics: Mechanics and Control,” Addison-Wesley, 1989.
• Yan, R., Peng, F., and Li, B., “A Method of General Stiffness Modeling for Multi-Axis Machine Tool,” Proc. of International Conference on Intelligent Robotics and Applications, pp. 1013-1021, 2008. [https://doi.org/10.1007/978-3-540-88518-4_108]