메탈 그리드 유연 투명 전극의 그리드 형태에 따른 유연 신뢰성 연구
1서울과학기술대학교 일반대학원 스마트생산융합시스템공학과2서울과학기술대학교 나노IT디자인융합대학원
2Graduate School of Nano IT Design Fusion Technology, Seoul National University of Science and Technology
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Recently, the metal grid electrode drew attention as a flexible transparent conductive electrode for touch screen panels. In metal grid electrodes, various shapes of grid patterns were used to avoid the moiré phenomenon. In this study, we investigated the effects of the metal grid shapes - such as the honeycomb, diamond, and square - on the flexibility and durability of the metal grid film using an experimental and numerical analysis. The flexibility of the metal grid film was evaluated via the following: bending, cyclic bending fatigue and stretching tests; it was compared with the numerical stress analysis. In the bending test, the resistance of the honeycomb grid sample increased by 10% at a bending radius of 10 mm. On the other hand, the diamond grid showed almost no change in resistance up to a bending radius of 6 mm. When the substrate was stretched to 5%, many cracks appeared on the surface of the honeycomb pattern sample. On the other hand, no cracks were found in the diamond pattern sample. Therefore, the diamond pattern exhibited superior flexibility and durability to the honeycomb pattern. The numerical stress analysis also showed that the honeycomb pattern had the highest stress and the diamond pattern had the lowest stress during bending and stretching, which corresponded with the experimental results.
Keywords:
Flexible transparent electrode, Metal grid, Flexible durability, Bending, Stretching키워드:
유연 투명 전극, 메탈 그리드, 유연 내구성, 굽힘, 인장1. 서론
최근 플렉서블 반도체 및 플렉서블 디스플레이, 플렉서블 터치 센서 등과 같은 유연전자(Flexible Electronics) 기술에 대한 관심이 크게 증대되고 있다.1 유연전자소자를 개발함에 있어서 가장 중요한 재료는 투명전극(Transparent Conductive Electrode)이다. 투명전극의 특성은 전자소자의 성능에 큰 영향을 미치며, 적용하는 소자의 종류에 따라 각기 다른 특성이 요구된다. 현재 가장 많이 사용되고 있는 투명전극은 ITO (Indium Tin Oxide) 이다. 인듐 주석 산화물인 ITO는 높은 투과도와 근적외선 반사도, 우수한 전기 전도도, 화학적 안정성과 우수한 식각 특성을 가지고 있어 투명전극으로 가장 널리 이용되고 있다.2 그러나 ITO는 소재의 희소성과, 고온의 제작 공정에 문제가 있다. 특히 ITO는 매우 Brittle하며, 기계적 유연성에 매우 취약하다. 따라서 기판을 굽히거나, 인장하였을 경우 ITO에 크랙이 쉽게 발생한다.3 ITO에 발생된 크랙은 쉽게 전파되어 주변의 박막 혹은 소자의 크랙을 발생시켜 소자의 파괴를 초래한다. 현재까지의 연구 결과, ITO 박막은 약 0.8-1.2%의 인장 응력에 파괴된다고 보고되고 있다.4,5 따라서 유연전자 소자의 개발에서 투명전극의 유연성 및 신뢰성 확보는 매우 중요한 요소이다.
기존의 ITO를 대체하기 위하여 Carbon Nanotubes,6 Graphenes,7 Conductive Polymers8 및 Silver Nanowires (AgNWs)9 같은 다양한 재료가 차세대 유연투명전극으로 개발되었다. 이러한 재료들 중에서 메탈 그리드(Metal Grid) 혹은 메탈 메쉬(Metal Mesh) 전극은 낮은 면저항과 롤투롤(Roll-to-Roll) 및 잉크젯 프린팅과 같은 다양한 프린팅 기술을 사용하여 비교적 간단하게 제작이 가능하다는 장점으로 인하여 많은 주목을 받고 있다. 또한 메탈 그리드 전극은 메탈 그리드의 선폭(Line Width) 및 피치(Pitch)를 변경함으로써 면저항 및 투과도 등을 손쉽게 조절할 수 있는 장점이 있다.10,11 메탈 그리드를 이용한 투명전극을 제작하는 방법은 다양하게 개발 및 발전되고 있다. Yu12 등은 Nanoimprint와 Rollto-Roll (R2R) 공정을 이용하여 메탈 그리드를 제작하였다. 니켈을 이용한 스탬프를 제작하여 유연 기판 위에 선폭 10 μm, 피치가 510 μm인 메탈 그리드 패턴을 구현하였다. Jin13 등은 포토리소그래피를 이용하여 메탈 그리드를 제작하였다. 마스크와 UV를 이용하여 메탈 그리드의 패턴을 형성한 후에, UV를 조사한 부분을 에칭을 통해 제거하여, 무전해도금 방식으로 구리를 채우는 방식을 개발하였다. Kang14 등은 유리 기판을 사용하여 메탈 그리드를 제작하고 폴리머 기판에 전사하는 Transfer Printing 기술을 이용하여 유연 기판에 메탈 그리드 패턴을 형성하였다. Kahng15 등은 메탈 메쉬와 그래핀을 합성하여 메탈 그리드를 제작하였다. 최근에는 Electrohydrodynamic (EHD) 잉크젯 프린팅 기술이 활발하게 적용되고 있다.16 EHD 잉크젯 프린팅 방법은 기존의 잉크젯 프린팅 방법에 비하여 달리 직경이 수십 μm인 노즐을 통하여 전기를 인가하면서 전극을 제작하기 때문에 10 μm 이하의 미세 선폭을 구현할 수 있다.
한편 메탈 그리드 투명전극은 시인성과 모아레(Moiré) 현상이 단점으로 지적되고 있다.17 시인성이란 완성된 제품 구현 시 메탈 그리드 패턴이 눈에 보이는 현상인데, 이는 메탈 그리드의 반사율 때문이다. 모아레 현상이란 메탈 그리드 패턴이 겹쳐지면서, 여기에 디스플레이의 격자 무늬가 더해져서 물결처럼 보이는 현상이다. 이를 해결하기 위한 방안으로 시인성 문제는 메탈 그리드의 선폭(두께)을 3 μm 미만으로 미세화 시킴으로써 해결할 수 있다. 또한 모아레 현상에 대한 문제는 메탈 그리드 패턴의 형상을 변경시킴으로써 해결할 수 있다. 특히 최근 모아레 현상을 해결하기 위하여 다양한 형태의 메탈 그리드 패턴에 대한 연구가 진행되었다. 메탈 그리드는 주로 정사각형 형태의 패턴이 주로 사용되고 있으나, 모아레 현상을 감소시키기 위해서 허니컴(Honeycomb) 구조 등 다양한 패턴에 대한 연구가 최근 수행되었다.17-19 Shin20 등은 말발굽(Horseshoe), 랜덤(Random), 정사각형 형태의 메탈 그리드를 제작하여 메탈 그리드 형태에 따른 모아레 현상을 관찰하였다. Wei21 등은 삼각형, 정사각형 및 육각형(Hexagon) 형태의 메탈 그리드 패턴을 제작하여 전기적 및 광학적 특성을 비교분석하였다. Hong 22 등은 삼각형, 정사각형, 허니컴 구조 패턴의 메탈 그리드에 대해서 레이저 경화 공정의 영향에 대한 연구를 수행한 바 있다.
메탈 그리드를 이용한 투명전극의 연구는 주로 재료의 개발 및 공정 기술에 초점을 맞추고 있다. 유연전자소자는 제조 공정, 취급 및 소비자 사용 과정에서 굽힘(Bending), 인장(Stretching) 및 Twisting 등 다양한 응력을 받게 되며 신뢰성 및 내구성에 대한 연구가 필수적이다. 그러나 현재까지 메탈 그리드의 다양한 기계적 응력에 대한 유연성 및 신뢰성에 대한 데이터는 미흡한 실정이다. 특히 다양한 형태의 패턴을 갖는 메탈 그리드의 유연성 및 내구성에 대한 연구는 거의 없다. 머지않아 접을 수 있는 폴더블(Foldable) 스마트폰 및 폴더블 전자소자가 출현할 것으로 기대되고 있다. 폴더블 전자소자의 경우 곡률 반경이 5 mm 이하 혹은 3 mm 이하가 될 것이며, 이때 메탈 그리드 전극에 작용하는 응력은 매우 클 것이다. 따라서 메탈 그리드 패턴에 따른 유연 신뢰성 연구가 필요할 것으로 사료된다.
따라서 본 연구에서는 현재 사용 중이거나, 사용이 고려되고 있는 대표적인 메탈 그리드 패턴인 정사각형 패턴, 다이아몬드 패턴 및 허니컴 패턴 전극에 대해서 굽힘, 굽힘 반복 피로 및 인장 실험을 수행하여 유연 내구성을 평가하였으며, 또한 수치해석에 의한 응력 해석을 통하여 각 패턴의 유연 내구성을 비교 평가하였다.
2. 제작 공정 및 실험 방법
2.1 메탈 그리드 필름 제작
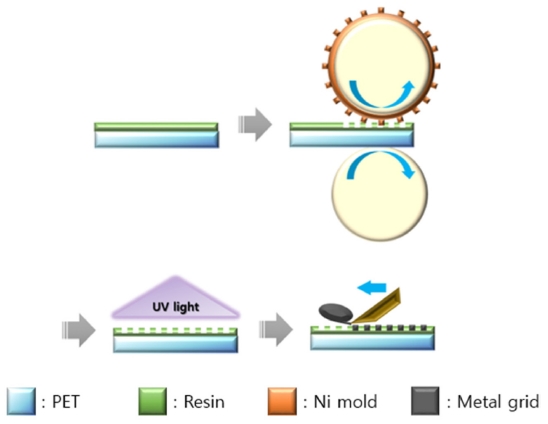
메탈 그리드 전극이 형성된 필름은 A사에서 롤-임프린팅(Roll-Imprinting) 공정을 이용하여 제작되었다. 롤-임프린팅 공정은 마이크로/나노 구조물을 효과적으로 형성할 수 있는 기술로서 기판 위에 코팅된 레진(Resin) 또는 포토레지스트(Photoresist)를 코팅한 후, 패턴이 형성된 몰드를 물리적으로 접촉시켜, 압력을 가해 주고 자외선(UV Light)을 통해 경화시켜 패턴을 복제하는 기술이다. 롤을 기반으로 한 임프린팅 공정은 연속적인 공정이 가능하므로 마이크로/나노 구조물을 대량 생산하기에 매우 효과적인 장점을 가지고 있다. Fig. 1은 유연 기판 위에 메탈 그리드 필름이 제작되는 과정을 도식적으로 나타낸다. 본 연구에서는 투과율이 높고 유연성이 좋은 두께 125 μm의 Polyethylene Terephthalate (PET) 기판을 사용하였다. PET 기판 위의 메탈 그리드 패턴은 유연 스탬프 몰드를 사용하여 패턴하였다. 유연 스탬프 몰드는 Ni (Nickel) 기판을 Electroforming 공정을 이용하여 제작하였으며, 제작된 Ni 기판을 롤에 감았다. PET 기판 위에 UV 레진을 도포시킨 후, 양각 패턴이 되어있는 유연 스탬프 몰드를 이용하여 압력을 가해 레진에 음각 패턴을 형성시켰다. 이후 자외선을 조사하여 레진층이 단단해지도록 경화시켰다. 패턴이 형성된 레진 안에는 Doctor Blade를 이용하여 실버 페이스트(Ag Paste)를 충진한 후, 레진 표면에 남아있는 잔여 페이스트를 세척 시켜주었다. 그 다음 메탈 그리드 필름을 오븐에서 140oC로 경화시키면, 메탈 그리드 전극이 완성된다. 실버 페이스트는 약 ~30 nm 크기의 Ag 나노입자들로 구성되어 있으며 Ag의 양은 약 85%이다. 제작된 메탈 그리드 전극의 선폭 및 두께는 각각 약 10 μm이며, 허니컴과 다이아몬드 패턴으로 각각 제작되었다. 좀더 자세한 공정 조건 등에 대해서는 회사의 보안사항이라 공개하기가 어려웠다.
2.2 실험 방법
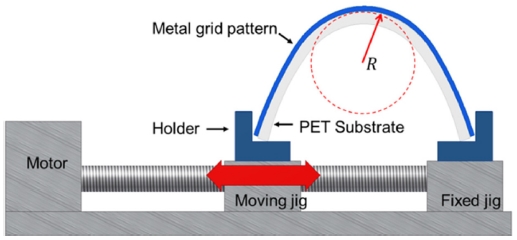
제작된 메탈 그리드 필름의 전기적 특성을 분석하기 위하여 4 Point Probe를 이용하여 면저항(Sheet Resistance)을 측정하였으며, 면저항 측정 시, 오차 범위를 줄이기 위해 총 5 번을 측정하여 평균값을 이용하였다. 메탈 그리드 전극의 광학적 특성으로서 UV–Visible Spectrophotometer (Cary 5000)를 사용하여 투과율(Transmittance)을 측정하였으며, 측정 시 파장은 가시광선 영역의 555 nm 에서 측정하였다. 메탈 그리드 필름의 유연성은 굽힘 시험, 굽힘 반복 피로 시험(Cyclic Bending Fatigue Test) 및 인장 시험을 통하여 평가하였다. 시험은 자체 제작한 굽힘 시험기(Bending Tester) 및 인장 시험기(Stretching Tester)를 이용하여 평가하였다. Fig. 2는 굽힘 시험기를 도시적으로 나타내고 있다. 굽힘 시험기의 시험 방법은 Convex 형태(∩)로 굽혀 시험하였으며, 이때 메탈 그리드 전극에는 인장 응력이 작용하게 된다. 굽힘 시험에서는 시편의 전체 길이 L을 변화시킴으로써 곡률반경을 변화시켰다. dL 만큼 변화시켰을 때 발생되는 곡률 반경(r)은 아래의 식(1)로 계산되었으며23
| Bending radius(r)=L2π√dLL-π2h2s12L2 | (1) |
여기서 L, dL/L 그리고 hs는 기판의 초기 길이, 기판의 전체 길이에 대한 기판의 이송거리, 그리고 기판의 두께를 각각 나타낸다. 한편 기판이 굽혀졌을 때 메탈 그리드 전극에서 발생하는 굽힘변형율(Bending Strain, ε)은 다음 식(2)와 같이 계산된다.
| ε = hs2r | (2) |
본 연구에서 사용된 굽힘 시험기에 대한 자세한 설명은 참고문헌에 기술되어 있다.24 굽힘 반복 시험은 시편이 굽혀지지 않은 상태에서 일정 곡률 반경까지 주기적으로 반복된 굽힘 변형을 주어 누적된 응력 피로에 의한 메탈 그리드 필름의 유연성 및 신뢰성을 확인할 수 있는 시험이다. 본 연구에서는 곡률 반경을 15 mm로 고정한 후, 샘플을 평평한 상태(곡률 반경은 ∞)에서 곡률 반경 15 mm까지 10,000 사이클을 반복적으로 굽혀 실험하였다. 굽힘 시험에 사용된 샘플의 크기는 25 mm × 25 mm이다. 시험은 샘플의 양단에 Ag 페이스트와 도선을 연결하여 2 point 탐침법으로 멀티미터(34401A, Agilent사)를 사용하여 실시간으로 전극의 저항 변화를 관찰하였으며, 동시에 광학현미경으로 전극 표면의 파괴 혹은 크랙 유무를 관찰하였다. 저항이 급격히 크게 변하거나, 전극의 표면에 크랙이 발생할 경우, 혹은 전극이 파손된 시점을 파괴 시점이라고 간주하고 시험을 중단하였다. 또한 Field Emission Scanning Electron Microscope (FE-SEM, Nova 200)을 이용하여 메탈 그리드 필름 표면의 크랙을 관찰하였다. 굽힘 시험은 각 시편에 대해서 각각 4번 수행하였다.
3. 유한요소해석
3.1 유한요소 모델링
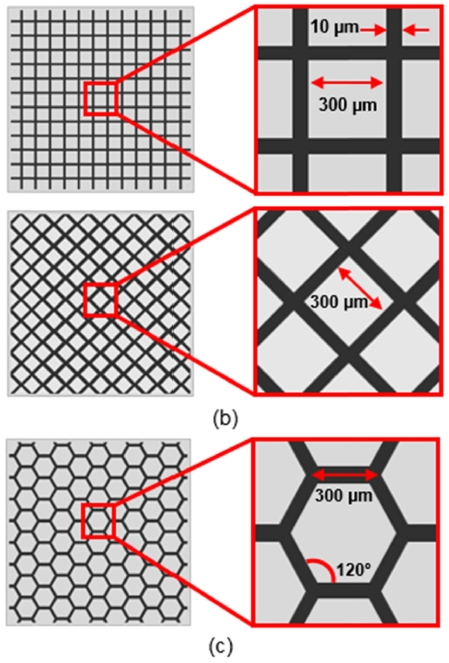
Fig. 3은 유한요소해석에 사용된 메탈 그리드의 패턴 구조에 따른 개념도이다. 각각의 패턴 구조에 따른 응력 분포의 차이를 예측하기 위해 정사각형 패턴, 다이아몬드 패턴, 허니컴 패턴의 세 종류로 구분하여 모델링 하였다. 해석에 사용된 메탈 그리드의 기본 구조는 PET 기판과 메탈 그리드로 구성되어 있다. 메탈 그리드패턴들의 선폭은 실험 샘플과 동일하게 10 μm로 모델링 하였으며, 패턴 사이의 간격 즉 피치는 300 μm로 일정하게 모델링하였다. 또한 메탈 그리드패턴들은 PET 기판에 음각의 형태로 임베디드(Embedded) 되어 있는 구조이다.
3.2 유한요소 해석 조건
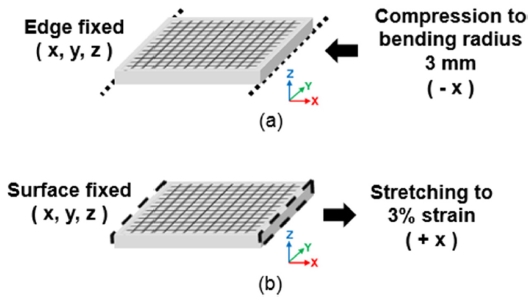
수치 해석은 범용 해석 프로그램인 ANSYS를 사용하여 유한요소해석을 수행하였으며, 해석 모델 모두 20절점 3차원 요소인 SOLID186을 사용하였다. 정사각형 패턴 모델의 경우 요소(Element)의 개수는 910,706개, 절점(Node) 수는 312,230개이다. 전술한 세 종류 모델에 대해서 굽힘 및 인장 시의 응력을 해석하였으며, 변위 및 경계 조건은 Fig. 4에 표시하였다. 굽힘 해석의 경우, 기판의 양쪽 끝 중, 한쪽 기판의 밑면 모서리를 모두 구속하고 반대쪽 기판의 밑면 모서리를 X 축 압축 방향으로 기판의 곡률반경이 3 mm가 되는 지점까지 구부려 진행하였다. 인장 해석의 경우, 변위 경계 조건은 기판의 양쪽 끝 면 중 한쪽 면에 대해 Global Coordinate X, Y, Z 축의 원점을 모두 구속하고, 반대쪽 면을 X 축으로 인장하여 기판의 변형율이 3%가 되도록 인장시켰다. 유한요소해석에서 사용된 각 재료의 물성은 탄성 영역 내에 있다고 가정하였으며, 기존 문헌에서 사용된 대표값을 사용하였다.25,26 PET 기판과 Ag 재료의 탄성계수 및 푸아송비(Poisson’s Ratio)는 각각 4 GPa, 0.35 및 82.5 GPa, 0.36이다.
4. 결과 및 고찰
Fig. 5는 실험에 사용된 허니컴 패턴 및 다이아몬드 패턴의 메탈 그리드 유연투명전극의 현미경 사진이다. 메탈 그리드 간의 간격(피치)는 허니컴 패턴의 경우, 평균적으로 약 300-400 μm이며, 다이아몬드 패턴의 경우 약 200 μm이다. 허니컴 패턴의 경우 시인성과 모아레 현상을 완화하기 위하여 약간의 랜덤 패턴으로 제작되었다. 허니컴 패턴과 다이아몬드 패턴의 면저항은 각각 7.4 Ω/square, 0.7 Ω/square이었다.

Optical microscope image of fabricated metal grid electrode, (a) Honeycomb pattern, (b) Diamond pattern
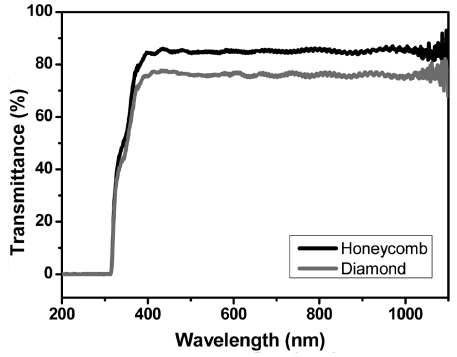
허니컴 패턴과 다이아몬드 패턴 샘플에 대한 투과도 특성은 Fig. 6에 나타나 있으며 투과도는 각각 84.8%, 75.7%이었다. 다이아몬드 패턴의 경우, 허니컴 패턴에 비하여 약간 더 조밀한 구조이며, 투명 필름에서 메탈 그리드 패턴이 차지하는 면적 비율은 다이아몬드 패턴의 경우는 9.4%, 허니컴 패턴은 6.4%이다. 즉 다이아몬드 패턴이 시편의 전체 면적 대비 차지하는 면적이 허니컴패턴보다 많기 때문에 면저항은 낮다. 반면에 투과도는 약간 감소하였다고 판단된다. 결론적으로 메탈 그리드가 차지하는 면적이 커질수록 전기적 특성(면저항)은 우수하나, 반면에 광학적 특성(투과도)은 저하된다고 할 수 있다. 이 결과는 메탈 그리드의 피치가 감소할수록 면저항은 향상되지만, 투과도는 저하된다는 다른 연구자들의 결과와 유사한 결과이다.16
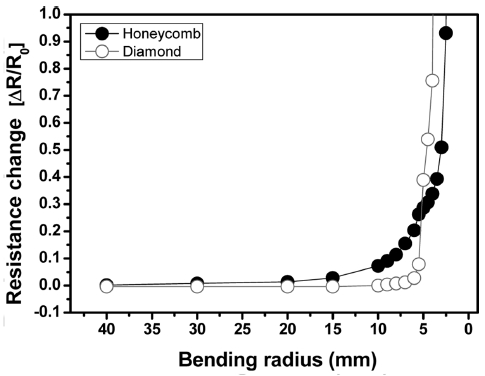
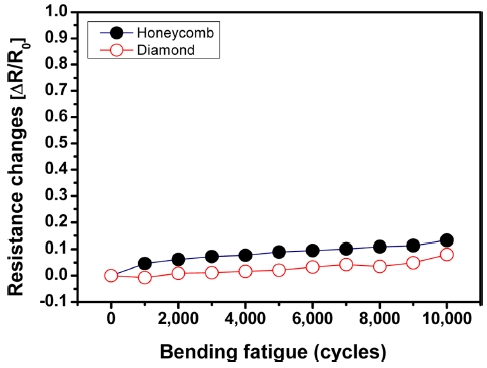
다음은 메탈 그리드 전극에 대한 기계적 유연성 내구성 시험을 진행하였다. Fig 7은 굽힘 반경에 따른 메탈 그리드 샘플의 굽힘 시험 결과이다. 여기에서 전극의 저항변화는 ΔR(=R-Ro)/Ro로 표시하였으며, Ro와 R은 굽힘 시험 전과 후의 저항을 각각 나타낸다. 허니컴 패턴의 메탈 그리드 샘플의 경우 곡률 반경 15 mm에서 저항이 서서히 증가하기 시작하여, 곡률 반경 10 mm에서는 약 10% 이상의 저항 증가가 있었다. 그 후 곡률 반경이 줄어들면서 저항이 지속적으로 증가하였으며, 곡률 반경 4 mm에서는 저항이 급격히 증가함을 알 수 있었다. 반면에 다이아몬드 패턴의 메탈 그리드의 경우 곡률 반경 6 mm까지 저항의 변화가 거의 없었으나, 5 mm 부터 저항이 급격히 증가함을 알 수 있었다. Fig. 8은 곡률 반경을 15 mm로 고정한 후, 샘플을 평평한 상태에서 곡률 반경 15 mm까지 10,000 사이클을 반복적으로 실험한 굽힘 피로 시험 결과이다. 허니컴 패턴 샘플의 경우 사이클이 증가하면서 저항이 서서히 증가함을 알 수 있으며, 7,000 사이클에서 저항이 약 10% 증가하였고, 최종 10,000 사이클에서 저항은 약 13% 증가하였다. 다이아몬드 패턴 샘플의 경우 10,000 사이클 굽힘 시험 후에 약 8%의 저항 증가가 있었다. 따라서 허니컴 패턴의 메탈 그리드 샘플보다 다이아몬드 패턴의 메탈 그리드 샘플이 굽힘에 더 우수한 강건성을 나타내는 것을 알 수 있다. 이러한 결과는 인장시험 결과에서 잘 나타나고 있다.
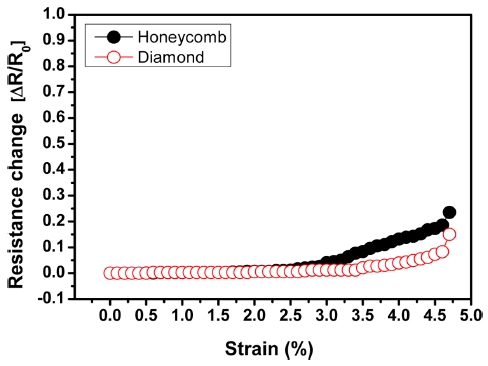
Fig. 9는 메탈 그리드 샘플들의 인장시험 결과이다. 인장 시편의 크기는 20 × 50 mm2이며, 시편의 한쪽을 그립(Grip)에 고정한 후 다른 한쪽을 20 mm/min의 속도로 서서히 당기면서 실험하였다. 허니컴 샘플의 경우 인장 변형율 약 3%부터 저항이 선형적으로 증가함을 알 수 있다. 반면에 다이아몬드 샘플의 경우 인장 변형율 약 4.5%부터 저항이 증가함을 알 수 있다. 따라서 허니컴 패턴 보다는 다이아몬드 패턴의 메탈 그리드 샘플이 굽힘 및 인장에 대한 강건성, 즉 유연성이 더 우수하다는 것을 알 수 있었다. Fig. 10은 인장 시험 후의 허니컴 메탈 그리드 샘플의 표면을 SEM으로 촬영한 사진이다. 허니컴 패턴 샘플의 경우 Metal Line에 다수의 크랙들이 존재함을 알 수 있었으며, 서로 연결된 전도성 나노입자들의 연결이 끊기거나 멀어지면서 저항이 증가하는 것으로 판단된다. 반면에 Fig. 11의 다이아몬드 패턴의 샘플의 경우 Metal Line 표면에 크랙이나 결함 등 특이한 파괴 현상은 발견되지 않았다.
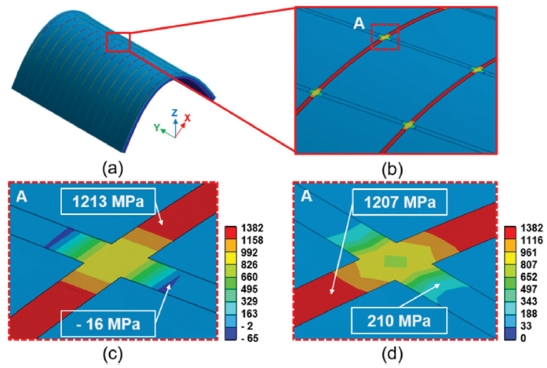
다음으로 메탈 그리드 전극의 굽힘 및 인장 시험 시의 응력을 수치해석으로 해석하였다. 전술한 실험들은 허니컴과 다이아몬드 패턴의 메탈 그리드에 대해서 수행하였으나, 실제 메탈 그리드의 패턴은 사각형 패턴, 말발굽 패턴, 지그재그 패턴 등 다양할 수 있기 때문에, 본 해석에서는 현재 기업에서 우선적으로 많이 사용되고 있는 다이아몬드, 허니컴 패턴 구조에 대해서 각각 수치 해석을 수행하였다. 한편 정사각형을 사용하는 경우도 있기 때문에 정사각형 패턴에 대해서도 수치해석을 부가적으로 수행하였다. 또한 허니컴 구조의 경우 실험에 사용된 허니컴은 약간의 랜덤 패턴을 하고 있으나, 랜덤 패턴이 국부적으로 각각 다르기 때문에 해석에서는 균일한 형태의 허니컴 패턴으로 해석하였다. Fig. 12는 정사각형 패턴의 메탈 그리드를 3 mm로 굽혔을 때의 응력 분포를 나타내고 있다. 곡률 반경 3 mm로 굽혔을 때의 메탈 그리드 전극에 가해진 굽힘 변형율은 식(2)로부터 계산되며, 계산 결과 굽힘 변형율은 2.1%이었다. 응력 분포는 X-방향의 인장응력(σxx)와 von Mises 응력(σMises)를 각각 나타내고 있다. 최대 인장응력은 1,213MPa이었으며, 최대 von Mises 응력은 1,207 MPa이였다. 최대응력이 걸리는 부분은 Grid 패턴이 서로 교차하는 지역이며, 굽히는 방향인 X-방향에서 최대 응력이 발생하고 있음을 알 수 있다. 인장응력분포의 경우 X-방향으로 인장이 발생하면서 Poisson’s Effect에 의하여 Y-방향으로는 압축이 발생하여 Y-방향의 메탈 그리드 패턴에는 압축 응력이 발생함을 알 수 있다.
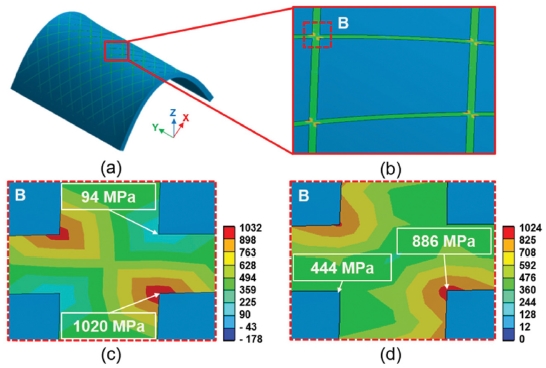
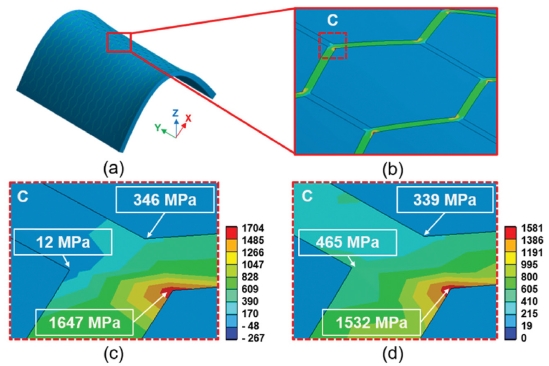
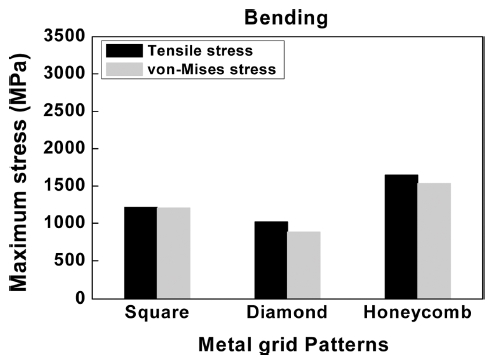
Fig. 13은 다이아몬드 패턴의 메탈 그리드를 3 mm 굽혔을 때의 응력 분포를 나타내고 있다. 최대응력은 패턴이 교차하는 모서리 부분에서 국부적으로 최대응력이 발생함을 알 수 있다. 최대 인장응력은 1020 MPa이었으며, 최대 von Mises 응력은 866MPa이었다. 다이아몬드 패턴의 응력은 정사각형 패턴의 응력에 비하여 인장 응력은 약 16%, von Mises 응력은 약 30% 낮음을 알 수 있었다. Fig. 14는 허니컴 패턴에 대한 응력 분포를 나타내고 있다. 최대 응력이 걸리는 지역은 역시 패턴이 교차되는 곳의 외곽 모서리 부분으로서, 최대 인장응력은 1,647 MPa이었으며, 최대 von Mises 응력은 1,532 MPa이었다. Fig. 15는 굽힘 시 3 가지 타입의 메탈 그리드 패턴의 최대응력을 정리해 놓은 그래프이다. 3 가지 타입의 Grid 패턴 중에서 허니컴 패턴의 응력이 최대임을 알 수 있었다. 또한 다이아몬드 패턴이 굽힘 시에 제일 적은 응력을 나타내고 있음을 알 수 있었다. 허니컴 패턴은 다이아몬드 패턴에 비하여 최대 인장응력이 약 61% 높았으며, 정사각형 패턴은 다이아몬드 패턴에 비하여 19% 높음을 알 수 있었다. 이는 Fig. 7의 굽힘 실험 결과에서 허니컴 패턴 보다는 다이아몬드 패턴 샘플이 굽힘에 대한 유연 신뢰성이 더 우수하다는 실험 결과와 잘 일치함을 보여주고 있다.
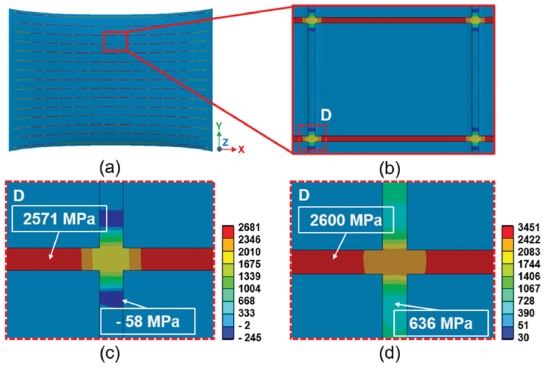
다음으로 인장 시 메탈 그리드 패턴의 응력을 수치해석으로 고찰하였다. Fig. 16은 정사각형 패턴에 대해서 인장 변형율 3%까지 인장했을 때의 응력분포를 나타내고 있다. 전술한 바와 같이 Poisson’s Effect에 의하여 인장 시 인장 방향에 수직인 방향(y 방향)으로 기판이 압축되는 것을 알 수 있다. 인장 시 최대응력은 인장 방향인 x-방향의 메탈 그리드 패턴 상에 걸리고 있음을 알 수 있다. 이때의 최대 인장응력은 2,571MPa이며, 최대 von Mises 응력은 2,600 MPa이었다.
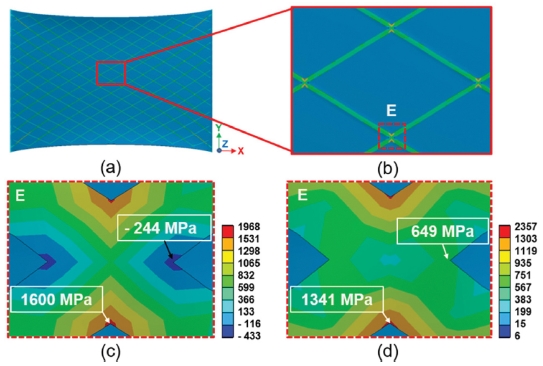
Fig. 17은 다이아몬드 패턴에 대한 인장 시의 응력분포를 나타내고 있다. 굽힘 시험의 결과와 유사하게 패턴이 교차되는 부분의 외곽 모서리에서 응력이 최대가 되며, 최대 인장응력은 1,600MPa이며, 최대 von Mises 응력은 1,341 MPa이었다.
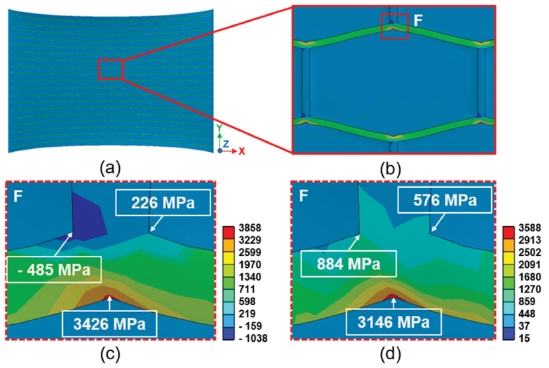
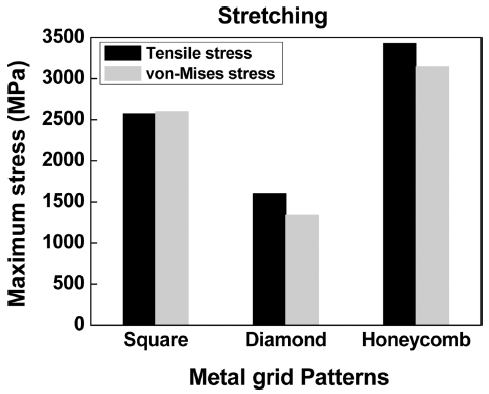
Fig. 18은 허니컴 패턴의 응력분포이다. 최대 인장응력은 3,426 MPa 이며, 최대 von Mises응력은 3,146 MPa이었다. 굽힘 시의 응력과 동일하게 허니컴 패턴의 응력이 가장 높았으며, 다이아몬드 패턴의 응력이 가장 낮았다. 이는 Fig. 9의 인장 실험 결과와도 잘 일치하는 결과이다. Fig. 19는 인장 시 3가지 타입의 Grid 패턴의 최대응력을 정리해 놓은 그래프이다. 굽힘 시와 동일하게 3 가지 타입의 메탈 그리드 패턴 중에서 허니컴 패턴의 응력이 최대이고, 다이아몬드 패턴이 제일 적은 응력을 나타내고 있음을 알 수 있었다. 허니컴 패턴은 다이아몬드 패턴에 비하여 최대 인장응력이 114% 높았으며, 정사각형 패턴은 다이아몬드 패턴에 비하여 61% 높음을 알 수 있었다. 특히 굽힘 보다는 인장했을 때 각 메탈 그리드 패턴에 따른 응력 차이가 많이 발생함을 알 수 있었다. 또한 실험결과와 수치해석에 의한 응력 해석결과가 잘 일치하고 있음을 알 수 있었다.
본 연구의 결과로부터 메탈 그리드의 패턴 형상이 메탈 그리드 전극 필름의 유연 내구성에 영향을 미치고 있음을 알 수 있었다. 현재 개발되고 있는 메탈 그리드의 패턴은 기업마다 매우 다양하다. 그러나 메탈 그리드의 패턴을 제작함에 앞서 굽힘 실험이나 수치해석을 통하여 유연내구성을 미리 파악하고 최적의 패턴을 설계하는 것이 중요함을 알 수 있었다.
5. 결론
본 연구에서는 유연 투명전극으로 개발되고 있는 메탈 그리드 투명전극의 메탈 그리드 패턴 형상에 따른 유연 내구성을 실험과 수치해석을 이용하여 비교 분석하였다. 메탈 그리드의 패턴으로는 허니컴, 다이아몬드 및 정사각형 패턴에 대해서 분석하였다. 굽힘 시험, 굽힘 반복피로시험 및 인장 시험을 통하여 메탈 그리드 필름의 유연내구성을 평가하였으며, 응력 해석을 통하여 시험결과와 비교하였다. 굽힘 시험 결과, 허니컴 패턴의 메탈 그리드 샘플의 경우 곡률 반경 15 mm에서 저항이 서서히 증가하기 시작하여, 곡률 반경 10 mm에서는 약 10% 이상의 저항 증가가 있었다. 반면에 다이아몬드 패턴의 경우 곡률 반경 6 mm까지 저항의 변화가 거의 없었다. 또한 10,000 사이클의 굽힘 피로시험 결과, 허니컴 패턴 샘플의 저항 증가율은 13%인 반면, 다이아몬드 패턴 샘플의 저항 증가율은 8%이였다. 기판을 5%까지 인장하였을 때 허니컴 패턴 샘플의 경우 메탈 그리드 표면에 다수의 크랙들이 존재함을 알 수 있었다. 반면 다이아몬드 패턴 샘플에는 크랙이나 결함이 발견되지 않았다. 따라서 허니컴 패턴 보다는 다이아몬드 패턴의 메탈 그리드가 굽힘 및 인장에 유연 내구성이 더 우수하였다. 굽힘 및 인장 시에 메탈 그리드에 응력을 해석한 결과, 허니컴 패턴이 응력이 가장 높았으며, 다이아몬드 패턴 샘플이 응력이 가장 낮았다. 이는 실험결과와 잘 일치하는 해석 결과임을 알 수 있었다. 굽힘 시 최대 인장응력을 비교한 결과, 허니컴 패턴은 다이아몬드 패턴에 비하여 응력이 61% 높았으며, 정사각형 패턴은 다이아몬드 패턴에 비하여 응력이 19% 높음을 알 수 있었다.
NOMENCLATURE
| r : | Bending radius |
| L : | Initial length of substrate |
| hs : | Substrate thickness |
| ε : | Bending strain |
| R : | Radius of curvature |
Acknowledgments
본 연구는 한국화학연구원의 지원을 받아 “유연 투명전극 소재의 기계적 특성 DB 구축” 과제로 수행되었습니다.
REFERENCES
-
Yu, J.-S., Yu, S., Kwak, S.-W., and Kim, J. S., “Fabrication of Transparent Conductive Film for Flexible Devices Using High-Resolution Roll Imprinting,” Journal of the Korean Society for Precision Engineering, Vol. 31, No. 11, pp. 975-979, 2014.
[https://doi.org/10.7736/KSPE.2014.31.11.975]

-
Hosono, H., “Recent Progress in Transparent Oxide Semiconductors: Materials and Device Application,” Thin Solid Films, Vol. 515, No. 15, pp. 6000-6014, 2007.
[https://doi.org/10.1016/j.tsf.2006.12.125]

-
Leterrier, Y., Medico, L., Demarco, F., Månson, J.-A., Betz, U., et al., “Mechanical Integrity of Transparent Conductive Oxide Films for Flexible Polymer-Based Displays,” Thin Solid Films, Vol. 460, Nos. 1-2, pp. 156-166, 2004.
[https://doi.org/10.1016/j.tsf.2004.01.052]

-
Cairns, D. R., Witte, R. P., Sparacin, D. K., Sachsman, S. M., Paine, D. C., et al., “Strain-Dependent Electrical Resistance of Tin-Doped Indium Oxide on Polymer Substrates,” Applied Physics Letters, Vol. 76, No. 11, pp. 1425-1427, 2000.
[https://doi.org/10.1063/1.126052]

-
Lewis, J., “Material Challenge for Flexible Organic Devices,” Materials Today, Vol. 9, No. 4, pp. 38-45, 2006.
[https://doi.org/10.1016/S1369-7021(06)71446-8]

- Trottier, C. M., Glatkowski, P., Wallis, P., and Luo, J., “Properties and Characterization of Carbon Nanotube Based Transparent Conductive Coating,” Journal of the Society for Information Display, Vol. 13, No. 9, pp. 759-763, 2005.
-
Huang, X., Zeng, Z., Fan, Z., Liu, J., and Zhang, H., “Graphene Based Electrodes,” Advanced Materials, Vol. 24, No. 45, pp. 5979-6004, 2012.
[https://doi.org/10.1002/adma.201201587]

-
Na, S. I., Kim, S. S., Jo, J., and Kim, D. Y., “Efficient and Flexible Ito Free Organic Solar Cells Using Highly Conductive Polymer Anodes,” Advanced Materials, Vol. 20, No. 21, pp. 4061-4067, 2008.
[https://doi.org/10.1002/adma.200800338]

-
Park, J. and Lee, C., “Roll-to-Roll Continuous Manufacturing System for Carbon-Nanotube-/Silver-Nanowire-Based Large-Area Transparent Conductive Film,” Journal of the Korean Society for Precision Engineering, Vol. 32, No. 8, pp. 673-680, 2015.
[https://doi.org/10.7736/KSPE.2015.32.8.673]

-
De, S., Higgins, T. M., Lyons, P. E., Doherty, E. M., Nirmalraj, P. N., et al., “Silver Nanowire Networks as Flexible, Transparent, Conducting Films: Extremely High DC to Optical Conductivity Ratios,” ACS Nano, Vol. 3, No. 7, pp. 1767-1774, 2009.
[https://doi.org/10.1021/nn900348c]

-
Zou, J., Yip, H.-L., Hau, S. K., and Jen, A. K.-Y., “Metal Grid/Conducting Polymer Hybrid Transparent Electrode for Inverted Polymer Solar Cells,” Applied Physics Letters, Vol. 96, No. 20, Paper No. 203301, 2010.
[https://doi.org/10.1063/1.3394679]

-
Yu, J.-S., Jung, G. H., Jo, J., Kim, J. S., Kim, J. W., et al., “Transparent Conductive Film with Printable Embedded Patterns for Organic Solar Cells,” Solar Energy Materials and Solar Cells, Vol. 109, pp. 142-147, 2013.
[https://doi.org/10.1016/j.solmat.2012.10.013]

-
Jin, Y., Deng, D., and Xiao, F., “Site-Selective Fabrication of Patterned Transparent Copper Mesh on Flexible Substrates at Mild Temperature for Green, Low Cost Electronics,” Proc. of IEEE 63th Electronic Components and Technology Conference (ECTC), pp. 1315-1319, 2013.
[https://doi.org/10.1109/ECTC.2013.6575742]

-
Kang, M.-G., Park, H. J., Ahn, S. H., and Guo, L. J., “Transparent Cu Nanowire Mesh Electrode on Flexible Substrates Fabricated by Transfer Printing and Its Application in Organic Solar Cells,” Solar Energy Materials and Solar Cells, Vol. 94, No. 6, pp. 1179-1184, 2010.
[https://doi.org/10.1016/j.solmat.2010.02.039]

-
Kahng, Y. H., Kim, M.-K., Lee, J.-H., Kim, Y. J., Kim, N., et al., “Highly Conductive Flexible Transparent Electrodes Fabricated by Combining Graphene Films and Inkjet-Printed Silver Grids,” Solar Energy Materials and Solar Cells, Vol. 124, pp. 86-91, 2014.
[https://doi.org/10.1016/j.solmat.2014.01.040]

-
Jang, Y., Kim, J., and Byun, D., “Invisible Metal-Grid Transparent Electrode Prepared by Electrohydrodynamic (EHD) Jet Printing,” Journal of Physics D: Applied Physics, Vol. 46, No. 15, Paper No. 155103, 2013.
[https://doi.org/10.1088/0022-3727/46/15/155103]

-
Shin, D.-K. and Park, J., “Angular Dependence of Moiré Fringes Induced by Metal Grids for Touch Screen Panels,” Journal of Display Technology, Vol. 11, No. 1, pp. 110-117, 2015.
[https://doi.org/10.1109/JDT.2014.2363198]

-
Jang, H. Y., Lee, S.-K., Cho, S. H., Ahn, J.-H., and Park, S., “Fabrication of Metallic Nanomesh: Pt Nano-Mesh as a Proof of Concept for Stretchable and Transparent Electrodes,” Chemistry of Materials, Vol. 25, No. 17, pp. 3535-3538, 2013.
[https://doi.org/10.1021/cm402085k]

-
Li, Y., Mao, L., Gao, Y., Zhang, P., Li, C., et al., “ITO-Free Photovoltaic Cell Utilizing a High-Resolution Silver Grid Current Collecting Layer,” Solar Energy Materials and Solar Cells, Vol. 113, pp. 85-89, 2013.
[https://doi.org/10.1016/j.solmat.2013.01.043]

-
Shin, D., Lee, J.-Y., Lee, J.-H., Choi, K.-J., Yoo, S.-h., et al., “Suppression of Moiré Fringes Induced by Metal Meshes for Touch Screen Panels,” Journal of Display Technology, Vol. 12, No. 6, pp. 632-638, 2016.
[https://doi.org/10.1109/JDT.2016.2515259]

-
Liu, W., Fang, Y., Xu, Y., Li, X., and Li, L., “The Effect of Grid Shape on the Properties of Transparent Conductive Films Based on Flexographic Printing,” Science China Technological Sciences, Vol. 57, No. 12, pp. 2536-2541, 2014.
[https://doi.org/10.1007/s11431-014-5683-1]

-
Hong, S., Yeo, J., Kim, G., Kim, D., Lee, H., et al., “Nonvacuum, Maskless Fabrication of a Flexible Metal Grid Transparent Conductor by Low-Temperature Selective Laser Sintering of Nanoparticle Ink,” ACS Nano, Vol. 7, No. 6, pp. 5024-5031, 2013.
[https://doi.org/10.1021/nn400432z]

-
Park, S. I., Ahn, J. H., Feng, X., Wang, S., Huang, Y., and Rogers, J. A., “Theoretical and Experimental Studies of Bending of Inorganic Electronic Materials on Plastic Substrates,” Advanced Functional Materials, Vol. 18, No. 18, pp. 2673-2684, 2008.
[https://doi.org/10.1002/adfm.200800306]

-
Jung, H. S., Eun, K., Kim, Y. T., Lee, E. K., and Choa, S.-H., “Experimental and Numerical Investigation of Flexibility of ITO Electrode for Application in Flexible Electronic Devices,” Microsystem Technologies, Vol. 23, No. 6, pp. 1961-1970, 2017.
[https://doi.org/10.1007/s00542-016-2959-3]

-
Alzoubi, K., Hamasha, M. M., Lu, S., and Sammakia, B., “Bending Fatigue Study of Sputtered ITO on Flexible Substrate,” Journal of Display Technology, Vol. 7, No. 11, pp. 593-600, 2011.
[https://doi.org/10.1109/JDT.2011.2151830]

-
Smith, D. R. and Fickett, F., “Low-Temperature Properties OF Silver,” Journal of Research of the National Institute of Standards and Technology, Vol. 100, No. 2, pp. 119-171, 1995.
[https://doi.org/10.6028/jres.100.012]