플랑크 상수를 이용한 킬로그램 재정의 및 실현
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In the current SI (International System of Units), the kilogram is defined by the mass of a material artefact. In this instance, because the artefact can be damaged during use, the present definition is inherently considered unstable. To overcome the shortcomings of the present kilogram definition, the SI will be redefined in near future. In the new SI, the kilogram will be redefined by fixing the numerical value of the Planck constant. After the kilogram redefinition, realization experiments which link the Planck constant to the mass will be necessary. In the new SI, the kilogram will be realized through experiments including the Kibble balance and the X-ray crystal density. The Kibble balance, which is named for the scientist Bryan P. Kibble, is an electromechanical device comparing mechanical power and electrical power. The electrical power is proportional to the Planck constant, because of the voltage and resistance are measured using the Josephson effect and the quantum Hall effect, respectively. The Planck constant is an invariant and not a characteristic of a man-made object, or a specific experiment. The new mass unit is more stable than the current one, and will pave the way for the advancement of precision measurement.
Keywords:
Kilogram, Mass standards, Electrical standards, Planck constant, Kibble balance, SI redefinition키워드:
킬로그램, 질량 표준, 전기 표준, 플랑크 상수, 키블 저울, 단위 재정의1. 서론
2019년 5월 20일은 정밀측정 연구자들에게 매우 중요한 날이다. 새로운 국제단위계가 이 날부터 시행되기 때문이다. 우리가 측정을 할 때 기준으로 삼아온 국제단위계 중에서 질량, 전기, 온도, 물질의 양 등 4개 단위는 시간에 따라 변할 수 있거나 한 점에서 정의되어 일정한 범위에서 벗어나면 실현하기 어렵다.
새로운 국제단위계에서는 변하지 않는 물리상수를 측정의 기준으로 삼는다. 물리상수는 사람이 만든 물체의 성질이 아니며 그 값이 변하지 않으므로 물리상수를 측정의 기준으로 삼게 되면 측정 정밀도를 높일 수 있다.
새로운 단위계에서는 플랑크 상수, 기본 전하, 볼츠만 상수, 아보가드로 상수 등 4개의 물리상수 값을 고정하여 각각 질량, 전기, 온도, 물질의 양 측정의 기준으로 삼는다. 질량의 단위인 킬로그램은 고정된 플랑크 상수 값을 기준으로 측정하게 된다.
플랑크 상수는 빛 에너지와 주파수의 관계를 설명하는 상수로서 원자물리 및 양자역학 등에서 중요한 상수이다. 새로운 단위계에서 킬로그램을 실현하기 위해서는 플랑크 상수와 킬로그램을 연결하는 실험 및 장비가 필요하다. 고정된 플랑크 상수 값을 이용해서 킬로그램을 실현하는 기술은 현재 키블저울과 XRCD (X-Ray Crystal Density) 방법이 있다.
본 논문에서는 2019년부터 시행되는 새로운 국제단위계에서 질량 단위를 실현하는 기술에 대하여 기술한다. 2장에서는 현재 질량 단위의 문제점을 기술한다. 3장과 4장에서는 새로운 단위계에서 질량 단위를 실현하는 기술인 키블저울에 대하여 설명한다. 5장에서는 새로운 단위계가 질량 측정에 미치는 영향에 대하여 기술한다. 6장에서는 XRCD 실험을 이용한 킬로그램 실현기술에 대하여 기술한다. 7장에서는 국내 및 국외에서 개발중인 키블저울에 대하여 간략하게 소개한다.
2. 현재 질량 단위의 문제점
현재 질량 단위로 사용하고 있는 킬로그램의 역사는 대혁명을 앞둔 프랑스 왕정 말기에 시작되었다.1 프랑스 과학자들은 지구의 둘레를 길이의 기준으로 정하기 위해 1792년에서 1799년까지 파리를 중심으로 프랑스 북부와 스페인을 지나는 거리를 측정하였다. 측정한 거리를 바탕으로 1799년에 순수한 백금으로 미터와 킬로그램 기준 물체를 만들었다.
1799년에 정한 프랑스 미터법은 잠시 폐지되었다가 나라간에 교역이 활발해짐에 따라 다시 필요성이 대두되었다. 전세계가 길이와 킬로그램의 기준을 함께 사용하기 위하여 1875년 미터 협약을 체결하였다. 미터 협약 이후에 국제 킬로그램 원기와 국가원기들을 제작하기 시작하였고 국제 미터 및 킬로그램 원기를 관리하는 국제기구로서 국제도량형국, 국제도량형위원회, 국제도량형총회를 만들었다.
1880년에 국제 킬로그램 원기를 제작할 때 기준으로 삼은 것이 1799년에 만들어진 킬로그램 기준 물체이다. 순수한 백금의 질량이 시간에 따라 변하므로 순수 백금보다 안정적인 백금 90%와 이리듐 10% 합금을 이용하여 원기를 제작하였으며 표면적을 줄이기 위하여 지름과 높이가 모두 39 mm인 원기둥으로 제작하였다. 제작한 원기 중 1799년 킬로그램 기준 물체와 질량이 같은 원기를 1889년에 열린 제1차 국제도량형총회에서 킬로그램의 기준인 국제 킬로그램 원기로 공인하였다.2
물체를 킬로그램의 기준으로 삼아 130년 가까이 사용해 왔으나 여러 가지 문제점이 발생하였다. 물체는 사용하면 닳을 수 있으므로 국제 킬로그램 원기를 보관하고 4번만 사용하였다. 국제 킬로그램 원기를 국제도량형국에 있는 금고에 보관하고 국제 킬로그램 원기의 안정성을 확인하기 위하여 공식 복제본을 함께 보관하였다. 1889년 당시에는 K1, 7, 8(41), 32번 등 4개 복제본을 국제 킬로그램 원기와 함께 보관하였으나 이후 43, 47번 2개가 추가되어 현재 6개 공식 복제본이 국제 킬로그램 원기와 같은 금고에 보관되어 있다.
공식 복제본과 국제 킬로그램 원기의 질량을 비교한 결과를 Fig. 1에 나타내었다.3,4 시간이 지남에 따라 공식 복제본과 국제 킬로그램 원기의 질량차이가 커짐을 알 수 있다. 공식 복제본은 국제 킬로그램 원기와 재질이 같으며 같은 환경에 있으므로 국제 킬로그램 원기가 공식 복제본보다 더 안정적이라고 볼 수 없다. 따라서 우리가 사용하고 있는 기준은 100년동안 수십 μg정도 변할 수 있는 셈이다.
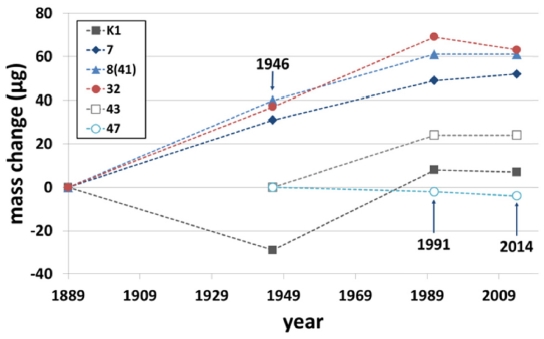
Mass changes of six official copies during four comparisons against the international prototype of the kilogram (IPK).3,4 Four official copies (K1, 7, 8(41), 32) have been measured since 1889, whereas two copies (43, 47) have been measured since 1946. The masses of the official copies, which are stored in the same environment as the IPK, change over time
3. 키블저울 원리
3.1 웨잉 모드
사람이 만든 금속 물체인 국제 킬로그램 원기는 시간이 지나면 오염되어 질량이 바뀔 수 있다. 또한 다른 물체와 질량을 비교하다가 손상될 수 있으므로 거의 사용하지 않는다. 하지만 변하지 않는 물리상수를 질량의 기준으로 삼으면 지금의 기준보다 안정적인 기준을 세울 수 있다.
물리상수 중 플랑크 상수를 질량의 기준으로 삼게 된 이유는 키블 저울을 이용하여 물체의 질량과 플랑크 상수를 연결하는 것이 가능하기 때문이다. 키블저울은 전기적 일률과 역학적 일률을 비교하는 실험이다. 일반적으로 두 가지 실험을 통하여 전기적 일률과 역학적 일률을 비교한다.
첫 번째 실험에서는 물체의 무게와 전자기력을 비교한다. 첫 번째 실험은 웨잉 모드 혹은 힘 모드라고 부르며 일반적인 전자저울의 동작원리와 비슷하다. 웨잉 모드의 모식도를 Fig. 2에 나타내었다.
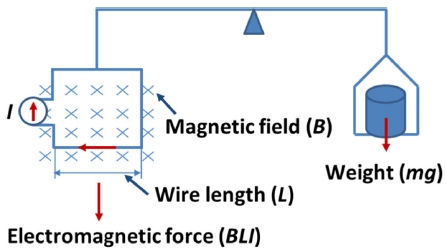
Conceptual diagram of the weighing mode for the Kibble balance experiments. Electric current passes through the coil, which is immersed in the magnetic field, to generate electromagnetic force. The electromagnetic force is compared to the weight of the test mass. The geometric factor, the quotient of weight and current, should be known to get the absolute mass
웨잉 모드에서는 양팔 저울 한쪽에 측정 대상을 놓고 다른 한 쪽에 전자기력을 이용하여 힘의 평형을 이루게 한다. 자기장을 균일하게 발생시킨 후 코일에 전류를 흐르면 전자기력이 발생한다. 웨잉 모드에서 중력과 전자기력 사이의 힘 평형 식은 다음 식(1)과 같다.
| (1) |
식(1)에서 m은 측정물체의 질량, g는 측정물체가 있는 위치에서의 중력가속도, B는 자기장, L은 코일 도선의 길이, I는 코일에 흐르는 전류이다.
일반적인 전자저울에서는 알고 있는 질량 ms를 가지는 표준분동을 이용하여 전류에 따른 저울 감도를 교정한 후 측정 대상의 질량 mx를 잰다. 이 때 사용하는 표준 분동의 질량 값 ms는 국제킬로그램원기로부터 교정한 값이다. 여기에서 현재 사용하고 있는 질량 단위의 문제점이 또 하나 나타난다.
국제킬로그램원기는 1 kg이므로 표준분동의 질량이 작아질수록 분동의 정밀도가 떨어진다. 원하는 표준분동이 1 mg이라면 이 분동을 교정하기 위해서 106배 큰 질량을 가지는 1 kg과 비교해야 한다. 1 kg과 비교하기 위해서 여러 차례 단계를 거치기 때문에 실험에 의하여 오차가 누적된다. 따라서 현재 표준분동 중 가장 정밀도가 높은 E1 분동의 경우 1 mg에서 50 kg사이의 분동만이 제작되고 있다. 더 작은 분동을 교정할 방법이 없는 셈이다.
식(1)을 역으로 생각하면 알고 있는 질량으로부터 국제단위계정의에 따른 전류를 실현할 수 있다. 전류단위인 암페어는 현재 국제단위계에서 두 도선 사이에 미치는 힘을 기준으로 정의되어 있다. 고정된 코일과 움직일 수 있는 코일에 전류를 흘리면 힘이 발생하고 발생한 전자기력을 국제 킬로그램 원기로부터 소급 받은 표준분동의 무게와 비교한다. 무게와 전류의 비례상수는 코일의 형상을 측정하여 결정한다. 일반적인 저울과 달리 전류 단위인 암페어를 실현하므로 암페어 저울이라 부른다.5
암페어 저울을 이용하여 암페어를 실현하기 위해서는 코일의 형상을 정확히 측정해야 한다. 코일 형상을 정확하게 측정하기 어려우므로 실제로는 사용하지 못하였다. 1975년 영국 NPL 과학자 키블은 암페어 저울의 정밀도를 획기적으로 향상시킬 수 있는 방법을 제안하였다.6 이것이 키블저울의 두 번째 실험이다.
3.2 무빙 모드
두 번째 실험은 무빙 모드 혹은 속도 모드라고 부르며 Fig. 3에 모식도를 나타내었다. 균일한 자기장에서 코일을 움직이면 패러데이 법칙에 의하여 코일 속도와 자기장의 곱에 비례하는 전압이 발생한다. 코일 속도와 전압과의 관계식은 다음 식(2)와 같다.
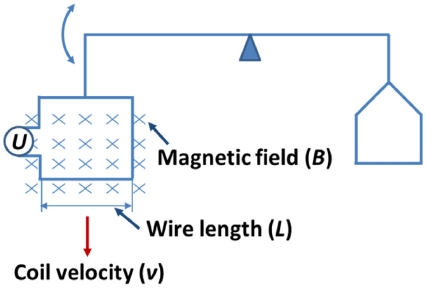
Conceptual diagram of the moving mode for the Kibble balance experiments. The coil is moved vertically to generate the voltage. The quotient of voltage and coil velocity in the moving mode is exactly same as the quotient of the weight and current in the weighing mode
| (2) |
식(2)에서 U는 코일을 움직일 때 발생하는 전압, v는 코일 속도이다. 전압과 속도의 비는 웨잉모드에서 구한 무게와 전류의 비와 정확하게 같다. 따라서 코일의 형상을 측정할 필요가 없으므로 암페어 저울의 정밀도를 향상시킬 수 있다. 무빙모드에서 발생하는 전압과 코일 속도의 비가 형상계수이므로 무빙모드를 교정모드라고도 부른다. 식(1)과 식(2)에서 형상계수를 제거하면 다음과 같다.
| (3) |
식(3)은 힘과 속도의 곱인 역학적 일률과 전압과 전류의 곱인 전기적 일률을 비교하는 식이다. 4장에서 기술하는 바와 같이 조셉슨 효과와 양자홀효과를 이용해서 전기적 일률을 측정하면 전기적 일률은 플랑크상수와 조셉슨 소자에 걸어주는 마이크로파 주파수에 비례한다. 역학적 일률은 킬로그램, 미터, 초 등 국제단위계로 표현된다. 따라서 역학적 일률과 전기적 일률을 비교하는 실험은 국제단위계를 이용하여 플랑크상수를 측정하는 실험이다.
키블저울 실험에서는 웨잉모드와 무빙모드 두 가지 독립적인 실험을 합해서 전기적 일률과 역학적 일률을 비교한다. 만약 두 가지 실험을 나누어 하지 않고 전기적 일률을 한번에 측정하면 도선 저항에 의해서 열 손실이 발생한다. 열 손실을 없애기 위해서는 저항이 없는 초전도 코일을 이용할 수 있지만 저온에서 동작하는 시스템을 개발해야 하는 어려움이 따른다. 또한 역학적 일률을 한번에 측정한다면 마찰에 의한 에너지 손실을 고려해야 한다.
일반적인 키블저울 실험에서는 웨잉모드에서 공급하는 전류와 무빙모드에서 발생하는 전압을 곱하므로 줄 발열에 의한 에너지 손실을 고려할 필요가 없다. 또한 웨잉모드에서 발생하는 힘과 무빙모드에서 코일을 움직이는 속도를 곱하므로 코일을 움직일 때 발생하는 마찰에 의한 손실을 고려할 필요가 없다. 즉 키블저울에서 비교하는 것은 실제 일률이 아니라 가상적인 일률이다. 키블저울은 결과적으로 역학적 일률과 전기적 일률을 비교하는 실험이므로 일률의 단위인 와트를 따서 와트저울이라고 불렸다. 2016년 키블이 타계한 이후 키블의 공적을 기려 키블저울로 부르기 시작하였다.
4. 키블저울과 플랑크상수
4.1 조셉슨 효과
키블이 무빙 모드를 제안한 당시에는 양자홀효과가 발견되기 이전이었으므로 키블저울의 목적은 전류, 전압과 같은 전기단위를 국제단위계를 이용하여 실현하는 것이었다. 조셉슨 효과를 이용한 전압표준기와 양자홀효과를 이용한 저항표준기가 개발된 이후 키블저울의 목적은 조셉슨과 양자홀과 같은 양자현상을 이용해서 국제 킬로그램 원기를 대체하는 것이 되었다.
조셉슨 효과는 초전도체가 부도체를 사이에 두고 가깝게 있을 때 초전도 전자쌍이 부도체 벽을 통과하며 나타나는 현상이다.7 조셉슨 소자에 마이크로파를 쏘아주면 두 초전도체 사이에 직류 전압이 발생한다. 직류전압이 플랑크상수, 기본전하, 마이크로파 주파수에만 의존하므로 안정적인 전압 기준으로 사용할 수 있다. 조셉슨 소자에서 발생하는 전압은 다음 식(4)와 같다.
| (4) |
식(4)에서 UJ는 조셉슨 전압, n은 정수, h는 플랑크상수, e는 기본 전하, f는 마이크로파 주파수, KJ는 조셉슨 상수이다.
조셉슨 소자는 주파수를 전압으로 바꾸어주는 주파수-전압 변환기이다. 주파수를 정밀하게 발생시킬 수 있으므로 조셉슨 소자에서 나오는 전압 역시 정밀하게 유지할 수 있다. 조셉슨 전압은 재현성이 우수하므로 1990년에 조셉슨 상수 값을 483,597.9 GHz V-1로 정하여 실제적인 전압 기준으로 사용하고 있다.
조셉슨 접합 1개에서 나오는 전압이 작으므로 접합을 직렬로 연결하여 1 V 혹은 10 V등 실험에서 사용할 수 있는 전압을 제공한다. 반도체 기술의 발전으로 초전도 박막 성장 및 식각 등 초전도 전자회로 공정기술 또한 발달하여 많은 접합을 한 칩에 집적할 수 있다. 현재 한국표준과학연구원 키블저울 실험에서 사용하고 있는 조셉슨 소자는 70,000개의 조셉슨 접합으로 이루어져 있으며 최대 2 V까지 원하는 전압을 만들어 낸다.
1990년에 정한 전압기준은 국제단위계는 아니며 재현성이 높은 조셉슨 효과를 사용하기 위하여 편의상 만든 기준이다. 2019년에 플랑크상수와 기본전하의 값이 고정되므로 조셉슨 상수 값 역시 고정된다. 따라서 새로운 국제단위계에서는 조셉슨 효과가 전압을 실현하는 기술이 된다. 고정되는 조셉슨 상수 값은 1990년 이후의 실험결과가 반영되므로 10-7정도 달라진다.
4.2 양자홀 효과
낮은 온도에서 자기장을 세게 걸면 2차원 전자계에서 홀 저항이 자기장과 전류에 관계없이 일정한 현상이 나타난다.8 이때 홀 저항이 자기장에 무관하므로 저항표준기로 사용할 수 있다. 양자 홀 저항은 다음 식(5)와 같이 나타난다.
| (5) |
식(5)에서 RH는 양자홀 저항, i는 정수, RK는 폰 클리칭 상수이다. 양자홀저항 역시 국제단위계로부터 정의되지 않지만 재현성이 우수하므로 실제적인 저항기준으로 삼고 있다. 1990년에 폰 클리칭 상수를 25,812.807 Ω으로 정하여 현재까지 사용하고 있다. 폰 클리칭 상수 역시 단위가 재정의 된 이후에는 그 값이 새로운 값으로 고정되므로 양자홀 효과를 저항 표준으로 사용할 수 있다.
4.3 키블 방정식
양자홀 효과와 조셉슨 효과를 이용하여 전압과 저항을 측정하면 전기적 일률을 플랑크상수로 나타낼 수 있다. 웨잉모드에서 코일에 흐르는 전류는 코일에 직렬로 연결한 표준저항 양쪽에 걸리는 전압 차이를 조셉슨 전압과 비교하여 측정한다. 표준저항은 양자홀 저항과 비교하여 얻는다. 따라서 키블저울실험에서 역학적 일률과 전기적 일률을 비교하는 식(3)은 다음 식(6)과 같이 표현된다.
| (6) |
식(6)에서 U1은 웨잉 모드에서 측정한 전압, f1은 웨잉 모드에서 전압을 측정할 때 조셉슨 소자에 걸어준 마이크로파 주파수, C는 조셉슨 전압 및 양자홀 저항을 이용하여 전압 및 저항을 측정할 때 얻어진 실험값이다.
식(6)과 같이 키블저울 실험을 통하여 플랑크 상수와 측정물체의 질량 사이의 관계식을 얻을 수 있다. 현재 국제단위계를 이용해서 플랑크상수를 측정하는 방법은 다음과 같다. 측정물체의 질량 값은 국제 킬로그램 원기로부터 소급된다. 측정 물체는 국가가 보유하고 있는 국가 킬로그램 원기를 이용하여 교정하며 국가원기는 국제도량형국에서 주기적으로 교정을 받는다. 국가원기의 불확도는 2014년에 약 3 μg이었으며 대략 2년에 1 μg 정도 불확도가 증가한다. 현재 한국표준과학연구원에서는 스테인리스 분동을 이용하여 실험을 하고 있다. 스테인리스 분동은 국가원기와 크기가 달라 공기에 의한 부력이 서로 다르다. 공기 부력 차이에 의하여 스테인리스 분동의 불확도가 대략 15 μg으로 증가한다.
측정물체 위치에서의 중력가속도는 별도의 장비를 이용하여 측정한다. 절대중력계를 이용하여 중력가속도를 측정한 후 상대 중력계를 이용해서 측정물체가 놓이는 위치와 절대중력계 측정 위치에서의 중력차이를 측정한다. 키블저울 시스템이 당기는 힘에 의한 중력 차이는 시스템 질량과 형상을 이용하여 수치적으로 계산한다.
절대중력을 측정하는 절대중력계는 원자중력계나 자유낙하 중력계를 사용한다. 자유낙하 중력계는 진공에서 코너큐브를 자유낙하시키고 간섭계를 이용해서 시간에 따른 위치변화를 측정하는 시스템이다. 절대중력, 상대중력, 중력계산을 포함한 중력가속도 측정불확도는 10-8정도이다.9 중력가속도와 무빙모드에서의 코일 속도는 세슘 주파수와 빛의 속도로 정의된 미터와 초로부터 소급된다. 따라서 킬로그램, 미터, 초 등 국제단위계에서 소급되는 역학적 일률을 이용하여 플랑크상수를 측정할 수 있다.
키블저울과 XRCD 방법을 이용하여 2017년 7월 1일까지 발표된 실험결과들을 가중 평균하여 단위재정의 이후 사용할 플랑크 상수 값이 결정되었다. CODATA TGFC에서 실험결과들을 모아서 가중 평균값을 계산하고 단위자문위원회 의결을 거쳐 국제도량형위원회에서 국제도량형총회에 제출한 플랑크 상수 값은 6.626 070 15 × 10-34 Js이다. 국제도량형위원회에서 제출한 플랑크 상수 값을 2018년 11월에 프랑스 베르사유에서 열리는 국제도량형총회에서 공인하면 2019년 5월 20일부터 고정된 플랑크 상수 값을 기준으로 하는 새로운 킬로그램의 정의가 시행된다.
새로운 국제단위계에서는 고정된 플랑크 상수 값을 기준으로 측정물체의 질량을 재게 된다. 얼핏 보면 측정대상과 측정기준을 맞바꾸는 순환논리에 불과하지만 질량측정 및 정밀측정 기술에 미치는 영향이 매우 크다. 다음 장에서 단위 재정의가 질량 측정에 미치는 영향을 살펴본다.
5. 킬로그램 재정의가 미치는 영향
5.1 현재 질량 단위
현재 질량단위의 기준은 금속 물체인 국제 킬로그램 원기이다. 국제 킬로그램 원기의 질량이 정확히 1 kg이며 미세 질량과 매우 큰 질량을 포함한 모든 물체의 질량은 1 kg인 국제 킬로그램 원기의 질량과 비교하는 소급체계를 가져야 한다. Table 1에 현재 국제단위계에서 사용되는 킬로그램 보급체계를 나타내었다.

Hierarchy for the mass calibration in the current SI based on the mass value of the international prototype of the kilogram
국제 킬로그램 원기는 취급도중 발생할 수 있는 손상을 방지하기 위하여 사용횟수를 제한하며 대략 30년에서 50년 주기로 다른 물체와 비교한다. 공식복제본은 6개 있으며 국제 킬로그램 원기와 같은 금고에 보관한다. 공식복제본은 2개씩 번갈아 가면서 10년 주기로 사용한다.
질량단위를 유지하기 위하여 국제도량형국이 보유하고 있는 원기는 12개이며 1년 내지 5년 주기로 원기질량을 서로 비교함으로써 시간에 따른 질량변화를 관찰한다. 12개 국제도량형국원기를 이용하여 각 나라 표준기관이 보유하고 있는 국가원기를 교정하여 전세계가 같은 질량단위를 유지하도록 한다.
우리나라가 보유하고 있는 국가원기는 72번과 84번이며 72번을 주로 사용한다. 시간이 증가하면 질량불확도가 증가하므로 5년주기로 국제도량형국에 방문하여 국제도량형국이 보유하고 있는 12개 원기 중 하나와 비교한다. 킬로그램 소급체계에서 국가 원기 상위에 있는 원기들은 백금과 이리듐 합금으로 만들어져 있지만 국가원기 하위에 있는 분동은 주로 스테인리스 강으로 만든다.
국가원기와 스테인리스 분동은 밀도가 다르므로 대략 2.5배 이상 부피가 다르다. 부피차이에 의하여 공기 부력이 다르며 온도, 대기압을 측정하여 공기 밀도를 계산하여 부력효과를 보정한다. 국가원기와 비교한 스테인리스 분동을 이용하여 산업체에서 저울을 교정하는 데 사용되는 표준분동을 교정한다.
1 kg 보다 작거나 큰 질량을 갖는 분동은 1 kg에서 시작하는 보급사슬을 따른다. 100, 200, 500 g 분동을 조합하여 1 kg을 만들고 이를 1 kg 표준분동과 비교함으로써 100, 200, 500 g 표준분동이 1 kg 원기에서 소급되도록 한다. 100 g 보다 작은 분동의 경우에도 마찬가지로 1/10, 1/5, 1/2 질량을 갖는 분동을 조합하여 비교한다. 1 kg 보다 작은 분동을 교정하기 위한 절차를 Fig. 4에 나타내었다.
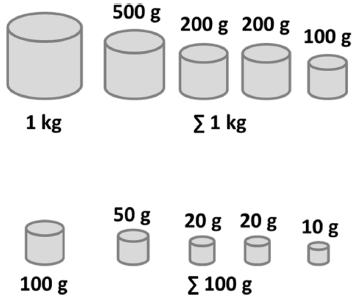
Calibration chain for the smaller weights than 1 kg weight. Combination of 100 g, 200 g, and 500 g weights is used to disseminate smaller weights than 1 kg weight. Using the similar subdivision, small masses up to 1 mg is calibrated within the maximum permissible error of E1 weights
현재와 같이 1 kg으로부터 교정을 시작하는 방법은 몇 가지 문제점이 있다. 1 kg 분동 두 개를 비교하는 질량비교기의 분해능은 최대 0.1 μg이다. 국가원기의 경우 국제도량형국에서 교정을 받을 때의 불확도는 3 μg이지만 수 년이 지나면 불확도가 10 μg 이상이 된다. 불확도가 10 μg 보다 큰 1 kg 스테인리스 분동을 이용하여 질량이 작은 분동을 교정하므로 측정대상의 질량이 작아질수록 상대불확도는 커진다.
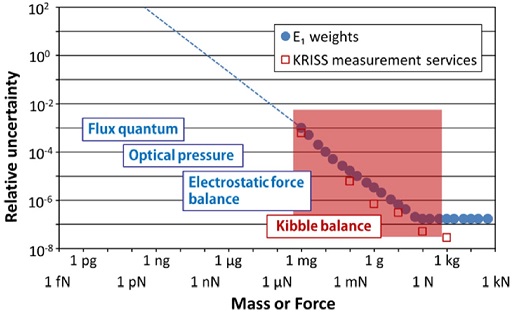
산업체에서 사용하는 분동은 표면상태, 자기장특성, 불확도에 따라 등급이 나뉘어있다.10 가장 높은 등급인 E1 분동은 국가원기로부터 소급이 가능한 교정 성적서를 가지고 있다. E1보다 낮은 등급을 갖는 분동은 상위 분동을 이용하여 교정한다. E1 분동의 질량 값에 따른 k = 2에서의 상대확장불확도 허용한계를 Fig. 5에 나타내었다. 1 kg에서 질량소급이 시작되므로 질량이 작아질수록 상대불확도가 커짐을 알 수 있다.
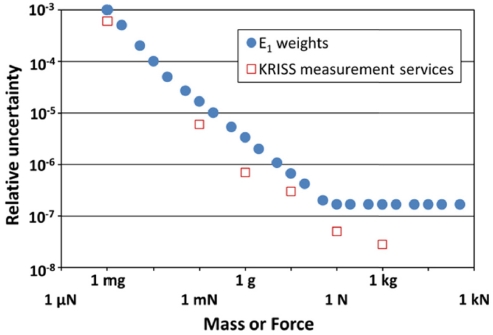
The relative uncertainty (k = 2) of E1 weights and the measurement capability of KRISS mass laboratory. The relative uncertainties of E1 weights, which are traceable to the IPK, increase as the mass of the weights are smaller
E1 분동은 1 mg에서 50 kg까지 있으며 더 작은 분동은 다루기가 어려워 잘 사용되지 않는다. 1 mg 분동의 확장불확도는 1 μg이며 상대불확도로 표현하면 10-3이다. 한국표준과학연구원에서 가지고 있는 측정능력을 Fig. 5에 함께 나타내었다. 한국표준과학연구원의 측정능력은 국외 표준기관과 국제비교를 통하여 검증한다.
현재 국제단위계에서는 작은 질량을 가지는 분동을 1 kg 분동을 이용하여 교정하므로 1 mg 미만의 분동을 교정하기가 어렵다. 또한 작은 분동은 다루기가 어려워 100 mg 미만의 분동을 국제 비교하는 절차가 없다.
5.2 새로운 질량 단위
새로운 국제단위계에서는 물체가 아니라 플랑크 상수를 질량 단위의 기준으로 삼는다. 임의의 질량을 갖는 분동을 플랑크 상수를 이용하여 직접 잴 수 있으므로 작은 질량을 지금보다 정확하게 잴 수 있다.
아직까지는 플랑크 상수를 이용하여 작은 질량을 실현하는 기술은 완성되어 있지 않다. 따라서 가까운 미래에는 키블 저울을 이용하여 1 kg 분동만 교정하고 작은 질량을 갖는 분동은 현재 질량 단위 보급체계를 유지할 것이다. 향후에는 1 kg에서 1 mg을 플랑크상수로부터 직접 실현하는 키블저울이 개발될 것이다. 미세질량을 플랑크상수를 이용하여 직접 실현하므로 측정정밀도를 향상시킬 수 있다.
1mg 미만의 질량은 정전기력, 광압, 자속양자 등을 이용하여 실현하는 기술이 개발될 것이다. 정전기력 저울은 물체의 무게와 정전기력을 비교하는 것으로 정전기력은 다음 식(7)과 같이 표현된다.
| (7) |
식(7)에서 FES는 정전기력, C는 용량, U는 전압이다. 수직 위치에 따라서 용량 변화가 일정하도록 전극을 설계하면 수직 위치에 둔감한 정전기력 저울을 만들 수 있다. 전압을 조셉슨 표준기를 이용하여 비교하고 전극 형상을 측정하면 국제단위계로부터 소급되며 계산이 가능한 힘을 발생시킬 수 있다.
단위재정의 이후 예상되는 질량실현 기술을 Fig. 6에 나타내었다. 단위재정의 이후에 개발되는 다양한 질량실현기술을 통하여 측정정밀도를 높이고 산업체에서 질량을 직접 실현할 수 있게 될 것이다.
6. XRCD 실험
키블저울을 이용하여 킬로그램, 미터, 초 등 국제단위계를 이용하여 플랑크상수를 측정할 수 있다. 하지만 키블저울 실험만으로 새로운 단위계에서 사용할 플랑크상수 값을 결정하면 오류가 발생할 수 있다. XRCD 실험을 이용하여 플랑크 상수를 측정함으로써 키블 저울에서 구한 플랑크 상수 값이 오류가 있는지 검증할 수 있다.
XRCD 실험은 실리콘 구안에 있는 실리콘 원자 개수를 세는 실험이다.11 원자 수를 실리콘 구에 있는 실리콘 몰 수로 나누면 아보가드로 상수를 얻을 수 있으므로 XRCD 실험을 아보가드로 실험이라고도 부른다. 아보가드로 상수와 플랑크 상수의 곱은 원자물리에서 얻어진 실험결과들로부터 잘 알려져 있다. 그러므로 XRCD에서 얻은 아보가드로 상수를 이용하여 플랑크 상수를 간접적으로 알아낼 수 있다.
실리콘 구 안에 있는 실리콘 원자개수는 다음 식(8)과 같다.
| (8) |
식(8)에서 N은 실리콘 원자 개수, V는 실리콘 구 부피, Va는 실리콘 원자 하나의 부피, a는 실리콘 격자상수이다.
실리콘 구 부피는 광학적인 방법으로 평균 지름을 측정하며 공기굴절률에 의한 오차를 줄이기 위하여 진공 중에서 측정한다. 실리콘 구를 회전시키면서 여러 지점에서 지름을 재어 평균 지름을 구한다. 구가 찌그러지면 부피 측정에 오차가 발생하므로 편차를 100 nm 미만으로 가공한다. 실리콘 격자상수는 X-선 광학계를 이용하여 측정한다.
실리콘 구안에 있는 실리콘 몰 수는 실리콘 구의 질량을 실리콘 몰 질량으로 나눈 것으로 다음과 같이 표현된다.
| (9) |
식 (9)에서 n은 실리콘 몰 수, m은 실리콘 구 질량, MSi은 실리콘 몰 질량이다. 실리콘 구의 질량은 국제킬로그램원기로부터 소급되며 수 μg불확도로 측정할 수 있다. 실리콘 몰 질량은 질량 분석기를 이용하여 12C와의 질량 비를 구한다. 12C 몰 질량이 12 g으로 정의되어 있으므로 몰 질량 측정은 국제단위계로부터 소급된다. 자연에 존재하는 실리콘은 동위원소가 있으므로 28Si 만을 99.999% 농축하여 실리콘 구를 제작한다.
XRCD 실험에서 아보가드로 상수와 측정량과의 관계식을 정리하면 다음과 같다.
| (10) |
식(10)와 같이 빛의 속도와 세슘 초미세 준위 주파수에 의하여 정의되는 미터, 12C 몰 질량, 국제 킬로그램 원기 등 국제단위계를 이용하여 아보가드로 상수를 측정할 수 있다. XRCD 실험에서 얻은 아보가드로 상수와 플랑크 상수의 관계는 리드버그 상수를 통해 알 수 있다. 수소원자의 전자에너지를 기술하는 리드버그 상수는 다음 식(11)과 같다.
| (11) |
식(11)에서 R∞는 리드버그 상수, c는 빛의 속도, me는 전자질량, Me는 전자 1몰의 질량, α는 미세구조상수이다. 리드버그 상수, 전자 몰질량, 미세구조상수는 매우 정확하게 알려져 있다. 따라서 식(11)을 통하여 XRCD에서 얻은 아보가드로 상수와 플랑크상수를 연결할 수 있다.
XRCD 실험과 키블저울 실험에서 얻은 플랑크 상수는 3 × 10-8 이내로 일치한다. 전혀 다른 원리에서 출발한 두 가지 실험이 이와 같이 낮은 측정불확도 이내에서 일치하는 것은 놀라운 사실이며 키블저울에서 측정한 플랑크상수에서 발생하는 오류가 위 불확도보다 작음을 말해준다. 새로운 단위계에서는 아보가드로 상수 값을 6.022 140 758 × 1023mol-1으로 고정하여 몰 단위의 기준을 삼는다.
새로운 단위계에서 키블저울 외에 XRCD실험을 통하여 킬로그램을 실현할 수 있다. 새로운 단위계에서는 XRCD 실험의 측정대상이 아보가드로 상수에서 실리콘 구의 질량으로 바뀐다. 식(10)을 다시 표현하면 다음 식(12)와 같다.
| (12) |
새로운 단위계에서는 플랑크 상수 값이 고정되므로 실리콘 구의 질량은 실리콘 구의 부피, 격자 상수, 실리콘 원자 질량과 플랑크 상수의 비를 측정하여 얻는다. 원자질량과 플랑크 상수의 비는 원자물리 실험결과로부터 잘 알려져 있다. 초기 속도를 가지는 원자에 빛을 흡수시키고 빛 에너지에 의하여 변하는 원자 속도를 측정하면 원자질량과 플랑크 상수의 비를 얻을 수 있다.
식(12) 역시 식(10)을 뒤집은 것에 불과한 것으로 보일 수 있다. 하지만 우리가 측정을 할 때 사용하는 기준이 변하는 물체에서 물리상수로 바뀌는 의미가 있다. 질량이 1 kg인 거시적인 물체를 기준으로 원자세계를 측량하는 것은 한계가 있다.
식(12)에서 플랑크상수 값을 고정하지 않고 실리콘 원자 질량값을 고정해도 XRCD 방법을 이용하여 킬로그램을 실현할 수 있다. 원자 질량 값을 고정하여 킬로그램을 정의하는 것은 직관적이며 이해하기 쉬우므로 원자질량을 기준으로 킬로그램을 재정의하자는 주장이 있어 왔으며 현재도 일부 연구자는 그러한 주장을 하고 있다.
원자의 질량 또한 물리상수이지만 특정한 원자의 질량보다는 물리법칙에 사용되는 플랑크 상수가 더 보편적이라 볼 수 있다. 또한 원자질량은 원자세계를 측량하는 데는 유리하지만 거시세계를 측정하는 데는 불리하다. 반면 플랑크 상수는 미시세계뿐 아니라 거시세계를 관측하는데 유리하다. 예를 들어 조셉슨 효과와 양자홀 현상을 이용하여 1 V, 1 kΩ을 측정할 수 있다.
XRCD 실험은 1 kg 및 일부 질량을 실현하는 데는 키블저울에 비하여 유용하지만 작은 질량이나 임의의 질량을 실현하는 것은 어렵다. 작은 질량을 실현하는 방법은 전에서 기술한 키블저울이나 전자기력 저울 등 전기단위를 이용한 방법들이 제안될 것이다.
7. 국내외 키블저울
단위재정의 이후 키블저울을 이용하여 킬로그램을 실현하므로 많은 표준기관에서 키블저울에 대한 연구를 진행하고 있다.
영국 NPL에서 개발한 키블저울은 2009년 캐나다 NRC로 이전되어 현재 NRC에서 운용하고 있다.12 NRC 키블저울은 Fig. 2에 보인 개념도와 유사한 구조로서 양팔저울을 사용하고 있다. 무빙 모드에서 코일을 수직 방향으로만 움직이기 위해서는 양팔저울의 팔 길이가 길어야 한다. NRC 저울의 팔 길이는 1.2 m이며 44 kg 알루미늄 합금으로 만들었다. NRC 저울은 코일 속도를 측정하기 위한 간섭계가 코일 중앙에 있다. 간섭계 위치가 코일 무게 중심과 일치하도록 간섭계 위치를 조절하여 아베 오차를 줄인다.
미국 NIST는 1980년부터 연구를 시작하였으며 양팔저울 대신에 도르래를 이용한다.13 NIST는 코일 가장자리에 3개의 간섭계를 설치하고 3개 간섭계 신호를 가중 평균하여 아베오차를 없앤다.
NIST와 NRC는 힘 비교와 구동을 같은 기구부를 이용하여 수행한다. 따라서 기구부가 무거워 판 스프링을 쓰지 않고 나이프에지를 이용하여 기구부를 지지한다. NIST와 NRC를 제외한 국가에서는 힘 비교기와 구동기를 분리하였다.
프랑스 LNE는 2000년부터 연구를 시작하였으며 양팔저울을 이용하여 힘을 비교한 후 양팔저울을 코일과 함께 움직인다.14 스위스 METAS는 1997년 연구를 시작하였으며 온도변화가 작은 영구자석을 사용하여 코일전류에 의한 온도상승이 실험에 미치는 영향을 줄였다.15 국제도량형국은 2002년 연구를 시작하였으며 코일을 움직이면서 동시에 힘을 비교하는 방식을 제안하였다.16 중국계량과학연구원은 키블저울에서 발생하는 전압을 적분하여 일률이 아니라 일을 비교하는 실험을 수행하고 있다.17
한국표준과학연구원은 단위 재정의에 기여하고 키블저울을 이용하여 킬로그램을 실현하기 위하여 2012년에 키블저울 연구를 시작하였다. 국내에서 제작중인 키블저울 모식도를 Fig. 7에 나타내었다.
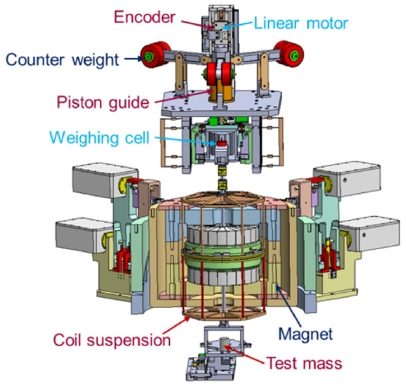
Schematics of the KRISS Kibble balance. The coil is immersed in the cylindrical permanent magnet. The difference between weight of the test mass and electromagnetic force is measured by a weighing cell. The parasitic movement of coil during the moving mode is reduced by piston guide, flexure guide, and voice coil motors
영구자석을 이용하여 반지름 방향으로 자기장이 형성되며 자석부를 연자성체로 둘러싸 생성된 자기장이 자석부 바깥으로 빠져 나오지 못하게 하였다. 무게와 전자기력의 차이는 질량비교기를 이용하여 측정하며 코일과 질량비교기를 함께 움직이도록 하였다.
리니어 모터를 이용하여 코일을 움직이며 리니어모터 측면에 있는 인코더를 이용하여 속도를 제어한다. 코일 속도는 3개의 호모다인 간섭계를 이용하여 측정하며 전압은 3개의 전압계를 조셉슨 전압과 비교 측정한다. 속도와 전압은 FPGA트리거 신호를 이용하여 동시에 측정한다.
코일을 수직 방향으로만 움직이기 위하여 피스톤과 실린더 공차를 이용한 피스톤 가이드, 판 스프링 가이드, VCM 구동기를 조합하여 가이드를 구성하였다. 코일 가장자리에 위치한 3개의 위치센서를 이용하여 VCM을 구동하여 코일이 수직으로만 움직이도록 한다. 무빙 모드에서 코일을 수직으로 10 mm 움직이는 동안 코일 수평위치 변화를 1 μm 이내로 제어하고 있다.
현재 진공중에서 키블저울 시스템을 시험 운영하고 있으며 10-7 수준의 반복도를 보이고 있다. 향후 기생 힘과 기생속도에 의한 정렬 불확도, 전기 측정 불확도 등을 향상시키는 연구를 수행할 예정이며 향후 3년이내에 10-8 수준의 불확도를 달성하여 국가 킬로그램 표준기로서 활용할 계획이다.
8. 결론
2019년에 킬로그램을 포함한 4개의 단위가 기본물리상수를 기준으로 바뀐다. 1983년 빛의 속도를 기준으로 길이 단위를 정의한 이후 가장 큰 변화이다. 1983년에 미터의 기준을 바꿀 수 있었던 것은 간섭계를 이용해서 레이저 파장 미만의 길이를 측정하는 기술이 있었기 때문이다. 빛의 속도를 기준으로 삼은 이후에 길이를 더욱 정밀하게 측정할 수 있게 되었다.
킬로그램의 기준이 사람이 만든 물체에서 플랑크 상수로 바뀜에 따라 빛의 속도 값을 고정하여 측정 정밀도가 높아진 것처럼 많은 과학적 발전이 있을 것으로 기대된다. 키블저울과 XRCD 방법을 이용하여 킬로그램을 실현하게 되므로 시간이 지나도 변하지 않는 기준을 만들 수 있다.
또한 키블저울 혹은 플랑크 상수와 질량을 연결하는 새로운 기술을 이용하여 임의의 질량을 실현하게 될 것이다. 예를 들면 1 mg 미만의 작은 질량 혹은 마이크로 캔틸레버의 스프링 상수와 같은 작은 힘을 플랑크 상수로부터 직접 구하여 측정 정밀도를 높일 수 있을 것이다. 플랑크 상수와 질량을 연결하는 장비를 교정기관이나 산업체에서 보유하게 되면 각 나라에 위치한 표준연구원에서 교정을 받지 않고 독자적으로 킬로그램을 실현할 수 있다. 단위가 재정의된 이후 플랑크 상수로부터 질량을 실현하는 새로운 기술 개발과 이를 기반으로 하는 나노 및 마이크로 분야, 정밀측정 분야의 발전을 기대한다.
NOMENCLATURE
| m : | Mass of the test mass |
| g : | Acceleration due to gravity |
| B : | Magnetic field |
| U : | Electromotive force |
| v : | Coil velocity |
| h : | Planck constant |
| e : | Elementary charge |
| KJ : | Josephson constant |
| RH : | Hall resistance |
| RK : | Von Klitzing constant |
| a : | Lattice constant |
| MSi : | Silicon molar mass |
| mSi : | Silicon atomic mass |
| NA : | Avogadro constant |
| R∞ : | Rydberg constant |
| c : | Speed of light in vacuum |
| α : | Fine structure constant |
| NPL : | National physical laboratory (UK) |
| CODATA TGFC : | CODATA task group for fundamental constants |
| BIPM : | International bureau of weights and measures |
| KRISS : | Korea research institute of standards and science |
| NRC : | National research council (Canada) |
| NIST : | National institute of standards and technology (USA) |
| LNE : | Laboratoire national de métrologie et d’essais (France) |
| METAS : | Federal institute of metrology (Switzerland) |
Acknowledgments
한국표준과학연구원에서 키블저울을 개발하는 데 도움을 준 연구자들에게 감사를 드립니다. 김종안과 김재완은 코일 위치 및 속도를 측정하는 광학계를 개발하였으며 김문석은 조셉슨 시스템을 구축하였습니다. 김완섭과 채동훈은 양자홀 시스템을 이용한 저항 측정, 최인묵은 중력측정, 이성준은 질량측정, 김민석은 광학계 정렬에 도움을 주었습니다.
REFERENCES
-
Alder, K., “The Measure of All Things,” Simon & Schuster, 2003.
[https://doi.org/10.5479/sil.743646.39088010915486]

-
Davis, R., “The SI Unit of Mass,” Metrologia, Vol. 40, No. 6, pp. 299-305, 2003.
[https://doi.org/10.1088/0026-1394/40/6/001]

-
Girard, G., “The Third Periodic Verification of National Prototypes of the Kilogram (1988-1992),” Metrologia, Vol. 31, No. 4, pp. 317-336, 1994.
[https://doi.org/10.1088/0026-1394/31/4/007]

-
Stock, M., Barat, P., Davis, R. S., Picard, A., and Milton, M. J. T., “Calibration Campaign Against the International Prototype of the Kilogram in Anticipation of the Redefinition of the Kilogram Part I: Comparison of the International Prototype with its Official Copies,” Metrologia, Vol. 52, No. 2, pp. 310-316, 2015.
[https://doi.org/10.1088/0026-1394/52/2/310]

- Rosa, E. B., Dorsey, N. E., and Miller, J. M., “A Determination of the International Ampere in Absolute Measure,” Journal of the Washington Academy of Sciences, Vol. 1, No. 8, pp. 211-218, 1911.
-
Kibble, B. P., “A Measurement of the Gyromagnetic Ratio of the Proton by the Strong Field Method,” Atomic Masses and Fundamental Constants, pp. 545-551, 1976.
[https://doi.org/10.1007/978-1-4684-2682-3_80]

-
Josephson, B. D., “Possible New Effects in Superconductive Tunneling,” Physics Letters, Vol. 1, No. 7, pp. 251-253, 1962.
[https://doi.org/10.1016/0031-9163(62)91369-0]

-
Klitzing, K. V., Dorda, G., and Pepper, M., “New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance,” Physical Review letters, Vol. 45, No. 6, pp. 494-497, 1980.
[https://doi.org/10.1103/PhysRevLett.45.494]

-
Choi, I.-M., Lee, K.-C., Lee, S., Kim, D., and Lee, H.-Y., “Gravity Measurement for the KRISS Watt Balance,” IEEE Transactions on Instrumentation and Measurement, Vol. 66, No. 6, pp.1317-1322, 2017.
[https://doi.org/10.1109/TIM.2017.2652598]

- OIML, R., “111-1 Weights of classes E1, E2, F1, F2, M1, M1-2, M2, M2-3, and M3,” International Organization of Legal Metrology, 2004.
-
Bartl, G., Becker, P., Beckhoff, B., Bettin, H., Beyer, E., “A New 28Si Single Crystal: Counting the Atoms for the New Kilogram Definition,” Metrologia, Vol. 54, No. 5, pp. 693-715, 2017.
[https://doi.org/10.1088/1681-7575/aa7820]

-
Wood, B. M., Sanchez, C. A., Green, R. G., and Liard, J. O., “A Summary of the Planck Constant Determinations Using the NRC Kibble Balance,” Metrologia, Vol. 54, No. 3, pp. 399-409, 2017.
[https://doi.org/10.1088/1681-7575/aa70bf]

-
Haddad, D., Seifert, F., Chao, L. S., Possolo, A., Newell, D. B., et al., “Measurement of the Planck Constant at the National Institute of Standards and Technology from 2015 to 2017,” Metrologia, Vol. 54, No. 5, pp. 633-641, 2017.
[https://doi.org/10.1088/1681-7575/aa7bf2]

-
Thomas, M., Ziane, D., Pinot, P., Karcher, R., Imanaliev, A., et al., “A Determination of the Planck Constant Using the LNE Kibble Balance in Air,” Metrologia, Vol. 54, No. 4, pp. 468-480, 2017.
[https://doi.org/10.1088/1681-7575/aa7882]

-
Baumann, H., Eichenberger, A., Cosandier, F., Jeckelmann, B., Clavel, R., et al., “Design of the New METAS Watt Balance Experiment Mark II,” Metrologia, Vol. 50, No. 3, pp. 235-242, 2013.
[https://doi.org/10.1088/0026-1394/50/3/235]

-
Bielsa, F., Lu, Y. F., Lavergne, T., Kiss, A., Fang, H., et al., “Alignment of the Magnetic Circuit of the BIPM Watt Balance,” Metrologia, Vol. 52, No. 6, pp. 775-782, 2015.
[https://doi.org/10.1088/0026-1394/52/6/775]

-
Li, Z., Zhang, Z., Lu, Y., Hu, P., Liu, Y., et al., "The First Determination of the Planck Constant with the Joule Balance NIM-2," Metrologia, Vol. 54, No. 5, pp. 763, 2017.
[https://doi.org/10.1088/1681-7575/aa7a65]