하중을 받는 대형 로터리 테이블의 변위 모델링

1. 서론

정밀 공작기계에서 가공물을 고정하거나 지지하는 역할을 위해 로터리 테이블을 널리 활용하고 있다. 최근 선박, 발전기, 항공분야 등에서 필요로 하는 대형 부품의 가공이 가능한 대형 공작기계에 대한 요구가 많아지고 있어 큰 하중을 지지하며 정밀한 이송을 수행해야 하는 대형 로터리 테이블의 수요 또한 증가하고 있다. 대형 부품을 지지해야 하는 로터리 테이블은 자체 하중과 공작물의 중량 및 가공 시 발생하는 외력성분 등에 의해 처짐이나 변형이 발생할 수 있으며 이는 가공 정밀도에 직접적인 영향을 미칠 수 있다. 특히 로터리 테이블을 구성하는 핵심 요소인 베어링의 특성은 이 같은 특성에 큰 영향을 미치는 것으로 알려져 있으며 공작기계의 성능 지표로도 활용되고 있어 이에 대한 정확한 평가가 필요하다.¹ 즉, 공작기계의 가공 정밀도 및 내구성 등의 성능 향상을 위해서는 로터리 테이블을 지지하는 베어링의 정확한 특성 예측이 필요하다.

대형 로터리 테이블의 수요가 증가하고 있지만 이에 대한 기술개발과 연구는 많지 않은 실정이다. 이는 대형 공작기계에 대한 요구 기술의 수준이 높고, 기술개발에 막대한 연구비와 전문 인력의 필요 등 높은 진입 장벽이 원인으로 작용하고 있기 때문이다. 대형 로터리 테이블에 대한 정확한 특성 예측이 어렵기 때문에 대부분의 로터리 테이블은 실험적으로 평가되어 왔다. 그러나 크고 대형의 공작물을 다루는 로터리 테이블의 특성으로 인해 실험적인 평가나 적정성 판단 등에도 난점이 있다.

로터리 테이블에 대한 특성 예측과 측정 방법이 많은 연구자들에 의해서 연구되어 왔다. Berend 등은 로터리 테이블을 지지하는 자기 베어링의 설계 방법을 제시 하였으나 소형테이블의 정밀 이송과 회전운동에 관한 연구로 국한하였다.² Ro 등은 유정압 안내면의 테이블 구조의 동적 모델을 제안하고 이론적 해석과 실험을 통해 모델을 검증하였다.³ Shim 등은 유정압 베어링 로터리 테이블의 회전운동정밀도, 구조루프 주파수 분석 및 모멘트 강성 실험을 통해 로터리 테이블의 성능을 실험적으로 분석하였다.⁴ 또한 로터리 테이블 회전요소로 사용되는 유정압 베어링에 대해서 Sasaki 등은 3 종류의 유정압 베어링의 압력 분포, 유량 부하 용량 등 이론적인 해를 구하고 이를 통해 동적 안전성, 최적 간극, 공급 유압 등의 베어링 설계 인자에 대해서 연구하였다.⁵ 특히 유정압 베어링에 대해 고하중의 대형 로터리 테이블이나 고속 운전 중 발생하는 진동 억제 등에 관한 연구가 진행되었다.

로터리 테이블의 오차에 관한 연구도 발표되어 왔다. Suh 등은 5축 로터리 테이블의 기하학적 오차에 대해 모델링하고 이를 실험적으로 검증하였다.⁶ 또한 오차를 측정하고 이를 보상하는 방법에 대한 연구를 진행하였다. Fan 등은 로터리 테이블의 구동 중 발생하는 열변형에 의한 오차에 대해서 측정하고 이를 보상하는 연구를 진행하였다.⁷ 그러나 하중에 의한 로터리 테이블의 변위와 이로 인한 오차에 관한 연구는 찾아 보기 어렵다.

한편 대부분의 롤러 베어링은 고하중을 지지하는 직선 이송계와 회전유니트에 주로 사용되고 있으며 대형 로터리 테이블에 적용된 연구는 아직 많지 않다. 최근 Hong⁸ 등은 대형 로터리 테이블에 적용되는 회전요소에 대한 모델링 방법을 제안하였다. 그러나 실제 로터리 테이블을 대상으로 한 해석 및 체계적인 검증은 이루어지지 않았다.

본 논문에서는 수직방향 하중을 지지하기 위해 단열 스러스트 롤러베어링을, 회전축에 대해 복열 원통 롤러 베어링을 채용한 대형 로터리 테이블에 내부, 외부 하중이 가해질 때의 정적 변형을 모델링 하였고 이를 실험적으로 검증하였다. 모델링을 위해, 충분한 강도를 갖도록 설계된 테이블 자체의 변형은 없다고 가정하였고, 롤러와 내외륜 접촉면에서 발생되는 접촉변형에 기안하는 베어링의 정적 변형에 의한 테이블 변위만을 고려하였다.

제안된 모델에 대한 실험적 검증을 위해 10 톤의 가공물을 테이블 상단에 인가하여 계산 결과와 실험 결과를 비교하였다 이를 통해 제안된 모델이 제작된 대형 로터리 테이블의 정적 특성을 효과적으로 반영하고 있음을 확인하였다. 마지막으로 제안된 모델을 이용하여 가공 중 예상되는 공작물의 자체 중량 및 절삭하중 등에 대한 테이블의 변위를 예측하였다.

2. 로터리 테이블 모델링

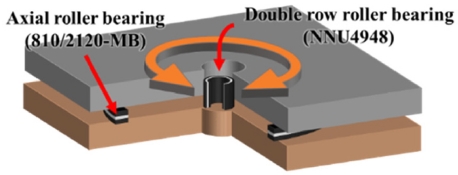
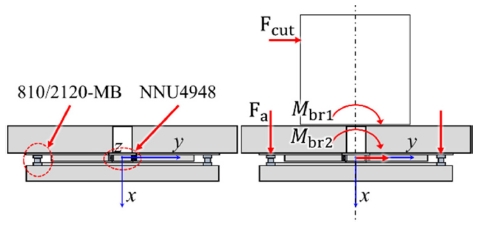
본 연구에서 고려하고 있는 대형 로터리 테이블은 3 m × 3 m로서 Fig. 1과 같이 구성된다. 축 방향 및 모멘트 하중을 지지하고 있는 스러스트 원통 롤러베어링(T-CRB, Thrust Cylindrical Roller Bearing: 810/2120-MB)과 로터리 테이블의 회전운동과 반경방향 하중을 지지하는 복열 원통 롤러베어링(D-CRB, Double Row Cylindrical Roller Bearing: NNU4948)이 사용되고 있다.

Fig. 1

Schematic diagram of the rotary table system

본 연구에서 사용한 로터리 테이블은 자체변형을 무시할 수 있도록 충분한 강도로 설계되어 베어링에서의 변형만을 고려하였다. 베어링의 변형을 계산하기 위해서는 외부하중에 의해 발생되는 베어링 접촉하중 및 이에 의한 변형식을 유도해야 한다. 베어링 접촉하중 계산 및 변형식 유도 과정은 de Mul⁹ 등에 의해 제시된 방법을 적용하였다.

2.1 스러스트 원통 롤러베어링 모델링

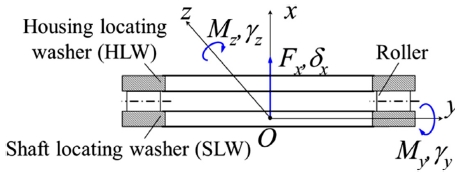
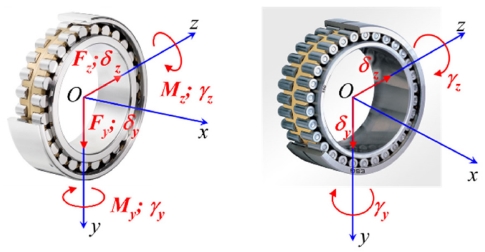
Fig. 2는 스러스트 롤러 베어링의 Oxyz 좌표계를 나타내고 있으며 베어링에 가해지는 외부하중 {F}와 변위 {δ}를 표시하였다. 하우징설치와셔(Housing Locating Washer, HLW)인 상판과 축설 치와셔(Shaft Locating Washer, SLW)인 하판 사이에 롤러가 위치하게 된다. 스러스트 롤러 베어링의 경우 반경방향이 구속되지 않으므로 3 자유도(Degree-of-Freedom)로 표현될 수 있다. 베어링 원점에 작용하는 외력과 변위는 다음과 같이 표현할 수 있다.

Fig. 2

Global coordinate system for T-CRB with loading and displacements

Fig. 3

Roller free body diagram for T-CRB

Fig. 4

Local coordinates system for T-CRB

$\[ \begin{array}{c}\left\{F\right\}={\left\{F_x M_y M_z\right\}}^T\\ \left\{\delta \right\}={\left\{{\delta }_x {\gamma }_y {\gamma }_z\right\}}^T\end{array} \]$

(1)

베어링의 평형 방정식을 유도하기 위해서는 각 롤러의 평형 방정식을 계산하여야 한다. 국부 좌표계 원점에서 정의되는 SLW 변위 {u}와 롤러의 변위 {v}는 다음과 같다.

$\[ \begin{array}{c}\left\{u\right\}={\left\{u_x \theta \right\}}^T\\ \left\{v\right\}={\left\{v_x \Psi \right\}}^T\end{array} \]$

(2)

이때 u_x, v_x는 SLW와 롤러의 축방향 변위를, θ, ψ는 각각의 각 변위를 나타낸다.

국부 좌표계 변위와 전역 좌표계 변위는 다음과 같은 관계로 표시된다.

$\[ \left\{u\right\}=\left[T_{\varphi }\right]\left\{\delta \right\} \]$

(3)

여기서, 좌표변환 행렬 [T_ϕ]는 다음과 같다.

$\[ \left[T_{\varphi }\right]=\left[\begin{array}{ccc}1 & r_p\sin \varphi & r_p\cos \varphi \\ 0& -\sin \varphi & \cos \varphi \end{array}\right] \]$

(4)

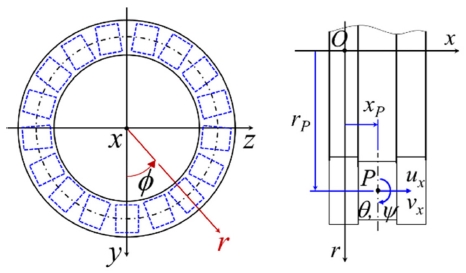
또 r_p는 원점으로부터 롤러 중심까지의 거리를 나타내며 ϕ는 롤러의 각도를 나타낸다.

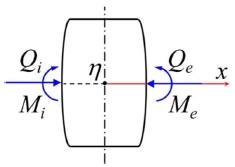
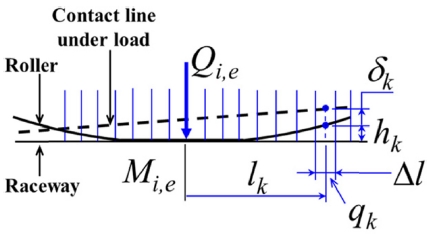
롤러와 SLW 사이의 접촉 하중 벡터{Q}를 구하기 위해서는 Fig. 5에 나타낸 슬라이싱 기법을 이용하며 롤러의 총 접촉하중을 다음과 같이 계산한다.^9-11

Fig. 5

Contact load modeling using slicing technique

$\[ q_k=c\times {\delta }_k^{10/9};\left({\delta }_k>0\right) \]$

(5)

$\[ Q_{i,e}={\sum }_{k=1}^s{q}_k;M_{i,e}={\sum }_{k=1}^s{q}_k{l}_k; \]$

(6)

여기서, c는 접촉상수이며 Harris¹¹식을 통해 정의된다.

한편 본 연구에서 사용한 롤러의 프로파일 h_k는 로그함수로 정의되며 다음과 같이 주어진다.¹²

$\[ h_k=0.0005D_a\ln \left(\frac{1}{\left(1-{\left\{\left[2\left|l_k\right|-\left(l_w-2.5D_a\right)\right]/2.5D_a\right\}}^2\right)}\right) \]$

(7)

여기서, D_a는 롤러의 직경, l_k는 슬라이스 k축의 축 방향 위치, l_w는 롤러 유효 길이를 나타낸다.

롤러와 SLW에 발생하는 변위로 인해 롤러와 SLW 및 HLW 사이에서의 접촉하중이 발생하게 된다. 롤러에 작용하는 평형 방정식을 표현하면 다음과 같다.

$\[ \left\{\begin{array}{c}{F}_x\\ M_{\eta }\end{array}\right\}=\left\{\begin{array}{c}{Q}_i-Q_e\\ M_i-M_e\end{array}\right\}=\left\{\begin{array}{c}0\\ 0\end{array}\right\} \]$

(8)

여기서, {Q}와 {M}은 롤러와 SLW 사이의 접촉하중과 모멘트를 나타내는데, 미지의 변수인 롤러 변위벡터{v}를 포함하고 있다. 이 식을 풀기 위해 본 연구에서는 Newton-Raphson법을 이용한 반복계산을 수행하였다.

롤러의 평형식을 통해 얻는 롤러의 접촉하중과 외력의 합으로부터 다음과 같은 평형식을 얻을 수 있다.

$\[ \left\{F\right\}+{\sum }_{j=1}^z\left({\left[T_{\varphi }\right]}^T{\left\{Q\right\}}_j\right)=\left\{0\right\} \]$

(9)

결국 식(9)를 풀게 되면 베어링 변위를 구할 수 있다. 식(9)는 비선형 방정식이기 때문에 앞서 언급한 Newton-Raphson법을 이용한 반복계산을 통해 베어링 변위{δ}를 계산하게 된다.

2.2 복열 원통 롤러베어링 모델링

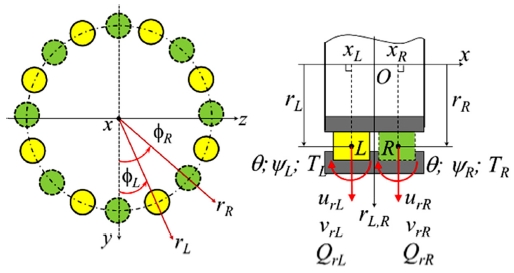
복열 원통 롤러베어링의 모델링을 위해 저자 등^13,14에 의해 제안된 해석적 모델을 사용하였다. 복열 베어링의 경우, 단열 베어링을 2개 조합한 모델을 활용할 수도 있으나 하중 조건 등을 설정할 때나 계산과정에서 오차를 유발할 수 있어 한 개의 통합된 모델을 갖는 것이 유리하다.¹⁵ Fig. 6은 복열 롤러베어링의 좌표계를 나타낸다. 원점 O는 베어링 내륜 중심에 위치한다. 복열 원통 롤러베어링의 경우 축방향으로 변위를 제외한 4개 좌표로 표현될 수 있다.¹³

Fig. 6

Double row CRB model with loading and displacement

$\[ \left\{Q_m\right\}=\left\{\begin{array}{c}-Q_i\\ -M_i\end{array}\right\} \left(m=L, R\right) \]$

(10)

Fig. 7은 특정 롤러에 대해 정의된 부분 좌표계를 보여준다. 그림에서의 왼쪽 열과 오른쪽 열의 내륜 중심을 기준점으로 정의한다.

Fig. 7

D-CRB cross-section at a particular roller

Fig. 8

Roller free body diagram for D-CRB

$\[ \left\{u_m\right\}={\left[u_{rm,}\theta \right]}^T; \left(m=L, R\right) \]$

(11)

여기서, 첨자 L, R은 각각 왼쪽, 오른쪽 열을 의미한다. 전역 좌표계를 기준으로 하는 내륜 변위벡터{δ}와 롤러의 변위벡터{u}는 다음과 같은 관계로 표현된다.

$\[ \begin{array}{c}\left[R_{{\varphi }_L}\right]=\left[\begin{array}{cccc}\cos {\varphi }_L& \sin {\varphi }_L& -r_L\sin {\varphi }_L& x_L\cos {\varphi }_L\\ 0& 0& -\sin {\varphi }_L& \cos {\varphi }_L\end{array}\right]\\ \left[R_{{\varphi }_R}\right]=\left[\begin{array}{cccc}\cos {\varphi }_R& \sin {\varphi }_R& -r_R\sin {\varphi }_R& x_R\cos {\varphi }_R\\ 0& 0& -\sin {\varphi }_R& \cos {\varphi }_R\end{array}\right]\end{array} \]$

(12)

롤러와 레이스 간의 접촉하중을 구하는 공식은 앞서 스러스트 롤러베어링과 마찬가지로 식(5), 식(6)으로 표현되며 내륜과 롤러 사이의 접촉 하중을 구하기 위해 스러스트 롤러 베어링에서와 마찬가지로 슬라이싱 기법이 이용되었다. 개별 롤러의 평형식은 다음과 같다.

$\[ \left\{\begin{array}{c}{Q}_i-Q_e+R_c\\ M_i-M_e\end{array}\right\}=\left\{\begin{array}{c}0\\ 0\end{array}\right\} \]$

(13)

식(13)을 풀면 개별 롤러의 변위벡터를 구할 수 있으며, 이를 이용해 롤러와 레이스 간의 접촉하중을 결정할 수 있다. 따라서 롤러로부터 내륜에 가해지는 접촉하중은 다음과 같다.

$\[ \left\{Q_m\right\}=\left\{\begin{array}{c}-Q_i\\ -M_i\end{array}\right\} \left(\text{m}=L, R\right) \]$

(14)

내륜의 평형식은 다음과 같이 쓸 수 있다.

$\[ \left\{F\right\}+{\sum }_{j=1}^n\left({\left[R_{\varphi L}\right]}^T{\left\{Q_L\right\}}_j\right)+{\sum }_{j=1}^n\left({\left[R_{\varphi R}\right]}^T{\left\{Q_R\right\}}_j\right)=\left\{0\right\} \]$

(15)

식(13)과 식(15)는 비선형이기 때문에 앞서 언급한 Newton-Raphson법을 이용한 반복계산을 통해 베어링 변위{δ}를 계산한다.

2.3 로터리 테이블 모델링 및 계산

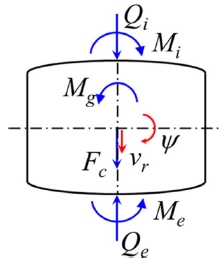
본 연구에서 고려한 시스템을 Fig. 9에서 보여주고 있다. 로터리 테이블과 테이블 상판에 고정되는 공작물을 같이 표시하였으며 가공 시 공작물에 작용되는 외력 또한 같이 나타내었다. 그림에 나타낸 바와 같이 로터리 테이블은 앞 서 기술한 두 가지 베어링의 조합에 의해 지지되고 있어 각각의 베어링에 작용하는 하중을 직접 유도하기 어려운 점이 있다.^16,17 특히 수직 하중과 달리 시스템 모멘트 평형식에는 스러스트 롤러 베어링과 복열 롤러 베어링에 작용하는 M_br1, M_br2라는 두 개의 미지 모멘트가 있어 평형식만으로 그 값을 결정할 수 없는 부정정계가 된다. 따라서 각 변위를 얻기 위해서는 모멘트 평형식에 대해 반복해법을 적용해야 한다.

Fig. 9

System configuration and loading condition

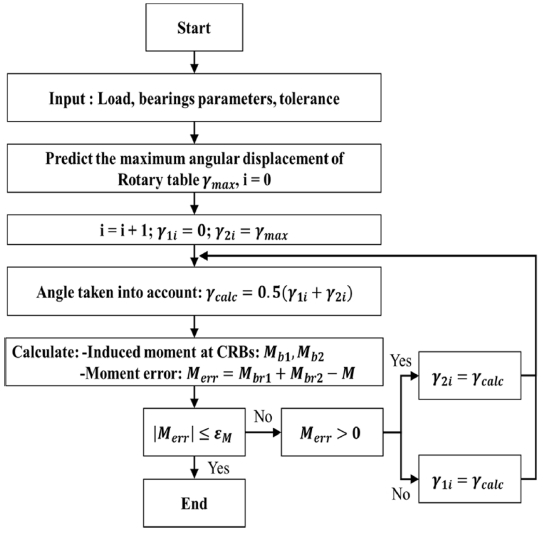
Fig. 10에 로터리 테이블에 대한 모멘트 및 각변위를 계산하는 알고리즘을 보여주고 있다. 본 연구에서는 모멘트를 결정하기 위해 이분법에 기초한 반복기법을 이용하였다. 먼저 절삭하중이나 공작물 편심에 의한 하중 등으로 인해 시스템 전체에 발생하는 모멘트 M과 공작물 및 테이블 자체 하중 F_a을 통해 스러스트 베어링의 수직변위와 각변위를 먼저 결정한다. 수직변위는 스러스트 베어링에만 의존하므로 여기서 결정된 값으로 확정한다. 각변위 결정을 위해서는 스러스트 베어링 만으로 얻어진 각변위를 최대각변위로 가정하고 각변위 0과 최대각변위 구간 내에서 이분법을 통해 실제 스러스트 베어링과 복열 롤러베어링에 발생하는 모멘트를 계산한다. 세부적인 계산알고리즘은 Fig. 10에 표현하였다.

Fig. 10

Calculation algorithm to determine the angular displacement of rotary table

3. 실험 및 모델 검증

3.1 실험 방법 및 실험 장치

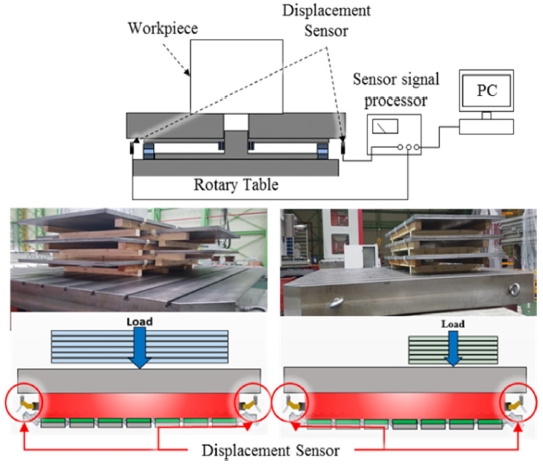
제안된 로터리 테이블의 하중에 대한 정적 변위 예측방법을 실험적으로 검증하기 위해 Fig 11과 같은 실험장치를 구성하였다. 적용된 로터리 테이블은 최대 부하 용량이 30 톤인 대형 복합 가공기의 로터리 테이블이다. 변위 센서를 Fig. 11과 같이 테이블 상판의 양 끝단에 2개를 설치하였으며 센서의 평균값을 이용하여 테이블의 수직 변위를, 센서 간의 변위 차이를 이용하여 각변위를 측정하였다. 측정에는 0-2 mm의 범위에서 0.3 μm의 분해능을 갖는 와전류형 센서를 사용하였다.

Fig. 11

Experimental setup and loading

로터리 테이블의 정적변위만을 측정하기 위해 테이블을 작동시키지 않고 고정한 상태에서 측정하였다. 측정을 위해 1 톤의 강판을 최대 10개까지 순차적으로 인가하였으며 테이블 중심에 가한 경우 및 인위적 편심을 준 경우로 실시하였다. 실험은 각각 3회를 반복하였다.

3.2 실험 및 계산 결과 비교

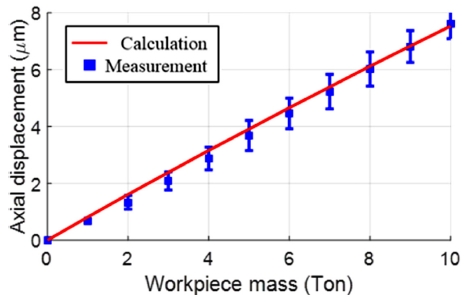
제안된 모델을 검증하기 위해 시뮬레이션 결과와 실험 결과를 비교하였다. Fig. 12에는 로터리 테이블 중심에 1 톤인 강판 10개를 순차적으로 인가하며 로터리 테이블의 처짐을 3회 반복 측정한 결과와 시뮬레이션 결과를 보여주고 있다. 테이블의 처짐은 수직 하중에 의해 발생하는 스러스트 롤러에서의 수직 변위를 나타낸다. 최대 하중인 10 톤의 하중에서 약 7.6 μm로 측정되었다. 시뮬레이션 결과는 7.5 μm로 실험 결과와 유사하게 나타나는 것을 볼 수 있다.

Fig. 12

Axial displacement of rotary table subjected to vertical load at the center

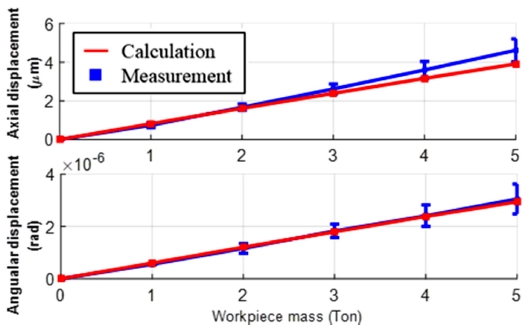
Fig. 13은 1 톤인 강판 5개를 테이블 중심에서 0.5 m 떨어진 위치에 단계별로 인가시키며 테이블 처짐을 반복 실험한 결과와 시뮬레이션 결과를 비교해서 보여주고 있다. 5 톤의 하중에서 수직 방향 처짐과 각변위는 약 4.62 μm, 각변위는 약 3.05 μrad로 측정되었다. 5 톤의 하중에 대한 시뮬레이션 결과는 수직변위 3.91 μm, 각변위는 2.94 μrad로 나타난다.

Fig. 13

Axial and angular displacements of rotary table subjected to eccentric vertical load

전체적으로 계산결과가 실험결과와 매우 유사하다는 것을 확인할 수 있으나 편심하중에 대한 수직변위 계산 결과가 다소 낮게 나타나는 것을 알 수 있다. 이는 모델링 과정에서 고려되지 않은 로터리 테이블의 회전축 변형으로 추정된다. 이를 확인하기 위해 로터리 테이블 및 축 계에 대한 추가적인 유한요소해석을 시행하였다.

본 연구에 사용된 로터리 테이블은 자체변형을 무시할 수 있도록 충분한 강도로 설계되어 있어 테이블 중앙에 인가되는 수직하중에 대해서는 무시할 수 있을 정도의 미미한 변위가 발생한다. 로터리 테이블에는 그 중심에 회전속도와 위치를 측정하기 위해 엔코더가 설치된다. 이로 인해 축과 테이블 사이가 직접적으로 결합되지 않고, 테이블 상판에 고정된 HLW 고정판에 의해 간접적으로 결합된다. 또한 축방향 하중을 지지할 수 없는 원통 롤러베어링으로 축을 지지하게 되므로 중심하중에 대한 직접적인 영향을 받지 않게 된다.

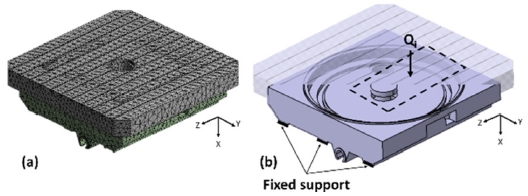
그러나 편심된 수직하중을 인가할 경우, 스러스트 베어링의 각변위로 인해 HLW의 고정판에 각변위가 발생하게 되고 이로 인해 테이블 상판의 하중이 축에 전달되어 축 변위가 발생할 수 있게 된다. 로터리 테이블 회전축의 탄성변형을 검토하기 위해 상용 유한요소해석 프로그램을 활용하였다. Fig. 14는 해석 대상 모델에 편심된 수직하중을 인가할 때의 구속 조건과 하중조건을 나타냈다. 탄성계수는 200 GPa, 밀도는 7850 kg/m³, 그리고 푸아송비는 0.3으로 하였다.

Fig. 14

FE model and loading conditions for rotary table: (a) FE model, (b) load condition

Fig. 15는 유한요소 해석 결과를 나타낸다. Fig. 15(a)는 편심된 하중 조건에서의 하판의 변형을 나타내고 있으며 그 절대크기는 크지 않다. Fig. 15(b)는 같은 조건에서 발생되는 축 변위만을 나타낸다. Fig. 16는 여기서 얻어진 축 변위를 반영하여 로터리 테이블의 변위를 계산한 결과와 축 변위를 고려하지 않은 모델의 계산 결과, 그리고 실험 결과를 비교해서 보여주고 있다. 그림을 통해 축 변형 효과를 고려하면 기존 결과보다 실험값에 더욱 잘 일치하는 것을 확인할 수 있다.

Fig. 15

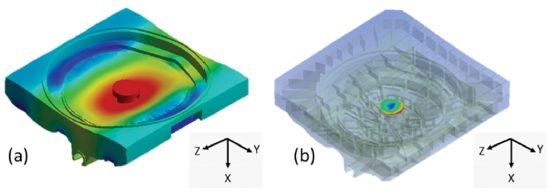
Axial displacement when eccentric load is applied deformation of lower table (b) deformation of shaft

Fig. 16

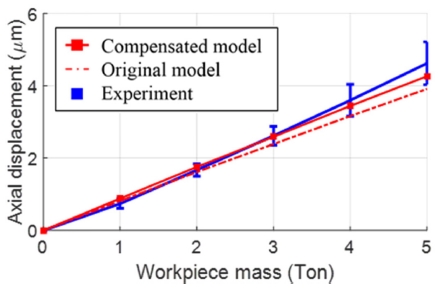
Comparison of vertical deflections of rotary table when eccentric load is applied (experiment and simulations with and without shaft deformation)

테이블 중심에 수직하중이 가해진 경우와 달리 편심하중에 의해 축 변형의 영향이 결과에 나타나고 있음을 확인하였다. 그러나 결과에 볼 수 있는 바와 같이 그 절대량은 크지 않으며 특히 실제 공작물을 설치할 때 공작물의 무게 중심이 중앙에서 크게 벗어나지 않도록 하게 된다는 점을 고려하면 편심하중에 의한 축 변형 효과는 실제적으로는 크지 않을 것으로 판단된다.

이상의 결과로부터 두 개의 지지 베어링을 모델링하여 내부/외부 하중을 받는 로터리 테이블의 정적 변위를 실험 결과와 유사하게 예측할 수 있음을 확인하였다. 따라서 제안된 모델은 본 연구에서 대상으로 고려하고 있는 대형 로터리 테이블 형태, 즉 스러스트 원통 롤러 베어링과 복열 원통 롤러 베어링을 채용한 대형 로터리 테이블에 대해 하중에 의한 변위 해석에 유용할 것으로 판단된다. 다음 장에서는 제안된 모델을 대형 로터리 테이블 위에 설치된 공작물에 절삭력이 가해질 때의 변위를 예측하는 데 활용한 예를 제시하였다.

4. 시뮬레이션

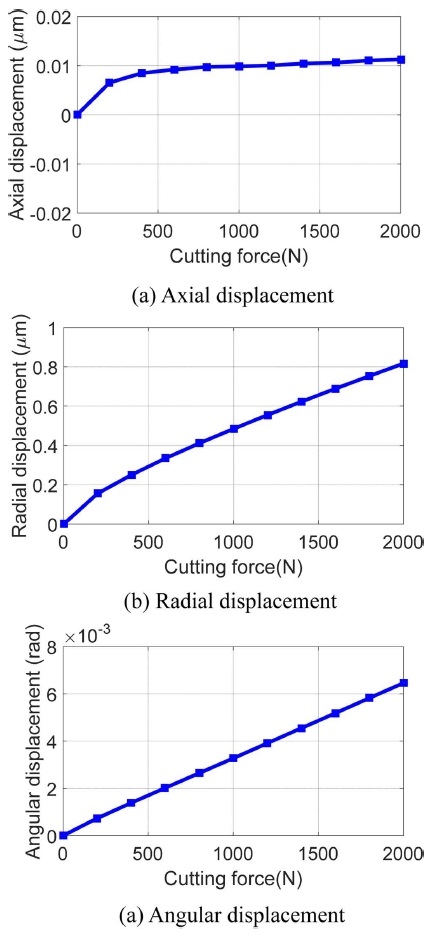
제안된 모델을 이용하여 가공 중 발생할 수 있는 외부 하중에 의한 변위를 계산하는 시뮬레이션을 수행하였다. 시뮬레이션을 위해 중량이 30 톤인 공작물이 테이블 중앙에 설치되었고, 테이블로부터 3 m 높이에서 Fig. 9와 같이 절삭이 이루어지고 있다고 가정하였으며, 절삭력에 따른 로터리 테이블의 변위를 분석하였다. Fig. 17은 절삭 력에 따른 로터리 테이블의 변위를 나타낸다. 그림에서 볼 수 있듯이 절삭력은 축방향 변위에는 미미한 영향을 미치나 각변위와 반경방향 변위에는 직접적으로 영향을 주는 것을 확인할 수 있다.

Fig. 17

Displacements due to cutting force

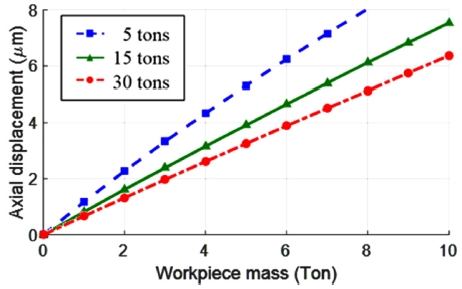
로터리 테이블의 변위는 테이블 자체의 중량 및 공작물의 중량에도 영향을 받게 된다. 테이블 자체 중량에 의한 예압 효과로 인해 같은 중량의 공작물을 테이블에 인가하여도 테이블 자체 중량에 따라 그 변위가 달라질 수 있다. Fig. 18은 로터리 테이블의 자체 중량에 의한 예압을 달리하였을 때 하중에 따른 상대적인 처짐량을 나타낸다. 테이블 중량을 변경시키면서, 공작물 하중 0-10 톤을 인가하였을 때의 변위를 비교해서 보여주고 있다. 결과에서 볼 수 있는 바와 같이 테이블의 자체 질량이 클수록 추가 하중에 의한 상대 변위량이 감소함을 확인할 수 있다. 이는 테이블의 중량이 증가함에 따라 롤러의 접촉면적이 증가하면서 강성 또한 증가하기 때문인 것으로 판단된다. 현재 테이블의 중량은 15 톤이며 이를 바꾸면 베어링 예압을 변경시키는 효과를 볼 수 있다. 이상 제안한 예는 공작물 하중 및 절삭력 등 로터리 테이블에 인가되는 하중에 의한 변위를 제공하게 됨으로써 가공 오차를 예측하거나 보상하는 데 유용하게 활용될 수 있을 것으로 예상된다.

Fig. 18

Variation of deflections due to the workpiece mass for three different masses of rotary table

5. 결론

본 연구에서는 스러스트 롤러 베어링과 복열 원통 롤러 베어링으로 지지되는 대형 로터리 테이블의 정적 특성을 모델링하고 계산하는 방법을 제안하였다. 사용된 2가지 베어링에 대한 수치적 모델을 도입하였고 복합 베어링 조건에서의 부정정계 특성을 고려한 반복해법을 적용하였다. 정적 하중에 대한 처짐을 시뮬레이션 하였으며 실험을 통해 개발된 모델 및 계산과정의 타당성을 검증하였다. 개발된 모델을 이용하여 공작물 하중 및 절삭력 등 로터리 테이블에 인가되는 하중에 의한 변위를 계산하는 예를 제시하였다. 개발된 모델은 대형 로터리 테이블이 장착된 대형 공작기계의 가공 시 오차를 예측하거나 보상하는 데 유용하게 활용될 수 있을 것으로 기대된다.

Acknowledgments

본 연구는 산업통상자원부와 한국 산업 기술 진흥원이 지원하는 경제 협력권 산업 육성 사업으로 수행된 연구 결과입니다.

REFERENCES

• Hong, S. W. and Tong, V. C., “Rolling-Element Bearing Modeling: A Review,” International Journal of Precision Engineering and Manufacturing, Vol. 17, No. 12, pp. 1729-1749, 2016. [https://doi.org/10.1007/s12541-016-0200-z]
• Denkena, B., Dahlmann, D., Floeter, F., and Bruehne, T., “Conceptual Design for Electromagnetic Guided Rotary Table in Machine Tools,” Procedia CIRP, Vol. 24, pp. 80-85, 2014. [https://doi.org/10.1016/j.procir.2014.08.010]
• Ro, S. K., Lee, C. H., and Park, C. H., “A Study on the Dynamic Modeling of a Hydrostatic Table,” Journal of the Korean Society for Precision Engineering, Vol. 15, No. 3, pp. 150-156, 1998.
• Shim, J. Y., Oh, J. S., Park, C. H., Shin, H. C., Park, W. S., et al., “Performance Evaluation of Hydrostatic Bearing Guided Rotary Table for Large Volume Multi-Tasking Vertical Lathe,” Journal of the Korean Society for Precision Engineering, Vol. 31, No. 7, pp. 635-642, 2014. [https://doi.org/10.7736/KSPE.2014.31.7.635]
• Sasaki, T., Mori, H., and Hirai, A., “Theoretical Study of Hydrostatic Thrust Bearings,” Bulletin of the Japan Society of Mechanical Engineers, Vol. 2 No. 5, pp. 75-79, 1959. [https://doi.org/10.1299/jsme1958.2.75]
• Suh, S. H., Lee, E. S., and Jung, S. Y., “Error Modelling and Measurement for the Rotary Table of Five-Axis Machine Tools,” International Journal of Advanced Manufacturing Technology, Vol. 14, No. 9, pp. 656-663, 1998. [https://doi.org/10.1007/BF01192286]
• Fan, K. C., Lin, J. F., and Lu, S. S., “Measurement and Compensation of Thermal Error on a Machining Center,” Proc. of the 29th International Matador Conference, pp. 261-268, 1992. [https://doi.org/10.1007/978-1-349-12433-6_33]
• Hong, S. W., Tong, V. C., and Park, W. S., “Modeling of Bearing Used for Rotary Table of a Large Machine Tool,” Proc. of the Korean Society of Manufacturing Technology Engineers Spring Conference, p. 126, 2017.
• De Mul, J. M., Vree, J. M., and Maas, D. A., “Equilibrium and Associated Load Distribution in Ball and Roller Bearings Loaded in Five Degrees of Freedom while Neglecting Friction- Part II: Application to Roller Bearings and Experimental Verification,” Journal of Tribology, Vol. 111, pp. 149-155, 1989. [https://doi.org/10.1115/1.3261865]
• Tong, V. C. and Hong, S. W., “Fatigue Life of Tapered Roller Bearing Subject to Angular Misalignment, Proceedings of Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 230, No. 2, pp. 147-158, 2016. [https://doi.org/10.1177/0954406215578706]
• Harris, T. A., “Rolling Bearing Analysis,” John Wiley & Sons, 4th Ed., 2006. [https://doi.org/10.1201/9781482275148]
• ISO/TS 16281, “Rolling Bearings Methods for Calculating the Modified Reference Rating Life for Universally Loaded Bearings,” International Organization for Standardization, 2008.
• Tong, V. C. and Hong, S. W., “Modeling and Analysis of Double-Row Cylindrical Roller Bearings,” Journal of Mechanical Science and Technology, Vol. 31, No. 7, pp. 3379-3388, 2017. [https://doi.org/10.1007/s12206-017-0627-x]
• Tong, V. C., Kwon, S. W., and Hong, S. W., “Fatigue Life of Cylindrical Roller Bearings,” Proceedings of Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, Vol. 231, No. 5, pp. 623-636, 2017. [https://doi.org/10.1177/1350650116668767]
• Tong, V. C. and Hong, S. W., “Analysis of the Stiffness and Fatigue Life of Double-Row Angular Contact Ball Bearings,” Journal of the Korean Society for Precision Engineering, Vol. 34, No. 11, pp. 813-821, 2017. [https://doi.org/10.7736/KSPE.2017.34.11.813]
• Tong, V. C., Bae, G. H., and Hong, S. W., “Dynamic Analysis of Spindle Supported by Multiple Bearings of Different Types,” Journal of the Korean Society for Precision Engineering, Vol. 32, No. 2, pp. 117-125, 2015. [https://doi.org/10.7736/KSPE.2015.32.2.117]
• Tong, V. C., Shin, H. C., and Hong, S. W., “A Study on Modeling of Large Size Rotary Table,” Proc. of the KSPE Spring Conference, p. 631, 2016.