정밀가공을 위한 CNC 알고리즘 연구 현황

1. 서론

다품종 소량생산 기술, 기계적 성능향상을 위한 자유곡면 등 복잡형상 가공, 티타늄과 탄소섬유복합재(Carbon Fiber Reinforced Plastic, CFRP)와 같은 난삭재 가공의 필요성 등이 증가하면서 최근 공작기계에 적용되는 수치제어(Computerized Numerical Control, CNC)의 고속 고정밀화를 구현하기 위한 다양한 연구가 이루어지고 있다. CNC는 공구경로계획의 생성, 이송계의 위치제어 등을 수행하는 자동화된 공작기계의 핵심 구성요소로서, 고속 고정밀화를 위해서는 CNC 보간 정밀도의 향상, 위치제어기의 성능 향상, CNC를 이용한 공작기계의 오차 보상제어의 구현 등이 필요하다.

CNC의 보간기에서 생성되는 공구경로계획은 공구의 위치, 공구이송 시의 가속도와 저크(Jerk)를 결정한다. 제어의 기준이 되는 공구경로가 계획단계에서 이미 공작기계가 수행할 수 있는 능력을 넘어설 경우 위치오차 및 장비의 진동 등을 유발하여 가공정밀도를 저하시키기 때문에 기구학적 한계와 가공정밀도를 고려하는 보간 방법에 대한 연구가 이루어지고 있다.¹

CNC의 위치제어기의 성능을 결정하는 윤곽오차는 작업물의 치수정밀도를 결정하기 때문에 윤곽오차 저감을 위한 다양한 제어 알고리즘이 연구되고 있다.^2,3

CNC 공작기계에는 기계부품의 기하학적인 부정확성, 조립 오차, 치수오차 등에 의한 기하학적 오차, 구동 중 발생한 열에 의한 열변형 오차 등이 존재하며, 이러한 오차는 공작기계의 가공정밀도를 저하시킨다. 또한 CNC 공작기계 이송계에 작용하는 마찰력과 같은 외란은 제어성능을 저하시킨다. 따라서 CNC제어기에는 기하학적 오차, 열변형 오차를 보상하기 위한 알고리즘과 마찰력과 같은 외란을 보상하기 위한 알고리즘이 포함되어 있으며, 기하학적 오차, 열변형 오차, 마찰력 등의 예측정확도를 높이고 이를 보상하기 위한 제어 알고리즘이 제안되고 있다.^4,5

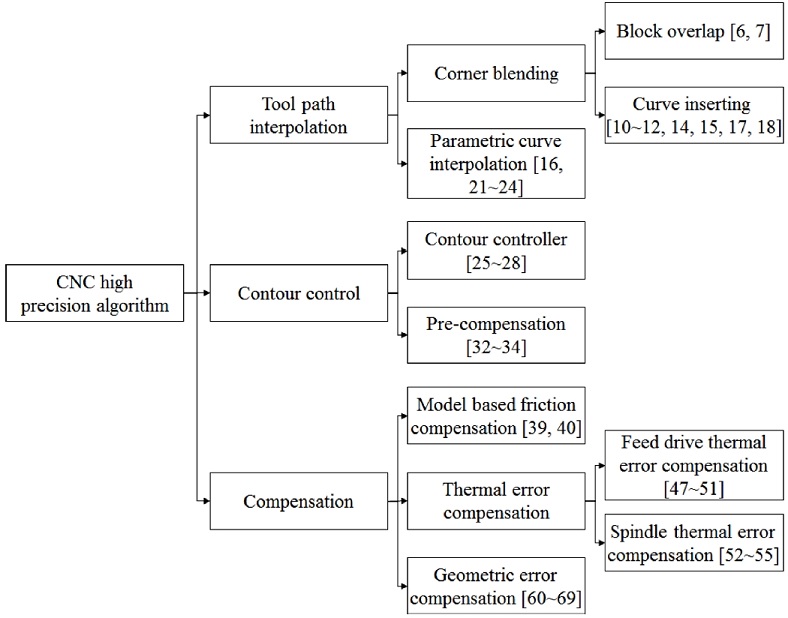
본 논문에서는 CNC의 제어 정밀도 향상을 위한 최근 연구동향을 정리하였다. 2절에서는 CNC 보간 알고리즘의 연구동향을 정리하였으며, 3절에서는 CNC 공작기계의 윤곽오차 저감을 위한 제어 알고리즘에 대해 살펴보았고, 4절에서는 기하학적 오차, 열변위, 마찰 보상을 CNC 에 구현하기 위한 알고리즘에 대해 정리하였다.

2. CNC 보간 알고리즘

2.1 코너 블렌딩 알고리즘

보간기(Interpolator)는 Computer-Aided Manufacturing (CAM) 소프트웨어에서 생성되거나 사용자가 입력한 파트프로그램을 이용하여 CNC 공작기계의 공구경로계획을 생성한다. CAM 소프트웨어는 작업물을 사용자가 설정한 허용오차 범위 내에서 G01 블록으로 근사하여 파트프로그램을 생성하는 기능을 제공한다. CNC 보간기는 G01 블록으로 구성된 파트프로그램의 보간 시, 급격한 가감속으로 인해 발생하는 CNC 공작기계의 진동과 충격을 방지하기 위해 G01 블록에 가감속 프로파일을 적용한다. 하지만 가감속으로 인하여 가공시간이 증가하기 때문에, CNC 보간기는 블록 오버랩(Block Overlap)을 적용하거나, 인접한 블록의 코너에 Kinematic 곡선, B-Spline 곡선, Pythagorean Hodograph (PH) 곡선 등을 삽입하여 지령된 종점을 지나지 않도록 공구경로 계획을 생성하는 코너 블렌딩(Corner Blending) 알고리즘을 적용하고 있다. 코너 블렌딩 적용 시 인접한 블록 사이의 코너 부근에서 항상 오차가 발생하기 때문에, 가공정밀도를 높이기 위해서 코너에서 발생하는 오차를 사용자가 정한 허용오차(Tolerance) 이내로 제한할 수 있는 코너 블렌딩 알고리즘이 연구되고 있다.

블록 오버랩 알고리즘은 속도 프로파일의 중첩을 통해 공구경로계획을 생성하며, 연산부하가 낮아 CNC 실시간 보간에 적용하기 용이하다는 장점이 있다. Sencer et al.⁶은 Finite Impulse Response (FIR) 필터를 적용한 Kinematic 프로파일의 블록 오버랩 시 중첩시간을 조절함으로써 코너링 오차(Cornering Error)를 제한하는 알고리즘을 제안하였다. 하지만 블록 내에서 지령된 이송속도에 도달하지 못하는 미소블록의 Kinematic 프로파일은 고려하지 않았기 때문에, 미소블록이 포함된 파트프로그램에 적용하는데 한계를 가진다. Lee et al.⁷은 미소블록을 고려하여 FIR 필터를 적용한 속도 프로파일을 생성하였고, 인접한 속도 프로파일의 중첩시간을 조절하여 경로계획오차(Tool Path Error)를 제한하는 알고리즘을 제안하였다.

Fig. 1과 같이 인접한 두 블록 사이에 곡선을 삽입하는 알고리즘⁸은 속도, 가속도 연속성의 보장과 가속도, 저크 제한을 적용한 공구경로계획의 생성이 용이하다는 장점이 있다. 상용 CNC에 코너링 오차의 제한이 가능한 코너 블렌딩을 위한 코드가 구현된 경우가 있으며, 해당 기능 적용 시 인접한 블록의 코너에 C² 연속성을 보장하는 4차 다항식 커브를 삽입한다.⁹ 최근에 연구되고 있는 알고리즘은 일반적으로 저크의 제한이 가능하고, 가속도의 연속성을 보장하는 저크 제한 가속 프로파일(Jerk Limited Acceleration Profile)을 적용하고 있다.^10-12 Zhao et al.¹⁰은 코너 블렌딩 시 허용오차 범위 내에서 C² 연속성을 보장하는 3차 B-Spline 커브를 삽입하는 알고리즘을 제안하였다. 또한 선독(Look-Ahead) 알고리즘을 적용하여 블록마다 제한조건을 만족하는 최적의 속도를 계산하였다. 하지만 B-Spline 곡선과 같은 매개변수형 곡선(Parametric Curve)은 공구경로계획 생성을 위해 실시간으로 매개변수(Parameter) 증분치를 계산하는데 높은 연산능력을 필요로 하기 때문에, Tajima et al.¹¹은 허용오차 범위내에서 Kinematic 곡선을 삽입하여 코너 블렌딩을 하는 알고리즘을 제안하였다.

Fig. 1

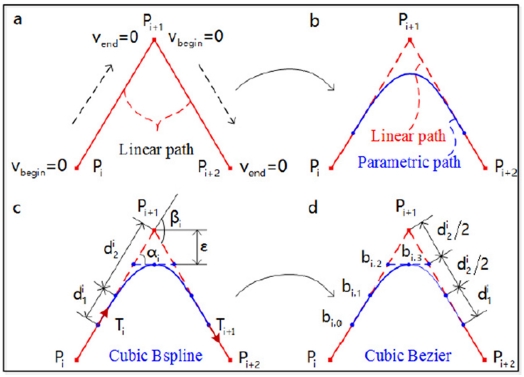
Corner blending by inserting curve between adjacent blocks8 (Adapted from Ref. 8 on the basis of open access)

커브 삽입을 통한 코너 블렌딩 알고리즘은 코너 삽입을 위한 충분한 거리가 확보되지 않으면 연속된 블록에서 삽입된 코너가 중첩될 수 있다. Tajima et al.¹²은 선독 알고리즘을 적용하여 삽입된 커브의 중첩 발생 유무를 미리 판단한 이후에, 중첩이 없는 경우에는 Kinematic 커브를 삽입하고, 중첩이 발생하는 경우에는 중첩구간에 대해서 새로운 Kinematic 커브를 생성하여 삽입하는 방식을 제안하였다.

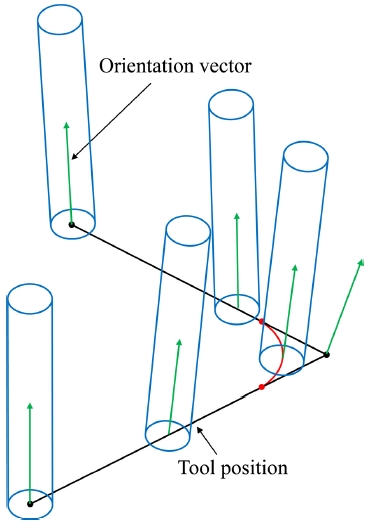
5축 CNC 공작기계는 회전축이 추가되기 때문에 코너 블렌딩 시 공구위치(Tool Position)와 공구방향(Tool Orientation)을 동시에 고려해야 하며, 공구위치 허용오차와 공구방향 허용오차를 고려해서 코너 블렌딩을 적용해야 한다. 5축 CNC 공작기계를 위한 보간 알고리즘에는 Fig. 2와 같이 3축 코너 블렌딩 기법을 적용해 생성된 2개의 곡선을 이용해 공구위치와 공구방향을 보간하는 방식이 있다.¹³ 또한 공구방향에 대해서는 3축 코너 블렌딩 기법을 적용하고, Fig. 3과 같이 공구방향에 대해 코너 블렌딩을 직접 적용하여 보간하는 방식이 있다.

Fig. 2

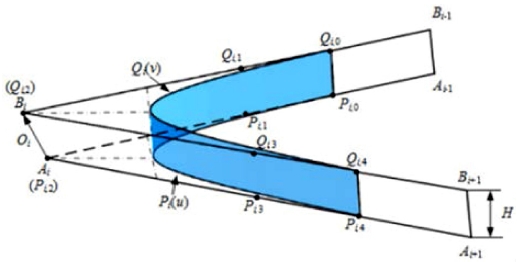
Five-axis interpolation algorithm using dual curve13 (Adapted from Ref. 13 on the basis of open access)

Fig. 3

Tool orientation interpolation algorithm applying direct corner blending at tool orientation

Beudaert et al.¹⁴은 5축 CNC 보간을 위해 3차 B-Spline 커브를 삽입하여 하단곡선(Bottom Curve)과 상단곡선(Top Curve)을 생성하고, 하단곡선을 공구위치 보간에 사용하고, 하단곡선과 상단곡선의 각도를 이용해 공구방향의 보간을 수행하는 알고리즘을 제안하였다. 직선 부분과 삽입된 곡선의 연결점에서 공구방향의 불연속을 막고, 하단곡선과 상단곡선의 매개변수의 동기화를 위해 Newton–Raphson방법을 사용해 매개변수를 최적화하는 알고리즘을 제안하였다. Shi et al.¹⁵은 하단곡선과 상단곡선의 코너 블렌딩에 5차 PH 곡선을 삽입하는 알고리즘을 제안하였다. 하단 곡선과 상단곡선의 매개변수 동기화 시 반복적 방법을 통한 최적화 알고리즘을 사용할 경우 시간이 많이 소요되어 실시간 보간에 적용하기 어려우므로, PH 곡선의 제어점(Control Point)사이의 길이를 조정함으로써 연결점에서 공구방향의 연속성을 보장하는 방법을 제안하였다. 하지만 두 개의 곡선을 사용하여 공구방향을 보간하는 방식은 공구위치 이송량은 작으나, 공구방향 이송량은 큰 경우에는 알고리즘의 성능이 저하된다.¹⁶

Tulsyan et al.¹⁷은 공구위치의 코너 블렌딩을 위해 C³ 연속성을 만족시키는 5차 Spline 곡선을 삽입하고, 공구방향의 코너 블렌딩을 위해서는 공구방향 허용오차 범위 내에서 정규화된 7차 B-Spline 커브를 삽입하는 알고리즘을 제안하였다. 보간을 통해 생성된 공구위치와 공구방향의 동기화를 위해 동일한 매개변수를 사용하였다. 하지만 공구방향의 제어점 위치 계산에 필요한 비선형 방정식의 해를 얻기 위해 반복적 기법인 Newton–Raphson 방법을 사용하였기 때문에 많은 계산시간이 필요하다. Yang et al.¹⁸은 공구위치와 공구방향의 코너 블렌딩을 위해 위해 C³ 연속성을 만족시키는 5차 B-Spline 곡선을 삽입하였다. 공구위치 및 공구방향의 동기화와 공구방향 오차 제한을 위한 해석적인 방법을 제시하여, 실시간 적용에 용이하도록 하였다.

2.2 매개변수형 곡선 보간 알고리즘

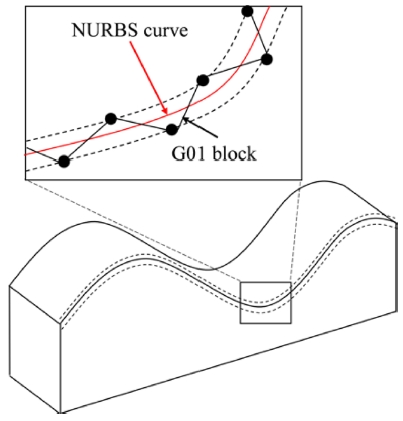
매개변수형 곡선은 자유곡면이 포함된 복잡한 형상을 정확하게 표현할 수 있으며, 동일한 작업물을 표현하기 위해 필요한 곡선의 개수도 G01 블록에 비해 적다. CAM 소프트웨어는 Non-Uniform Rational B-Spline (NURBS) 곡선과 같은 매개변수형 곡선으로 허용오차 범위 내에서 근사하여 파트프로그램을 생성하는 기능을 제공하고 있다. CNC 보간기는 매개변수형 곡선관련 정보로 구성된 파트프로그램의 실시간 보간을 위한 알고리즘을 제공하고 있으며, 이송속도를 고려하여 계산된 매개변수 증분치와 제어점, 제어점에 대한 가중치(Weight)를 이용하여 실시간으로 공구경로계획을 생성한다. 또한 Fig. 4와 같이 G01 블록으로 구성된 경로를 매개변수형 곡선으로 근사한 이후에 보간하는 알고리즘도 제공하고 있다. Yuen et al.¹⁶은 파트프로그램이 G01 블록으로 구성된 경우에는, G01 블록을 미리 선독하여 허용오차 범위 이내에서 G01 블록들을 매개변수 곡선으로 근사하는 알고리즘을 제안하였다. 상용 CNC에 구현된 방법으로는 G01 블록을 허용오차 범위 내 에서 NURBS 커브로 근사한 이후에 보간을 수행하는 나노 스무딩(Nano Smoothing) 기능과¹⁹ G01 블록을 매개변수형 곡선으로 근사하여 보간하는 Compressor 방식이 있다.²⁰

Fig. 4

Approximation the G01 blocks as a parametric curve

매개변수형 곡선 보간 알고리즘은 공구경로계획 생성을 위해 서 매개변수 증분치와 원호길이(Arc Length)를 계산해야 한다. 하지만 직선과 원호의 경우를 제외하고는 원호길이를 구하기 위한 해석적인 관계가 없고, 매개변수 증분치와 원호길이 사이에도 해석적 관계가 없기 때문에, 매개변수 증분치와 원호길이를 계산하기 위해서는 보간 알고리즘을 적용해 근사값을 계산한다. 또한 계산된 매개변수 증분치와 원호길이의 정확도가 낮을수록 이송속도의 변동폭이 크게 발생한다. 계산 정확도를 높이기 위해 복잡한 알고리즘을 적용할수록 계산부하가 커져 실시간 보간 적용에 한계를 가진다. 따라서 실시간 보간에 적용가능하며 매개변수 증분치와 원호길이를 정확하게 계산하기 위한 다양한 연구가 이루어지고 있다.

매개변수형 곡선에서 C⁰ 연속성을 가지거나, 곡률이 큰 부분을 높은 이송속도로 지날 경우 가속도와 저크가 크게 발생하고, 위치정밀도가 저하된다. Lee et al.²¹은 NURBS 곡선을 C⁰ 연속성을 가지거나, 곡률이 큰 점을 기준으로 작은 NURBS 곡선 블록으로 나눈 후에 NURBS 보간을 수행하는 알고리즘을 제안하였다. 가속도, 저크, 코드오차(Chord Error) 제한값을 고려하여 NURBS 곡선 블록의 종점에서 허용가능 이송속도를 계산하였으며, 사인 곡선 속도 프로파일을 적용하여 이송속도 스케줄링(Feederate Scheduling)을 하였다. 원호길이 계산을 위해 Adaptive Lobatto Quadrature Method를 사용하였다. NURBS 곡선을 작은 NURBS 곡선 블록으로 나누는 알고리즘, 허용가능 이송속도 계산 알고리즘, 이송속도 스케줄링을 실시간으로 구동할 경우 높은 연산능력을 필요로 하기 때문에 오프라인으로 구동하였다. NURBS 곡선 보간기는 실시간으로 구동하였으며, 설정된 이송속도 오차 범위 내에서 매개변수 증분치를 계산하기 위해 Predictor-Corrector Interpolator (PCI) 알고리즘을 사용하였다. Jia et al.²²은 코드오차, 가속도, 저크 제한과 이송계의 윤곽오차 제한값을 고려하여 전체 NURBS 곡선에 대해 허용가능 이송속도를 계산하고, 허용가능 이송속도가 지령된 이송속도보다 작은 구간(Feederate-Sensitive Region)에서 이송속도를 등속으로 변경하는 이송속도 스케줄링 알고리즘을 제안하였다. 원호길이 계산을 위해서는 Simpson’s Rule과 Adaptive Bisection Technique을 적용하였다. 제안된 알고리즘에서도 이송속도 스케줄링은 오프라인으로 구동하였다. NURBS 보간 시 저크 제한 가속 프로파일을 적용하여 매 보간주기마다 이송거리를 계산하였으며, 매개변수 증분치 계산 정확도를 높이기 위해 2차 Runge-Kutta 방법과 매개변수 보상 방법을 결합한 알고리즘을 제안하였다. 제안된 NURBS 보간기를 적용하여 이송계 구동 시 코드오차, 가속도, 저크, 윤곽오차가 제한 값 이내로 제한되는 것을 실험적으로 검증하였다. 이송속도 스케줄링과 NURBS 보간기를 오프라인과 온라인으로 나누어 구동하는 경우 상대적으로 연산부하가 적어져, 매개변수 증분치 및 원호길이 계산 정확도를 높이기 위해 복잡한 알고리즘을 적용할 수 있다. 하지만 오프라인 알고리즘을 구동하는데 추가적인 시간이 소요되기 때문에 전체 가공시간이 증가하는 단점이 있다. Liu et al.²³은 이송속도 스케줄링과 NURBS 보간기를 온라인으로 구동하였으며, 연산부하를 저감시키기 위해 원호길이 계산에는 Simpson’s Rule과 Adaptive Bisection Technique을 사용하였으며, 파라미터 보간에는 원호길이와 매개변수의 관계식을 3차 다항식으로 근사하는 Re-Mapping 알고리즘을 적용하였다. NURBS 곡선을 C⁰ 연속성을 가지거나, 코드오차와 구심가속도가 제한조건보다 크게 발생하는 점을 기준으로 작은 NURBS 블록으로 나누고, 저크 제한 가속 프로파일을 적용하여 이송속도를 스케줄링하는 알고리즘을 제안하였다.

5축 CNC 공작기계에서는 회전축이 추가되어 작업물 좌표계와 기계좌표계가 비선형 관계를 가지기 때문에, 공구를 기준으로 기구학적 제한조건을 만족시키더라도 각 축에서는 기구학적 제한조건을 만족시키지 못할 수 있다. Sun et al.²⁴은 5축 CNC 공작기계의 코드오차, 공구의 접선방향 가속도, 공구의 접선방향 저크, 공구의 각속도, 각 축의 속도, 가속도, 저크 제한조건을 고려하여 이송속도를 스케줄링하는 오프라인 전처리 알고리즘을 제안하였다. 한 번의 계산으로 허용가능 이송속도의 계산이 가능한 Neighbor-Independent (NI) 제한조건과 반복적 계산이 필요한 Neighbor-Dependent (ND) 제한조건으로 구분하여 허용가능 이송속도를 계산하였다. ND 제한조건에서 허용가능 이송속도 계산 시 수정된 이송속도로 인해 이송속도의 변동폭이 크게 발생하는 것을 줄이기 위해 Curve Evolution 방법을 적용하였다.

3. CNC 윤곽제어 알고리즘

윤곽오차는 공작기계의 목표경로와 현재위치 사이의 최단거리로서, 작업물의 치수정밀도를 결정하는 주요 요소이다. 최근 5축 공작기계를 활용한 복잡한 형상 가공이 보편화 됨에 따라 임의의 자유곡면 형상에 적용하기 위한 윤곽제어 알고리즘, 5축 공작기계에 적용하기 위한 윤곽제어 알고리즘, 공구경로계획 보정을 통한 윤곽제어 알고리즘 등이 연구되고 있다.

Rahaman et al.²⁵은 고속가공 시 적용 가능한 Cross-Coupled Control (CCC), Zero Phase Error Tracking Control (ZPETC)과 Real-Time Frequency Modulated Interpolation (FMI) 알고리즘의 성능을 비교하였다. 기존 알고리즘보다 윤곽오차 저감 효과를 높이기 위해 Linearized Cross-Coupled Control (LCCC) 과 FMI를 조합한 윤곽제어 알고리즘을 제안하였으며, 고속 이송 시 코너 부분에서의 윤곽오차 저감에 효과적임을 실험적으로 검증하였다. Huo et al.²⁶은 기존의 CCC 알고리즘이 직선, 원호 또는 미리 정의된 비선형 곡선에 대해서만 적용이 가능하다는 한계를 극복하기 위해 임의의 자유곡면 형상에도 적용 가능한 Generalized Cross-Coupled Control (GCCC) 알고리즘을 제안하였다. 위치 지령만을 이용하여 윤곽오차를 예측하였으며, 이를 이용해 CCC제어기의 게인 값을 설정하였다. 또한, 매개변수형 곡선의 위치 지령에 대해서도 제안한 알고리즘이 적용 가능함을 보였다. 기존에 제안된 Taylor Series Expansion Error Compensation (TSEEC)²⁷은 CNC 공작기계 이송계 모델을 기반으로 테일러 급수를 활용하여 각 축의 윤곽오차 보상량을 계산하였다. 하지만 이는 직선 또는 원호 형태 경로의 윤곽제어에만 적용 가능하였다. 이에 Huo et al.²⁸은 TSEEC를 확장하여 일반적인 임의의 자유곡면 형상에도 적용할 수 있도록 Generalized TSEEC 를 제안하였다. 위치지령과 현재 위치 사이의 거리를 순차적으로 비교함으로써 임의의 곡선에서 윤곽오차를 계산하는 알고리즘을 제안하였다. 기존에 제안된 ZPETC와 CCC 알고리즘과의 성능비교를 통해 제안된 알고리즘의 성능을 검증하였다.

3축 CNC 공작기계는 공구위치 윤곽오차만을 고려하지만, 5축 CNC 공작기계는 Fig. 5와 같이 공구방향 윤곽오차도 고려해야 한다. Altintas et al.²⁹은 5축 공작기계의 윤곽오차 저감을 위해 다중입력 다중출력 슬라이딩 모드 제어기(Multi-Input Multi-Output Sliding Mode Controller)를 설계하였다. 공구위치 윤곽오차 저감을 위해 병진운동을 하는 축으로 구성된 슬라이딩 모드 제어기를 설계하였고, 공구방향 윤곽오차 저감을 위해 회전운동을 하는 축으로 구성된 슬라이딩 모드 제어기를 설계하였다. Yang et al.³⁰은 5축 공작기계의 윤곽오차를 실시간으로 예측하고, 보상하는 알고리즘을 제안하였다. 일반화된 5축 자코비안 함수를 사용하여 임의의 5축 공작기계 구성에 적용가능 하도록 하였다. 기존의 5축 윤곽제어 알고리즘은 윤곽오차 예측 시 정기구학(Forward Kinematics)과 역기구학(Inverse Kinematics)을 필요로 하는 반면, 제안된 알고리즘에서는 기구학 모델을 사용하지 않고, 자코비안 함수만을 이용하여 윤곽오차와 각 축의 윤곽오차 성분을 계산하였다. 계산된 윤곽오차 성분을 이용하여 축 별 윤곽제어 폐루프(Closed-Loop)를 구성하였고, 알고리즘의 성능을 실험적으로 검증하였다. Li et al.³¹은 5축 공작기계 윤곽오차 예측을 위해 매개변수형 곡선을 이용하는 알고리즘을 제안하였고, 윤곽오차 저감을 위해 이중 슬라이딩 모드 윤곽제어 알고리즘(Dual Sliding Mode Contouring Control)을 제안하였다. 기존의 슬라이딩 모드 제어기를 사용한 5축 윤곽제어 알고리즘은 역자코비안(Inverse Jacobian) 및 자코비안 변화량의 계산을 필요로 하기 때문에 높은 연산능력을 필요로 한다. 이에 반해, 제안된 알고리즘에서는 윤곽오차 예측 알고리즘을 이용하여 추종오차와 윤곽오차 저감을 위한 PD 형태의 슬라이딩 평면을 독립적으로 각각 설계하였다. 기존의 5축 윤곽오차 예측 방법과³⁰ 제안된 윤곽오차 예측 알고리즘의 성능을 윤곽오차 예측정확도 비교를 통해 검증하였고, 실험을 통해 제안한 알고리즘의 윤곽오차 저감성능을 검증하였다.

Fig. 5

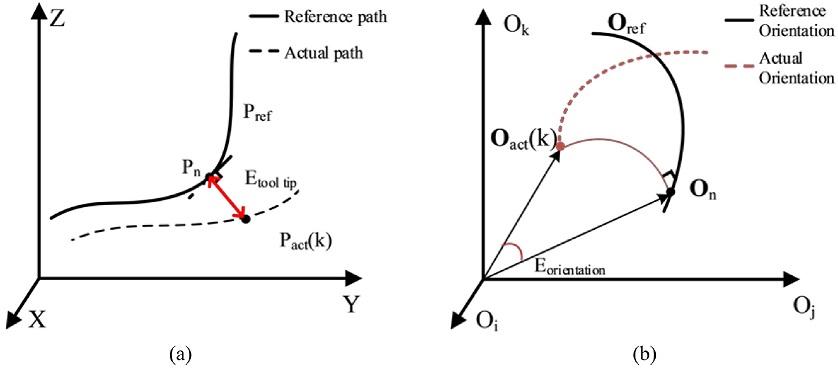
Contour errors in 5-axis machine tools: (a) Tool tip contour error (Etooltip) and (b) Tool orientation contour error (Eorientation)

윤곽오차 저감을 위한 실시간 제어기 설계 방법 외에도 공구경로계획 보정 방법 또한 연구되고 있다. 공구경로계획 보정 알고리즘은 예측된 윤곽오차를 보상하도록 공구경로계획을 사전에 보정하는 방법으로 제어기 구조를 변경하지 않기 때문에 일반적인 제어 알고리즘에 비해 현장에서의 적용이 용이하다. Zhang et al.³²은 공구경로계획 보정을 통한 5축 공작기계 윤곽오차 저감 알고리즘을 제안하였다. 공구경로계획의 속도, 가속도, 저크 연속성을 위해 이를 5차 다항식으로 근사 후 선형화된 이송계의 전달함수를 이용하여 각 축의 추종오차를 예측하였고, 이를 이용하여 5축 공작기계의 윤곽오차를 예측하였다. 예측된 윤곽오차를 저감하도록 각 축의 공구경로계획을 보정하였고 제안된 알고리즘의 성능을 실험을 통해 검증하였다. 기존의 공구경로계획 보정 알고리즘은 다음 보간주기의 공구경로계획에 대해서만 윤곽오차를 예측하기 때문에 공구경로계획 중 곡률이 큰 부분에서는 오차 저감 성능이 떨어지는 한계가 존재한다. 이러한 단점을 극복하기 위해 Yang et al.³³은 모델기반 예측 제어 방법을 조합한 공구경로 보정 방법을 제안하였다. 정해진 보간주기만큼 공구경로계획을 미리 생성하고, 각각의 공구경로계획에서 윤곽오차를 계산 한 후에 각 위치 별 가중치를 설정하여 전체 윤곽오차가 저감되도록 설계하였다. 실험을 통해 기존 공구경로계획 보정 방법과 제안한 알고리즘의 성능을 비교하였다. Zhang et al.³⁴은 반복적인 공구경로 보정을 통해 윤곽오차를 저감하는 알고리즘을 제안하였다. 이송계의 선형모델과 역전파(Back Propagation) 신경망으로 모사한 외란 모델을 이용하여 각 축의 추종오차를 예측하였다. 예측된 추종오차를 이용하여 윤곽오차를 계산하였고, 이 값이 특정 값 이하가 될 때까지 추종오차를 보상하도록 공구경로 보정 과정을 반복하였다.

4. CNC 보상 알고리즘

4.1 마찰력 보상 알고리즘

CNC 공작기계 이송계에 작용하는 비선형 마찰력은 스틱슬립(Stick-Slip), 리밋 사이클(Limit Cycle), 정상상태오차(Steady State Error) 등을 야기하며, 이로 인해 이송계의 위치 정밀도가 저하된다. 이는 가공 정밀도의 저하로 이어지기 때문에 이송계에 작용하는 마찰력을 마찰모델을 이용해 예측하고, 예측된 마찰력을 보상함으로써 정밀도를 향상시키기 위한 연구가 수행되었다.

모델 기반의 마찰력 보상 알고리즘의 성능은 마찰력 예측 정확도에 영향을 받기 때문에, 이송계에 작용하는 마찰력의 모델링이 중요하다. 고전마찰모델(Classical Friction Model)은 속도에 대한 함수로 나타나는 쿨롱 마찰력(Coulomb Friction), 점성 마찰력(Viscous Friction), 스트라이벡 마찰력(Stribeck Friction)과 같은 정적 마찰 특성을 모델링 하기 위해 사용되었다. Bui et al.³⁵은 고전마찰모델이 속도 구간마다 나타나는 마찰력의 정점을 표현하지 못하기 때문에, 쿨롱 마찰력과 점성 마찰력에 정점을 표현하기 위한 가우시안 함수를 추가한 마찰모델을 제안하였다. 제안한 마찰모델을 이용한 피드포워드 제어(Feed-Forward Control)를 적용한 결과, 고전마찰모델과 비교하였을 때 고속 구간에서 마찰력 예측정확도와 위치정밀도가 향상됨을 검증하였다. Bui et al.³⁶은 볼스크류(Ball Screw)와 너트(Nut)의 편심에 의해 이송계의 위치에 따라서 주기적으로 나타나는 마찰력 변화를 리드 스크류(Lead Screw)와 너트 접촉부위에서 가상의 용수철의 압축과 인장으로 나타내는 마찰모델을 제안하였다. 실험을 통해 고전마찰모델과 비교하였을 때 제안된 마찰모델이 위치와 속도에 따른 마찰력 예측 정확도가 높음을 검증하였다. 또한 제안된 모델을 이용한 마찰력 보상을 수행하였을 때 고전마찰모델을 이용하여 마찰력을 보상할 때보다 위치정밀도가 향상되었다.

하지만 고전마찰모델은 저속에서 발생하는 스틱슬립, 리밋 사이클, 히스테리시스(Hysteresis)와 같은 동적 마찰 특성을 예측할 수 없다. 따라서 정적 마찰 특성과 동적 마찰 특성을 모두 예측하기 위해 LuGre 마찰모델,³⁷ Leuven 마찰모델과³⁸ 같은 마찰모델이 제안되었다. Ruderman³⁹은 LuGre 마찰모델보다 평균 마찰 예측 정확도가 높은 2SEP(Two-State Dynamic Friction Model with Elastoplasticity) 마찰모델을 이용한 마찰력 관측기(Friction Observer)를 설계하였다. 비례제어와 2SEP 모델 기반의 마찰력 관측기를 사용한 경우, 최적화된 게인을 갖는 비례-적분제어기를 사용하였을 때에 비해 위치정밀도가 향상됨을 확인하였다. Lee et al.⁴⁰은 LM 가이드(Linear Motion Guide)-볼스크류 타입의 이송계를 사용하는 CNC 공작기계에서 LM 가이드와 볼스크류의 마찰 특성이 다르므로, LM 가이드와 볼스크류의 마찰력을 각각 모델링하였다. 이송계에 작용하는 마찰력을 집중 모델(Lumped Model)이 아닌 분산 모델(Distributed Model)로 표현하였고, 실험에서 얻은 마찰력 데이터를 유전자 알고리즘으로 처리하여 구성 부품별로 LuGre 마찰모델의 파라미터를 식별하였다. Fig. 6은 집중 모델과 제안된 분산 모델의 마찰력 예측 결과를 비교한 것으로, 분산 모델 사용 시 마찰력 예측 정확도가 향상됨을 검증하였다. 또한 제안된 분산 모델에 기반한 마찰력 관측기를 제안하였으며, 집중 모델을 사용하였을 때에 비해 위치정밀도가 향상됨을 실험적으로 검증하였다.

Fig. 6

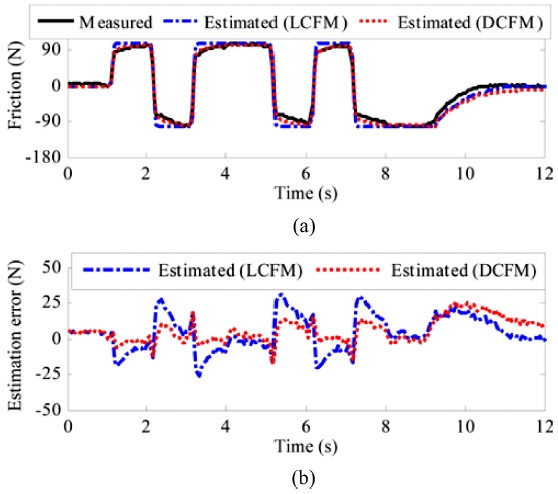
Comparison of (a) estimated friction, (b) friction estimation error40 (Adapted from Ref. 40 with permission)

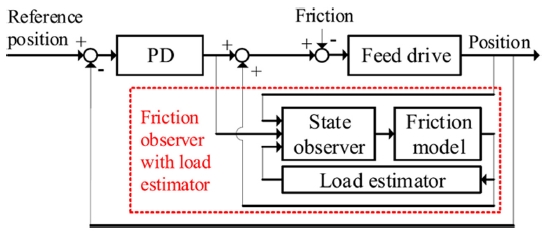
모델 기반의 마찰력 보상 알고리즘에서 마찰모델 파라미터의 불확실성과 마찰모델의 불확실성은 보상 알고리즘의 성능을 저하시키는 원인이 된다. Lee et al.⁴¹은 식별된 파라미터의 불확실성을 줄이기 위해 적응 제어를 이용하여 LuGre 마찰모델의 파라미터를 실시간으로 예측하는 알고리즘을 제안하였다. 제안된 마찰력 보상 적응 제어기를 쿨롱 마찰력과 점성 마찰력을 보상하는 제어기, LuGre 모델 파라미터의 일부만 예측했던 적응 제어기와 비교한 결과, 제안된 제어기의 위치정밀도가 높음을 확인하였다. Lee et al.⁴²은 이송계에 가해지는 하중에 따르는 쿨롱 마찰력의 변화를 예측하기 위하여 Fig. 7과 같은 하중 예측기(Load Estimator)를 제안하였다. 하중에 따라서 변하는 쿨롱 마찰력을 LuGre 마찰모델에 포함하였고, 하중 예측기를 이용한 새로운 마찰력 관측기를 제안하였다. 하중 예측기의 검증을 위하여 하중의 변화를 가할 수 있는 특수한 이송계를 제작하였다. 비례-미분제어기와 하중 예측기를 포함하는 마찰력 관측기를 함께 이용하는 경우, 하중 예측기를 사용하지 않는 마찰력 관측기를 사용할 때보다 위치정밀도가 높음을 보였다.

Fig. 7

Block diagram of load estimator42 (Adapted from Ref. 42 with permission)

이송계에 마찰력 외의 외란이 작용할 경우 외란에 의하여 제어성능이 저하될 수 있다. 따라서 모델 기반의 마찰력 보상 알고리즘에 외란 관측기(Disturbance Observer)를 추가하여 마찰력 외의 외란을 보상하는 알고리즘이 연구되고 있다. Lin et al.⁴³는 속도의 3차 다항함수로 표현되는 마찰모델을 도입하여 피드포워드 제어를 적용하였고, 마찰력 외의 외란을 예측하기 위해 외란 관측기를 적용하였다. 또한 이송계 모델의 불확실성에 의해서 발생하는 외란 관측기의 성능 저하에 대비하여 강인성을 높인 가변 구조 제어기(Variable Structure Controller)를 추가하였다. 가변 구조 제어기 사용 시 불연속 스위칭(Discontinuous Switching)에 의해서 발생하는 채터링(Chattering)을 제거하기 위하여 1차 필터를 추가하였다. 제안된 제어기를 비례-적분-미분 제어와 외란 관측기를 이용한 제어기, 비례-적분-미분 제어와 외란 관측기와 마찰력 피드포워드 제어를 이용한 제어기 등과 비교하였을 때 위치 정밀도가 향상됨을 확인하였다. Lin et al.⁴⁴은 리니어 모터(Linear Motor)를 이용한 이송계에서 발생하는 비선형 마찰력을 표현하기 위해 정적 마찰력은 Hsieh-Pan 모델, 동적 마찰력은 LuGre 모델로 각각 모델링하였다. 또한 외란 관측기를 사용하여 마찰력 외의 외란을 예측하여 보상하고, 입자 군집 최적화(Particle Swarm Optimization)를 이용하여 최적화된 파라미터를 갖는 가변 구조 제어기를 사용하여 외란에 대한 강인성을 높였다. 실험 결과에서 비례-적분-미분 제어기에 외란 관측기를 적용한 제어기와 비교하였을 때 위치 정밀도가 향상됨을 보였다.

4.2 열변형 오차 보상 알고리즘

공작기계 구동 중 발생하는 열에 의한 열변형 오차는 전체 공작기계 오차 중 50-70%를 차지한다.⁴⁵ 따라서 가공정밀도를 향상시키기 위해 공작기계의 열변형오차를 예측하고 보상하는 알고리즘의 적용이 필요하며, 열변형 오차 예측을 위한 모델링 알고리즘과 모델링에 필요한 적절한 온도 측정 위치와 수를 결정하는 알고리즘에 관한 연구가 수행되고 있다.

CNC 공작기계에는 LM 가이드-볼스크류 타입의 이송계가 주로 사용 되고 있다.⁴⁶ 볼스크류의 열변형 오차는 이송계의 위치 오차에 영향을 미쳐 가공 정밀도를 감소시킨다. 따라서 공작기계 정밀도 향상을 위해 볼스크류의 열변형 오차를 보상하는 연구가 이루어지고 있다. Thiem et al.⁴⁷은 열변형 오차와 이송계 구조의 상관관계를 고려한 열변형 오차 모델을 제작하였으며, 열변형 오차 모델의 파라미터를 최적화 기법을 이용해서 계산하는 알고리즘을 제안하였다. 파라미터 최적화 기법 적용 시 Fig. 8과 같이 열변형 오차 모델의 정확도가 증가함을 시뮬레이션을 통해 검증하였다. Li et al.⁴⁸은 열 전도 방정식을 이용한 실시간 열변형 오차 모델을 제안하였다. 유한요소해석을 통해 이송속도에 따른 볼스크류의 온도를 예측하고, 이를 토대로 이송속도와 측정한 온도에 따른 열변형 오차 모델을 제작하였다. 실험을 통해서 열변형 오차 모델의 정확도를 확인하였다. Li et al.⁴⁹은 볼스크류의 열변형 오차 모델의 정확도를 향상시키기 위해서 온도뿐 아니라 스핀들 속도, 가공이력을 변수로 사용하였다. 다중회귀모델(Multiple Regression)과 역전파 기법을 이용하여 열변형 오차 모델을 제작하였다. 온도만을 고려해 제작한 열변형 오차 모델과 스핀들 속도, 가공 이력을 추가적으로 고려해 제작한 모델을 비교하여 정확도가 향상됨을 보였다. Shi et al.⁵⁰은 LM 가이드-볼스크류 타입의 이송계에서 발생한 열로 인한 오차와 볼스크류 열 팽창의 관계를 수학적으로 모델링하고 실험을 통해 검증하였다. 볼스크류 온도와 축 변형을 측정하여 볼스크류의 열팽창계수를 추정하였고, 다중 선형 회귀 기법(Multiple Linear Regression Method)을 이용하여 볼스크류 위치에 따른 열변형 오차의 관계식을 계산하고 실험을 통해 검증하였다. Feng et al.⁵¹은 LM 가이드-볼스크류 타입의 이송계에서 볼스크류의 열변형 오차의 원인을 마찰열에 의한 동적 피치 오차로 가정하고, 볼스크류의 열적 특성을 분석하여 동적 피치 오차를 모델링하였다. 볼스크류의 열적 특성이 볼스크류의 위치에 따라 동일하지 않기 때문에 볼스크류를 여러 구간으로 나누어 모델을 만들고 중첩시켜 전체 오차 모델을 완성하였다. 실험을 통해 제안한 모델을 검증하고 보상 알고리즘을 통해 LM 가이드-볼스크류 타입의 이송계의 열변형 위치 오차가 50% 감소됨을 확인하였다.

Fig. 8

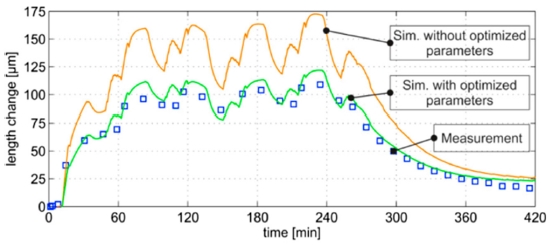
Effect of parameter adjustment on simulated thermal error47 (Adapted from Ref. 47 on the basis of open access)

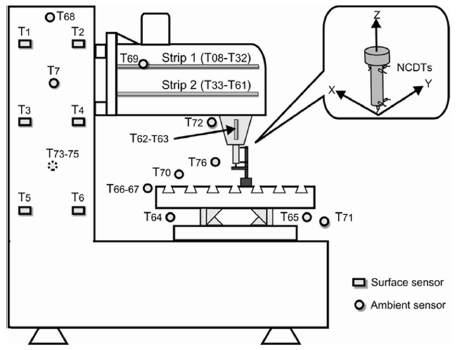
공작기계에서 스핀들은 주요 열원 중 하나이며 스핀들에 발생하는 열변형 오차는 최종 가공 정밀도에 영향을 미치기 때문에 이를 모델링하고 보상하는 연구도 활발하게 진행되고 있다. Huang et al.⁵²은 고속 스핀들 시스템에서 스핀들에 발생한 열변형 오차를 역전파 기법과 유전자 알고리즘(Genetic Algorithm)을 결합하여 모델링하였다. 기존의 역전파 기법을 이용한 모델링은 역전파 모델의 초기 가중치를 임의의 값으로 설정하고 학습을 통하여 모델을 생성한다. 제안한 모델은 유전자 알고리즘을 이용하여 최적화된 값을 역전파 모델의 초기 가중치로 설정하여 학습을 진행하였다. 그 결과, 제안한 모델이 기존 역전파 기법을 이용한 모델보다 수렴 속도가 빠르고, 예측 정확도가 향상됨을 검증하였다. Abdulshahed et al.⁵³은 Fuzzy C-Means Clustering 방법을 이용하여 열변형 오차와 높은 상관관계를 가지는 측정 온도의 위치를 선정하고, 적응형 뉴로-퍼지 추론시스템(Adaptive Neuro Fuzzy Inference System)을 이용하여 열변형 오차를 모델링하였다. Fig. 9는 기계 시스템의 온도 측정 센서와 스핀들의 축방향과 원주방향의 열변형 오차 측정 시스템 나타낸 것이다. Liu et al.⁵⁴은 스핀들의 원주방향의 열변형 오차를 예측하고, 이를 보상하는 방법을 제시하였다. 스핀들 하우징의 상하에 센서를 부착해 온도를 측정하고, 측정한 온도와 스핀들 변형의 기구학적 모델을 이용하여 스핀들 원주방향의 열변형 오차를 모델링하였다. 모델링한 열변형 오차만큼 오프셋을 주어 오차를 보상하는 알고리즘을 제시하고 실험을 통해서 검증하였다. Tan et al.⁵⁵은 공작기계 스핀들의 열변형 오차를 최소 자승법 서포트 벡터 머신(Least Squares Support Vector Machine) 방법을 이용하여 모델링하였다. 열변형 오차 예측 정확도를 보장하면서 스핀들의 온도 측정 수를 줄이기 위해서 Least Absolute Shrinkage and Selection Operator (LASSO)를 이용하였다. 회색 모델, 다중 선형 회귀 기법을 이용한 열변형 오차 모델과 제안한 모델을 비교하여 예측 정확도가 향상됨을 검증하였다.

Fig. 9

Location of thermal sensors on the machine53 (Adapted from Ref. 53 on the basis of open access)

열변형 오차 모델의 정확도와 강건성은 모델링에 사용한 온도의 측정 위치에 영향을 받기 때문에 온도 측정 위치 선정이 중요하다. Miao et al.⁵⁶은 다양한 조건에서 측정한 열변형 오차와 온도를 이용하여 Least Squares Multiple Linear Regression Model (LS-MLR), Least Absolute Multiple Linear Regression Model (LA-MLR), Distributed Lag Model (DL), Support Vector Machine Regression Model (SVR)의 성능을 비교하였다. 하나의 배치(Batch) 데이터로 모델링 할 경우 DL 모델의 정확도가 가장 높았으나 강건하지 못하였고, SVR 모델이 강건하면서 정확도가 높았다. 여러 개의 배치 데이터로 모델링한 경우 LS-MLR, LA-MLR, DL 모델은 강건성이 높아졌으나 SVR 모델은 감소하였다. Miao et al.⁵⁷은 공작기계의 온도 측정 위치의 변화에 따른 열변형 오차 보상 모델의 정확도와 강건성을 연구하였다. 공작기계에서 측정한 온도 값 간의 공선성(Collinearity)으로 인해 열변형 오차 모델의 예측 정확도가 강건하지 못함을 확인하였다. 주성분회귀 알고리즘(Principal Component Regression Algorithm)을 이용하여 측정한 온도 간의 공선성을 제거한 열변형 오차 보상 모델을 제시하였다. 또한 열변형 오차 모델의 정확도를 향상시키기 위해서 트래버스 최적화 기법(Traverse Optimization Method)을 이용하여 온도 측정 위치를 결정하였다. 또한 Liu et al.⁵⁸은 능형회귀 알고리즘(Ridge Regression Algorithm)을 이용하여 측정 온도 간의 공선성을 최소화하면서 동시에 측정 온도와 열변형 오차의 상관관계의 변동성을 줄이는 모델을 제시하고 이를 검증하였다.

4.3 기하학적 오차 보상 알고리즘

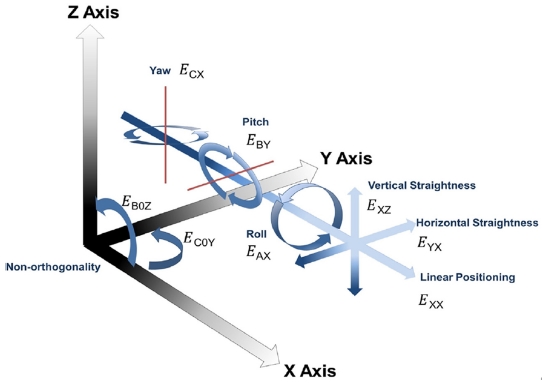
기하학적 오차는 CNC 공작기계 구성 요소의 기하학적인 부정확성, 조립 과정에서 발생하는 정렬오차, 치수오차 등에 의해 발생하는 공작기계의 오차이다. 일반적인 3축 공작기계에서는 각 축의 선형위치(Linear Position), 수직 및 수평 진직도(Vertical and Horizontal Straightness), 롤(Roll), 피치(Pitch), 요(Yaw)와 X-Y, Y-Z, Z-X축의 직각도(Squareness) 오차의 총 21가지 기하학적 오차가 발생하며, Fig. 10은 3축 공작기계에서 발생할 수 있는 기하학적 오차를 나타낸 것이다.⁵⁹ 기하학적 오차는 장비가 구동되는 동안 지속적으로 위치정밀도를 저하시키는 원인이 되기 때문에 상용 CNC에는 기하학적 오차를 보상하기 위한 기능을 제공하고 있다.²⁰ 또한 기하학적 오차를 모델링하고, 보상하려는 다양한 연구가 수행되고 있다.

Fig. 10

Geometric error of linear axis59 (Adapted from Ref. 59 on the basis of open access)

Feng et al.⁶⁰은 갠트리 타입의 대형 밀링 센터의 진직도 오차를 실시간으로 보상하기 위한 연구를 수행하였다. 공간상의 진직도 오차를 B-Spline 커브를 이용해 근사하였고, 상용 CNC에서 제공하는 EMOO (External Mechanical Origin Offset) 기능을 이용하여 다수의 오차를 실시간으로 보상하여 진직도 오차가 90% 이상 감소함을 확인하였다. Zha et al.⁶¹은 갠트리 타입 그라인딩 장비의 유정압 안내면에서 발생하는 진직도 오차의 모델링 및 보상에 관한 연구를 하였다. 오차의 평균화 기법을 이용하여 유정압 안내면의 진직도 오차를 모델링 하였고, 오차를 보상하여 Y-Slider의 수직방향 진직도 오차를 크게 감소시킬 수 있음을 확인하였다.

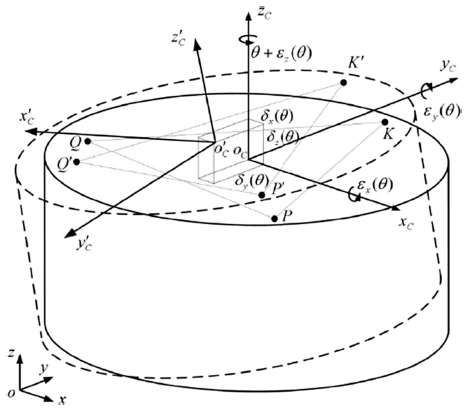
3축 CNC 공작기계에 2개의 회전축이 추가된 5축 CNC 공작기계는 복잡한 형상을 가공할 수 있다는 장점이 있지만, 기구학적으로 복잡한 형상을 가지게 되며 회전축의 추가로 인해 3축 대비 20개 증가한 41개의 기하학적 오차가 발생할 수 있다. Fig. 11은 회전축에서 발생할 수 있는 6가지의 위치 의존적 기하학적 오차(Position Dependent Geometric Error)를 나타낸 것이다.⁶² 이러한 기하학적 오차는 5축 공작기계의 정밀도를 하락시키는 원인 중 하나로, 가공정밀도 향상을 위해 5축 CNC 공작기계에서 발생하는 기하학적 오차의 측정, 모델링 그리고 보상하기 위한 다양한 연구가 수행되고 있다.

Fig. 11

Six geometric error in C-axis62 (Adapted from Ref. 62 on the basis of open access)

Zhu et al.⁶³은 각 회전축에서 발생하는 6 종류의 기하학적 오차를 모델링 하고, 볼바(Ball Bar)를 이용한 오차 식별 방법을 제안하였다. 제안한 방식은 다축 공작기계의 구성 방식에 관계없이 적용할 수 있다는 장점이 있다. 또한 제안한 모델을 기반으로 가공에 사용되는 파트 프로그램을 수정하여 기하학적 오차를 보상하였다. He et al.⁶⁴은 5축 CNC 공작기계의 2개의 회전축에서 발생하는 12가지의 기하학적 오차를 측정하기 위해 Dual Optical Path Measurement Method (DOPMM)를 제안하였다. DOPMM은 두 개의 레이저 간섭계(Laser Interferometer)에서 측정한 값을 이용하여 변위 오차와 각도 오차를 계산하는 측정 방식이다. 기존의 볼바를 이용한 측정 방식이 두 개 이상의 축을 동시에 움직이는 반면, DOPMM은 하나의 축만을 움직이며 측정할 수 있다. 또한 기존의 측정 방식은 오차 측정 시 기하학적 오차의 모델링이 필요한 반면, 제안된 방법은 별도의 오차 모델링 없이 기하학적 오차를 계산할 수 있다. Chen et al.⁶⁵은 Denavit-Hartenberg Theory를 기반으로 하는 B, C 회전축의 기하학적 오차 모델을 제안하였다. 제안한 모델을 기반으로 Double Ball Bar (DBB)를 이용하여 회전축에서 발생하는 12개의 위치 오차와 12개의 모션 오차를 측정하였다. Zhong et al.⁶⁶은 DBB 측정법에 기초한 5축 공작기계의 공간 오차(Volumetric Error)를 평가하기 위한 새로운 측정 방식인 Spherical Deviation Measurement Method를 제안하였다. ISO 10791-6의 부속서A에서 정의된 기구학적 오차 테스트 방법인 Circular Deviation 방식은 하나의 테스트 경로의 오류만을 반영할 수 있지만, 제안한 방식은 다른 테스트 경로 사이의 오프셋 오류도 반영할 수 있으며, 3차원 공간에서 다섯 축의 정확도를 종합적으로 정량화할 수 있는 장점이 있다. Xia et al.⁶⁷은 DBB를 이용한 회전축의 위치 독립적 기하학적 오차(Position Independent Geometric Error, PIGE)와 위치 의존적 기하학적 오차(Position Dependent Geometric Error, PDGE)의 판별 방법을 제안했다. 변위 오차와 각도 오차를 분리하여 측정하기 위한 DBB의 설치 방식을 제안하였으며, 제안한 방식은 장비의 오차, 설치 오차 등의 오차에 영향을 적게 받는 것을 확인하였다.

Zhong et al.⁶⁸은 대형 5축 공작기계의 위치 기하학적 오차에 관한 모델링과 식별 및 보상 알고리즘을 제안하였다. 공작기계를 강체 다물체 시스템(Rigid Multi-Body System)으로 간주하여 모델링하였다. 직선축과 회전축의 오차 측정을 위해 각각 레이저 간섭계와 레이저 트래커(Laser Tracker)를 사용하였다. 임의의 위치에서 오차의 크기를 계산하기 위해 위치 오차를 Least-Square 알고리즘을 이용하여 다항식으로 근사하였으며, 위치 오차를 재귀적 방식을 통해 보상한 결과 Y축의 오차는 약 97%, B 축의 오차는 약 93% 감소하였다. Xiang et al.⁶⁹은 나선 이론을 이용하여 5축 공작기계의 정기구학, 역기구학을 모델링하고, 기하학적 오차를 Error Twist로 표현하였다. 직선축의 오차 성분은 레이저 간섭계로, 회전축의 오차 성분은 볼바를 사용하여 측정하였으며 가상 공작기계와 상용 CNC에 의해 제어되는 공작기계에 기하학적 오차를 Look-Up Table 형식으로 입력하여 보상을 하였다.

Fig. 12

CNC high precision algorithm for increasing machining accuracy

5. 결론

CNC 공작기계에 요구되는 가공정밀도가 높아짐에 따라 고속에서 높은 위치정밀도를 구현할 수 있는 제어기를 구현하기 위한 다양한 연구가 수행되고 있다. 본 리뷰논문에서는 CNC 공작기계에 적용하기 위한 보간 알고리즘, 윤곽오차 제어 알고리즘 및 오차 및 외란보상 제어 기술의 최근 연구동향을 정리하였다.

새로운 알고리즘의 개발, CNC 장비의 정밀도 및 속도의 향상, 5축 공작기계 및 다축 복합가공기의 보편화 등의 결과로 새로운 제어기술이 제안되고 있다.

특히, 최근에는 새로운 컴퓨터 기술을 CNC 제어기술에 활용하는 연구가 활발하게 시도되고 있다. 현재까지는 CNC 제어기의 성능 한계를 고려하여 제한된 연산능력 범위 안에서 정밀도를 향상시키는 것이 중요한 연구목표의 하나였다면, CNC에 적용되는 프로세서 및 통신의 속도가 높아짐에 따라, 향후에는 고성능 컴퓨터와 Cyber Physical System을 활용한 CNC의 정밀도 향상에 대한 연구가 활발히 이루어질 것으로 예상된다.

Acknowledgments

본 연구는 산업통상자원부의 기계산업핵심기술개발 사업(No. 10053248, 과제명: 탄소섬유복합재(CFRP) 가공시스템 개발) 및 제조기반 생산시스템 사업(No. 10067754, 과제명: 중소형 공작기계용 2계통 제어 CNC와 서보, 스핀들 구동 유닛 국산화 개발) 및 한국기계연구원 주요사업(고속 고정밀 기계장비의 메카트로닉스 최적화 기술 개발)의 지원으로 수행되었다.

REFERENCES

• Bi, Q., Shi, J., Wang, Y., Zhu, L., and Ding, H., “Analytical Curvature-Continuous Dual-Bézier Corner Transition for Five-Axis Linear Tool Path,” International Journal of Machine Tools and Manufacture, Vol. 91, pp. 96-108, 2015. [https://doi.org/10.1016/j.ijmachtools.2015.02.002]
• Wu, J., Liu, C., Xiong, Z., and Ding, H., “Precise Contour Following for Biaxial Systems via an A-Type Iterative Learning Cross-Coupled Control Algorithm,” International Journal of Machine Tools and Manufacture, Vol. 93, pp. 10-18, 2015. [https://doi.org/10.1016/j.ijmachtools.2015.03.005]
• Wu, J., Xiong, Z., and Ding, H., “Integral Design of Contour Error Model and Control For Biaxial System,” International Journal of Machine Tools and Manufacture, Vol. 89, pp. 159-169, 2015. [https://doi.org/10.1016/j.ijmachtools.2014.11.011]
• Wan, A., Song, L., Xu, J., Liu, S., and Chen, K., “Calibration and Compensation of Machine Tool Volumetric Error Using a Laser Tracker,” International Journal of Machine Tools and Manufacture, Vol. 124, pp. 126-133, 2018. [https://doi.org/10.1016/j.ijmachtools.2017.10.004]
• Shen, J.-C., Lu, Q.-Z., Wu, C.-H., and Jywe, W.-Y., “Sliding-Mode Tracking Control with DNLRX Model-Based Friction Compensation for the Precision Stage,” IEEE/ASME Transactions on Mechatronics, Vol. 19, No. 2, pp. 788-797, 2014. [https://doi.org/10.1109/TMECH.2013.2260762]
• Sencer, B., Ishizaki, K., and Shamoto, E., “High Speed Cornering Strategy with Confined Contour Error and Vibration Suppression for CNC Machine Tools,” CIRP Annals, Vol. 64, No. 1, pp. 369-372, 2015. [https://doi.org/10.1016/j.cirp.2015.04.102]
• Lee, C. Y., Min, J., and Min, B. K., “Limiting Tool Path Error Generated by Corner Blending of CNC Interpolator,” J. Korean Soc. Precis. Eng., Vol. 34, No. 10, pp. 695-700, 2017. [https://doi.org/10.7736/KSPE.2017.34.10.695]
• Du, X., Huang, J., and Zhu, L.-M., “An Analytical Transition Algorithm for Real-Time CNC Machining of Linear Tool Path,” Procedia CIRP, Vol. 56, pp. 344-348, 2016. [https://doi.org/10.1016/j.procir.2016.10.037]
• Yutkowitz, S. J., “Apparatus and Method for Smooth Cornering in a Motion Control System,” US Patent, 6922606B1, 2005.
• Zhao, H., Zhu, L. M., and Ding, H., “A Real-Time Look-Ahead Interpolation Methodology with Curvature-Continuous B-Spline Transition Scheme for CNC Machining of Short Line Segments,” International Journal of Machine Tools and Manufacture, Vol. 65, No. pp. 88-98, 2013. [https://doi.org/10.1016/j.ijmachtools.2012.10.005]
• Tajima, S. and Sencer, B., “Kinematic Corner Smoothing for High Speed Machine Tools,” International Journal of Machine Tools and Manufacture, Vol. 108, pp. 27-43, 2016. [https://doi.org/10.1016/j.ijmachtools.2016.05.009]
• Tajima, S. and Sencer, B., “Global Tool-Path Smoothing for CNC Machine Tools with Uninterrupted Acceleration,” International Journal of Machine Tools and Manufacture, Vol. 121, pp. 81-95, 2017. [https://doi.org/10.1016/j.ijmachtools.2017.03.002]
• Yan, Y. C., Zhang, L. Q., and Zhang, K., “Corner Smoothing Transition Algorithm for Five-Axis Linear Tool Path,” Procedia CIRP, Vol. 56, pp. 604-609, 2016. [https://doi.org/10.1016/j.procir.2016.10.119]
• Beudaert, X., Lavernhe, S., and Tournier, C., “5-Axis Local Corner Rounding of Linear Tool Path Discontinuities,” International Journal of Machine Tools and Manufacture, Vol. 73, pp. 9-16, 2013. [https://doi.org/10.1016/j.ijmachtools.2013.05.008]
• Shi, J., Bi, Q., Zhu, L., and Wang, Y., “Corner Rounding of Linear Five-Axis Tool Path by Dual PH Curves Blending,” International Journal of Machine Tools and Manufacture, Vol. 88, pp. 223-236, 2015. [https://doi.org/10.1016/j.ijmachtools.2014.09.007]
• Yuen, A., Zhang, K., and Altintas, Y., “Smooth Trajectory Generation for Five-Axis Machine Tools,” International Journal of Machine Tools and Manufacture, Vol. 71, pp. 11-19, 2013. [https://doi.org/10.1016/j.ijmachtools.2013.04.002]
• Tulsyan, S. and Altintas, Y., “Local Toolpath Smoothing for Five-Axis Machine Tools,” International Journal of Machine Tools and Manufacture, Vol. 96, pp. 15-26, 2015. [https://doi.org/10.1016/j.ijmachtools.2015.04.014]
• Yang, J. and Yuen, A., “An Analytical Local Corner Smoothing Algorithm for Five-Axis CNC Machining,” International Journal of Machine Tools and Manufacture, Vol. 123, pp. 22-35, 2017. [https://doi.org/10.1016/j.ijmachtools.2017.07.007]
• Otsuki, T., Ogino, H., Ide, S., and Chiba, T., “Curve Interpolation Method,” US Patent, 6823234B2, 2004.
• Siemens, Milling with SINUMERIK 5-Axis Machining, DocOrder No. 6FC5095-0AB10-0BP1, 2009.
• Lee, A.-C., Lin, M.-T., Pan, Y.-R., and Lin, W.-Y., “The Feedrate Scheduling of NURBS Interpolator for CNC Machine Tools,” Computer-Aided Design, Vol. 43, No. 6, pp. 612-628, 2011. [https://doi.org/10.1016/j.cad.2011.02.014]
• Jia, Z.-Y., Song, D.-N., Ma, J.-W., Hu, G.-Q., and Su, W.-W., “A NURBS Interpolator with Constant Speed at Feedrate-sensitive Regions Under Drive and Contour-Error Constraints,” International Journal of Machine Tools and Manufacture, Vol. 116, pp. 1-17, 2017. [https://doi.org/10.1016/j.ijmachtools.2016.12.007]
• Liu, M., Huang, Y., Yin, L., Guo, J., Shao, X., and Zhang, G., “Development and Implementation of a NURBS Interpolator with Smooth Feedrate Scheduling for CNC Machine Tools,” International Journal of Machine Tools and Manufacture, Vol. 87, pp. 1-15, 2014. [https://doi.org/10.1016/j.ijmachtools.2014.07.002]
• Sun, Y., Zhao, Y., Bao, Y., and Guo, D., “A Smooth Curve Evolution Approach To The Feedrate Planning on Five-Axis Toolpath With Geometric and Kinematic Constraints,” International Journal of Machine Tools and Manufacture, Vol. 97, pp. 86-97, 2015. [https://doi.org/10.1016/j.ijmachtools.2015.07.002]
• Rahaman, M., Seethaler, R., and Yellowley, I., “A New Approach to Contour Error Control in High Speed Machining,” International Journal of Machine Tools and Manufacture, Vol. 88, pp. 42-50, 2015. [https://doi.org/10.1016/j.ijmachtools.2014.09.002]
• Huo, F. and Poo, A.-N., “Improving Contouring Accuracy by Using Generalized Cross-Coupled Control,” International Journal of Machine Tools and Manufacture, Vol. 63, pp. 49-57, 2012. [https://doi.org/10.1016/j.ijmachtools.2012.07.012]
• Xi, X.-C., Poo, A.-N., and Hong, G.-S., “Taylor Series Expansion Error Compensation for a Bi-Axial CNC Machine,” Proc. of IEEE International Conference on Systems, Man and Cybernetics, pp. 1614-1619, 2008.
• Huo, F., Xi, X.-C., and Poo, A.-N., “Generalized Taylor Series Expansion for Free-Form Two-Dimensional Contour Error Compensation,” International Journal of Machine Tools and Manufacture, Vol. 53, No. 1, pp. 91-99, 2012. [https://doi.org/10.1016/j.ijmachtools.2011.10.001]
• Altintas, Y. and Sencer, B., “High Speed Contouring Control Strategy for Five-Axis Machine Tools,” CIRP Annals, Vol. 59, No. 1, pp. 417-420, 2010. [https://doi.org/10.1016/j.cirp.2010.03.019]
• Yang, J. and Altintas, Y., “A Generalized On-Line Estimation and Control of Five-Axis Contouring Errors of CNC Machine Tools,” International Journal of Machine Tools and Manufacture, Vol. 88, pp. 9-23, 2015. [https://doi.org/10.1016/j.ijmachtools.2014.08.004]
• Li, X., Zhao, H., Zhao, X., and Ding, H., “Dual Sliding Mode Contouring Control with High Accuracy Contour Error Estimation for Five-Axis CNC Machine Tools,” International Journal of Machine Tools and Manufacture, Vol. 108, pp. 74-82, 2016. [https://doi.org/10.1016/j.ijmachtools.2016.05.007]
• Zhang, K., Yuen, A., and Altintas, Y., “Pre-Compensation of Contour Errors in Five-Axis CNC Machine Tools,” International Journal of Machine Tools and Manufacture, Vol. 74, pp. 1-11, 2013. [https://doi.org/10.1016/j.ijmachtools.2013.07.003]
• Yang, S., Ghasemi, A. H., Lu, X., and Okwudire, C. E., “Pre-Compensation of Servo Contour Errors Using a Model Predictive Control Framework,” International Journal of Machine Tools and Manufacture, Vol. 98, pp. 50-60, 2015. [https://doi.org/10.1016/j.ijmachtools.2015.08.002]
• Zhang, D., Chen, Y., and Chen, Y., “Iterative Pre-Compensation Scheme of Tracking Error for Contouring Error Reduction,” The International Journal of Advanced Manufacturing Technology, Vol. 87, Nos. 9-12, pp. 3279-3288, 2016. [https://doi.org/10.1007/s00170-016-8735-9]
• Bui, B. D., Uchiyama, N., and Sano, S., “Nonlinear Friction Modeling and Compensation for Precision Control of a Mechanical Feed-Drive System,” Sensors and Materials, Vol. 27, No. 10, pp. 971-984, 2015.
• Bui, B. D., Uchiyama, N., and Simba, K. R., “Contouring Control for Three-Axis Machine Tools Based on Nonlinear Friction Compensation for Lead Screws,” International Journal of Machine Tools and Manufacture, Vol. 108, pp. 95-105, 2016. [https://doi.org/10.1016/j.ijmachtools.2016.06.001]
• De Wit, C. C., Olsson, H., Astrom, K. J., and Lischinsky, P., “A New Model for Control of Systems with Friction,” IEEE Transactions on Automatic Control, Vol. 40, No. 3, pp. 419-425, 1995. [https://doi.org/10.1109/9.376053]
• Swevers, J., Al-Bender, F., Ganseman, C. G., and Projogo, T., “An Integrated Friction Model Structure with Improved Presliding Behavior for Accurate Friction Compensation,” IEEE Transactions on Automatic Control, Vol. 45, No. 4, pp. 675-686, 2000. [https://doi.org/10.1109/9.847103]
• Ruderman, M., “Tracking Control of Motor Drives Using Feedforward Friction Observer,” IEEE Transactions on Industrial Electronics, Vol. 61, No. 7, pp. 3727-3735, 2014. [https://doi.org/10.1109/TIE.2013.2264786]
• Lee, W., Lee, C.-Y., Jeong, Y. H., and Min, B.-K., “Distributed Component Friction Model for Precision Control of a Feed Drive System,” IEEE/ASME Transactions on Mechatronics, Vol. 20, No. 4, pp. 1966-1974, 2015. [https://doi.org/10.1109/TMECH.2014.2365958]
• Lee, T. H., Tan, K. K., and Huang, S., “Adaptive Friction Compensation with a Dynamical Friction Model,” IEEE/ASME Transactions on Mechatronics, Vol. 16, No. 1, pp. 133-140, 2011. [https://doi.org/10.1109/TMECH.2009.2036994]
• Lee, W., Lee, C.-Y., Jeong, Y. H., and Min, B.-K., “Friction Compensation Controller for Load Varying Machine Tool Feed Drive,” International Journal of Machine Tools and Manufacture, Vol. 96, pp. 47-54, 2015. [https://doi.org/10.1016/j.ijmachtools.2015.06.001]
• Lin, C.-J. and Lee, C.-Y., “Observer-based Robust Controller Design and Realization of a Gantry Stage,” Mechatronics, Vol. 21, No. 1, pp. 185-203, 2011. [https://doi.org/10.1016/j.mechatronics.2010.10.005]
• Lin, C.-J., Yau, H.-T., and Tian, Y.-C., “Identification and Compensation of Nonlinear Friction Characteristics and Precision Control for a Linear Motor Stage,” IEEE/ASME Transactions on Mechatronics, Vol. 18, No. 4, pp. 1385-1396, 2013. [https://doi.org/10.1109/TMECH.2012.2202679]
• Li, Y., Zhao, W., Lan, S., Ni, J., Wu, W., and Lu, B., “A Review on Spindle Thermal Error Compensation in Machine Tools,” International Journal of Machine Tools and Manufacture, Vol. 95, pp. 20-38, 2015. [https://doi.org/10.1016/j.ijmachtools.2015.04.008]
• Altintas, Y., Verl, A., Brecher, C., Uriarte, L., and Pritschow, G., “Machine Tool Feed Drives,” CIRP Annals-Manufacturing Technology, Vol. 60, No. 2, pp. 779-796, 2011. [https://doi.org/10.1016/j.cirp.2011.05.010]
• Thiem, X., Kauschinger, B., and Ihlenfeldt, S., “Structure Model Based Correction of Thermally Induced Motion Errors of Machine Tools,” Procedia Manufacturing, Vol. 14, pp. 128-135, 2017. [https://doi.org/10.1016/j.promfg.2017.11.015]
• Li, T.-J., Zhao, C.-Y., and Zhang, Y.-M., “Adaptive Real-Time Model on Thermal Error of Ball Screw Feed Drive Systems of CNC Machine Tools,” The International Journal of Advanced Manufacturing Technology, Vol. 94, Nos. 9-12, pp. 3853-3861, 2017. [https://doi.org/10.1007/s00170-017-1076-5]
• Li, Y., Zhao, W., Wu, W., Lu, B., and Chen, Y., “Thermal Error Modeling of the Spindle Based on Multiple Variables for the Precision Machine Tool,” The International Journal of Advanced Manufacturing Technology, Vol. 72, Nos. 9-12, pp. 1415-1427, 2014. [https://doi.org/10.1007/s00170-014-5744-4]
• Shi, H., Ma, C., Yang, J., Zhao, L., Mei, X., and Gong, G., “Investigation into Effect of Thermal Expansion on Thermally Induced Error of Ball Screw Feed Drive System of Precision Machine Tools,” International Journal of Machine Tools and Manufacture, Vol. 97, pp. 60-71, 2015. [https://doi.org/10.1016/j.ijmachtools.2015.07.003]
• Feng, W., Li, Z., Gu, Q., and Yang, J., “Thermally Induced Positioning Error Modelling and Compensation Based on Thermal Characteristic Analysis,” International Journal of Machine Tools and Manufacture, Vol. 93, pp. 26-36, 2015. [https://doi.org/10.1016/j.ijmachtools.2015.03.006]
• Huang, Y., Zhang, J., Li, X., and Tian, L., “Thermal Error Modeling by Integrating GA and BP Algorithms for the High-Speed Spindle,” The International Journal of Advanced Manufacturing Technology, Vol. 71, Nos. 9-12, pp. 1669-1675, 2014. [https://doi.org/10.1007/s00170-014-5606-0]
• Abdulshahed, A. M., Longstaff, A. P., and Fletcher, S., “The Application of ANFIS Prediction Models for Thermal Error Compensation on CNC Machine Tools,” Applied Soft Computing, Vol. 27, pp. 158-168, 2015. [https://doi.org/10.1016/j.asoc.2014.11.012]
• Liu, K., Sun, M., Zhu, T., Wu, Y., and Liu, Y., “Modeling and Compensation for Spindle’s Radial Thermal Drift Error on a Vertical Machining Center,” International Journal of Machine Tools and Manufacture, Vol. 105, pp. 58-67, 2016. [https://doi.org/10.1016/j.ijmachtools.2016.03.006]
• Tan, F., Yin, M., Wang, L., and Yin, G., “Spindle Thermal Error Robust Modeling Using LASSO and LS-SVM,” The International Journal of Advanced Manufacturing Technology, Vol. 94, Nos. 5-8, pp. 2861-2874, 2018. [https://doi.org/10.1007/s00170-017-1096-1]
• Miao, E.-M., Gong, Y.-Y., Niu, P.-C., Ji, C.-Z., and Chen, H.-D., “Robustness of Thermal Error Compensation Modeling Models of CNC Machine Tools,” The International Journal of Advanced Manufacturing Technology, Vol. 69, Nos. 9-12, pp. 2593-2603, 2013. [https://doi.org/10.1007/s00170-013-5229-x]
• Miao, E., Liu, Y., Liu, H., Gao, Z., and Li, W., “Study on the Effects of Changes in Temperature-Sensitive Points on Thermal Error Compensation Model for CNC Machine Tool,” International Journal of Machine Tools and Manufacture, Vol. 97, pp. 50-59, 2015. [https://doi.org/10.1016/j.ijmachtools.2015.07.004]
• Liu, H., Miao, E. M., Wei, X. Y., and Zhuang, X. D., “Robust Modeling Method for Thermal Error of CNC Machine Tools Based on Ridge Regression Algorithm,” International Journal of Machine Tools and Manufacture, Vol. 113, pp. 35-48, 2017. [https://doi.org/10.1016/j.ijmachtools.2016.11.001]
• Miller, J. E., Longstaff, A. P., Parkinson, S., and Fletcher, S., “Improved Machine Tool Linear Axis Calibration through Continuous Motion Data Capture,” Precision Engineering, Vol. 47, pp. 249-260, 2017. [https://doi.org/10.1016/j.precisioneng.2016.08.010]
• Feng, W., Yao, X., Azamat, A., and Yang, J., “Straightness Error Compensation for Large CNC Gantry Type Milling Centers Based on B-Spline Curves Modeling,” International Journal of Machine Tools and Manufacture, Vol. 88, pp. 165-174, 2015. [https://doi.org/10.1016/j.ijmachtools.2014.09.006]
• Zha, J., Xue, F., and Chen, Y., “Straightness Error Modeling And Compensation for Gantry Type Open Hydrostatic Guideways in Grinding Machine,” International Journal of Machine Tools and Manufacture, Vol. 112, pp. 1-6, 2017. [https://doi.org/10.1016/j.ijmachtools.2016.10.002]
• Zhenjiu, Z., Mingjun, R., and Mingjun, L., “A Modified Sequential Multilateration Scheme and Its Application in Geometric Error Measurement of Rotary Axis,” Procedia CIRP, Vol. 27, pp. 313-317, 2015. [https://doi.org/10.1016/j.procir.2015.04.085]
• Zhu, S., Ding, G., Qin, S., Lei, J., Zhuang, L., and Yan, K., “Integrated Geometric Error Modeling, Identification and Compensation of CNC Machine Tools,” International Journal of Machine Tools and Manufacture, Vol. 52, No. 1, pp. 24-29, 2012. [https://doi.org/10.1016/j.ijmachtools.2011.08.011]
• He, Z., Fu, J., Zhang, L., and Yao, X., “A New Error Measurement Method to Identify all Six Error Parameters of a Rotational Axis of a Machine Tool,” International Journal of Machine Tools and Manufacture, Vol. 88, pp. 1-8, 2015. [https://doi.org/10.1016/j.ijmachtools.2014.07.009]
• Chen, D., Dong, L., Bian, Y., and Fan, J., “Prediction and Identification of Rotary Axes Error of Non-Orthogonal Five-Axis Machine Tool,” International Journal of Machine Tools and Manufacture, Vol. 94, pp. 74-87, 2015. [https://doi.org/10.1016/j.ijmachtools.2015.03.010]
• Zhong, L., Bi, Q., and Wang, Y., “Volumetric Accuracy Evaluation for Five-Axis Machine Tools by Modeling Spherical Deviation Based on Double Ball-Bar Kinematic Test,” International Journal of Machine Tools and Manufacture, Vol. 122, pp. 106-119, 2017. [https://doi.org/10.1016/j.ijmachtools.2017.06.005]
• Xia, H.-J., Peng, W.-C., Ouyang, X.-B., Chen, X.-D., Wang, S.-J., et al., “Identification of Geometric Errors of Rotary Axis on Multi-Axis Machine Tool Based on Kinematic Analysis Method Using Double Ball Bar,” International Journal of Machine Tools and Manufacture, Vol. 122, pp. 161-175, 2017. [https://doi.org/10.1016/j.ijmachtools.2017.07.006]
• Zhong, G., Wang, C., Yang, S., Zheng, E., and Ge, Y., “Position Geometric Error Modeling, Identification and Compensation for Large 5-Axis Machining Center Prototype,” International Journal of Machine Tools and Manufacture, Vol. 89, pp. 142-150, 2015. [https://doi.org/10.1016/j.ijmachtools.2014.10.009]
• Xiang, S. and Altintas, Y., “Modeling and Compensation of Volumetric Errors for Five-Axis Machine Tools,” International Journal of Machine Tools and Manufacture, Vol. 101, pp. 65-78, 2016. [https://doi.org/10.1016/j.ijmachtools.2015.11.006]