자기변형 에너지 하베스팅 장치의 고유진동수 조절에 관한 연구
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This paper presents a proposed means of frequency-tuning a magnetostrictive energy harvester(EH). This end may be accomplished by decreasing the distance between two permanent magnets (PM) located at free end of the cantilever and at the opposite, resulting in increase of a repulsive force between the PMs. The EH consists of a coil-wound Galfenol cantilever with PMs, a mover connected to the cantilever, and a rotating wheel with PMs. The rotating wheel driven by a motor provides a forced vibration to the EH. To direct inspection, It is noted that the maximum output voltage continually changes depending upon the the distance between the PMs And itmight therefore be deduced that the resonant frequency of the harvester may be adjusted to attain maximum, or optimal, voltage output. The rotational speed of the wheel (for the purpose of attaining maximum output voltage) is changed from 325 rpm to 265 rpm at a distance of 10 mm. It can be concluded that the practice of frequency-tuning with two PMs is a potentially positive application with respect to the EH.
Keywords:
Vibration energy, Magnetostriction, Frequency-tuning키워드:
진동에너지, 자기변형, 고유진동수 조절1. 서론
에너지 하베스팅(Energy Harvesting)은 일상생활에서 사용하지 못하고 버려지는 빛, 열, 진동 등의 에너지를 사용 가능한 전기에너지로 변환하는 기술을 의미한다. 풍력, 태양광 등을 이용하는 대규모의 에너지 하베스팅은 이미 상용화되어, 국내의 경우 전기 생산량의 0.8%를 이와 같은 신재생에너지로부터 얻고 있으며 그 비율을 점진적으로 늘리고 있다. 반면 열이나 진동 등을 이용하는 소규모의 에너지 하베스팅 기술은 발전량이 적어 주목받지 못하다가, 소모전력이 적은 센서 등의 개발로 인해 그 가치를 재조명 받고 있으며, 무선센서네트워크(Wireless Sensor Network, WSN)나 웨어러블 기기 등의 전력원으로서 사용가능성에 대한 검증이 논의되고있다.1
일상생활에서 가장 쉽게 볼 수 있는 에너지로는 진동 에너지가 있으며, 압전(Piezoelectric),3 정전기(Electrostatic),4 전자기(Electromagnetic)5 등의 다양한 방식을 이용한 연구가 진행되고 있다. 이 중 압전 방식의 에너지 하베스팅은 단위 면적당 발생 전력이 높고, 가격이 저렴하며, 복잡한 시스템을 요구하지 않는다는 장점이 있어 가장 활발히 연구되고 있다. 그러나 압전 재료는 대부분 납(Pb)을 포함하고 있어 인체적합성이 떨어지고 환경오염을 유발할 수 있으며, 납을 포함하지 않는 재료는 납 기반 재료만큼 높은 특성을 나타내기 힘들고 가격이 비싸다. 또한 압전 재료는 취성이 강해 반복적인 진동을 인가할 경우 파손되기 쉽고, 이를 지속적으로 교체해야 할 경우 배터리를 대체한다는 에너지 하베스팅의 취지에 부합하지 못한다.
자기변형(Magnetostriction) 방식은 압전 방식과 유사한 매커니즘을 가지고 있어 압전 방식의 에너지 하베스팅 연구와 접목이 가능하며, 압전 재료의 단점을 해소할 수 있다. 갈륨(Ga)과 철(Fe)의 합금인 갈페놀(Galfenol)과 같은 자기변형 재료는 연성이 높아 쉽게 파손되지 않으므로 압전 재료보다 큰 변형을 일으킬 수 있으며, 반복적인 진동에 적합하다. 또한 인체에 쉽게 흡수되지 않아 휴대형·소형 전자기기와 같은 인체와 접촉하는 곳에도 사용이 가능하며, 높은 인장강도와 퀴리온도(Qurie Temperature)를 가져 시스템의 기대수명이 높다.
진동 에너지 기반의 에너지 하베스팅 연구는 효율을 높이기 위해 공명현상(Resonance)을 이용한다. 공명현상은 시스템이 갖는 고유진동수와 일치하는 주파수를 인가할 경우 시스템의 거동이 크게 변하는 현상으로, 출력이 변형량에 비례하는 진동 에너지 기반의 에너지 하베스팅 장치의 효율을 높일 수 있다. 그러나 일상생활에서 발생하는 진동 에너지는 진동수가 가변적이며, 시스템이 갖는 고유진동수에 비해 매우 작아 공명현상을 유도하기 힘들다.

List of vibration sources with their maximum acceleration magnitude and frequency of peak acceleration6
이를 해결하기 위해 최근에는 주파수 상승 변환(Frequency Up-Conversion)에 대한 연구가 진행되고 있다. 주파수 상승 변환은 시스템에 인가하는 진동의 주파수를 높이는 방법으로, 기계적 구조 또는7 자석을 이용하여8 인가주파수를 상승시킨다. 그러나 이러한 주파수 상승 변환은 인가되는 주파수와 시스템의 고유진동수가 크게 차이가 나는 미세전자기계시스템(Micro Electro Mechanical Systems, MEMS) 구조에서 유리한데, 주파수 상승 변환을 위한 복잡한 구조가 필요해 소규모 에너지 하베스팅에는 적합하지 않다. 다른 해결법으로 고유진동수 조절(Resonance Frequency Tuning)에 대한 연구가 제시되고 있다. 고유진동수 조절은 수동 조절(Passive Tuning)9과 능동 조절(Active Tuning)10로 나뉘는데, 능동 조절 방법의 경우 조절능력이 제한되고, 출력되는 전력보다 고유진동수 조절에 들어가는 비용이 높다는 단점이 있다.
본 논문에서는 압전 재료의 단점을 해결하기 위해 자기변형 재료인 갈페놀을 이용한 에너지 하베스팅 장치를 고안하고, 축 방향의 외력인가가 시스템의 고유진동수에 미치는 영향을 분석하여 고유진동수 조절 가능성을 확인하고, 이를 통해 에너지 하베스팅 장치의 출력을 향상시키고자 한다.
2. 자기변형 에너지 하베스팅 장치 설계
2.1 자기변형 에너지 하베스팅 이론
자성체는 각각의 자기편극(Magnetic Polarization) 영역인 자구(Magnetic Domain)을 갖는다. 철이나 코발트와 같은 강자성체에 자기장을 인가하면 자구가 자기장의 방향으로 정렬하고, 이로 인해 자성체의 체적 변화가 발생한다. 이러한 현상을 줄 효과(Joule Effect) 또는 자기변형 효과라고 하며, 주로 잉크젯 헤드와 같은 구동기에 이용된다. 반대로 자성체에 외력을 인가할 경우 자구의 정렬이 바뀌면서 내부 자화(Magnetization)의 방향이 바뀌는데, 이를 빌라리 효과(Villari Effect) 또는 역자기변형 효과(Inverse Magnetostriction Effect)라고 하며, 주로 센서에 이용된다.
자기변형 에너지 하베스팅 장치는 이러한 빌라리 효과를 이용해 구현할 수 있다. 자성체에 코일을 감은 후, 외력을 인가하면 자성체 내부 자화의 방향이 바뀌게 된다. 패러데이의 전자기유도 법칙(Faraday’s Law of Electromagnetic Induction)에 의하면 자속의 변화로 인해 유도전류가 발생하게 되므로, 기계적 에너지를 전기적 에너지로 변환하는 에너지 하베스팅이 이루어진다. 식(1)은 패러데이의 전자기유도 법칙에 대한 식이다.
| (1) |
자성체의 자속밀도는 변형률과 자계강도의 합으로써 나타낼 수 있다.11
| (2) |
자성체의 변형률은 식(3)과 같이 나타낼 수 있다.
| (3) |
식(1), 식(2), 식(3)을 통해 자기변형 에너지 하베스팅 장치의 출력 모델을 얻을 수 있다.
| (4) |
식(4)를 통해 자기변형 에너지 하베스팅 장치의 출력 전압은 코일의 권선 수와 단면적에 비례하며, 재료의 변형률의 변화량에 비례하는 것을 알 수 있다.
보 요소에 가해지는 힘과 모멘트에 대한 평형방정식은 다음과 같다.
| (5) |
| (6) |
모멘트와 전단력의 관계는 다음과 같다.
| (7) |
식(5), 식(6), 식(7)을 통해, 외력이 가해질 때의 보의 운동방정식은 다음과 같다.
| (8) |
영구자석간의 반발력을 통해 자기변형 에너지 하베스팅 장치에 진동을 인가하거나, 축 방향으로 외력을 인가한다. 두 영구자석 사이에서 발생하는 힘은 다음과 같이 나타낼 수 있다.12
| (9) |
자석간의 간격이 가까울수록 반발력이 커지므로, 이를 통해 자기변형 에너지 하베스팅 장치에 인가하는 외력의 크기를 조절할 수 있다.
2.2 자기변형 에너지 하베스팅 장치 설계
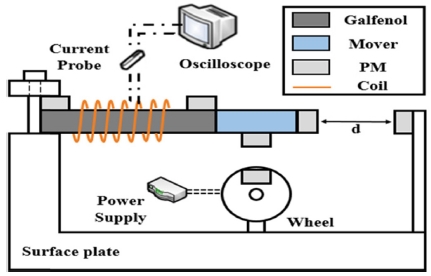
자기변형 에너지 하베스팅 장치는 자기변형재료인 갈페놀을 외팔보형태로 고정하고, 그 위에 전력을 회수할 수 있는 코일이 감겨져 있다. 갈페놀의 양단에는 영구자석이 극성이 반대가 되도록 부착되어 갈페놀의 자구 방향을 정렬하며, 자유단에는 무버(Mover)가 연결되어 외력을 대신 인가받아 자기변형 재료의 파손을 방지한다. 무버에는 2개의 영구자석이 부착되어 축 방향 외력을 인가받거나, 외부로부터 진동을 인가받는다. 외부 진동은 영구자석을 부착한 바퀴를 이용해 인가하며, 바퀴가 회전할 때 바퀴와 무버에 각각 부착된 영구자석간의 반발력을 이용한다. Fig. 1은 자기변형 에너지 하베스팅 장치의 개략도이다.
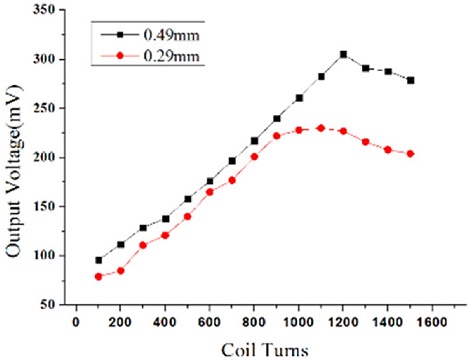
Output voltage of magnetostrictive energy harvester device by changing coil’s diameter and number of turns
실험에 사용한 갈페놀은 직육면체 형태로 가로 15 mm, 세로 100 mm, 두께 3 mm의 외형 치수를 갖는다. Fig. 3은 코일의 직경이 각각 0.29 mm, 0.49 mm일 때 바퀴의 회전속도에 따른 자기변형 에너지 하베스팅 장치의 출력 전압을 나타낸 그래프이다.
출력 전압은 바퀴를 300 rpm으로 회전시켰을 때 발생하는 전압의 최댓값이다. 코일 직경이 0.29 mm일 때는 코일 권선 수가 900 턴 일 때 최댓값을 나타내고, 0.49 mm일 때는 1200 턴 일 때 최댓값을 나타낸다. 코일 직경에 따라 출력값이 바뀌는 것은 코일의 허용전류 때문이고, 전압값이 일정 권선 수 이상에서 더 이상 증가하는 것은 코일의 권선 수 증가로 인한 전력생성량보다 갈페놀의 진동을 방해하는 에너지 손실이 더 크기 때문이다. 실험 결과에 따라 갈페놀에 직경이 0.49 mm, 권선 수가 1200 턴인 코일을 감았다.
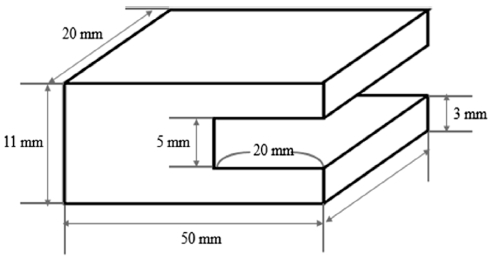
갈페놀의 변형량이 클수록 자기변형 에너지 하베스팅 장치의 출력이 높아지므로, 휨 모멘트(Bending Moment)가 큰 외팔보 형태로 고정하였다. 알루미늄 무버는 ㄷ자 형태로 갈페놀의 자유단에 연결될 수 있으며, 외형은 Fig. 3과 같다.
무버에는 가로 15 mm, 세로 10 mm, 두께 5 mm의 외형 치수를 갖는 NdFeB37 영구자석을 Scotch-3M 社의 SGAD-875A 접착제를 이용해 부착하였다. 축 방향 외력 인가를 위한 바퀴와 무버에 부착된 영구자석간에 발생하는 반발력은 갈페놀의 허용응력을 넘지 않아야 한다. 허용응력은 갈페놀의 인장강도와 안전율과의 관계로부터 구할 수 있다.
| (10) |
갈페놀의 인장강도는 350 MPa이고, 진동 또는 반복하중일 때의 안전율은 6이다. 따라서 허용응력은 58.33 MPa이 된다. 영구자석간의 반발력의 크기가 F이고 외팔보의 총 길이를 a라고 할 때, 모멘트의 크기는 다음과 같다.
| (11) |
모멘트는 허용응력과 단면계수의 곱으로써 나타낼 수 있다.
| (12) |
단면계수는 단면이차모멘트를 중심축에서 최외곽거리로 나누어 얻을 수 있다. 단면이 직사각형이고, 중심축이 중앙에 있는 균일보라고 가정하면 단면계수는 다음과 같이 나타낼 수 있다.
| (13) |
영구자석은 무버의 중앙에 부착되어, 갈페놀의 고정단으로부터 107.5 mm 떨어진 곳에 부착된다. 영구자석간의 반발력을 집중하중으로 가정하면 식(12), 식(13)으로부터 허용응력을 넘지 않는 모멘트가 0.87495 N/m2임을 얻을 수 있다. 이 결과를 식(11)에 대입하면 허용응력을 넘지 않는 영구자석간의 반발력은 8.1391 N 이하여야 하며, 영구자석의 자속밀도는 1.23 T 이므로 식(9)로부터 반발력이 8.1391 N이 되는 영구자석간의 거리는 11.27 mm가 된다. 본 연구에서는 바퀴와 무버에 부착된 영구자석간의 거리는 11.5 mm로 하였다.
3. 실험 및 결과
바퀴는 지름이 4 cm이며, DC 모터에 연결되어 회전을 한다. 실험에 사용한 DC 모터는 Maxon Motor 社의 MSC 130238 모델이며, DC 모터에 전원공급은 Agilent 社의 U8031A 모델 전원공급기를 이용해 이루어진다. DC 모터의 회전속도는 전원공급량에 의해 결정되고, 바퀴의 회전속도는 Inparo 社의 디지털 타코미터를 사용해 측정하였다. 전압 측정은 Tektronix 社의 TDS3014B 모델의 오실로스코프를 사용하였다.
바퀴가 회전함에 따라 영구자석간의 반발력으로 인해 외팔보가 진동하고, 이 때 코일에서 발생하는 전압의 최댓값을 회전속도에 따라 측정하였다. 또한 무버의 끝단에 부착된 영구자석에 축방향 외력을 인가하고 그 크기를 조절해가면서 동일한 실험을 반복하였다. 회전속도는 165 rpm부터 10 rpm씩 증가시켜서 335 rpm까지 측정하였고, 축 방향 외력은 영구자석간 거리를 각각 20 mm, 15 mm, 10 mm일 때를 측정하였다.
3.1 축 방향 외력이 없는 경우
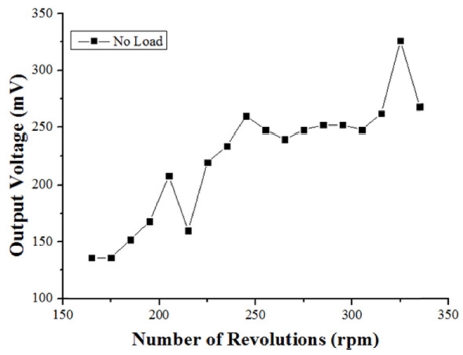
무버의 자유단에 부착된 영구자석은 반대편에 위치한 영구자석과의 반발력을 통해 자기변형 에너지 하베스팅 장치에 외력을 인가하는 역할을 한다. 거리가 가까울수록 외력의 크기가 세지며, 외력이 없는 경우는 두 영구자석간의 거리가 충분히 멀어 반발력이 존재하지 않는다. Fig. 4는 외력이 없는 경우일 때 자기변형 에너지 하베스팅 장치의 출력전압을 나타낸 그래프이다.
출력전압은 325 rpm일 때 326 mV로 가장 높으며, 이 때의 출력전류는 25.47 m이다. 따라서 생성되는 전력은 8302.8 μW이다.
3.2 축 방향 외력이 있는 경우
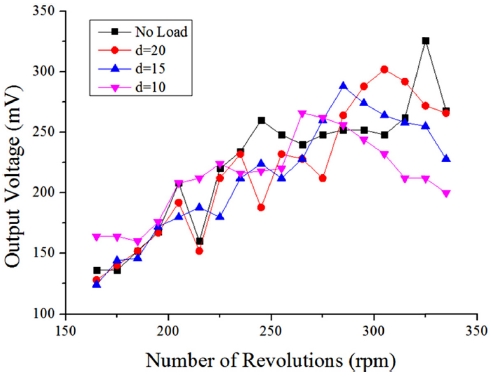
축 방향 외력은 영구자석간의 거리를 통해 조절한다. Fig 5(a)-5(c)는 영구자석간 거리가 각각 20 mm, 15 mm, 10 mm일 때의 출력전압을 나타낸 그래프이다.
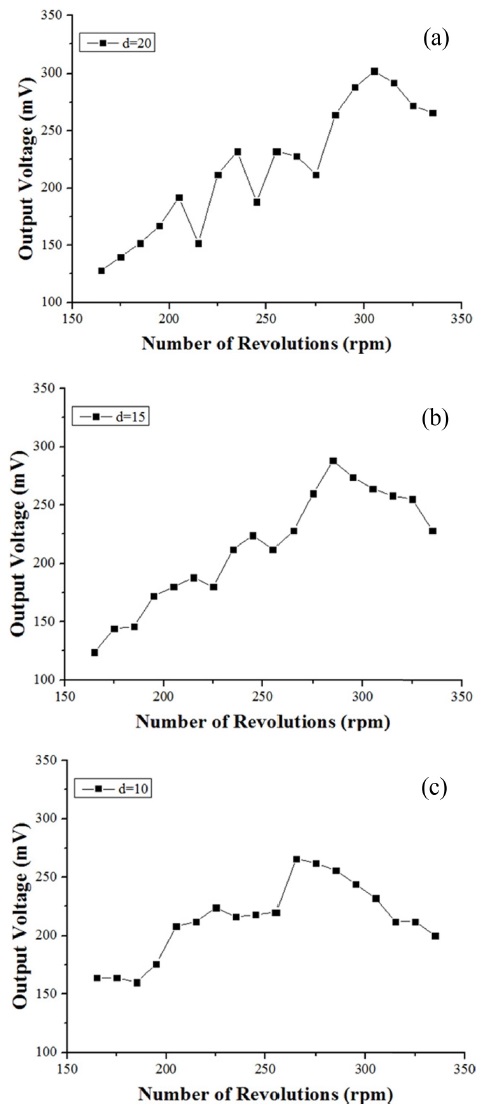
(a) Output voltage of energy harvesting device with preload (d = 20 mm), (b) Output voltage of magnetostrictive energy harvesting device with preload (d = 15 mm), (c) Output voltage of magnetostrictive energy harvesting device with preload (d = 10 mm)
d = 20mm인 경우, 출력전압은 305 rpm일 때 302 mV로 가장 높으며, 이 때의 출력전류는 23.59 mA이다. 따라서 생성되는 전력은 7125.3 μW이다. d = 15mm인 경우, 출력전압은 285 rpm일 때 288 mV로 가장 높으며, 이 때의 출력전류는 22.50 mA이다. 따라서 생성되는 전력은 6480.0 μW이다. d = 10mm인 경우, 출력전압은 265 rpm일 때 266 mV로 가장 높으며, 이 때의 출력전류는 20.78 mA이다. 따라서 생성되는 전력은 5527.8 μW이다. 진동 에너지 기반의 에너지 하베스팅 장치는 출력이 시스템의 변형량과 비례하므로, 출력이 가장 높은 지점이 변형량이 가장 크다는 것을 알 수 있고, 해당 지점에서 공명현상이 일어난 것을 유추할 수 있다. 또한 축 방향으로 외력이 가해질 경우, 그 크기가 커짐에 따라 전체적인 출력은 감소하지만, 출력의 최댓값이 나타나는 회전속도 또한 감소한다. 이를 통해 축 방향 외력이 고유진동수를 조절할 수 있음을 입증하였다. Fig. 6은 모든 출력 결과를 한번에 나타낸 그래프이다.
4. 결론
본 연구에서는 축 방향으로 외력을 인가한 자기변형 에너지 하베스팅 장치 설계 및 제작하였고, 인가하는 외력의 크기에 변화를 주었을 때 회전속도에 따른 출력전압의 비교를 통해 에너지 하베스팅 장치의 고유진동수 조절 가능성을 입증하였다. 축 방향 외력은 시스템의 출력을 81.60% 수준으로 저하시키나, 고유진동수 또한 81.54% 수준으로 낮아지므로, 인가하는 진동의 주파수가 낮더라도 공명현상을 유도할 수 있다. 따라서 이러한 고유진동수 조절을 이용하면 일상생활에서 발생하는 진동의 주파수처럼 크기가 작은 주파수가 인가될 경우에도 에너지 하베스팅 장치의 출력을 보장할 수 있다.
NOMENCLATURE
| Σa : | Allowable stress |
| A : | Cross sectional areas of magnet |
| Ac : | Cross sectional areas of coils |
| b : | Base of mover |
| B : | Magnetic flux density |
| d : | Distance between magnets |
| e* : | Coupling coefficient between strain and magnetic field under constant stress |
| E : | Modulus of elasticity |
| h : | Height of mover |
| H : | Magnetic field intensity |
| I : | Area moment of inertia |
| l : | Length of mover |
| M(x, t) : | Moment distribution along length of beam |
| N : | Number of coils |
| P : | Axial load |
| Q(x, t) : | Shearing force distribution |
| S : | Strain |
| SH : | Mechanical compliance under constant magnetic field |
| T : | Stress |
| V : | Electromotive force |
| V(x, t) : | Beam displacement |
| Zx : | Modulus of section |
| μs : | Permeability under constant stress |
| ρ : | Mass per unit length of beam |
| ω : | Circular frequency of vibration |
Acknowledgments
이 논문은 충남대학교 2016년 자체연구(CNU 학술연구지원사업)비 지원에 의하여 연구됨(No. 2016-1584-01).
REFERENCES
-
Park, C.-W., Kwon, K.-S., Kim, W.-B., Min, B.-K., Park, S.-J., et al., “Energy Consumption Reduction Technology in Manufacturing-A Selective Review of Policies, Standards, and Research,” Int. J. Precis. Eng. Manuf., Vol. 10, No. 5, pp. 151-173, 2009.
[https://doi.org/10.1007/s12541-009-0107-z]

- Lee, M. W., Gong, D., Tan, K., Chan, T., Wang, N., et al., “Energy Harvesting for IoT,” National University of Singapore, 2015.
-
Erturk, A. and Inman, D. J., “An Experimentally Validated Bimorph Cantilever Model for Piezoelectric Energy Harvesting from Base Excitations,” Smart Materials and Structures, Vol. 18, No. 2, Paper No. 025009, 2009.
[https://doi.org/10.1088/0964-1726/18/2/025009]

-
Torres, E. O. and Rincón-Mora, G. A., “Electrostatic Energy-Harvesting and Battery-Charging CMOS System Prototype,” IEEE Transactions on Circuits and Systems, Vol. 56, No. 9, pp. 1938-1948, 2009.
[https://doi.org/10.1109/TCSI.2008.2011578]

-
Beeby, S. P., Torah, R., Tudor, M., Glynne-Jones, P., O'donnell, T., et al., “A Micro Electromagnetic Generator for Vibration Energy Harvesting,” Journal of Micromechanics and Microengineering, Vol. 17, No. 7, Article No. 1257, 2007.
[https://doi.org/10.1088/0960-1317/17/7/007]

- Roundy, S. J., “Energy Scavenging for Wireless Sensor Nodes with a Focus on Vibration to Electricity Conversion,” University of California, Berkeley, 2003.
-
Rastegar, J., Pereira, C., and Nguyen, H.-L., “Piezoelectric-Based Power Sources for Harvesting Energy from Platforms with Low-Frequency Vibration,” Proc. of International Society for Optics and Photonics in Industrial and Commercial Applications of Smart Structures Technologies, Paper No. 617101, 2006.
[https://doi.org/10.1117/12.657464]

-
Kulah, H. and Najafi, K., “Energy Scavenging from Low-Frequency Vibrations by Using Frequency Up-Conversion for Wireless Sensor Applications,” IEEE Sensors Journal, Vol. 8, No. 3, pp. 261-268, 2008.
[https://doi.org/10.1109/JSEN.2008.917125]

-
Challa, V. R., Prasad, M., Shi, Y., and Fisher, F. T., “A Vibration Energy Harvesting Device with Bidirectional Resonance Frequency Tunability,” Smart Materials and Structures, Vol. 17, No. 1, Paper No. 015035, 2008.
[https://doi.org/10.1088/0964-1726/17/01/015035]

-
Peters, C., Maurath, D., Schock, W., Mezger, F., and Manoli, Y., “A Closed-Loop Wide-Range Tunable Mechanical Resonator for Energy Harvesting Systems,” Journal of Micromechanics and Microengineering, Vol. 19, No. 9, Paper No. 094004, 2009.
[https://doi.org/10.1088/0960-1317/19/9/094004]

-
Berlincourt, D. A., Curran, D. R., and Jaffe, H., “Piezoelectric and Piezomagnetic Materials and Their Function in Transducers,” Physical Acoustics: Principles and Methods, Vol. 1, pp, 182-188, 1964.
[https://doi.org/10.1016/B978-1-4832-2857-0.50009-5]

-
Chung, T. K., Lee, D. G., Ujihara, M., and Carman, G. P., “Design, Simulation, and Fabrication of a Novel Vibration-based Magnetic Energy Harvesting Device,” Proc. of International Transducers in Solid-State Sensors, Actuators and Microsystems Conference, pp, 867-870, 2007.
[https://doi.org/10.1109/SENSOR.2007.4300268]