PD 제어 및 신경망제어를 결합하여 평행한 슬라이더시스템의 궤적 제어
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
The parallel slider system can be configured as a parallel robot by combining with other link devices. Therefore, the degree of positioning of the parallel slider would have considerable influence on the smooth operation of the parallel robot. In order to examine the degree of positioning of each slider, the following trajectory is equally presented, and the possibility of tracking the slider trajectory examined by application of the PD and PND control. From the experimental results, the dynamic characteristics of the slider show different responses to differing equivalent frictional forces acting on the slider. The PND control can make the rise time shorter than the PD control, and the PND control and PD control can smoothly follow the same trajectory given to each slider. It is therefore anticipated that the PND control and the PD control could be successfully implemented to follow the trajectory of a parallel robot based on a parallel slider system. It would then be necessary to fabricate slider experimental equipment capable of generating torque of sufficient magnitude to successfully reduce the trajectory error of the slider.
Keywords:
Ball screw, Slider system, PD control, PND control, Trajectory control키워드:
볼나사, 슬라이더시스템, 비례미분제어, 비례신경망미분제어, 궤적제어1. 서론
볼나사1는 마찰저항이 작고 구름운동으로 회전운동을 직선운동으로 변환시키므로 로봇, 공작기계, 반도체제조 장비, 의료 및 보조기기 등 정밀도 높은 직선 이송장치에 널리 응용되고 있다. 볼나사와 슬라이더를 조립한 장치를 2개의 평행 안내판 위에 각각 설치한 슬라이더시스템에 링크장치를 추가2 하여 체결된 링크의 끝부분이 로봇의 말단장치역할을 함으로써 병렬로봇으로 구성할 수 있다. 이러한 로봇은 강성이 높고, 속도가 빠르고, 동작이 민첩하여 기본적으로 제품을 집어서 정해진 위치로 이동시키는 작업3뿐만 아니라 절삭작업,4 고속 고출력작업,5 고속 고정밀도작업,6 밀링작업7 등에 활용할 수 있다. 이러한 작업을 원활하게 수행하기 위해 병렬로봇이 주어진 작업궤적을 추종할 수 있는 제어기술이 요구된다. Takegaki 등8은 로봇이 마이크로컴퓨터로 쉽게 제어될 수 있는 PD 제어를 개발하여 허용오차범위 안에서 로봇 궤적을 제어하였다. Brad 등9은 PD 제어에서 관성력을 보상하여 로봇 궤적을 제어하였다. Seul 등10은 PD 제어를 피드백으로 하고 신경망제어를 피드포워드로 하여 로봇 궤적을 제어하였다. Jun 11은 PD 제어 및 신경망제어를 결합하면서 신경망제어의 은닉층은 복합삼각함수를 이용하였다.
2개의 평행한 슬라이더시스템은 2개의 슬라이더가 각각 독립적으로 동시에 움직이면서 병렬로봇의 작업을 수행한다. 이러한 슬라이더의 동작은 모터 동작에서 발생되는 마찰력, 볼나사 동작에서 발생되는 마찰력, 안내판과 슬라이더 테이블 사이에서 발생되는 마찰력 등의 등가마찰력이 슬라이더시스템의 위치결정에 중대한 영향을 미치게 된다. 본 연구에서는 각 슬라이더시스템의 동특성을 통하여 등가마찰력의 영향을 검토하고, 동일한 궤적에 대해 PD 제어 및 PD 제어와 신경망제어를 결합한 PND 제어를 적용하여 슬라이더의 궤적을 제어하여 병렬로봇의 작업가능성을 검토하고자 한다.
2. 슬라이더시스템의 궤적제어
2.1 슬라이더시스템의 실험장치 구성
본 연구에서 구축한 평행한 슬라이더시스템은 이러한 시스템을 기저로 새롭게 구성할 수 있는 병렬로봇의 위치결정 정도에 중대한 영향을 미친다. Fig. 1에서 보여준 슬라이더시스템은 각 슬라이더의 위치결정 정도를 검토하기 위해 동일하게 제시된 슬라이더 궤적의 추종 가능성을 연구할 수 있는 실험장치이다. 슬라이더시스템은 LS 메카피온에서 제작한 LM 가이드,12 Maxon Motor의 모터와 모터 제어기,13 TI의 TMS320F28335 마이크로 제어기14로 구성된 보드 및 컴퓨터 등으로 구성되어 있다. 슬라이더의 궤적은 컴퓨터에서 작성된 궤적제어알고리즘을 마이크로 제어기가 실행시킨 제어기보드에서 전압을 출력으로 내보내고 이를 모터제어기가 입력으로 받아 모터를 작동시켜 슬라이더의 궤적을 추종하도록 한다.
TI의 제어기로 구성된 제어기보드는 -10~+10 V를 출력으로 내보낸다. 맥슨모터의 제어기는 전류를 이용한 토크제어를 하는데 제어기의 입력과 출력은 -10~+10 V 사이의 전압으로 나타내고 출력전압의 0.8 V가 약 1 A에 해당된다. 모터의 위치는 모터에 장착된 엔코더로 검출되며 2000 펄스가 모터 1회전에 해당하고 모터 감속비가 26 : 1이다. LM 가이드는 모터, 볼나사, 슬라이더테이블 및 안내판 등으로 구성되어 있으며 스트로크는 500 mm, 볼 나사 리드는 10 mm이다.
2.2 슬라이더시스템의 운동방정식
슬라이더시스템의 운동방정식15은 컴퓨터 시뮬레이션을 이용한 슬라이더 궤적제어에 사용되고 식(1)과 같이 구할 수 있다.
| (1) |
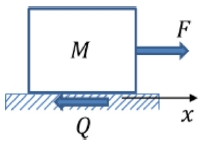
여기서, M은 안내판 위에 있는 볼나사 및 슬라이더 테이블 등을 포함한 등가질량으로 슬라이더로 하고, F는 슬라이더를 움직이게 하는 등가구동력, Q는 모터에서 발생하는 마찰력, 볼나사에서 발생하는 마찰력, 안내판과 슬라이더 사이에서 발생하는 마찰력을 포함한 등가마찰력, x는 슬라이더의 변위, 는 슬라이더의 가속도를 나타낸다.
2.3 슬라이더시스템의 궤적제어 알고리즘
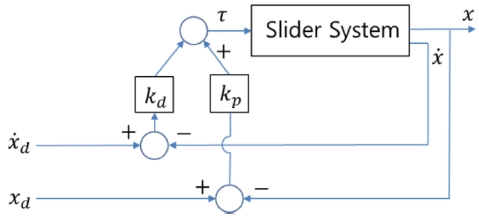
슬라이더 시스템을 대상으로 2가지 방법으로 슬라이더의 궤적을 제어하고 관성력을 보상하여 질량관성의 영향을 검토한다. 첫째는 비례제어와 미분제어를 결합한 PD 제어이고, 둘째는 PD 제어 및 신경망제어를 결합한 PND 제어이다. PD 제어를 이용한 슬라이더의 궤적제어는 Fig. 3의 블록선도에서 본 바와 같이 슬라이더의 입력 τ를 다음 식과 같이 구할 수 있다.
| (2) |
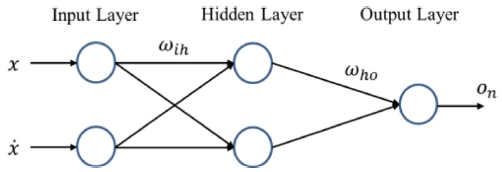
신경망제어에서는 슬라이더의 변위 및 속도를 입력으로 하는 다층신경망구조에서 조정 가중치 ωih와 ωho를 갱신하는 역전파 알고리즘16을 이용한다. 다층신경망은 Fig. 4와 같은 구조를 이루고 있으며 활성함수로써 식(3)와 같은 로지스틱 함수를 이용한다.
| (3) |
여기서 a, b, c는 임의의 상수이다.
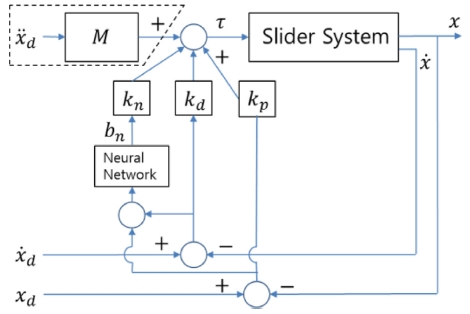
PND제어를 이용한 슬라이더의 궤적제어는 Fig. 5의 블록선도에서 본 바와 같이 슬라이더의 입력 τ를 다음 식과 같이 구할 수 있고, bn은 신경망제어에서 구한 것이다. 또한 점선 다각형으로 표시한 부분은 관성력보상을 나타낸 것으로 PND와 관성력보상을 결합하여 PNDM 제어라고 한다.
| (4) |
3. 실험 결과
슬라이더시스템을 대상으로 모터제어기의 출력인 전압을 전류로 변환하여 발생하는 토크를 이용하여 PD 및 PND 제어로 슬라이더 궤적을 제어하는데 있어, 슬라이더의 응답시간은 50초로 한다.
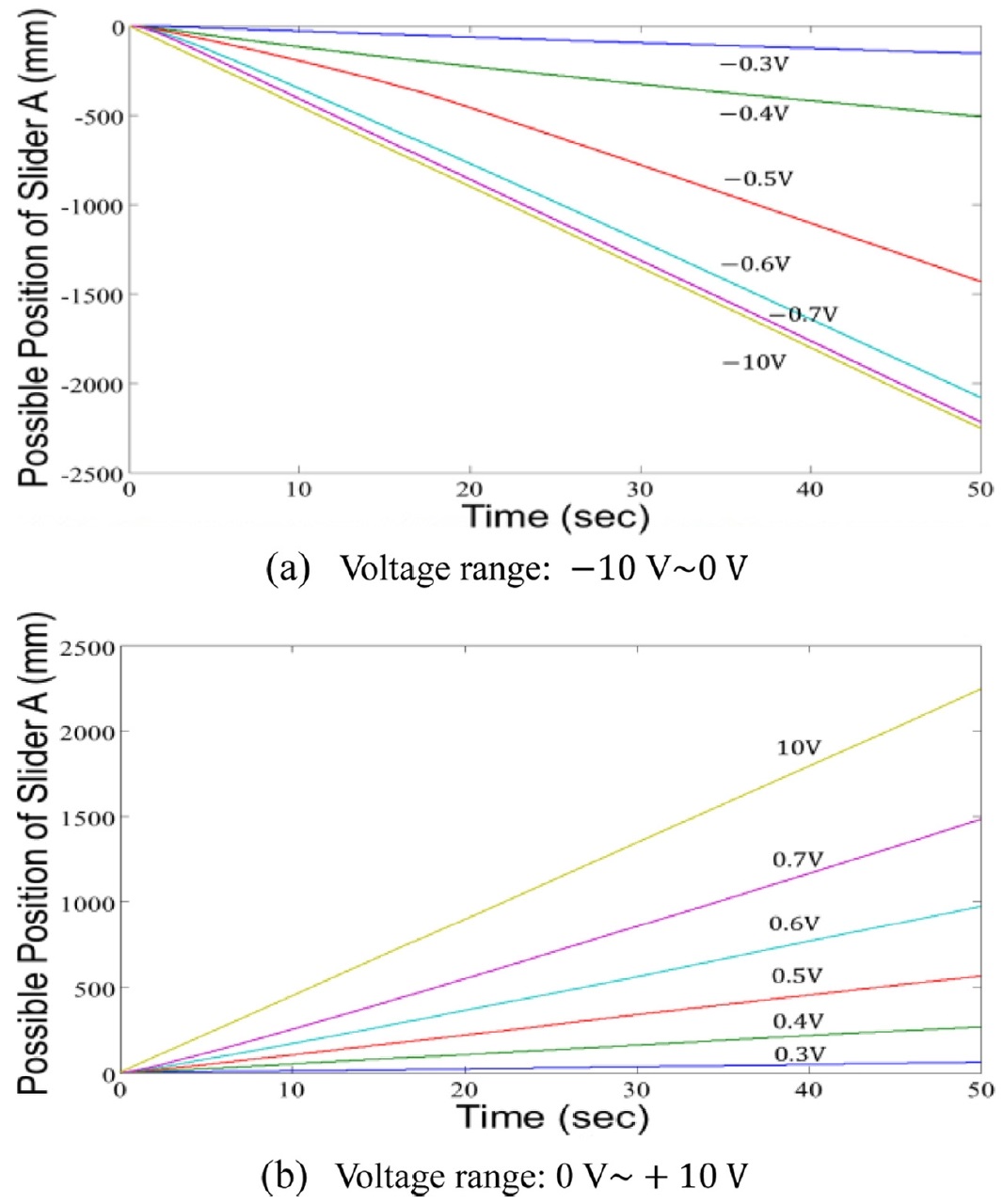
Fig. 6은 토크입력을 입력전압의 범위 -10~+10 V 할 때 모터의 동특성을 슬라이더 A가 이송이 가능한 위치를 나타낸 것으로 거의 선형으로 나타난다. -0.3 V <Vin < 0 V, 0 V <Vin < +0.3 V에서는 모터가 작동하지 않는 것으로 보아 모터의 마찰력이 영향을 준 것으로 보인다. -0.7 V ≤ Vin ≤ -0.3 V, +0.3 V ≤ Vin ≤ +0.7 V 입력범위에서의 직선의 기울기 변화가 -10 V ≤ Vin ≤ -0.7 V, +0.7 V ≤ Vin ≤ +10 V보다 크므로 입력구간이 좁더라도 슬라이더 A의 운동변화가 클 수 있다.
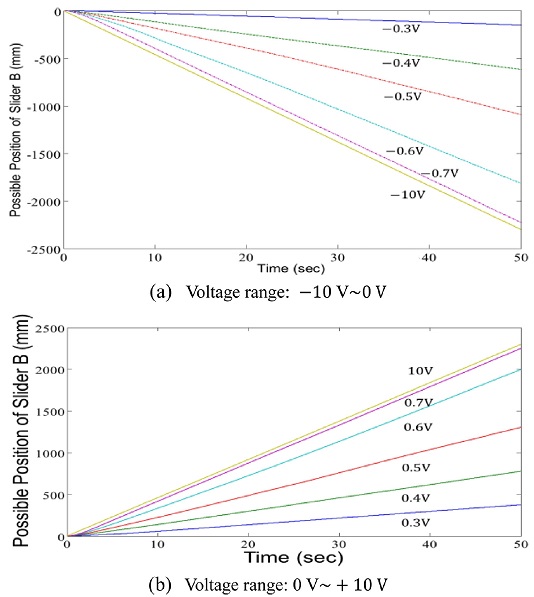
Fig. 7은 토크입력을 입력전압의 범위 -10~+10 V 할 때 모터의 동특성을 슬라이더 B가 이송이 가능한 위치를 나타낸 것으로 거의 선형으로 나타난다. -0.3 V <Vin < 0 V, 0 V <Vin < +0.3 V에서는 모터가 작동하지 않는 것으로 보아 모터의 마찰력이 영향을 준 것으로 보인다. -0.7 V ≤ Vin ≤ -0.3 V, +0.3 V ≤ Vin ≤ +0.7 V 입력범위에서의 직선의 기울기 변화가 -10 V ≤ Vin ≤ -0.7 V, +0.7 V ≤ Vin ≤ +10 V보다 크므로 입력구간이 좁더라도 슬라이더 B의 운동변화가 클 수 있다.
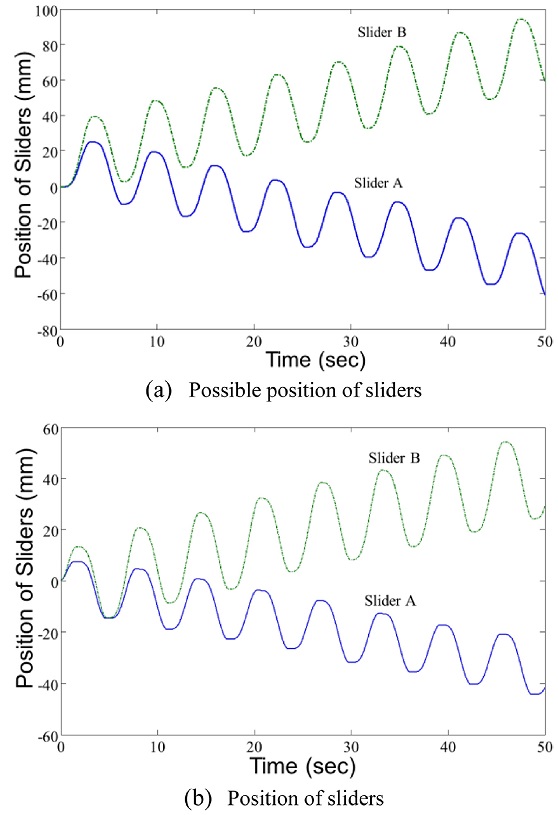
Figs. 6과 7의 토크입력 +0.7 V에서 슬라이더 B가 슬라이더 A보다 직선기울기가 훨씬 큰 것을 근거로 토크입력을 0.7 cost로 할 때 슬라이더들의 동특성을 Fig. 8에 나타낸다. Fig. 8(a)는 모터만을 구동시켰을 때 모터 A, B의 회전량을 위치로 나타낸 것이다. 모터 A의 포락선은 아랫쪽으로, 모터 B의 포락선은 윗쪽으로 진행하고 있는데, 모터 마찰력이 다르게 작용하는 것을 알 수 있다. Fig. 8(b)는 슬라이더 A, B의 변위를 나타낸 것으로 모터의 동특성과 유사하지만 변위 폭은 줄어들고 있다. 이것은 볼나사의 마찰력과 안내판과 슬라이더 테이블 사이의 마찰력이 다르게 작용하는 것을 알 수 있다.
PD 제어 및 PND 제어에서 이용되는 비례, 미분 및 신경망 이득상수를 설정하기 위해, 우선 설계자가 만족할만한 PD 제어응답이 나타나도록 비례 및 미분 이득상수를 조정한다. 그리고 PND 제어에서는 PD 제어에서 조정된 비례 및 미분 이득상수를 이용하고 설계자가 만족할만한 응답이 나타나도록 신경망 이득상수를 조정한다.
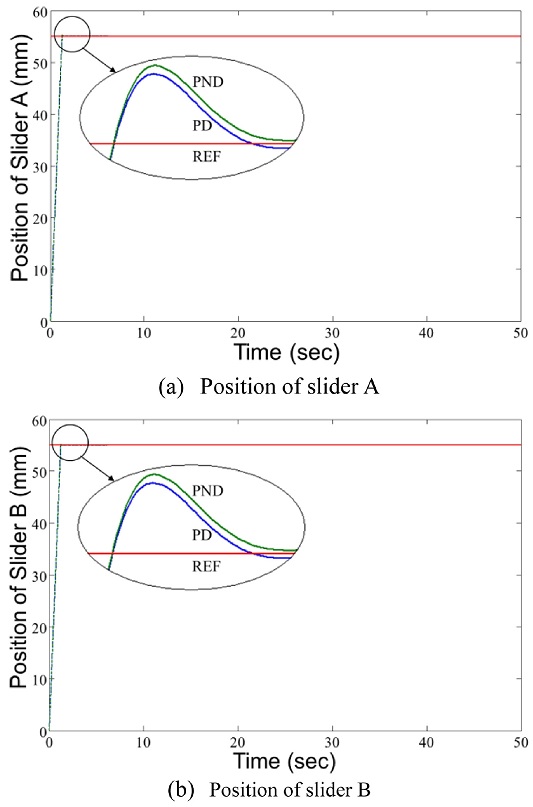
Fig. 9는 각 슬라이더의 목표위치를 55 mm로 할 때 나타낸 응답이다. PD 제어에서 슬라이더 A의 상승시간은 1.260초, 첨두율은 0.40%이고 슬라이더 B의 상승시간은 1.260초, 첨두율은 0.45%이다. PND 제어에서 슬라이더 A의 상승시간은 1.244초, 첨두율은 0.44%이고 슬라이더 B의 상승시간은 1.242초, 첨두율은 0.48%이다. PND 제어는 PD 제어보다 첨두율이 크더라도 목표궤적에 큰 영향을 미친다고 볼 수 없지만 상승시간을 짧게 하는 효과를 가지고 있다.
Figs. 10부터 12에서 슬라이더의 목표궤적을 추종하는데 이용한 제어기법은 PD 제어, PND 제어 및 PNDM 제어를 적용하고, 목표궤적은 다음 식17을 활용하고 계수 a1, a2, a3은 임의의 상수이다.
| (5) |
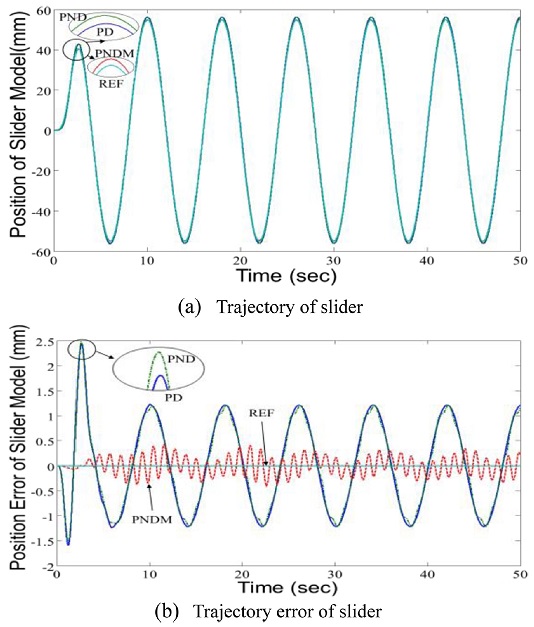
Fig. 10은 슬라이더시스템의 운동방정식을 이용한 컴퓨터 시뮬레이션으로 슬라이더의 궤적을 제어한 결과이다. Fig. 10(a)는 슬라이더의 궤적 제어한 결과를, Fig. 10(b)는 슬라이더의 궤적오차를 나타낸 것이다. 관성력의 영향을 받은 PNDM 제어가 PD 제어나 PND 제어보다 오차를 뚜렷하게 줄이는 것을 알 수 있다.
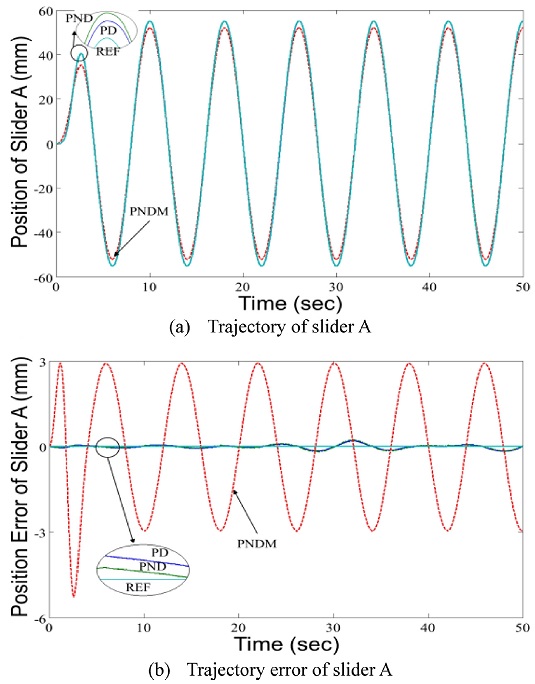
Fig. 11은 슬라이더시스템의 실험장치로 슬라이더 A의 궤적을 제어한 결과이다. Fig. 11(a)는 슬라이더 A의 궤적 제어한 결과를, Fig. 11(b)는 슬라이더 A의 궤적오차를 나타낸 것이다. PD 제어나 PND 제어가 PNDM 제어보다 오차를 뚜렷하게 줄이는 것을 알 수 있다.
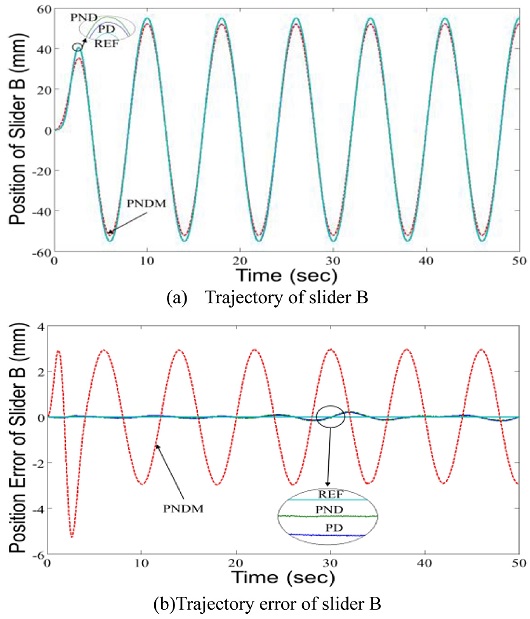
Fig. 12는 슬라이더시스템의 실험장치로 슬라이더 B의 궤적을 제어한 결과이다. Fig. 12(a)는 슬라이더 B의 궤적 제어한 결과를, Fig. 12(b)는 슬라이더 B의 궤적오차를 나타낸 것이다. PD 제어나 PND 제어가 PNDM 제어보다 오차를 뚜렷하게 줄이는 것을 알 수 있다. Figs. 10에서 12의 결과로부터 PD 제어, PND 제어 및 PNDM 제어는 평행한 슬라이더시스템으로 구성된 병렬로봇의 궤적을 제어할 수 있는 것으로 판단할 수 있고 PND 제어는 상승시간을 짧게 하는데 영향을 미친다.
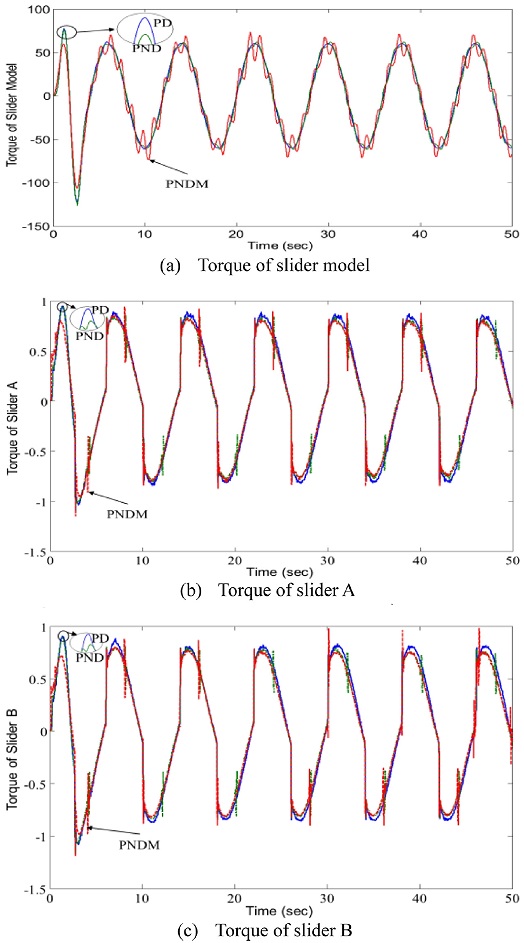
Fig. 13은 슬라이더시스템을 제어할 때 구한 토크 그래프로써, Fig. 13(a)는 식(1)의 슬라이더 모델 식을 이용하여 시뮬레이션으로 구한 슬라이더 모델의 토크, Figs. 13(b)와 13(c)는 실험으로 구한 슬라이더 A와 B의 토크를 나타낸다. 시뮬레이션의 토크그래프에서 PNDM 제어는 PD 제어 및 PND 제어보다 토크크기가 초기 토크영역에서 크고 토크크기의 첫번째 첨두율에서 PD 제어 및 PND 제어보다 작게 나타난다. 마찬가지로 실험에서의 초기토크 및 첫 번째 첨두율의 토크크기도 시뮬레이션의 토크크기 특성과 유사하고, 응답시간 동안 시뮬레이션 및 실험에서의 그래프의 개형도 비슷하지만, 실험에서 구한 토크크기의 영역은 시뮬레이션의 토크크기의 영역보다 상대적으로 크게 떨어진다.
Brad 등9은 로봇 관절의 궤적을 대상으로 한 시뮬레이션에서 관성력을 보상한 PDM 제어가 PD 제어보다 궤적오차가 줄어드는 것을 보여준다. Figs. 10부터 12에서 본 바와 같이 슬라이더시스템의 궤적제어에서 PNDM 제어는 시뮬레이션에서 PD 제어 및 PND 제어보다 슬라이더의 궤적오차를 줄이지만 실험에서 PD 제어 및 PND 제어보다 슬라이더의 궤적오차를 크게 한다. PNDM 제어는 PD 제어 및 PND 제어보다 궤적오차를 줄이기 위해 시뮬레이션에서 구한 토크크기에 해당하는 만큼 토크를 발생해야 하지만 Fig. 13에서 본 바와 같이 실험에서 구한 토크크기는 현저하게 떨어진다. 따라서 실험에서 PNDM 제어가 PD 제어 및 PND 제어보다 궤적오차를 줄이기 위해서는 시뮬레이션에서 구한 토크크기를 발생할 수 있는 실험장치를 구성할 필요가 있다.
4. 결론
평행한 슬라이더시스템은 다른 링크장치와 결합하여 병렬로 봇으로 구성할 수 있고 이러한 병렬로봇이 원활한 작업을 수행하는데 평행한 슬라이더의 위치결정 정도가 중대한 영향을 미친다. 각 슬라이더의 위치결정 정도를 검토하기 위해 슬라이더가 추종하는 궤적을 동일하게 제시하고, PD 및 PND 제어를 적용하여 슬라이더 궤적의 추종 가능성을 조사하였다. 본 시스템을 대상으로 한 실험결과로부터 슬라이더에 작용하는 서로 다른 등가마찰력 때문에 동일한 입력에 대한 슬라이더 동특성은 서로 다른 응답으로 나타나서 위치결정 정도가 떨어진다. PD 및 PND 제어를 적용한 결과에서, PND 제어가 PD 제어 보다 과도응답의 상승시간을 짧게 할 수 있고 PND 제어 및 PD 제어는 각 슬라이더에 주어진 동일한 궤적을 원활하게 추종할 수 있었다. 따라서 PND 제어 및 PD 제어를 이용하여 평행한 슬라이더시스템으로 구성된 병렬로봇의 궤적제어 가능성을 기대할 수 있다.
또한 관성력 보상제어가 관성력 비보상제어보다 슬라이더의 궤적오차를 줄이기 위해서 슬라이더 실험장치는 슬라이더 모델에서 구한 토크크기를 발생할 수 있는 장치로 구성될 필요가 있다.
NOMENCLATURE
| F : | Equivalent driving force |
| M : | Equivalent mass |
| Q : | Equivalent friction force |
| bn : | Output of neural network control |
| kd : | Differential gain constant |
| kn : | Neural network gain constant |
| kp : | Proportional gain constant |
| x : | Slider displacement |
| : | Slider velocity |
| : | Slider acceleration |
| xd : | Desired slider displacement |
| : | Desired slider velocity |
| : | Desired slider acceleration |
| τ : | Input torque |
| ωih : | Weights between input layer and hidden layer |
| ωho : | Weights between hidden layer and output layer |
Acknowledgments
이 논문은 2017년도 정부(교육부)의 재원으로 한국연구재단의 대학중점연구소지원사업으로 수행된 연구임(2010-0020089).
REFERENCES
-
Min, B.-K., Cao, L., Khim, G., Park, C.-H., and Chung, S.-C., “Modeling and Uncertainty Analysis of Ballscrew Nut Stiffness,” J. Korean Soc. Precis. Eng., Vol. 32, No. 5, pp. 415-422, 2015.
[https://doi.org/10.7736/KSPE.2015.32.5.415]

-
Liu, X., Wang, J., and Pritschow, G., “On the Optimal Kinematic Design of the PRRRP 2-DOF Parallel Mechanism,” Mechanism and Machine Theory, Vol. 41, No. 9, pp. 1111-1130, 2006.
[https://doi.org/10.1016/j.mechmachtheory.2005.10.008]

-
Pierrot, F., Baradat, C., Nabat, V., Company, O., Krut, S., et al., “Above 40 g Acceleration for Pick-and-Place with a New 2-DOF PKM,” Proc. of the International Conference on Robotics and Automation, pp. 1794-1800, 2009.
[https://doi.org/10.1109/ROBOT.2009.5152193]

-
Long, Y., Wang, L., Ye, P., and Wang, J., “Kinematic Analysis and Netton-Euler Equations of a Novel Hybrid Machine Tool,” Chinese Journal of Mechanical Engineering, Vol. 15, pp. 132-138, 2002.
[https://doi.org/10.3901/CJME.2002.supp.132]

- Tang, X., Wang, J., and Wang, L., “Analysis and Design of a Novel 4-Axis Hybrid Machine Tool Based on a 2-DOF Parallel Mechanism,” Proc. of the International Conference on Robotics, Intelligent System and Signal Processing, pp. 991-995, 2003.
- Chu, Z., Qu, D., Sun, L., and Cui, J., “Research of 2-DOF Planar Parallel High Speed/High Accuracy Robot,” Proc. of the World Congress on Intelligent Control and Automation, pp. 4715-4719, 2004.
-
Hao, Q., Guan, L., Wang, L., and Shao, H., “Dynamic Feedforward Control of the 2-DOFs Parallel Manipulator of a Hybrid Machine Tool,” Proc. of the International Conference on Control and Automation, pp. 528-533, 2010.
[https://doi.org/10.1109/ICCA.2010.5524164]

-
Takegaki, M. and Arimoto, S., “A New Feedback Method for Dynamic Control of Manipulators,” Journal of Dynamic Systems, Measurement, and Control, Vol. 103, No. 2, pp. 119-125, 1981.
[https://doi.org/10.1115/1.3139651]

-
Paden, B. and Panja, R., “Globally Asymptotically Stable ‘PD+’Controller for Robot Manipulators,” International Journal of Control, Vol. 47, No. 6, pp. 1697-1712, 1988.
[https://doi.org/10.1080/00207178808906130]

-
Jung, S. and Hsia, T. C., “Neural Network Inverse Control Techniques for PD Controlled Robot Manipulator,” Robotica, Vol. 18, No. 3, pp. 305-314, 2000.
[https://doi.org/10.1017/S0263574799002064]

- Ye, J., “Compound Control of a Compound Cosine Function Neural Network and PD for Manipulators,” International Journal of Control, Vol. 87, No. 10, pp. 2118-2129, 2014.
- LS Mecapion, “Industrial Robot System,” http://www.lsmecapion.com/contents/sub02/sub03_01_03.php?writemode=view&code=catalog&seq=8230&page=1, (Accessed 23 DEC 2017)
- Maxon Motor, “Maxon Motor Control,” https://www.maxonmotor.com/medias/sys_master/root/8803609444382/145391-ADS-50-5-Operating-Instructions-En.pdf, (Accessed 23 DEC 2017)
- Texas Instruments, “TMS320F2833x Digital Signal Controllers (DSCs),” http://www.ti.com/lit/ds/symlink/tms320f28335.pdf, (Accessed 23 DEC 2017)
-
Zhang, J., Zhang, H., Du, C., and Zhao, W., “Research on the Dynamics of Ball Screw Feed System with High Acceleration,” International Journal of Machine Tools and Manufacture, Vol. 111, pp. 9-16, 2016.
[https://doi.org/10.1016/j.ijmachtools.2016.09.001]

-
Wu, C.-J. and Huang, C.-H., “Back-Propagation Neural Networks for Identification and Control of a Direct Drive Robot,” Journal of Intelligent & Robotic Systems, Vol. 16, No. 1, pp. 45-64, 1996.
[https://doi.org/10.1007/BF00309655]

-
Dawson, D. M., Carroll, J. J., and Schneider, M., “Integrator Backstepping Control of a Brush DC Motor Turning a Robotic Load,” IEEE Transactions on Control Systems Technology, Vol. 2, No. 3, pp. 233-244, 1994.
[https://doi.org/10.1109/87.317980]