절대 거리 측정을 위한 편광 기반 이중 기준 경로 분광 간섭계의 개발

1. 서론

절대 거리 측정(Absolute Distance Measurement)은 단색광 레이저 간섭계를 이용한 증분식 변위 측정과는 다르게 측정 거울을 연속적으로 이동하면서 위상 정보를 누적하지 않고도 한번에 거리 정보를 획득할 수 있는 방법이다. 이와 같은 장점으로 인해, 절대 거리 측정은 간섭 신호를 연속적으로 누적하여 획득하기 어려운 대형 구조물의 조립 공정, 대형 광학계의 정렬, 초정밀 스테이지의 위치 결정, 3차원 공간상의 좌표 측정, 불연속적인 단차 및 두께 측정 등의 다양한 정밀 공학 분야에 널리 활용될 수 있다. 절대 거리 측정을 구현하는 대표적인 광학식 원리로는 다파장 간섭계(Multi-Wavelength Interferometer),^1-3,22 파장 쓸기 간섭계(Wavelength Sweeping Interferometer),^4,5,22 분광 간섭계(Spectral-Domain Interferometer),^6-10,21,22 비행 시간법(Time of Flight)^11,12 등이 연구되고 있다.

이와 같은 절대 거리 측정 방법 중 분광 간섭계는 광대역 광원을 사용하여 기준 경로와 측정 경로를 진행한 빛들에 의해 생성된 간섭 스펙트럼(Interference Spectrum)을 획득하여 그 간섭 스펙트럼의 주기를 계산함으로써, 단색광 간섭계에서는 필수적인 위상 천이 기법(Phase-Shifting Technique)과 같은 과정없이 실시간으로 거리를 측정할 수 있다. 이러한 장점에도 불구하고, 분광 간섭계에는 근원적으로 방향 모호성 문제(Directional Ambiguity Problem)와 측정 불가 영역(Non-Measurable Range)이 존재한다. 이와 같은 근원적인 문제 해결을 위해 이색 광분할기(Dichroic Beam Splitter)를 이용하여 간섭계의 기준 경로를 2개로 나누고, 측정되는 간섭 스펙트럼도 두 영역으로 나누어 각 영역에서 측정되는 거리에 오프셋(Offset)을 주어 측정 불가 영역 문제를 해결하는 연구,¹³ 기준 경로에 분산 물질을 삽입하여 간섭 스펙트럼 위상에 비선형성을 발생시킴으로써 비선형 성분 부호가 측정 거리에 따라 바뀜을 이용하여 방향 모호성 문제를 해결하고자 하는 연구들이 수행되었다.^14,15 그러나 이색 광분할기 사용으로 인해 분광 스펙트럼 샘플링 한계가 존재하고, 분산 물질 삽입에 의한 간섭 신호 가시도 저하라는 문제가 발생하게 된다. 또 다른 연구에서는, 측정 불가 영역과 방향 모호성을 해결하기 위해 반사율이 다른 2개의 기준 거울을 사용한 이중 기준 경로 분광 간섭계를 제안하였다.¹⁶ 이 연구에서는 마이켈슨 형태의 간섭계(Michelson’s Interferometer)를 기반으로 측정하고자 하는 거리에서 3개의 서로 다른 간섭 신호인 1) 측정 거울과 높은 반사율을 갖는 기준 거울 사이의 강한 간섭 신호(주 간섭 신호), 2) 측정 거울과 낮은 반사율을 갖는 기준 거울 사이의 약한 간섭 신호(부 간섭 신호), 3) 기준 거울 사이의 간섭 신호(두 기준 거울 사이의 간섭 신호)를 얻을 수 있다. 주 간섭 신호와 부 간섭 신호에서 계산된 거리 값의 크기를 비교하여 분광 간섭계의 방향 모호성 문제를 해결하였고, 주 간섭 신호가 측정불가 영역에 포함될 경우에도 부 간섭 신호를 통해 거리 측정이 가능하도록 하여 측정 불가 영역을 극복하였다. 이 선행 연구에서는 분광 간섭계의 근원적인 문제인 방향 모호성 문제와 측정 불가 영역 문제가 잘 해결됨을 보였지만, 2개의 기준 거울 사이에서 생성되는 자체 간섭 신호와 절대 거리 정보를 포함하는 간섭 신호가 겹칠 경우, 신호 구분의 어려움과 겹쳐진 신호의 비대칭성으로 인해 측정하고자 하는 절대 거리 신호에 왜곡을 줄 수 있다.

본 논문에서는 서로 수직한 편광을 갖는 두 기준 경로를 생성하여 기존 연구의 장점을 유지하면서도 두 기준 거울로부터 돌아오는 빛들 간의 간섭 신호를 제거함으로써, 절대 거리 측정값의 왜곡을 해결하는 편광 기반 이중 기준 경로 분광 간섭계를 제안하고 구현하고자 한다.

2. 기본 이론

분광 간섭계는 광대역 광원을 사용하여 광경로차(Optical Path Difference, OPD)에 의해 생기는 간섭 스펙트럼을 획득하여 절대 거리 l을 측정한다. 광주파수(f ) 영역에서 간섭 스펙트럼 I (l,f )는 측정하고자 하는 절대 거리에 따라 주기가 변화하며, 식(1)과 같이 표현된다. 여기서, c는 진공에서의 빛의 속도를 나타낸다.

식(1)과 같이 획득한 간섭 스펙트럼의 주기를 계산하기 위해, 일반적으로 푸리에 변환(Fourier Transform)을 활용한다. 푸리에 영역에서는 2개의 첨두 신호(Peak Signal)를 관찰할 수 있으며, 이는 1) 광원 자체의 배경광 분포인 I₀ (f )을 포함하는 DC, 저주파 첨두 신호와 2) 광경로차인 l에 따른 첨두 신호이다. 광원의 분포가 이상적으로 무한대 영역에서 균일한 광량을 가질 수 없다면, 광경로차가 작을 때 첨두 신호는 배경광 분포에 의한 저주파 첨두 신호 영역에 포함되어 절대 거리 측정을 할 수 없는 ‘측정 불가 영역(Non-Measurable Range)’이 근원적으로 발생한다. 또한, 광원인 광 빗(Optical Comb)의 반복률(Repetition Rate)에 의해 일정한 거리에 따라 반복적으로 같은 형태의 간섭 스펙트럼이 관찰되며, 반복되는 간섭 스펙트럼은 서로 다른 2개의 측정값을 갖는 ‘방향 모호성(Direction Ambiguity)’ 문제가 발생하게 된다. 이는 샘플링 이론에서 폴딩(Folding) 현상으로도 알려져 있다.¹⁷

이를 해결하기 위해 제안된 이중 기준 경로 분광 간섭계의 광학적 구성도는 Fig. 1과 같다. 광원인 펨토초 펄스 레이저(Femtosecond Pulse Laser)에서 발진한 광 빗은 광분할기A (BSA)에 의해 기준 경로와 측정 경로로 나뉜다. 기준 경로는 광분할기B (BS-B), 기준 거울A (RM-A), 기준 거울B (RM-B)에 의해 2개의 경로인 L_R1과 L_R2가 생성된다. 측정 경로인 L_T는 측정 거울(TM)로 진행한 빛의 이동 거리이다. 간섭 스펙트럼은 분광기(Spectrometer)에 의해 획득되며, 이는 3가지 간섭 신호인 1) 기준 거울A와 측정 거울 사이의 거리(|L_R1 - L_T|) 정보를 갖는 주 간섭 신호, 2) 기준 거울B와 측정 거울 사이의 거리(|L_R2 - L_T|) 정보를 갖는 부 간섭 신호, 3) 기준 거울A와 기준 거울B 사이의 거리(|L_R1 - L_R2|) 정보를 갖는 두 기준 거울 사이의 간섭 신호이다. 또한, 2개의 기준 경로에 의한 광경로차인 |L_R1 - L_T|와 |L_R2 - L_T|를 포함하는 간섭 신호를 구별하기 위해 기준 거울A와 기준 거울B의 반사율을 달리하여 간섭 신호의 크기를 조절하였다. 식(2)는 이중 기준 경로 간섭계를 통해 얻어지는 간섭 스펙트럼을 식으로 표현한 것이다.

Fig. 1

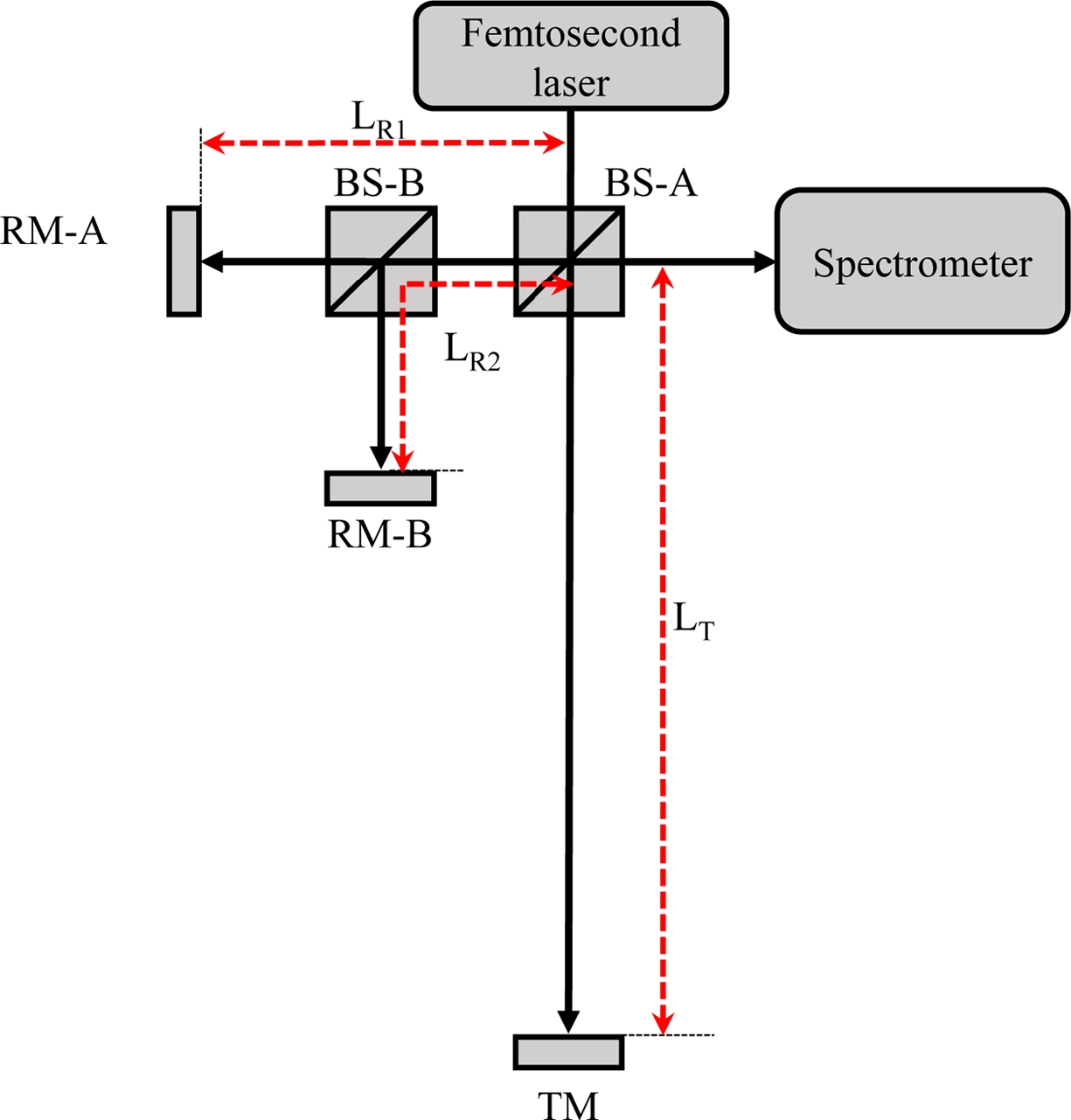
Optical layout of spectral-domain interferometer with dual reference paths (TM: target mirror, BS-A, BS-B: beam splitters, RM-A, RM-B: reference mirrors A, B, LT: target distance, LR1, LR2: reference distances)

여기서, I₀ (f )는 광원 자체의 배경광 분포이며, P_A, P_B, P_AB는 각각 주 간섭 신호의 진폭, 부 간섭 신호의 진폭, 두 기준 거울 사이 간섭 신호의 진폭이다. 본 논문에서는 편의상 주 간섭 신호와 부 간섭 신호를 구별하기 위해 P_A > P_B라고 가정하였다.

분광기를 통해 획득된 간섭 스펙트럼의 주기를 결정하기 위해 푸리에 변환을 적용하게 되면, Fig. 2와 같이 푸리에 영역에서 4개의 첨두 신호들을 관찰할 수 있다. 이들은 각각 1) |L_R1 - L_T|의 정보를 갖는 주 간섭 신호인 P_A, 2) |L_R2 - L_T|의 정보를 갖는 부 간섭 신호인 P_B, 3) |L_R1 - L_R2|의 정보를 갖는 두 기준 거울 사이 자체 간섭 신호인 P_AB 및 4) 광원의 광량 분포에 해당하는 DC 및 저주파 영역 신호이다. 폴딩 현상에 의해 발생하는 방향 모호성 문제는 Figs. 2(a)와 2(b) 같이 P_A 및 P_B의 거리 값의 크고 작음을 비교함으로써 해결할 수 있고, 측정 불가 영역 문제는 DC 및 저주파 영역에 P_A 신호가 묻히더라도 Fig. 2(c)와 같이 P_B 신호를 분석하여 절대 거리를 측정함으로써 극복할 수 있다. 그러나, Fig. 2(d)와 같이 P_A 신호가 P_AB 신호와 겹치는 경우, 절대 거리 정보를 가지고 있는 P_A 신호가 두 신호의 겹침 정도에 따라 측정값의 왜곡을 가져올 수 있다.

Fig. 2

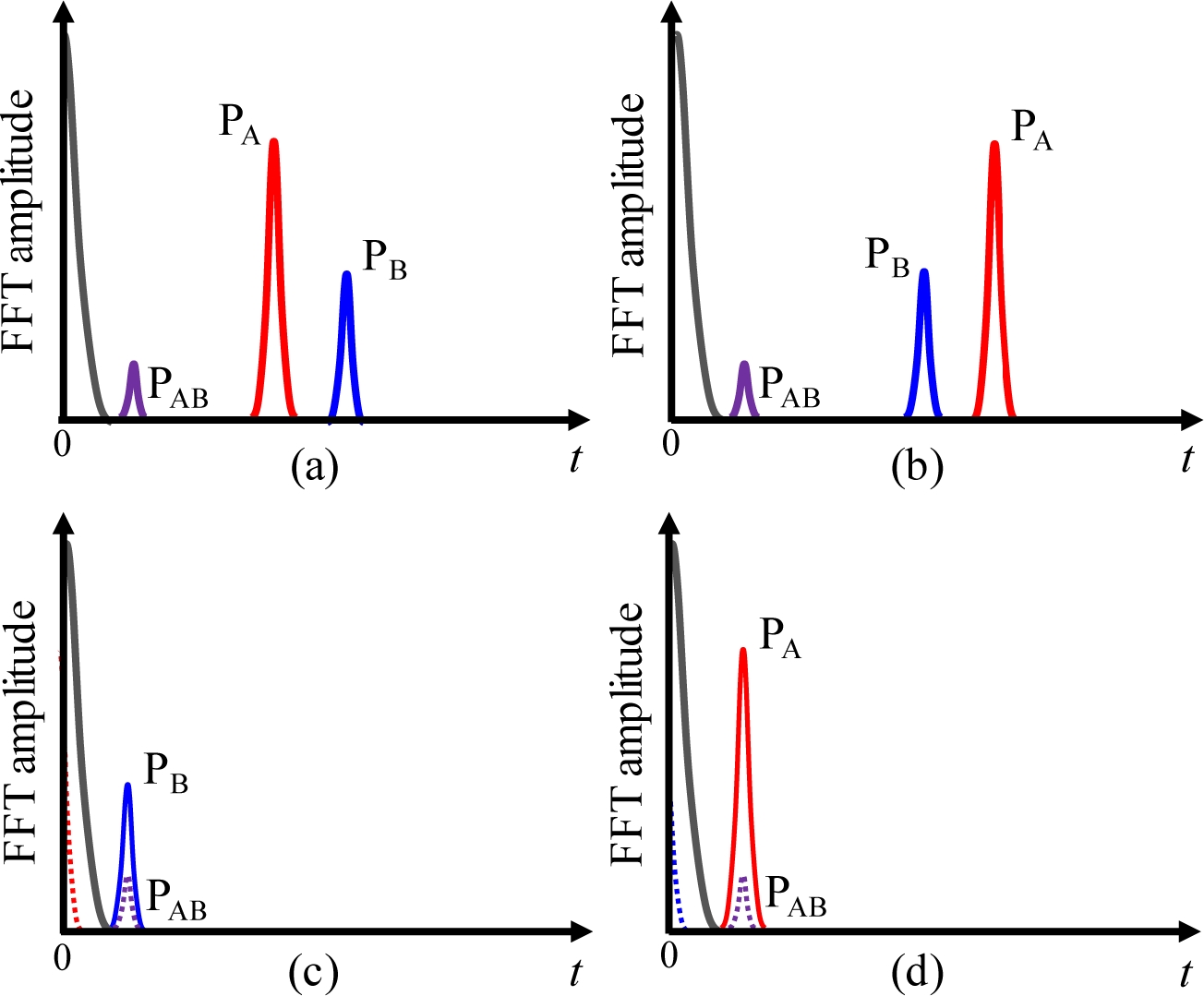
Examples of Fourier-transformed results in case of (a) Clearly separated three peaks when |LR2 - LT| > |LR1 - LT|, (b) Clearly separated three peaks when |LR1 - LT| > |LR2 - LT|, (c) Overlap of PB and PAB, and (d) Overlap of PA and PAB (PA: peak signal having an OPD of |LR1 - LT|, PB: peak signal having an OPD of |LR2 - LT|, PAB: peak signal having an OPD of |LR1 - LR2|)

물론, P_A 신호가 P_AB 신호가 이상적으로 완벽히 겹친다면 신호 왜곡은 발생하지 않는다. 두 신호의 겹침 정도에 따라 절대 거리 측정값의 정량적인 오차는 3장에서 언급할 수치 시뮬레이션(Numerical Simulation)의 결과를 통해 확인할 수 있다.

3. 수치 시뮬레이션 및 절대 거리 측정 실험

앞선 2장에서 논의한 바와 같이, 간섭 신호들의 겹침에 의해 생길 수 있는 측정값의 왜곡을 정량적으로 분석하기 위해 수치 시뮬레이션을 수행하였다. 선행 연구의 경우, Fig. 2와 같이 기준 거울들 사이에서 생긴 자체 간섭이 푸리에 영역에서 P_AB의 형태로 항상 존재하게 된다. 본 연구에서는 Fig. 2(d)와 같이 P_AB 신호와 주 간섭 신호인 P_A가 겹침에 의해 발생할 수 있는 절대 거리 측정값의 왜곡을 분석하기 위해, P_A와 P_AB가 완벽히 겹치는 위치를 원점으로 두고, 이 원점을 기준으로 ±100 μm인 총 200 μm 영역에서 P_A와 P_AB의 겹침 정도에 따른 절대 거리를 분석하여 보았다. 수치 시뮬레이션 조건은 본 연구에서 수행한 실험 조건을 반영하여, 광원은 중심 파장 1550 nm에서 40 nm의 반치폭(Full Width at Half Maximum)의 가우시안 포락선(Gaussian Envelope)을 갖는 반복률이 250 MHz인 광 빗이다. 또한 식(2)로 주어지는 각 간섭 신호 항들을 크기로 모든 측정 영역에서 구분될 수 있도록 각 항의 진폭비 P_A : P_B : P_AB를 선행연구¹⁸를 바탕으로 1 : 0.67 : 0.14로 결정하였다. 두 기준 거울 사이의 거리 |L_R1 - L_R2|는 250 μm로 설정하였다.

수치 시뮬레이션의 분석 결과에 따르면, Fig. 3과 같이 간섭 신호의 겹침 정도에 따라 최대 1 μm의 절대 거리 측정 오차가 발생할 수 있음을 알 수 있다. P_A 신호와 P_AB 신호가 완벽히 겹치는 경우에는 이론상 절대 거리 분석값의 왜곡 현상이 완전히 사라지지만, 다른 겹침 상태에서는 절대 거리 분석값의 왜곡이 발생된다. 이런 절대 거리 측정값의 왜곡은, 본 연구에서 제안하는 방법에 따라 기준 거울 자체 간섭 신호를 제거한다면, Fig. 3의 붉은색 그래프와 같이 0.1 μm 이하의 일반적인 수준으로 유지될 수 있다. 다만, 실제 측정에서는 간섭 신호들의 진폭비에 따라 절대 거리의 왜곡 값이 달라질 수 있다.

Fig. 3

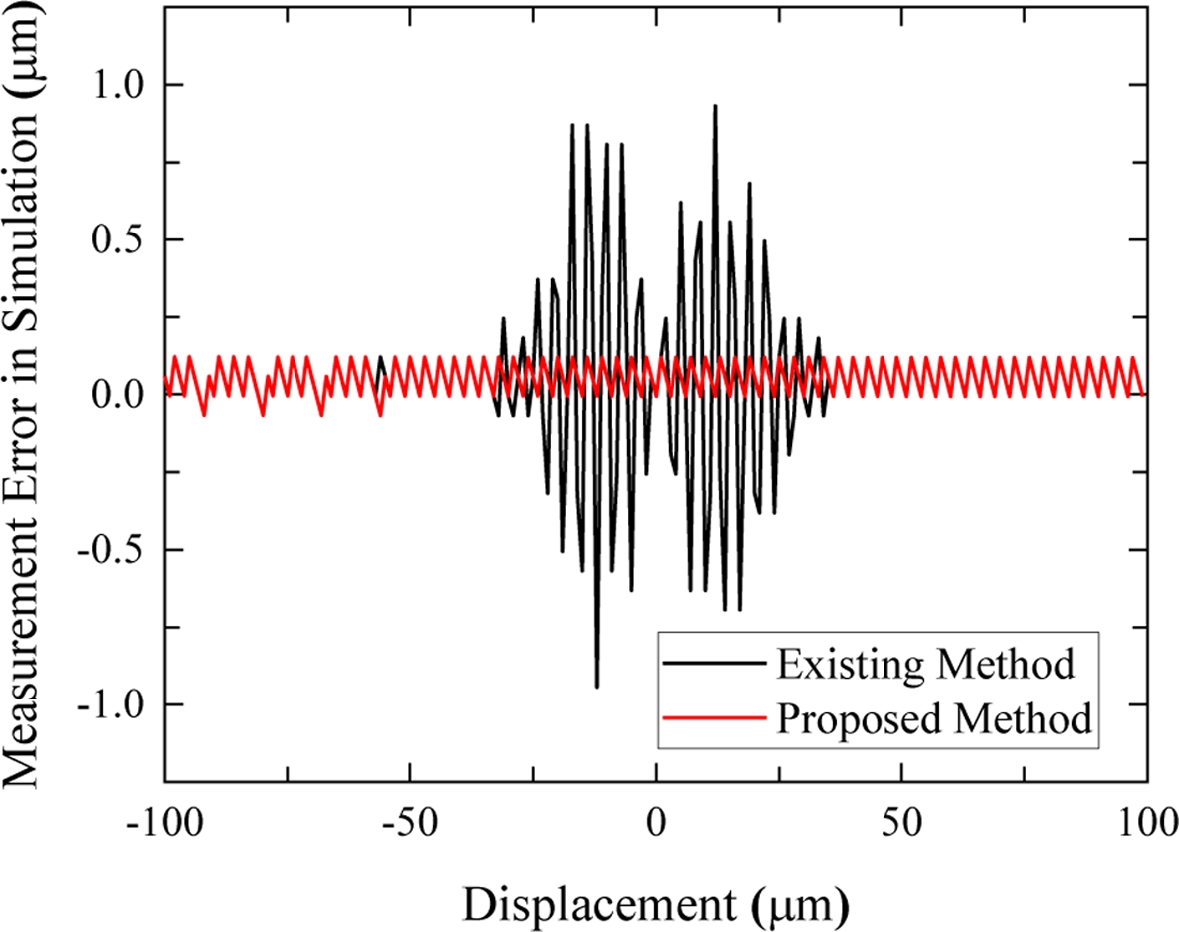
Simulation results of measurement error by existing method (Black dashed curve) and proposed method (Red curve)

본 연구에서 제안하는 편광 기반 이중 기준 경로 분광 간섭계의 광학 구성도는 Fig. 4(a)와 같다. 기준 경로는 Fig. 1과 같이 기존의 방법과 동일하게 2개이지만, 2개의 기준 경로 사이의 간섭을 막기 위해 광분할기 대신 편광 광분할기(Polarizing Beam Splitter, PBS)를 사용하여 두 기준 경로를 통과하는 빛의 편광을 서로 수직하게 하였다. 한편, 기준 거울들과 측정 거울에서 반사된 빛들은 여전히 간섭을 해야 하므로 선형 편광자(Linear Polarizer, LP)를 사용하여 측정 경로로 진행하는 빛이 45° 내외로 선형 편광된 빛(Linearly Polarized Light)이 되도록 조절하였다. 이때, 편광 소자들로 인한 편광 섞임(Polarization Mixing)에 의해 발생하는 신호는 편광 소자들의 편광 비율을 고려하면 무시할 만큼 작은 크기를 갖기 때문에, 거리 측정에 주요한 영향을 주지 못한다.

Fig. 4

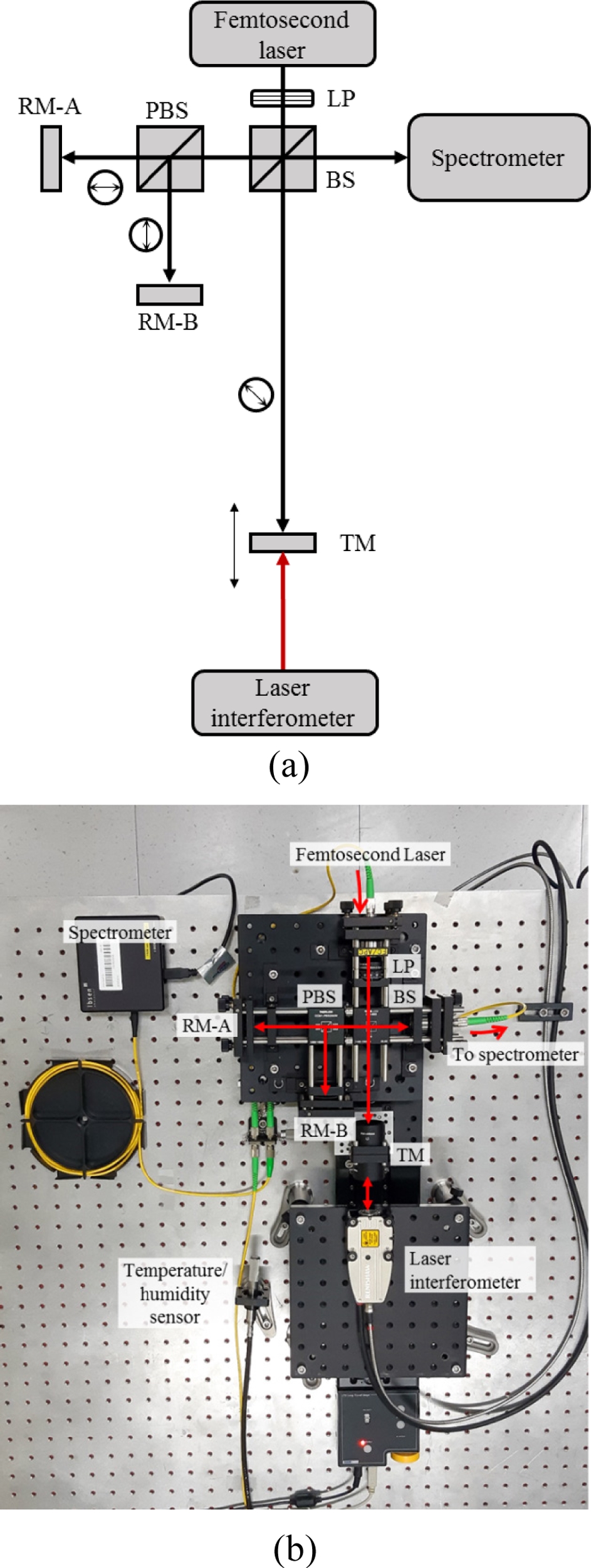
(a) Optical layout and (b) Photographical view of spectraldomain interferometer with polarization-based dual reference paths (LP: linear polarizer, PBS: polarizing beam splitter, BS: beam s plitter, RM-A, RM-B : reference mirrors, TM: target mirror)

제안한 방법의 실험적 검증을 위해 측정 거울은 선형 모터 구동 스테이지(Linear Motorized Stage) 위에 설치되었고, 수치 시뮬레이션과 동일한 조건에서 간섭 스펙트럼 데이터를 획득하였다. 광원은 1550 nm 중심 파장에서 약 40 nm의 반치폭을 갖고 반복률이 250 MHz인 광섬유 기반의 펨토초 펄스 레이저를 사용하였다. 분광기는 1500-1600 nm의 파장 영역에서 512 픽셀(Pixel)로 간섭 스펙트럼을 샘플링(Sampling)한다. 간섭 스펙트럼은 해닝 윈도우(Hanning Window) 함수를 적용 후 푸리에 변환하여 주변 잡음을 최소화하였다. 본 실험에서의 측정 영역은 200 μm이며, 측정 간격은 1 μm이다. 이 영역은 본 연구에서 해결하고자 하는 주 간섭 신호와 두 기준 거울 사이의 간섭 신호의 겹침 현상을 관찰하기에는 충분하다. 또한, 선형 모터 구동 스테이지의 정확한 이동 위치를 측정하기 위해 상용 단색광 레이저 간섭계(RLE Fiber Optic Laser Encoder, Renishaw Plc.)를 설치하여 절대 거리 측정과 동시에 이동 변위를 측정하였다. 단색광 레이저 간섭계를 통한 거리 측정을 위해 Fig. 4(b)에서 보이는 것처럼, 분광 간섭계의 측정 거울 뒷면에 단색광 레이저 간섭계의 측정 거울을 설치하였다. 단색광 레이저 간섭계의 측정 분해능은 10 nm이다. 실험실의 온도와 습도는 24.7°C와 40% R.H.로 유지되었으며, 이를 통해 공기의 굴절률을 계산하여 측정값을 보정하였다.^19,20

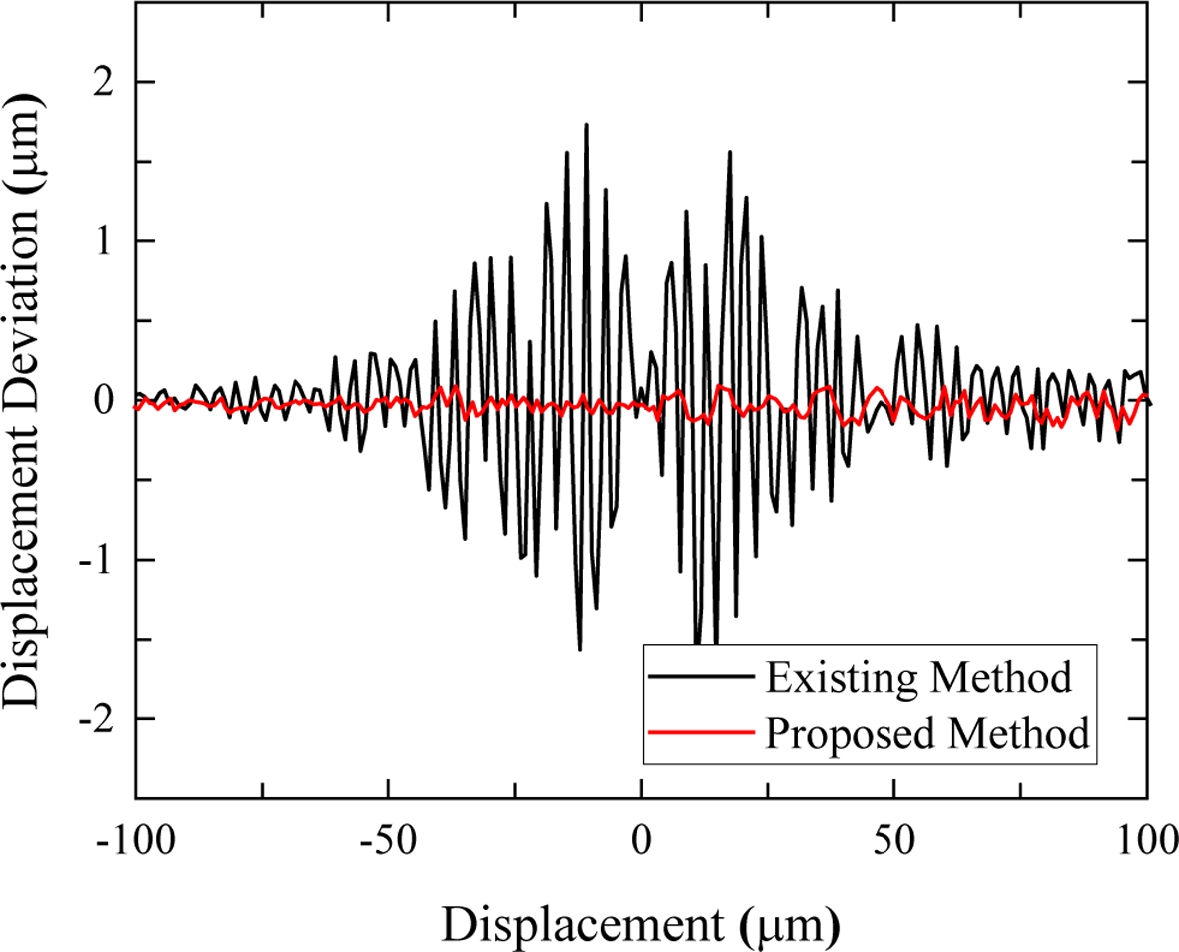
절대 거리 측정은 선행 연구에서 제안된 방법과 본 연구에서 제안한 방법으로 각각 수행되었다. Fig. 5는 2가지 방법으로 측정한 절대 거리 측정 결과들을 보여준다. 수치 시뮬레이션을 통해 예상한 바와 같이, 선행 연구에서 제안한 방법은 주 간섭 신호인 P_A 신호와 두 기준 거울 간의 간섭 신호인 P_AB 신호가 겹치는 영역에서는 절대 거리 측정값의 왜곡이 발생함을 확인할 수 있다. 반면에, 본 연구에서 제안한 방법은 2개의 기준 거울 사이의 간섭 신호를 제거함으로써, 최대 1.5 μm 수준의 절대 거리 측정값의 왜곡이 없어지고, 약 0.1 μm 수준의 측정 오차가 유지됨을 확인할 수 있다.

Fig. 5

Displacement deviations of existing method (Black) and proposed method (Red) from displacement results using monochromatic laser interferometer

4. 결론

본 연구는 분광 간섭계에서 발생하는 ‘측정 불가 영역’ 문제와 ‘방향 모호성’ 문제를 해결하기 위해 보고된 선행연구에서 간섭 신호 겹침에 의해 발생하는 절대 거리 측정값의 왜곡을 제거하기 위한 목적으로 수행되었다. 이를 위해 편광 기반 이중 기준 경로 분광 간섭계를 제안하고 구현하였다. 간섭 신호 겹침에 의해 발생하는 절대 거리 측정값의 왜곡을 정량적으로 분석하기 위해 실험 조건과 유사한 조건으로 수치 시뮬레이션을 수행하였다. 수치 시뮬레이션 결과에 따르면, 주 간섭 신호와 두 기준 거울 사이의 간섭 신호가 겹치는 영역에서는 최대 1 μm의 절대 거리 측정값의 왜곡이 생길 수 있음을 확인할 수 있었다.

펨토초 펄스 레이저를 이용한 절대 거리 측정 실험도 수행되었다. 본 연구에서 제안한 측정법의 동작 여부를 실험적으로 검증하기 위해 선행 연구에서 제안된 방법과 본 연구에서 제안된 방법을 모두 활용하였다. 측정 영역은 수치 시뮬레이션과 같이 주 간섭 신호와 두 기준 거울 사이의 간섭 신호가 겹치는 총 200 μm 영역을 선정하였다. 또한, 기준 거울의 변위를 정확하게 측정하기 위해 단색광 레이저 간섭계도 함께 설치하였다.

선행 연구를 활용한 실험 결과에 따르면, 수치 시뮬레이션에서 예상되는 것과 같이 절대 거리 측정값의 왜곡을 확인할 수 있었다. 반면에, 본 연구에서 제안된 방법을 활용한 실험 결과에서는 두 기준 거울 사이의 간섭을 제거하여 간섭 신호들의 겹침 현상을 피함으로써 절대 거리 측정값이 왜곡되지 않음을 실험적으로 검증하였다. 이로부터 수치 시뮬레이션 및 실험에서 얻어진 결과들의 유사성을 확인할 수 있었다.

본 연구의 또 다른 실질적인 장점은 기준 경로로 진행하는 빛이 서로 다른 편광을 갖도록 간단하게 조절함으로써, 기존 연구에도 쉽게 적용할 수 있는 것이다. 또한, 간섭 신호들의 명확한 구별을 위한 가시도 조절도 선행 연구에서 제안한 기준 거울 반사율 변화가 아닌 선형 편광자의 편광축 각도 조절을 통해 조절할 수 있기 때문에 보다 쉽고 정밀하게 조절할 수 있다는 장점을 갖는다. 이는 분광 간섭계 기반 절대 거리 측정을 수행함에 있어 선행연구에서 보고된 근원적인 문제점 해결과 함께 간섭 신호 겹침 현상이 발생하는 특정 영역에서의 측정값 왜곡을 해결하기 위해 유용하게 활용될 수 있을 것으로 기대한다.

Acknowledgments

본 연구는 한국표준과학연구원 ‘1-2-01. 광학 측정표준기술 고도화’ 과제(No. 20011030)의 지원으로 수행되었습니다.

References

• Bourdet, G. and Orszag, A., “Absolute Distance Measurements by CO₂ Laser Multiwavelength Interferometry,” Applied Optics, Vol. 18, No. 2, pp. 225-227, 1979. [https://doi.org/10.1364/AO.18.000225]
• Jin, J., Kim, Y. J., Kim, Y., Kim, S. W., and Kang, C. S., “Absolute Length Calibration of Gauge Blocks Using Optical Comb of a Femtosecond Pulse Laser,” Optics Express, Vol. 14, No. 13, pp. 5968-5974, 2006. [https://doi.org/10.1364/OE.14.005968]
• Jang, Y. S., Wang, G., Hyun, S., Kang, H. J., Chun, B. J., et al., “Comb-Referenced Laser Distance Interferometer for Industrial Nanotechnology,” Scientific Reports, Vol. 6, No. 1, pp. 1-10, 2016. [https://doi.org/10.1038/srep31770]
• Coe, P. A., “An Investigation of Frequency Scanning Interferometery for the Alignment of the ATLAS Semiconductor Tracker,” Ph.D. Thesis, Oxford University, 2011.
• Dale, J., Hughes, B., Lancaster, A. J., Lewis, A. J., Reichold, A. J., et al., “Multi-Channel Absolute Distance Measurement System with Sub Ppm-Accuracy and 20 m Range Using Frequency Scanning Interferometry and Gas Absorption Cells,” Optics Express, Vol. 22, No. 20, pp. 24869-24893, 2014. [https://doi.org/10.1364/OE.22.024869]
• Schwider, J. and Zhou, L., “Dispersive Interferometric Profilometer,” Optics Letters, Vol. 19, No. 13, pp. 995-997, 1994. [https://doi.org/10.1364/OL.19.000995]
• Joo, K. N. and Kim, S. W., “Absolute Distance Measurement by Dispersive Interferometry Using a Femtosecond Pulse Laser,” Optics Express, Vol. 14, No. 13, pp. 5954-5960, 2006. [https://doi.org/10.1364/OE.14.005954]
• Maeng, S., Park, J., Byungsun, O., and Jin, J., “Uncertainty Improvement of Geometrical Thickness and Refractive Index Measurement of a Silicon Wafer Using a Femtosecond Pulse Laser,” Optics Express, Vol. 20, No. 11, pp. 12184-12190, 2012. [https://doi.org/10.1364/OE.20.012184]
• Park, J., Bae, J., Jin, J., Kim, J. A., and Kim, J. W., “Vibration-Insensitive Measurements of the Thickness Profile of Large Glass Panels,” Optics Express, Vol. 23, No. 26, pp. 32941-32949, 2015. [https://doi.org/10.1364/OE.23.032941]
• Van Den Berg, S. A., Van Eldik, S., and Bhattacharya, N., “Mode-Resolved Frequency Comb Interferometry for High-Accuracy Long Distance Measurement,” Scientific Reports, Vol. 5, No. 1, pp. 1-10, 2015. [https://doi.org/10.1038/srep14661]
• Coddington, I., Swann, W. C., Nenadovic, L., and Newbury, N. R., “Rapid and Precise Absolute Distance Measurements at Long Range,” Nature Photonics, Vol. 3, No. 6, pp. 351-356, 2009. [https://doi.org/10.1038/nphoton.2009.94]
• Lee, J., Kim, Y. J., Lee, K., Lee, S., and Kim, S. W., “Time-of-Flight Measurement with Femtosecond Light Pulses,” Nature Photonics, Vol. 4, No. 10, pp. 716-720, 2010. [https://doi.org/10.1038/nphoton.2010.175]
• Joo, K. N., “Dichroic Spectrally-Resolved Interferometry to Overcome the Measuring Range Limit,” Measurement Science and Technology, Vol. 26, No. 9, Paper No. 095204, 2015. [https://doi.org/10.1088/0957-0233/26/9/095204]
• Yun, Y. H., Seo, Y. B., and Joo, K. N., “Elimination of the Direction Ambiguity and the Dead Zone in Spectrally Resolved Interferometry,” Measurement Science and Technology, Vol. 27, No. 3, Paper No. 035004, 2016. [https://doi.org/10.1088/0957-0233/27/3/035004]
• Yun, Y. H., Kim, D. H., and Joo, K. N., “Optimal Dispersion Condition to Distinguish OPD Directions of Spectrally-Resolved Interferometry,” Journal of the Korean Society for Precision Engineering, Vol. 34, No. 4, pp. 259-264, 2017. [https://doi.org/10.7736/KSPE.2017.34.4.259]
• Park, J., Jin, J., Kim, J. A., and Kim, J., “Absolute Distance Measurement Method without a Non-Measurable Range and Directional Ambiguity based on the Spectral-Domain Interferometer Using the Optical Comb of the Femtosecond Pulse Laser,” Applied Physics Letters, Vol. 109, No. 24, Paper No. 244103, 2016. [https://doi.org/10.1063/1.4971836]
• Proakis, J. and Manolakis, D., “Digital Signal Processing: Principles Algorithms and Applications,” New York Macmillan Publishing Company, 3rd Ed., 1992.
• Dorrer, C., Belabas, N., Likforman, J. P., and Joffre, M., “Spectral Resolution and Sampling Issues in Fourier-Transform Spectral Interferometry,” Journal of the Optical Society of America B, Vol. 17, No. 10, pp. 1795-1802, 2000. [https://doi.org/10.1364/JOSAB.17.001795]
• Edlen, B., “The Refractive Index of Air,” Metrologia, Vol. 2, No. 2, pp. 71-80, 1966. [https://doi.org/10.1088/0026-1394/2/2/002]
• Birch, K. and Downs, M., “Correction to the Updated Edlen Equation for the Refractive Index of Air,” Metrologia, Vol. 31, No. 4, pp. 315-316, 1994. [https://doi.org/10.1088/0026-1394/31/4/006]
• Jin, J., “Dimensional Metrology Using the Optical Comb of a Mode-Locked Laser,” Measurement Science and Technology, Vol. 27, No. 2, Paper No. 022001, 2015. [https://doi.org/10.1088/0957-0233/27/2/022001]
• Park, J., Kim, J. A., Ahn, H., Bae, J., and Jin, J., “A Review of Thickness Measurements of Thick Transparent Layers Using Optical Interferometry,” International Journal of Precision Engineering and Manufacturing, Vol. 20, No. 3, pp. 463-477, 2019. [https://doi.org/10.1007/s12541-019-00105-0]