직선 이송축의 3자유도 오차 보정을 위한 미세 구동 스테이지 개발 및 성능 평가

1. 서론

IT, 광학, 의료 등의 첨단 산업에서 서브 마이크로 미터 수준의 소형 부품 수요 증가로 인해 정밀 가공 기술이 주목 받고 있다.^1-3 정밀 가공 기술은 복잡한 형상을 가진 소형 부품을 제조할 수 있는 장점을 가진다.⁴ 이러한 부품의 형상 정확도는 정밀 기계의 공구와 공작물간의 위치 정확도에 의해 직접적인 영향을 받는다. 위치 정확도에 악영향을 끼치는 주요 오차로는 준정적 오차와 동적 오차 등이 있다. 준정적 오차는 기계의 구성 부품들의 불완전에 의해 야기된 기하학적 오차와 열원에 의한 구조의 열적 팽창 및 수축에 의한 오차로 구분한다. 동적 오차는 구동축의 가속력, 공작기계의 진동 그리고 제어기 오차 등에 의해 발생한다.^5,6 이러한 오차들에 의한 공구와 공작물간의 상대 자세는 공간상의 6자유도 오차를 포함한다.

따라서, 위치 정확도를 향상하기 위한 오차 측정 및 보정에 관한 연구가 진행되고 있다.^7,8 Lee는⁹ 정전용량 센서와 기준 미러를 사용한 5자유도 측정 시스템을 개발하고 직선 이송축의 기하학적 오차를 측정하였다. 그리고 Lee는¹⁰ 직선 이송축의 5자유도 이송 성능을 정량적으로 평가하기 위해 국제 표준 규격 ISO 230-2 기반의 측정 방법을 제안하였다. Gao는^11,12 이송축의 6자유도 기하학적 오차를 보정하기 위해 레이저 간섭계, 오토콜리메이터, 정전용량 센서를 사용한 측정 방법을 제안하고 다양한 측정 시스템의 측정 및 비교 분석을 통해 타당성을 검증하였다. 또한 소형 공작기계를 대상으로 기하학적 오차 측정을 위한 방법이 제안되었다.¹³ 그러나 대부분의 기존 연구는 보정 전/후의 결과가 명시되지 않았다. 또한 대부분의 오차가 실시간 측정이 아닌 오프라인 오차 측정을 함으로써 시변 오차에 의해 야기된 다자유도 오차는 정확하게 보정하기가 어렵다.

따라서, 본 연구에서는 단일 직선 이송축을 대상으로 위치 정확도 향상을 위해 3자유도 오차(선형 변위 오차, 수평 진직도 오차, 요 오차)의 측정 및 보정을 위한 미세 구동 스테이지를 개발한다. 레이저 간섭계를 이용하여 측정된 선형 변위 오차는 오프라인 보정 방법을 이용하고 정전용량 센서를 이용하여 이송축의 2자유도 오차(수평 진직도 오차, 요 오차)를 실시간 측정 및 보정한다. 2장에서는 스테이지의 구조와 정/역기구학을 이용하여 분석한 이송 영역 및 오차 보정을 위한 구동기의 길이 계산 방법을 설명한다. 3장에서는 개발한 스테이지를 활용하여 직선 이송축의 3자유도 오차 측정 및 보정 실험 결과를 기술한다. 마지막으로 4장에서는 본 연구를 정리 및 요약하여 결론을 나타내고 활용방안을 제시한다.

2. 미세 구동 스테이지 설계 및 기구학 분석

2.1 평면형 3자유도 스테이지 설계

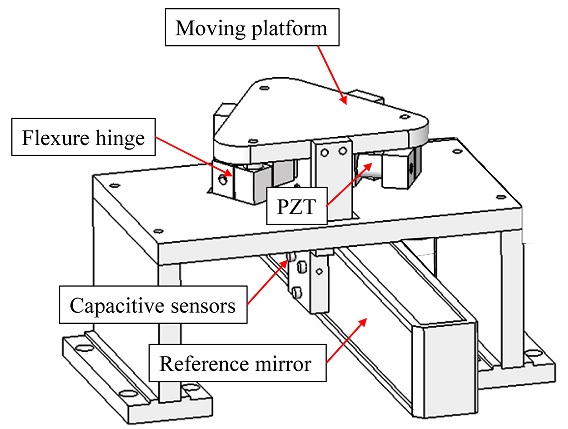
스테이지는 Fig. 1과 같이 3개의 압전 구동기와 6개의 유연 힌지 기반의 조인트로 구성되며 평면상의 3자유도 운동(2자유도 위치 운동, 1자유도 회전 운동) 구현이 가능하다. 유연 힌지 기반의 조인트는 기계적 조인트의 한계인 스틱 슬립 마찰, 마모 등의 문제점을 최소화하기 위해 사용되며 초정밀 위치 정확도 구현이 용이하다. 그리고 압전 구동기는 빠른 응답 속도 및 위치 재현성 확보를 위해 이용된다.

Fig. 1

Structure of a suggested fine stage

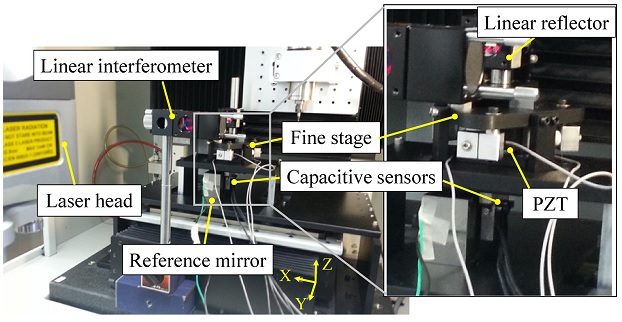
단일 직선 이송축의 3자유도 오차 측정을 위해 레이저 간섭계, 정전용량 센서와 기준 미러 (Reference Mirror)가 사용된다. 레이저 간섭계는 선형 변위 오차를 측정하고 2개의 정전용량 센서 (s₁, s₂)는 수평 진직도 오차와 요 오차 측정에 활용한다. 제안한 스테이지는 이송축 테이블에 고정하고 기준 미러는 외부 치구에 설치한다. 오차 측정을 위해 사용된 정전용량 센서와 기준 미러로 인해 단축 방향의 오차 측정 및 보정만이 가능하다. 따라서 제안한 미세 구동 스테이지를 활용하여 다축 직선 이송축의 실시간 오차 측정 및 보정을 위해서는 임의의 위치에서의 오차 측정이 가능한 측정 시스템 개발이 요구된다.¹⁴

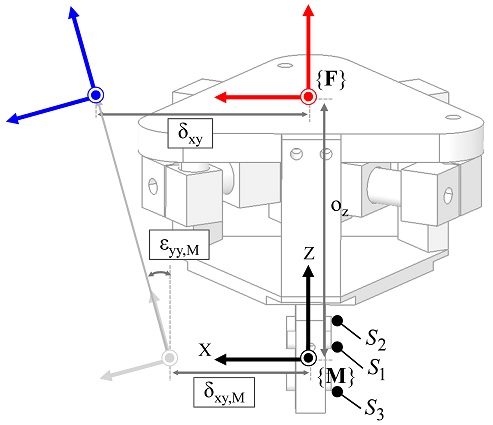
정확한 오차 측정 및 보정을 위해 기준 좌표계 {F}는 무빙 플랫폼 (Moving Platform)의 중심에 위치한다. 그러나 구조적인 한계로 인해 측정 좌표계 {M}와 기준 좌표계 {F}간의 아베 옵셋 (o_x, o_y, o_z)이 발생한다. 좌표계간의 아베 옵셋에 의해 기준 좌표계와 측정 좌표계에서 위치 오차는 Fig. 2와 같이 상이한 결과를 보인다.¹⁵ 위치 오차는 이송 방향에 대한 회전 오차에 의해 영향을 받는다. 따라서 아베 오차의 영향의 최소화를 위해 롤 오차는 추가 센서 (s₃)를 이용하여 측정된다. 측정된 3자유도 오차와 보정값간의 관계는 식(1)과 같다.

$\[ \begin{array}{l}{\delta }_{xy}={\delta }_{xy,M}+{\epsilon }_{yy,M}\times o_z\\ {\epsilon }_{zy}={\epsilon }_{zy,M}\end{array} \]$

(1)

Fig. 2

Abbe’s offsets between reference coordinates system {F} and measuring coordinates system {M}

Fig. 3

Maximum stress of the fine stage

여기서, δ_xy는 좌표계 {F}에서 정의된 Y축 방향의 진직도 오차를 나타내며 ε_zy는 Z축 방향의 회전 오차를 의미한다. 마찬가지로, δ_xy,M, ε_yy,M, ε_zy,M는 좌표계 {M}에서 측정된 위치 및 회전 오차이고 o_z는 Z축 방향의 아베 옵셋이다.

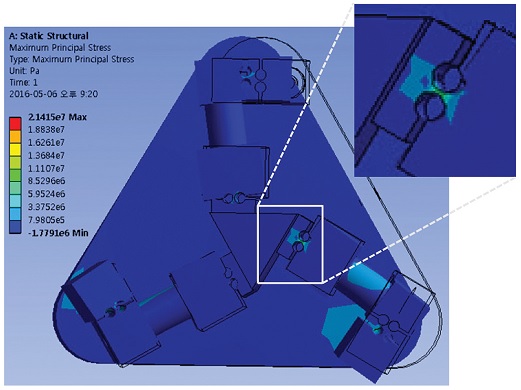
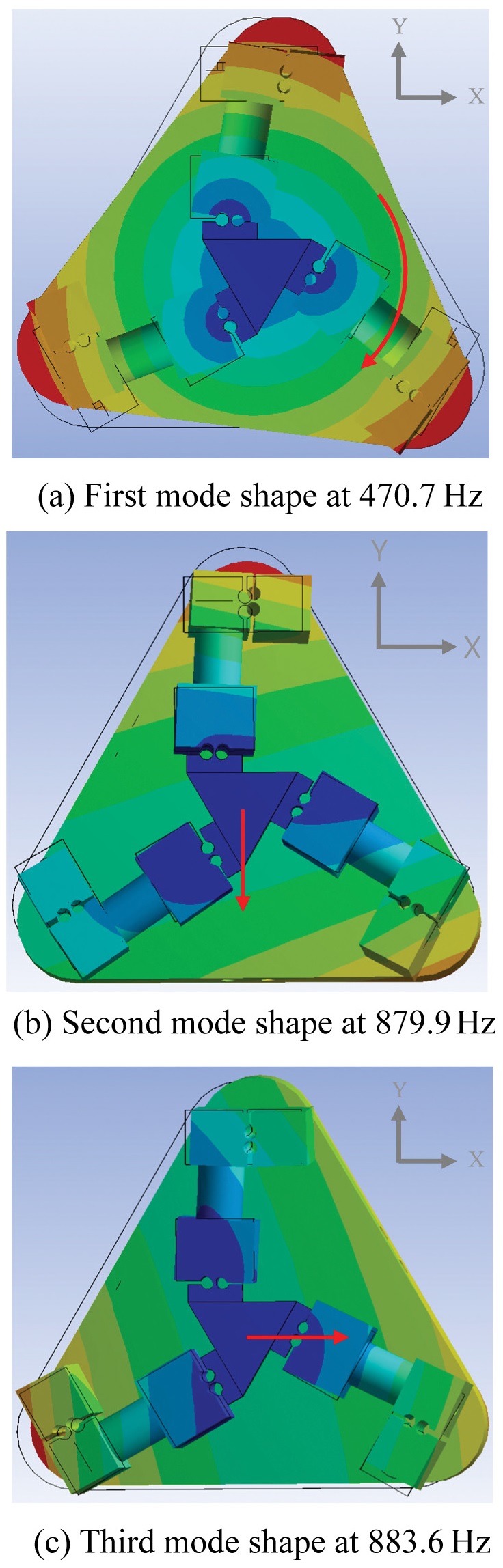
스테이지는 유연 힌지 기반의 조인트를 활용하기 때문에 탄성 영역 이내에서 구동되어야만 한다. 그리고 실시간 구동에 의한 유연 힌지에서 발생하는 최대 응력은 ANSYS를 활용하여 분석한다. 스테이지는 300 Hz이내에서 구동되며 이때 무빙 플랫폼의 변위는 ± 6.2·sin (300·2 π·t)이다. 변위에 따른 유연 힌지에서 발생하는 최대 응력은 스테이지 재질인 AL 6061의 항복 강도의 16.2%인 21 MPa이다. 따라서, 유연 힌지는 스테이지의 모든 이송 범위 내에서 탄성변형을 한다. 또한 스테이지의 모드 형상을 분석한 결과는 Fig. 4와 같다. 1 - 3차에서는 Z축 방향의 회전 운동과 X, Y축 방향의 병진 운동을 보인다. 이때, 각 모드 형상의 고유 진동수는 각각 470.7 Hz, 879.9 Hz, 883.6 Hz이다.

Fig. 4

Mode shapes of the fine stage

2.2 기구학 해석

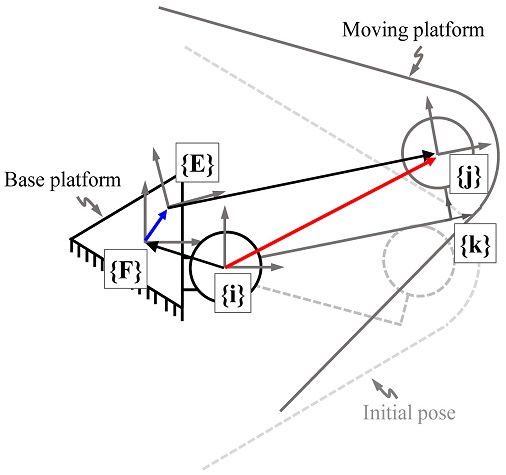
3자유도 오차 보정을 위한 각 압전 구동기의 길이 l_i (i = 1, 2, 3)는 역기구학을 이용하여 계산한다. 스테이지의 각 조인트 좌표계와 기준 좌표계 {F}는 Fig. 5와 같이 설정한다. 기준 좌표계 {F}는 기저 플랫폼 (Base Platform)의 중심에 위치하고 좌표계 {E}는 임의의 위치와 방향을 가지는 무빙 플랫폼의 중심에 위치한다. 그리고 좌표계 {i}, {j}는 각각 기저 플랫폼과 무빙 플랫폼에 연결된 조인트 좌표계이고 좌표계 {k}는 링크 좌표계이다. 좌표계간의 관계는 기구학 체인에 의해 식(2)와 같다. 여기서, τ_i^j는 좌표계 {i}에서 정의된 좌표계 {j}의 상대적인 위치와 방향을 나타내는 동차변환행렬이다. 그리고 P_i^j는 좌표계 {i}, {j}의 원점간 상대적 위치 벡터를 의미한다. 각 조인트 좌표계 {i}, {j}의 위치와 방향은 초기 설계 값에 의해 결정되며, 정전용량 센서에 의해 측정된 3자유도 오차를 기반으로 좌표계 {E}의 위치와 방향이 계산된다. 그리고 좌표계 {j}, {k} 간의 관계인 τ_j^k는 초기 설계에 의해 결정된 동차변환행렬이다. 압전 구동기의 길이 l_i (i = 1, 2, 3)를 계산하기 위한 좌표계 {i}, {k}간의 관계는 식(3)과 같다. 3자유도 오차 보정을 위한 압전 구동기의 길이 l_i (i = 1, 2, 3)는 식(4)와 같이 계산한다. 여기서, l₀는 압전 구동기의 초기 길이이다.

$\[ {\tau }_F^i{\tau }_i^k{\tau }_k^j={\tau }_F^E{\tau }_E^j \]$

(2)

$\[ {\tau }_i^k={\left({\tau }_F^i\right)}^{-1}{\tau }_F^E{\tau }_E^j{\left({\tau }_k^j\right)}^{-1} \]$

(3)

여기서,

$\[ \begin{array}{l}{\tau }_F^E=\left[\begin{array}{cc}\mathrm{R}& \mathrm{T}\\ 0& 1\end{array}\right]\\ \mathrm{R}=\left[\begin{array}{ccc}1& -{\epsilon }_z& 0\\ {\epsilon }_z& 1& 0\\ 0& 0& 1\end{array}\right]\\ 0=\left[\begin{array}{ccc}0& 0& 0\end{array}\right]\\ \mathrm{T}={\left[\begin{array}{ccc}{\delta }_x& {\delta }_y& 0\end{array}\right]}^T\end{array} \]$

$\[ l_i=\left|{\mathrm{P}}_i^k\right|-l_0 \]$

(4)

$\[ f_i\left({\delta }_x,{\delta }_y,{\epsilon }_z\right)=\left|{\mathrm{P}}_i^k\right|-\left(l_i+l_0\right)=0 \]$

(5)

Fig. 5

Coordinates systems establishment for kinematic analysis

미세 구동 스테이지의 이송영역은 직선 이송축의 3자유도 오차 범위를 포함해야만 한다. 설계된 스테이지의 이송 영역은 정기 구학을 이용하여 분석한다. 압전 구동기의 길이 l_i (i = 1, 2, 3)와 평면상의 3자유도 오차와의 관계는 식(4)를 이용하여 식(5)와 같이 함수 f_i (δ_x, δ_y, ε_z), (i = 1, 2, 3)로 나타낸다.

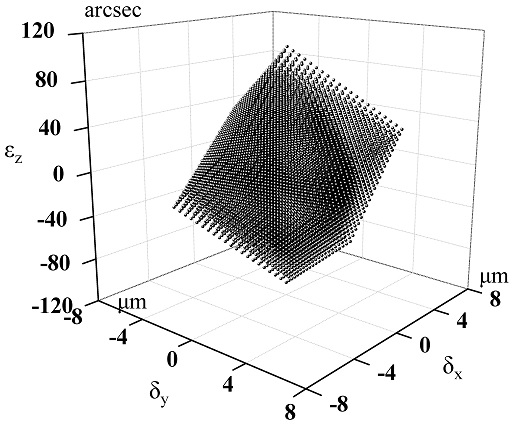
비선형 방정식의 해를 해결하기 위해 가우스-뉴턴 방법이 사용된다. 실험에 사용된 압전 구동기의 구동 범위인 ± 7.5 μm내에서 설계된 스테이지의 최대 위치 및 회전 이송 영역은 Fig. 6과 같다. 각각의 이송 영역은 ± 6.3 μm, ± 107 arcsec이다. 모의 실험 결과에서 회전 이송 값의 증가 또는 감소에 따라 위치 이송 영역이 감소하는 경향을 보인다. 그럼에도 불구하고 스테이지의 이송 영역은 초정밀급 직선 이송계의 위치 및 회전 오차 범위를 포함한다. 따라서 직선 이송계의 오차를 보정하기 위해 설계한 미세 구동 스테이지는 충분한 이송 영역을 가진다.

Fig. 6

Workspace of designed 3-DOF fine stage

3. 보정 알고리듬 설계 및 평면형 3자유도 미세 구동 스테이지 성능 검증

3.1 3자유도 오차 보정 알고리듬 설계

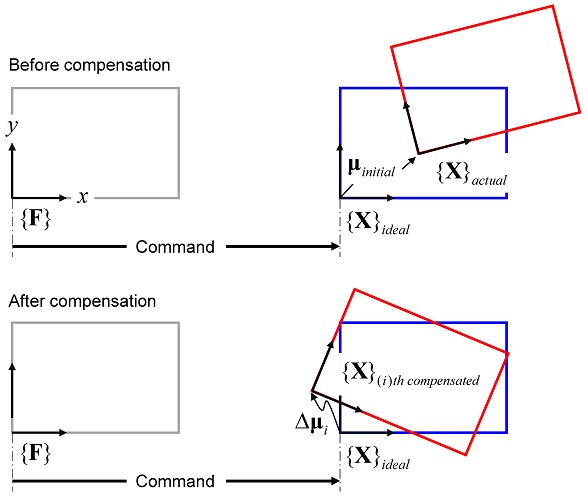
단일 직선 이송축의 정확한 위치 결정 구현을 위해서는 동적/열 변형/정적 오차에 의한 3자유도 오차를 위한 보정 알고리듬이 필요하다. 제안한 보정 알고리듬 기본 개념은 Fig. 7과 같다. 직선 이송축 좌표계 {X}_ideal는 기준 좌표계 {F}의 X축을 따라 이송해야만 하지만 앞서 언급한 오차들에 의해 왜곡된 자세 {X}_actual를 가진다. 여기서, μ는 정전용량 센서에 의해 측정된 위치 오차(수평 진직도)와 각도 오차(요)를 나타낸다. 직선 이송축 좌표계 {X}_actual를 {X}_ideal로 일치시키는 것이 보정 알고리듬의 주요 목적이다. i 번째 보정 후의 이송축 좌표계 {X}_{ith compensated}는 잔류 오차 Δμ_i을 포함하며 잔류 오차가 설정된 허용 범위 이내에 값에 수렴하기 전까지 보정 작업을 반복적으로 수행한다. 따라서 직선 이송축의 좌표계 {X}_actual는 허용 범위 이내에서 좌표계 {X}_ideal와 일치한다.

Fig. 7

The principle concept of compensation algorithm

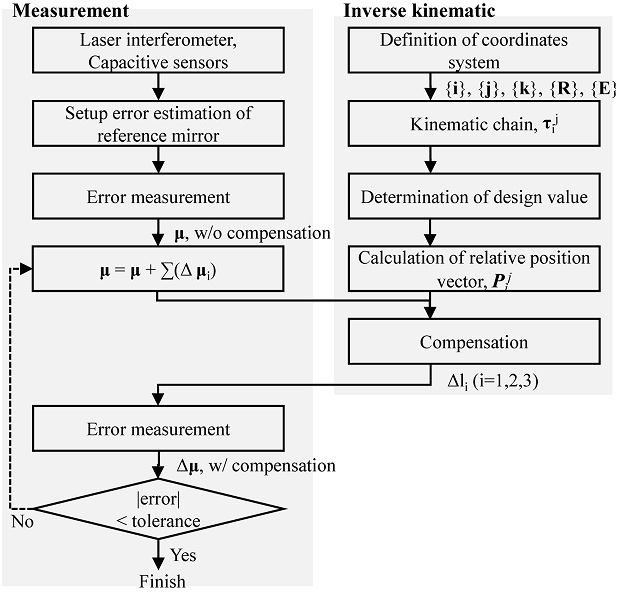
단일 직선 이송축의 3자유도 오차를 위한 보정 절차는 Fig. 8과 같다. 3자유도 오차는 레이저 간섭계와 정전용량 센서를 이용하여 측정한다. 이때 기준 미러와 이송축간의 불일치로 인해 측정된 진직도 오차는 증가 또는 감소하는 경향을 보인다. 따라서 진직도 오차의 기울기 값을 계산하여 셋업 오차의 영향을 제거한다. 레이저 간섭계에 의해 측정된 선형 변위 오차는 오프라인 보정방법을 이용하고, 그 외 2자유도 오차는 실시간 측정 및 보정을 수행한다. 오차 보정을 위한 압전 구동기의 길이 l_i (i = 1, 2, 3)는 역기구학에 의해 계산된다. 이 때 보정값 Δl_i은 잔류 오차 Δμ_i가 허용 범위 이내의 값을 가지도록 결정된다.

Fig. 8

Flow chart of compensation procedure

3.2 오차 측정 및 보정 실험

오차 측정 및 보정 실험을 위해 Fig. 9와 같이 제작된 미세 구동 스테이지는 3축 공작기계에 설치된다. Y축을 대상으로 3개의 기하학적 오차 및 보정 실험을 진행한다. 실험에는 압전 구동기 (P-840.10, PI GmbH, Germany), 정전용량 센서 (4810 Module, 2805 Probe, ADE Technology Inc., U.S.A.)와 레이저 간섭계 (XL-80 Laser System, Renishaw Plc., U.K.)가 사용된다. 실험에 사용한 측정 및 구동 장비의 성능은 Table 1과 같다.

Fig. 9

Installation for experiment at 3-axis machine tool

Table 1

Specification of used instrument in experiments

미세 구동 스테이지는 이송축의 테이블에 고정하고 기준 미러는 측정된 위치 오차의 표준 불확도를 최소화하기 위해 테이블 외부에 설치된 치구에 고정한다.⁹ 그리고 레이저 간섭계를 이용하여 사전에 측정된 선형 변위 오차는 오프라인 보정에 이용한다. 정전용량 센서에 의해 진직도 오차와 요 오차는 실시간 측정된다.

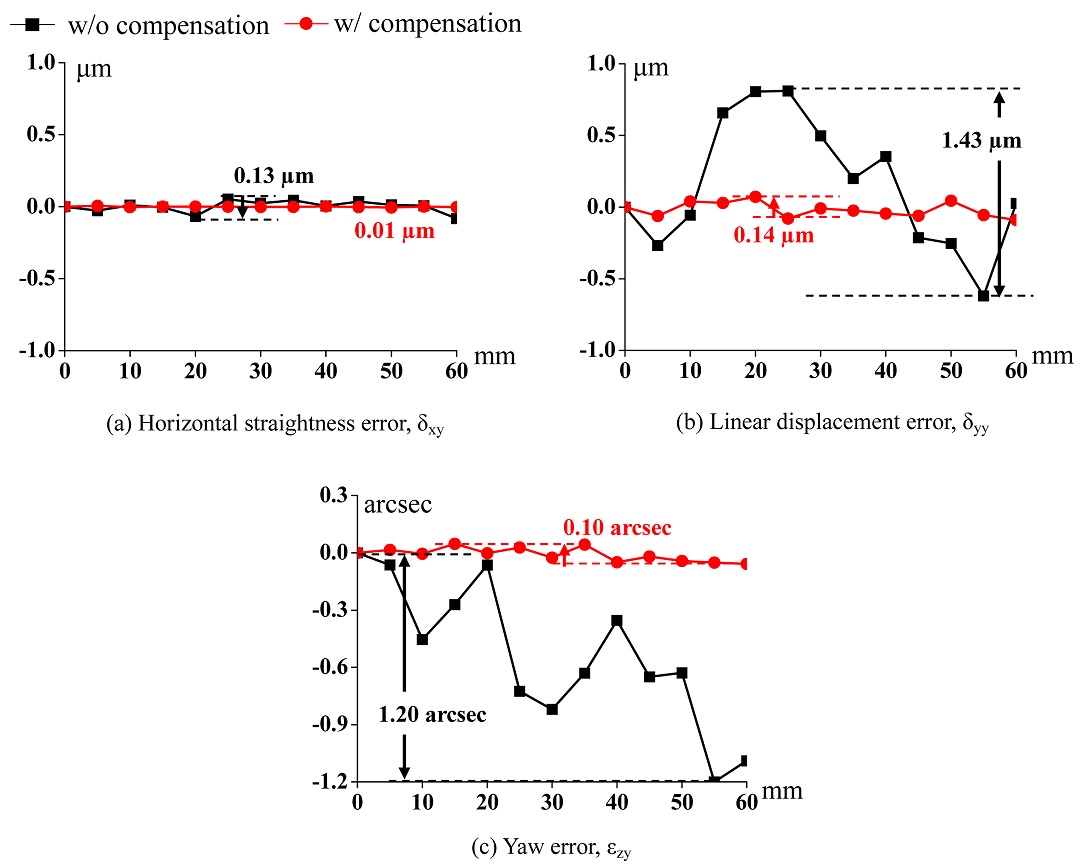
오차 측정 및 보정 실험은 이송 구간 60 mm 범위 내에서 5mm 간격으로 5회 반복적으로 수행한다. 측정된 기하학적 오차는 Fig. 10과 같고 위치 오차와 각도 오차의 PV (Peak to Valley)값은 각각 1.43 μm, 1.20 arcsec이다. 보정 전후의 오차는 Table 2와 같고 보정 후 오차의 PV 값은 각각 0.14 μm, 0.10 arcsec로 90%이상 감소한다. 마찬가지로 보상 전후 오차의 RMSE (Root Mean Square Error)는 0.05 μm, 0.04 arcsec로 88% 이상 감소한다. 선형 변위 오차는 오프라인 보정 방법을 활용하기 때문에 보정 후 측정값에서 상대적으로 수평 진직도 오차에 비해 큰 PV 값을 가진다. 오차 보정 실험 결과는 개발한 미세 구동 스테이지의 성능을 검증하였다. 또한 위치 정확도는 직선 이송축의 3자유도 오차를 보정함으로써 상당히 향상되었다.

Fig. 10

Measurement and compensation of geometric errors of a linear axis

Table 2

Experimental results(Unit: μm, arcsec)

4. 결론

본 연구에서는 직선 이송축의 초정밀 위치 구현을 위해 3자유도 오차 보정을 위한 평면형 미세 구동 스테이지를 제안한다. 위치 정확도 향상을 위해 유연 힌지 기반의 조인트가 활용된다. 그리고 정밀 오차 측정을 위해 아베 오차에 의한 영향을 최소화한 방법이 제안되고 설계한 스테이지의 이송 영역은 기구학을 이용하여 평가된다. 또한 개발한 스테이지를 활용하여 3자유도 오차를 측정하고 보정함으로써, 직선 이송축의 위치 정확도가 향상된다.

차후 가공 실험에 적용함으로써, 정밀 가공을 구현하고자 한다. 또한 실시간 오차 측정 및 보정은 이송축 성능 향상에 기여할 수 있을 것으로 사료된다. 이는 직선 이송축의 위치 정확도를 향상시켜 최종적으로 공작물의 형상 정확도 향상에 기여할 것으로 기대된다.

Acknowledgments

이 논문은 2015년도 정부(교육부, 미래창조과학부)의 재원으로 한국연구재단의 대학중점연구소지원사업(2010-0020089)과 기초연구사업(2013R1A2A2A01067917)으로 수행된 연구임.

REFERENCES

• Luo, X., Cheng, K., Webb, D., and Wardle, F., “Design of Ultraprecision Machine Tools with Applications to Manufacture of Miniature and Micro Components,” Journal of Materials Processing Technology, Vol. 167, No. 2, pp. 515-528, 2005. [https://doi.org/10.1016/j.jmatprotec.2005.05.050]
• Zhang, S., To, S., Wang, S., and Zhu, Z., “A Review of Surface Roughness Generation in Ultra-Precision Machining,” International Journal of Machine Tools and Manufacture, Vol. 91, pp. 76-95, 2015. [https://doi.org/10.1016/j.ijmachtools.2015.02.001]
• Ehmann, K. F., Bourell, D., Culpepper, M. L., Hodgson, T. J., Kurfess, T. R., et al., “International Assessment of Research and Development in Micromanufacturing,” DTIC Document, 2005. [https://doi.org/10.21236/ADA466761]
• Filiz, S., Conley, C. M., Wasserman, M. B., and Ozdoganlar, O. B., “An Experimental Investigation of Micro-Machinability of Copper 101 Using Tungsten Carbide Micro-Endmills,” International Journal of Machine Tools and Manufacture, Vol. 47, No. 7, pp. 1088-1100, 2007. [https://doi.org/10.1016/j.ijmachtools.2006.09.024]
• Ramesh, R., Mannan, M. A., and Poo, A. N., “Error Compensation in Machine Tools - A Review Part I: Geometric, Cutting-Force, Induced and Fixture Dependents Errors,” International Journal of Machine Tools and Manufacture, Vol. 40, No. 9, pp. 1235-1256, 2000. [https://doi.org/10.1016/S0890-6955(00)00009-2]
• Schwenke, H., Knapp, W., Haitjema, H., Weckenmann, A., Schmitt, R., et al., “Geometric Error Measurement and Compensation of Machines-An Update,” CIRP Annals-Manufacturing Technology, Vol. 57, No. 2, pp. 660-675, 2008. [https://doi.org/10.1016/j.cirp.2008.09.008]
• Lee, D.-M., Zhu, Z., Lee, K.-I., and Yang, S.-H., “Identification and Measurement of Geometric Errors for a Five-Axis Machine Tool with a Tilting Head Using a Double Ball-Bar,” Int. J. Precis. Eng. Manuf., Vol. 12, No. 2, pp. 337-343, 2011. [https://doi.org/10.1007/s12541-011-0044-5]
• Fan, K.-C., Chen, M.-J., and Huang, W., “A Six-Degree-of-Freedom Measurement System for the Motion Accuracy of Linear Stages,” International Journal of Machine Tools and Manufacture, Vol. 38, No. 3, pp. 155-164, 1998. [https://doi.org/10.1016/S0890-6955(97)00055-2]
• Lee, K.-I., Lee, J.-C., and Yang, S.-H., “The Optimal Design of a Measurement System to Measure the Geometric Errors of Linear Axes,” The International Journal of Advanced Manufacturing Technology, Vol. 66, Nos. 1-4, pp. 141-149, 2013. [https://doi.org/10.1007/s00170-012-4312-z]
• Lee, K.-I., Lee, J.-C., and Yang, S.-H., “Performance Evaluation of Five-DOF Motion in Ultra-Precision Linear Stage,” Int. J. Precis. Eng. Manuf., Vol. 15, No. 1, pp. 129-134, 2014. [https://doi.org/10.1007/s12541-013-0315-4]
• Gao, W., Arai, Y., Shibuya, A., Kiyono, S., and Park, C. H., “Measurement of Multi-Degree-of-Freedom Error Motions of a Precision Linear Air-Bearing Stage,” Precision Engineering, Vol. 30, No. 1, pp. 96-103, 2006. [https://doi.org/10.1016/j.precisioneng.2005.06.003]
• Gao, W., Saito, Y., Muto, H., Arai, Y., and Shimizu, Y., “A Three-Axis Autocollimator for Detection of Angular Error Motions of a Precision Stage,” CIRP Annals-Manufacturing Technology, Vol. 60, No. 1, pp. 515-518, 2011. [https://doi.org/10.1016/j.cirp.2011.03.052]
• Lee, J. H., Liu, Y., and Yang, S.-H., “Accuracy Improvement of Miniaturized Machine Tool: Geometric Error Modeling and Compensation,” International Journal of Machine Tools and Manufacture, Vol. 46, No. 12, pp. 1508-1516, 2006. [https://doi.org/10.1016/j.ijmachtools.2005.09.004]
• Wilkening, G. and Koenders, L., “Nanoscale Calibration Standards and Methods,” Wiley-VCH, 2005. [https://doi.org/10.1002/3527606661]
• Steinmetz, C., “Sub-Micron Position Measurement and Control on Precision Machine Tools with Laser Interferometry,” Precision Engineering, Vol. 12, No. 1, pp. 12-24, 1990. [https://doi.org/10.1016/0141-6359(90)90004-I]