6 DOF 정합을 이용한 대 영역 실리콘 웨이퍼의 3차원 형상, 두께 측정 연구
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this investigation, we describe a metrological technique for surface and thickness profiles of a silicon (Si) wafer by using a 6 degree of freedom (DOF) stitching method. Low coherence scanning interferometry employing near infrared light, partially transparent to a Si wafer, is adopted to simultaneously measure the surface and thickness profiles of the wafer. For the large field of view, a stitching method of the sub-aperture measurement is added to the measurement system; also, 6 DOF parameters, including the lateral positioning errors and the rotational error, are considered. In the experiment, surface profiles of a double-sided polished wafer with a 100 mm diameter were measured with the sub-aperture of an 18 mm diameter at 10x10 locations and the surface profiles of both sides were stitched with the sub-aperture maps. As a result, the nominal thickness of the wafer was 483.2 μm and the calculated PV values of both surfaces were 16.57 μm and 17.12 μm, respectively.
Keywords:
Wafer metrology, Silicon wafer, Low coherence scanning interferometry, 6 DOF stitching, Near infrared light키워드:
웨이퍼 측정, 실리콘 웨이퍼, 저간섭성 주사 간섭계, 6 자유도 정합, 근적외선 광1. 서론
최근 반도체 산업의 발전에 따라 디스플레이, LCD, 스마트폰 및 반도체 메모리 칩의 제조가 늘어나고 있는 추세이며, 고품질 실리콘 웨이퍼 (Silicon Wafer)의 생산성 또한 요구되고 있다. 이에 따라 반도체의 대량 생산 및 단가 하락을 위해서 웨이퍼의 크기가 점차적으로 증가하고 있고,1 그에 따른 이슈인 웨이퍼의 결함 (Defect), 평탄도 (Surface Flatness)에 대한 검사가 중요시 되고 있다. 이러한 웨이퍼의 형상 측정, 검사 방식은 크게 점 측정과 면적 측정으로 나눌 수 있는데, 점 측정 방식에는 대표적으로 정전 용량 센서 (Capacitive Sensor)2를 이용한 방식이 있다. 정전 용량 센서는 측정 프로브 (Measurement Probe)와 측정 대상체 사이에 축전되는 정전기량을 측정하여 거리를 측정하는 방식으로 빠른 응답특성과 높은 정밀도를 가진다. 그러나 이러한 점 측정 방식은 웨이퍼의 전체 영역을 검사하는 것이 아니라 임의의 영역만 측정한다는 한계가 있으며 양면 연마 웨이퍼(Double Side Polished Wafer, DSP)의 경우에는 앞면과 뒷면에서 각각 측정 해야 하는 단점이 있다. 한편, 웨이퍼의 형상을 한번에 측정하기 위해서 면적 측정 방식이 도입되었고, 그 중 대표적인 기술이 광학 간섭계 (Optical Interferometer)를 이용하는 방법이다. 그러나 가시광 대역의 광원을 이용한 간섭계는 양면 연마 웨이퍼를 측정 시 앞면과 뒷면을 각각 측정해야 하기 때문에 측정 시스템이 다소 복잡해지는 문제점이 있다.3 이를 해결하기 위한 방법으로 근적외선 (Near Infrared, NIR) 광원을 사용함으로써 근적외선의 투과 특성을 이용하여 웨이퍼의 두께 형상을 측정하는 연구가 진행되었으나, 이는 웨이퍼의 앞면과 뒷면의 형상 차이를 이용하여 전 영역에 대한 두께 변화를 주로 측정하였기 때문에 웨이퍼의 각 면에 대한 형상 및 두께를 측정하는 것에는 한계를 가지고 있다.4
한편, 광학 간섭계 중에서 저간섭성 주사 간섭계 (Low Coherence Scanning Interferometry)5는 짧은 가간섭 거리(Coherence Length)를 이용하여 시편의 절대 높이 값을 측정할 수 있기 때문에 산업계에서 3차원 형상 측정으로 많이 사용되고 있다. 하지만 점차 커지고 있는 웨이퍼의 전체 면적에 대해 일반적인 저간섭성 주사 간섭계로 측정, 검사를 할 경우 간섭계에 사용되는 광학 부품들은 측정하는 시편에 비례하여 커져야 하는 단점이 있다. 이러한 단점은 광학 부품의 교체로 인한 비용 증가, 광학계의 부피 증가로 넓은 공간 확보가 요구된다. 이러한 문제점을 해결하기 위한 방법으로 웨이퍼의 임의의 위치에서 비교적 작은 영역이 형상을 측정한 후, 이를 정합하여 웨이퍼 전체의 형상을 복원하는 정합 (Stitching)하는 기술은 비용적인 측면이나 측정 정밀도 측면에서 매우 효율적이다.6 그러나 성공적인 정합을 위해서는 측정된 영역들 상의 기하학적 관계가 정확해야 하기 때문에 기본적인 정합 이론과 더불어 측정 영역들 사이에서 발생할 수 있는 정렬 오차들을 보상해야 할 필요가 있다.
본 논문에서는 대 영역 실리콘 웨이퍼의 3차원 형상 및 두께측정을 하기 위한 근적외선 정합 저간섭성 주사 간섭계를 구성하고 이를 검증하였다. 근적외선 저간섭성 주사 간섭계 원리를 적용하여 웨이퍼의 앞면과 뒷면 형상을 동시에 측정한 후, 이를 이용하여 웨이퍼의 두께 및 균일도를 측정하였다. 또한 웨이퍼 전체의 측정 결과를 위해 6 자유도 (Degree of Freedom, DOF)를 기반으로 하여 측정 결과들을 정합하는 알고리즘을 적용하였다.
2. 근적외선 정합 간섭계의 원리
2.1 근적외선 저간섭성 주사 간섭계
일반적으로 가시광 영역의 빛은 실리콘 웨이퍼를 투과하지 못하고 대부분 반사한다. 그러나 1 μm 파장 대역 이상의 적외선 및 근적외선 대역의 빛은 두께 및 도핑 정도에 따라 차이를 보이기는 하지만 Fig. 1의 녹색 그래프와 같이 실리콘 웨이퍼를 부분적으로 투과하는 특성을 보인다.7 이와 더불어 1 μm 파장 대역의 빛은 고가의 적외선 대역 이미지 센서를 사용하지 않더라도 Fig. 1의 파란색 그래프와 같이 가시광 대역의 일반적인 센서에서 광 검출이 가능하다는 특징이 있다.
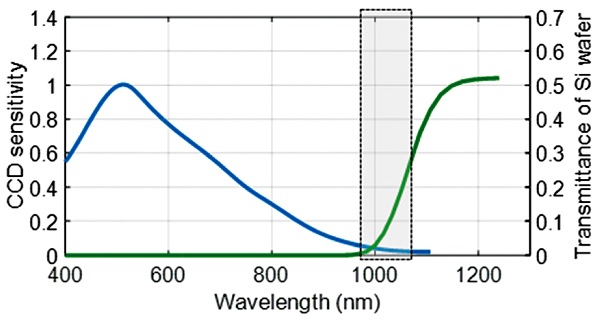
Transmittance of Si wafer (Green line) and visible CCD sensitivity (Blue line) corresponding to the wavelength
그래서 광원으로 1 μm 파장 대역의 SLD (Super-Luminescent Diode)와 같은 근적외선 저간섭성 광원을 이용하면 고가의 특별한 적외선 이미지 센서를 사용하지 않고 저간섭성 주사 간섭계를 구성할 수 있다. 이 경우, 1 μm 파장 근처에서 실리콘 웨이퍼의 투과 특성이 50% 이하로 비교적 낮고, 이미지 센서의 감도도 가시광에 비해 매우 작은 편이나 양면 연마 웨이퍼의 경우 표면에서 비교적 높은 크기의 반사광을 검출 할 수 있어 간섭 신호 획득이 충분히 가능하다.8
기본적으로 저간섭성 주사 간섭계는 넓은 주파수 대역을 가지고 있는 저간섭성 광원이 수십 마이크로 이하의 짧은 가간섭 거리를 가지고 있다는 점을 이용한다. 간섭계에서 광 분할기(Beam Splitter)를 통해 기준 면에서 반사된 기준 광과 측정 면에서 반사된 측정 광의 광경로 차이 (Optical Path Difference)가 0에 근접하면, 간섭 현상이 발생하여 간섭 신호가 나타나고, 이 신호를 푸리에 방법 (Fourier Method)9을 통해 해석하여 거리를 측정한다. 저간섭성 주사 간섭계는 간섭 신호가 가간섭 거리 영역에서만 나타나는 특징으로 인해 단차가 있는 시편의 형상을 측정할 수 있는 장점이 있고, 또한 웨이퍼와 같은 앞, 뒷면의 형상을 가지는 대상체의 경우에도 광경로 차이를 조절하여 각 면에 해당하는 간섭 신호 획득이 가능하다. 그러면 이러한 간섭 신호들로부터 측정된 높이 정보를 통해 실리콘 웨이퍼의 3차원 형상 및 두께 측정이 가능하다.
2.2 6 DOF 정합을 이용한 근적외선 저간섭성 주사간섭계
근적외선을 이용한 저간섭성 주사 간섭계는 실리콘 웨이퍼의 형상 및 두께를 동시에 측정하기에 경제적으로 효율적이며 높은 정밀도를 가진다. 그러나 실리콘 웨이퍼의 전체 영역에 대한 3차원 측정을 위해서는 간섭계에 사용되는 여러 광학 부품의 크기도 동시에 커져야 하는 문제가 발생한다. 그래서 본 연구에서는 이러한 근적외선 저간섭성 주사 간섭계 기반으로 실리콘 웨이퍼의 전체 영역과 같은 넓은 영역을 측정하기 위해 정합 방법(Stitching Technique)을 도입하였다. Fig. 2는 본 연구에서 제안하는 근적외선 정합 저간섭성 주사 간섭계의 구성도를 나타낸다. 간섭계는 마이켈슨 간섭계 (Michelson Interferometer) 타입으로 구성하였으며, 1050 nm 대역의 근적외선 광원을 사용하여 측정 대상물인 실리콘 웨이퍼의 앞면과 뒷면의 3차원 형상 및 두께를 효과적으로 측정할 수 있고, 종축 방향과 횡축 방향의 구동을 위해 3축으로 모터 구동 스테이지를 구성하여 측정하였다. 구성된 간섭계는 실리콘 웨이퍼의 전체 면적보다 비교적 작은 개구의 FOV (Field of View)를 가지기 때문에 웨이퍼 전체를 한번에 측정하는 것이 아니라, 웨이퍼의 일정 부분의 면적을 측정하게 되며 횡축 방향 구동을 통해 전체 실리콘 웨이퍼의 부분별 앞, 뒷면의 형상을 측정한다. 이후, 측정된 결과들을 정합하여 전체 웨이퍼의 형상을 복원하게 된다. 그래서 제안하는 간섭계는 넓은 측정 영역에서 높은 공간 분해능을 확보할 수 있는 장점을 가지며 또한 시스템 비용을 줄이는 효과가 있다.3
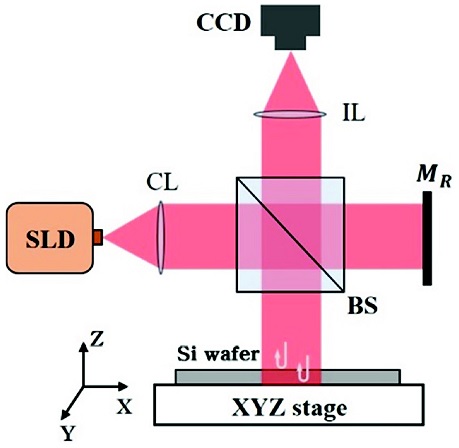
Optical configuration of stitching interferometry for measuring Si wafer, SLD: Super-Luminescence Diode, CL: Collimating Lens, BS: Beam Splitter, IL: Imaging Lens, MR: Reference Mirror
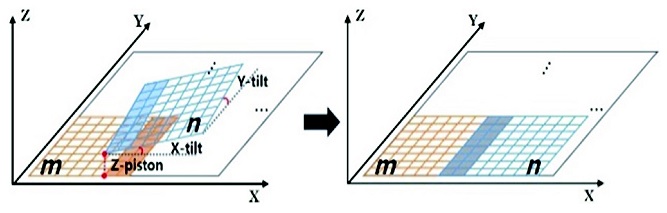
정합은 작은 개구 (Sub-Aperture)로 측정한 형상 데이터들의 서로 겹치는 영역을 동일하게 맞춤으로써 전체적인 3차원 형상 데이터를 생성시키는 기술이다. 일반적으로 3차원 형상 정합 방법에는 겹침 영역에 포함되는 몇개의 높이값을 추출하여 이러한 특징점들을 일치시키는 방법과, 겹침 영역의 평면 (Plane) 정보를 가지고 두 데이터 간의 차이를 최소로 만드는 방법이 있다.10 본 연구에서는 형상 오차로부터 비교적 둔감한 겹침 영역의 평면 정보로 3차원 형상을 정합하는 방법을 이용하였으며, 기본적인 3 DOF (Degree of Freedom) 정합 방법과 더불어 횡방향 구동 오차를 보정하기 위한 XY 위치오차 및 광축 (Z) 기준 회전 오차까지 보정하는 6 DOF 정합을 구현하였다.
먼저, 3 DOF의 정합 알고리즘에서는 Fig. 3과 같이 측정된 3차원 형상 데이터들을 평면으로 가정하고 이로부터 X축 기울기(X-Tilt), Y축 기울기 (Y-Tilt), 높이 방향 옵셋 (Z-Piston)인 3개의 변수값을 추출한다. 그리고 인접한 3차원 형상 데이터들과의 겹침 영역에서 추출된 이러한 3개의 변수값들을 서로 동일하게 맞춤으로써 정합을 수행한다. 3차원 형상 측정에서의 정합 과정을 수학적으로 표현하면 다음과 같다. 간섭계에서 측정된 형상 데이터 (Z)는 평면으로 간주되어 식(1)과 같이 나타낼 수 있다.
| (1) |
여기서 a, b, c 는 각각 X축 기울기, Y축 기울기, 높이 방향 옵셋을 나타낸다. 그러면 서로 근접하여 겹쳐져 있는 임의의 m평면 (Zm)과 n평면 (Zn)은 다음과 같은 수식으로 각각 표현할 수 있다.
| (2) |
이때, 두 평면의 겹치는 영역은 Zm과 Zn에서 각각 Zm,n과 Zn,m으로 나타낼 수 있고, 또한 식(1)과 같이 기울기와 옵셋으로 다음과 같이 나타낼 수 있다.
| (3) |
정합 과정에서는 두 평면 상의 겹침 영역이 서로 같은 평면이 되도록 식(3)에서의 기울기와 옵셋이 동일하게 되도록 조정되고, 그때 발생하는 기울기 변화와 옵셋 변화는 식(2)에서 표현한 전체 평면의 기울기와 옵셋에 적용되어 결국 정합을 위한 두 평면의 방정식 (Zm, Zn)은 식(4)와 같이 표현할 수 있다.
| (4) |
그러면 겹치는 영역의 임의의 한점 (Xsj, Ysj)에 대하여 식(2)부터 식(4)까지 정의한 정합 이전 및 이후의 평면의 기울기들과 옵셋들 간에는 식(5)와 같은 관계를 만족한다.
실제 측정한 3차원 형상 데이터에서 식(2)와 식(3)에서 표현되는 기울기들과 옵셋은 평면 맞춤 (Plane Fitting)을 통해 추출할 수 있기 때문에, 겹침 영역에서의 측정점들을 통해 행렬을 이용하여 식(5)에서 정합을 위한 기울기 변화 및 옵셋 변화를 계산할 수 있고, 이를 통해 식(4)의 정합을 위한 기울기 및 옵셋을 추출하여 정합을 수행하였다.
| (5) |
그러나 이러한 3 DOF 정합 방법은 기본적으로 횡방향의 좌표가 비교적 정확하다는 가정에서 진행되기 때문에, 작은 개구로 측정되는 형상들 간의 횡방향 구동 오차가 포함되는 경우 정합이 수행될 수 없다. 또한 측정시 시편의 광축 방향 회전이 발생하는 경우에도 정합 수행이 오차를 유발하게 된다. 이를 극복하기 위해 정밀한 횡방향 구동 스테이지가 필요하나 이는 시스템 비용을 증가시키는 요인이다. 그래서 본 연구에서는 효율적이고 정밀한 3차원 형상 정합을 위해 횡방향 구동 오차 및 회전 오차를 보상한 6 DOF 정합법을 구현하였다. 6 DOF 정합은 Fig. 4(a)와 같이 횡방향 위치 및 회전에 따른 근접한 평면들 각각의 겹침 영역들 간의 차이가 최소가 되는 최적의 횡방향 위치와 회전 각도를 추출한다. 이때, 초기에 겹치는 2개의 평면은 주어진 XY 좌표를 바탕으로 겹침 영역이 설정되고, 겹침 영역에 해당하는 2개의 평면상의 데이터들의 높이 차이는 식(6)과 같이 RMS (Root Mean Square) 값으로 계산된다. 이때, 각각의 평면들의 XY 기울기와 Z축 옵셋은 제거된다. 식(6)에서 F (X,Y,θZ)는 XY위치 오차 및 Z축 회전 오차를 보상하기 위한 목적 함수로 이용되어, 구동기의 사양에 따라 오차의 범위가 결정되면, 그 오차범위 내에서 값이 최소화가 되도록 최적화가 이루어지고 이를 통해 각 평면의 횡방향 좌표가 재설정된다.
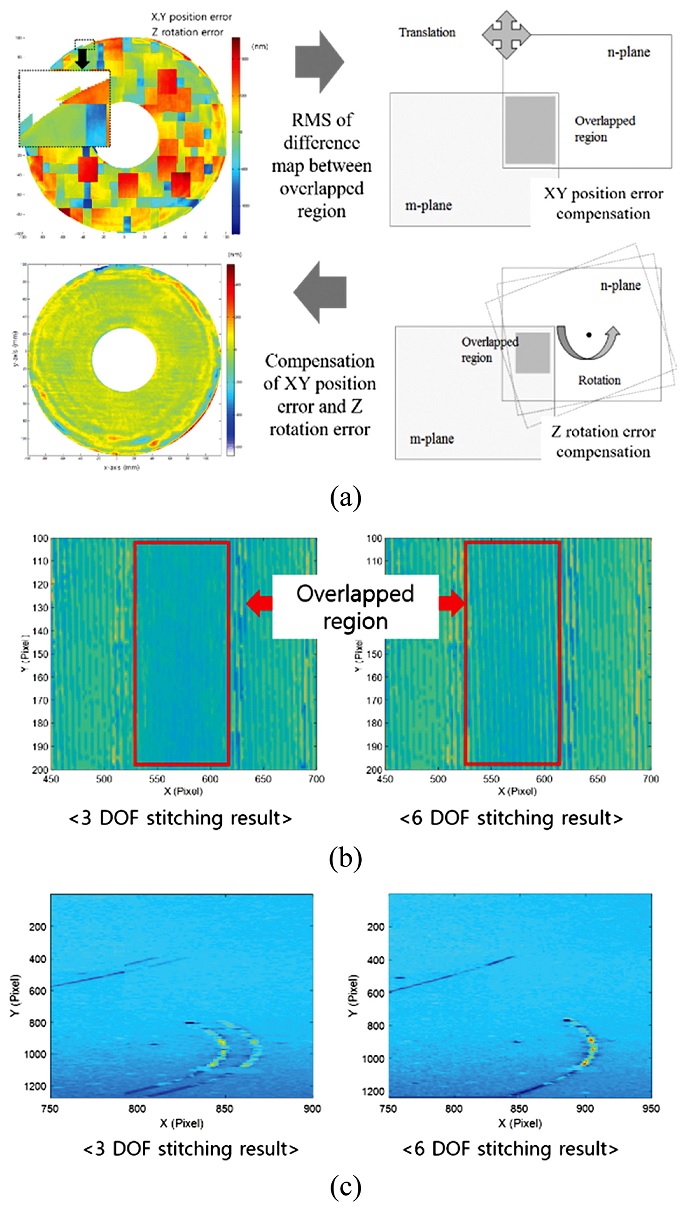
(a) Stitching procedure of 6 DOF (3 DOF with XY-Tilt and Z-Piston correction), (b) and (c) Comparisons between 3 DOF and 6 DOF stitching results of a machined surface and a flat surface
그러면 겹치는 영역의 좌표가 일치하는 경우 F(X,Y,θZ)가 최소가 되기 때문에 XY 위치 오차와 Z축 회전 오차를 보상할 수 있다.
| (6) |
여기서 Z'm,n과 Z'n,m는 m과 n 평면의 겹침 영역 (Zm,n과 Zn,m)에서 X, Y 기울기와 Z축 옵셋을 각각 제거한 평면을 나타낸다. 각 평면들의 횡방향 좌표가 결정되면, 이후에 3 DOF 정합이 수행되고 이를 통해 전체 형상을 복원할 수 있다. Fig. 4(b)는 백색광 주사 간섭계의 측정 결과를 통해 비교한 3 DOF와 6 DOF의 정합 결과를 나타낸다. Fig. 4(b)는 가공을 통한 비구면 시편의 측정 형상에 대한 일부분을 나타내며, Fig. 4(c)는 거울 면의 평면 형상 측정 결과를 보여준다. 이들 결과에서 알 수 있듯이, XY 위치 오차 및 Z축 회전 오차가 포함되는 경우, 표면 상의 패턴 및 형상이 정합 후에 명확히 드러나지 않거나 크기가 커지는 현상이 발생하지만 6 DOF 정합 이후에는 표면의 형상 및 패턴이 명확히 관찰되는 것을 확인할 수 있다. 이를 통해, 횡방향 구동기의 정밀도가 비교적 높지 않더라도, 알고리즘 상에서 구동 오차를 정합 과정에서 보상할 수 있다. 참고로, 정합 과정에서 횡방향 구동 오차를 보상하기 위한 방법으로 겹침 영역들에 대한 Correlation을 추출하는 방법10을 적용할 수 있지만, Correlation 방법은 일반적으로 3차원 형상에 임의의 패턴이 포함되는 경우에 사용되는 방법으로 본 연구에서 측정하고자 하는 실리콘 웨이퍼 측정에는 한계를 가지고 있음을 확인하였다.
3. 실험 결과 및 분석
3.1 단일 개구를 통한 실리콘 웨이퍼 측정
본 연구에서는 제안한 근적외선 정합 저간섭성 주사 간섭계를 검증하기 위해 100 mm 직경과 475 ± 25 μm의 두께를 가지는 양면 연마 실리콘 웨이퍼 (Double Sided Polished Si Wafer, DSP Si Wafer)의 형상 및 두께 측정을 수행하였다. 정합을 통한 전체 웨이퍼의 측정을 수행하기 전에 우선 단일 개구에서의 웨이퍼 측정 실험을 수행하였다.
Fig. 5는 실험을 수행하기 위한 광학 구성을 나타내며, 광원의 중심 파장은 1050 nm, 반치폭 (Full Width at Half Maximum, FWHM)은 50 nm를 갖는 SLD (Super-Luminescent Diode) 광원을 이용하였다. 넓은 면적을 조사하기 위해 빔 확장기 (Beam Expander)를 이용하였으며, 0.3x의 결상 렌즈 시스템을 통해 단일 개구의 측정 영역은 직경 18 mm로 설정하였다. 영상 검출기로는 (1280×1024) 해상도를 가지는 CCD 카메라를 사용하여 각각의 축을 X축과 Y축으로 설정하였다. 간섭무늬 획득을 위해 광축 (Z축)으로는 스텝 모터 구동기를 사용하였고, 영상의 샘플링 간격은 650 nm로 서브 샘플링 기법 (Sub-Sampling)을 이용하였다.

Photograph of constructed NIR stitching white light scanning interferometry, SLD: Super-Luminescence Diode, BS: Beam Splitter, MR: Reference Mirror.
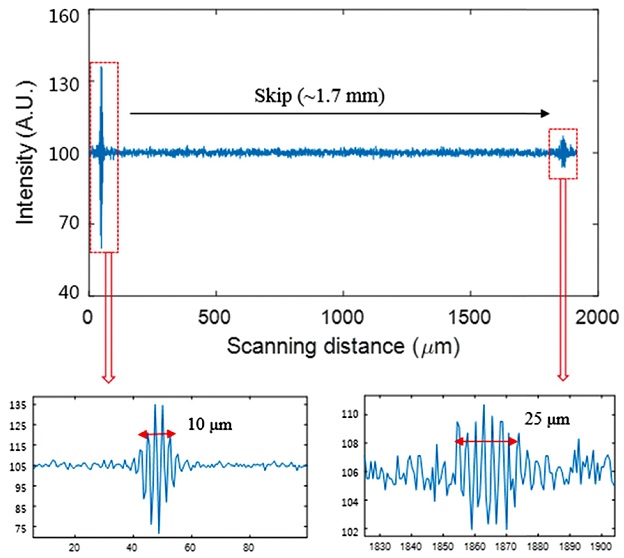
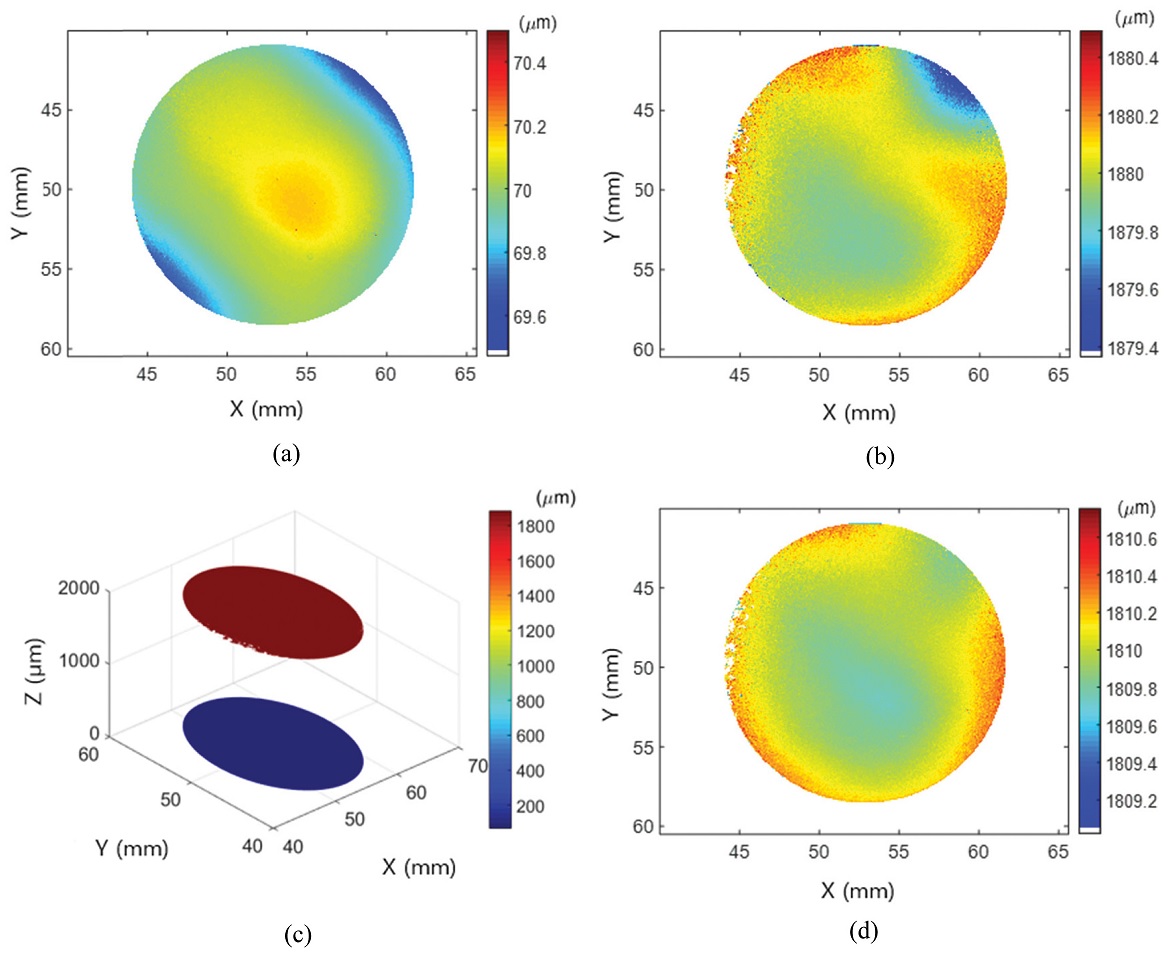
Fig. 6은 웨이퍼의 임의의 한 점에서 저간섭성 주사로 획득한 간섭 신호를 나타낸다. Fig. 6에서 알 수 있듯이 비록 웨이퍼의 앞면과 뒷면에 해당하는 간섭 신호의 가시도가 투과율에 의해 차이가 있고 또한 분산 영향으로 인해 뒷면의 간섭 신호가 비교적 넓어지기는 하지만 1050 nm 대역의 근적외선을 이용하여 실리콘 웨이퍼 투과가 가능한 동시에 이를 통해 웨이퍼의 앞면과 뒷면의 형상 측정이 가능함을 확인하였다. Fig. 7은 실리콘 웨이퍼의 중앙 부분에 대한 단일 개구의 측정 결과를 보여준다. 측정결과, 1050 nm 대역의 근적외선을 이용하여 웨이퍼 투과가 가능한 동시에 이를 통해 웨이퍼의 앞면과 뒷면의 형상 측정이 가능함을 확인하였다. 또한 두 면의 측정 결과와 실리콘 웨이퍼의 군굴절률을 이용하여 Figs. 7(c) 및 7(d)와 같이 두께 및 두께의 균일도를 추출하였다. 이때 평균 두께는 480.1 μm, 두께 형상은 PV (Peak to Valley) 값으로 0.8 μm였다.
3.2 6 DOF 정합을 이용한 실리콘 웨이퍼의 전체 영역 측정
100 mm 직경의 실리콘 웨이퍼의 전체 영역을 측정하기 위해 단일 개구에 대한 실리콘 웨이퍼 측정을 기반으로 6 DOF 정합 간섭계에 대한 실험을 수행하였다. 단일 개구 실험에서와 같은 광학 구성에서 실리콘 웨이퍼의 전체 영역인 100 mm 측정을 위해 횡축 방향 (X, Y)으로 구동 거리가 긴 스텝 모터 구동기를 추가하였다. 일반적으로 정합 간섭계에서 정합의 정확도는 겹침영역의 크기에 따라 결정되며, 겹침 영역이 증가할 경우에는 정합의 정확도가 높아지지만 측정해야 하는 작은 개구 형상 데이터 수가 증가한다. 반대로 겹침 영역이 작아질 경우에는 측정 데이터 수는 감소하지만 정합 시 오차를 유발할 수 있다. 그래서 정합 간섭계에서 겹침 영역의 크기 결정은 매우 중요하며, 본 연구에서는 정합을 위한 겹침 영역을 고려하여 횡축 구동기를 10 mm씩 구동하면서 겹침 비율 (Overlapping Ratio)을 30% 정도 되도록 유지하였고, 이때 인접한 데이터의 겹침 영역(Overlapped Area)은 8 mm로 설정하였다.
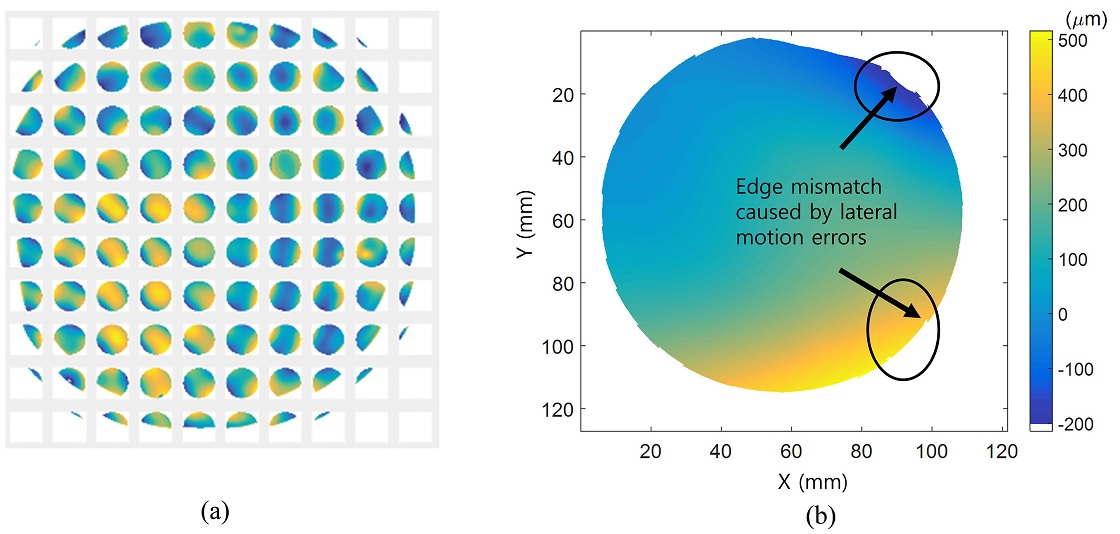
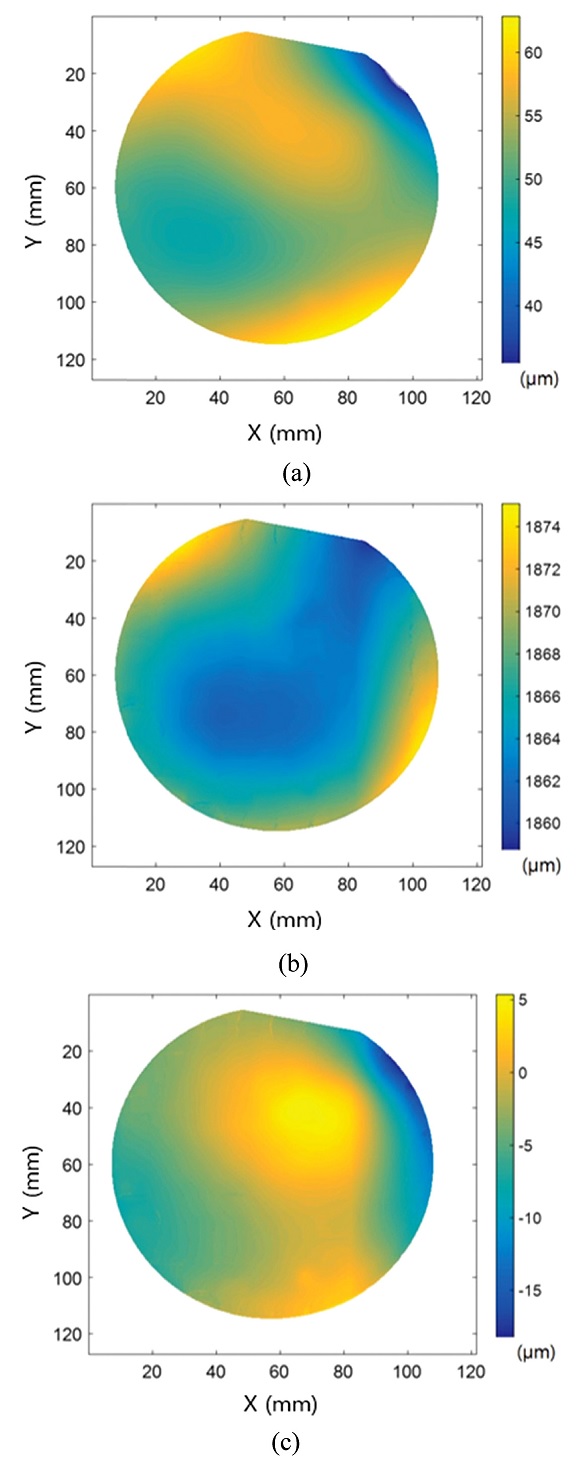
Fig. 8(a)는 100 mm 직경의 실리콘 웨이퍼 앞면에 대해 측정한 100개 (10×10)의 단일 개구 (18 mm 직경) 형상 데이터를 나타낸다. 100개의 형상 데이터 중에서도 웨이퍼의 측정 영역을 벗어나는 부분은 간섭 신호의 가시도를 기준으로 제거하였으며 이후 정합을 시도하였다. Fig. 8(b)는 횡축 방향 구동기의 좌표를 바탕으로 3 DOF 정합을 수행한 결과를 보여준다. 그러나 구성한 정합 간섭계에 사용된 횡축 방향 구동기는 정밀 제어를 수행하지 않았기 때문에 횡방향 구동 오차를 포함하고 있고 이로 인해 정합시 웨이퍼의 가장자리 부분이 부드럽게 나타나지 않음을 확인할 수 있다. 횡방향 구동기의 횡방향 오차를 보상하기 위해 본 연구에서 제안한 6 DOF 정합 방법을 적용하였으며, 그 결과 Fig. 9와 같이 웨이퍼의 전체 영역에 대한 양면의 3차원 형상 및 두께를 측정하였다. 측정 결과 웨이퍼의 광학적 두께는 1812.5 μm로 실리콘 굴절률을 고려하여 계산하면 실제 측정 두께 값은 483.2 μm으로 나왔다. 그리고 앞면, 뒷면, 두께에 대한 PV 값은 16.57 μm, 17.12 μm, 13.54 μm임을 확인할 수 있었다.
3.3 고찰 및 논의
본 연구에서 제안한 근적외선 저간섭성 주사 간섭계는 실리콘 웨이퍼를 투과할 수 있는 1 μm 파장 대역의 광을 이용하여 가시광 영역 대의 CCD 나 CMOS 카메라 등에서 영상을 획득할 수 있기 때문에 기존의 적외선 간섭계 등에 비해 시스템 비용을 줄일 수 있는 장점이 있다. 또한 대면적 측정을 위해 6 DOF 정합 기술을 도입하여 전체적인 광학계의 크기는 줄이면서 측정 영역은 확대할 수 있다. 그러나 제안하는 간섭계는 다음과 같은 한계를 가지고 있다.
먼저 측정 대상인 실리콘 웨이퍼가 순수한 실리콘이 아닌 다른 반도체 등에 의한 도핑 (Doping)이 되어 있는 경우 투과율이 현저히 낮아진다. 순수한 실리콘 웨이퍼의 경우에도 두께에 따라 근적외선 투과율이 달라지며 Fig. 6에서 알 수 있듯이 웨이퍼를 투과한 광에 의한 간섭 신호는 광량 감소로 인해 현저히 작음을 알 수 있다. 이를 극복하기 위해서는 광원부에 광증폭기 (Amplifier)를 추가적으로 구성하여 전체적인 광량을 높이는 방법을 생각할 수 있으나 이 경우 웨이퍼의 앞면에서 반사하는 광량을 고려하여 조절해야 할 필요가 있다.
두번째로 정합을 이용하여 웨이퍼의 전체 면적에 대한 3차원 형상을 측정하는 경우, 웨이퍼의 표면이 비교적 매끄러워 정합을 위한 겹침 영역에서 횡방향 오차가 발생하더라도 Fig. 8(b)와 같이 정합이 성공적으로 수행되었다고 판단될 수 있다. 이는 3 DOF 정합시 기울기와 옵셋을 이용하여 정합이 진행되기 때문에, 정합의 성공 여부를 판단하기 위해서는 정합된 형상의 매끄러운 정도 및 정합 자국의 유무뿐만 아니라 전체 측정 영역의 복원 여부도 포함해야 한다. 본 연구에서 수행한 6 DOF 정합 과정에서는 이러한 요소들을 고려하여 정합을 진행하였고 성공적으로 정합이 이루어졌음을 확인하였다.
4. 결론
본 연구에서는 최근 생산성 증대를 위해 크기가 점차 커지고 있는 실리콘 웨이퍼의 3차원 형상을 측정하기 위한 간섭계를 구성하고 연구를 수행하였다. 직경이 100 mm, 두께가 475 ± 25 μm인 양면 연마 실리콘 웨이퍼를 근적외선의 투과 특성으로 앞면과 뒷면의 3차원 형상 및 두께를 측정하였다. 또한, 작은 개구로 측정을 함으로써 높은 분해능으로 웨이퍼의 전체 영역을 측정하였으며, 6 DOF 정합 방법을 통해 전체 형상을 복원하였다. 측정결과 실리콘 웨이퍼의 앞면과 뒷면에 해당하는 3차원 형상 정보와 두께 483.2 μm를 계산할 수 있었으며, 앞면과 뒷면에 해당하는 평균 PV 값은 16.57 μm, 17.12 μm을 확인할 수 있었다. 이를 통해 저간섭성 주사 간섭계 기반의 정합 간섭계로 대 영역 실리콘 웨이퍼의 3차원 형상 및 두께 측정에 활용될 수 있음을 확인하였다.
NOMENCLATURE
| a : | X-Tilt for a measure surface |
| b : | Y-Tilt for a measure surface |
| c : | Z-Piston for a measure surface |
| z : | Polynomial for stitching algorithm |
Acknowledgments
이 논문은 2014년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업 (NRF-2014R1A1A2056691)의 연구 결과입니다.
REFERENCES
-
Hahn, P. O., “The 300 mm Silicon Wafer-A Cost and Technology Challenge,” Microelectronic Engineering, Vol. 56, No. 1, pp. 3-13, 2001.
[https://doi.org/10.1016/S0167-9317(00)00499-8]

-
Bugg, C. D., “Noncontact Surface Profiling Using a Novel Capacitive Technique: Scanning Capacitance Microscopy,” Proc. of the International Society for Optics and Photonics, pp. 216-224, 1992.
[https://doi.org/10.1117/12.57765]

-
Jansen, M., Schellekens, P., and Haitjema, H., “Development of a Double Sided Stitching Interferometer for Wafer Characterization,” CIRP Annals-Manufacturing Technology, Vol. 55, No. 1, pp. 555-558, 2006.
[https://doi.org/10.1016/S0007-8506(07)60481-8]

- Schmitz, T. L., Davies, A., Evans, C. J., and Parks, R. E., “Silicon Wafer Thickness Variation Measurements Using the National Institute of Standards and Technology Infrared Interferometer,” Optical Engineering, Vol. 42, No. 8, pp. 2281-2290, 2003.
-
Haruna, M., Ohmi, M., Mitsuyama, T., Tajiri, H., Maruyama, H., et al., “Simultaneous Measurement of the Phase and Group Indices and the Thickness of Transparent Plates by Low-Coherence Interferometry,” Optics Letters, Vol. 23, No. 12, pp. 966-968, 1998.
[https://doi.org/10.1364/OL.23.000966]

-
Jansen, M. J., Haitjema, H., and Schellekens, P. H. J., “A Scanning Wafer Thickness and Flatness Interferometer,” Proc. of the International Society for Optics and Photonics, pp. 334-354. 2004.
[https://doi.org/10.1117/12.515650]

-
Green, M. A., “Self-Consistent Optical Parameters of Intrinsic Silicon at 300K Including Temperature Coefficients,” Solar Energy Materials and Solar Cells, Vol. 92, No. 11, pp. 1305-1310, 2008.
[https://doi.org/10.1016/j.solmat.2008.06.009]

-
Kim, Y. G., Seo, Y. B., and Joo, K.-N., “Low Cost Wafer Metrology Using a NIR Low Coherence Interferometry,” Optics Express, Vol. 21, No. 11, pp. 13648-13655, 2013.
[https://doi.org/10.1364/OE.21.013648]

-
Lee, H.-J. and Joo, K.-N., “Optical Interferometric Approach for Measuring Geometrical Dimension and Refractive Index Profiles of a Double-Sided Polished Undoped Si Wafer,” Measurement Science and Technology, Vol. 25, No. 7, Paper No. 075202, 2014.
[https://doi.org/10.1088/0957-0233/25/7/075202]

-
Lee, D.-H., Ahn, J.-H., and Cho, N. G., “Development and Evaluation of Stitching Algorithm with Five Degrees of Freedom for Three-Dimensional High-Precision Texture of Large Surface,” Journal of the Korean Society of Manufacturing Technology Engineers, Vol. 23, No. 2, pp. 118-126, 2014.
[https://doi.org/10.7735/ksmte.2014.23.2.118]