오차를 기반으로한 RBF 신경회로망 적응 백스테핑 제어기 설계
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
2-Axis Pan and Tilt Motion Platform, a complex multivariate non-linear system, may incur any disturbance, thus requiring system controller with robustness against various disturbances. In this study, we designed an adaptive backstepping compensated controller by estimating the disturbance and error using the Radial Basis Function Neural Network (RBF NN). In this process, Uniformly Ultimately Bounded (UUB) was demonstrated via Lyapunov and stability was confirmed. By generating progressive disturbance to the irregular frequency and amplitude changes, it was verified for various environmental disturbances. In addition, by setting the RBF NN input vector to the minimum, the estimated disturbance compensation process was analyzed. Only two input vectors facilitated compensatory function of RBF NN via estimating the modeling and control error values as well as irregular disturbance; the application of the process resulted in improved backstepping controller performance that was confirmed through simulation.
Keywords:
RBF nueral network, Adaptive backstepping, Disturbance observer, 2-Axis pan-tilt키워드:
RBF 신경회로망, 적응 백스테핑, 외란관측기, 2축 팬틸트1. 서론
2축 팬 틸트는 카메라 짐벌 및 터렛, 레이더 서보 메커니즘으로 민간 및 군사응용 분야에 광범위하게 사용되는 시스템이다.1 이 때문에 어떠한 외란이 시스템에 영향을 미칠지 모른다. 또한, 2축 팬 틸트는 복잡한 다 변수 비선형 시스템 일 뿐 아니라, 외란에 영향을 많이 받는 시스템 이다.1 이러한 이유로 다양한 외란에도 정밀한 제어가 가능한 강건한 제어기가 필요하다.
2축 팬 틸트 비선형 시스템은 순궤환 형식 (Strict Feedback Form)으로 나타낼 수 있으며,1 이를 제어하는 방법 중 강력한 방법이 백스테핑 기술이다.2 백스테핑 제어기법은 가상의 제어입력을 순궤환 형식에 대입하여 복잡한 비선형제어를 단계적으로 설계하여 Lyapunov 이론에 의해 가상제어 값과의 오차를 단계적으로 0으로 수렴시켜 가상제어 값으로 플랜트를 제어한다.3 이러한 백스테핑 제어기법은 단계적으로 Lyapunov 이론을 적용하기 때문에 전체 안정성을 쉽게 확보하며 제어할 수 있다. 하지만 정확하지 않은 매개변수들과 외란 등의 문제로 정확한 제어를 하는데 한계가 있다. 그러므로 알지 못하는 매개변수 및 오차들을 추정 보상하여 제어할 수 있는 기술이 필요하다.
이러한 문제를 해결하려는 방법으로 외란 관측기를 추가하여 문제를 해결하는 방법들이 연구되고 있다.4-12 이 중 RBF (Radial Basis Function) 신경회로망을 통해 불확실한 플랜트와 외란의 영향으로부터의 발생한 오차를 추정, 보상하여 제어기 성능을 향상하는 연구가 진행되어 왔다.9-12 이러한 앞선 연구들에서는 RBF 신경회로망이 외란에 대해 추정 및 보상을 통하여 제어오차가 0으로 수렴한다는 것만 나타내고 있다.10,11 하지만 RBF 신경회로망이 제어 수렴속도와 수렴오차에 어떠한 영향이 미치는지에 관한 세분화된 분석이 필요하다. 또한, 외란을 고정된 주파수 혹은 정해진 범위의 외란만을 가지고 RBF 신경회로망을 검증을 하였다.11,12 하지만 실제 환경에서는 다양한 외란이 발생한다. 따라서 주파수와 크기가 불규칙하게 변화하는 외란에 대해 RBF 신경회로망의 성능 검증이 필요하다.
본 연구에서는 다 변수 비선형 시스템인 2축 팬 틸트를 비선형 동역학 식을 기반으로 백스테핑 제어기를 설계하고, RBF 신경회로망을 이용하여 불확실한 플랜트와 외란의 영향으로부터의 발생한 오차를 추정, 보상하여 백스테핑 제어기의 성능을 향상시킨다. 또한, 외란 이외의 제어 오차를 보상하여 제어 응답속도를 높여 제어기 성능향상에도 기여한다는 것을 보여준다. 그리고 고정된 주파수의 외란이 아닌 시간에 따라 주파수와 크기가 변화하는 외란의 환경 속에서 제어기를 검증한다. 이것을 통해 제어가 힘든 외란 환경 속에서도 강건한 제어기임을 증명한다. 또한, 이 과정에서 RBF 신경회로망의 입력 값과 노드점을 최소화하여 설계하고, UUB (Uniformly Ultimately Bounded)로 안정성을 증명한다. 이렇게 설계된 RBF 신경회로망이 백스테핑 제어기성능 향상에 어떻게 기여하는지를 살펴보아 RBF 신경회로망 역할을 설명하고자 한다.
본 논문의 구성은 다음과 같다. 2장에서는 본 연구에서 다루는 시스템에 관한 서술과 RBF 신경회로망에 대한 내용을 간략히 정리하였다. 3장에서는 RBF 신경회로망 적응 백스테핑 제어기 설계 과정을 기술하고, 설계한 제어입력을 넣은 전체 폐루프 시스템의 안정성 판별에 대하여 언급한다. 4장에서는 다양한 외란에 대해 모의실험을 하기 위해, 시간에 따른 주파수와 크기가 바뀌는 외란들을 제시한다. 5장에서는 백스테핑 제어기와 RBF 신경회로망 적응 백스테핑 제어기의 성능 비교를 통하여, RBF 신경회로망의 제어 응답향상 기여도를 확인한 후, 4장에서 제시한 외란을 가지고 모의 실험을 하여 오차 보상과정을 보여준다. 6장에서는 연구에 관한 결과를 정리하여 결론을 맺는다.
2. 관련이론
2.1 2축 팬 틸트 모델
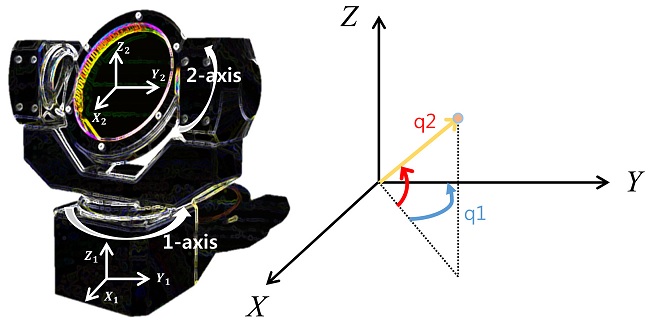
2축 팬 틸트는 다음 그림과 같이 나타내어 진다. 밑의 부분을 1축 위의 부분을 2축이라고 하며, 1축에 의해 구동되는 각을 q1, 2축에 의해 구동되는 각을 q2라고 정의한다.
주어진 시스템의 동적 모델은 라그랑주 방정식을 사용 하여 다음 식(1)처럼 유도된다.
| (1) |
위 시스템은 두 개의 입력 토크와 2차 MIMO 시스템이며 출력은 두 개의 각도 위치이며 식(2)와 같이 나타내어 진다.
| (2) |
, 은 각각 1축의 각 위치, 각 속도, 각 가속도를 , 은 각각 2축의 각 위치, 각 속도, 각 가속도를 나타낸다. 위 식을 다음과 같은 순궤환 시스템으로 나타낼 수 있다.
| (3) |
여기서 x1= [x11, x12]T= [q1, q2]T, x2= [x21, x22]T= []T은 상태 변수를 나타내며, u = [u1, u2]T= [τ1, τ2]T, y는 시스템의 제어 입력과 출력 각각 나타낸다.
2.2 RBF 신경회로망
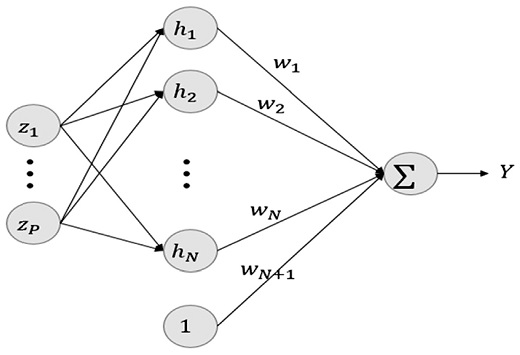
RBF (Radial Basis Function) 신경회로망은 은닉층과 출력 층으로 구성된 전 방향 지도 학습 알고리즘을 갖는 신경망이다. 기본적인 구조는 다음 Fig. 2와 같이 구성되어 있다
Fig. 2과 같이 RBF 신경회로망은 은닉 층이 단 한 층만으로 구성되며 입력 층과 은닉 층의 연결은 연결강도를 갖지 않고 입력 값을 그대로 받아 들이며, 은닉 층은 많은 노드가 이루어져 있으며, 각 노드는 연결강도에 의해 출력된다. 또한, 출력 층은 노드와 연결강도의 곱의 합들로 출력되며 다음과 같이 나타내어진다.
| (4) |
여기서 Z = [z1, z2,...zp]T, W = [w1, w2,...wN, wN+1]T은 각각 입력층의 입력벡터와 은닉 층과 출력 층 사이의 연결강도 벡터이다. H = [h1, h2,...hN, 1]T는 은닉 층의 출력벡터이며 i번째 노드의 비선형 활성 함수로써 다음과 같은 형태를 갖는 가우스 함수로 표현된다.
| (5) |
여기서 ci는 중심점을, bi는 가우스 함수의 폭을 나타내며 이 두개의 값은 고정된다. 즉, 위의 함수 식에서 나타내는 것은 중심에서 가장 큰 값을 갖고 중심에서 멀어질수록 0으로 감소하는 함수를 나타낸다는 것을 알 수 있다.
3. RBF 신경회로망을 이용한 백스테핑 제어기
3.1 RBF 신경회로망 적응 백스테핑 제어기 설계
불확실한 플랜트와 외란의 영향으로 정확하게 알 수 없는 상태변수들이 결합되어 있는 복잡한 다 변수 비선형 시스템인 2축 팬 틸트를 제어하기 위해서, 적응칙을 유도하고 전체 폐루프 시스템의 안정성을 보장하는 제어입력을 구하여 RBF 신경회로망 외란 관측기를 활용한 백스테핑 제어기를 다음과 같이 설계한다. 먼저 2장에서 구한 식(3)을 알 수 없는 외란 D를 추가하여 시스템을 다음과 같이 정의한다.
| (6) |
ㆍ백스테핑 제어기 설계
아래와 같이 새로운 상태변수를 정의한다.
| (7) |
| (8) |
여기서 x1,d, x2,d는 각각 x1, x2의 명령추종입력이다. 식(7)을 미분하면, 아래의 식(9)와 같다.
| (9) |
그리고, 다음과 같이 Lyapunov함수를 정의한다.
| (10) |
| (11) |
식(11)이 0보다 작거나 같게 되는 안정화 함수를 다음과 같이 선택한다.
| (12) |
여기서, k1은 양의 제어이득이다. 식(12)에 의해 x2,d는 다음과 같이 선택된다.
| (13) |
식(13)에 의하여 식(8)과 식(9)는 다음과 같이 정의된다.
| (14) |
| (15) |
| (16) |
따라서 식(6)과 식(16)을 통해 최종적으로 다음과 같이 나타내어진다.
| (17) |
그리고, 다음과 같은 Lyapunov를 정의한다.
| (18) |
| (19) |
식(19)가 0보다 작거나 같게 되는 안정화 함수를 만족하는 입력 u는 다음과 같이 선택된다.
| (20) |
하지만 여기서 D는 알 수 없는 값이다. 이것을 RBF 신경회로망 외란 관측기를 이용하여 근사화하여 보상한다.
ㆍRBF 신경회로망 설계
식(20)에서 D를 RBF 신경회로망으로 근사화 하기 위해 다음과 같이 정의한다.
| (21) |
여기서 Z = [e1, e2]T는 입력 벡터, W*는 이상적인 연결강도 값, ε는 근사 오차이다. 그리고 |ε| ≤ U, U > 0을 만족하는 W*가 존재한다고 가정한다. 하지만 W*를 알 수 없으므로, W* 추정을 통해 최종적으로 D를 추정하여 다음과 같이 정의한다.
| (22) |
여기서 은 이상적인 연결강도의 추정 값이고, 은 알 수 없는 외란 D의 추정 값이다. 이 값을 식(18)에 대입하면, 식(23)과 같다.
| (23) |
식(21)과 식(23)에 의하여 식(17)은 다시 다음과 같이 나타내어진다.
| (24) |
여기서 는 연결강도 추정오차이다. 그리고, 다음과 같이 Lyapunov를 정의한다.
| (25) |
| (26) |
위 식(26)으로부터 연결강도에 대한 적응칙을 구하면 식(27)과 같다.
| (27) |
하지만, W*를 알 수 없으므로, 도 알 수 없다. 그러므로 식(27) 대신 다음과 같은 식을 사용하여 연결강도를 추정한다.
| (28) |
여기서, γ는 양의 적응 이득이고, σ는 양의 작은 상수 값이다.
3.2 안정성 판별
시스템의 안정성을 판별하기 위해 Lyapunov 함수를 활용하였다. 또한 UUB (Uniformly Ultimately Bounded)를 통하여 증명하였다. Lyapunov 함수는 식(26)과 같으며, 적응칙과 입력 값은 식(27), 식(28)과 같이 구해진다. 여기서 k1 ≥ λ/2, k2 ≥ (λ + 1)/2, σ ≥ λ/γ을 만족하도록 σ, γ를 선택하고, 앞에서 언급한 연결강도 추정오차의 정의인 를 이용하여 안정성을 확인해보면 다음과 같다.
| (29) |
위 식(29)에서, ε2/2 + (λW*TW*)/(2γ) = ρ라고 하면 최종식은 식(30)과 같다.
| (30) |
즉 식(30)에 의하여 V3는 |V3| ≤ ρ/λ를 만족할 때까지 지수적으로 감소하며, ρ/λ로 Bounded된다. 또한, k1, k2를 충분히 큰 값으로
ㆍ백스테핑 제어기에 외란이 없을 때
선택하면 Lyapunov 함수 V3의 e1, e2, 는 UUB (Uniformly Ultimately Bounded)된다. 즉, k1, k2 값이 증가하면 λ 값이 증가하여 ρ/λ 값은 작아져 e1, e2, 는 작아진다. 따라서, UUB (Uniformly Ultimately Bounded) 안정성을 확인할 수 있다.
4. 모의 실험을 위한 외란 발생
강인한 제어기임을 보이기 위해 외란을 시간에 따라 주파수와 크기가 다양하게 변화하도록 발생한다. 외란은 q1과 q2에 각각 다음과 같이 발생시킨다.
위 Figs. 3과 4에서 보이듯이 주파수가 불규칙하게 바뀌고 있다. 처음 주파수는 30 rad/sec에서 시작하며 주파수가 바뀌는 시간은 다음 Table 1과 같다.
ㆍRBF 신경회로망 적응 백스테핑 제어기일 때
5. 모의실험
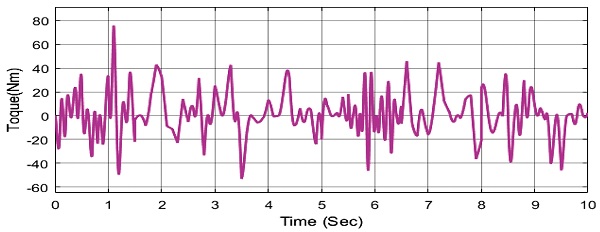
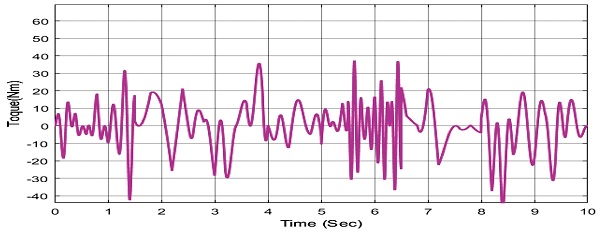
설계한 RBF 신경회로망을 이용한 백스테핑 제어기의 성능을 검증하고, 분석하기 위해 외란이 있을 때와 없을 때, RBF 신경회로망이 있을 때와 없을 때를 나누어 모의실험을 한다. RBF 신경회로망의 설계 상수는 bi = 0.5, γ = 10000, σ = 0.01, k1 = 10, k2 = 10, 노드 수는 100개이며 모터 토크 입력 값은 200 Nm를 넘지 않도록 하였다.
위의 Figs. 5-8을 통해 시스템의 모델링이 정확하게 되었다면 제어성능이 만족할 만큼 나온다는 것을 알 수 있다. 여기에 RBF 신경회로망 적응 백스테핑 제어기를 사용하여 제어 오차를 관측하면 다음과 같다.
ㆍ백스테핑 제어기에 외란만 있을 때
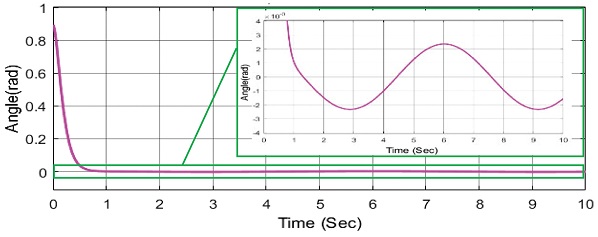
위 Figs. 9과 10을 통하여 RBF 신경회로망을 통하여 백스테핑 제어기 성능향상이 된 것을 확인할 수 있다. 성능향상의 원인을 알아보기 위해 RBF 신경회로망의 관측 값을 알아보았다.
위의 Figs. 11과 12에서 보이듯이 RBF 신경회로망이 e2의 값을 추종하고 있다. 위의 그림에서 빨간 실선은 e2에 게인 570 값이 곱해진 570e2를 나타내고 있다. 즉, RBF신경회로망은 e2의 게인 값이 곱해진 만큼을 추종하여 제어기에 보상을 해주고 있다는 말이다. 이 과정에서 제어기 성능 향상이 이루어 진다는 것을 알 수 있다.
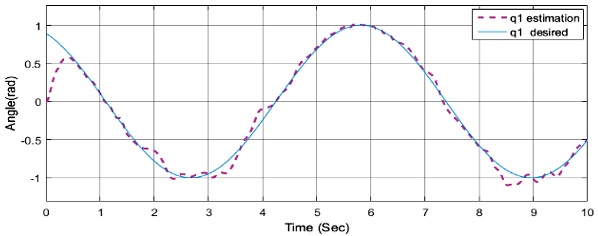
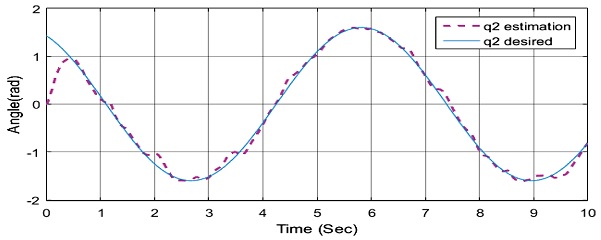
위 Figs. 13-16에서처럼 백스테핑 제어기에 외란이 추가가 되면 모델링에 알 수 없는 값이 추가가 되기 때문에 제어가 되지 않는 것을 확인할 수 있다. RBF 신경회로망 적응 백스테핑 제어기를 사용하여 제어 성능을 확인해보면 다음과 같다.
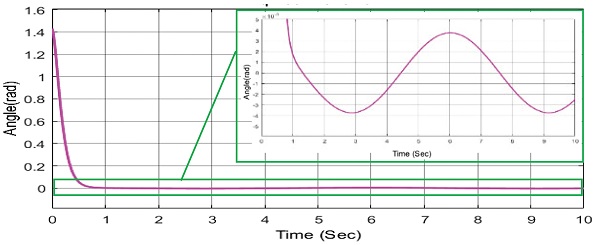
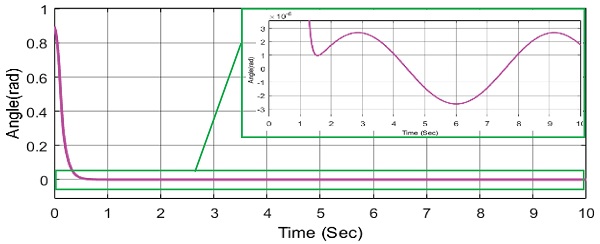
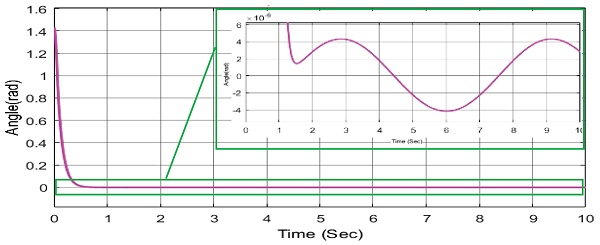
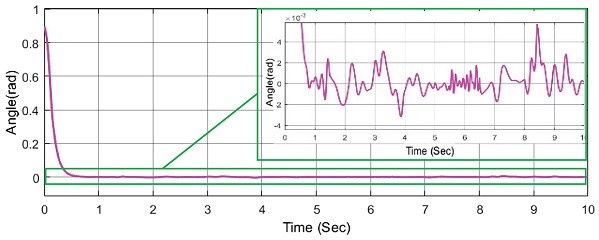
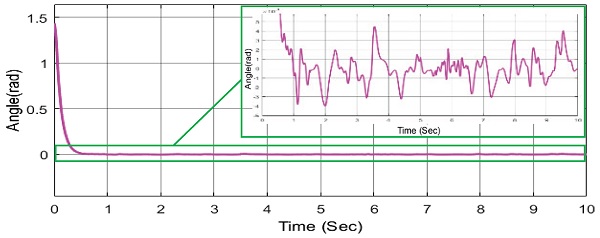
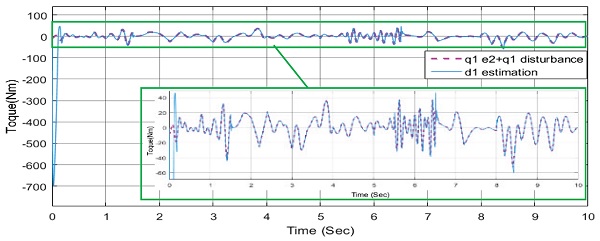
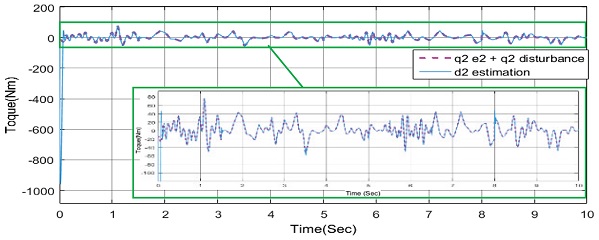
위 Figs. 17과 18을 통하여 RBF 신경회로망을 통하여 백스테핑 제어기 성능향상이 된 것을 확인할 수 있다. 성능향상의 원인을 알아보기 위해 RBF 신경회로망의 관측 값을 알아보았다.
ㆍRBF 신경회로망 적응 백스테핑 제어기일 때
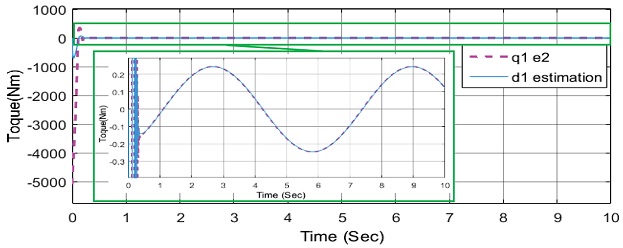
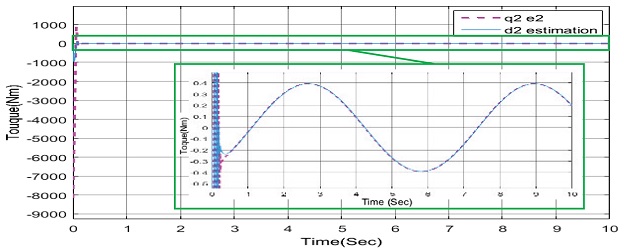
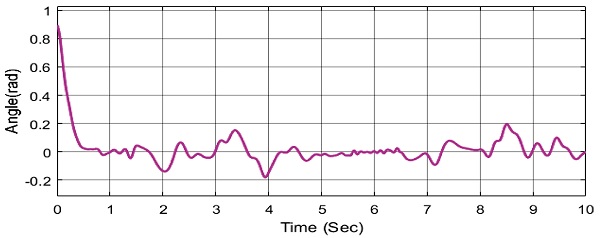
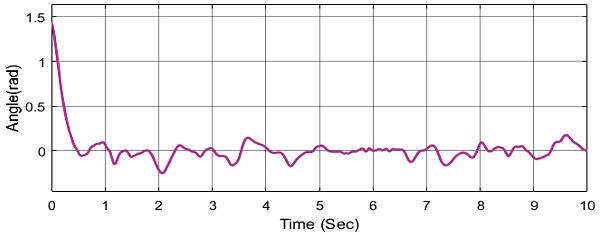
위의 Figs. 19와 20에서 보이듯이 RBF 신경회로망 이 e2값과 외란 값을 추종하고 있다. 위의 그림에서 빨간 실선은 e2와 외란의 합을 나타내고 있다. 즉, RBF신경회로망은 외란 뿐 아닌 오차 값인 e2도 같이 추종하여 제어기에 보상을 해주고 있다는 말이다. 이 과정을 통해 제어기 성능 향상이 이루어 진다는 것을 알 수 있다.
6. 결론
본 논문에서는 2축 팬 틸트 시스템을 가지고 시간에 따라 주파수와 크기가 불규칙하게 변화하는 상황에서 RBF 신경회로망적응 백스테핑 제어기 성능향상을 확인해보았다. 이 과정에서 최소한의 입력벡터와 노드점으로 RBF신경회로망을 설계하고, RBF 신경회로망의 역할을 분석하여 성능향상의 이유를 알아 보았다.
먼저 백스테핑 제어기에서 외란은 e1, e2 변수만으로 표현이 가능할 것이라 생각하여 RBF 신경회로망 설계시 입력 벡터를 e1, e2 두 개로만 하여 적은 입력 벡터로 RBF 신경회로망을 설계하여 외란 추정의 성능을 평가 하였다.
Matlab Simullink 모의실험에서는 RBF 신경회로망 적응 백스테핑 제어기 성능향상의 이유를 찾고, RBF 신경회로망의 역할을 알아보고자 다양한 상황을 만들어 실험을 하였다. 첫 번째 상황에서는 외란이 없는 상황에서 RBF 신경회로망을 사용하지 않은 백스테핑 제어기를 사용한 경우와 RBF 신경회로망 적응 백스테핑 제어기를 사용한 경우를 나누어 각각 성능을 비교해 보았다. 결과는 RBF 신경회로망 적응 백스테핑 제어기를 사용한 경우가 성능이 더 좋게 나왔다. 그 이유를 파악해보고자 관측 값을 찾아 보았다. 그 결과, RBF 신경회로망은 e2에 게인값이 곱해진 만큼을 추정하여 보상해 주고 있었다. 이것을 토대로, RBF 신경회로망은 외란 뿐 아니라, 모델링 오차값, 제어 오차값등을 함께 보상해주어 제어기 성능을 향상해 준다는 가정을 세웠다. 이것을 확인하기 위하여 외란을 추가하여 RBF 신경회로망을 사용하지 않은 백스테핑 제어기를 사용한 경우와 RBF 신경회로망적응 백스테핑 제어기를 사용한 경우를 나누어 제어기의 성능 비교와 관측값을 확인 하였다. 확인 한 결과, RBF 신경회로망 적응 백스테핑 제어기를 사용한 경우가 더 성능이 좋았다. 또한 관측값을 확인해본 결과 외란과 함께 e2을 더한값을 RBF 신경회로망이 추정하는 것을 볼 수 있었다. 이것을 통해 RBF 신경회로망은 외란 뿐 아닌, 모델링 오차, 제어 오차값을 같이 추정하여 보상해 주어 제어 성능을 향상시킨다는 것을 알 수 있다.
Acknowledgments
이 논문은 국방과학연구소 생존성 기술 특화연구센터의 사업으로 지원받아 연구되었다(계약번호 UD150013ID).
REFERENCES
- Elkoteshy, Y., Shuyuan, Y., and Hegazy, M., “RBF Based Adaptive Backstepping Neural Control of a Dual-Axis Motion Platform,” Proc. of the 32nd Control Conference (CCC), pp. 3083-3088, 2013.
-
Kanellakopoulos, I., Kokotovic, P. V., and Morse, A. S., “Systematic Design of Adaptive Controllers for Feedback Linearizable Systems,” IEEE Transactions on Automatic Control, Vol. 36, No. 11, pp. 1241-1253, 1991.
[https://doi.org/10.1109/9.100933]

- Hassan, K. K., “Nonlinear Control,” Pearson, Global Ed., 2015.
-
Chen, W.-H., “Disturbance Observer Based Control for Nonlinear Systems,” IEEE/ASME Transactions on Mechatronics, Vol. 9, No. 4, pp. 706-710, 2004.
[https://doi.org/10.1109/TMECH.2004.839034]

-
Oh, Y. and Chung, W. K., “Disturbance-Observer-Based Motion Control of Redundant Manipulators Using Inertially Decoupled Dynamics,” IEEE/ASME Transactions on Mechatronics, Vol. 4, No. 2, pp. 133-146, 1999.
[https://doi.org/10.1109/3516.769540]

-
Kim, E., “A Fuzzy Disturbance Observer and Its Application to Control,” IEEE Transactions on Fuzzy Systems, Vol. 10, No. 1, pp. 77-84, 2002.
[https://doi.org/10.1109/91.983280]

-
Kwan, C. and Lewis, F. L., “Robust Backstepping Control of Nonlinear Systems Using Neural Networks,” IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans, Vol. 30, No. 6, pp. 753-766, 2000.
[https://doi.org/10.1109/3468.895898]

-
Zhang, T., Ge, S. S., and Hang, C. C., “Adaptive Neural Network Control for Strict-Feedback Nonlinear Systems Using Backstepping Design,” Automatica, Vol. 36, No. 12, pp. 1835-1846, 2000.
[https://doi.org/10.1016/S0005-1098(00)00116-3]

-
Li, Y., Qiang, S., Zhuang, X., and Kaynak, O., “Robust and Adaptive Backstepping Control for Nonlinear Systems Using RBF Neural Networks,” IEEE Transactions on Neural Networks, Vol. 15, No. 3, pp. 693-701, 2004.
[https://doi.org/10.1109/TNN.2004.826215]

-
Choi, J. Y. and Farrell, J. A., “Adaptive Observer Backstepping Control Using Neural Networks,” IEEE Transactions on Neural Networks, Vol. 12, No. 5, pp. 1103-1112, 2001.
[https://doi.org/10.1109/72.950139]

-
Chen, W., “Adaptive Backstepping Dynamic Surface Control for Systems with Periodic Disturbances Using Neural Networks,” IET Control Theory and Applications, Vol. 3, No. 10, pp. 1383-1394, 2009.
[https://doi.org/10.1049/iet-cta.2008.0322]

-
Stepanyan, V. and Hovakimyan, N., “Robust Adaptive Observer Design for Uncertain Systems with Bounded Disturbances,” IEEE Transactions on Neural Networks, Vol. 18, No. 5, pp. 1392-1403, 2007.
[https://doi.org/10.1109/TNN.2007.895837]