지형 기울기에 의한 항공 수심 라이다 수심 측정 오차 보정

2.1 해저지형 모델링

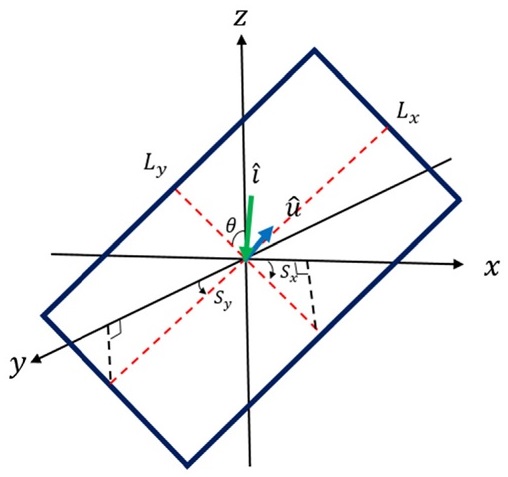
해저지형은 중심의 깊이 z를 중심으로 x, y 축 두 방향으로 기울어진 것으로 일반화할 수 있다. Fig. 1과 같이 빔의 진행방향에 평행한 방향과 수직한 방향 두 방향으로 기울기를 주고, y 축 방향을 평행방향, x 축 방향을 수직 방향으로 정하였을 때, 모델링된 해저지형은 두 방향의 기울기 S_x, S_y와 두 방향의 길이 L_x, L_y를 갖고 N_x, N_y개로 분할된다. 두 방향의 기울기에 따라 지형의 길이 L_x와 L_y가 변하는 데, 그 관계는 다음과 같다.

Fig. 1

Parameters of the seafloor tilted in two directions

여기서 L_x0, L_y0는 S_x, S_y가 모두 0일 때의 두 방향의 길이이다.

분할 개수 N_x와 N_y는 고정되어 있으므로 기울기가 커질수록 분할된 해저 지형 하나당 면적은 증가하게 된다. 이는 시뮬레이션의 해상도 문제를 일으킬 수 있는데, 두 방향의 기울기가 최대일 때, 밀도 및 넓이의 변화가 시뮬레이션 결과에 영향을 주지 않도록 N_x, N_y를 충분히 크게 설정하여 이를 방지하였다. 해저는 Lambertian reflection을² 하는 이상적인 산란체로 가정하였으며, 산란된 빔이 모두 지형에 도달할 수 있도록 충분히 크게 하였다. 해저 지형을 나타내기 위한 7개의 인자는 지형의 분할 개수, 분할된 지형 각각의 x, y, z 좌표, 넓이, 법선벡터, 반사율이다.

지형의 기울기는 좌표계를 기준으로 x, y 축으로 구분되었지만, 입사하는 빔과 지형 사이의 각도는 하나의 각도 θ로 표현될 수 있다. Fig. 1에서 볼 수 있듯이 θ는 π/2에서 입사빔 벡터와 지형의 법선벡터가 이루는 각도를 뺀 것이다. θ, 입사빔 벡터 $$ \widehat{i}$$, 지형의 법선벡터 $$ \widehat{u}$$의 관계는 다음과 같다.

본 논문에서는 모델링의 일반화와 간소화를 위해 θ를 기준으로 하여, θ의 변화에 따른 라이다 신호의 왜곡을 다룰 것이다.

2.2 Small Angle Scattering Approximation (SASA)

우리가 관심을 갖는 일정 정도 이상의 탁도를 가진 수중에서의 빔의 산란의 대부분은 빔의 진행방향과 작은 각도를 이룬다. 이 가정이 Small Angle Scattering Approximation (SASA)인데, 이는 실험적으로 증명되었고,⁸ 수중에서의 빔의 진행 및 수중 라이다 연구에서 폭넓게 받아들여지고 있다.^4,6,9-14 Table 1은 다른 두 종류의 물에서 관측된 흡수계수, 산란계수, 소산계수(Attenuation Coefficient) 등 광학적 특성을 실험으로 측정한 결과를 보여준다.⁸ b는 물의 산란계수이며, 값이 클수록 산란이 일어날 확률이 크다. ψ는 빔의 진행방향에서부터 산란되는 빔 중 50%가 산란되는 각도를 나타낸 것으로, 두 수중 환경에서 평균 약 4°로 SASA에 부합하는 것을 볼 수 있다.

Table 1

Inherent optical properties of the water8

SASA를 이용하면 시뮬레이션에서의 복잡한 문제를 단순화시킬 수 있다. Fig. 2에서 빔의 수면에서의 위치는 좌표계의 원점에 해당한다. 그 원점에서 출발한 뒤 산란되면서 진행하여 해저 지형에 도달하였을 때, 그 빔은 수많은 산란을 거쳐 도달하게 된다. 하지만 SASA의 가정 아래, 수면에부터 산란된 빔이 해저 지형의 특정 지점에 도달하는데 걸리는 시간은 빔의 수면에서의 위치와 도달한 해저 지점 사이의 직선 거리를 수중에서의 빔의 속도로 나눈 것으로 근사할 수 있다.

Fig. 2

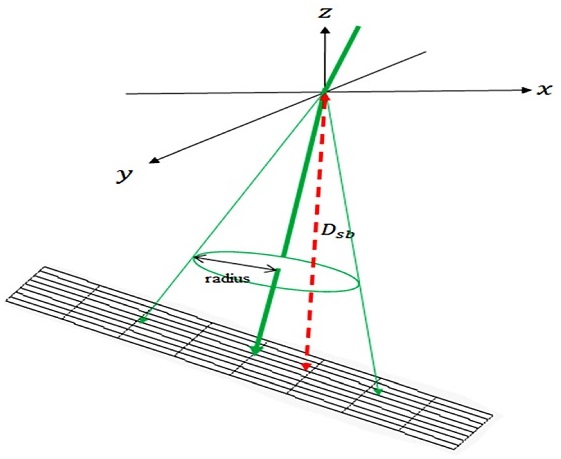
Diagram of beam propagation in water representing the radius of beam and the distance between the surface point and a bottom point (Dotted line)

여기서 t_s,b는 수표면부터 특정 해저지점까지 빔의 이동 시간, D_s,b는 수표면부터 특정 해저 지점 까지의 거리, c_w는 수중에서 빔의 속도이다. 또한 SASA는 빔의 수중에서의 진행에 따른 공간적 에너지 분포 계산에서 사용되는 중요한 가정이다. 이는 2.3절에서 다룰 것이다.

2.3 수중에서의 산란

공기 중에서와는 달리, 수면을 지나 수중을 진행하는 빔은 매질에 의해 퍼지면서 진행한다. 빔의 수중에서의 퍼짐에 영향을 주는 세 가지 요소는 바람에 의한 수면의 기울기, 수면에 입사하는 빔의 수면에서의 지름, 수중 입자에 의한 산란이다.² 우리가 관심 있는 부분은 해저 지형의 변화에 의한 신호의 왜곡이므로 수면의 기울기에 의한 영향과 수면에서의 지름의 영향은 없다고 가정하였다. 즉, 수중의 입자에 의한 산란만을 고려대상으로 하였고, 이로 인한 빔의 이동 경로의 방사상 분산은 McLean et al.의 연구¹²의 2차 공간모멘트를 사용하였으며 다음과 같다.

여기서 a는 물의 흡수계수, z_w는 빔의 진행거리, μ_τ와 $$ {\sigma }_{\tau }^2$$는 빔의 총 이동시간에서 산란에 의해서만 소요된 시간인 다중경로 시간의 평균과 분산이다. SASA를 적용하여 다중경로 시간을 0으로 근사하여 Lutomirski el al.의 결과를¹³ 인용하면 다중경로 시간의 평균과 분산은 다음과 같다.¹²

여기서 이다. 비대칭적 인자(Asymmetry Parameter)인 <cosθ>는 빔이 빔의 진행 방향과 얼마나 작은 각도를 이루며 산란하는지 보여주는 지표이며, 1에 가까울수록 빔의 진행방향과 작은 각도를 이루며 산란할 확률이 높다는 것을 의미한다. Mobley의 문헌에⁸ 따르면 일반적인 해양 조건에서 0.8 - 0.95의 값을 갖는다.

식(7)의 분산을 적용하여, 빔이 수중에서의 진행 거리와 Principal Ray와의 거리 ρ에 따른 에너지 분포는 다음과 같이 나타낼 수 있다.

여기서 Φ(z_w)는 수중에서 z_w만큼 이동한 뒤의 빔의 총 에너지이다. 위 식과 2.1 절에서의 해저 지형 정보를 적용하여 각각의 분할된 해저 지형에서 반사된 빔이 수신부에 도달하는 에너지, 시간 등을 계산하여 수신부에서의 Return Full-Waveform이 완성된다.

2.4 시스템 및 환경 변수

Tables 2와 3은 본 연구의 시뮬레이션에 사용된 라이다 시스템, 환경 변수 및 해저 지형 조건이다. 라이다 시스템의 변수는 상용 라이다인 Hawkeye의 시스템 변수를 사용하였다.¹⁴ 하지만 2.3절에서 언급한 이유로, 시스템 변수 중 DIV와 FOV는 시뮬레이션에서 고려되지 않았다. 환경변수는 Mobely와⁸ Michael Tulldah et al.의 연구에서² 인용하였으며, 일반적인 해양 환경을 기준으로 하였다.

Table 2

System parameters14

Table 3

Environmental parameters2,8

2.5 시뮬레이터 검증

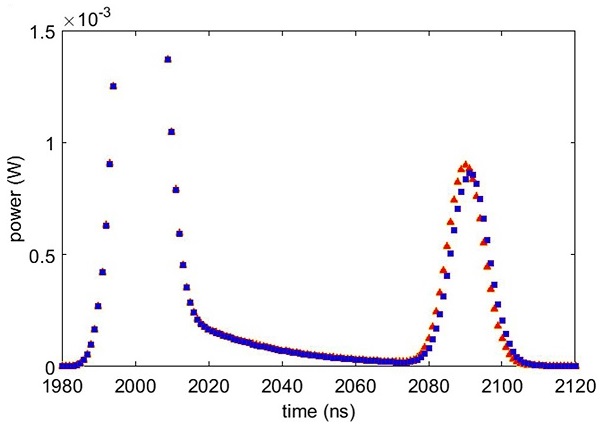
본 논문에서 사용한 시뮬레이터의 유효성을 검증하기 위해 같은 시스템, 환경 조건에서 10 m 깊이와 기울기가 없는 지형을 가정하였을 때, 선행 연구에서 사용한 시뮬레이터 Wa-LID와¹⁴ 본 연구에서 개발한 시뮬레이터의 수신파형을 비교하였다. 두 시뮬레이터는 모두 Matlab으로 구현하였으며 Wa-LID를 구현하기 위해 해당 논문의 식을 사용하였다.

Fig. 3에서 지형 깊이 10 m, 기울기 0°일 때의 본 연구의 시뮬레이터의 수신 파형과 Wa-LID의 수신파형을 비교하였다. 첫 번째 파형이 수면 파형, 두 번째 파형은 지형 파형이다. 지형 파형은 본 연구의 수신 파형의 크기가 더 작은데, 이는 본 연구의 시뮬레이터는 미리 설정된 한정된 너비의 지형 파형인데 반해, 선행 연구는 해당 깊이의 한 점을 가정한 수신파형이기 때문이다. 또한 본 연구의 지형 파형의 피크가 선행연구의 피크보다 늦는데, 이는 빔의 이동경로가 짧은 지형의 중심점의 한 점의 수신 에너지보다 이동경로가 더 긴 중심점 주변의 분할 지형들의 수신 에너지 합이 더 크기 때문이다. 위 두 가지 차이점의 원인은 모두 본 연구의 모델이 한정된 면적의 지형을 가정하였기 때문이다. 특정 조건에서 선행연구와 본 연구의 시뮬레이터의 수신파형의 차이와 그 원인을 검토함으로써 본 연구의 시뮬레이터의 유효성을 검증하였다.

Fig. 3

Comparison between return signals of our simulator (Square) and Wa-LID (Triangular)

3.1 과소추정 분석

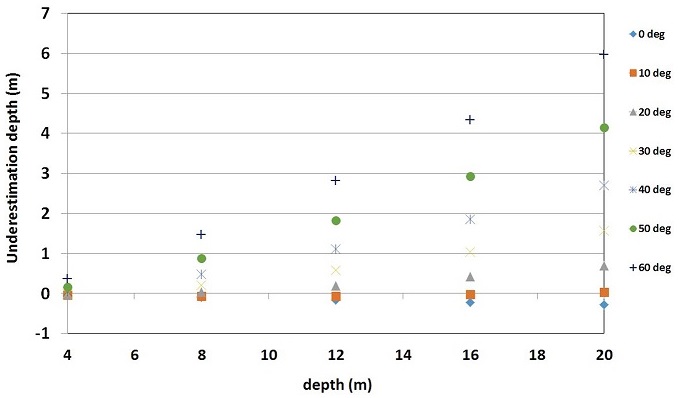
Fig. 4는 지형의 기울기 θ를 변화시킬 때, 각기 다른 평균 깊이 Z에서 해저 지형의 깊이의 과소추정을 보여주는 그래프이다. 가로축은 Z, 세로축은 과소추정 깊이 U이다. Z는 4 m부터 4 m 간격으로 20 m까지, θ는 0°부터 10°씩 60°까지 증가시키며 과소추정 깊이 값을 구하였다. 지형의 기울기가 클수록 과소추정이 커지는데, 이는 지형이 기울어지면서 수심이 얕아진 지형에 빔이 반사하여 짧은 거리를 이동해 수신부에 도달하기 때문이다. 또한 지형이 깊을수록 과소추정의 증가폭이 커지는데, 이는 빔이 수중에서 진행하는 시간이 길어질수록 산란에 의해 펄스폭이 증가하여 중심부터의 거리에 따른 에너지 감소 비율이 줄어들어 수평면에서 중심에서 더 먼 거리의 지점에서 반사된 이동거리가 짧은 빔이 피크에 기여하기 때문이다. 약 10° 이하의 기울기의 지형에서는 깊이에 관계없이 과소추정이0보다 작다. 이는 가장 짧은 이동거리를 지나는 하나의 중심 지점에서의 수신 신호의 세기보다 산란에 의해 조금 더 긴 이동거리를 지나는 하나의 중심 지점에서의 수신 신호의 세기보다 산란에 의해 조금 더 긴 이동거리를 지나지만 여러 개의 지점에서 반사되어 수신된 신호의 세기의 합이 더 크기 때문이다.

Fig. 4

Underestimation of the water depth with varying θ and Z

3.2 과소추정 방정식 유도

위 시뮬레이션 결과를 바탕으로 비선형 fitting을 통해 지형의 기울기 θ와 지형의 평균 깊이 Z를 변수로 하는 과소추정 방정식을 유도하였다. Z 값을 특정하였을 때, 과소추정 식 U(Z, θ)는 Z, θ에 대한 지수식이며 다음과 같이 나타낼 수 있다.

이 때 위 식의 계수 A(Z), B(Z), C(Z)는 Z에 대한 다항식으로 식(10)과 같다.

식(10)의 계수들은 Table 4에 정리하였다. 위에서 얻어진 과소 추정식에 라이다 측정에서 얻어진 데이터의 지형의 기울기 정보 θ와 깊이 정보 Z를 대입하여 얻어진 과소추정 값을 이용하여 본 데이터를 보정하면 더욱 정확한 해저 지도를 생성할 수 있다.

Table 4

Coefficients of underestimation Eq. (10)

위 식을 적용하여 라이다 데이터를 보정하는 과정은 4절에서 다룰 것이다.

3.3 선행 연구와의 비교

지형의 깊이와 기울기를 변화시킬 때, 본 연구의 시뮬레이터에서의 과소추정 결과와 Anis Bouhaoui et al.의 결과를⁷ 비교하였다. 선행 연구와 본 연구에서 사용한 시스템 변수는 동일하게 H. Abdallh et al.에서¹⁴ 인용하였다.

선행 연구의 과소추정 분석 결과로서 도출되는 지면의 평균 깊이 Z, 기울기 θ, 수면에서의 Footprint 지름 F_p를 변수로 하는 과소추정 방정식은 식(11)과 같이 지수형태로 표시되며, 계수 a, b는 식(12)와 같이 F_p, Z의 식으로 표현 가능하다. 이를 식(11)에 대입하면 식(13)과 같이 식을 구할 수 있고, 비선형 곡선맞춤을 통해 구한 식(13)의 계수는 Table 5와 같다.

Table 5

Coefficients of underestimation Eq. (13)

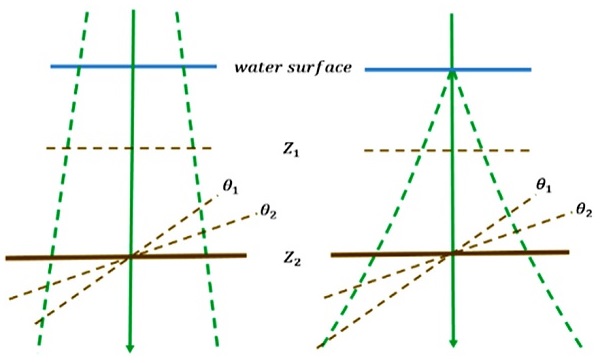
Fig. 5는 기존연구와 본 연구의 과소추정 결과의 비교를 보여준다. 선행 연구의 F_p= 10m일 때 평균 깊이를 Z = 8과 20 m로 변화시킨 결과는 지형 기울기에 따른 측정 깊이의 오차가 무시할 만큼 적게 계산된다. 그러나 본 연구의 결과는 깊이 측정오차는 지형의 깊이와 기울기 변화의 변수에 모두 민감하게 변한다는 것을 알 수 있다. 또한 3.1절에서 언급했듯이, 빔이 산란에 의해 깊이가 증가할수록 펄스폭이 증가한다면 기울기가 작은 지형에서의 과소추정 값은 0 m보다 작아야 하지만 선행연구의 결과에서 기울기가 없을 때의 과소추정 값은 모두 0 m이다. 본 경향성으로부터 Fig. 6과 같은 모델링의 차이를 유추할 수 있다. Fig. 6은 두 모델에 대해서 깊이는 Z₁, Z₂로, 기울기는 θ₁, θ₂로 변화시킬 때의 모식도이다. 같은 깊이에서 기울기를 변화시킬 때와 같은 기울기에서 깊이를 변화시킬 때, 가장 먼저 지형에 도달하는 빔과 가장 나중에 도달하는 빔의 거리차는 본 연구의 모델의 경우에서 상대적으로 큰 것을 확인할 수 있다. Fig. 6의 왼쪽과 같은 기존의 모델은 물의 산란계수를 매우 작게 설정하거나 물에서의 산란을 모델링에 포함시키지 않을 때이다. 또한 선행 연구 조건이라면 시스템의 고도가 500 km로, F_p를 10 m로 가정하면 레이저의 발산각은 약 0.05 mrad로 본 연구의 가정인 7 mrad의 1/140이다. 이 때 수면에 닿는 빔의 모든 영역 안에서 빔은 수면과 수직을 이룬다고 가정할 수 있으므로, 빔의 수중에서의 진행 중, 퍼짐을 작게 하는 요인이 된다. 이는 기존 연구에서 F_p의 값이 클수록, 즉, 발산각이 클수록 과소추정 값이 증가한다는 사실로 뒷받침 된다. 기존 연구에서 사용한 시뮬레이터 Wa-LID를 다룬 문헌에서는¹⁴ 빔의 물속에서의 산란에 대한 고려를 자세히 언급하지 않았기 때문에 본연구에서 사용한 시뮬레이터에서 SASA의 가정 하에 산란에 따른 빔의 해저 지형 도달 시간 차이를 계산한 만큼의 산란에 대한 고려가 선행되었는지는 확인할 수 없었다. 하지만 수중에서의 빔의 산란은 수중에서의 빔의 진행 경로 변화와 그에 따른 수신 파형 변화에 중요한 역할을 하므로 반드시 신중히 고려되어야 한다.

Fig. 5

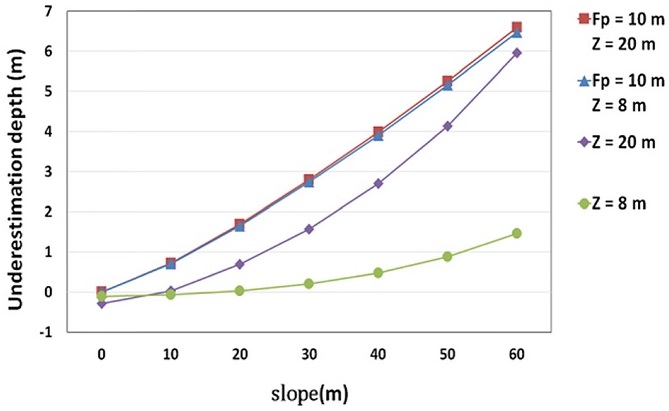
Comparison between the underestimation of the water depth of existing research and this paper, with varying parameters

Fig. 6

Diagram of model of existing research (Left) and this paper’s model (Right)

4.1 가상의 해저 지형 설정

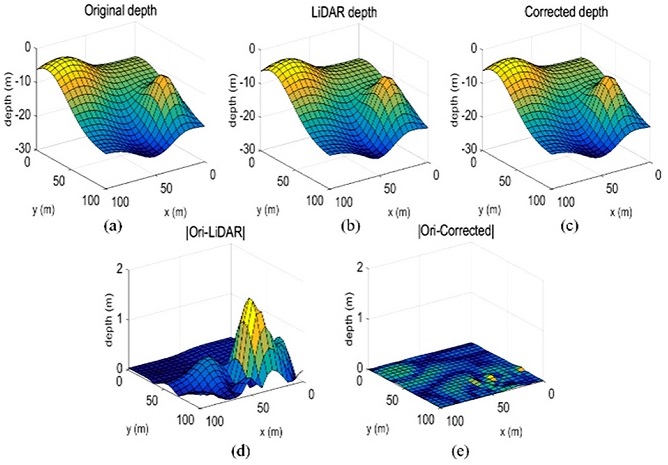
Fig. 7(a)와 같이 가상의 3차원 해저지형을 설정하였다. Fig. 7(b)는 시뮬레이션을 통해 얻은 라이다 지형 지도, Fig. 7(c)는 4.2절의 보정 알고리즘을 이용하여 보정한 지형 지도이며, Fig. 7(d)는 각 지점에서 실제 지형과 보정 전 라이다 지형의 수심 오차 절대값, Fig. 7(e)는 보정 후 라이다 지형의 수심 오차 절대값을 나타내는 지도이다. 지형의 크기는 100 × 100 m이며, 측정점의 개수는 21 × 21개, 각 측정점 간 간격은 5 m이다. 지형의 최소 깊이와 최대 깊이는 각각 2.64 m, 24.46 m이며, 입사빔과 지형이 이루는 각도의 최소와 최대는 각각 0.07°, 38.61°이다.

Fig. 7

Correction Results: (a) Original map, (b) LiDAR map, (c) Corrected map, (d) Error between original and LiDAR map, (e) Error between original and corrected map

4.2 수심 보정 과정

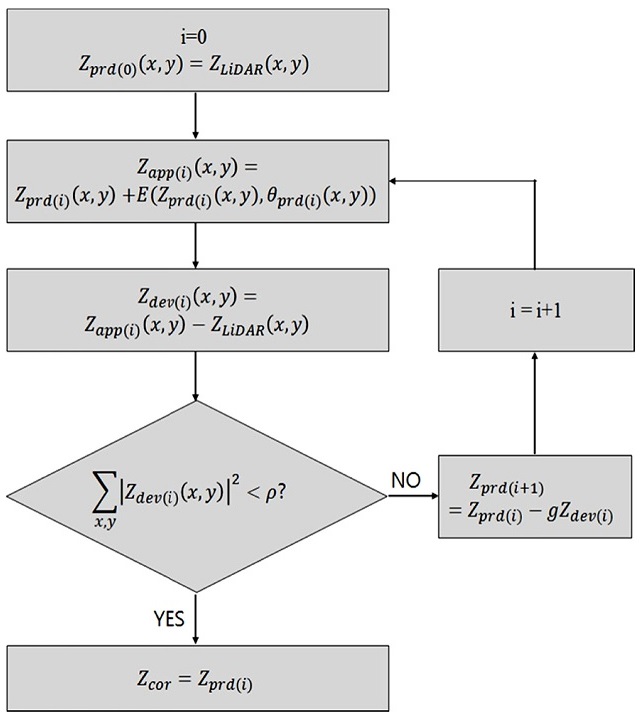
설정된 지형 지도의 각 측정점의 기울기와 깊이 정보를 시뮬레이터에 입력하여 출력되는 수신파형의 수면 신호 피크와 해저 신호 피크 사이의 시간을 수중에서의 빔의 속도로 나누어 각 측정점의 깊이를 계산한다. 각 측정점에 입사하는 빔은 수면과 수직을 이루는 것으로 가정하였으며, 각 측정점의 지형은 기울기 변화가 작고 완만한 2.2절의 지형모델과 같이 특정한 기울기와 깊이를 가진 충분히 크고 평평한 지형으로 근사하였다. 위의 과정을 거쳐 시뮬레이션을 통해 얻어진 지형 지도는 실제 실험에서는 라이다를 통해 얻은 지형 지도로 간주할 수 있다. 라이다에서 얻은 지형 지도에 과소추정식을 적용해 실제 지형 정보를 역추적하여 실제 지형과 최소한의 오차를 갖는 지형 지도를 만들 수 있다. 보정 순서도는 Fig. 8과 같다. 한 지점의 실제 지형 수심 예상 값이 Z_prd(x, y)라고 할 때, 그 지점에서의 깊이 Z_prd(x, y), 기울기 θ_prd(x, y)를 과소추정식에 대입하여 오차 E(Z_prd(x, y), θ_prd(x, y))를 얻는다. 과소추정 값 U(Z_prd(x, y), θ_prd(x, y))와의 관계는 다음과 같다.

Fig. 8

Flow chart of correction process

만약 Z_prd(x, y)이 실제 지형 지도의 깊이라면 Z_prd(x, y)에 E(Z_prd(x, y), θ_prd(x, y))를 더한 값 Z_app(x, y)은 라이다 측정 값 Z_LiDAR(x, y)와 같아야 한다. 하지만 아직 보정되지 않은 상태에서 두 값 사이의 차이가 있으며, 이 차이는 Z_dev(x, y)이다.

모든 x, y 지점에서의 Z_dev(x, y)의 제곱의 합이 일 정 상수 ρ이하라는 보정 완료 조건을 만족하면 Z_prd(x, y)는 실제 지형 수심으로 충분히 보정되었다고 판단되어 보정 과정은 끝난다. 위의 조건을 만족시키지 못하면 Z_prd는 -gZ_app 만큼 보정되며, 조건을 만족할 때까지 위 과정을 반복한다. 여기서 g는 0에서 1 사이의 실수이다.

4.3 수심 보정 결과

Table 6는 실제 지형인 Fig. 7(a)와 라이다 지형 지도 Fig. 7(b)간, 그리고 실제 지형과 보정 후 지형 지도 Fig. 7(c)간의 각 지형 지점에서의 오차의 절대값의 평균, 최대, 최소, 표준편차를 나타낸다. Table 6에서 확인할 수 있듯이, 보정 후 전체적으로 오차가 줄어든 것을 확인할 수 있으며 지형 지도와의 깊이 평균오차는 약 0.21 m에서 0.013 m, 최대오차는 1.67 m에서 0.06 m로 각각 90% 이상 감소하였다.

Table 6

Error values before and after correction