티타늄 합금의 나노유체 극미량 윤활 밀링 공정 열특성에 관한 수치 해석 연구

1. 서론

밀링 가공에 발생하는 에너지는 대부분 열로 변환되며 이러한 절삭열은 공구의 마멸을 증가시키고 온도상승에 의한 가공품 표면 열손상으로 인해 표면 품질에 악영향을 미친다. 특히 난삭재로 분류되는 티타늄 합금의 경우 매우 낮은 열전도도로 인해 가공 시 발생되는 열이 원활하게 배출되지 않는 문제가 있다. 따라서 티타늄 합금의 밀링 가공 중 가공물의 열적 거동에 대한 분석이 필수적이다.

밀링 가공에서의 절삭 메커니즘은 매우 복잡하여 열원의 크기 및 분포 예측이 어려운데, 이는 가공에 사용된 공구 및 가공물의 특성이 온도에 따라 변하기 때문이다. 20세기초부터 이러한 현상을 이해하기 위해 이론적 해석과 실험적 분석이 진행되고 있으며 그 중에서 절삭온도의 측정을 통한 절삭열 규명과 분석이 수행되고 있다.¹

이러한 절삭열을 제거하기 위해 절삭유를 사용하는데 절삭유는 냉각제(Coolant)나 윤활제(Lubricant) 역할을 한다. 절삭유를 사용함에 있어서 환경오염 및 인체유해성을 포함한 문제를 해결하기 위한 추세로 산업 현장에서는 친환경 생산기술(Green Manufacturing)개발이 중요한 문제로 대두되고 있다.² 또한, 절삭유 처리 비용과 설비 유지 비용이 증가함에 따라 관리 비용은 총 생산 비용의 7 - 17%로 공구비용의 네 배 이상이라는 통계도 발표되었다.^3,4

이러한 상황에서 최근 절삭유 사용을 최소화하는 절삭유 가공기술 중의 하나인 극미량 절삭유(Minimum Quantity Lubrication, MQL) 기술의 적용이 대두되고 있으며 냉각 및 윤활 특성을 향상시키기 위해 나노입자를 추가한 나노유체 MQL 기술도 산업현장에서의 적용성이 적극적으로 검토되고 있는 상황이다.

따라서, MQL 및 나노유체 MQL 기술이 적용되었을 때 가공물에 발생하는 절삭열 감소의 효과성을 분석하는 연구가 필요하며 이를 위해 실험적 방법과 수치해석적 방법이 필요하다. 특히, 수치해석적 관점에서는 밀링 가공 환경 유한요소해석 모델을 개발하고 전산유체역학(Computational Fluid Dynamics, CFD) 기법을 적용하고 가공물의 온도를 계산하여 절삭유 분사 시의 가공물 냉각효과를 예측하는 연구가 진행되었으나 MQL 및 나노유체 MQL 기술이 적용된 밀링 가공에서의 열특성 수치해석 연구는 구체적으로 수행되지 않았다.^5,6

따라서 본 논문에서는 MQL 및 나노유체 MQL을 적용한 티타늄 합금 밀링 공정에서의 가공물의 열특성 분석을 위해 가공물에 설치된 열전대를 통해 각 윤활조건에서의 온도를 측정하고 또한 밀링 가공 환경을 모사하기 위해 개발된 CFD 기반 수치해석 모델로부터 가공물 온도를 계산하여 이를 측정값과 비교하여 수치해석 모델의 타당성을 검증하였다. 본 연구에서 고려된 윤활조건은 Pure MQL, Hexagonal Boron Nitride (hBN) 나노유체 MQL, Nanodiamond (ND) 나노유체 MQL이며 실험의 경우 가공물에 설치된 3개의 열전대를 통해 가공물 온도를 측정하였으며 수치해석 모델은 실제 실험 환경과 유사하게 구현하기 위해 공구 회전, 가공물의 이동, 나노유체 극미량 분사, 가공물의 절삭 운동이 구현되었고 각 조건에서의 밀도, 점도 및 열전도도를 입력하여 수치해석을 수행하였다.

2. 나노유체 MQL 밀링 가공 실험

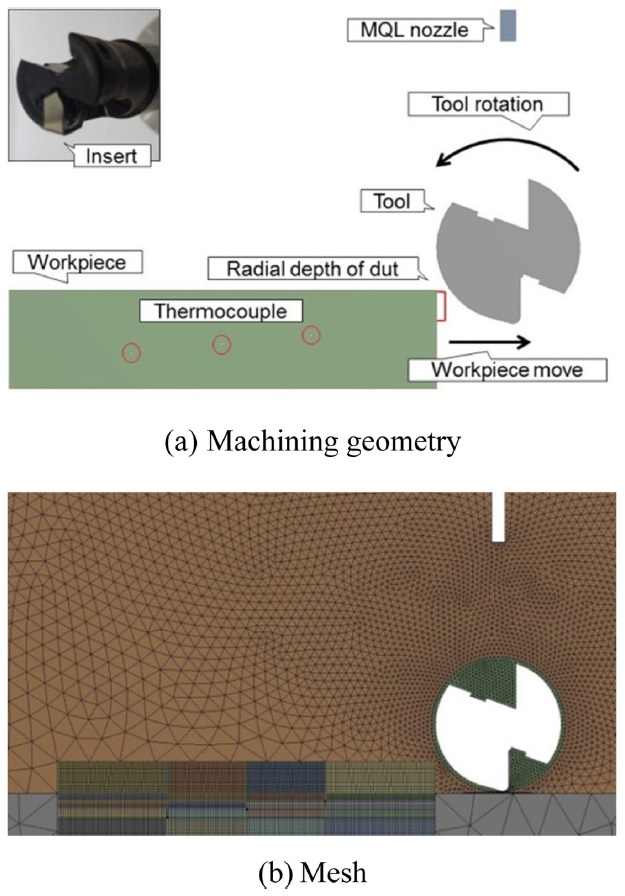
나노유체 종류에 따른 밀링 가공 시 가공물의 온도를 측정하기 위해 Fig. 1과 같이 실험 시스템을 구현하였다. 구현된 실험 장치는 CNC 머시닝 센터(NVD 4000 DCG, DMG MORI SEIKI), 공구(R390-016A16L-11L, SANDVIK), 인서트(R390-11 T3 08M-KMH13A, SANDVIK), 가공물(Ti-6Al-4V Grade 5), 분사 시스템(UNIMAX 202F, UNIST), 열전대(5SC-TT-K-30-36, OMEGA) 및 데이터 수집장치(NI9211, NI)로 구성되어 있다.

Fig. 1

Experimental setup

밀링 가공 시 발생하는 티타늄 합금 가공물의 온도는 절삭 표면 아래에 설치된 3개의 열전대를 통해 측정되었다. 열전대는 표면으로부터 깊이 5, 6, 7 mm 위치에 설치하였고, 각 열전대 사이의 간격은 10 mm이다. 밀링 가공 실험 조건을 Table 1과 같이 구성하였다. 실험 설계는 사이드 밀링 공정으로 나노유체 종류만을 다르게 하여 총 3가지 조건으로 실험을 수행 하였다.

Table 1

Experimental conditions

열전대를 통해 측정된 온도를 이용하여 가공물표면의 평균 표면 온도를 계산하였고, 이는 추후 수치해석의 입력값으로 사용되었다.

3. 나노유체 MQL 밀링 가공 수치해석

3.1 해석 모델 구성

본 연구를 수행하기 위해 상용 프로그램인 ANSYS FLUENT를 통해 Fig. 2(a)와 같이 실제 실험 환경을 고려한 2차원 수치해석 모델을 구성하였다. 공구의 형상은 나노유체 분사 시 유체의 흐름에 상당한 영향을 미치므로 실제 공구의 치수를 기반으로 모델링 하였고, 노즐 형상은 유체가 분사되는 홀(Hole)의 형상이 영향을 미치므로 외부 구조는 생략하고 홀 부분의 모델링만을 수행하였다. 가공물은 실제 사이즈인 48×48 mm로 모델링 하였고 가공물의 표면으로부터 5, 6, 7 mm 거리만큼 떨어진 위치에 실제 직경인 0.25 mm인 열전대 3개를 모델링 하였다.

Fig. 2

Machining geometry and mesh in the numerical model

해석 수행 시 실제 실험과 동일하게 공구는 2,387 RPM 속도의 회전을 고려하였고, 가공물은 공구 방향으로 날당이송량 0.1 mm/tooth의 이동을 고려하였다. 이 때 실제 반경방향 절삭 깊이만큼 절삭되는 운동을 고려하였다. 격자 형상은 Fig. 2(b)에 주어져 있으며 유체가 이동하는 곳에는 삼각형, 가공물은 사각형으로 구현하였고, 노드 수는 64,180 개, 격자 수는 85,086 개이다.

3.2 수치해석 방법

밀링 가공 시 나노유체 분사에 따른 가공물의 열 특성을 수치해석으로 분석하기 위해 에너지 방정식을 활성화 하였으며 지배 방정식은 식(1)과 같다.⁷

$\[ \rho C_p\left(u\cdot \mathrm{\nabla }\right)T=k{\mathrm{\nabla }}^{2}T \]$

(1)

난류 모델로는 Standard k−ε의 변종으로 회전에 대한 유동을 잘 예측할 수 있는 Realizable k−ε 모델을 적용하였다. 노즐 출구에서 분사되는 MQL 종류에 따른 Inlet 조건은 압력 0.5 MPa과 유량 3 ml/min으로 적용하였고, 사각형으로 이루어진 전체 유동영역의 바깥 면은 Pressure Outlet으로 설정하였다. 가공물에 발생하는 열이 나노유체 MQL에 의해 감소하면서 온도가 낮아지게 되고, 공구는 열전달이 없는 단순 벽(Wall)으로 작용한다.

해석 Solver는 Simple을 선택하였고, 압력에 대한 Discretization Scheme은 Standard로 적용하였다. Turbulent Kinetic Energy, Turbulent Dissipation Rate은 First Order Upwind으로 설정하였다. 공구의 회전 구현 방법으로는 과도해석(Transient Analysis)에 적용되는 해석 도메인이 좌표계와 함께 움직이는 MRF (Moving Reference Frames)기법을 사용하여 실제 공구 회전 속도인 2,387 RPM을 구현하였다.^7,8 즉, 공구가 회전하면서 가공물을 절삭하는 운동을 구현하기 위한 목적으로 MRF 기법이 사용되었는데 이는 공구가 가공물을 절삭하면서 열전대가 표면으로부터 드러나는 깊이가 달라지게 되고, 노즐에서 분사되는 유체에 의한 냉각 효과나 공구가 가공물에 접촉되는 거리가 달라지게 되므로 열전대에 전달되는 열의 영향을 고려하기 위함이다.

노즐에서 분사되는 유체는 Pure MQL의 경우 공기와 순정오일, 나노유체 MQL의 경우 공기와 각각 0.5 wt.%의 농도를 갖는 hBN 나노유체 및 ND 나노유체이다. 이 때 Pure MQL은 나오미테크사의 순정오일을 사용하였고 hBN 및 ND 나노입자는 각각 XG-Science, 링크코리아 사 제품이다.

수치해석의 사용되는 공기의 물성치는 FLUENT에서 제공하는 Data Sheet을 사용하였다. 순정오일의 밀도는 나오미테크사의 Data Sheet를 사용하였고, hBN 나노유체와 ND 나노유체는 0.5 wt.%의 농도를 고려하여 나노입자 중량비와 순정오일 밀도를 고려하여 계산하였다.

나노유체의 점도와 열전도도는 각각 Core-Tech 사의 Viscometer (SV-10), Julabo 사의 Refrigerated/Heating Circulator (FP-50)장치를 사용하여 측정된 값을 사용하였다. 해석에 사용된 공기, 순정오일, 각 나노유체 및 가공물 Ti-6Al-4V (Grade 5) 물성치는 Table 2에 주어져 있으며 순정오일 및 각 나노유체의 열전도도는 Table 3에 주어져 있다.

Table 2

Density and viscosity

Table 3

Thermal conductivity

절삭 시 발생하는 온도를 입력조건으로 사용하기 위해 실험 중 3개의 열전대로부터 측정된 온도를 기반으로 열전달 Fourier 법칙을 적용하여 평균 표면 온도를 계산하였다. 이 온도가 공구가 가공물을 절삭하는 동안의 개발된 해석 모델에의 각 윤활 조건을 고려한 입력 온도이다. 또한 입력 온도의 구체적인 적용을 위해 본 실험 조건에서 공구가 가공물에 접촉하는 길이를 계산하였으며 이 때의 접촉 길이에 입력 온도값이 작용함을 고려하면 공구가 가공물을 절삭하는 동안 가공물 아래 방향으로의 열전달량을 계산할 수 있게 된다.⁹ 즉, 이를 통해 공구와 가공물 간 접촉부에서의 마찰열 효과와 윤활 조건으로 인한 공기 중으로의 열전달 효과를 모두 고려하게 된다. 이 때 해석 모델을 통해 계산된 열전달량은 노즐로부터 공급되는 공기 및 순정오일, 나노유체 등의 분사를 고려한 결과이며 Table 4에 각 경우의 계산된 평균 표면온도값이 주어져 있다.

Table 4

Calculated surface temperatures

밀링 가공 시 열전대가 온도를 측정하는 시간 간격은 0.05초이므로 실험 환경과 동일한 조건을 위해 수치해석에서도 동일한 0.05 Time Step Size를 설정하였다. 실험에서 총 밀링 가공 시간이 15초였으므로 수치해석에서 동일한 시간을 고려하기 위해 300 Time Step Size의 해석을 수행하였다. 구체적인 수치해석 조건은 Table 5에 요약되어 있다.

Table 5

Numerical analysis conditions

3.3 수치해석 결과

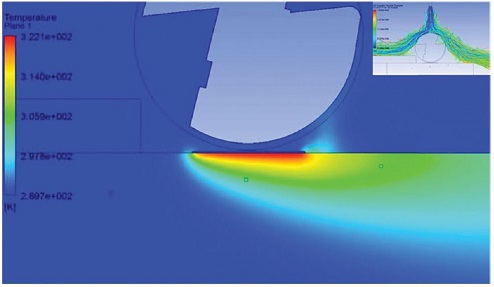
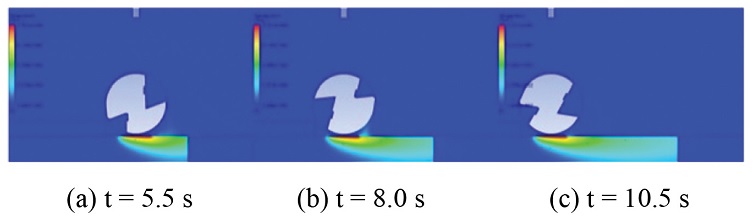
3.2 절에서 기술한 수치해석 방법을 기반으로 해석을 수행한 온도 분포의 가시화 결과가 Fig. 3에 주어져 있다. 또한, 공구가 이동하면서 가공물에 설치되어 있는 3 개의 열전대에서 각 열전대에 가장 근접했을 때의 순간 운동은 Fig. 4에 나타내었다. 공구가 첫 번째 열전대에 근접하게 위치했을 때 시간은 5.5 s이고, 두번째 열전대는 8 s, 세 번째 열전대는 10.5 s이다. 각 열전대 사이 이동 시간 간격은 2.5 s이며, 노즐에서 분사되는 유체는 외부 온도와 동일하기 때문에 온도 변화는 확인할 수 없었다.

Fig. 3

Estimated temperature distribution around the milling region from the numerical model

Fig. 4

Estimated temperature distributions as the milling process proceeds

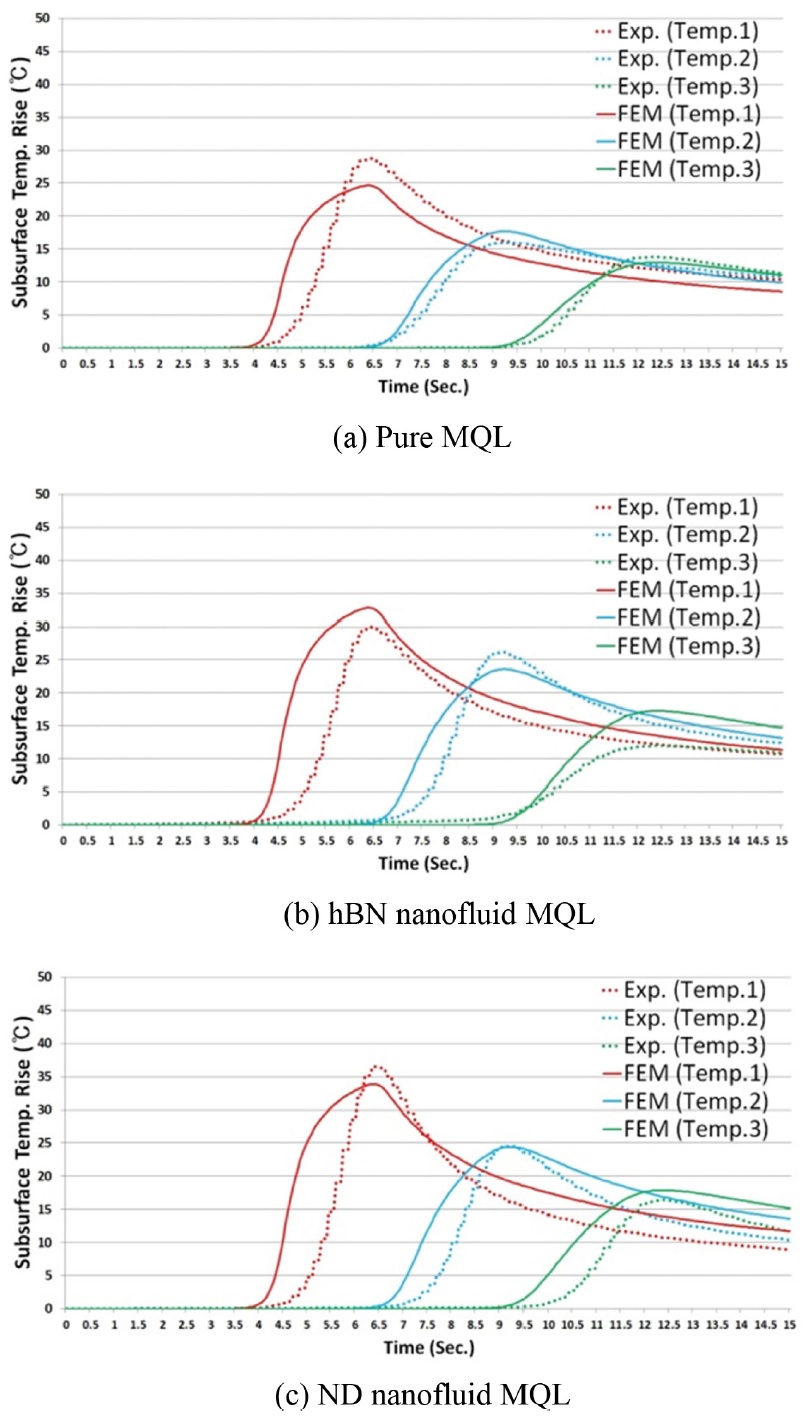
수치해석 모델로부터 계산된 가공물의 설치된 열전대 위치에서의 표면 아래 온도(Subsurface Temperature)의 증가량 결과가 Fig. 5에 주어져 있다. 즉, 나노유체 종류에 따른 시간영역에서의 가공물의 온도 증가 그래프가 주어져 있는데 실험과 수치해석으로 얻은 온도 그래프 형상이 유사한 것을 알 수 있다.

Fig. 5

Sub-Surface temperature rises in the cases of pure MQL, hBN nanofluid MQL and ND nanofluid MQL

실험과 수치해석 그래프를 보면 첫 번째 열전대에서 온도가 증가하기 시작하는 시간은 3.5 s 이후이고, 두 번째 열전대는 6 s, 세번째 열전대는 8.5 s로 열전대 사이 온도 증가 시간 간격은 2.5 s로 동일하다. 이 시간 간격은 공구가 다음 열전대로 이동하는 데에 걸리는 시간과 동일하다. 또한, 최대온도에 도달하는 시간의 경우, 첫 번째 열전대에서의 시간은 6.4 s, 두 번째 열전대는 9.2 s, 세 번째 열전대는 12.4 s이다. 최대 온도가 측정되는 열전대 간의 시간 간격은 온도가 측정되는 시간과 달리 일정하지 않다. 첫 번째 열전대와 두 번째 열전대 사이 시간 간격은 2.8 s, 두 번째 열전대와 세 번째 열전대 사이 시간 간격은 3.2 s이다. 여기서 공구가 첫 번째 열전대에 가장 근접했을 때의 시간은 5.5 s인 것과 달리 최대 온도가 측정된 시간은 6.4 s이다.

이는 공구가 열전대에 가장 근접한 위치에 접근하였지만 열이 열전대로 전달되는데 약간의 시간이 소요되기 때문이다. 공구가 첫 번째 열전대에 가장 근접했을 때의 시간과 최대 온도가 측정된 시간차는 0.9 s이며, 두 번째 열전대의 시간차는 1.2 s, 세 번째 열전대의 시간차는 1.9 s이다. 다음 열전대로 갈수록 시간차가 벌어지는 것은 1 mm 간격으로 열전대가 더 깊게 박혀있기 때문으로 분석된다. 또한 Fig. 6에는 Pure MQL, hBN Nanofluid MQL, ND Nanofluid MQL의 각 경우에 있어서 표면 아래 온도 증가량의 최대값이 주어져 있으며 실험 및 수치해석으로부터 얻은 결과가 유사함을 알 수 있다.

Fig. 6

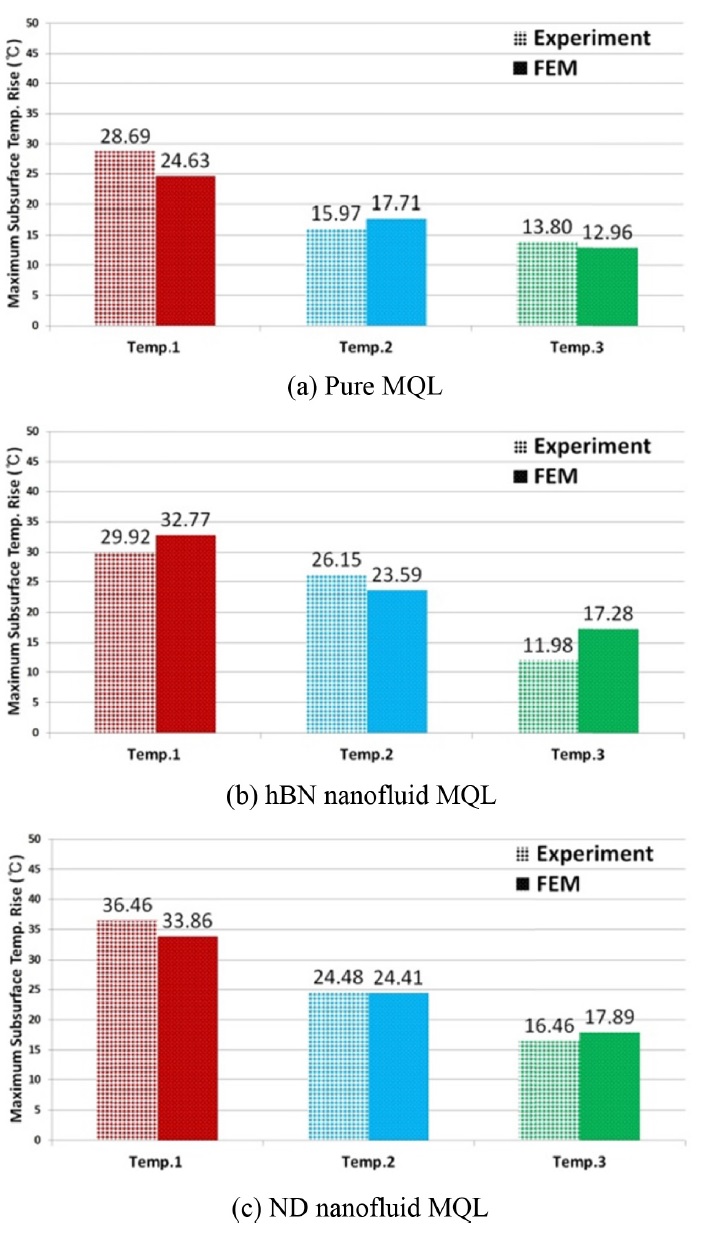
Measured and calculated maximum subsurface temperature rises in the cases of pure MQL, hBN nanofluid MQL and ND nanofluid MQL

Figs. 5와 6으로부터 개발된 밀링 가공 시 티타늄 합금 가공물의 열특성 해석 모델이 실제 실험값과 유사한 결과를 도출함을 알 수 있으므로 해석 모델의 타당성이 검증되었다고 할 수 있다.

추가적으로 Tables 2와 3에 주어진 열물성치가 각 윤활 조건별로 유사하나 Table 4에 주어진 것처럼 열전대로 측정한 표면 아래 온도값으로부터 예측된 가공물 표면온도가 각 조건별로 상이하므로 이를 입력값으로 사용하는 수치해석 모델의 계산결과가 다르게 나타남으로 분석할 수 있다.

4. 결론

본 연구에서는 순정오일과 hBN 및 ND 나노유체를 사용한 극미량 윤활 환경에서 티타늄 합금의 밀링 가공 시 발생하는 가공물의 온도값을 계산하는 열특성 분석 수치해석 모델을 개발하였고 실험으로부터 측정된 온도값과의 비교를 통해 개발된 해석 모델의 타당성을 검증하였다.

수치해석 모델 개발에 있어서 상용 프로그램인 ANSYS FLUENT를 이용하여 공구, 노즐 및 가공물을 고려한 2차원 모델을 구성하였고 MRF 기법을 도입하여 공구회전 및 공구와 가공물 간 상대 운동을 구현하였다. 해석 수행에 있어서 가공물 표면으로부터 서로 다른 깊이에 설치된 3개의 열전대로부터 측정한 온도값을 이용하여 Fourier 방법을 통해 표면온도를 추정한 후 이 온도값을 해석 모델에 입력하여 가공물 내 열전대 위치에서의 온도값을 계산하였다. Pure MQL 및 나노유체 MQL 조건의 각 경우에 있어서 해석으로부터 도출한 가공물 온도곡선과 각 열전대 위치에서의 최대 온도 증가량을 실험값과 비교하였을 때 유사함을 확인하였고 이를 통해 개발된 수치해석 모델의 타당성을 검증하였다.

Acknowledgments

본 연구는 한국산업기술평가관리원의 산업핵심기술개발사업의 일환으로 수행하였음(No. 10048871).

REFERENCES

• Kitagawa, T., Kubo, A., and Maekawa, K., “Temperature and Wear of Cutting Tools in High Speed Machining Inconel 718 and Ti-6Al-6V-2Sn,” Wear, Vol. 202, No. 2, pp. 142-148, 1997. [https://doi.org/10.1016/S0043-1648(96)07255-9]
• Kang, J. H., Lee, C. H., Song, J. Y., and Lee, J. K., “Environmentally Conscious Machining Technology Considered Economic View,” Proc. of KSPE Autumn Conference, pp. 972-975, 2000.
• NIOSH, “Criteria for a Recommended Standard Occupational Exposure to Metalworking Fluids,” U. S. Department of Health and Human Services, CDC, 1998.
• Chang, Y. S. and Kim, Y. S., “Optimization of Milling Process Considering the Environmental Impact of Cutting Fluids,” J. Korean Soc. Precis. Eng., Vol. 15, No. 12, pp. 14-20, 1998.
• Lazoglu, I. and Bugdayci, B., “Thermal Modeling of End Milling,” CIRP Annals-Manufacturing Technology, Vol. 63, No. 1, pp.113-116, 2014. [https://doi.org/10.1016/j.cirp.2014.03.072]
• Duchosal, A., Werda, S., Serra, R., Leroy, R., and Hamdi, H., “Numerical Modeling and Experimental Measurement of MQL Impingement Over an Insert in a Milling Tool with Inner Channels,” International Journal of Machine Tools and Manufacture, Vol. 94, pp. 37-47, 2015. [https://doi.org/10.1016/j.ijmachtools.2015.04.003]
• ANSYS, Inc., “ANSYS Fluent Tutorial Guide,” 2013.
• ANSYS, Inc., “ANSYS Fluent User’s Guide,” 2013.
• Zhang, S., Li, F. J., and Jiang, F., “Tool Wear and Cutting Forces Variation in High-Speed End-Milling Ti-6Al-4V Alloy,” The International Journal of Advanced Manufacturing Technology, Vol. 46, Nos. 1-4, pp. 69-78, 2010. [https://doi.org/10.1007/s00170-009-2077-9]