방향 판별 분산간섭계의 최적 분산 조건 연구
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Spectrally resolved interferometry (SRI) is an attractive technique to measure absolute distances without any moving components. In the spectral interferogram obtained by a spectrometer, the optical path difference (OPD) can simply be extracted from the linear slope of the spectral phase. However, SRI has a fundamental measuring range limitation due to maximum and minimum measurable distances. In addition, SRI cannot distinguish the OPD direction because the spectral interferogram is in the form of a natural sinusoidal function. In this investigation, we describe a direction determining SRI and propose the optimal conditions for determining OPD direction. Spectral phase nonlinearity, caused by a dispersive material, effects OPD direction but deteriorates spectral interferogram visibility. In the experiment, various phase nonlinearities were measured by adjusting the dispersive material (BK7) thickness. We observed the interferogram visibility and the possibility of direction determination. Based on the experimental results, the optimal dispersion conditions are provided to distinguish OPD directions of SRI.
Keywords:
Spectrally-resolved interferometry, Nonlinear phase, Dispersion, Direction ambiguity, Dispersive material, Visibility키워드:
분산간섭계, 비선형 위상, 분산, 방향 모호성, 분산 물질, 가시도1. 서론
분산간섭계(Spectrally-Resolved Interferometry, SRI)는 변위측정 간섭계(Displacement Measuring Interferometry)와는 달리 고정된 길이를 바로 측정할 수 있는 거리측정 간섭계(Distance Measuring Interferometry)인 동시에, 실시간 고속으로 거리 및 형상 측정이 가능하여 산업계에서 널리 사용되고 있다.1 분산간섭계는 일반적으로 넓은 주파수 대역의 광원을 이용하여 기준광(Reference Beam)과 측정광(Measurement Beam) 사이의 광학적 거리 차이(Optical Path Difference, OPD)를 측정하며, 분광기(Spectrometer)를 통해 광주파수 별 간섭 신호(Spectral Interferogram)를 획득하기 때문에 백색광 주사 간섭계(White Light Scanning Interferometry)와 달리 구동부 없이 거리 측정이 가능한 장점이 있다.2 하지만 분산간섭계는 측정 영역에 있어 최대 측정 거리(Lmax)와 최소 측정 거리(Lmin)가 존재하고, 이로 인해 측정 영역에 한계가 있다.
분산간섭계를 통해 측정할 수 있는 Lmax는 간섭 신호를 획득하는 분광기의 주파수 분해능에 의해 다음과 같이 결정된다.3
| (1) |
여기서 c0는 진공에서의 빛의 속도, Ν는 매질의 군굴절률(Group Index of Refraction)을 나타내며, δv는 분광기의 주파수 분해능을 의미한다. 식(1)을 살펴보면, 분광기의 분해능이 작을수록 Lmax가 증가하지만, 현실적으로 분광기의 분해능은 유한한 한계를 가지기 때문에 실제로 Lmax는 mm 이상의 값을 가지기 어렵다. 이러한 한계점을 극복하기 위해, 펨토초 레이저(Femtosecond Pulse Laser)를 이용한 최대 측정 거리를 개선한 연구가 제안되었으며, 펨토초레이저의 주파수 모드들을 분광기에서 각각 분리하고, 모드들의 좁은 선폭(Linewidth)을 이용하여 최대 측정 거리를 확장하였다.4
한편, 분산간섭계의 최소 측정 영역은 광원의 주파수 대역폭(Spectral Bandwidth)에 의해 결정되는데, 광원의 유한한 대역폭에 의해 다음의 수식과 같이 표현된다.3
| (2) |
여기서 Δv는 광원의 주파수 대역폭을 나타낸다. 식(2)에서 알 수 있듯이, 결국 Δv가 넓을수록 최소 측정 거리는 짧아지지만, 이 역시 유한한 Δv에 의해 한계를 가진다. 텅스텐 할로겐 램프(400 nm - 700 nm)를 광원으로 하는 경우, Lmin은 수 μm 정도가 되어 OPD가 0인 지점에서 Lmin까지 측정이 불가능하다. 최근, 이러한 한계점을 극복하기 위해 DBS (Dichroic Beam Splitter)를 이용한 분산간섭계가 제안되었으며 최소 측정 영역을 제거하는 연구가 진행되었다.5 광원의 파장 영역을 기준 거울부에서 DBS를 이용하여 나누고 이를 통해 주파수 영역이 서로 다른 동시에 측정 거리가 서로 다른 2개의 간섭 신호로 분산간섭계의 최소 측정 영역을 제거할 수 있었다.
그러나 분산간섭계는 위와 같은 두 가지 한계점을 개선하더라도 OPD의 방향성에 의해 전체 측정 영역의 1/2만을 사용할 수 밖에 없는 문제점이 있다. 이는 기준거울이 측정 거울보다 같은 거리만큼 가깝거나 멀 경우, 동일한 간섭 신호가 획득되기 때문에 발생하는 현상으로 광의 파동적 성질에 기인한다. 결국, 분산간섭계는 OPD의 방향 모호성(Direction Ambiguity)으로 인해 OPD가 0인 점을 기준으로 한쪽 영역만을 사용해야 한다. 이를 보상하기 위해 기준광 경로에 분산 물질(Dispersive Material)을 추가하여 분산 영향에 의해 방향성 판별이 가능한 연구가 제안되었고 실험적으로 검증되었다.6 하지만 기존의 연구는 방향성 판별 방법에 대해 이론적인 검증과 기초실험이 진행되어 방향 판별 유무에 대한 가능성을 확인한 정도이며, 보다 심층적인 논의는 되지 않았다. 특히, 분산 물질을 추가하게 되면 분산에 의해 간섭 신호의 가시도(Visibility)가 저하되는 문제점이 발생되는데, 이러한 문제점에 대해서 방향 판별 유무와 더불어 종합적으로 고려할 필요가 있다. 그래서 본 연구에서는 분산간섭계에서 OPD의 방향성 판별을 위한 분산 물질의 두께 변화에 따른 가시도 저하와 방향성 판별 유무에 대해 실험적으로 검증하고, 최적의 두께를 찾는 연구를 진행하였다.
2. 방향 판별 분산간섭계 최적 조건
2.1 분산간섭계의 방향성 판별 이론
일반적으로 분산간섭계는 Fig. 1과 같이 광원에서 출사되는 빔이 광분활기(Beam Splitter, BS)를 통해 기준광과 측정광으로 분리되어, 각각의 거울에서 반사되어 되돌아오며, 다시 광분활기에서 합쳐져 간섭을 일으킨다. 이때 간섭 신호는 분광기를 통해 파장 별로 획득되며, 측정된 신호는 다음과 같이 나타낼 수 있다.6
| (3) |
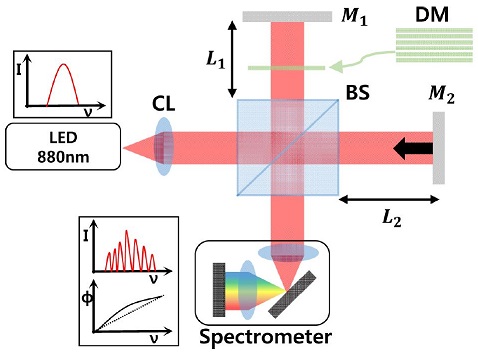
Optical configuration of the direction deterministic SRI, (CL: Collimating lens, BS: Beam splitter, M1, M2, Mirror, DM: Dispersive material) It is noted that L1 and L2 indicate distances between the end surface of BS and mirrors (M1 and M2), respectively
여기서 A(ν)는 광원의 광주파수 분포(Spectral Density)를, B(ν)는 간섭 신호의 포락선(Envelope)을 나타내며, (n1L1)과 (n2L2)은 기준광과 측정광 각각의 광학적 거리이며, L1과 L2는 BS의 표면과 거울간의 기하학적 거리를 나타낸다(이 경우, BS 내에서의 광경로는 동일함). 이때 분산간섭계에서는 보통 매질이 공기이기 때문에 n1과 n2는 1로 가정할 수 있고, 또한 분산 효과는 미미하다.
식(3)에서 광주파수 별 위상을 추출하기 위해서 푸리에 변환(Fourier Transformation)과 역푸리에 변환(Inverse Fourier Transformation)을 이용할 수 있고,4 이를 통해 획득되는 위상은 다음과 같이 표현된다.
| (4) |
식(4)에서 알 수 있듯이, 측정 거리 (L2 - L1)은 위상의 기울기를 통해 다음과 같이 나타낼 수 있다.
| (5) |
그러나 실제로 분산간섭계의 간섭 신호는 식(3)에서와 같이 사인파(Sinusoidal Function)의 형태를 보이고 있으며 이로 인해 측정되는 위상의 부호에 모호성이 발생한다.6 즉, 분산간섭계의 측정값은 (L2 - L1)이 아닌 |L2 -L1|이 되어, Fig. 3(a)와 같이 OPD가 0인 지점을 중심으로 부호가 서로 다른 영역에서 방향성이 없이 동일해진다. 그래서 분산간섭계의 거리 측정은 선형성(Linearity)이 유지되는 한쪽 영역에서만 수행되고, 이로 인해 측정 영역이 제한되는 문제점이 있다. 이를 극복하기 위해 Fig. 1과 같이 기준 경로에 분산 물질을 삽입하여 간섭 신호를 통해 방향성 판별이 가능하게 된다.6 이때 분광기를 통해 측정되는 간섭 신호는 식(3)과 비슷하지만, BS의 표면과 M1 사이의 거리 L1'은 분산 물질의 두께 t와 삽입하는 분산 물질의 굴절률(nd) 을 통해 다음과 같이 다르게 표현된다.
| (6) |
식(6)을 이용하여 광주파수 별 위상 ϕ'(v)을 정리하면 다음과 같다.
| (7) |
이때 nd를 광주파수에 대한 1차 함수(nd = n0 + n1v)로 가정하면, 식(7)은 다음과 같이 v에 대한 2차 함수의 형태로 나타낼 수 있다.
| (8) |
식(8)에서 알 수 있듯이, 이때 ϕ'(v)의 광주파수에 대한 1차 선형 기울기로부터 (L2 - L1)을 추출할 수 있다. 한편, 분산 물질에 의해 생기는 비선형성을 가지는 2차 성분은 L1, L2의 거리 차이에 따라 부호가 바뀌는 현상이 발생하고 이를 이용하여 방향을 판별한다. 예를 들어, L2가 L1'에 비해 긴 경우에는 ϕ'(v)의 분산간섭계 측정값인 |L2 - L1'|는 L2 - L1'로 표현되지만 그 반대의 경우에는 L1' - L2가 되며, 이로 인해 광주파수에 따른 위상의 2차 성분의 부호가 바뀌게 된다. 기존 분산간섭계에서는 간섭 신호인 Cosine 함수의 우함수 특성상, 위상은 양인 경우와 음인 경우를 구분할 수 없고 그로 인해 방향성이 모호해진다. 그러나 본 논문에서 제안하는 방법에서는 위의 경우와 같이 OPD의 부호에 따라 위상의 2차 성분 부호가 달라진다. 그래서 ϕ'(v)의 2차 계수 성분(4πtn1/c0)을 비선형 계수(Nonlinear Coefficient)로 정의하여, 비선형 계수의 부호에 따라 분산간섭계의 방향성 판별이 가능하다.
2.2 분산에 의한 가시도 변화
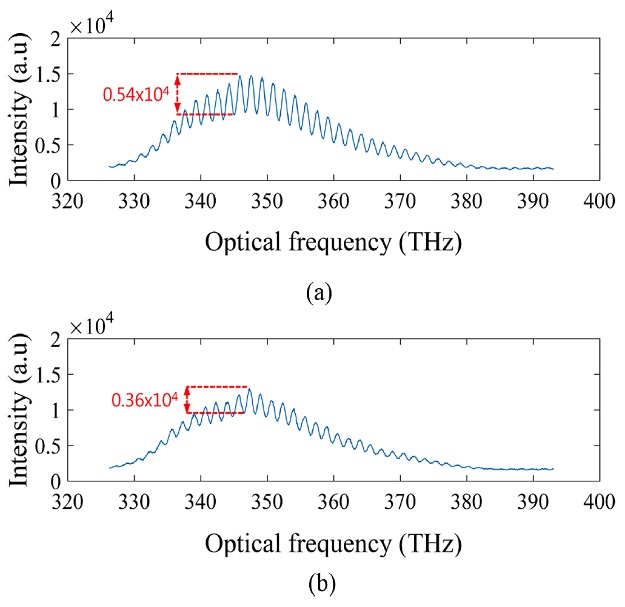
분산간섭계는 앞서 설명한 바와 같이 분산 물질의 삽입을 통해 방향성 판별이 가능하다. 그러나 간섭계의 한쪽 경로에 분산 물질을 삽입하는 경우, 분산 효과로 인해 측정되는 간섭 신호의 가시도가 저하되는 문제가 발생한다.7 이론적으로 분산간섭계에서 각 주파수에 해당하는 간섭 신호만을 획득하면 이러한 간섭 신호의 가시도의 저하가 발생하지 않지만, 실제의 경우에는 분광기의 각 주파수에서 일정한 주파수폭을 가지고 간섭 신호를 획득하기 때문에 분산에 의해서 획득되는 주파수 폭 내의 간섭 신호들의 위상차가 발생하게 되면 측정되는 간섭 신호의 가시도는 저하된다. Fig. 2에서 알 수 있듯이, OPD가 동일한 위치에서 분산량의 증가는 간섭 신호의 가시도 저하를 유발하는 것을 확인할 수 있다. 분산간섭계에서 가시도의 저하는 측정 정밀도 및 측정 영역에 있어서 제한을 주기 때문에, 방향 판별 분산간섭계에서는 위상의 비선형 성분뿐만 아니라 분산량 및 간섭 신호의 가시도가 동시에 고려되어야 한다.
방향 판별 분산간섭계에서 발생하는 분산량을 계산하기 위해 분산 물질의 굴절률을 식(9)와 같은 셀마이어 방정식(Sellmeier Equation)을 이용하여 파장의 함수로 나타내었다.8
| (9) |
여기서 λ는 빛의 파장, B1,2,3, C1,2,3은 매질에 따른 셀마이어 계수이다. 이때 본 분산간섭계에서 이용하는 색분산(Chromatic Dispersion, dn/dλ)은 식(9)의 n(λ)을 분산 이론에 따라 1차 미분을 통해 계산된다. 참고로 BK7의 경우, 광원의 중심 파장(880 nm)에서 색분산은 -0.016689 μm-1이다. 그래서 분산간섭계에서 발생하는 분산량은 삽입하는 분산 물질의 두께(t)와 색분산의 곱으로 나타낼 수 있다.
한편, 분산 물질의 두께 변화에 따라 측정되는 간섭 신호의 가시도를 비교하기 위해 본 연구에서는 광주파수 별 간섭 신호의 푸리에 변환 결과에서 검출되는 첨두(Peak)의 크기를 이용하였다. 첨두의 푸리에 크기(Fourier Amplitude)는 간섭 신호의 가시도에 대한 정확한 표현은 아니지만, 가시도의 변화에 따라 동일한 경향성을 가지기 때문에, 이를 이용하여 분산 물질의 두께에 따른 가시도를 비교하였다.
3. 실험
3.1 분산 물질을 이용한 방향성 판별 확인
먼저, 일반적인 분산간섭계의 방향 모호성을 확인하기 위하여 분산 물질을 삽입하지 않은 일반적인 분산간섭계로 간섭 신호를 획득하였다. 광원은 880 nm 중심파장에서 50 nm의 대역폭을 가지는 LED를 이용하였고, 거리 측정을 위해 측정거울(M2)을 모터구동 스테이지에 설치하여 6 μm의 간격으로 0.9 mm까지 이동하며 분광기를 통해 간섭 신호를 측정하였다. 측정된 간섭 신호로부터 푸리에 변환 기반 측정 알고리즘을 통해 식(8)과 같은 광주파수 별 위상을 추출하였으며, Fig. 3과 같이 (a)거리 및 (b)비선형 계수와 이를 이용한 방향 보상 거리 결과를 계산하였다. Fig. 3(a)에서 볼 수 있듯이 일반적인 분산간섭계에서의 측정 길이가 (L1 - L2)의 부호에 상관없이 동일하게 측정되는 것을 통하여 방향 모호성을 확인하였다. 또한 분산 물질을 삽입하지 않는 일반적인 분산간섭계에서는 비선형 효과가 생기지 않아야 하지만, 분산간섭계의 간섭 신호를 푸리에 변환하여 획득되는 위상의 위상잡음(Phase Noise)으로 인하여 Fig. 3(b)와 같이 불규칙하게 측정되는 것을 확인하였고 이로 인해 Fig. 3(c)와 같이 방향성 보상이 이루어지지 않음을 확인하였다. 참고로, 분산간섭계에서 발생하는 위상 잡음은 주로 광원의 광주파수 분포의 푸리에 변환 결과에 의해 발생하며, 푸리에 변환시 적용되는 윈도우 함수(Window Function)에 의해서도 발생한다.
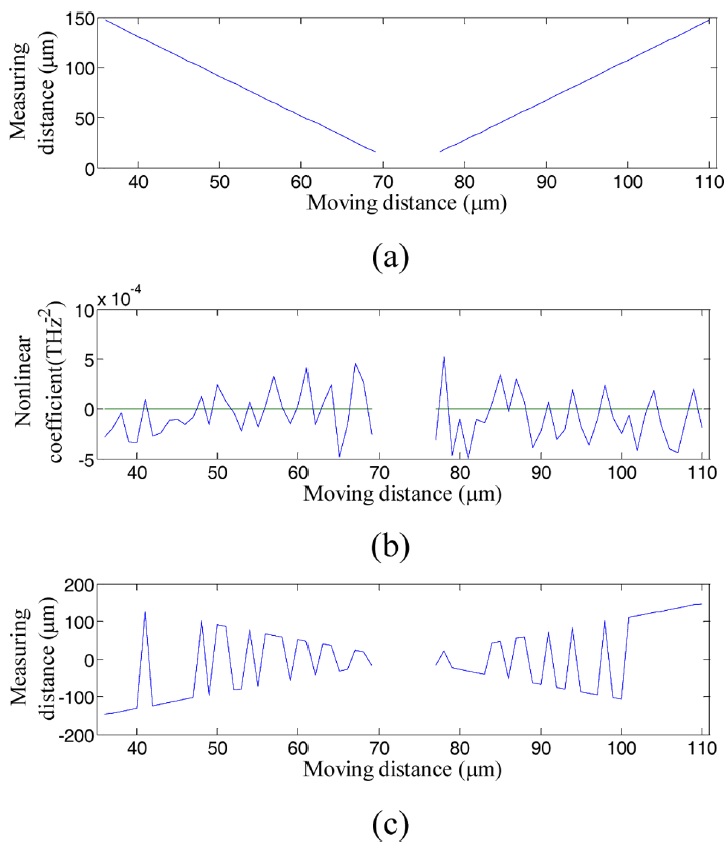
(a) Measured distances, (b) Nonlinear coefficient, (c) Calibrated distance of SRI without the dispersive material
본 실험 구성에서 Lmin과 Lmax는 이론적으로 각각 6.84 μm, 193 μm이고, 실험적으로는 15.48 μm, 148 μm로 측정되었다. 실험적으로 측정한 Lmin 과 Lmax는 분산간섭계의 간섭 신호를 푸리에 변환한 후, 검출되는 거리 신호에 따른 첨두 신호에 의한 거리측정 유무로 결정하였다. 측정 거리가 Lmin보다 짧은 경우에는 첨두 신호가 광원의 스펙트럼에 의한 첨두 신호와 겹치게 검출이 불가능하였으며, 측정 거리가 Lmax보다 긴 경우에는 첨두 신호의 크기가 매우 작아 검출이 불가능하였다.
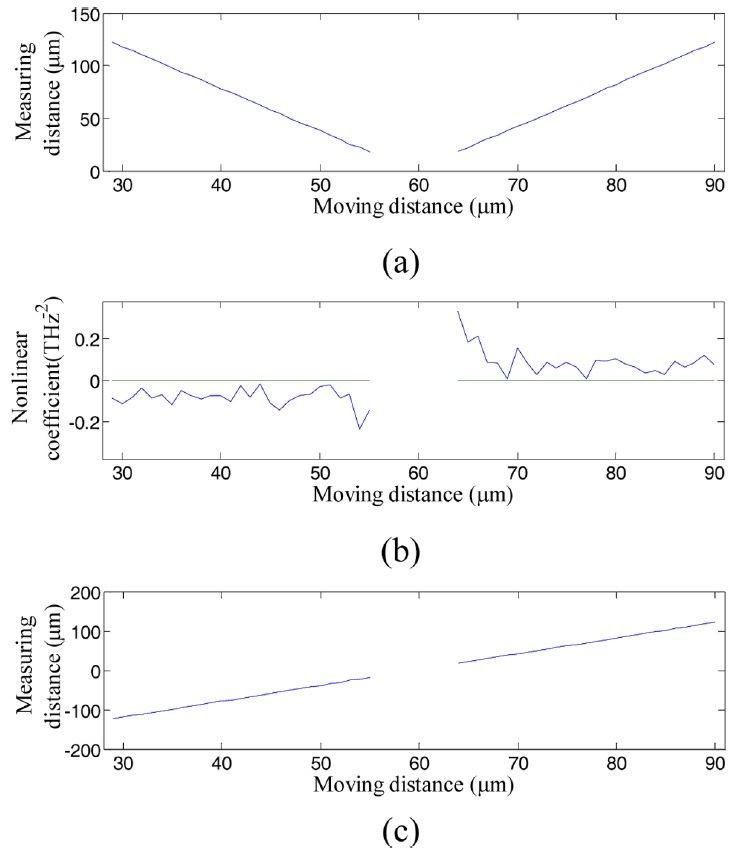
두번째로 분산간섭계의 방향 모호성을 해결하기 위하여 Fig. 1과 같이 기준광 경로에 분산 물질(DM)을 삽입하였다. 이때 광원과 BS, 분광기는 일반적인 분산간섭계와 동일한 조건으로 구성하였다. 삽입하는 분산 물질로는 1 mm 두께의 BK-7을 사용하여 실험하였고, Fig. 4(b)는 분산 물질에 의해 발생하는 측정 거리에 따른 비선형 계수를 보여준다. Fig. 4(b)에서 알 수 있듯이 60 μm 근처의 OPD 가 0인 위치를 기준으로 방향에 따라 부호가 바뀌고 있음을 확인하였다. 그리고 이를 이용하여 Fig. 4(a)의 측정 거리결과에 대한 방향성을 판별 하였을 때 Fig. 4(c)와 같이 보상된 결과를 얻어 방향 모호성이 해결되는 것을 확인하였다.
3.2 분산 물질의 두께에 따른 가시도 변화 및 방향판별 유무
분산량에 따른 가시도의 변화와 방향성 판별 유무를 확인하기 위해 분산 물질의 두께를 변화시키면서 방향 판별 분산간섭계에서 거리를 측정하였다. 분산 물질로는 BK7으로 만들어진 현미경용 커버 유리(Cover Glass)를 이용하였고, 분산량 변화는 단순하게 커버 유리를 겹치는 형태로 구현하였으며, 커버 유리 표면의 반사에 의한 영향을 고려하여 광량을 일정하도록 조절하였다. 사용한 커버 유리들은 간섭계의 광축과 어긋나게 정렬하여 내부 반사 효과를 최소화하였다. 본 실험에서는 0 - 1.5 mm까지 두께를 0.15 mm 두께를 가지는 커버 유리의 개수를 달리하면서 분산 간섭 신호를 획득하였다.
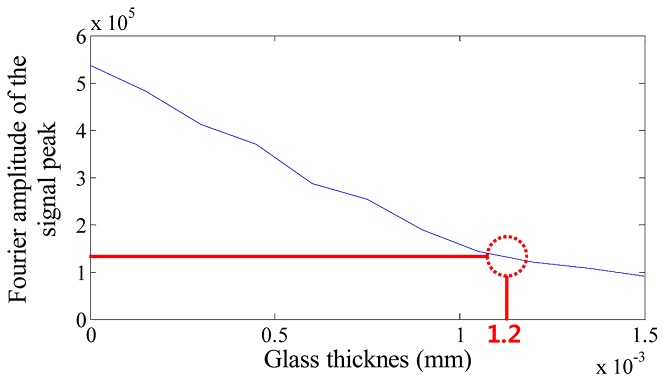
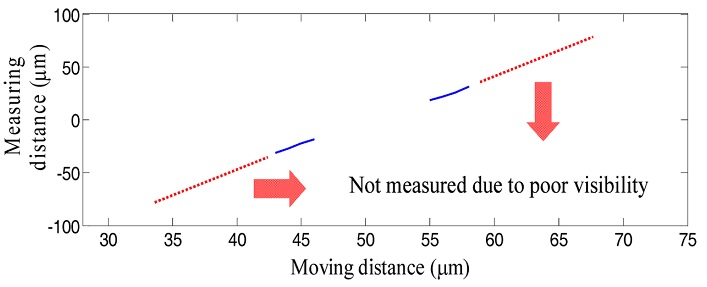
푸리에 변환을 통해 간섭 신호에 해당하는 첨두를 검출하였고 Fig. 5와 같이 첨두의 크기로부터 가시도를 비교하였다. 참고로 분산간섭계의 간섭 신호를 푸리에 변환하는 경우, Fig. 2에서 나타난 간섭 신호의 진폭은 푸리에 변환에 의한 신호 첨두의 크기와 선형적으로 비례하는 관계를 가지고 있고, 실험 상에서 광원의 광량을 일정하게 유지하는 경우 푸리에 첨두의 크기는 가시도와 비례한다. Fig. 5에서 알 수 있듯이 BK7의 두께가 증가할수록 가시도가 점차적으로 낮아지고 있음을 확인하였고, 두께가 1.2 mm 이상부터 가시도가 낮아 Fig. 6과 같이 거리 측정이 제대로 수행되지 않음을 확인하였다. 이때 간섭계에서 발생한 분산량은 -20.03 μm/μm로 계산되었다.
한편, 분산 물질의 두께에 따른 방향성 판별 유무를 확인하기 위해 각각의 경우에 대해 Fig. 7과 같이 측정 위상의 비선형 계수를 측정하였다. Fig. 7에서 알 수 있듯이 분산 물질의 두께가 얇을 경우에는 위상 잡음으로 인해 방향 판별이 어려우며, 분산 물질이 0.45 mm 이상의 두께를 가질 때부터 위상의 비선형 성분이 측정 길이의 부호에 따라 상이하게 나와 방향의 모호성을 해결됨을 알 수 있다. 이때 분산량은 -7.510 μm/μm 값임을 확인하였다.
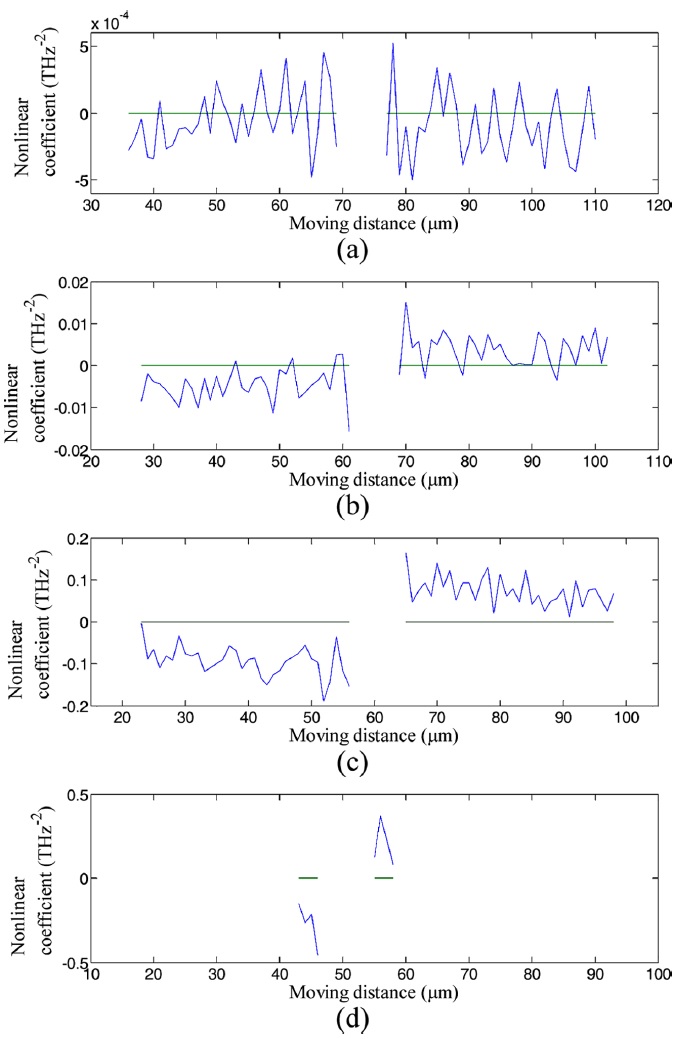
Measured nonlinear coefficients with the BK7 cover glass thickness of (a) 0 mm, (b) 0.3 mm, (c) 0.45 mm, (d) 1.2 mm
또한, 분산 물질의 두께가 1.2 mm 이상에서는 방향성 판별이 가능하지만 가시도의 저하로 인해 측정 영역이 극히 제한됨을 확인하였다. Table 1은 BK7의 두께에 따른 방향 판별 간섭계에서의 위상 비선형 계수와 간섭 신호의 푸리에 진폭, 분산 물질에 의한 분산량 및 방향 판별 유무를 정리하였다. Table 1에서 알 수 있듯이, 분산간섭계에서 방향 판별을 위해 삽입하는 분산 물질은 적절한 두께 및 분산량을 가지고 있어야 함을 알 수 있고, BK7을 분산 물질로 이용할 경우에는 0.45 mm - 1.05 mm 두께의 범위 내에서 사용할 경우, 가시도 저하 등으로 인한 거리 측정 한계 등의 추가적인 문제를 해결할 수 있다.

Summary of the direction deterministic SRI with the thickness of BK7 (t), nonlinear coefficients (4πtn1/c0), Fourier amplitude, chromatic dispersion (dn/dλ) and possibility of determining direction (Dir.)
Table 1에서 삽입하는 분산 물질의 두께에 따른 비선형 계수(4πtn1/c0)는 분산간섭계의 전체 측정 영역에서 계산되는 비선형 계수들의 절대 평균값(Absolute Mean Value)으로 나타내었다. 이론적으로 비선형 계수는 분산 물질의 두께가 증가함에 분산량이 증가하기 때문에 동일하게 증가해야 하지만, Table 1에서 알 수 있듯이 측정 값이 오히려 감소하는 현상이 발생하였다. 이는 측정 오차와 더불어 FFT (Fast Fourier Transformation)를 이용할 때 발생되는 윈도우(Window)에 의한 위상 오차, 비교적 작은 위상 변화에 대한 광주파수의 2차 곡선 맞춤(Second Order Polynomial Fitting)에서 발생하는 오차에 기인한다. 실제로 FFT를 적용할 때, 윈도우의 크기에 따라 위상이 달라지는 것을 확인하였고, 이로 인해 2차 곡선 맞춤에 의한 비선형 계수 값이 변화하는 것을 알 수 있었다.
그러나 실험 결과에서 알 수 있듯이 전체적으로 측정된 비선형 계수값들은 분산 물질의 두께가 증가함에 따라 증가하는 경향성을 보이고 있고, 또한 본 연구에서 도출한 분산 최적 조건에서 비선형 계수의 부호는 측정 방향에 따라 정확히 달라지는 것을 확인하였다.
4. 결론
본 연구에서는 방향 판별 분산간섭계에 대해 방향 판별 유무와 더불어 가시도, 분산량 등을 이론적, 실험적으로 제시하고 이를 통해 최적의 조건을 확인하였다. 일반적인 분산간섭계의 한계인 방향 모호성을 해결하기 위해 분산 물질을 이용한 방향 판별 이론을 설명하였고 이를 실험적으로 검증하였다. 또한 방향성 판별에 대한 분산량의 최적의 조건을 찾기 위해 가시도 변화와 위상의 비선형 성분을 동시에 측정하였다. 실험 결과, 가시도는 분산 물질의 두께가 증가함에 따라 저하되는 것을 확인하였으며, BK7의 두께가 1.2 mm 이상일 때 가시도 저하로 인해 측정 영역이 제한되었다. 또한 분산 물질의 두께에 따른 위상의 비선형 계수는 BK7의 두께가 0.45 mm부터 측정 거리에 따라 부호가 상이하게 나오는 것을 확인하였다. 방향 판별 분산간섭계에서 방향성 판별에 대한 최적의 분산량은 위상의 비선형 효과가 측정 길이에 따라 부호가 상이하게 나오는 -7.510 μm/μm 부터 가시도가 측정길이에 영향을 미치지 않는 -20.03 μm/μm 이하가 최적 조건임을 확인하였다.
NOMENCLATURE
| Lmax : | Maximum measurable distance |
| Lmin : | Minimum measurable distance |
| c0 : | Speed of light in vacuum |
| nd : | Refractive index of a dispersive material |
| N : | Group index of refraction |
| δv : | Resolution of a spectrometer |
| Δv : | Spectral bandwidth of a light source |
| t : | Thickness of a dispersive material |
| B, C : | Coefficients of Sellmeier equation |
| dn/dλ : | Chromatic dispersion |
Acknowledgments
본 논문은 2016학년도 조선대학교 학술연구비의 지원을 받아 연구되었음.
REFERENCES
-
Schnell, U., Zimmermann, E., and Dandliker, R., “Absolute Distance Measurement with Synchronously Sampled White-Light Channelled Spectrum Interferometry,” Pure and Applied Optics, Vol. 4, No. 5, pp. 643-651, 1995.
[https://doi.org/10.1088/0963-9659/4/5/016]

-
Hlubina, P., “Experimental Demonstration of the Spectral Interference between Two Beams of a Low-Coherence Source at the Output a Michelson Interferometer,” Journal of Modern Optics, Vol. 44 No. 1, pp.163-173, 1997.
[https://doi.org/10.1080/09500349708232906]

-
Schnell, U., Dandliker, R., and Gray, S., “Dispersive White-Light Interferometry for Absolute Distance Measurement with Dielectric Multilayer Systems on the Target,” Optics Letters, Vol. 21, No. 7, pp. 528-530, 1996.
[https://doi.org/10.1364/OL.21.000528]

-
Joo, K.-N. and Kim, S.-W., “Absolute Distance Measurement by Dispersive Interferometry Using a Femtosecond Pulse Laser,” Optics Express, Vol. 14, No. 13, pp. 5954-5960, 2006.
[https://doi.org/10.1364/OE.14.005954]

-
Joo, K.-N., “Dichroic Spectrally-Resolved Interferometry to Overcome the Measuring Range Limit,” Measurement Science and Technology, Vol. 26, No. 9, Paper No. 095204, 2015.
[https://doi.org/10.1088/0957-0233/26/9/095204]

-
Yun, Y. H., Seo, Y. B., and Joo, K.-N., “Elimination of the Direction Ambiguity and the Dead Zone in Spectrally Resolved Interferometry,” Measurement Science and Technology, Vol. 27, Paper No. 035004, 2016.
[https://doi.org/10.1088/0957-0233/27/3/035004]

-
Hitzenberger, C. K., Baumgartner, A., Drexier, W., and Fercher, F. A., “Dispersion Effects in Partial Coherence Interferometry: Implications for Intraocular Ranging,” Journal of Biomedical Optics, Vol. 4, No. 1, pp. 144-151, 1999.
[https://doi.org/10.1117/1.429900]

-
Ghosh, G., “Sellmeier Coefficients and Dispersion of Thermo-Optic Coefficients for Some Optical Glasses,” Applied Optics, Vol. 36, No. 7, pp. 1540-1546, 1997.
[https://doi.org/10.1364/AO.36.001540]