능동형 위상보정을 이용한 정밀 속도리플 제어기의 개발

1. 서론

모터는 그 구조와 쓰임새 및 형태에 따라 AC모터, DC모터, 브러쉬리스 모터 및 리니어 스테이지 등 다양한 종류가 존재하는데, 그 구조상 필연적으로 토크 리플이 발생하며 이는 속도 리플 발생의 원인이 된다. 특히 반도체 생산 장비등에서는 매우 정밀한 등속구동성능이 요구되기 때문에 시스템 자체 또는 외부에서 발생하는 속도 리플은 장비의 성능을 저하시키는 주요 요인이 된다.

속도 리플이 발행하는 주요원인 중 하나인 토크 리플의 저감에 대한 연구를 크게 분류하면, 내부 구조에 따른 토크 리플을 분석하고 해당 결과를 통해 내부 모델 구조를 변경시켜 토크 리플을 감소시키는 연구가^1-3 있으며 모터 드라이버의 전류 또는 전압제어의 개선을 통해 토크 리플을 감소시키는 연구가^4-7 있다. 그런데 속도 리플과 토크 리플은 그 원인이 구조적인 문제나 여자의 위상차이 등에서만 생성되는 것이 아니라, 코일전류의 오프셋, 자석의 불균질성, 코일의 저항차이 등 모터의 개별적인 특성에서도 기인하기 때문에 같은 모델의 모터라 하더라도 개별적인 특성이 달라지므로 위의 기술들로는 이미 완성된 제품 단계에서 보정하기가 매우 어렵다. 이렇게 구조적, 하드웨어적으로 토크 리플을 보정하는 방법은 시스템을 복잡하게 만들며 높은 비용문제가 있어서 제품화 및 상용화하기 어렵다는 단점이 있다. 다른 방법으로는 모터에 대한 적응제어 기법을 통해 토크리플을 줄이는 방법이^8,9 있으며 또는 모터를 구동하여 특정 위치나 속도에 따른 리플을 측정해 모델링하여 보상 신호를 생성한 후 ROM Table을 구성해 피드포워드 방식으로 보상하는 연구가¹⁰ 있는데 이는 미세하게 변화하는 속도 리플을 추적하기 힘든 문제점이 있다. 또한 개선된 PID 속도 제어기를 통해 상위 제어기에서 속도 리플을 감소시키는 연구가¹¹ 있으나 에러가 발생해야 구동하는 피드백 제어기의 특성상 등속구간으로의 정착시간이 증가로 인해 장비 구동시간이 늘어나는 단점이 존재한다.

실제 생산 공정에서는 정속제어시 발생하는 속도 리플이 다양한 원인을 가지며, 고정되어 있지 않고 위상이 미세하게 시간이 흐름에 따라 드리프트하며 변화하는 특징을 가지고 있다. 따라서 피드백으로 상쇄하지 못하는 속도리플에 대하여 단순하게 고정된 피드포워드를 이용한 속도 보정은 실제적으로는 활용이 매우 어렵게 된다.

본 논문에서는 기존의 리플 보상기들의 단점을 극복하여, 시간에 따라 위상값이 변화하는 경우에도 속도 리플을 실시간으로 추적하여 정밀 보정할 수 있고, 상위제어기에서 소프트웨어로 쉽게 구현이 가능하며, 개별 제품의 특징 변동에도 문제없이 적용할 수 있는 능동형 위상보정 속도리플제어기를 설계하였다. 실시간으로 발생하는 속도 리플 신호와 보상 신호의 위상차 에러를 특별한 형태의 적분기를 통하여 판별하고 능동적으로 이를 피드백 형태로 구현하여 실시간으로 추적 및 보상할 수 있도록 설계하였다.

제안된 방식의 알고리듬은 모터 내부 구조특성에서 발생한 리플 뿐만 아니라 베어링, 무게중심 등 외부적 요인으로부터 발생하는 속도 리플도 능동적으로 제거할 수 있다.

2. 리플의 정의와 피드포워드 제어기

2.2 기존의 피드포워드 리플보상

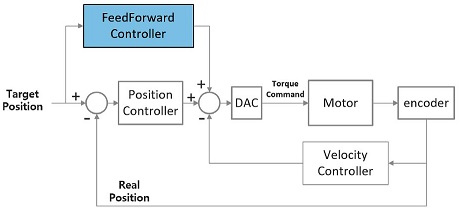
피드포워드 제어는 에러가 발생해야 출력을 발생시키는 피드백 제어기와는 달리, 시스템의 모델을 이용하여 원하는 출력이 나오도록 미리 입력을 넣어주므로, 시간지연에 따른 에러를 최소화할 수 있는 방법이다. Fig. 1과 같이 서보 시스템에서는 주로 목표궤적의 빠른 추종을 위하여 피드포워드 제어기가 주로 사용된다.

Fig. 1

Motor feedforward control

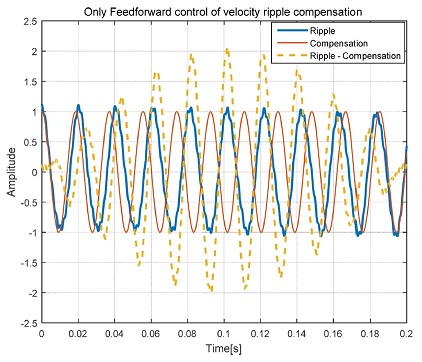
속도 리플의 제거에 있어서도 시간지연의 영향을 최소화 하기 위하여 피드포워드 보상 방식을 사용하여야 하는데, 만약 일반적인 고정형 피드포워드 제어기를 사용하게 되면, 변하지 않는 일정한 형태의 속도 리플의 경우에는 에러의 감소효과를 볼 수 있으나, 실제 현장에서 발생하는 리플은 Fig. 2과 같이 리플의 위상이 시간에 따라 조금씩 흐르며 변화하는 경우가 대부분이며, 이러한 경우 그래프의 약 0.1초의 구간에서 볼 수 있듯이, 보상신호와 리플신호의 위상 차이가 180°로 반대되면 오히려 리플을 두 배로 증폭시키기 때문에 시스템의 안정성의 문제를 야기할 수 있다.

Fig. 2

Velocity ripple feedforward control

3. 속도 리플 능동제어기 설계

3.1 능동제어 방식의 속도 리플 제어기

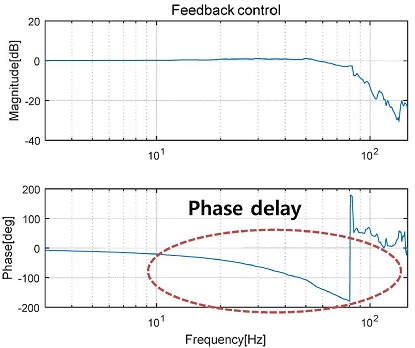
발생하는 속도 리플의 주파수가 피드백 제어 밴드폭 안에 있더라도, Fig. 3의 위상 선도에서 볼 수 있는 위상지연 때문에 피드백제어만으로는 리플의 보상이 깨끗하게 이루어지지 못한다. 그래서 속도 리플의 보정 출력은 대부분 피드포워드를 사용하여 보정할 수 밖에 없는데 실제 상황에서 발생하는 리플은 상기한 것처럼 시간에 따라 조금씩 흐르거나 주파수의 미세한 변동을 동반하는 경우가 대부분이다.

Fig. 3

Motor feedback control Bode diagram

기존의 연구에서는 발생하는 리플이 고정되어 주파수 및 위상을 정확히 측정할 수 있는 경우에 한하여 많이 연구되었는데, 실제 상황에서의 속도리플은 미세하게 위상의 변화가 발생하는 경우가 대부분이어서 기존의 알고리듬은 적용될 수 있는 대상이 매우 제한되었다.

본 연구에서는 별도의 센서를 사용하지 않고 속도제어에 사용되는 단순 속도 측정신호만을 사용하여 속도 리플의 위상변화 및 드리프트를 실시간으로 추적하여 보정할 수 있는 새로운 형식의 위상 보정기(Phase Compensator) 가 추가된 능동형 피드포워드 방식의 속도 리플 제어기를 개발하였다. 본 연구에서 제안된 알고 리듬은 속도 리플의 원인과는 상관없이 최종단계에서 발생하는 속도 리플에 대하여 범용으로 사용이 가능하므로 실용성이 매우 높으며, 상품화된 모션 전용 제어기의 라이브러리로 실장이 가능하다.

제안된 속도 리플 제어기 VRAC (Velocity Ripple Active Controller)는 첫째로 속도 리플을 추출하는 하는 단계, 둘째로 추출된 주파수의 리플신호의 위상변화를 알아내는 단계, 마지막으로 보상 신호의 위상차를 보정하여 최종 보상신호로 출력하는 단계로 구성되어 있다.

3.2 속도리플 추출기(Velocity Ripple Extractor)

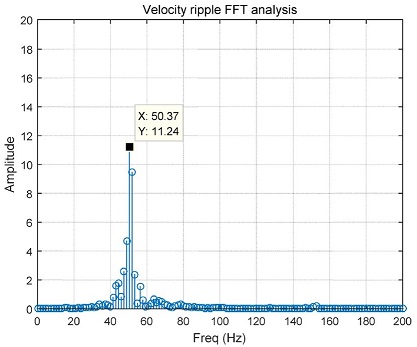
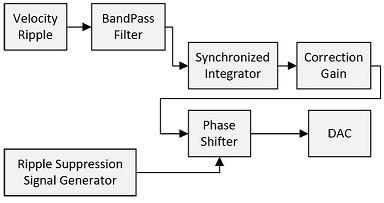
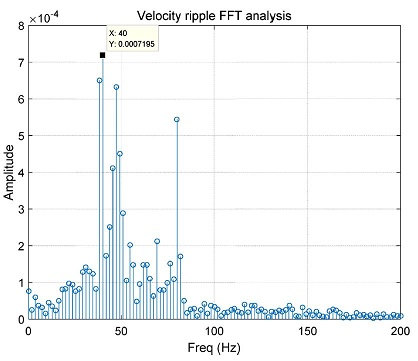
속도 리플 추출단계에서는 사전에 Fig. 4와 같이 FFT 분석을 거쳐서 가장 큰 영향을 미치는 핵심 리플주파수를 알아내고, 밴드패스 필터를 사용하여 레퍼런스 속도를 제외한 리플을 실시간으로 추출한다. 이렇게 추출되어진 주파수로부터 시스템으로 입력 되어질 보상 신호의 진폭을 알아내며, 이를 토대로 리플 보상 신호를 생성한다. 속도 리플은 이 필터를 거쳐 DC 성분이 제거된 핵심 주파수에 해당하는 값만 추출되며 이는 리플 신호와 보상 신호 사이의 위상차를 추적하기 위해 다음 단계인 위상 보정기(Phase Compensator)에 입력된다.

Fig. 4

FFT analysis of velocity ripple

3.3 위상 보정기(Phase Compensator)

실제의 속도 리플은 수시로 위상과 주파수가 조금씩 변화하므로, 이를 보정해 주지 못하면 지속적으로 누적 오차가 발생하게 된다. 만약 발생하는 속도 리플의 위상이 드리프트하여 보상신호의 기준 위상과 반대가 되면 오히려 속도 리플을 더 크게 만들게 된다. 따라서 실시간으로 매 주기마다 두 신호 사이의 위상차를 판별하고 보정해주는 것이 위상 보정기(Phase Compensator)이다.

이 모듈에서는 Fig. 5에서 보는 것처럼 속도 리플 추출기(Velocity Ripple Extractor)에서 밴드패스 필터를 거친 핵심 주파수에 해당하는 속도 리플을 동기화 적분기(Synchronized Integrator)를 통해 보상 신호와 리플 신호 사이의 위상차를 판별하며, PI제어기로 이루어진 보정 게인(Correction Gain)을 통해 위상 보정 신호를 출력한다. 출력된 보정 신호는 VRAC의 마지막 단계인 위상 시프터(Phase Shifter)에 입력된다.

Fig. 5

Block diagram of phase compensator

3.3.1 동기화 적분기(Synchronized Integrator)

정속구동 중에 발생하는 리플을 보상신호가 위상차이 없이 피드포워드로 잘 제어하고 있을 때는 속도 리플이 발생하지 않는다. 하지만 시간이 지남에 따라 리플의 위상변화가 생기기 시작하면 위상차의 방향과 크기의 변화를 즉각적으로 계산하여 보상신호를 조정해 주어야 하는데, 제어를 하고 있는 상황에서는, 틀어지기 시작한 리플의 측정값이 매우 작으며 신호자체에 많은 고조파 및 노이즈가 섞여 있어서 위상값의 변화를 정확하게 계산하는 것이 쉽지 않다.

본 연구에서는 많은 시뮬레이션과 실험을 거쳐서 실시간으로 제어상태에서 속도 리플의 위상값의 변화를 추출해 낼 수 있는 특별한 적분기 형태의 알고리듬을 개발하였다. 동기화 적분기(Synchronized Integrator)라 부르는 이 적분기는 주기신호로 표현되는 리플신호와 보상신호 차이 값을 매 주기마다 특별한 방법으로 적분하여 위상차를 알아내도록 설계되었다.

리플신호와 보상신호 사이에서 위상차가 발생하면 이는 특정 각도를 기준으로 ±90도 간격으로 부호가 바뀌게 된다. 이러한 관계로 동기화 적분기의 적분구간은 동기화 기준 위상각으로부터 ±90도로 설정해야 하며 동기화 기준 위상각은 다음과 같은 방법으로 계산한다. 최초 보상신호가 출력되는 시점을 기준으로 리플과 보상신호의 오차를 적분하면 다음과 같다. p는 기준 위상각, α는 위상차를 나타낸다.

식(8)의 기본적인 출력이 정현파를 기반으로 하므로 전체 주기를 그냥 적분해서는 에러 증감에 따른 위상변화의 부호를 알아낼 수 없다. 따라서 본 연구에서 개발된 동기화 적분기에서는 위상차이에 따른 함수의 결과가 단조함수가 되는 특정 구간만을 추출하여 적분하여 한 주기내의 일정 영역 안에서 에러함수의 증분과 위상의 선행과 지연사이의 관계식을 도출해 내었다.

$\[ \begin{array}{l}y=\underset{p}{\overset{p+\frac{\pi }{2}}{\int }}\left(\sin \theta -\sin \left(\theta +\alpha \right)\right)d\theta \\ {=\left[-\cos \theta \right]}_p^{p+\frac{\pi }{2}}+{\left[-\cos \left(\theta +\alpha \right)\right]}_p^{p+\frac{\pi }{2}}\\ =-\cos \left(p+\frac{\pi }{2}\right)+\cos p+\cos \left(p+\frac{\pi }{2}+\alpha \right)-\cos \left(p+\alpha \right)\\ =\sin p+\cos p-\sin \left(p+\alpha \right)-\cos \left(p+\alpha \right)\\ =\sqrt{2}\sin \left(p+\frac{\pi }{4}\right)-\sqrt{2}\sin \left(p+\frac{\pi }{4}+\alpha \right)\end{array} \]$

(8)

위 결과가 단조함수가 되기 위해서는 미분한 결과가 단조 증가의 경우 0보다 크거나 같고 단조 감소의 경우 0보다 작거나 같은 기준 위상각 p를 구하면 된다. 기울기를 계산하기 위하여 식(8)을 미분하면 다음과 같다.

$\[ \begin{array}{c}{y}^{\text{'}}=\sqrt{2}\cos \left(p+\frac{\pi }{4}\right)-\sqrt{2}\cos \left(p+\frac{\pi }{4}+\alpha \right)\\ =2\sqrt{2}\sin \left(p+\frac{\pi }{4}+\frac{\alpha }{2}\right)\sin \frac{\alpha }{2}\end{array} \]$

(9)

위 결과가 단조 증가로 가정하는 경우 식(9) 결과가 0보다 커야하므로,

$\[ \sin \left(p+\frac{\pi }{4}+\frac{\alpha }{2}\right)\ge 0 \mathrm{a}\mathrm{n}\mathrm{d} \sin \frac{\alpha }{2}\ge 0 \]$

(10)

$\[ \sin \left(p+\frac{\pi }{4}+\frac{\alpha }{2}\right)\le 0 \mathrm{a}\mathrm{n}\mathrm{d} \sin \frac{\alpha }{2}\le 0 \]$

(11)

식(10), 식(11)과 같이 정리할 수 있으며 식(10)이 0 ≤ α/2 ≤ π와 같은 조건을 가질 때,

$\[ 0\le p+\frac{\pi }{4}+\frac{\alpha }{2}\le \pi \]$

(12)

기준 위상각 p의 범위는 식(12)와 같고,

$\[ \begin{array}{c}-\frac{\pi }{4}\le p\le \frac{3\pi }{4}, \because \alpha =0\\ -\frac{5\pi }{4}\le p\le -\frac{\pi }{4}, \because \alpha =2\pi \end{array} \]$

(13)

각 α의 조건에 따른 p의 범위는 식(13)과 같이 구할 수 있다.

마찬가지로 식(11)이 π ≤ α/2 ≤ 2π일 때,

$\[ \pi \le p+\frac{\pi }{4}+\frac{\alpha }{2}\le 2\pi \]$

(14)

기준 위상각의 범위는 식(14)와 같이 나타나며,

$\[ \begin{array}{c}-\frac{\pi }{4}\le p\le \frac{3\pi }{4}, \because \alpha =2\pi \\ -\frac{5\pi }{4}\le p\le -\frac{\pi }{4}, \because \alpha =4\pi \end{array} \]$

(15)

위와 같이 정리할 수 있다.

또한 단조 감소로 가정하는 경우, 식(9)의 결과가 0보다 작아야 하므로,

$\[ \sin \left(p+\frac{\pi }{4}+\frac{\alpha }{2}\right)\ge 0 \mathrm{a}\mathrm{n}\mathrm{d} \sin \frac{\alpha }{2}\le 0 \]$

(16)

$\[ \sin \left(p+\frac{\pi }{4}+\frac{\alpha }{2}\right)\le 0 \mathrm{a}\mathrm{n}\mathrm{d} \sin \frac{\alpha }{2}\ge 0 \]$

(17)

식(16), 식(17)과 같이 정리할 수 있으며 식(16)이 π ≤ α/2 ≤ 2π와 같은 조건을 가질 때 기준 위상각 p의 범위는 식(12)와 같으며,

$\[ \begin{array}{c}-\frac{5\pi }{4}\le p\le -\frac{\pi }{4},\because \alpha =2\pi \mathrm{ }\\ -\frac{9\pi }{4}\le p\le -\frac{5\pi }{4},\because \alpha =4\pi \end{array} \]$

(18)

각 α의 조건에 따른 p의 범위는 식(18)과 같이 구할 수 있다.

그리고 식(17)이 0 ≤ α/2 ≤ π일 때, 기준 위상각의 범위는 식(14)와 같이 나타나며,

$\[ \begin{array}{c}\frac{3\pi }{4}\le p\le \frac{7\pi }{4},\mathrm{ }\because \alpha =0\mathrm{ }\\ -\frac{\pi }{4}\le p\le \frac{3\pi }{4},\because \alpha =2\pi \end{array} \]$

(19)

위와 같이 정리할 수 있다.

단조 증가 또는 감소함수의 조건에서 p가 0보다 크기 때문에 단조증가 시 상기 식들을 만족하는 p는 3π/4로 구해지며 이를 적용하여 식(8)을 다시 계산하면 다음과 같다.

$\[ \begin{array}{l}y=\underset{\frac{3\pi }{4}}{\overset{\frac{3\pi }{4}+\frac{\pi }{2}}{\int }}\left(\sin \theta -\sin \left(\theta +\alpha \right)\right)d\theta \\ =\sqrt{2}\sin \left(\pi \right)-\sqrt{2}\sin \left(\pi +\alpha \right)\\ =-\sqrt{2}\sin \left(\pi +\alpha \right)\end{array} \]$

(20)

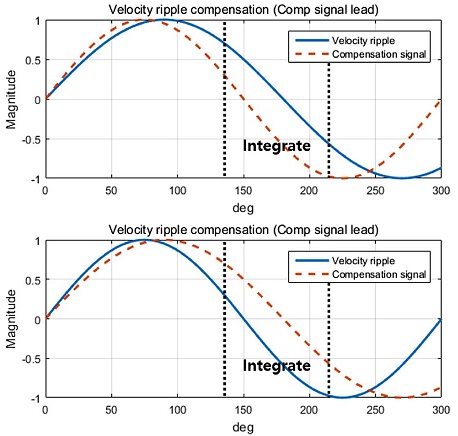
위에서 계산된 결과, 기준 위상각 p가 3π/4이고, −π/2 ≤ α ≤ π/2일 때, 단조 증가 함수를 보이는 것을 알 수 있으며, 식(20)을 이용하여 실시간으로 리플신호 및 보상신호 사이의 차이를 수치적분하고 아크사인 함수를 사용하면 Fig. 6과 같이 현재 출력되고 있는 보상신호와 리플 신호의 위상차이와 앞섬 또는 뒤쳐짐을 실시간으로 계산할 수 있다.

Fig. 6

Integration of difference in value between two signals

3.4 리플 보상 신호 생성기 및 위상 쉬프터(Ripple Suppression Signal Generator & Phase Shifter)

최종적으로 위상 이동기는 이전단계를 거치며 얻은 핵심 주파수에 해당하는 리플 신호의 정보들을 토대로 속도 리플 보상 신호를 생성한다.

FFT 분석으로 얻은 리플 데이터를 토대로, 실제 장비를 구동하며 리플 크기가 최소화되는 보상 신호 진폭 데이터 및 시스템과 제어기에서 발생하는 지연시간을 사전에 측정하여 리플 신호와 180°로 반대되는 위상을 가지도록 하는 보정 값을 가지고 만들어진 출력 신호는 위상 보정기(Phase Compensator)에서 만들어진 위상차 보정 신호와 함께 위상 시프터(Phase Shifter)로 입력된다.

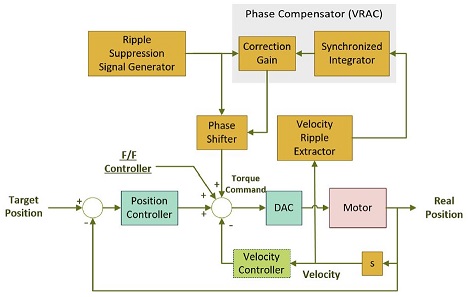
이 곳에서는 보상 신호가 다음 주기 때 변화된 리플 신호를 추적할 수 있도록 입력된 두 신호의 보정 작업을 진행하여 최종적인 속도 리플 보상 피드포워드 신호를 생성한다. Fig. 7에는 전체적인 시스템의 흐름에 대한 블록선도가 나와있으며 VRAC은 기존의 다른 피드포워드 제어기와 함께 적용 가능하다.

Fig. 7

Block diagram of velocity ripple active controller

4. 속도 리플 보상 실험

4.1 모의 실험 장비

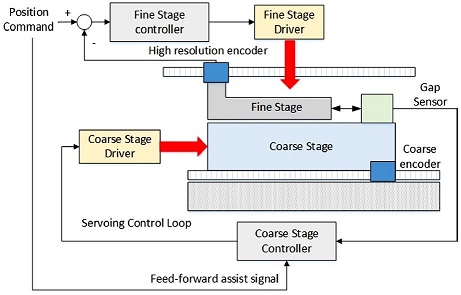
제안된 속도리플 제어기 VRAC (Velocity Ripple Active Controller)의 성능 평가를 위해서 Fig. 8과 같은 테스트용 단축 스테이지를 구성하였다. 이는 미동과 조동 스테이지가 적층형 마스터-슬레이브 방식으로 결합된 듀얼 스테이지이다. 미동과 조동 스테이지는 각각 보이스코일 모터와 리니어 모터가 사용되었으며 제어기는 TI사의 TMS320F28335 DSP를 MCU로 사용하였다. 제어 주파수는 4 kHz이고, 스테이지 위치를 측정하기 위한 갭센서와 절대 위치 엔코더가 부착되어 있다.

Fig. 8

Test equipment system

실험은 제안된 속도 리플 제어기를 적용하여 장비에서 발생하는 리플의 저감되는 정도를 측정 및 비교하기 위해 실행되었다.

4.1.1 마스터 - 슬레이브 구동

실험 스테이지는 마스터-슬레이브 방식으로 구동하며 이는 듀얼 스테이지 제어방법 중 한가지로, 미동 스테이지가 마스터, 조동 스테이지가 슬레이브가 되어 마스터가 움직일 때 발생하는 갭(Gap)을 항상 일정한 값으로 유지하려는 방향으로 슬레이브가 구동한다. 이는 결과적으로 두 스테이지가 단일 스테이지처럼 구동할 수 있게 해 주며, 각각의 스테이지는 Fig. 9와 같이 구성하였다.

Fig. 9

Master-Slave principle dual stage

4.2 실험 내용

상기한 실험용 스테이지에서, 실제상황과 유사하게 핵심 주파수로부터 약 ±1 Hz로 변화하는 40 Hz 주파수의 속도 리플이 발생하는 경우에 대하여 단순 피드포워드 제어기와 본 연구에서 제안한 알고리듬의 비교실험을 진행하였다.

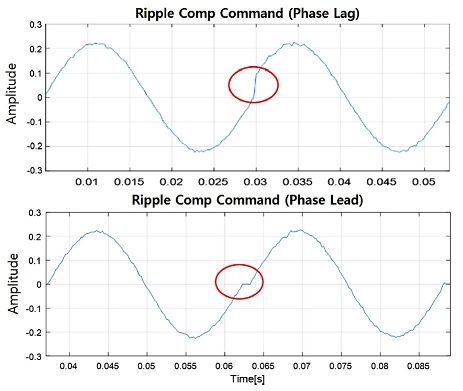
제어기의 속도 리플 추출기에 사용된 밴드패스필터는 2차 Butterworth 필터가 사용되었으며, 필터의 컷오프 주파수는 37 - 43 Hz이다. Fig. 10은 속도 리플 추출기에서 FFT 분석한 결과이며 이를 통해 40 Hz가 핵심이 되는 주파수임을 알 수 있었으며, Fig. 11은 실제 최종 리플 보상 신호의 일부분을 확대한 그림이다. 위의 그래프에서는 보상 신호가 리플 신호보다 25° 위상이 더 늦는 상황이며, 이를 토대로 다음 주기의 보상 신호 위상을 당겨서 보정하는 모습을 확인할 수 있다. 또한 Fig. 11 아래의 그래프에서는 반대로 보상 신호가 리플 신호보다 10° 위상이 더 빠르기 때문에 리플 보상신호가 느려지는 방향으로 보정되는 것을 확인할 수 있다.

Fig. 10

The FFT result in 40 Hz velocity ripple

Fig. 11

Velocity ripple compensation signal one part

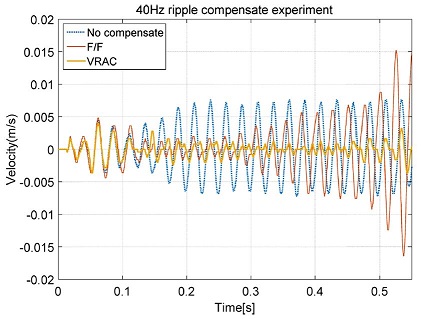
Fig. 12는 40 Hz의 속도 리플이 발생할 때의 리플 Raw 신호와 피드포워드 형태의 제어기를 적용 했을 때, 그리고 개발된 속도리플 제어기 VRAC (Velocity Ripple Active Controller)을 적용했을 때의 실험 결과 그래프를 각각 도시한 것이다. 단순히 고정된 피드포워드 형태로 리플 보상이 이루어지는 경우, 시작 부분에서는 리플 저감이 대체로 잘 이루어지나 등속 구간이 길어질수록 누적오차가 발생하여 리플 신호가 오히려 더 커지는 상황이 발생했다. 반면에 개발된 제어기를 적용했을 때에는 리플 신호의 위상변화를 능동적으로 추적하여 보상하는 모습을 보였다.

Fig. 12

40 Hz velocity ripple compensation result

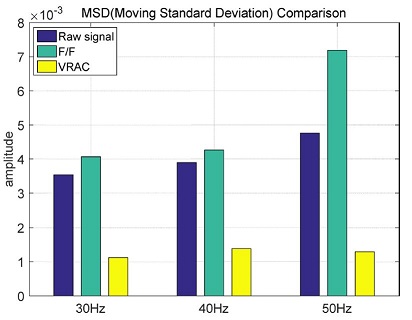
Fig. 13과 Table 1에는 위의 실험에 추가로 30 Hz와 50 Hz 실험을 진행했을 때의 결과를 MSD (Moving Standard Deviation)로 나타낸 값이 나와있다. 30 Hz, 40 Hz, 50 Hz의 속도 리플을 각각 단순 피드포워드로 보상했을 때 평균적으로 25% 정도 리플이 더 커지는 반면 개발된 제어기로 보상했을 때 리플이 평균적으로 69%정도 크게 감소되는 것을 확인할 수 있다.

Fig. 13

MSD comparison in variable frequency velocity ripple

Table 1

Comparison of measured velocity ripple data

5. 결론

본 논문에서는 변화하는 속도 리플을 실시간으로 능동적으로 추적하여 보상할 수 있는 피드포워드 방식의 제어기를 개발하였다. 사전에 핵심주파수를 측정하고 모델링하여 보상신호를 생성 및 적용함과 동시에 실시간으로 동기화 적분기(Synchronized Integrator)라는 특별한 적분기를 통해 속도리플 신호와 보상 신호 사이의 위상차를 능동적으로 판별하고 추적하여 보상할 수 있다.

개발된 제어기는 기존의 하드웨어 개선방법에 관한 연구와 다르게 저비용, 고효율성과 상위제어기에서 쉽게 구현할 수 있다는 큰 장점이 있으며 단순한 피드포워드 제어기에서 발생하는 위상차에 따른 누적오차를 제거할 수 있다. 또한 리플의 원인과 관련없이 정밀한 등속제어가 요구되는 장비의 상품성을 크게 향상시킬 수 있다.

Acknowledgments

본 연구는 2015 년도 산업통상자원부의 재원으로 한국산업기술평가원의 지원(No.10050532)과, 서울과학기술대학고 21C 다빈치형 인재양성센터 지원에 의하여 작성되었음.

REFERENCES

• Kim, D. H., Choi, J. H., Son, C. W., and Baek, Y. S., “Theoretical Analysis and Experiments of Axial Flux PM Motors with Minimized Cogging Torque,” Journal of Mechanical Science and Technology, Vol. 23, No. 2, pp. 335-343, 2009. [https://doi.org/10.1007/s12206-008-0814-x]
• Kwack, J. H. and Min, S. J., “Structural Optimization of Interor Permanent Magnet Motor for Torque Ripple Reduction Considering Speed Range,” Proc. of the Korean Society of Automotive Engineers Annual Conference, pp. 3045-3049, 2009.
• Bianchi, N., Bolognani, S., and Cappello, A., “Reduction of Cogging Force in PM Linear Motors by Pole-Shifting,” IEE Proceedings-Electric Power Applications, Vol. 152, No. 3, pp. 703-709, 2005. [https://doi.org/10.1049/ip-epa:20045082]
• Lee, D. H., “A Torque Ripple Reduction of Miniature BLDC Using Instantaneous Voltage Control,” Journal of The Korean Society of Mechanical Engineers, Vol. 31, No. 1, pp. 18-25, 2007.
• Song, J. H., Jang, J. S., and Kim, B. T., “Reduction of Torque Ripple in a BLDC Motor Using an Improved Voltage Control,” Journal of Institute of Control, Robotics and Systems, Vol. 16, No. 2, pp. 145-150, 2010. [https://doi.org/10.5302/J.ICROS.2010.16.2.145]
• Lee, G. H., Choi, W. C., Kim, S. I., Kwon, S. O., and Hong, J. P., “Torque Ripple Minimization Control of Permanent Magnet Synchronous Motors for EPS Applications,” International Journal of Automotive Technology, Vol. 12, No. 2, pp. 291-297, 2011. [https://doi.org/10.1007/s12239-011-0034-8]
• Won, T. H., Park, H. W., and Lee, M. H., “Torque Ripple Minimization of BLDC Motor including Flux-Weakening Region,” Journal of Institute of Control Robotics and Systems, Vol. 8, No. 6, pp. 445-454, 2002. [https://doi.org/10.5302/J.ICROS.2002.8.6.445]
• Kim, H. B., Lee, B. H., Han, S. O., and Huh, K. S., “Nonlinear Adaptive Control for Linear Motor through the Estimation of Friction Forces and Force Ripples,” The Korean Society of Mechanical Engineers, Vol. 31, No. 1, pp. 18-25, 2007. [https://doi.org/10.3795/KSME-A.2007.31.1.018]
• Choi, Y. M., Gweon, D. G., and Lee, M. G., “Adaptive Force Ripple Compensation and Precision Tracking Control of High Precision Linear Motor System,” J. Korean Soc. Precis. Eng., Vol. 22, No. 12, pp. 51-60, 2005.
• Butler, H., “Magnetic Disturbance Compensation for a Reticle Stage in a Lithographic Tool,” Mechatronics, Vol. 23, No. 6, pp. 559-565, 2013. [https://doi.org/10.1016/j.mechatronics.2013.04.011]
• Kim, H. M., Choo, Y. B., and Lee, D. H., “Design of the Modified PID Speed Controller to Reduce the Speed Ripple,” Journal of the Transactions of Korean Institute of Power Electronics, Vol. 17, No. 2, pp. 135-145, 2012. [https://doi.org/10.6113/TKPE.2012.17.2.135]
• Jang, H. Y., Park, K. C., and Jang, P. H., “Compensation of Torque Ripple of Brushless DC Motor Usign Feedforward Method,” Journal of Institute of Control Robotics and Systems, No. 10, pp. 736-739, 1997.
• Zhao, S. and Tan, K. K., “Adaptive Feedforward Compensation of Force Ripples in Linear Motors,” Control Engineering Practice, Vol. 13, No. 9, pp. 1081-1092, 2005. [https://doi.org/10.1016/j.conengprac.2004.11.004]