안내 로봇 실용화를 위한 비 관성센서 기반 옥외용 위치평가
2제주관광대학교 해군기술부사관계열
2Major of Technical Petty Officer, Jeju Tourism University
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This paper introduces a new outdoor localization method for practical application to guide robots. This method uses only encoder data from the robot’s wheels and non-inertial sensors, such as GPS and a digital compass, to guarantee ease of use and economy in real world usage without cumulative error. Position and orientation information from DGPS (Differential Global Positioning System) and a digital compass are combined with encoder data from the robot’s wheels to more accurately estimate robot position using an extended Kalman filter. Conventional robot guidance methods use different types of fusion that rely on DGPS. We use a very simple and consistent method that ensures localization stability by using the validation gate to evaluate DGPS reliability and digital compass data that can be easily degraded by various noise sources. Experimental results of the localization are presented that show the feasibility and effectiveness of the methods using a real robot in real world conditions.
Keywords:
Outdoor localization, Guide robot, Non-inertial sensors, Differential global positioning system, Digital compass키워드:
옥외 위치평가, 안내로봇, 비관성센서, 위성항법보정시스템, 전자나침반1. 서론
최근 지능로봇 기술을 실제에 응용하기 위한 연구가 다양하게 이루어지고 있다. 안내로봇은 가장 흥미로운 서비스 로봇 응용분야 중 하나이다. 안내로봇은 관광지에서 관광객, 대학교와 같은 대규모 시설의 탐방 객, 그리고 박물관 관람객 등을 인솔하면서 안내를 하는 로봇을 말한다. 안내로봇은 여러 곳으로 내방객을 스스로 안내하여야 하므로 자율주행능력이 있어야 하며 내방객과의 상호작용, 즉 자신이 위치한 장소에 대한 필요한 안내를 수행할 수 있는 능력이 필요하다.1 이와 같은 자율주행이나 위치에 따른 필요한 안내를 수행하기 위해서는 기본적으로 로봇 자신의 위치를 인식하는 위치인식(Localization)이 가장 중요하다.2
지금까지 실내 안내로봇에 대한 연구는 많이 수행되어왔다. 독일 본 대학에서는 박물관 안내용 로봇인 Rhino3를 개발하였으며, 미국의 카네기 멜론 대학에서는 Minerva4 안내로봇을 개발하여 Smithsonian 국립박물관에서 안내를 수행하게 하였다. 또한 연회장 웨이터역할을 하는 로봇 Alfred,5 학회 안내를 도와주는 도우미 로봇 Grace6 등이 개발되었다. 이 안내로봇들은 초음파, 카메라 및 레이저 센서 등을 사용하여 주변 환경을 인식하며 Markov 위치평가 방법을 이용하였다.7
그러나 이와 같은 기존의 안내로봇들을 실내안내용이기 때문에 옥외 안내로봇에 적용하기에는 적합하지 않다. 옥외 환경은 실내 환경에서처럼 위치정보를 제공하기에 알맞은 벽과 같은 구조화된 물체가 없으며 물체와 로봇이 이동할 수 있는 자유공간의 구별이 뚜렷하지 못할 뿐만 아니라, 활동 공간이 넓기 때문에 실내에서 주로 사용하는 스타게이저와 같은 위치 센서 등을 설치하기가 어렵기 때문에 실내 위치평가와는 달리 정밀한 위치평가가 어렵다.
또한 옥외환경은 실내와는 달리 구조화되지 않은 환경으로서 실내 위치평가에 많이 사용하는 환경지도와 같은 사전 환경정보 제공이 불가능하다. 아울러 옥외 지형은 실내 바닥보다 평탄하지 못하며 요철이 심하기 때문에 실내 위치평가에 주로 이용되는 Dead-Reckoning 위치평가 시에 오차가 심하게 발생한다. 이상과 같은 이유로 인해 옥외 위치평가는 기존 실내 위치평가 방법을 그대로 적용할 수 없으며 위치평가 성능 또한 실내보다 떨어질수 밖에 없다.
이에 따라 옥외 위치평가는 GPS에 의존 할 수 밖에 없다. 그러나 GPS는 기본적으로 위치 정밀도가 낮으며, 위성상태에 따라 일시적으로 위치정보를 주지 못하는 경우가 발생할 뿐만 아니라 위성궤도오차, 시계오차, 대기권 및 전리층 영향, 수신기 오차, 그리고 수신주변 환경에 따른 다중반사 효과 등으로 인해 위치정보의 신뢰성이 떨어지는 경우가 자주 발생한다. 따라서 자율 주행을 위한 로봇의 위치평가에 GPS를 단독으로 이용하기에는 적합하지 않다.
이와 같은 GPS의 문제점을 보완하기 위해 옥외 위치평가에는 자이로 및 가속도계 등으로 구성된 관성항법시스템(Inertial Navigation System, INS)을 추가적으로 이용하는 경우가 대부분이다.8-11 그러나 관성항법시스템은 유지 보수가 까다로울 뿐만 아니라 오차가 시간에 따라 누적되는 단점이 있다. 또한 영상 이미지나 레이저 스캐너를 GSP와 융합하여 위치평가를 수행하는 연구도 수행되었다.12-14
비 관성센서 만을 GPS와 융합하여 위치평가를 하는 연구도 수행되었다. Ohono와15 Thrapp16 등은 DGPS와 주행계를 융합하여 위치평가를 시도하였다. 또한 Zhang17 등은 주행계와 지자기센서를 GPS와 융합하는 방법을 제시하였는데, 이 들은 GPS 위치정보 신뢰성에 따라 위치평가 방법을 달리하는 스위칭 방법을 이용하였다. 이와 같은 비 관성센서들은 관선센서에 비해 정밀도가 떨어지므로 비 관성센서 기반 연구들은 대부분 정밀한 고가의 GPS를 이용하고 있으며, 위치정보의 신뢰성에 따른 일정한 조건을 경험적으로 정하고 그 조건에 따라 서로 다른 위치정보 융합방법을 이용하고 있다. 이와 같은 고가의 센서사용, 그리고 시스템 및 환경에 따라 달라질 수 있는 경험적인 정보 신뢰도 조건 설정 등은 안내로봇의 실용화라는 관점에는 적합하지 못하다.
Lim은1 저가의 저 정밀도 GPS와 엔코더 정보를 융합하여 위치를 평가하는 옥외 위치평가 방법을 제안하였다. 이 연구에서는 저가의 비 관성 센서 만을 사용함에도 불구하고 직선 경로에서는 위치평가 성능이 어느 정도 보장되었지만 곡선 경로에서는 그렇지 못하다는 결과를 보였다. 이것은 GPS는 위치정보는 제공하지만 방향정보를 제공하지 못하기 때문에 로봇의 방향은 전적으로 엔코더 정보에만 의존하기 때문이다.
본 논문에서는 옥외용 안내로봇 실용화 관점에서 경제적이고 유지관리가 쉬우며 적용이 용이한 비 관성센서 기반 옥외용 위치 평가 방법을 제안한다. 이 방법은 정밀도가 낮은 저가의 DGPS (Differential Global Positioning System)와 디지털 컴퍼스 및 로봇 바퀴에 부착된 엔코더 정보를 이용하여 로봇의 위치를 평가하는 것으로서, 기존 방법과는 달리 곡선 경로 및 DGPS신호가 수신되지 못하는 곳에서도 위치평가 신뢰성이 보장될 뿐만 아니라, 단순하고 일관성 있는 정보 신뢰성 평가 방법을 적용함으로써 DGPS와 디지털컴퍼스의 오차에 따른 정보 신뢰성 변화에 대해 위치평가의 안정성을 확보할 수 있다. 또한 개발된 방법의 효율성과 적용가능성을 실제 실험을 통하여 분석한다.
2. 위치평가
본 연구에서는 옥외용 안내로봇 실용화라는 관점에서 경제적인 저 정밀도 DGPS와 디지털컴퍼스 기반 위치평가방법으로서, DGPS의 위치정보(x, y) 및 디지털 컴퍼스의 방향정보 θ를 확장칼만필터(Extended Kalman Filter, EKF)를 이용하여 엔코더 정보와 융합함으로써 로봇의 최적의 위치를 평가한다. EKF 기반 위치평가는 엔코더 정보로부터 로봇의 현재 위치를 추정하는 위치추정 단계와 위치 센서로부터 측정된 위치 정보를 이용하여 추정된 위치를 갱신하는 위치갱신 단계로 구성된다.
2.1 시스템 및 측정모델
시스템 모델은 주어진 제어 입력 u(k)와 시간의 흐름에 따라 로봇의 위치 X(k) = (x(k), y(k), θ(k))T가 어떻게 변해 가는 지를 표현한 것으로서 일반적으로 다음과 같이 표현된다.
| X(k+1)=F(X(k), u(k)+w(k) | (1) |
여기서 F(X(k), u(k))는 비선형 상태천이함수이며 w(k)는 평균이 0이고 공분산이 Q(k)인 가우시안 잡음으로 가정한다.18
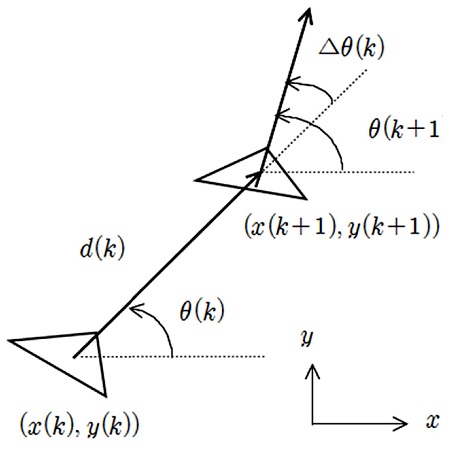
상태 천이함수 F(X(k), u(k))는 Fig. 1과 같은 관계에 의해 다음과 같이 표현된다.
| F(X(k), u(k))=(x(k)+d(k)cosθ(k)y(k)+d(k)sinθ(k)θ(k)+∆ | (2) |
여기서 제어입력인 u(k) = [d(k), Δθ(k)]T이며 d(k)는 이동거리, Δθ(k)는 회전을 나타낸다.
측정모델은 센서의 측정값과 로봇의 위치를 관계 짓는 모델로서 다음과 같이 표현된다.
| (3) |
여기서 v(k) 평균이 0이고 공분산이 R(k)인 가우시안 잡음으로 가정한다. z(X(k))는 로봇의 현재 위치 및 방향을 변수로 하는 측정 함수이다.
그러나 DGSP와 디지털 컴퍼스의 측정값은 로봇의 위치와는 아무런 기하학적 관계가 없기 때문에 z(X(k))는 단순히 두 센서의 측정값으로 구성된다. 즉,
| (4) |
여기서 (x, y)는 DGPS의 측정값이며 θ는 디지털 컴퍼스의 측정 값이다.
2.2 위치 및 측정값 예측
시스템 모델과 제어입력 u(k)를 이용하여 시간 k + 1에서의 새로운 로봇 위치 를 다음과 같이 예측한다.19,20
| (5) |
여기서 기호 ^은 예측 값을 의미한다. 이 예측에 연관된 공분산 P(k + 1|k)는 다음과 같이 표현된다.
| (6) |
이 식에서 ∇F는 상태 천이함수인 의 자코비안으로서 다음과 같다.
| (7) |
로봇의 새로운 위치에서 실제로 관측된 DGSP 및 디지털 컴퍼스의 값으로 구성되는 실측 값 m(k + 1)은 다음과 같이 표현된다.
| (8) |
다음으로 로봇의 새로운 위치 에서 측정할 경우 예측되는 DGPS 및 디지털 컴퍼스의 측정값 은 다음과 같이 추정한다. 즉, DGSP와 디지털 컴퍼스는 별다른 기하학적인 연관 없이 단지 에서의 위치와 방향정보를 제공하는 것이므로 는 단순히 그 자체로 표현된다.
| (9) |
2.3 측정값의 신뢰성 평가
성공적인 위치평가를 위해서는 부정확한 측정값의 배제가 필수적이다. 따라서 위성 상태, 대기권 및 통신상태, 주변 장애물 상태 등에 따라 발생하는 외란의 영향을 받아 신뢰성이 떨어진 DGPS 및 디지털 컴퍼스의 측정값을 제거하기 위하여 측정값의 신뢰성을 평가하여야 한다. 이를 위해 먼저 각 센서에 대응되는 예측 값과 실측 값의 차로 구성되는 Innovation 행렬 V(k + 1)을 다음과 같이 평가한다.
| (10) |
이 평가에 수반되는 공분산 s(k + 1)는 식(3)을 제곱하고 예측값을 중심으로 평균을 취함으로써 다음과 같이 구해진다.
| (11) |
여기서 ∇z는 식(4)의 자코비안이다.
이제 측정값의 신뢰성은 Maximum Likelihood 평가에서의 “Validation Gate”로 잘 알려져 있는 Mahalanobis 거리 δd를 다음과 같이 계산하여 결정한다.21
| (12) |
여기서 γ는 설계 변수이다. 만약 식(12)가 만족되면 그 측정값은 신뢰할 수 있는 것으로 판단하고, 그렇지 아니한 측정값은 신뢰할 수 없는 것으로 판단하여 EKF 위치평가에서 제외시킴으로써 위치평가의 신뢰성을 확보할 수 있다.
3. 시뮬레이션 평가
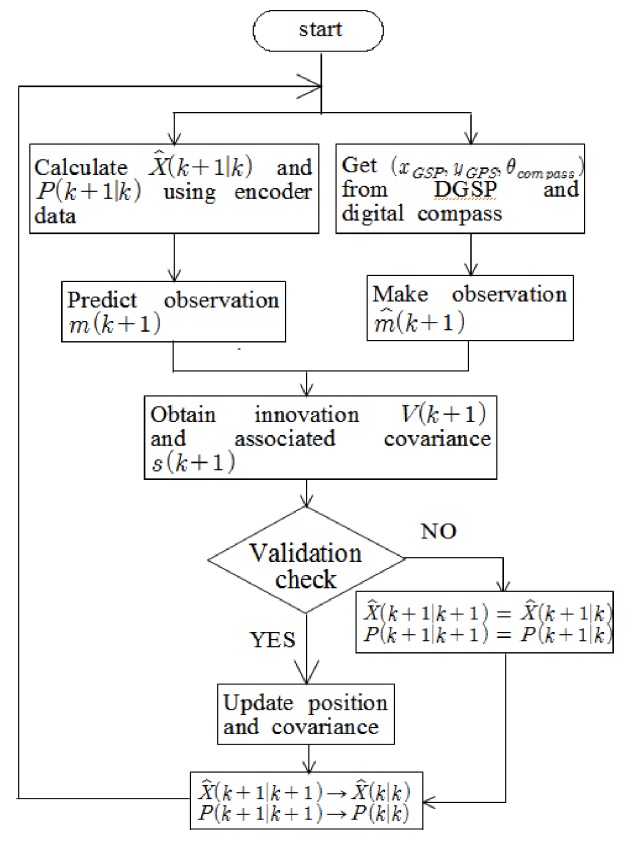
이상과 같이 개발된 옥외용 위치평가 방법의 성능을 시뮬레이션을 통하여 평가하였다. Table 1은 시뮬레이션에 필요한 통계학적 오차 특성을, 그리고 Fig. 2는 시뮬레이션을 위한 흐름도를 나타낸다. DGPS 및 디지털컴퍼스의 오차 특성은 제조사가 제공한 값을 이용하였다. 또한 DR 위치평가에서는 방향에 대한 오차가 가장 크게 누적되므로 방향에 대한 계통오차를 회전각도의 10%정도로 크게 가정하였다.
먼저 식(12)의 최적의 γ를 찾기 위해 여러 번의 시뮬레이션을 수행하였다. 그 결과 γ가 2에서 10사이의 값인 경우 안정한 위치 평가가 이루어짐을 알 수 있었으며 이에 따라 그 중간 값인 5를 γ값으로 설정하였다.
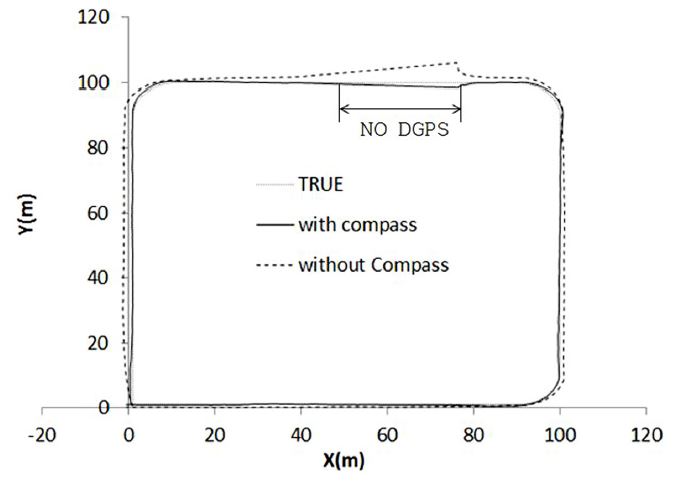
그림 3은 위치평가 시뮬레이션 결과를 나타낸다. 그림에서 붉은 색은 DGPS 및 디지털 컴퍼스 측정값을 모두 이용한 EKF 위치평가 결과이고 파란색은 디지털 컴퍼스를 제외한 EKF 위치평가 결과이다. 그림에서 “No DGPS”로 표시된 구간은 DGPS 정보가 제공되지 아니하거나 오차가 큰 정보가 제공된 구간으로서 단지 엔코더와 디지털 컴퍼스만으로 EKF 위치평가기 수행된 구간을 나타낸다. 이 구간의 길이는 약 60 m 정도이며 위성상태로 인해 DGPS 정보가 두절되거나 위성상태, 전리층 상태 또는 주변 장애물에 의해 DGPS 위치오차가 크게 발생한 상황을 시뮬레이션 한 것이다. 그림에서 알 수 있듯이 디지털 컴퍼스가 사용되지 아니한 위치 평가에서는 No DGPS 구간에서 위치 오차가 급격하게 발생하고 있지만 디지털 컴퍼스의 방향정보를 이용한 위치평가에서는 오차가 크지 않음을 보이고 있다.
일반적으로 엔코더 정보만으로 위치를 평가하는 경우 10 m 이내의 단거리 주행 시에는 위치오차가 크게 발생하지 않지만 주행 거리가 늘어남에 따라 방향오차가 누적되어 위치오차가 크게 발생한다. 그러나 Fig. 3의 결과는 엔코더만의 위치평가에 디지털 컴퍼스를 추가로 이용할 경우 방향오차가 누적되지 않기 때문에 위치오차가 현격히 줄어든다는 것을 나타낸다.
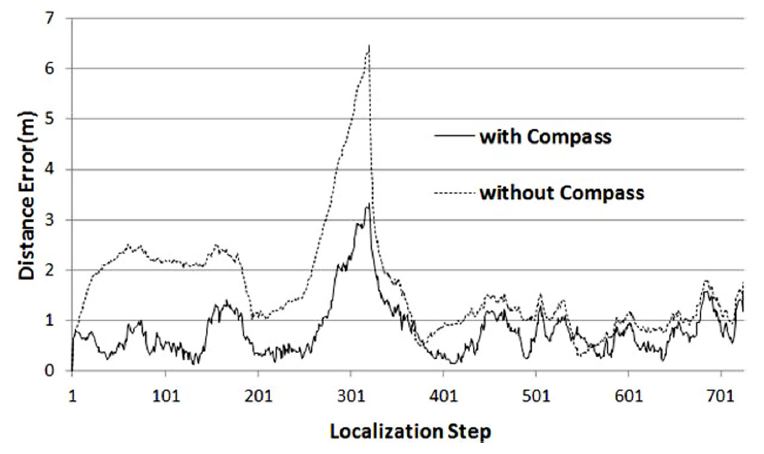
Fig. 4는 위치오차 특성을 나타낸다. 그림에서 위치평가 스텝 300 좌우에서 위치오차가 크게 발생한 것은 No DGPS 구간이기 때문이다. 디지털 컴퍼스가 없는 경우의 오차 평균과 표준편차는 각각 1.7 m 및 1.1 m였으나 컴퍼스가 사용 된 경우는 평균이 0.8 m, 표준편차가 0.5 m로 나타났다. 따라서 엔코더와 DGPS만의 위치평가 보다 디지털 컴퍼스를 추가로 사용함으로써 위치오차를 현저히 줄일 수 있다는 것을 알 수 있다.
4. 실험 및 결과
4.1 실험방법
Fig. 5는 실험에 이용된 Pioneer-3DX 로봇을 나타낸다. 이 로봇에는 저가 저 정밀도의 DGPS와 디지털 컴퍼스가 장착되어 있으며 그 사양은 Table 2에 나타내었다. 실험 장소는 Fig. 6과 같은 운동장이었으며, 그림에 X 표로 나타낸 6곳을 기준위치로 설정하였다. 로봇 경로상의 모든 위치의 실제 좌표를 알기 힘들기 때문에 사전에 6곳의 실제좌표를 측정 한 후 이것을 기준좌표로 설정한 것이다.
리모컨을 이용하여 로봇이 각 기준위치를 통과하게 주행시킨 후 각 기준위치에 대한 오차를 평가하는 방법으로 실험을 수행 하였으며 로봇의 이동 속력은 평균 0.4 m/s이었다. DGP의 경위도 좌표는 로봇의 좌표와 통일시키기 위해 가상원점에 대해 m단위의 TM (Transverse Mercator) 좌표계로 환산하여 사용하였다.
4.2 실험결과
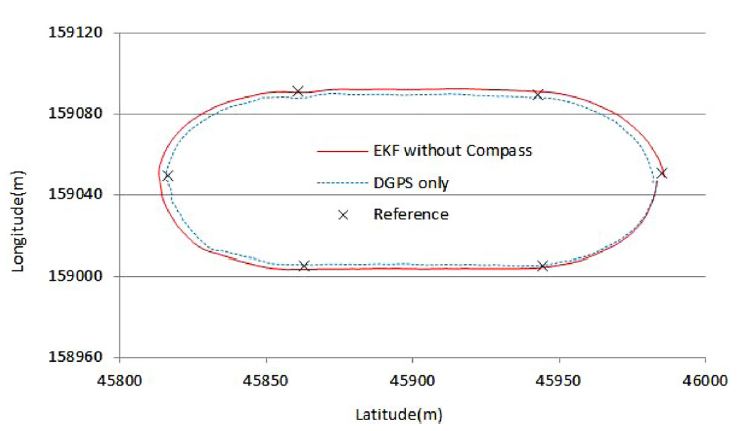
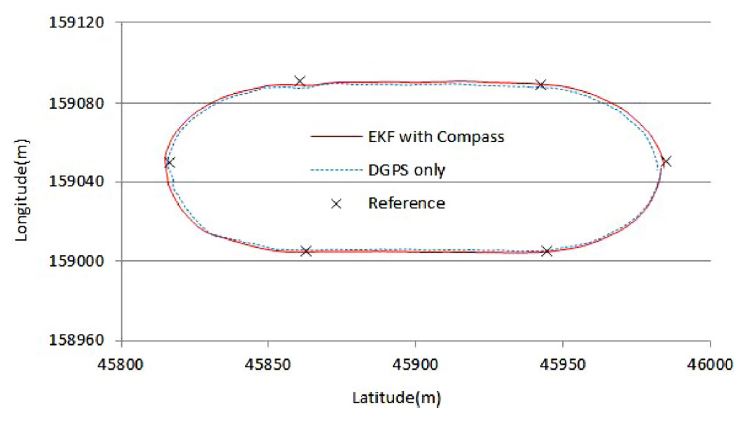
Figs. 7과 8은 한번의 주행 시에 컴퍼스를 사용하지 아니한 경우와 사용한 경우의 위치평가를 동시에 수행하여 나타낸 결과이다. 실험 전체경로는 약 430 m이며 각 그림에서 점선은 DGPS 단독에 의한 위치평가 결과이며 실선은 EKF 위치평가 결과를 나타낸다.
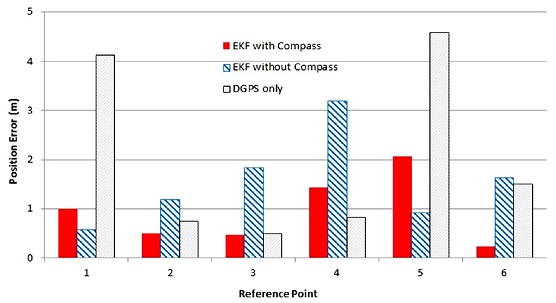
두 위치평가의 성능을 정량적으로 비교하기 위해 각 기준 위치에서의 오차를 Fig. 9에 나타내었다. 컴퍼스를 사용하지 아니한 경우는 4곳의 기준위치에서 DGPS 단독인 경우보다 위치평가 성능이 떨어지는데 반해 컴퍼스를 이용하는 경우에는 한곳의 기준위치를 제외하고는 모든 기준위치에서 DGPS 단독의 경우보다 우수한 결과를 보이고 있다.
Table 3에는 각 위치평가 오차의 특성을 나타내었다. 표를 분석해 보면 컴퍼스를 사용하는 경우가 가장 위치평가 성능이 우수하며 DGPS 단독의 경우가 가장 성능이 낮다. 또한 DGPS 단독의 위치평가에 비해 컴퍼스를 쓰는 경우는 평균오차 기준으로 60%이상 위치정밀도가 개선되는데 반해 컴퍼스를 쓰지 않는 경우는 크게 개선되지 않음을 알 수 있다.
DGPS 단독의 경우 최대오차는 4.6 m 정도로서, 이는 로봇이 자율적으로 주행을 하기 위해서는 최소 도로 폭이 9m 이상은 되어야 한다는 것을 의미한다. 반면에 컴퍼스를 사용하는 EKF 위치평가의 최대오차는 2.2 m 정도이므로 도로 폭이 4 m 정도이면 자율 주행이 가능하다. 따라서 제안된 저가의 DGPS 및 디지털 컴퍼스를 이용한 위치평가 방법은 관광안내로봇, 캠퍼스 안내로봇, 그리고 골프장 캐디로봇과 같은 비교적 정밀도가 덜 요구되는 옥외용 로봇의 자율 주행에 실질적으로 적용될 수 있을 것으로 사료된다.
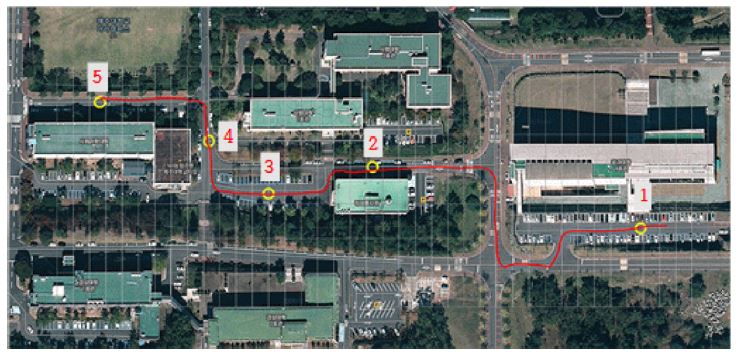
Fig. 10은 위치센서에 영향을 줄 수 있는 장애물 및 경사지 환경에서의 위치평가 결과를 나타낸다. 경로의 길이는 약 700 m 정도이며 출발점(Fig. 10의 1 위치)과 최종지점(Fig. 10의 5 위치) 사이의 고도 차는 약 20 m이고, 원으로 표시된 5곳의 위치에서 오차를 측정하였으며, 최대오차는 2 위치에서 2.7 m로 관측되었다. 2 위치는 건물이 밀집한 지형으로서 DGPS및 디지털 컴퍼스가 장애물의 영향을 영향을 받아 위치정보에 오차가 크게 발생한 것으로 판단된다. 그러나 전체적인 평균 오차는 1.4 m 정도로서 비교적 양호한 결과라 할 수 있다.
5. 결론
본 논문에서는 옥외용 로봇의 자율주행에 실질적으로 적용 가능한 비관성센서 기반 위치평가 방법을 제안하고 그 성능을 시뮬레이션 및 실험으로 평가하였다. 이 방법은 정밀도가 낮은 저가의 DGPS와 디지털 컴퍼스의 위치 및 방향정보의 신뢰성을 평가하여 신뢰성이 있는 정보 만을 확장 칼만 필터를 이용하여 엔코더 정보에 의해 예측된 위치와 융합하여 최적의 위치를 평가하는 방법이다. 또한 디지털 컴퍼스를 도입함으로써 엔코더와 DGPS 만의 위치평가에 비해 성능이 향상됨을 보였다. 실제 로봇을 이용한 실험 결과 제안된 위치평가 방법은 비교적 정밀도가 덜 요구되는 옥외용 안내 로봇의 자율 주행에 실질적으로 적용할 수 있을 정도의 성능이 확보 됨을 보였다.
Acknowledgments
이 논문은 2016년도 제주대학교 교원성과 지원사업에 의하여 연구되었음.
REFERENCES
- Lim, J. H., “A Study on a Localization System for Tour Guide Robot,” J. Korean Soc. Precis. Eng., Vol. 26, No. 1, pp. 1-8, 2009.
-
Lim, J. H. and Leonard, J. J., “Mobile Robot Relocation from Echolocation Constraints,” IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 22, No. 9, pp. 1035-1041, 2000.
[https://doi.org/10.1109/34.877524]

- Buhmann, J., Burgard, W., Cremers, A. B., Fox, D., Hofmann, T., et al., “The Mobile Robot RHINO,” Ai Magazine, Vol. 16, No. 2, pp. 31-38, 1995.
-
Thrun, S., Beetz, M., Bennewitz, M., Burgard, W., Cremers, A. B., et al., “Probabilistic Algorithms and the Interactive Museum Tour-Guide Robot Minerva,” International Journal of Robotics Research, Vol. 19, No. 11, pp. 972-999, 2000.
[https://doi.org/10.1177/02783640022067922]

- Maxwell, B., Meeden, L., Addo, N., Brown, L., Dickson, P., et al., “Alfred: The Robot Waiter Who Remembers You,” Proc. of the AAAI Workshop in Robotics, pp. 1-12, 1999.
-
Simmons, R., Coldberg, D., Goode, A., Montemerlo, M., Roy, N., et al., “GRACE: An Autonomous Robot for the AAAI Robot Challenge,” Ai Magazine, Vol. 24, pp. 51-72, 2003.
[https://doi.org/10.21236/ADA434943]

-
Fox, D., Burgard, W., and Thrun, S., “Markov Localization for Mobile Robots in Dynamic Environments,” Journal of Artificial Intelligence Research, Vol. 11, pp. 391-427, 1999.
[https://doi.org/10.1613/jair.616]

-
Toledo-Moreo, R., Zamora-Izquierdo, M. A., Ubeda-Miarro, B., and Gomez-Skarmeta, A. F., “High-Integrity IMM-EKF-Based Road Vehicle Navigation with Low-Cost GPS/SBAS/INS,” IEEE Transactions on Intelligent Transportation Systems, Vol. 8, No. 3, pp. 491-511, 2007.
[https://doi.org/10.1109/TITS.2007.902642]

-
Almagbile, A., Wang, J., and Ding, W., “Evaluating the Performances of Adaptive Kalman Filter Methods in GPS/INS Integration,” Journal of Global Positioning Systems, Vol. 9, No. 1, pp. 33-40, 2010.
[https://doi.org/10.5081/jgps.9.1.33]

-
Han, S. and Wang, J., “Integrated GPS/INS Navigation System with Dual-Rate Kalman Filter,” GPS Solutions, Vol. 16, No. 3, pp. 389-404, 2012.
[https://doi.org/10.1007/s10291-011-0240-x]

-
Chen, X., Shen, C., Zhang, W. B., Tomizuka, M., Xu, Y., et al., “Novel Hybrid of Strong Tracking Kalman Filter and Wavelet Neural Network for GPS/INS during GPS Outages,” Measurement, Vol. 46, pp. 3847-3854, 2013.
[https://doi.org/10.1016/j.measurement.2013.07.016]

-
Agraw, M. and Konolige, K., “Real-Time Localization in Outdoor Environments Using Stereo Vision and Inexpensive GPS,” Proc. of the 18th International Conference on Pattern Recognition, pp. 1063-1068, 2006.
[https://doi.org/10.1109/ICPR.2006.962]

-
Limsoonthrakul, S., Dailey, M. N., and Parnichkun, M., “Vehicle Localization Using GPS, Compass, and Machine Vision,” Proc. of the International Conference on Intelligent Robots and Systems, pp. 3981-3986, 2009.
[https://doi.org/10.1109/IROS.2009.5354042]

-
Kümmerlem, R., Triebel, R., Pfaff, P., and Burgard, W., “Monte Carlo localization in Outdoor Terrains Using Multilevel Surface Maps,” Journal of Field Robotics, Vol. 25, No. 6, pp. 346-359, 2008.
[https://doi.org/10.1002/rob.20245]

- Ohno, K., Tsubouchit, T., Shigematsut, B., Maeyamas, S., and Yuta, S., “Outdoor Navigation of a Mobile Robot between Buildings Based on DGPS and Odometry Data Fusion,” Proc. of the IEEE International Conference on Robotics and Automation, pp. 1978-1984, 2003.
- Thrapp, R., Westbrook, C., and Subramanian, D., “Robust Localization Algorithms for an Autonomous Campus Tour Guide,” Proc. of the IEEE International Conference on Robotics and Automation, pp. 2065-2071, 2001.
-
Zhang, Y. and Chong, K. T., “A GPS/DR Data Fusion Method Based on the GPS Characteristics for Mobile Robot Navigation,” International Journal of Control and Automation, Vol. 7, No. 10, pp. 119-132, 2014.
[https://doi.org/10.14257/ijca.2014.7.10.12]

- Gelb, A, C., “Applied Optimal Estimation,” MIT Press, 1973.
-
Smith, R. and Cheeseman, P., “On the Representation and Estimation of Spatial Uncertainty,” International Journal of Robotics Research, Vol. 5, No. 4, pp. 56-68, 1987.
[https://doi.org/10.1177/027836498600500404]

-
Leonard, J. J. and Durrant-White, H. F., “Direct Sonar Sensing for Mobile Robot Navigation,” Springer, 1992.
[https://doi.org/10.1007/978-1-4615-3652-9]

-
Bar-Shalom, Y., Fortman, T. E., and Cable, P. G., “Tracking and Data Association,” Journal of the Acoustical Society of America, Vol. 87, No. 2, pp. 918-919, 1990.
[https://doi.org/10.1121/1.398863]