비행체 내진설계를 위한 동흡진기 설계와 유한요소해석 모델 구축 및 시험

1. 서론

지상용 이동형 장비, 항공기, 무인기 등의 기계 시스템은 그 시스템의 활용도 향상을 위해 다양한 성능의 탑재체를 설치하여 운용한다. 이때 기계 시스템에 설치된 탑재체는 기계 시스템과 목표물과의 거리, 방향 등의 정보를 파악하여 운용자에게 전달하며, 운용자가 그 정보를 활용하도록 하는 역할을 수행한다.

기계 시스템에 설치된 탑재체는 시스템의 운용환경에 따라 각각의 설계 요구조건을 갖게 된다. 특히 비행구조물 등의 고기동 플랫폼에 설치되는 탑재체의 경우 타 시스템에 비해 가혹한 운용 환경에 노출된다. 비행구조물의 운용 시 비행구조물에는 추진력, 공력, 구조물의 관성 및 탄성 등의 상호작용에 의해 진동이 발생하게 되며, 이때 발생한 진동은 비행구조물과 탑재체의 인터페이스를 통해 탑재체 내부로 전달된다. 이렇게 전달된 진동은 탑재체 내부 전자장비 및 구동장비의 구동특성에 영향을 주어 탑재체 성능에 악영향을 줄 뿐만 아니라 내구성에 영향을 미쳐 탑재체의 수명을 악화 시킨다.

탑재체를 설치한 비행구조물의 기동성능 향상 추세에 따라 비행구조물의 추진력은 점점 증가되는 반면, 경량화 소형화 설계에 대한 요구가 증가하고 있다. 비행구조물의 추진력 증가는 탑재체 와의 인터페이스를 통해 전달되는 진동을 증가시키며, 따라서 탑재체 내부의 진동응답 역시 증가하게 된다. 또한 탑재체의 경량화, 소형화 설계는 탑재체 강성을 저하시켜 탑재체 내부 진동응답을 크게 증폭시키기 때문에 이를 감소 혹은 소산시키는 설계가 진행되어야 한다. 이런 탑재체에 작용하는 진동은 여러 가지 진동모드의 조합형태를 가지는데 먼저 저주파 진동모드에 의한 진동은 탑재체 주 구조물의 강성에 의해 발생하게 된다. 저주파 진동모드의 진동은 변위가 크기 때문에 탑재체 내부 구동장비의 구동 성능에 영향을 미치고, 플랫폼 파손 원인이 된다. 반면 고주파 진동모드는 탑재체 운용 시 내부 구성품 간 상대운동에 의해 발생되어 탑재체 내부 전자모듈 성능에 영향을 준다. 따라서 탑재체 플랫폼 및 전자모듈 파손 방지를 위해 저주파 및 고주파 모드의 진동을 모두 감소 시키는 것을 고려해야 한다.

기존 외팔 보 형태를 갖는 구조물에 발생하는 진동응답을 줄이는 방법으로 구조물 설계 시 구조보강을 통하여 구조물 강성을 증가시켜 구조물 유연모드에 의한 리셉턴스(Reacceptance)를 줄이는 방법이 주로 사용되었다. 이후 복합재료의 발달로 구조물에 점탄성물질 적용 및 설계 최적화를 통해 외팔보 형태를 갖는 구조물의 진동을 최소화 하는 방법에 대한 이론적, 시험적 연구가 진행되었다. 하지만 구조물의 강성을 증가시키는 방법은 탑재체 플랫폼의 무게를 증가시켜 탑재체의 소형화, 경량화 개발 목적에 부합하지 않으며, 탑재체 무게중심의 변화로 인한 불균형을 초래한다. 또한 고온 환경에 노출되는 탑재체는 내부 열에 의해 점탄성 재료의 변형 및 성능 저하가 발생할 수 있기 때문에 적용에 한계가 있다.^1-3

외팔보 형태의 구조물에 발생하는 진동응답 저감 방법으로 감쇠기를 적용하는 연구가 진행되었는데 Eric. Kathe는 포신의 진동응답 감소를 위해 포신 끝단에 스프링 로드(Spring Rod)다발과 진동흡수용 감쇠질량(Absorber Mass)을 단 수동형 질량 감쇠기의 스프링 로드의 개수에 따른 진동감쇠 효과에 대한 연구를 수행하였다. 이런 수동형 질량 감쇠기의 설치는 공간 및 중량에 제한을 가지고 있어 탑재체 적용에 어려움을 가지고 있다.^4,5

2011년 곽동기 등은 외팔보 형태를 갖는 포신의 진동응답 감쇠를 위해 동흡진기를 적용하고 이에 대한 이론적, 시험적 및 해석적 검증을 진행하였다. 화포 포신의 경우 외팔보의 형태를 갖는 구조물 중에서도 가장 단순한 구조를 갖기 때문에 이론해를 구해는 것이 가능하다.^6,7

탑재체는 외팔보의 형태를 갖는 기계 구조물이다. 외팔보 형태를 갖는 대부분의 기계 구조물의경우 오일러 보 이론(Euler Beam Theory) 혹은 티모센코 보 이론(Timoshenko Beam Theory)을 활용하여 이론해를 도출할 수 있다. 하지만 탑재체의 경우 기계 구조물과 다양한 전자 모듈로 구성되어 있고, 특히 세장비가 작아 이론해를 구하는데 제약을 가지고 있다. 이와 같이 이론해를 구하기 어려운 경우 유한요소해석(Finite Element Analysis, FEA)을 설계에 활용할 수 있다.^8,9

동흡진기는 기계 구조물 중 일정 진동수로 진동하는 큰 진동체에 작은 질량-스프링계를 부착하여 진동을 줄이는 방법으로, 일정 진동수로 진동하는 진동체에 부착된 질량-스프링계의 동흡진기 고유진동수를 진동체의 진동수와 같도록 만들어 진동체의 진동을 줄이거나 없앨 수 있는 감쇠장치 이다. 이런 동흡진기는 큰 공간 및 중량증가 없이 설치 가능하여, 공간 제약으로 인해 감쇠장치를 설치할 수 없는 경우 및 감쇠장치를 통한 진동 저감에 한계가 있는 경우, 구조물의 정렬이 매우 중요한 설계요구사항 이어서 감쇠 장치 설치로 인해 발생되는 변위가 문제되는 경우, 이미 설계가 완료된 기계 시스템에 진동 저감이 필요한 경우 또는 국부진동모드에 대한 진동저감이 필요할 경우 유용하다. 따라서 이런 동흡진기의 특성활용 시 탑재체가 가지는 무게, 공간 등의 문제를 최소한의 설계변경으로 해결할 수 있다.

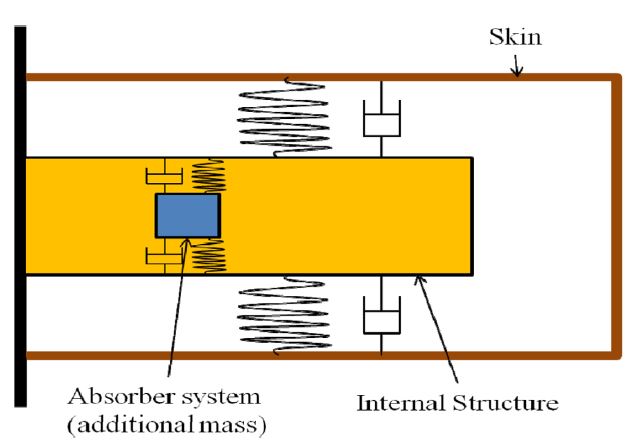
본 연구에서는 기존에 제작된 탑재체의 설계변경을 최소화 하면서 탑재체 내부 진동응답 저감방안으로 탑재체 내부 구성품 설계 및 배치 시 동흡진기의 운용 개념을 적용하는 것에 대한 연구를 진행하였다(Fig. 1).

Fig. 1

Concept of dynamic vibration absorber

운용환경에서 탑재체의 안전성 및 신뢰성 검증을 위해 유한요소해석을 수행하여, 탑재체의 진동응답을 도출하였고, 구조진동시험을 통해 검증하였다.

2. 본론

2.1 FEA 모델 구축 절차

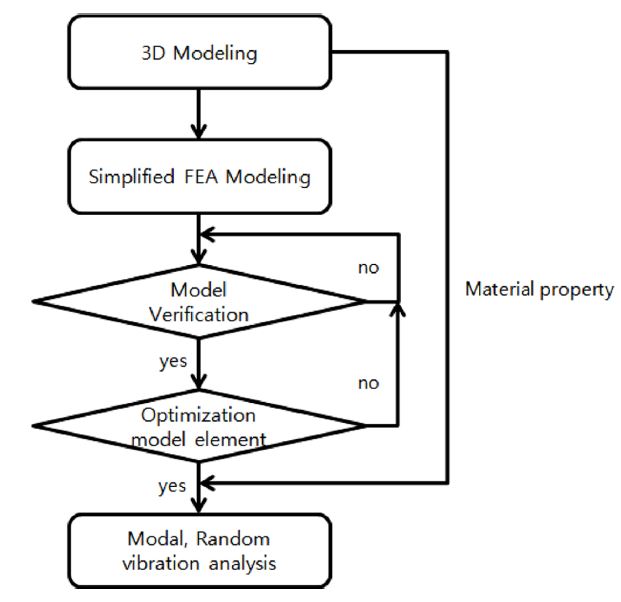
탑재체 내부 전자모듈 및 케이블 등 모든 구성품을 고려한 FEA 모델 구축 및 유한요소해석 진행 시 많은 비용이 소요된다. 따라서 이런 비용을 최소화 하기 위해 최소의 절점 및 요소로 구성하면서도 탑재체의 동적 특성을 정확하게 반영하여 해석해야 한다. 운용환경에서 탑재체가 받게 되는 진동 및 그 진동응답은 1, 2, 3차 주요 모드에 영향 받는데 이런 특성을 반영하고, 해석에 요구되는 비용을 최소화 하기 위해 탑재체의 단순화 모델(Simplified-FEA)을 모델링 하였다. 모델링 시 구조물의 주요모드에 미치는 영향이 큰 플랫폼 강성은 고려하고, 구조물의 주요모드에 미치는 영향이 작은 내부 전자모듈의 강성은 무시하여 집중질량으로 처리하여 해석에 소모되는 비용을 최소화 하였다.

탑재체 FEA 모델의 해석 값과 시험 결과의 비교 검증을 위해 구조진동시험의 조건을 반영하여 Fig. 2의 절차를 통해 탑재체의 FEA 모델을 모델링 하였다.

Fig. 2

Finite element modeling procedure

2.2 FEA 모델 해석

2.2.1 시험 치구 공진주파수 검증 해석

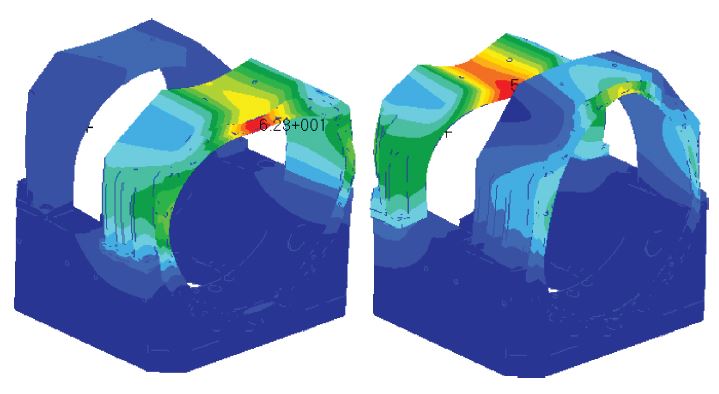
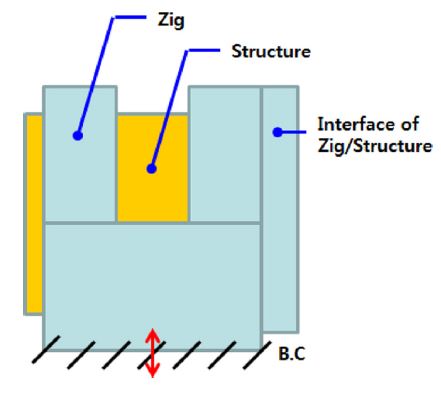
탑재체의 설계 개념과 설치 방안을 고려할 때 탑재체는 외팔보구조물로 분류할 수 있다. 따라서 탑재체 진동시험 수행 시 탑재체와 비행구조물의 인터페이스를 경계조건으로 하는 치구를 설계하여 시험에 반영할 때 실제 운영조건과 가장 유사한 시험 결과를 얻을 수 있다고 판단된다. 하지만 장비의 가치 및 안전성을 고려하여 탑재체 인터페이스 및 동체(Skin)를 같이 구속하는 형태의 치구를 설계하였으며, Mode 해석을 통해 치구의 동특성을 확인하였다(Fig. 3).

Fig. 3

FEA model of zig

탑재체 시험용 치구 해석 결과 치구의 1, 2차 공진주파수는 각각 843, 1199 Hz로 확인된다. 이는 기 제작되어 운용되고 있는 탑재체의 1, 2, 3차 주요모드의 공진주파수 영역인 100 - 500 Hz 대역과 충분히 이격 되어있어 진동 시험 및 해석에 적용 가능하다고 판단된다(Fig. 4) (Table 1).

Fig. 4

FEA modal result (Zig) of mode 1, 2

Table 1

Result of modal analysis of zig

2.2.2 탑재체 해석 모델

동흡진기가 적용된 탑재체의 동적 거동 예측을 하기 위해 우주항공분야에서 주로 사용하고 있는 전문 구조해석 프로그램인 MSC. Patran 2012와 Nastran 2012을 사용하여, 유한요소 모델을 구축하였다.

탑재체의 구조 특성을 감안하여 Tet 10, Hex 8 등의 3D Solid 요소와 Quad 4의 2D Shell 요소를 사용하였으며, 힌지 및 체결부는 RBE 2와 Bush, Beam 요소를 적용 단순화 하였다. 탑재체 주요모드에 강성으로서 미치는 영향이 작은 내부 전자모듈은 집중 질량으로 표현하여 RBE 3요소로 연결하였으며,최종적으로 완성된 해석 모델을 632,466개의 절점과 389, 249요소로 구성하였다(Fig. 5).

Fig. 5

FEA modeling of structure

2.2.3 해석 조건

탑재체에 적용된 동흡진기의 진동저감 효과를 유한요소해석으로 비교하기 위해 매개변수연구를 진행하였다.

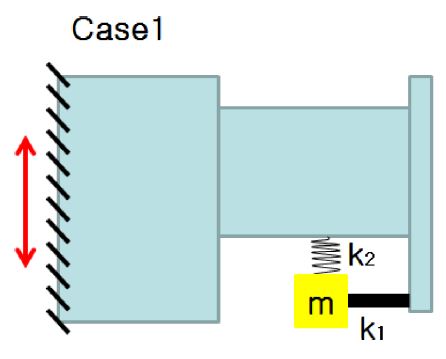
Case 1 은 외팔보 형태의 동흡진기를 적용한 모델이며, 2개의 스프링 요소로 구성된다(Fig. 6).

Fig. 6

Case 1 structure with 2 spring vibration absorber

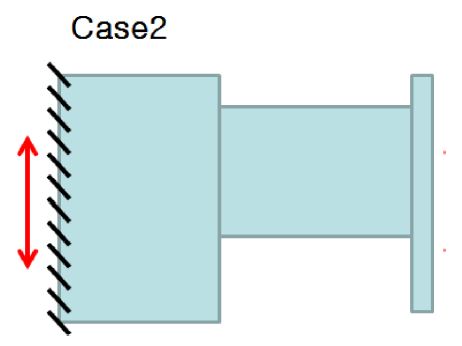
Case 2 는 동흡진기가 적용되지 않은 탑재체이다(Fig. 7).

Fig. 7

Case 2 structure without vibration absorber

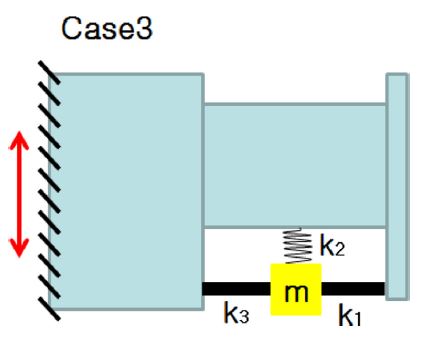
Case 3 은 외팔보 형태의 동흡진기를 적용한 모델이며, 3개의 스프링 요소로 구성된다(Fig. 8).

Fig. 8

Case 3 structure with 3spring vibration absorber

탑재체 FEA 모델의 해석 조건과 구조 진동시험 조건 일치를 위해 구조진동시험 치구 모델을 FEA 모델에 적용하였으며, 해석에 적용한 물성치는 Table 2과 같다.

Table 2

Material property of structure

2.2.4 해석 결과

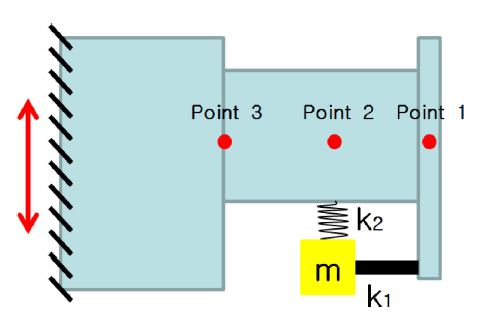
탑재체 FEA 모델 진동응답을 확인하기 위해 Random Vibration 해석을 진행하였다. 동흡진기의 설치위치 확정을 위해 치구를 제외한 탑재체의 단독 FEA 모델의 모드 해석을 별도로 수행하였으며, 그 결과를 통해 진동응답 측정위치 및 동흡진기 설치 위치를 도출하였다. 진동응답 측정위치는 동흡진기 설치 위치와의 연관성, 탑재체 내 구동부 및 주요 전자모듈 위치, 탑재체 내 큰 진동응답 발생 위치 등을 고려하여 선정하였으며, 각 위치의 진동응답 해석결과를 비교하였다(Fig. 9).

Fig. 9

The vibration measuring points of structure

탑재체 진동해석 하중조건은 치구 바닥 가진 조건이며, 시험진동 규격 MIL-STD-810 g의 진동규격을 적용하였다(Fig. 10).

Fig. 10

The boundary condition of structure

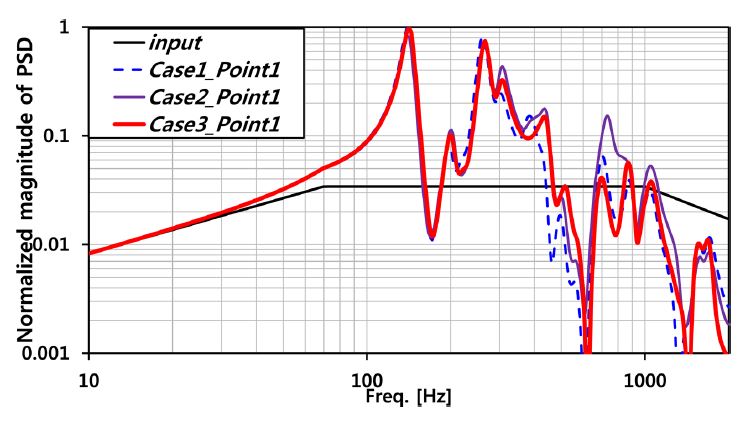
Point 1 위치의 해석결과 비교 시 동흡진기 설치 유무에 따라 300 - 1000 Hz 주파수영역에서 진동응답 변화가 발생하며, 동흡진기가 설치되지 않은 Case 2의 경우 보다 진동응답이 저감됨을 확인하였다(Fig. 11). 동흡진기가 설치된 Case 1, 3의 경우 각각 11%, 9%의 진동저감 효과를 확인할 수 있다(Table 3).

Fig. 11

Comparison results (FEA) of the point 1

Table 3

Normalized grms result of point 1

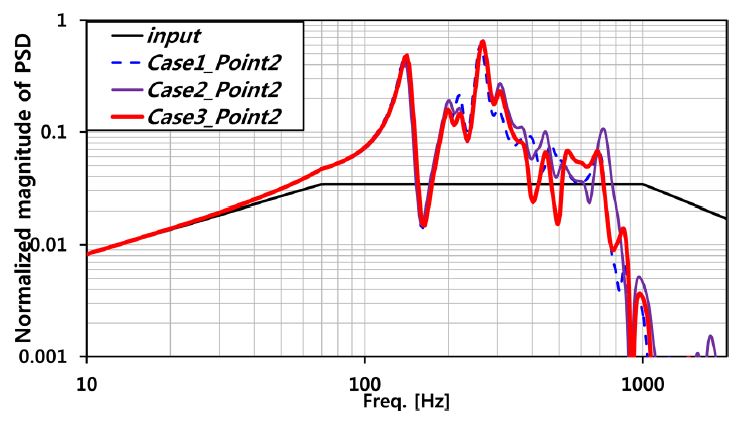
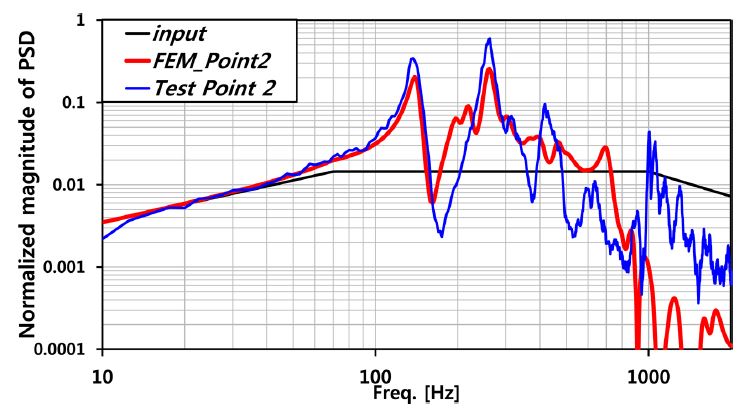
Point 2 위치의 해석결과 비교 시 300 - 1000 Hz 주파수영역에서 진동응답 변화가 발생함을 확인하였다(Fig. 12). 동흡진기가 설치된 Case 1, 3에서 각각 7%, 6%의 진동저감 효과를 확인할 수 있다(Table 4).

Fig. 12

Comparison results (FEA) of the point 2

Table 4

Normalized grms result of point 2

Table 5

Normalized grms result of point 3

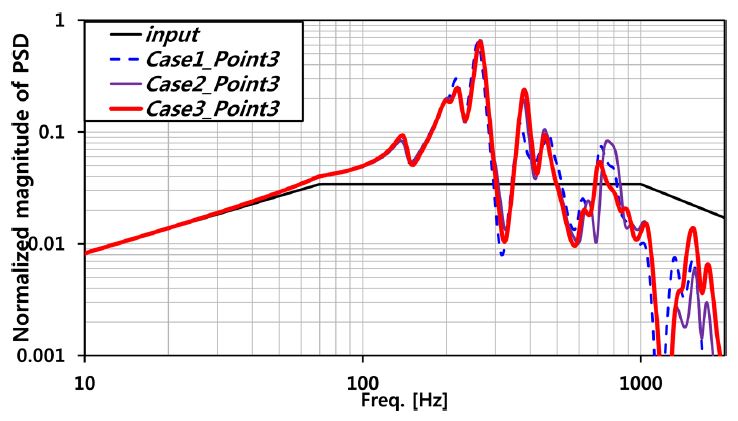
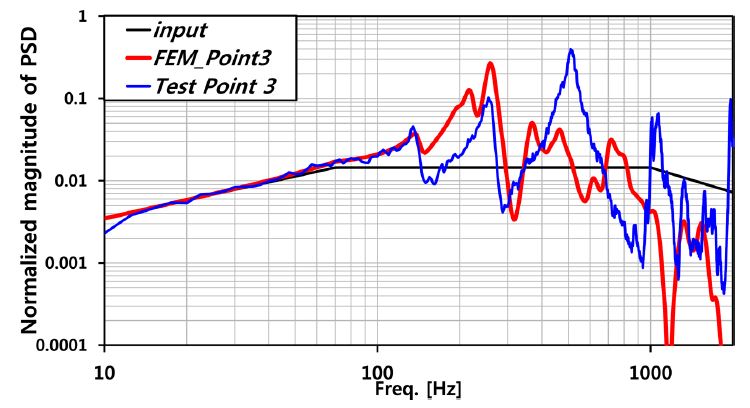
동흡진기가 설치 부에서 가장 먼 곳이 위치한 Point 3은 동흡진기 설치에 따른 진동응답 저감 효과가 거의 발생하지 않았다(Fig. 13) (Table 4).

Fig. 13

Comparison results (FEA) of the point 3

해석 결과 동흡진기를 설치 위치에서 가까운 Point 1, 2의 경우 상당한 진동저감 효과가 있음을 확인하였다. 기존 탑재체 설계 시 탑재체의 강성을 증가시켜 진동응답을 감소시키는 방법이 주로 고려되었고, 그에 따라 체결 부를 추가하는 설계가 많이 진행되었다. 동흡진기의 역시 체결 부위가 증가하면 진동응답이 완화될 것으로 예상하였으나 해석 결과 체결부위가 많은 Case 3 보다 Case 1이 더 큰 진동저감 효과를 가짐을 확인하였다.

2.3 탑재체 구조시험 결과 비교 검증

동흡진기의 진동저감효과 검증을 위해 가장 많은 진동저감이 발생한 Case1에 해당하는 탑재체를 제작하여 구조진동시험을 수행하였고, 이를 FEA 모델 해석 결과와 비교 검증하였다. 해석 및 시험간 오차를 줄이기 위해 구조시험용 치구 구성품 중 상부 덮개를 제외한 부분을 일체형으로 제작하였다. 구조진동시험은 Famtech 사의 Gt-800 m 가진기를 이용하였으며, 정확한 진동 입력을 위하여 2개의 컨트롤 센서를 시험 치구 양단에 설치하였다(Fig. 14).

Fig. 14

Set of random vibration test

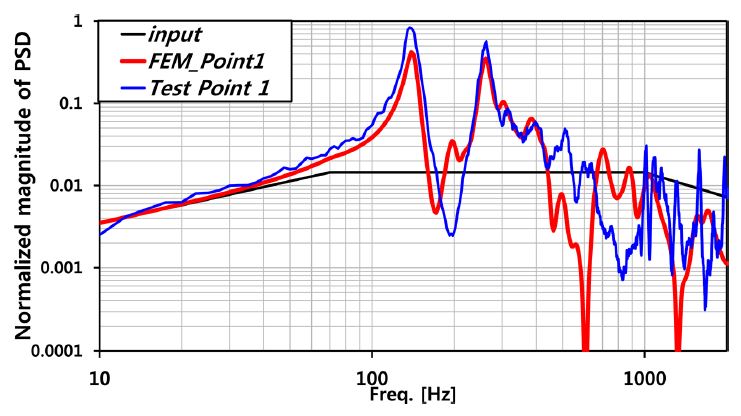
Figs. 15부터 17은 Point 1, 2, 3의 탑재체 FEA 모델 해석 결과와 시험 결과를 비교한 결과이다. Point 1, 2의 진동응답은 탑재체의 주요모드인 1, 2차 모드에 크게 영향 받음을 확인할 수 있으며, 탑재체 구조해석 결과와 시험결과의 1, 2차 공진주파수가 1% 오차 이내로 일치함을 확인하였다. Point 3의 진동응답은 탑재체 2차 모드와 내부 모듈에 의한 국부 모드에 주로 영향 받음을 확인할 수 있으며, 고 주파수 영역에서 해석결과와 시험결과가 오차가 발생함을 확인할 수 있다.

Fig. 15

Comparison results of the point 1

Fig. 16

Comparison results of the point 2

Fig. 17

Comparison results of the point 3

고 주파수 영역에서 발생한 시험과 해석간 오차는 다음의 원인에서 기인한다고 판단된다.

첫 번째 원인은 진동시험 치구 모델 및 탑재체 간 인터페이스 접촉 조건 단순화 과정에서 발생된 오차로 판단된다. 실제 탑재체와 시험 치구 간 고정은 후방 인터페이스의 체결, 탑재체/시험 치구 간 실리콘 패드 면 접촉 2가지로 구분된다. 이중 실리콘 패드의 면 접촉 조건을 1D Spring Bush 요소와 RBE2 MPC 구속 조건으로 단순화 하였는데 그 결과 치구 모델의 공진주파수인 843, 1199 Hz 의 공진이 해석 결과에 제대로 반영되지 않고 시험결과와의 오차를 발생하게 만든 원인이라고 판단된다.

두 번째 원인은 FEA 모델의 단순화 과정에서 내부 전자모듈을 집중질량으로 표현한 결과 발생되었다고 판단된다. 구조 시험 결과 전자모듈 설치 부에서 국부적으로 고주파 영역의 진동이 발생하였다. 반면 전자모듈을 집중질량으로 표현한FEA 모델에서는 고주파 영역에서의 진동이 잘 표현되지 않았다. 이로 인해 발생한 차이는 Point 1에서 Point 3으로 갈수록 커지는 것을 확인할 수 있는데 이는 Point 3의 위치로 갈수록 전자모듈에 의한 국부 모드가 진동응답에 미치는 영향이 커지기 때문이다.

실질적으로 탑재체의 Random vibration에 의한 Grms는 주로 탑재체의 1, 2차 모드의 영향 받는다. 또한 1000 Hz 이상의 영역에서 발생하는 고주파 진동은 변위가 작아 탑재체 구조물에 파손을 일으키지 않을 것이라고 판단되어 무시 가능하다고 판단된다. 또한 실제 제작된 탑재체의 운용환경 시험을 통해 동흡진기 적용 시 탑재체의 운용성능 향상 및 정상 운용됨을 확인하였다.

4. 결론

본 연구에서는 탑재체 구동부 및 전자모듈의 구조 건전성 확보를 위한 동흡진기 적용 효과를 구조해석으로 확인하고, 실제 시제품을 제작하여 확인하고자 하였다.

설계 제한 등의 사유로 변경이 어려운 탑재체구조에 구조해석 및 시험으로 확인된 파손 예상위치에 동흡진기를 적용함으로써 파손 예상 부에서 발생하는 특정주파수 영역의 진동을 저감할 수 있었고, 이를 구조해석 및 시험으로 검증하였다.

본 연구를 통하여 기 제작되어 설계가 확정된 탑재체의 설계를 크게 변경하지 않는 선에서 소형화, 경량화를 설계를 진행할 수 있었다. 또한 차후 최초 설계가 진행되는 추가 탑재체의 동흡진기 설계 적용에 대한 연구가 진행 중이며, 비행구조물에 설치될 탑재체에 동흡진기 설계 적용에 대한 다음과 같은 설계 고려사항을 얻을 수 있었다.

(1) 동흡진기 설치 시 설치 위치의 진동응답을 완화할 수 있다. 따라서 구조해석 또는 기 제작 시제의 시험을 통해 파손이 우려되는 위치를 확인해야 한다.

(2) 동흡진기는 특정 주파수영역의 진동응답에 영향을 미친다. 따라서 시제품 제작 전 구조해석 또는 기 제작 시제의 시험을 통해 구조물의 위험 주파수 영역을 확인해야 한다.

(3) 구조물 내부 모듈을 활용한 동흡진기 설계 시 모듈의 형상에 따라 정확한 주파수 영역을 예측이 어려운 경우가 많다. 따라서 설계 적용에 따른 진동응답완화 효과를 구조해석을 통해 확인해야 한다.

(4) 구조물 내에서 동흡진기로 설계된 모듈은 타 구성품에 비해 강한 진동응답을 받는다. 따라서 진동에 대한 내구성 및 모듈 운용성능을 고려하여 동흡진기로 적용될 모듈을 선정해야 한다.

REFERENCES

• Kathe, E. L., “Gun Barrel Vibration Absorber,” US Patent, 6167794 B1, 2001.
• Kathe, E., “Lessons Learned on the Application of Vibration Absorbers for Enhanced Cannon Stabilization,” Shock and Vibration, Vol. 8, Nos. 3-4, pp. 131-139, 2001. [https://doi.org/10.1155/2001/983024]
• Lim, J. H., Baek, P. G., Lee, J. Y., and Chung, B. G., “A Study on the Stabilization of Gun Barrel by Viscoelastic Damping Material,” Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 9, No. 4, pp. 714-719, 1999.
• Littlefield, A., Kathe, E., Messier, R., and Olsen, K., “Gun Barrel Vibration Absorber to Increase Accuracy,” Proc. of the 19th American Institute of Aeronautics and Astronautics Conference, p. 1228, 2002. [https://doi.org/10.2514/6.2001-1228]
• Littlefield, A. G., Kathe, E. L., and Durocher, R., “Dynamically Tuned Shroud for Gun Barrel Vibration Attenuation,” Proc. of the in SPIE 9th Annual International Symposium on Smart Structures and Materials, pp. 89-97, 2002. [https://doi.org/10.21236/ADA405870]
• Kwag, D.-G., Bae, J.-S., Hwang, J.-H., and Kim, H.-S., “A Study on the Vibration Damping of a Barrel Using Vibration Absorber,” Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 21, No. 5, pp. 408-415, 2011. [https://doi.org/10.5050/KSNVE.2011.21.5.408]
• Kwag, D.-G., Bae, J.-S., Hwang, J.-H., and Kim, H.-S., “An Experimental Study on the Vibration Absorber for Vibration Attenuation of Cantilever Beam Structure,” Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 21, No. 11, pp. 991-996, 2011. [https://doi.org/10.5050/KSNVE.2011.21.11.991]
• Lee, J.-H., Ryu, G.-H., Yang, S.-C., Kim, J.-E., and Jung, D.-Y., “Simplified Finite Element Model Building of an External Mounting Pod for Structural Dynamic Characteristics Analysis of an Aircraft,” Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 22, No. 6, pp. 495-501, 2012. [https://doi.org/10.5050/KSNVE.2012.22.6.495]
• Kim, J. S., Kim, S. J., Lee, H., Ha, S. K., and Lee, Y.-H., “Forced Vibration Modeling of Rail Considering Shear Deformation and Moving Magnetic Load,” Transactions of the Korean Society of Mechanical Engineers A, Vol. 37, No. 12, pp. 1547-1557, 2013. [https://doi.org/10.3795/KSME-A.2013.37.12.1547]