고경도 장갑판재 배열이 고속충격거동에 미치는 영향
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this study, a numerical analysis on the impact response of HHA (High Hardness Armor Plate) sequences under a 7.62 mm projectile impact was performed to obtain the fundamental design data for a combat-vehicle platform. Recently, the ballistic-protection levels for combat vehicles have increased, and ballistic-protection designs should now be able to deflect multi-hit projectiles. To study the ballistic-impact characteristics, armor-plate sequences of one or two layers with a gap of 0 mm to 2 mm between the front and rear plate were defined under the same weight and thickness. For the certification of the reliability of the numerical model, ballistic tests and an analysis of the single plate under the 7.62 mm projectile impact were performed and analyzed. On the basis of a valid numerical model, a numerical analysis was performed and analyzed. Lastly, it was proved that the performances of the two-layer sequence with the 2 mm gap regarding the impact-response acceleration, deflection efficiency, and penetration depth are the highest.
Keywords:
Ballistic impact characteristics, High hardness armor plate, Penetration depth, Impact response acceleration, Deflection키워드:
피탄 충격 특성, 고경도 장갑판재, 관통 깊이, 충격 응답 가속도, 처짐1. 서론
일반적으로 군용 장갑차 및 전차 등의 군용 전투차량에서 차체는 특수한 재질의 고강도 장갑판재가 사용되고 있으며 차량에 탑승하고 있는 승무원들의 생존성을 높이기 위해서 철갑탄 및 지뢰, 급조 폭발물(Improvised Explosive Device, IED)과 같은 발사체에 대한 방호설계가 요구된다. 최근 중동지역을 중심으로 소규모 분쟁발생과 전 세계적인 테러로 인하여 선진국을 중심으로 신규 개발 전투용 차량들의 방호성능을 점점 높여 설계하고 있다. 따라서 장갑차 차체를 구성하는 장갑판의 방호성능을 향상시키기 위해서 차체의 형상 최적 설계 뿐 아니라 차체 외부에 추가적으로 장착하여 운용하는 부가장갑(Add-on Armor)의 성능을 개선하여 방호성능을 향상시키기 위한 연구들이 활발히 진행되고 있다. Mahfuz는1 부가장갑 개발을 위해서 복합재(Phenolic Composites), 세라믹, 고무, 복합재(S2-Glass/Vinyl) 등으로 구성된 부가장갑의 방호성능을 확인하기 위해서 FSP (Fragment-Simulating Projectile)탄 충격시 동적거동을 유한요소해석과 시험을 동시에 병행하여 복합적층 구성된 부가장갑의 각 층간 분리 및 파손특성이 전체 방호성능에 미치는 영향을 연구하였다. Gama는2 부가장갑 개발을 위해서 기존에 많이 사용되었던 세라믹, 복합재, 고무 등으로 구성된 다층판에 충격 에너지 흡수능력이 뛰어난 발포 알루미늄을 추가하여 발사체 고속 충격시 알루미늄 폼의 충격에너지 흡수 성능을 유한요소해석과 실험을 통해서 확인하였다. 또, Fernandez-Fdz은3 부가장갑의 구성재료인 세라믹의 고속충격 특성을 연구하였는데, 발사체 고속충격시 세라믹 파쇄와 부가장갑 파손과의 관계식을 나타내는 구조모델을 제시하였다. 그러나, 모든 부가장갑은 일정한 두께, 배열로 이루어져 차체를 구성하는 장갑판재에 볼트 등으로 조립되므로 높은 방호성능을 갖는 부가장갑 개발을 위해서는 차체를 구성하는 장갑판재의 철갑탄에 대한 충격 특성을 알아야 된다. 금속 장갑판재는 균질의 소재로서 두께와 발사체 충돌각도에 따라서 충격특성 차이가 발생하는데, 방호 성능 뿐 만 아니라, 충격에너지 전달량 차이가 발생한다. 방호성능 외에도 내부 탑승 승무원들의 상해를 최소화 해야 하므로 철갑탄에 의한 발생된 충격에너지 크기 또한 동시에 고려해야 한다. Kurtaran은47.62 mm 탄을 발사체로 하여 군용차량 문을 단순화 모델링한 충격해석을 수행하였고, 발사체 충돌속도 변화에 따른 장갑판의 내부 및 운동에너지 관계를 규명하였다. 일반적인 부가장갑은 차체 외부에 조립되어 방호성능을 높이기 위해서 세라믹, 고무, 알루미늄 폼 및 복합재 등으로 구성되어 있어서 방호성능 및 충격에너지 흡수능력은 뛰어나지만, 두께가 매우 두껍고, 제작과 조립의 복잡성과 비용, 중량이 증가하는 단점이 있다. 따라서, 최근에는 두꺼운 부가장갑을 고경도 장갑판재로 대치하기 위한 개발을 진행해오고 있다.
Flores-Johnson은5 7.62 mm 탄을 발사체로 하여 서로 다른 장갑판재 재질인 알루미늄과 스틸판 조합의 단일판, 2중판, 3중판 배열들을 대상으로 발사체 변화에 따른 충격시험 및 동일조건의 해석을 수행하였는데, 발사체 충돌시 발사체 속도변화에 따른 각각의 배열구성과 발사체 잔류속도의 상관관계를 분석하였다. 또, Bobbili는6 7.62 mm 탄을 발사체로 하여 단일판재 및 2중 장갑판재를 대상으로 충격 시험 및 해석을 통해서 장갑판재의 등가응력, 스트레인 및 충격흡수성능과의 상관관계를 통계적인 분석을 통해서 제시하였다. 이와 같이 얇은 고경도 장갑판재의 2층, 3층 배열 구조로 방호성능 뿐 아니라, 충격량 전달을 최소화하기 위한 다양한 연구 가 진행되고 있다.7 고경도 장갑판재를 기존의 세라믹, 복합재 및 고무 등으로 구성된 부가장갑 대체용으로 사용할 경우에 두께 감소, 조립성 향상과 소재, 제작 비용감소 등의 장점 등이 있고, 특히, 방호 성능면에서 장갑판재가 균질성의 금속이므로 다탄(Multi-Hit) 방호, 즉, 발사체 충격시 바로 인접위치에서의 방호성능을 확보할 수가 있다. 따라서, 본 연구에서는 장갑차 차체재료로 사용되는 고경도 장갑판재를 대상으로 하였고, 대상모델은 전면판과 후면판으로 구성되며 전면판, 후면판은 각각 부가장갑과 차체 장갑판재로 정의하였고, 7.62 mm 철갑탄을 발사체로 한 충격해석을 상용코드인 LS-DYNA를 사용하여 수행하였다. 차체 장갑판재와 부가장갑용 장갑판재는 동일한 크기와 두께로 하였고, 두 판재 사이에 일정한 거리를 유지하게 한 후 발사체 충격시 관통저지성능, 충격응답가속도, 최대 수직변위와 같은 피탄 충격 특성과 판재구성모델과의 상관관계를 확인 하였으며, 또한, 동일 중량의 단일 판재와의 비교를 통해서 부가장갑으로서 적용 타당성을 확인하였다.
2. 충격해석 모델
일반적으로 고속충격해석에 사용되는 해석 물성모델은 Ls-Dyna에서 사용되는 물성모델인 소성 운동 물성모델(Mat_Plastic-Kinematic Model)과 존슨-쿡 물성모델(Mat_Johnson-Cook Model)이 사용 된다.8 이 모델들은 재료의 변형경화, 변형률 경화, 온도에 의한 연화, 파괴 또는 손상 등의 거동을 모사하는 방법상에 차이가 있으므로, 고속충격해석의 목적에 따라서 사용자가 연구에 적합한 해석모델을 결정해서 사용해야 한다.
본 연구의 충격해석은 비교적 얇은 판을 대상으로 하고, 충격 시 접촉에 의한 요소소실이 매우 중요하므로 존슨-쿡 모델을 사용하였다. 존슨-쿡 모델은 고속충격 해석시 판재의 변형률, 온도 영향 및 점소성 효과를 고려한 모델로써, 발사체 충격해석시 가장 많이 사용된다. 충격시 발생하는 재료연화에 영향을 주는 큰 범위의 변형률, 온도 변화에 의한 요소소실(Failure of Element) 등을 모사하는 모델로써 본 연구에서는 관통현상의 정확한 거동을 구현하기 위해서 이 모델을 사용하였으며, 변동 응력식은 식(1)과 같다.
| (1) |
여기서, σY : 유효응력, ε : 유효 소성 변형률, : 표준화된 유효소성 변형률 속도, A, B, C, m, n : 재료상수이며, 온도 성분 T*는 식(2)로 정의할 수 있다.
| (2) |
여기서, T : 절대 온도, Troom : 상온, Tmelt : 녹는점이다. 존슨-쿡 모델에서 요소소실은 식(3)의 누적손상법칙에 따라서 발생하며 다음과 같다.9
| (3) |
여기서,
| (4) |
이며, Δε : 하중 증가 동안의 유효소성변형 증가분, σ* : 유효응력에 의해 일반화된 평균응력, D1, D2, D3, D4, D5는 파괴상수이다.
요소소실은 식(3)에서 D = 1일 때 발생하며, 파괴변형, εf과 손상누적, D는 평균응력, 변형률 및 온도의 함수로 나타낼 수 있는데, 고속충격 해석시 파손된 요소성분들은 관통거동이 진행되는 동안에 유한요소 모델로부터 제거 된다. 충격해석에 필요한 장갑판재물성 및 존슨-쿡 모델의 상수는 Tables 1부터 4에 도시하였다.10,11
또, 재료의 압력과 체적 그리고 내부에너지의 상관관계는 상태 방적식으로 정의할 수 있다. Zukas12는 속도범위 500 - 2000 m/s의 솔리드-솔리드 충격시 적당한 압력이 발생하는데, 이것이 재료의 강도와 필적하는 값으로 빠르게 부식한다고 했다. 따라서, 충격해석에서 상태방정식은 충격대상 재료의 관통깊이를 결정하는 중요한 요소이며, 비선형 상태방정식이 많이 사용 된다.13-15
본 연구에서 사용한 고속충격해석에서는 Mie-Gruneisen16 상태방정식이 사용되었으며, 압축된 재료의 압력은 식(5)로 나타낼 수 있다.
| (5) |
여기서, E0 : 단위 체적당 내부에너지, Csp : 충격 및 입자속도 그래프의 인터셉트, S1, S2, S3 : 충격 및 입자속도 그래프의 기울기계수, γ : Gruneisen 계수, α : 체적누적 인자이며, 압축 인자인 μ = ρ/ρ0 − 1로 나타낼 수 있다. 철갑탄의 상태방정식 계수 및 상수는 Niezgoda, and Morka17로부터 인용하였고, 장갑판재의 상태 방정식 계수 및 상수는 Espinosa14, Gailly15, Flores-Johnson5로부터 인용하였으며, Table 5에 도시하였다.
Tables 1부터 5의 고속충격해석 모델에 사용되는 물성치는 일반적으로 군용차량의 소재특성연구를 위한 고속충돌 해석에 사용되는 장갑판재의 물성치로써 일반화되어 사용되고 있으며, 이 물성치를 사용한 충격해석모델의 신뢰성 확인을 위해서 3장에서 충격해석 및 시험결과 비교를 수행하였다.
3. 충격해석 모델 검증
3.1 충격 시험
본 연구에서 확인하고자 하는 장갑판재의 피탄충격 특성을 획득하기 위해서는 고속충격 해석 모델의 신뢰성이 중요하므로, 기수행했던 7.62 mm 철갑탄을 발사체로 한 충격시험과 동일 조건의 해석결과를 비교하여 본 연구에서 사용할 충격해석 모델의 신뢰성을 검증하고자 하였다.
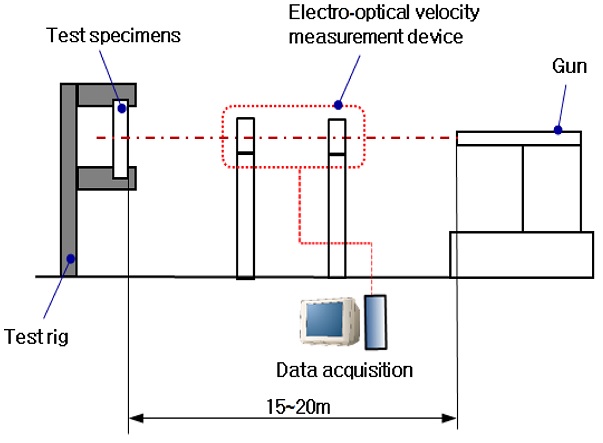
Fig. 1은 일반적으로 수행하는 철갑탄 발사체 충격시험의 개념도를 나타낸 것이다. 시편을 시험지그에 고정하고 시편과의 거리 약 15 - 20 m 위치에 발사체 지지대를 설치하였으며, 중간에는 발사체 속도를 측정할 수 있는 속도측정 장치를 설치하였다.
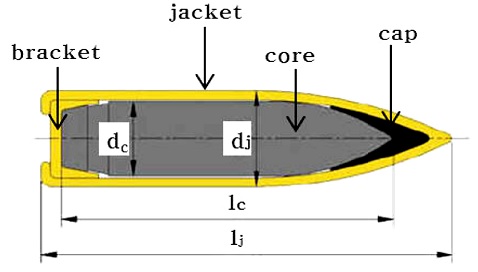
Fig. 2 및 Table 6은 고속충격해석모델 검증용 발사체 충격시험에 사용된 7.62 mm 철갑탄의 형상과 제원18을 나타낸 것이다.
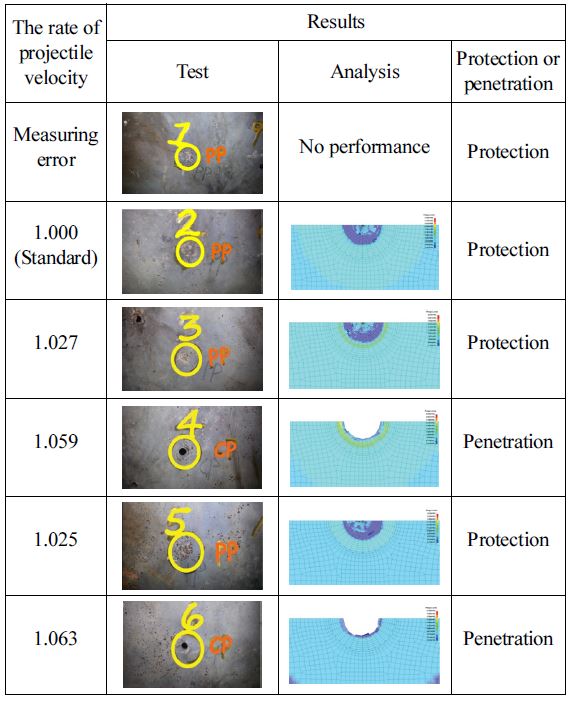
Fig. 3은 경도 500 HB 6.35 mm 두께의 장갑판재를 대상으로 7.62 mm 철갑탄19의 충격시험을 수행한 결과이며, Table 7은 장갑판재 1 - 6번 위치에서의 발사체 충격속도 비율을 나타낸 것이다. 총 6개의 방호 또는 관통결과에 대한 경향성을 얻을 수 있었는데, Fig. 3 결과로부터 측정위치 4번과 6번은 관통되었고, 나머지 1, 2, 3, 5번은 관통되지 않았음을 확인하였다. 1번의 경우는 속도가 측정 되지 않아서 2번을 기준 탄 속도로 정하였고, Table 7의 속도 비율 1.059, 1.063에서 완전 관통이 되었음을 확인할 수 있었다.
3.2 충격 해석
3.1절의 충격시험과 동일한 조건으로 2 - 6번에 대한 충격해석을 수행하였고, 속도가 측정되지 않은 1번은 해석에서 제외하였다.
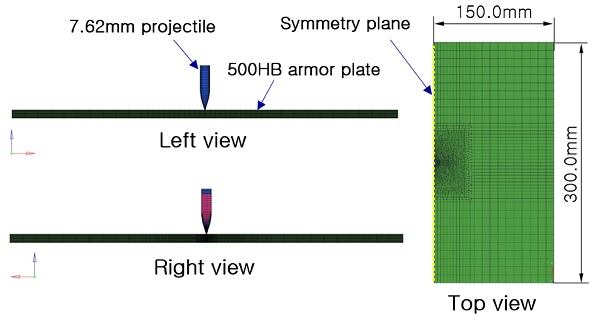
Fig. 4는 7.62 mm 철갑탄의 충격해석을 위한 유한요소모델을 나타낸 것이며, 총 해석시간을 줄이기 위해서 대칭모델로 구성하였고, 해석시간은 발사체와 장갑판재가 충돌이 일어난 후 충분한 시간을 정해서 0.0005초로 하였다.
Fig. 5는 판재모델 2 - 6번의 총 5개의 발사체 속도비에 따라서 수행한 충격해석 및 시험결과 형상을 비교해서 나타낸 것으로써, 방호 및 관통성능에 대한 유사 경향성을 확인할 수 있었다.
4. 충격해석
4.1 충격 해석 조건
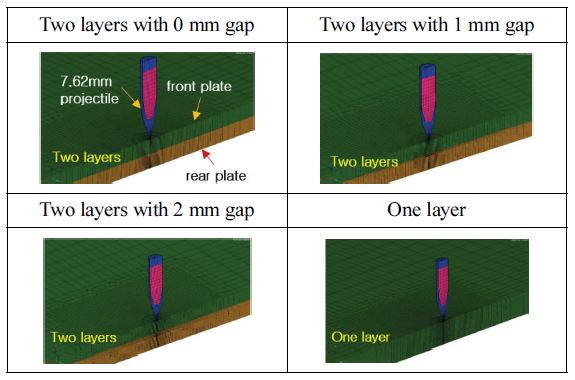
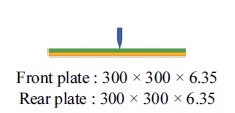
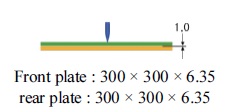
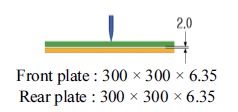
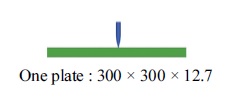
3장의 충격해석 결과로부터 7.62 mm 철갑탄 충격시 시험결과 속도에 따른 장갑판재 방호 및 관통결과와 유사한 경향성이 나타남을 확인하였고, 이 해석모델을 사용하여 7.62 mm 철갑탄 충격시 발사체 속도변화에 따른 장갑판재 배열변화가 장갑판재의 충격특성에 미치는 영향을 확인하기 위해서 Table 8에 충격해석 대상이 되는 총 4 종의 장갑판재 형상 및 배열을 나타내었다. 2중 배열판은 6.35 mm 2개의 장갑판재를 두께 방향으로 각각 전면판과 후면판의 간격이 0 mm, 1 mm, 2 mm를 유지하도록 하였다. 단일판은 두께 12.7 mm의 단일 장갑판재를 사용하였고, 4종 모델의 두께 합과 중량을 동일하게 하였다. Table 9는 Table 8의 충격해석 모델에 대한 발사체의 4가지 충돌속도를 나타낸 것이다.
4.2 유한요소모델 및 경계조건
Fig. 6은 각 해석종류별 유한요소모델을 나타낸 것으로써, 발사체 충격시 두께방향의 관통현상을 구현하기 위해서 총 122,976개의 솔리드 요소를 사용하였다. 고속충격인 경우에는 접촉부 거동현상이 요소크기에 민감하므로 발사체와 장갑판재 접촉부위 요소 크기는 0.027로 하였고, 비접촉 부위의 요소크기는 최대 10.0으로 모델링하였다. 구속조건은 Fig. 4의 충격해석 검증모델과 동일하게 장갑판재의 3면의 모서리부를 구속하였다. 총 해석시간을 줄이기 위해서 면대칭 조건으로 구성하였고, 해석시간은 발사체와 장갑판재가 충돌이 일어난 후 충분한 시간을 정해서 0.0005초로 하였다. 충격시 발사체와 장갑판재의 접촉이 발생하고, 발사체에 의한 관통현상을 구현하기 위해서 발사체와 장갑판재의 접촉부에는 파손접촉(Eroding Contact) 조건을 적용하였다. 또, 2개 배열 장갑판재는 충격시 전면판이 발사체에 의한 처짐이 발생할 경우 후면판과 접촉이 발생하므로 전면판과 후면판 사이에 자동접촉(Automatic Contact) 조건을 적용하였다.
5. 결과 및 고찰
7.62 mm 철갑탄 충격시 발사체 속도 및 장갑판재 배열 변화가 발생할 때 장갑판재의 관통저지성능, 충격응답가속도 및 두께방향의 처짐 경향성 등의 충격특성을 확인하기 위해서 충격해석을 수행하였다.
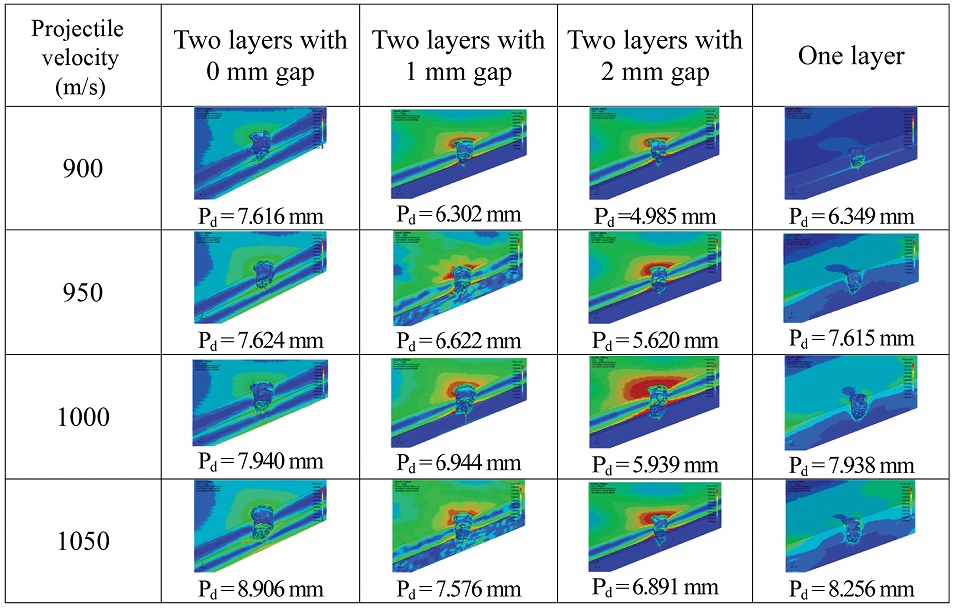
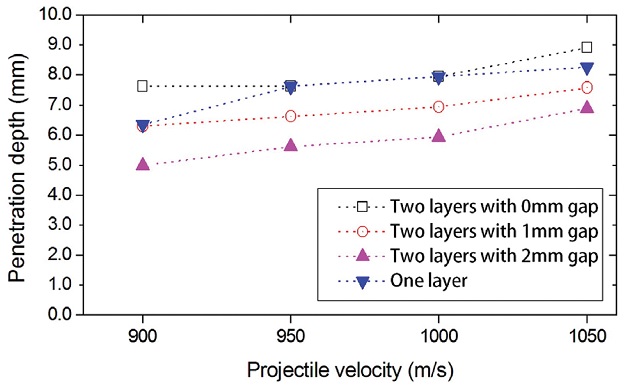
Figs. 7과 8은 발사체 속도변화에 따른 해석모델의 관통깊이를 나타낸 결과로서, Fig. 7은 해석모델의 관통형상을 나타낸 것이고, Fig. 8은 속도에 따른 관통깊이를 그래프로 나타낸 것이다. 해석 결과의 2중 배열판 관통깊이는 판 사이 간격을 제외한 관통깊이를 측정하였으며, 발사체 속도 증가에 따라서 4가지 모델의 관통 깊이도 점차 증가하는 경향성을 확인할 수 있다. 단일판과 판 사이 간격이 0 mm인 2중 배열판의 관통 깊이는 속도 증가에 따른 관통깊이 경향성이 비교적 유사하게 나타나지만, 판 사이 간격이 1 mm, 2 mm인 2중 배열판의 관통깊이는 단일판에 비해서 작게 나타남을 확인할 수 있다. 특히, 판 사이 간격 2 mm인 2중 배열판의 관통깊이가 가장 작게 나타나고 관통성능이 가장 우수함을 확인할 수 있다.
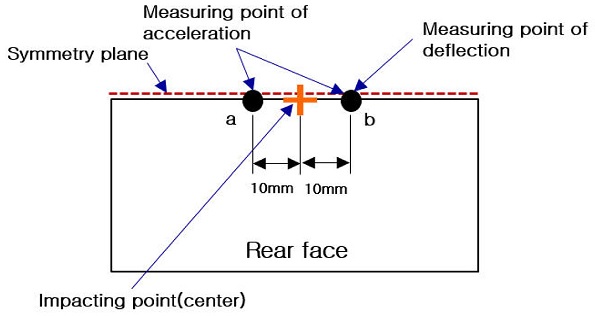
Fig. 9는 장갑판 후면부 측정위치를 나타낸 그림이며, 가속도 측정인 경우 발사체 충돌부위를 중심으로 좌, 우측으로 10 mm 떨어진 위치에서 측정하였는데, 측정값이 민감하여 발사체 충격 시 장갑판 좌, 우측 변형 편차에 의한 좌, 우측 가속도 값 편차가 나타날 수 있어서 좌측(Fig. 9(a)), 우측(Fig. 9(b))의 최대값을 측정한 후 최대값의 평균값을 계산하여 비교하였다, 또, 처짐인 경우에는 좌, 우 편차가 거의 없으므로 한쪽 위치만 측정하였다.
Table 10은 좌, 우측 최대 충격응답가속도의 평균값을 나타낸 것이다. 일반적으로 발사체 속도가 증가할수록 운동에너지가 증가하므로 각 동일 모델의 최대 충격응답가속도는 점점 증가하는 경향을 나타낸다. 각 속도 구간에서의 모델별 경향은 단일판의 경우에 최대 충격응답가속도가 가장 크게 나타남을 확인할 수 있고, 2중 배열판이 상대적으로 작게 측정됨을 확인할 수 있다. 2중 배열판의 장갑판 간격이 0 mm에서 2 mm로 증가한 경우 최대 충격 응답가속도의 값이 반대로 감소함을 확인할 수 있다. 원인으로는 발사체와 장갑판의 충돌이 일어나기 시작할 때, 운동에너지가 내부에너지로 변환되기 시작하여 장갑판에 전달되는데, 2중 배열판인 경우 전면판이 먼저 발사체와 충돌이 일어나고, 전면판과 후면판의 접촉에 의해서 후면판에 충격 에너지가 전달된다. 이때 충격 에너지 전달시 접촉면 넓이에 따라서 에너지 전달율 차이가 발생되기 때문에 2중 배열판이 단일판에 비해서 충격응답가속도가 작게 측정된 것으로 판단된다. 따라서, 2중 배열판 중 두 판재 접촉 거리가 가장 먼 2 mm인 모델의 최대 충격응답가속도가 가장 작게 나타남을 확인할 수 있다. 그러나, 두 판재 접촉거리가 0 mm인 모델은 발사체와 충돌이 일어날 때 단일판과 비슷한 거동을 하기 때문에 최대 응답가속도 또한 비슷한 수준의 값을 나타냄을 Table 10의 결과에서 확인 할 수 있다. 따라서, Table 10의 결과로부터 단일판 대비 두 판재 접촉거리가 2 mm인 모델의 최대 충격 응답가속도는 속도 증가에 따라서 55.1% - 76.7% 차이가 발생함을 확인할 수 있다.
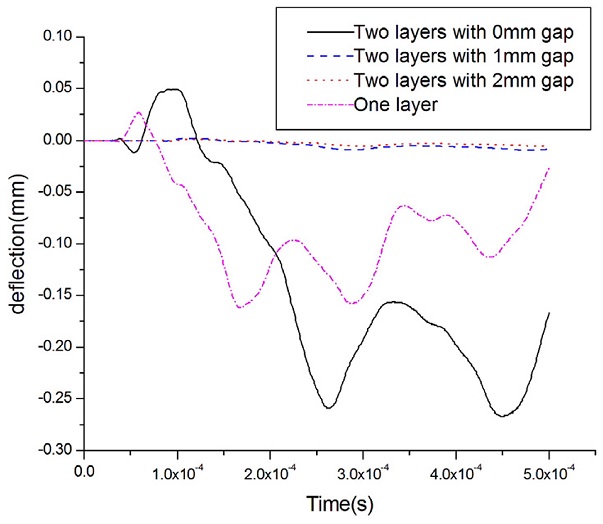
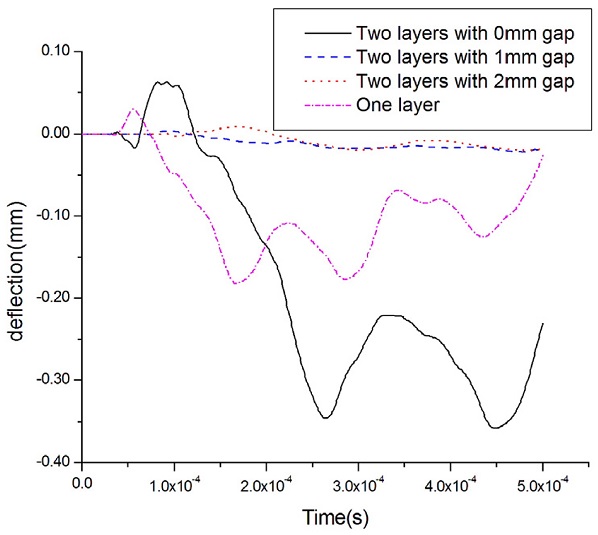
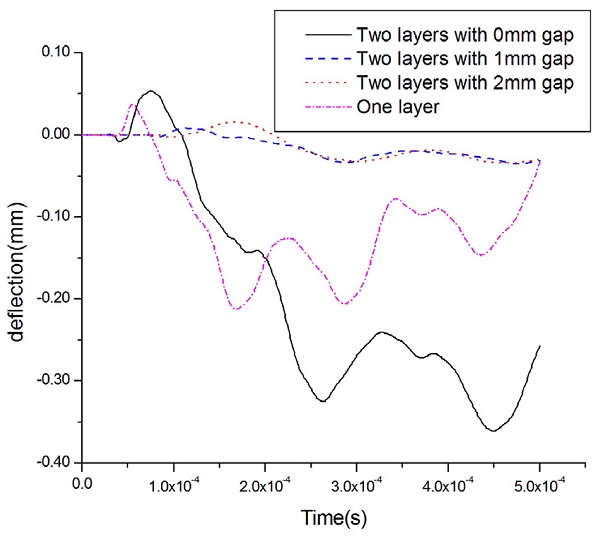
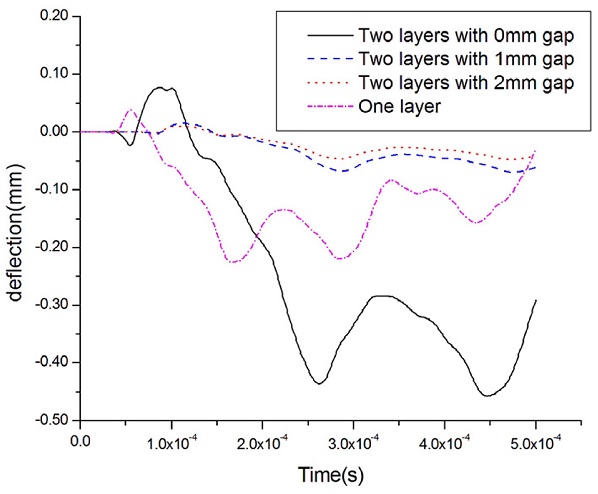
Figs. 10-13은 발사체 속도 변화에 따른 장갑판 후면에서의 처짐량을 측정한 그래프이고, Table 11은 최대 처짐량을 나타낸 것으로써, 장갑판 후면부 처짐량은 발사체 속도 증가에 비례하여 증가하는 경향을 보이고 있다. 4가지 모델 중 2중 배열판의 두 판재 접촉거리가 0 mm인 모델이 모든 발사체 속도 조건에서 처짐량이 가장 크게 측정되었고, 두 번째로는 단일판의 처짐량이 크게 측정되었다. 첫 번째 모델인 경우에는 발사체 충격시 충돌에 의한 전면판 처짐을 유발하고 다시 전면판 처짐이 후면판과의 접촉 발생후에 후면판 처짐변형을 유발하기 때문인 것으로 판단된다. 4가지 모델 중에서 2중 배열판의 두 판재 접촉거리가 1 mm, 2 mm인 모델은 4가지 발사체 속도 조건에서 상대적으로 처짐량이 작게 측정되었는데, 이유로는 발사체 충격시 충돌에 의한 전면판 처짐이 발생되고, 이 처짐이 두 판재 접촉거리 내에서 발생하므로 전면판이 후면판 접촉변형에 거의 영향을 주지 않기 때문이라 판단된다. 따라서, 발사체가 7.62 mm 철갑탄인 경우에는 12.7 mm 단일판 보다는 6.35 mm 2중 배열판이 처짐량을 최소화할 수 있으며, 특히 발사체 충격시 전면판의 변형을 고려하여 2개의 판재 접촉거리를 1 - 2 mm 일정하게 유지한 경우에 처짐량을 최소화할 수 있음을 확인할 수 있었다. Table 11 결과로부터 단일판과 판재 접촉거리 2 mm인 2중 배열판의 처짐량 차이는 속도변화에 따라서 80.5% - 96.7%가 발생하며 2중판 배열이 우수함을 확인하였다.
6. 결론
7.62 mm 철갑탄을 발사체로 선정하여 고경도 장갑판 6.35 mm의 2중 배열판 3종(2개의 판재 접촉거리 0 mm, 1 mm, 2 mm)과 12.7 mm의 단일판 1종 등 총 4종을 대상으로 발사체의 4가지 속도변화에 따른 총 16가지의 충격해석을 수행하였고, 해석결과로부터 판재의 관통저지성능, 충격응답가속도 및 후면부 처짐량 등과 같은 충격특성에 대한 결론을 다음과 같이 얻을 수 있었다.
(1) 발사체 충격시 관통저지성능은 동일중량의 6.35 mm 장갑판 2 중 배열판이 단일 장갑판에 비해서 우수한 것을 확인할 수 있었고, 특히, 2중 배열판 중 판 사이 거리가 2 mm인 배열이 가장 우수함을 확인하였다.
(2) 발사체 충격시 장갑판 후면부에서의 최대 충격응답가속도는 6.35 mm 장갑판 2중 배열판이 12.7 mm 단일 장갑판 보다 작게 측정됨을 확인할 수 있었다. 특히, 판재 접촉거리 2 mm인 2중 배열판이 최소 충격응답가속도를 나타내었고, 단일판 대비 속도별 55.1% - 76.7% 우수함을 확인하였다.
(3) 발사체 충격시 장갑판 후면부의 최대 처짐량은 2중 배열판이 단일판 보다 우수한 경향을 나타내고 있으며, 특히 2중 배열판 중 판재 접촉거리가 1 - 2 mm인 모델이 최소값을 나타내었고, 판재 접촉거리 2 mm인 배열이 단일판에 비해서 80.5% - 96.7% 우수함을 확인하였다.
본 연구에서는 고경도 장갑판재의 부가장갑으로서 뿐 만 아니라, 장갑차 차체 기본재료로서의 충격거동특성을 확인하였다. 군용전투차량 및 장갑차 차체로 사용되는 고경도 장갑판재의 플랫폼 방호 구조설계시 활용이 가능하며 차량차체의 관통저지 성능뿐 아니라, 차량 내부 탑승 승무원의 상해 및 전장품을 보호하기 위한 최대 충격응답가속도, 차량 내부의 처짐량 최소 설계에 기초 자료로 활용이 가능 할 것으로 판단된다.
REFERENCES
-
Mahfuz, H., Zhu, Y., Haque, A., Abutalib, A., Vaidya, U., et al., “Investigation of High-Velocity Impact on Integral Armor Using Finite Element Method,” International Journal of Impact Engineering, Vol. 24, No. 2, pp. 203-217, 2000.
[https://doi.org/10.1016/S0734-743X(99)00047-0]

-
Gama, B., Bogetti, T., Fink, B., Yu, C., Claar, T., et al., “Aluminum Foam Integral Armor: a New Dimension in Armor Design,” Composite Structures, Vol. 52, No. 3, pp. 381-395, 2001.
[https://doi.org/10.1016/S0263-8223(01)00029-0]

-
Fernandez-Fdz, D., Zaera, R., and Fernandez-Saez, J., “A Constitutive Equation for Ceramic Materials Used in Lightweight Armors,” Computers and Structures, Vol. 89, No. 23, pp. 2316-2324, 2011.
[https://doi.org/10.1016/j.compstruc.2011.08.003]

-
Kurtaran, H., Buyuk, M., and Eskandarian, A., “Ballistic Impact Simulation of GT Model Vehicle Door Using Finite Element Method,” Theoretical and Applied Fracture Mechanics, Vol. 40, No. 2, pp. 113-121, 2003.
[https://doi.org/10.1016/S0167-8442(03)00039-9]

-
Flores-Johnson, E. A., Saleh, M., and Edwards, L., “Ballistic Performance of Multi-Layered Metallic Plates Impacted by a 7.62 mm APM2 Projectile,” International Journal of Impact Engineering, Vol. 38, No. 12, pp. 1022-1032, 2011.
[https://doi.org/10.1016/j.ijimpeng.2011.08.005]

-
Bobbili, R., Paman, A., Madhu, V., and Gogia, A. K., “The Effect of Impact Velocity and Target Thickness on Ballistic Performance of Layered Plates Using Taguchi Method,” Materials and Design, Vol. 53, pp. 719-726, 2014.
[https://doi.org/10.1016/j.matdes.2013.06.005]

-
Abdel-Kader, M. and Fouda, A., “Mild Steel Plates Impacted by Hard Projectiles,” Journal of Constructional Steel Research, Vol. 99, No. 4, pp. 57-71, 2014.
[https://doi.org/10.1016/j.jcsr.2014.04.003]

- Johnson, G. and Cook, W., “A Constitutive Model and Data for Metals Subjected to Large Strain, High Strain Rates and High Temperatures,” Proc. of the 7th International Symposium on Ballistic, pp. 541-547, 1983.
-
Vo, T. P., Guan, Z. W., Cantwell, W. J., and Scheyer, G. K., “Modelling of the Low-Impulse Blast Behavior of Fibre-Metal Laminates Based on Different Aluminum Alloys,” Composites Part B: Engineering, Vol. 44, No. 1, pp. 141-151, 2013.
[https://doi.org/10.1016/j.compositesb.2012.06.013]

-
Yuen, S., Langdon, G., Nurick, G., Pickering, E., and Balden, V., “Response of V-Shape Plates to Localized Blast Load: Experiments and Numerical Simulation,” International Journal of Impact Engineering, Vol. 46, pp. 97-109, 2012.
[https://doi.org/10.1016/j.ijimpeng.2012.02.007]

-
Kılıç, N. and Ekici, B., “Ballistic Resistance of High Hardness Armor Steels Against 7.62 mm Armor Piercing Ammunition,” Materials and Design, Vol. 44, pp. 35-48, 2013.
[https://doi.org/10.1016/j.matdes.2012.07.045]

- Zukas, J. A., Nicholas, T., Swift, H. F., Greszczuk, L., and Curran, D., “Impact Dynamics,” Wiley, pp. 39-45, 1982.
- Livermore Software Technology Corporation (LSTC), “LS-DYNA Keyword User’s Manual Vol. 1,” http://thyme.ornl.gov/fhwa/tractortrailer/resources/manuals/l971k_1.pdf, (Accessed 10 MAY 2017)
-
Espinosa, H. D., Dwivedi, S., Zavattieri, P. D., and Yuan, G., “A Numerical Investigation of Penetration in Multi-Layered Material/Structure Systems,” International Journal of Solid Structures, Vol. 35, No. 22, pp. 2975-3001, 1998.
[https://doi.org/10.1016/S0020-7683(97)60353-4]

-
Gailly, B. A. and Espinosa, H. D., “Modelling of Failure Mode Transition in Ballistic Penetration with a Continuum Model Describing Microcracking and Flow of Pulverized Media,” International Journal of Numeric Methods Engineering, Vol. 54, No. 3, pp. 365-398, 2002.
[https://doi.org/10.1002/nme.427]

-
Jiang, L., Guan, M. Q., Li, X. J., and Liao, H. H., “High Rotating Speed Projectile Penetrating into Moving Vehicle Door at Different Incident Angle,” Theoretical and Applied Fracture Mechanics, Vol. 55, No. 2, pp. 113-117, 2011.
[https://doi.org/10.1016/j.tafmec.2011.04.002]

- Niezgoda, T. and Morka, A., “On the Numerical Methods and Physics of Perforation in the High-Velocity Impact Mechanic,” World Journal of Engineering, pp. 414-417, 2010.
-
Borvik, T., Dey, S., and Clausen, A., “Perforation Resistance of Five Different High-Strength Steel Plates Subjected to Small-Arms Projectiles,” International Journal of Impact Engineering, Vol. 36, No. 7, pp. 948-964, 2009.
[https://doi.org/10.1016/j.ijimpeng.2008.12.003]

-
Jena, P., Mishra, B., Kumar, K., and Bhat, T., “An Experimental Study on the Ballistic Impact Behavior of Some Metallic Armor Materials Against 7.62 mm Deformable Projectile,” Material and Design, Vol. 31, No. 7, pp. 3308-3316, 2010.
[https://doi.org/10.1016/j.matdes.2010.02.005]