[ SPECIAL ]

Journal of the Korean Society for Precision Engineering - Vol. 34, No. 9, pp.591-596

ISSN: 1225-9071 (Print) 2287-8769 (Online)

Print publication date 01 Sep 2017

Received 20 Jun 2017 Revised 27 Jul 2017 Accepted 16 Aug 2017

DOI: https://doi.org/10.7736/KSPE.2017.34.9.591

고속비행체 비행진동 규격 설정에 관한 연구

황동기¹^{, #} ; 송오섭²

1국방과학연구소
2충남대학교 기계공학부

A Study on Making Flight Vibration Specification of High Speed Vehicle

Dongkee Hwang¹^{, #} ; Ohseop Song²

1Agency for Defense Development
2School of Mechanical Engineering, Chungnam National University

Correspondence to: ^#E-mail: leo7303@add.re.kr, TEL: +82-42-821-3441, FAX: +82-42-823-3400

Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

Defining an appropriate flight vibration specification is a critical issue at an initial design phase, for optimized design of components in a surface-to-air missile (SAM). As the related document (MIL-STD-810G) doesn’t provide detailed value, appropriate procedures for estimation of flight vibration specification are required for design of a surface-to-air missile. In this study, the method-making appropriate specification without an actual flight test is introduced. Comparison between a theoretical approach using the beam theory and FEA is conducted to attain a natural vibration frequency under thrust force. Transient response analysis using commercial S/W is conducted to establish an envelope curve for flight vibration.

Keywords:

Surface-to-air missile, Flight vibration specification, Beam theory, Finite element analysis, Natural vibration frequency, Transient response analysis

키워드:

지대공유도탄, 비행진동규격, 보 이론, 유한요소해석, 고유진동수, 과도응답해석

1. 서론

지대공유도탄(Surface-to-Air Missile)은 다른 유도탄에 비해 비행속도 및 기동(Maneuvering) 성능이 매우 큰 특징을 가지며, 이를 위해 유도탄은 세장비(Fineness Ratio)가 크고, 무게는 가벼우며, 구조적 유연성을 갖는다. 특히 무게는 유도탄 비행 성능에 직접적으로 영향을 미치게 되므로, 구조물 무게를 낮추기 위한 방향으로 설계가 발전되고 있다.

유도탄 환경규격에 참조되는 MIL-STD-810G¹는 유도탄 비행 진동에 관해 실제 계측 후 사용하기를 권하고 있으며, 이전 버전인 MIL-STD-810C²는 규격을 제시하고 있으나 과도한 수준의 진동 규격을 제시하고 있어 구성품 제작비 증가 및 유도탄 무게 증가의 원인이 된다. 즉, 유도탄 환경규격 수준은 유도탄 제조원가 증가의 원인, 유도탄 기동성능 저하의 원인 등과 밀접한 관계를 가지므로, 최적의 규격 제시가 요구된다. 그러나 개발 기간 및 비용 절감이 요구되는 작금의 상황에서는 설계 이전 단계부터 최적의 환경규격을 요구하게 되므로 환경규격, 특히 비행진동 규격에 대해 적절한 해석방법이 요구된다. 따라서 본 논문에서는 국내에서 개발된 지대공유도탄을 기반으로 지대공유도탄 개발 시 적용 가능한 비행진동 환경규격 설정 방법을 제시하고자 한다.

최승혁³은 비행시험을 통해 계측된 비행진동 데이터를 기반으로 규격을 생성하고, 이를 비행시험 전 유도탄 신뢰성 시험에 적용하였다. Piesol⁴은 비행 탑재 구성품에 대한 진동시험 규격을 개발하는 절차에 대해 기술하고, 진동 수준과 평균 및 표준편차와의 관계를 제시하였다. Bendat⁵등은 비행체 진동 발생 원인 및 추력에 따른 진동 크기를 분류한 후 통계적인 방법으로 문제를 해결하는 방법을 제시하였다. Bokaian⁶은 압축하중을 받는 단일 물성치 Euler 보의 고유진동수를 산출하는 방법을 제시하였다. Joshi⁷, Pourtakdoust등⁸은 비행체 축에 추력 작용 시, 여러 개의 Euler 보로 이루어진 조립체에 대한 고유진동수와 모드를 산출하는 방법을 제시하였다.

이외에 다수의 논문에서 자체모델에 대한 진동환경을 모사하기 위한 노력은 있었으나, 유도탄 비행진동 환경에 대한 제시 방법은 없다. 따라서 본 논문에서는 보 모델을 이용한 이론적 접근 및 보 모델을 이용한 FEA (Finite Element Analysis), 비행시험 데이터와의 비교 등을 통해 유도탄 개발 초기에 설계 규격으로 제시 가능한 비행진동 환경규격을 개발하는 방법을 보였다.

2. 보 모델을 이용한 이론적 접근

2.1 보 모델 운동방정식

추력하중을 받는 Bernoulli-Euler 보의 운동방정식은 식(1)과 같이 표현된다.^6-8

∂ 2 ∂ x 2 E l ∂ 2 y ∂ x 2 + ∂ ∂ x T ∂ y ∂ x = - ρ A ∂ 2 y ∂ t 2

(1)

여기서 E는 탄성계수, I는 면적관성모멘트, ρA는 단위길이당 질량(ρ는 밀도, A는 단면적), T는 추력, x는 보의 외쪽 끝에서부터의 거리, y는 횡방향 변위(y(x, t))이다.

식(1)의 해를 y(x, t) = Y(x)F(t)라 놓고, EI가 일정하며, $- F t ¨ F t = ω 2$ 라면, 식(1)은 식(3)으로 표현된다.

E I ρ A Y (x) d Y (x) d x 4 + T ρ A Y (x) d 2 Y (x) d x 2 = - F (t) ¨ F (t)

(2)

d 4 Y x d x 4 + T E I d 2 Y x d x 2 - ρ A E I ω Y x = 0

(3)

유도탄 비행 중 경계 조건은 양 끝단에서 모멘트와 전단력이 없으므로 식(4), 식(5)와 같이 표현된다.

즉, x = 0, L에서, 여기서 L은 보의 길이, Y(x)는 모달 변위, ω는 고유진동수(= 2πf)이다.

d 2 Y (x) d x 2 = 0

(4)

d 3 Y (x) d x 3 + T E I d Y (x) d x = 0

(5)

비행체가 여러 연결부로 나뉘어져 있고, 추력이 길이 방향으로 분포되었다 가정하면, 식(3)은 식(6)과 같이 표현된다.

d 4 Y i d x i - 4 + 2 U i d 2 Y i d x i - 2 - Ω i 2 Y i = 0

(6)

여기서

x ¯ i = x i L, 0 ≤ x ¯ i ≤ l ¯ i, l ¯ i = l i L,

(7-1)

U i = T i L 2 2 (E I) i,

(7-2)

Ω i 2 = (ρ A) i ω 2 L 4 (E I) i

(7-3)

이며, l_i는 i번째 연결부의 길이를 나타낸다.

식(6)의 해는 식(8)과 같이 표현된다.

Y i x = C 1 i sinh ⁡ M i x - i + C 2 i cosh ⁡ M i x - i + C 3 i s i n N i x - i + C 4 i c o s (N i x - i)

(8)

여기서

M i 2 = (U i 2 + Ω i 2) - U i

(9-1)

N i 2 = (U i 2 + Ω i 2) + U i

(9-2)

이다.

만일 비행체가 n개의 연결부로 나뉘어졌다면, 1번째와 n번째 연결부에서의 경계조건은 식(10-1), 식(10-2)와 같이 표현되고, 연결부와 연결부 사이에서의 조건은 식(11-1)부터 식 (11-4)와 같이 표현된다.

a t x ¯ 1 = 0, d 3 Y 1 d x 1 - 3 = 0, d 3 Y 1 d x 1 - 3 + 2 U 1 d Y 1 d x 1 - = 0

(10-1)

a t x ¯ n = l ¯ n, d 2 Y n d x n - 2 = 0, d 3 Y n d x n - 3 + 2 U n d Y n d x n - = 0

(10-2)

Y i l ¯ i = Y i + 1 0

(11-1)

Y' i l ¯ i = Y' i + 1 0

(11-2)

Y'' i l ¯ i = Y'' i + 1 0

(11-3)

Y''' i l ¯ i + 2 U i Y' i l ¯ i = Y''' i + 1 0 + 2 U i + 1 Y' i + 1 0

(11-4)

결국 4개의 경계조건과 4(n-1)개의 연결성 조건에 의해 4n개의 C_1n, C_2n, C_3n, C_4n이 결정되고, 식(10), 식(11)은 고유치 문제 풀이에 의해 고유진동수 ω를 구할 수 있다.

2.2 이론 보 모델 구성

Bokaian⁶은 물성치가 동일한1개의 보를 이용하여 고유진동수와 모드를 계산하였고, Joshi⁷는 연결부를 8개 이상으로 구성하여도 모드해석 결과에 영향을 주지 않는다는 것을 제시하였으며, Pourtakdoust⁸는 유도탄을 10개의 연결부로 나누어 모드해석을 수행하였다.

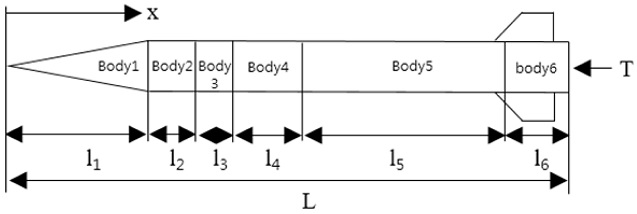
보통의 지대공유도탄은 Fig. 1과 같이 5-6개의 연결부로 구성된다. 본 논문에서는 Bokaian 방법을 이용 한 1개의 물성치로 만들어진 모델과 Joshi, Pourtadoust 등의 방법을 이용한 6개의 서로 다른 물성치를 가진 연결부로 구성된 모델에 대해 국내에서 개발된 지대공유도탄의 물성치를 이용하여 계산을 수행하고, 실제 동특성시험 및 비행시험에서 추출된 결과와 비교하였다.

Fig. 1

Analytic model for surface-to-air missile

1개 물성치 사용 모델은 복잡한 형상의 유도탄을 1개 물성치로 단순화하여 표현해야 하므로, 평균화한 물성치(I, E, ρ 및 동일 무게 기준 직경)로 바꾸어서 적용하였다. 6개 물성치 사용 모델 역시 각각의 연결부 무게를 맞추기 위하여 무게 등가 직경으로 변경하여 계산을 수행하였다.

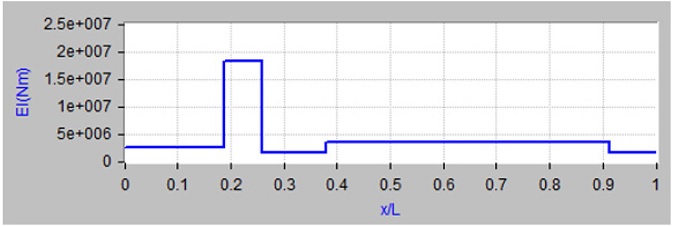
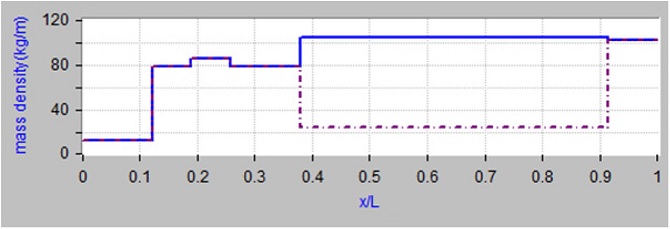
모델을 위한 무차원화된 길이대 굽힘강성 관계는 Fig. 2와 같으며, 무차원화된 길이대 단위 질량 관계는 Fig. 3과 같다.

Fig. 2

Distribution of bending stiffness

Fig. 3

Distribution of mass density (Propellant initial/burnout)

3. FE 모델링

상용 S/W (NX I-DEAS)를 이용한 FE 모델은 해석모델과 동일하게 보 요소를 이용하여 작성하고 계산을 수행하였다. 해석모델과 비교를 위하여 물성치가 동일하게 구성된 보 요소와 물성치가 서로 다른 6개 보 요소로 구성된 모델을 만들어 모드해석을 수행하였다. 비행진동 규격을 위한 과도응답해석을 수행하기 위하여 41개 보 요소로 구성된 모델을 만들어 계산된 자료들 간의 비교 및 시험결과와 비교를 수행하였다.

3.1 FE 모델 작성

FE 모델은 3개를 구성하였다. 첫 번째는 Bokaian⁶의 이론에 따른 보 모델로 물성치를 1개 사용하고, 6개의 보 요소로 구현하였고, 두 번째는 6개의 서로 다른 물성치로 10개의 보 요소로 이루어진 모델, 세 번째는 서로 다른 물성치를 가진 41개 보로 이루어진 모델이다. 각 모델에 사용되는 물성치는 Figs. 2와 3을 기본으로 하였고, 이론 보 모델과 비교를 위하여 첫 번째와 두 번째 FE 모델은 이론 모델과 각각 동일하게 적용하였다. 작성된 FE 모델은 다음과 같다.

3.2 외력 구성

유도탄은 비행 중 다양한 외력⁵의 영향을 받는다. 특히 추진기관 연소 시의 외력, 유도탄 동체에 부과되는 공력 변화에 따른 외력, 구동장치의 조종날개 작동력 및 조종면에 부과되는 공력 변화력 등이 주 외력으로 여겨진다.

본 논문에서는 FE 모델에 위 3가지 외력(조종날개 작동력 제외) 작용 시의 응답을 확인하였다.

3.2.1 추진기관 추력

추력은 유도탄 설계 목적에 따라 대상 표적과의 교전 성능과 연관되어 결정된다.⁹ 그러나 과도응답해석(Transient Response Analysis) 를 위해 진동이 필요하고, 이를 위해 본 논문에서는 개발 시 적용된 추력과 추력의 6.5% 진폭을 갖는 랜덤 진동을 만들어 입력하였다.

각 연결부에 작동되는 추력은 식(12)와 같이 정의^7,8,11 된다.

T i = T - T M 0 {∑ k = i n ρ A k l k + 12 ρ A i l i}

(12)

여기서 T는 총 추력, M₀은 유도탄 최초 무게이다.

3.2.2 유도탄 동체 및 조종날개 동압

추진기관 추력이 결정되면, 유도탄 속도가 결정되고, 이로부터 앙각에 따른 공력 중심 및 공력이 계산된다. 이 역시 과도응답해석을 위해 유도탄 동체 및 조종날개에 작용되는 하중 크기의 10% 진폭 랜덤 진동을 만들어 FE 모델에 입력하였다. 공력을 계산하기 위한 관련 식은 다음과 같다.

(1) 추력과 유도탄 속도 관계¹⁰

d u = F m d t = c m ˙ m d t = (c m ˙) d t m 0 - m p t t p

(13)

du는 속도변화, c는 노즐유효 출구속도(= Isp·g), $m ˙$ 는 시간당 추진제 연소소모량, m_p는 추진제 무게, m₀는 유도탄 무게, t_p는 연소시간

(2) 앙각에 따른 동체의 공력 중심⁹

x A C B l n = 0.63 1 - sin 2 ⁡ α + 0.5 l b l n sin 2 ⁡ α

(14)

(X_AC)_B은 공력중심 위치, l_n는 유도탄 노즈(Nose) 길이, α는 앙각(Angle of Attack), l_b는 유도탄 길이

(3) 동압¹

q = 12 ρ 0 V e s t 2

(15)

q는 동압, ρ₀는 해면에서 공기밀도, V_est는 비행체 등가 속도

(4) 공기 밀도¹²

ρ (h) = 1.2 E x p (- 2.9 × 10 - 5 × h 1.15)

(16)

h는 고도

(5) 공력⁹

D = C d q S r e f

(17)

C_d는 항력계수, q는 동압, S_ref는 공력작용 면적

4. 해석 결과

4.1 고유진동수 계산 결과

Bokaian 방법(추력 하중 하) 계산, Fig. 4의 FE 모델에 의한 계산, 대상 유도탄에 대한 모달시험 결과 및 비행시험 시 획득한 고유진동수(Hz)는 Table 1과 같다. Bokaian제시 방법에 의한 결과로부터 추력은 고유진동수에 미소하게 영향을 미치는 것으로 나타났다. FEA (Normal Mode 해석) 및 모달시험에서는 추력 가진 하의 고유진동수 계산을 할 수 없는 단점이 있다. 비행시험 시 계측된 자료 대비 Bokaian 방법(추력 50,000 N시)에 의해 계산된 고유진동수는 1차, 2차 모드에서 약 1.8% 오차를 보이며, 3차 모드에서 약 0.2% 오차를 보이고 있어, 비행 중 고유진동수를 확인하기 위해서는 이론적 방법을 적용하여도 유효한 결과를 얻는 것으로 확인되었다.

Fig. 4

FE model based on bokaian method

Table 1

Comparison of bokaian method result and others

Joshi, Pourtakdoust 방법, Fig. 5의 FE 모델, 대상 유도탄에 대한 모달시험 결과 및 비행시험 시 획득한 고유진동수(Hz)는 Table 2와 같다. 시험결과와 비교 시 이론적 방법(추력 50,000 N시)은 1차 모드에서 약 8.8% 오차를, 2차 모드에서 약 0.6% 오차를, 3차 모드에서 약 1.9% 오차를 보이고 있다. 이는 모델의 부정확성에 따른 것으로, 모델 구성 시 유도탄 무게를 맞추기 위하여 직경 변화 등을 통해서 수정을 가함으로써 발생한 것으로 실제 형상을 정확히 모사하지 못해서 발생하였다.

Fig. 5

FE model consisted of 10 beam element

Table 2

Comparison of joshi/pourtakdoust method result and others

Bokaian 방법과 Fig. 6의 FE 모델, 대상 유도탄에 대한 모달시험 결과 및 비행시험 시 획득한 고유진동수(Hz)는 Table 3과 같다. FE 모델을 자세히 구성함으로써 비행시험 계측치와 유사한 결과가 도출되었고, 따라서 Fig. 6의 FE 모델을 응답해석 모델로 이용하였다.

Fig. 6

FE model consisted of 41 beam element

Table 3

Comparison of bokaian method result and others

4.2 응답해석 및 시험 데이터 비교

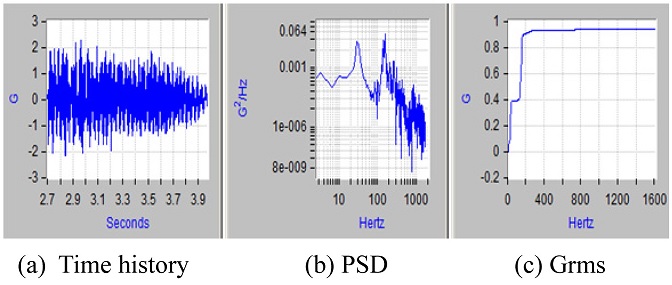
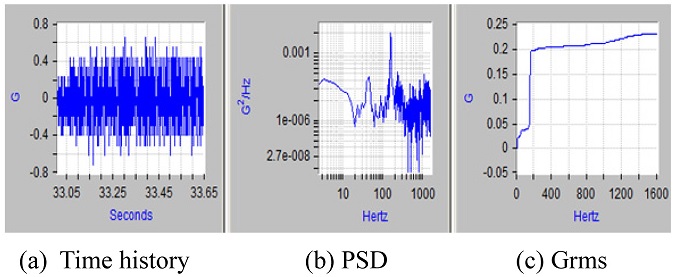
Figs. 7과 8은 국내 개발 지대공유도탄 비행시험 시 획득한 진동 데이터로, Fig. 7은 추진기관 연소 시작 직후 속도 Mach. 0.4-0.8 수준의 데이터이며, Fig. 8은 추진기관 연소 종료 후의 속도 Mach. 2.0 수준의 데이터로, 본 연구에서 검토한 특정한 한 부위에서 측정한 결과이다. 각 그림에서 첫 번째는 Time History를, 두 번째는 PSD (Power Spectrum Density)를, 세 번째는 Grms (G Root Mean Square)를 나타내고 있다.

Fig. 7

Measured vibration data (Time 2.7-3.9 sec.)

Fig. 8

Measured vibration data (Time 33 sec.)

비행시험 데이터는 원격측정장치(Telemetry)를 통해 수집되는데, 원격측정장치의 채널 한계성에 의해 Sampling Frequency를 3.2 kHz로 측정하였고, 이로부터 비행진동 환경규격 영역인 20-2,000 Hz를 모두 만족하는 영역을 측정하지는 못했다. 그러나 고주파수 영역이 구조물의 Grms에 크게 영향을 끼치지 못하고 있으므로 현 수준으로 2,000 Hz까지 확장하여 사용하여도 큰 영향이 없을 것으로 판단된다.

또한 PSD와 Grms 데이터 비교 시 추력 가진이 있을 때가 추력이 사라진 후의 진동데이터에 비해 매우 큼을 알 수 있다. 비행진동 환경 규격은 비행 중 모든 이벤트를 포함해야 하므로, 추력중 발생하는 진동데이터를 이용한 규격 생성이 타당하다.

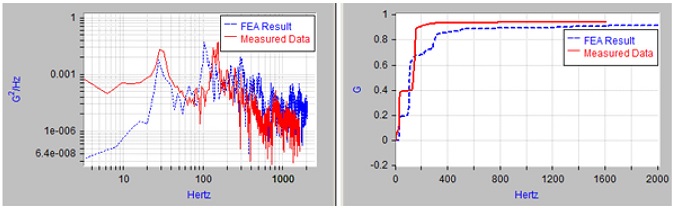
Fig. 9는 FE 모델을 이용한 과도응답해석 결과와 Fig. 7 (PSD, Grms)을 같이 도시하였다. 1차 모드 이하의 저주파수 영역에서 FE 모델이 실제 데이터를 충분히 따라가지 못하고 있으며, 200 Hz 이상의 주파수에서는 측정 데이터보다 다소 높은 수준 결과를 얻었다. 또한 Grms 측면에서는 해석 결과가 측정결과보다 미소하게 낮게 계산되었다. 이는 FE 모델의 부정확성에 따른 영향으로, 실제 형상과의 단면형상 모사 오차 및 물성치 모사 오차, 저주파수 및 고주파수 영역에 대한 댐핑의 부정확한 모사 등이 원인이라 판단된다.

Fig. 9

Result of FEA and measured data

일반적으로 비행진동 환경시험 규격을 정할 때 측정된 데이터의 PSD를 둘러싸는 Envelop을 작성하므로, 저주파수 영역을 제외하면 FE 모델에 의해 제시된 응답해석 결과를 환경규격으로 사용하여도 무리가 없을 것으로 판단된다.

FE 응답해석에 적용된 댐핑(Damping Factor)은 Table 4와 같다. 200 Hz 수준까지는 기존 모달시험에서 얻은 댐핑을 적용하였으며, 200 Hz 이상의 고주파수 영역에서는 4-5(%) 댐핑을 적용하였다.

Table 4

Damping factors for FEA

4.3 비행환경 규격 생성

Piesol⁴은 비행체 구성품 진동 규격 수준을 식(18)과 같이 제시하였다.

T f = μ f + k σ (f)

(18)

여기서 μ(f) 는 평균, σ(f) 는 표준편차, k는 상수(2 ≤ k ≤ 3)이다.

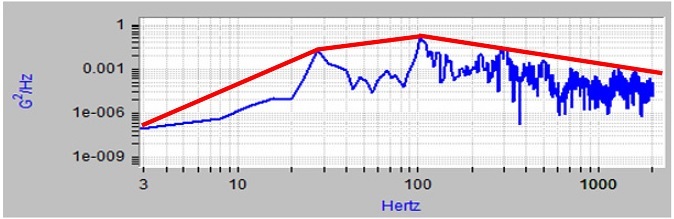
식(18)과 랜덤과정(Random Process)¹³을 적용하면, Grms는 1σ이고, k = 3일 경우, 비행진동 규격은 Fig. 9의 곡선을 덮은 Smoothed Spectrum의 3배와 같으며, Fig. 10으로 표현된다.

Fig. 10

Proposed flight vehicle vibration spec.

앞서 언급했던 것처럼, 유도탄은 5-6개의 연결부로 조립된 형상이며, 각각의 연결부에는 많은 센서들과 전자장비를 탑재하고 있다. 또한 각 연결부는 각기 다른 응답특성이 있다. 따라서 1개의 비행진동 규격으로 유도탄 구성품에 동일하게 적용하는 것은 바람직하지 않다. 따라서 본 논문에서 제시한 방법을 기준으로 각 연결부에 대한 과도응답해석을 수행하고, 이를 각 연결부 별로 비행진동 규격을 설정하는 것이 최적의 설계가 될 것으로 판단된다.

5. 결론

본 논문에서는 지대공유도무기 개발 초기, 내부 구성품의 최적 설계를 위해 요구되는 비행진동 규격을 설정하는 방법을 제시하였다.

비행진동 규격을 설정하기 위한 첫 번째 단계로 단순한 빔 이론을 이용한 방법과 FEA를 이용한 방법으로 고유진동수를 찾았고, 그 크기를 비교하였다. 두 번째 단계는 41개의 보 요소로 구성된 FE 모델에 기존에 모달시험에서 구한 댐핑을 이용한 응답해석을 수행하였다. 세 번째 단계는 구해진 PSD를 포함하는 Smoothed Spectrum의 3배를 취하여 비행진동 환경규격을 설정하였다. 이는 표준정규분포에서 99.7% 이상의 확률을 가지게 됨을 의미한다.

대상체의 물성치를 평균화하여 얻은 값으로 계산한 Bokaian 방법이 세분화한 FE 모델과 대등 수준의 고유진동수를 얻었다. 세분화한 FE 모델을 이용한 응답해석은 비행시험에서 얻은 데이터와 비교 시 1차 굽힘 모드 이하의 주파수에서 다소 차이를 보이나 그 형태나 크기가 유사성을 보여 비행환경 규격을 설정함에 무리가 없음을 확인하였다.

NOMENCLATURE


E :	Young’s modulus
I :	Second moment of area
ρ :	Mass density
A :	Cross section area
T :	Thrust force
x :	Distance from the left-hand end of the beam
$x ¯ i$ :	Dimensionless distance (x_i/L)
y :	Transverse displacement, y (x, t)
Y :	Modal displacement
L :	Beam length
l_i :	Segment length of beam
$l ¯ i$ :	Dimensionless length of segment beam (l_i/L)
ω :	Circular natural frequency
t :	Time

REFERENCES

MIL-STD-810G, “Environmental Engineering Considerations and Laboratory Tests,” 514-7D-19, 2014.
MIL-STD-810C, “Military Standard Environmental Test Methods,” 514.2-36, 1975.
Choi, S. H., “Flight Environment Simulation Test for Reliability Improvement of Precise Guided Missile,” J. Korean Soc. Precis. Eng., Vol. 33, No. 10, pp. 781-787, 2016. [https://doi.org/10.7736/KSPE.2016.33.10.781]
Piersol, A. G., “The Development of Vibration Test Specifications for Flight Vehicle Components,” Journal of Sound and Vibration, Vol. 4, No. 1, pp.88-115, 1966. [https://doi.org/10.1016/0022-460X(66)90156-8]
Bendat, J. S., Enochson, L. D., Klein, G. H., and Pieesol, A. G., “The Application of Statistics to the Flight Vehicle Vibration Problem,” ASD Technical Report, pp. 61-123, 1961.
Bokaian, A., “Natural Frequencies of Beam under Compressive Axial Loads,” Journal of Sound and Vibration, Vol. 126, No. 1, pp. 49-65, 1988. [https://doi.org/10.1016/0022-460X(88)90397-5]
Joshi, A., “Free Vibration Characteristics of Variable Mass Rockets Having Large Axial Thrust/Acceleration,” Journal of Sound and Vibration, Vol. 187, No. 4, pp. 727-736, 1995. [https://doi.org/10.1006/jsvi.1995.0559]
Pourtakdoust, S. H. and Assadian, N., “Investigation of Thrust Effect on the Vibrational Characteristics of Flexible Guided Missile,” Journal of Sound and Vibration, Vol. 272, No. 1, pp. 287-299, 2004. [https://doi.org/10.1016/S0022-460X(03)00779-X]
Fleeman, E. L., “Tactical Missile Design,” American Institute of Aeronautics and Astronautics, pp. 82-137, 2006.
Sutton, G. P. and Biblarz, O., “Rocket Propulsion Elements,” John Wiley & Sons, pp. 104-113, 2001.
Chen, G., Rui, X. R., Yang, F., and Zhang, J., “Study on the Natural Vibration Characteristics of Flexible Missile with Thrust by Using Riccati Transfer Matrix Method,” Journal of Applied Mechanics, Vol. 83, No. 3, Paepr No. 031006, 2016. [https://doi.org/10.1115/1.4032049]
Komerath, N., “AE 6450 Rocket Propulsion,” Georgia Institute of Technology, 2005.
Bendat, J. S. and Piersol A. G., “Random Data,” John Wiley & Sons, 2010. [https://doi.org/10.1002/9781118032428]

Mode (Hz)	Bokaian	Method	FEA	Modal	Test
	Thrust, N
	50,000	500,000	None	None	-
1st	29.14	29.13	27.11	29.16	29.7
2nd	78.24	78.23	74.52	77.17	79.7
3rd	145.74	145.74	145.88	144.66	146.1

Mode (Hz)	Joshi, Pourtakdoust method		FEA	Modal	Test
	Thrust, N
	50,000	500,000	None	None	-
1st	27.06	25.12	32.88	29.16	29.7
2nd	79.19	77.58	90.67	77.17	79.7
3rd	148.94	147.65	159.72	144.66	146.1

Mode (Hz)	Bokaian	Method	FEA	Modal	Test
	Thrust, N
	50,000	500,000	None	None	-
1st	29.14	29.13	29.3	29.16	29.7
2nd	78.24	78.23	78.2	77.17	79.7
3rd	145.74	145.74	147.0	144.66	146.1

Frequency (Hz)	Damping (%)
~30	0.38
30~120	1.03
120~200	1.76
200~300	4
300~2000	5