통계적 기법과 유한요소해석을 활용한 복합재 적층판 설계 허용치 예측
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This paper presents a method to predict the design allowable for composite laminates subjected to a tensile load with finite element analysis. The mechanical properties were obtained by conducting tensile and compressive lamina tests. The statistically-based properties were acquired using an in-house tool to calculate the design allowable. A tensile load was imposed on the FE model of the laminate, and each ply stress was compared to the design allowable of the lamina test. The load was considered as the failure load when the ply stress reached the allowable value. This load was applied to a laminate model to perform finite element analysis, and the laminate strength was calculated. The calculated strength and design allowable of the laminate were compared, and as a result, the difference between the results of analysis and test was found to be within 10%.
Keywords:
Statistical method, Pooling method, Design allowable, Finite element analysis키워드:
통계 기법, 합동 방법, 설계 허용치, 유한요소해석1. 서론
복합재료는 금속재료에 비해 비강성과 비강도가 높고 내마모성, 피로 특성이 우수하기 때문에 항공, 우주, 국방 산업 등과 같이 경량화가 요구되는 분야에 많이 적용되고 있다. 하지만 금속재료에 비해 높은 변동성(Variability)을 내재하고 있기 때문에 이에 대한 신뢰성 확보를 위해 재료의 특성 및 환경 요인에 의한 강도 저하 등에 대한 다양한 평가를 수행하고 있다. 이러한 평가 방법의 대부분이 시험 위주로 이루어져 있기 때문에 설계 허용치(Design Allowable)를 계산하기 위한 데이터 획득을 위해서 보다 더 많은 반복 시험이 요구된다. 그럼에도 불구하고 복합재료는 이방성으로 인한 다양한 시험과 높은 시험 비용으로 인해 구축된 데이터베이스가 금속재료에 비해 충분하지 못한 것이 현실이다. 따라서, 복합재료의 기계적 물성에 대한 합리적인 설계 허용치를 도출하기 위해서는 변동성을 고려하여 신뢰할 수 있는 통계 이론을 적용하는 것이 보다 효율적이다.1 CMH-17에는 통계 분석 기법으로 합동 방법(Pooling Method)와 점 추정 방법(Single Point Method)을 제시하고 있다.2 이러한 통계 기법을 사용하여 Kim3등은 국내에서 사용되고 있는 항공용 복합재료 프리프레그의 물성치를 데이터베이스화하였다. Quayle4은 통계기법을 사용하여 위성 구조에 적용한 10 종의 탄소섬유/시아네이트 에스테르(Carbon Fiber/Syanate Ester) 복합재료에 대한 설계 허용치를 재평가하였다. Zureick5등은 섬유강화복합 재료의 기계적 물성을 기록하기 위해 통계적으로 유효한 방법을 제시하였다.
또한 통계이론을 적용한 복합재 불확도 해석에 관한 연구가 많이 수행되어 왔다. Nam6등은 라미나 시험 데이터의 통계 분포를 반영한 표본을 생성하여 유한요소 해석을 통해 라미네이트의 설계 허용치를 예측하였으며, Astill7와 Oh8는 몬테카를로 시뮬레이션(MCS)을 적용하여 탄소섬유강화 복합재료의 강도를 평가하였다. Barbero9등은 Weibull 분포 함수를 사용하여 복합재의 기계적 물성을 통계적으로 분석하였다.
라미네이트 시험은 적층 순서에 따라 시험 조합의 수를 무한대로 볼 수 있으므로 부분적으로 일부 조합에 대해서만 시험을 수행해야 한다. 하지만, 라미나 시험은 단방향 시편을 이용하여 시험하므로 시험 수량이 상대적으로 제한적이다. 따라서, 라미나 물성을 이용하여 라미네이트의 설계 허용치를 예측할 수 있다면 시간 및 비용을 최소할 수 있는 이점이 있다.
본 연구에서는 라미나의 인장, 압축 시험을 통해 기본 물성(강성 및 강도)을 획득하고, 자체 개발한 EXCEL 기반의 통계 처리 프로그램으로 강도에 대한 설계 허용치를 계산하였다. 그리고 획득한 라미나 물성을 사용한 유한요소해석을 통해 라미네이트 강도의 설계 허용치를 예측해보고자 한다.
해석을 통해 예측된 라미네이트의 설계 허용치를 실제 시험으로 획득한 라미네이트 강도의 설계 허용치와 비교, 분석하였다.
2. 본론
2.1 시험
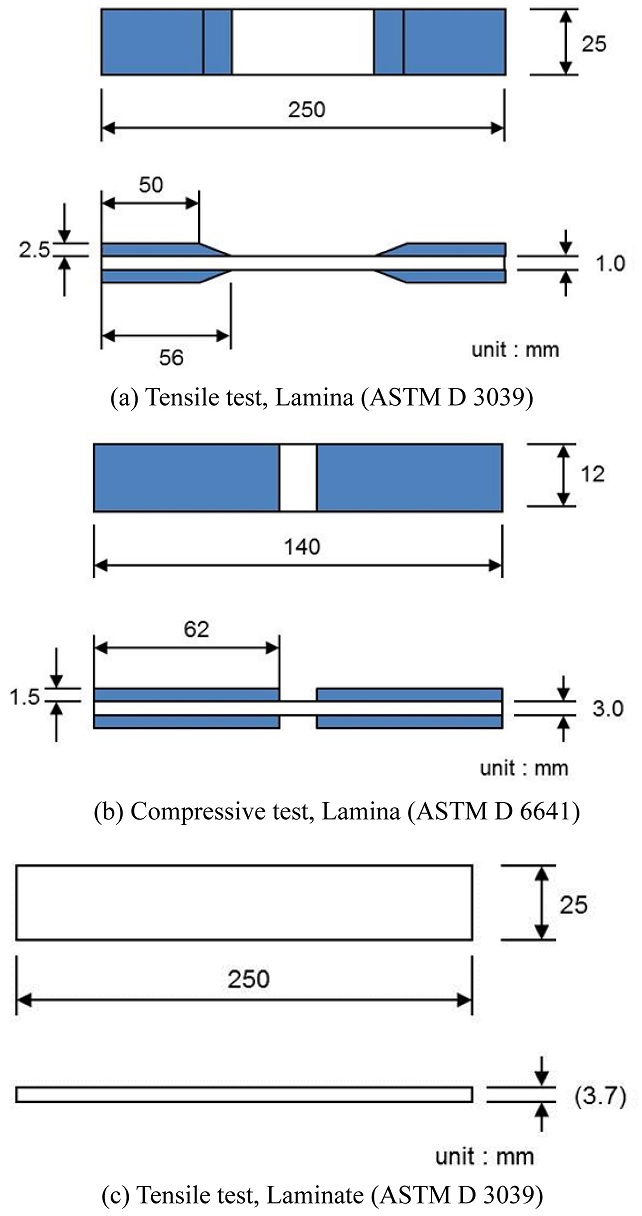
본 연구에서 사용한 소재는 일방향(UD)과 직조형(Fabric)의 탄소섬유/에폭시 프리프레그이다. 소재의 각 방향 별 기본 물성을 얻기 위한 라미나 시편은 ASTM D 3039(인장)과 ASTM D 6641(압축)을 참고하였다. 두 가지 프리프레그로 적층한 라미네이트의 강도를 획득하기 위한 라미네이트 시편은 ASTM D 3039(인장)을 참고하였다.
시편은 오토클레이브 성형으로 제작하였으며, 라미나 및 라미네이트 시편 형상을 Fig. 1에 나타내었다.
시편 수량은CMH-17에서 제시하는 허용치 기준 중 하나인 B-Basis Reduced Sampling 해당하는 3뱃치(Batch)에 18개이다(뱃치 당 6개).
소재의 각 방향에 대한 기본 물성을 획득하기 위해 라미나의 인장, 압축 시험을 수행하였다.
먼저 일방향 라미나의 0°와 90° 방향에 대한 인장 탄성계수, 인장강도 및 포아송비를 획득하기 위하여 인장 시험을 수행하였다. 축 방향과 횡 방향 스트레인 게이지를 통해 측정된 변형률을 이용하여 포아송비를 계산하였다. 직조형 라미나는 0°와 90° 방향의 물성이 동일하다고 보고 90° 방향에 대한 시험은 생략하였다.
다음으로 압축 강도를 획득하기 위하여 압축 시험을 수행하였으며, 인장 시험과 마찬가지로 직조형 라미나는 90° 방향에 대한 시험은 생략하였다. 특히, 압축 시험에서는 시편의 좌굴 현상의 발생 여부가 시험 결과에 영향을 주기 때문에 이를 방지하기 위한 치구를 이용하여 시험을 수행하였다.
라미네이트는 축방향으로 인장 시험을 수행하여 강도를 측정하였다. 예측한 라미네이트의 설계 허용치를 비교하는 목적의 시험이므로 파손 하중을 측정하여 강도데이터를 획득하였다.
복합재료 운용 및 보관 환경 조건에 따라 물성 저하가 발생하기 때문에 온도와 습도 환경을 고려할 필요가 있다. 본 연구에서는 일반적인 상온 건조(RTD) 상태와 가장 급격한 물성 저하 현상을 보이는 고온 다습(ETW) 상태 2 가지 환경 조건에서 라미나의 인장, 압축 시험과 라미네이트의 인장 시험을 수행하였다. 고온다습 환경은 ASTM D 5229에 따라 환경화 과정을 완료한 후 시험을 진행하였다.
2.2 설계 허용치(Design Allowable) 획득
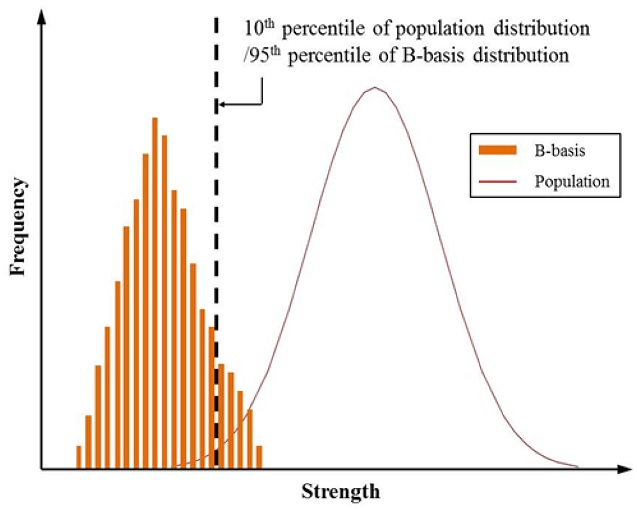
앞서 수행한 라미나 및 라미네이트 시험 결과를 통계 처리하여 설계 허용치로 B-Basis를 계산하였다. B-Basis는 측정값들의 지정된 모집단의 백분위 수에 관한 95% 신뢰한계이다. 즉, 지정된 모집단의 상위 90%에 대한 95% 공차 한계(Tolerance Limit)를 의미한다. B-Basis는 각 요소 파괴로 인한 적용 하중이 다른 하중전달 요소에 안전하게 배분되는 다중화 구조에 대하여 사용이 가능하다.
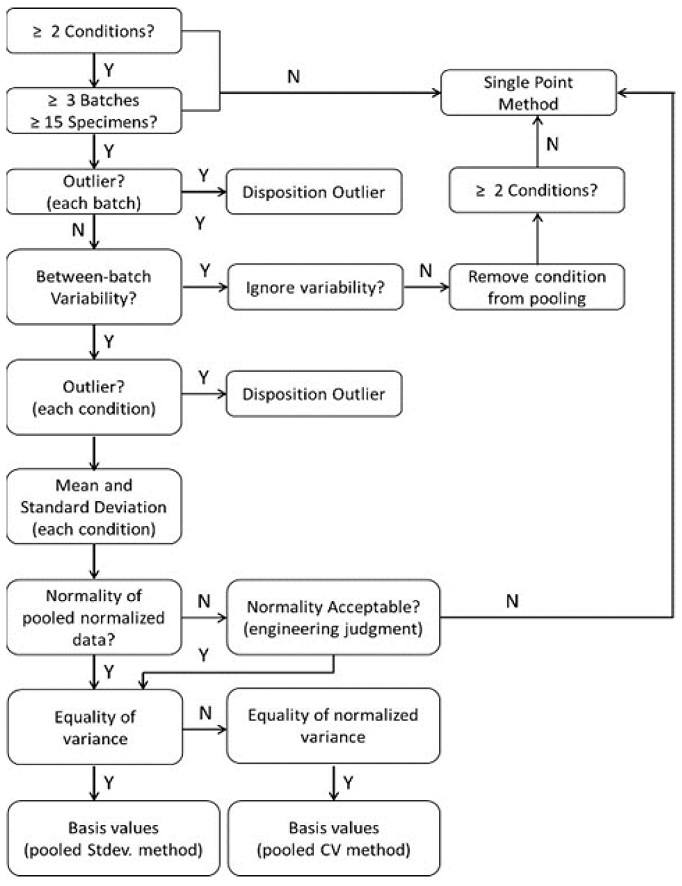
시험 결과 정리에 적용한 합동 방법은 서로 다른 데이터 집합(환경 조건)을 결합하여 보다 큰 데이터 집합을 구성하는 방법으로 설계 허용치를 획득할 수 있는 원천 데이터가 풍부해지기 때문에 통계적으로 보다 안정적인 설계 허용치를 획득하는 것이 가능하다. 합동 방법을 사용하여 설계 허용치를 계산하는 과정은 아래와 같다.
(1) 각 환경 조건 데이터 집합 내 뱃치 간 변동성이 무시할 수 있을 정도인지 확인하기 위해 K-Sample Anderson-Darling Test를 수행한다. ADK 검정통계량과 임계값(ADC)을 비교하여 뱃치 간 변동성이 무시할 만한 수준인지 판단한다.
| (1) |
| (2) |
(2) 합동 방법을 적용하기 위해서는 합동된 데이터가 정규분포를 이루어야 하며, 이를 확인하기 위해 Anderson-Darling Test를 사용하여 정규분포에 대한 적합도(Goodness-of-Fit) 평가를 진행한다. 관측 유의 수준(OSL)이 0.05보다 큰 경우 정규분포를 이룬다고 판단할 수 있다.
(3) Levene’s Test를 사용하여 각 데이터 집합의 중간값(Median)과 각 데이터 간의 편차를 계산 후 F-Test를 수행한다.
| (3) |
(4) 각 환경 조건 데이터 집합 내 뱃치 간 변동성이 무시할 수 있을 정도인지 확인하기 위해 K-Sample Anderson-Darling Test를 수행한다. ADK 검정통계량과 임계값(ADC)을 비교하여 뱃치 간 변동성이 무시할 만한 수준인지 판단한다.
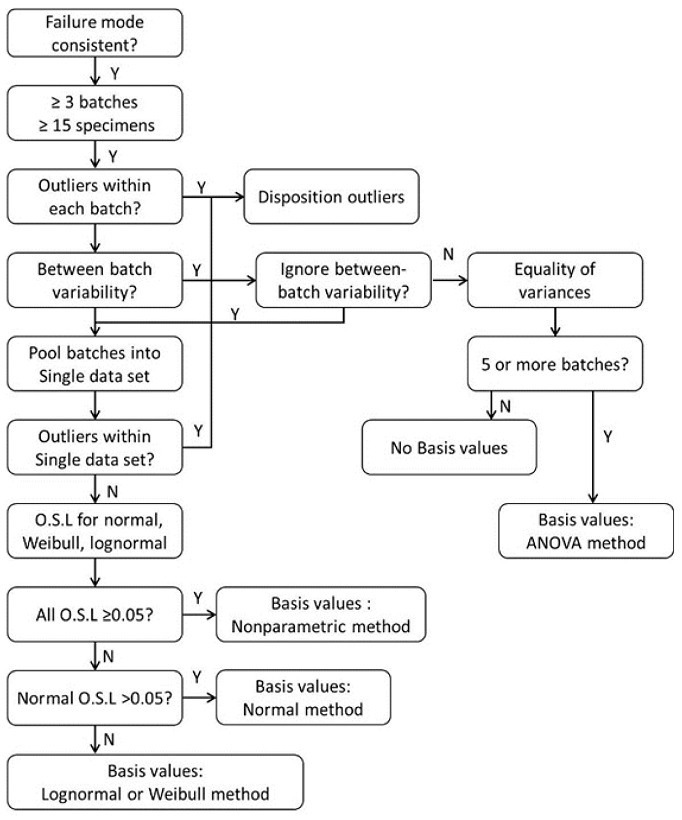
합동 방법의 절차를 따른 계산 과정에서 합동이 불가하다고 판단하는 경우에는 점 추정 방법을 사용하여 설계 허용치를 구하게 된다. 합동 방법과 달리 점 추정 방법은 개별 데이터 집합에 대한 분포 적합성 검증을 수행하다. 분포 적합성 검증 결과에 따라 개별 데이터 집합에 맞는 분포 모델에서 설계 허용치를 계산한다. 점 추정 방법으로 설계 허용치를 계산하는 과정을 다음에 기술하였다.
합동 방법과 동일한 절차로 뱃치 간 변동성 이 무시할 만한 수준인지 확인하기 위해 K-Sample Anderson-Darling Test를 수행한다.
각 데이터 집합에 대한 정규 분포(Normal Distribution), 로그 정규분포(Lognormal Distribution), 2모수 와이블 분포(2-Parameter Weibull Distribution)에 해당하는 각각의 OSL을 계산한다.
개별 데이터 집합 별로 세 분포에 대한 OSL이 0.05이하이면 비모수(Nonparametric) 방법으로 설계 허용치를 계산한다. 이는 데이터 집합이 특정 분포를 따르지 않는다는 것을 의미한다.
(3)의 조건을 만족하지 못하면 우선 정규 분포 OSL과 0.05를 비교하여 0.05보다 크면 정규 분포로 설계 허용치를 계산한다.
정규분포 OSL이 0.05보다 작으면 로그정규분포 또는 2 모수 와이블 분포로 설계 허용치를 계산한다. 물론 이 과정에서 두 분포에 대한 OSL은 0.05보다 커야 한다.
(1)의 과정에서 뱃치 간 변동성이 무시할 만한 수준이 아닌 경우에는 합동 방법 절차 (3)의 방법으로 분산 동등성을 검정한 후 5뱃치 또는 이상 조건을 만족하는 경우 ANOVA 방법으로 설계 허용치를 계산한다.
2.3 라미나 / 라미네이트 시험 결과
Fig. 1에 제시한 시편을 사용하여 라미나(인장 및 압축)와 라미네이트(인장)에 대한 시험을 수행하였다. 라미나 시험을 통해 해석을 위한 기본 물성(강성, 포아송비)을 획득하였고, 강도를 통계 처리하여 라미나의 설계 허용치를 계산하였다. 또한 라미네이트 시험을 통해 획득한 강도를 통계 처리하여 라미네이트의 설계 허용치를 계산하였다. 일방향 라미나, 직조형 라미나 및 라미네이트의 물성을 Tables 1-3에 각각 제시하였다.
2.4 라미네이트의 강도 예측
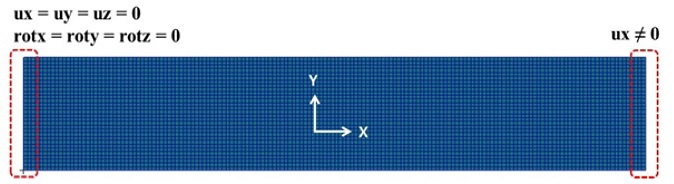
본 논문에서는 유한요소해석을 수행하여 라미네이트의 강도를 예측하였다. 재료 물성은 Tables 1과 2에 제시한 값을 사용하였다. MSC. Patran/Nastran으로 해석을 수행하였고, Fig. 5에 유한요소 모델을 나타내었다.
변위 하중을 점차적으로 증가시키면서 각 단층의 응력 상태와 전체 하중을 확인하였다. 각 단층에 대하여 응력 성분들을 확인하여 이 값이 해당 단층의 라미나 설계 허용치에 도달하면 파손된 것으로 간주하였다. 그리고 이 때의 하중을 라미네이트의 파손 하중으로 보고 이를 이용하여 라미네이트의 설계 허용치를 계산하였다.
해석 결과, 10번째 단층에 위치한 직조형 라미나의 시편 축 방향(X 방향) 응력이 가장 먼저 라미나 설계 허용치에 도달하는 것을 확인할 수 있었다. 직조형 라미나의 시편 축 방향 설계 허용치는 731.741 MPa 이다. 라미나의 응력이 설계 허용치에 도달할때 시편 전체에 작용하는 하중은 66,727.97 N 이다. 해당 하중 상태에서 라미네이트의 설계 허용치는 716.93 MPa이다.
라미네이트의 해석 결과와 시험결과를 통계 처리하여 계산한 라미네이트 강도의 설계 허용치를 비교한 결과를 Table 4에 나타내었다. 약 9.2% 오차 범위에서 예측됨을 확인하였다.
3. 결론
본 논문에서는 복합재 라미나의 설계 허용치를 계산하고 이를 이용한 유한요소해석을 통해 라미네이트의 설계 허용치를 예측하는 방법에 대해 연구하였다. 라미네이트의 설계 허용치 예측 과정을 요약하면 다음과 같다.
(1) 탄소섬유복합재료의 기계적 물성을 구하기 위해CMH-17 및 ASTM에 제시된 규격과 절차에 따라 시편 제작 및 시험을 수행하였다. 시편 수량은 B-Basis Reduced Sampling 기준(3 뱃치/18개)에 따라 제작하였고, 2가지 환경 조건(RTD, ETW)에서 인장과 압축 시험을 진행하였다.
(2) CMH-17에서 제시하는 통계 기법 절차를 따라 자체 제작한 EXCEL 기반의 In-House Tool을 사용하여 합동 방법(Pooling Method)으로 설계 허용치(B-Basis)를 계산하였다.
(3) 라미나 시험으로 획득한 물성을 이용하여 유한 요소 해석을 수행하였다. 변위 하중을 점차적으로 증가시키면서 라미네이트 각 단층의 응력 상태를 확인하였고, 각 단층의 응력이 해당 단층의 라미나 설계 허용치에 도달하면 파손된 것으로 간주하였다. 그리고 이 때의 하중을 라미네이트의 파손 하중으로 보고, 라미네이트의 설계 허용치를 계산하였다.
(4) 유한요소해석으로 예측한 라미네이트의 설계 허용치와 실제 라미네이트 시험 결과를 통계 처리한 설계 허용치를 비교한 결과, 약 9.2%의 오차 범위에서 예측됨을 확인하였다.
NOMENCLATURE
| ADK : | K-Sample anderson-darling statistics |
| ADC : | Critical value for ADK |
| ANOVA : | Analysis of variance |
| ETW : | Evaluated temperature wet |
| F : | F statistics |
| MNR : | Maximum normed residual |
| OSL : | Observed significance level |
| RTD : | Room temperature dry |
| α : | Significant level |
REFERENCES
-
Rhee, S. Y., “Pooling-Across-Environments Method for the Generation of Composite-Material Allowables,” Journal of Aerospace System Engineering, Vol. 10, No. 3, pp. 63-69, 2016.
[https://doi.org/10.20910/JASE.2016.10.3.63]

- CMH-17, “Polymer Matrix Composites: Guidelines for Characterization of Structural Materials,” SAE International, Vol. 1, 2012.
-
Kim, J. and Lee, H., “Statistical Characteristics of Domestic Composite Material Prepregs,” Journal of Aerospace System Engineering, Vol. 10, No. 1, pp. 103-110, 2016.
[https://doi.org/10.20910/JASE.2016.10.1.103]

- Quayle, A., “Design Allowables Re-Evaluation of Ten Composite Materials; Mechanical Testing and Porosity Examination of M55J Fabric Coupons,” Space Systems / Loral, 2013.
-
Zureick, A.-H., Bennett, R. M., and Ellingwood, B. R., “Statistical Characterization of Fiber-Reinforced Polymer Composite Material Properties for Structural Design,” Journal of Structural Engineering, Vol. 132, No. 8, pp. 1320-1327, 2006.
[https://doi.org/10.1061/(ASCE)0733-9445(2006)132:8(1320)]

-
Nam, K., Park, K. J., Shin, S., Kim, S. J., and Choi, I.-H., “Estimation of Composite Laminate Design Allowables Using the Statistical Characteristics of Lamina Level Test Data,” International Journal of Aeronautical and Space Sciences, Vol. 16, No. 3, pp. 360-369, 2015.
[https://doi.org/10.5139/IJASS.2015.16.3.360]

-
Oh, K. P., “A Monte Carlo Study of the Strength of Unidirectional Fiber-Reinforced Composites,” Journal of Composite Materials, Vol. 13, No. 4, pp. 311-328, 1979.
[https://doi.org/10.1177/002199837901300405]

-
Astill, C., Imosseir, S., and Shinozuka, M., “Impact Loading on Structures with Random Properties,” Journal of Structural Mechanics, Vol. 1, No. 1, pp. 63-77, 1972.
[https://doi.org/10.1080/03601217208905333]

-
Barbero, E., Fernández-Sáez, J., and Navarro, C., “Statistical Analysis of the Mechanical Properties of Composite Materials,” Composites Part B: Engineering, Vol. 31, No. 5, pp. 375-381, 2000.
[https://doi.org/10.1016/S1359-8368(00)00027-5]