CNC 보간기의 코너 블렌딩에 의한 경로계획오차의 한계설정
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
Computer numerical control (CNC) part programs generated by computer-aided manufacturing software are frequently composed of numerous G01 blocks. CNC interpolator applies acceleration and deceleration to generate velocity profile of each block. Therefore, the machining time is increased when the number of G01 blocks is increased. To reduce the machining time, corner blending has been used to smooth the corner shape of adjacent blocks. Because the tool path generated by corner bending dose not reach the commanded endpoint, error of the interpolated tool path exists. The objective of this study was to present a method to determine block overlap time to limit tool path error generated by corner blending. An algorithm to calculate tool path error with respect to block overlap time was also proposed. Performance of the proposed algorithm to limit tool path error was demonstrated in this study.
Keywords:
Machine tool control, Position control, Precision machining키워드:
공작기계 제어, 위치 제어, 정밀가공1. 서론
Computer-Aided Manufacturing (CAM) 소프트웨어는 공작물의 도면을 입력 받아 CNC 공작기계의 구동에 필요한 파트 프로그램을 생성한다. CNC 공작기계에서는 직선보간(G01)과 원호보간(G02, G03)으로 구성된 파트 프로그램이 보편적으로 사용되고 있기 때문에, CAM소프트웨어는 일반적으로 자유곡면을 설정된 허용오차를 만족하는 짧은 직선 세그먼트로 근사하여 G01 블록으로 파트 프로그램을 생성하는 용도로 사용된다. 공작물 형상 내 곡률이 큰 자유곡면이 많아지거나, 허용오차를 작게 할수록 직선 세그먼트의 개수가 증가한다. CNC는 급격한 가속 및 감속으로 인해 발생하는 오차와 공작기계의 충격을 방지하기 위하여 이송지령에 가감속을 적용하기 때문에 G01 블록의 개수가 증가할수록, 전체 가공시간이 증가하여 생산성이 저하된다.
가공속도를 향상시키기 위하여 G01 블록으로 구성된 경로를 설정된 오차범위 내에서 매개변수형 곡선으로 근사하여 보간하는 기술이 연구되고 있다. Wang1은 G01 블록을 미리 선독하여 짧은 직선 세그먼트로 구성된 경로만을 NURBS 커브로 근사하고, 이송 속도 스케쥴링을 적용하여 가공시간을 줄이는 방법을 제안하였다. Zhao2는 선독한 G01 블록을 G2 연속성이 보장되는 B-Spline 커브로 근사하여 곡률의 불연속성으로 인한 가속도의 진동을 방지하고, 가공시간을 저감시키는 방법을 제안하였다. 그러나 매개변수형 곡선에 근사할 때 정확한 곡선의 곡률을 계산하는 것이 어렵고3, 이송 속도의 변동이 크게 발생할 수 있으며4, 계산과정이 복잡하여 높은 연산 성능을 요구하기 때문에 CNC에 적용하는데 한계를 가진다.
코너 블렌딩 기술은 인접한 두 G01 블록 사이의 코너를 매끄러운 곡선으로 이어주는 방식으로 계산부하가 적어 CNC의 실시간 보간에 주로 적용되고 있다. 코너 블렌딩을 적용하여 경로계획을 생성할 경우 지령된 종점에 도달하지 못하기 때문에 코너 부근에서 항상 오차가 발생하고, 이는 가공된 작업물의 형상오차를 초래한다. 따라서 허용되는 오차범위 내에서 코너 블렌딩을 적용하는 것이 필요하다. Tulsyan5 은 코너에 허용오차 제한과 C3 연속성을 만족시키는 B-Spline 커브로 블렌딩을 하는 방법을 제안하였다. Tajima6는 저크 제한과 허용오차 제한을 만족시키는 Kinematic 커브를 이용하여 코너를 블렌딩 하는 방법을 제안하였다. Sencer7는 FIR 필터를 적용한 속도 프로파일의 중첩시간을 조절하여 코너에서 발생하는 오차를 조절하는 방법을 제안하였다. 이 방법은 코너에서 블렌딩을 위한 커브를 삽입하기 위해 충분한 거리가 확보되어야 하기 때문에, 미소블록들이 이어지는 파트 프로그램에는 적용하기 어렵다.
본 논문에서는 3축 CNC 공작기계의 실시간 보간에 적용하기 위하여 FIR 필터가 적용된 속도 프로파일에서 중첩시간을 조절하여 경로계획오차를 제한하는 코너 블렌딩 기술을 제안하였다. 경로계획오차 제한을 적용하기 위하여 중첩시간에 따라 경로계획에서 발생하는 오차를 계산하였다. 제안된 알고리즘은 미소블록이 연속되는 경우와 블록간 이송속도가 변하는 경우에도 적용이 가능하다.
2. 코너에서 발생하는 경로계획오차
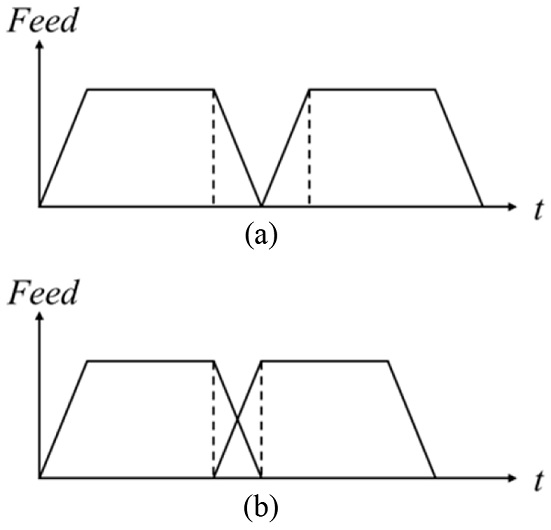
G61과 G64는 CNC에서 절삭가공 시 인접한 두 블록의 속도 프로파일의 중첩을 설정하기 위한 파트 프로그램 명령어이다. Fig. 1은 G61과 G64를 설정하였을 때 생성되는 접선방향 속도 프로파일을 비교한 것이다. G61은 지령된 종점에 공구가 정확히 도달해야 하는 경우 사용이 되며, G61을 지령하였을 시 Fig. 1(a)와 같이 지령된 종점에 도달한 이후에 다음 속도 프로파일을 실행한다. G64는 인접한 두 블록의 코너에서 블렌딩을 지원하기 위한 명령어로, 가감속으로 인한 가공시간 증가를 줄이기 위해 사용된다. G64 지령 시 현재 블록의 감속이 시작되는 구간부터 다음 블록의 가속을 동시에 수행한다. 가속구간과 감속구간의 중첩에 의해 CNC에서 생성된 경로계획이 지령된 종점에 도달하지 못한다. 따라서 G64를 지령할 경우, 인접한 두 블록 사이의 코너 부근에서는 파트 프로그램으로 지령한 기준경로와 CNC에서 생성된 경로계획 간에 항상 오차가 발생한다.
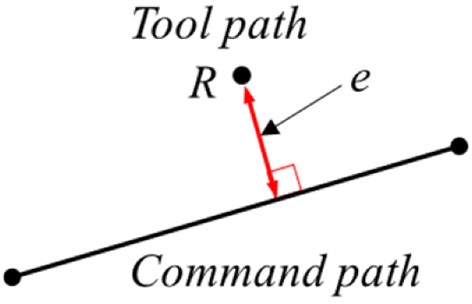
작업물의 윤곽오차는 기준경로와 공작기계 공구의 실제위치 사이의 최단거리로써 공작기계를 이용한 가공 시 작업물의 형상오차를 나타내기 위해 사용된다. 경로계획오차는 Fig. 2와 같이 기준경로와 CNC에서 생성된 경로계획 사이의 최단거리로 정의할 수 있으며, 보간 정확도를 평가하기 위해 사용된다.8 공작기계 구동부의 위치제어 시 경로계획을 목표 위치로 사용하기 때문에 일반적으로 파트 프로그램의 보간 시 경로계획오차의 평균값이 작아질수록 작업물의 윤곽오차는 감소할 것이다. 따라서 파트 프로그램의 보간 단계에서 경로계획오차를 제한함으로써, 작업물의 형상정밀도를 향상시킬 수 있다.
경로계획오차를 계산하기 위해서는 경로계획과 모든 기준경로 사이의 거리를 계산하여 최단거리를 찾아야 한다. 하지만 파트 프로그램 내 블록 수가 많아질수록 계산량이 증가하게 되기 때문에, CNC의 실시간 보간에 적용하기 어렵다. 따라서 경로계획오차는 중첩이 일어나는 두 블록만을 고려하여 계산을 하였다.
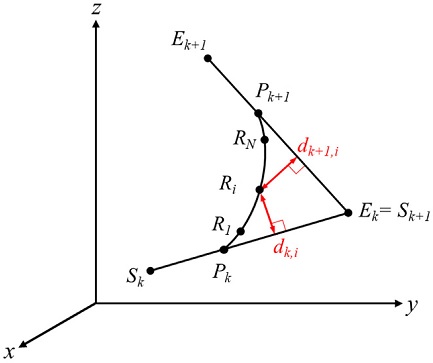
경로계획오차를 계산하기 위하여 먼저 중첩구간에서 경로계획의 좌표를 구하였다. Fig. 3은 인접한 두 블록의 속도 프로파일의 중첩에 의해 생성된 경로계획을 나타낸 것이다. 가감속시간(tA)과 중첩시간이 동일하므로, 중첩이 일어나는 구간에서 경로계획의 개수(N)는 식(1)과 같다.
| (1) |
식(1)에서 tI는 보간주기이다. 중첩구간 내의 i번째 경로계획 R의 좌표(Rxi, Ryi, Rzi)는 식(2)와 같이 계산할 수 있다.
| (2) |
식(2)에서 Pxk, Pyk, Pzk 는 k번 블록에서 감속이 일어나기 직전 경로계획 Pk의 좌표이다. Vxk,i, Vyk,i, Vzk,i는 k번 블록의 감속구간에서 i번 경로계획의 각 축의 속도이며, Vk+1,i, Vyk+1,i, Vzk+1,i는 k+1번 블록의 가속구간에서 i번 경로계획의 각 축의 속도이다.
경로계획과 k, k+1번 블록까지의 거리(d)는 식(3)과 같다.
| (3) |
식(3)에서 Pk+1은 k+1번 블록에서 가속이 종료된 직후의 경로계획이다. 는 파트 프로그램 블록의 방향벡터이며, 식(4)와 같이 계산할 수 있다.
| (4) |
식(4)에서 Sk, Ek 는 각각 k번 블록의 시작점과 종점이고, Sk+1, Ek+1는 각각 k+1번 블록의 시작점과 종점이다. i번 경로계획에서 경로계획오차(e)는 식(5)와 같다.
| (5) |
따라서 k, k+1번 블록의 중첩구간에서 발생하는 최대경로계획 오차(eMax)는 식(6)과 같다.
| (6) |
3. 경로계획오차 제한 알고리즘
경로계획오차는 인접한 두 블록의 가속구간과 감속구간의 중첩 시간을 감소시킴으로써 줄일 수 있다. 그러나 중첩시간(tO)이 감소하면 가공시간이 증가하게 되므로 경로계획오차 한계치(ε)를 만족시키는 중첩시간 중에 가장 큰 값을 적용해야 한다.
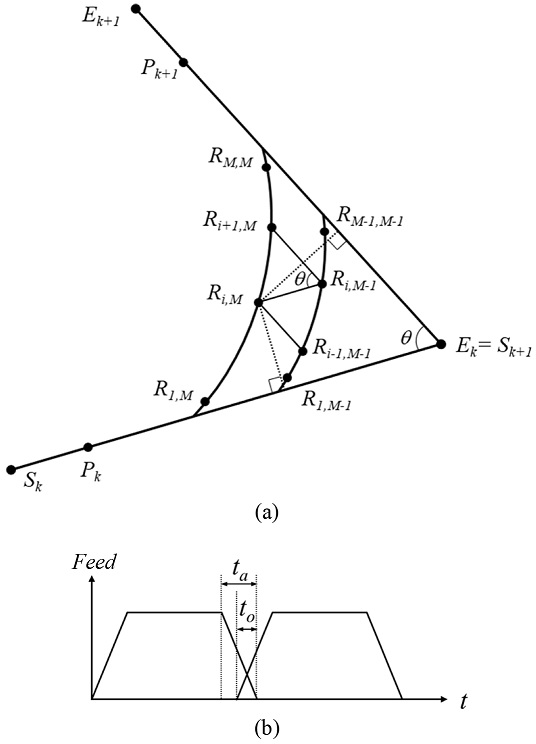
Fig. 4는 중첩시간이 각각 tO와 tO-tI 일 때, 중첩구간에서의 경로 계획을 나타낸 것이다. M은 중첩구간에서 경로계획의 개수이며, 식(7)과 같이 계산할 수 있다.
| (7) |
중첩구간의 개수가 M일 때, i번 경로계획에서 각 축의 좌표는 식(8)과 같다.
| (8) |
| (9) |
| (10) |
즉 Ri,M과 Ri,M-1 두 점을 잇는 직선은 k번 블록의 방향벡터와 평행하므로, Ri,M과 Ri,M-1에서 k번 블록까지의 길이는 동일하다.
| (11) |
또한 Ri,M과 Ri-1,M-1을 잇는 직선은 k+1번 블록의 방향벡터와 평행하므로, 두 점과 k+1번 블록까지의 길이는 같다.
| (12) |
따라서 중첩시간이 tO-tI일 때, i번 경로계획에서 경로계획오차는 식(13)과 같다.
| (13) |
식(10)에 의해 은 k+1번 블록의 방향벡터와 평행하다. 따라서 벡터가 이루는 각도가 θ일 때, dk,i,M와 dk+1,i,M의 관계는 식(14)와 같다.
| (14) |
식(14)에 따라 i가 커질수록, 경로계획과 k번 블록까지의 거리는 증가한다. 식(9)에 의해 은 k+1번 블록의 방향벡터와 평행하고, 방향은 반대이다. 따라서 dk+1,i,M 와 dk+1,i+1,M의 관계는 식(15)와 같다.
| (15) |
식(15)에 의해 i가 증가할수록, 경로계획과 k+1번 블록까지의 거리는 감소한다.
중첩시간이 tO일 경우 최대경로계획오차가 발생하는 경로계획이 Rj,M이라고 가정한다. 이 때, 중첩시간이 tO-tI인 경우의 최대경로계획오차를 계산한다. 먼저 dk,j,M ≤ dk+1,j,M일 경우의 최대경로계획오차를 계산한다. 가정에 의해 Rj,M에서 최대경로계획오차는 dk,j,M이다. 식(14)와 식(15)에 의해 1, … , j-1번 경로계획에서는 식(16)과 같은 관계가 성립한다.
| (16) |
식(13)과 식(16)에 의해 1, … , j-1번 경로계획까지의 경로계획 오차는 식(17)과 같다.
| (17) |
j번 경로계획에서 경로계획오차는 식(13)에 의해 식(18)과 같다.
| (18) |
경로계획 Rj+1,M에서 k, k+1번 블록까지의 길이는 각각 dk,j+1,M, dk+1,j+1,M이다. dk,j,M ≤ dk,j+1,M이고, Rj,M에서의 경로계획오차가 최대라고 가정하였기 때문에, Rj+1,M에서 경로계획오차는 dk+1,j+1,M이다. 즉 dk,j+1,M ≥ dk+1,j+1,M이다. 따라서 식(14)와 식(15)에 의해 j+1과 M-1번 경로계획에서는 식(19)와 같은 관계가 성립한다.
| (19) |
식(13)과 식(19)에 의해 j+1, … , M-1번 경로계획까지의 경로계획오차는 다음과 같다.
| (20) |
1, … , j-1번 경로계획에서 경로계획오차의 최대값은 식(14)에 의해 j-1번 경로계획에서 발생한다. j번 경로계획에서 경로계획오차가 dk+1,j+1,M이라고 하면, 식(15)에 의해 j, … , M-1번 경로계획에서는 j번 경로계획오차의 값이 최대값이다. dk,j,M ≤ dk,j+2,M이고,Rj,M에서의 경로계획오차가 최대라고 가정하였기 때문에, Rj+2,M에서 경로계획오차는 dk+1,j+2,M이다. 따라서 다음과 같은 관계가 성립한다.
| (21) |
식(21)에 의해 j번 경로계획에서 경로계획오차가 dk,j,M이라고 하면, j, … , M-1번 경로계획에서는 j번 경로계획오차의 값이 최대 값이다. 따라서 중첩시간이 tO-tI일 때, 최대경로계획오차는 항상 j-1번 경로계획과 j번 경로계획에서 발생한다.
| (22) |
다음으로 dk,j,M > dk+1,j,M일 때, 최대경로계획오차를 계산한다. 식(14)와 식(15)에 의해 j, … , M-1번 경로계획에서는 다음과 같은 관계가 성립한다.
| (23) |
식(13)과 식(23)에 의해 j, … , M-1번 경로계획까지의 오차는 다음 식(24)와 같다.
| (24) |
Rj-1,M에서 k, k+1번 블록까지의 길이는 dk,j-1,M, dk+1,j-1,M이다. dk+1,j-1,M > dk+1,j,M이고, Rj,M에서의 경로계획오차가 최대라고 가정 하였으므로, Rj-1,M에서 경로계획오차는 dk,j-1,M이다. 즉 dk,j-1,M < dk+1,j-1,M 이다. 따라서 1, … , j-1번 경로계획에서는 식(25)와 같은 관계가 성립한다.
| (25) |
식(13)과 식(25)에 의해 1, … , j-1번 경로계획까지의 경로계획오차는 식(26)과 같다.
| (26) |
식(14)에 의해서 j, … , M-1번 경로계획에서는 j번 경로계획에서 경로계획오차가 가장 크다. 또한 식(15)에 의해서 1, … , j-1에서는 j-1번 경로계획에서 경로계획오차가 가장 크다. 따라서 dk,j,M > dk+1,j,M일 때, 최대경로계획오차는 식(27)과 같다.
| (27) |
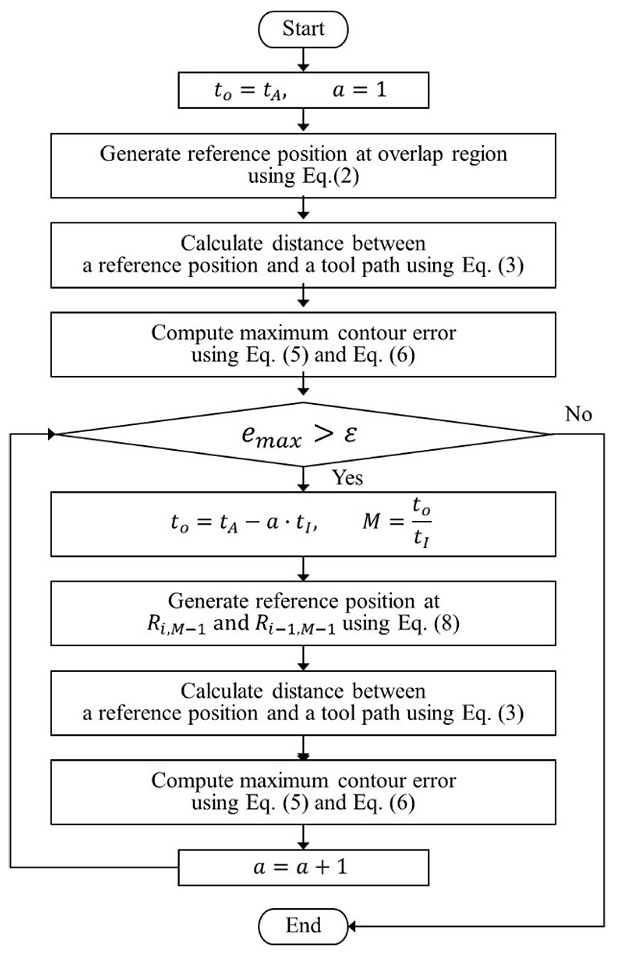
최대경로계획오차가 발생하는 경로계획이 Rj,M일 때, 식(22)와 식(27)에 의하여 중첩시간이 tO-tI인 경우에는 최대경로계획오차가 항상 Rj-1,M-1, Rj,M-1에서 발생한다. 이를 이용해 중첩시간을 줄여가며 최대경로계획오차를 경로계획오차 한계치로 제한하는 알고리즘을 제작하였으며, Fig. 5는 알고리즘의 흐름도를 나타낸 것이다.
4. 알고리즘 성능평가
제안한 경로계획오차 제한 알고리즘의 성능을 평가하였다. 먼저 다이아몬드 형상의 경로에 대해서 알고리즘을 적용하였다. 가감속을 위해 직선형 디지털 FIR 필터를 적용하였으며, 가감속 시간은 100 ms, 보간 주기는 1 ms로 설정하였다. 경로계획오차 한계치는 50 μm 로 설정하였다. 이송속도가 다른 파트 프로그램 블록 사이에서도 알고리즘이 적용되는 것을 검증하기 위하여, 이송 속도를 1200 mm/min, 600 mm/min, 1500 mm/min, 900 mm/min으로 변경하였다. Fig. 6은 경로계획오차 제한 알고리즘 적용 전후의 결과를 비교한 것이다. 알고리즘을 적용하기 전 3개의 모서리 부분에서 최대경로계획오차는 각각 170.5, 187.3, 237.2 μm 였지만, 알고리즘을 적용한 후에는 49.1, 49.1, 48.3 μm로 제한되었다. 알고리즘 적용 전의 이송시간은 3.728 s였으나, 알고리즘 적용 후에는 3.879 s로 이송시간이 증가하였다.
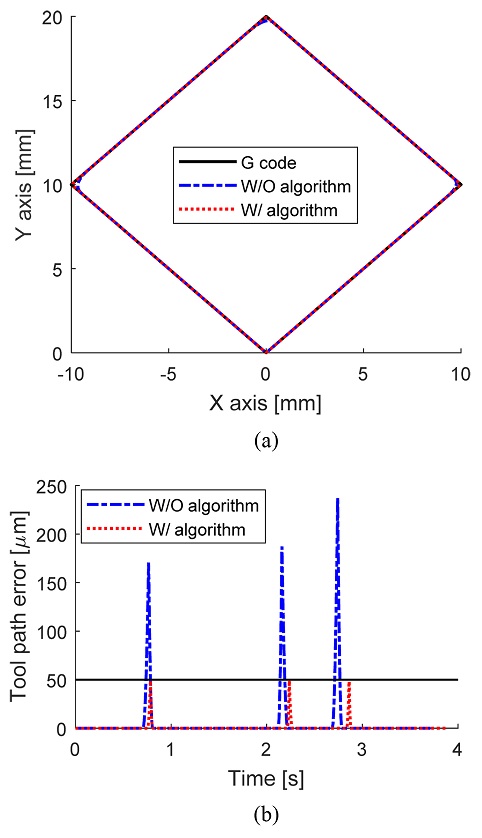
Comparison of (a) diamond-shaped tool path, (b) tool path error before and after applying tool path error constrain algorithm
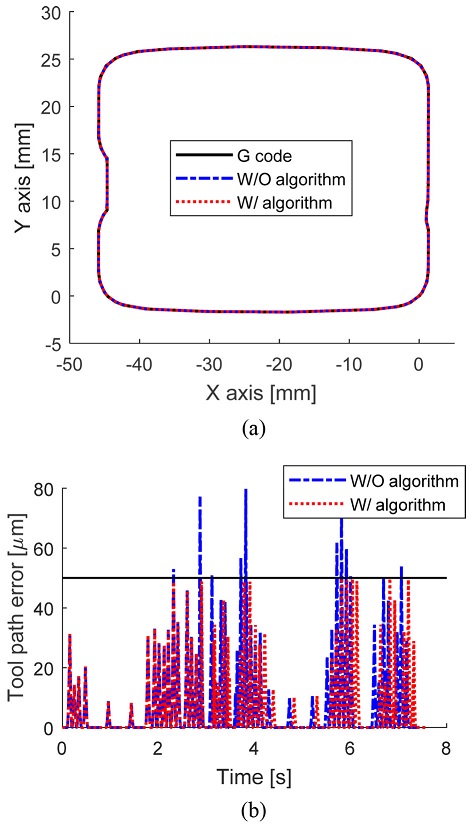
일반적으로 CAM 을 통해 생성되는 파트 프로그램에는 지령된 시점과 종점내에서 이송속도까지 가감속이 이루어지지 않는 미소블록들이 포함이 된다. 미소블록이 포함된 경우에도 경로계획오차 제한 알고리즘이 적용되는지 검증하기 위하여 보간을 수행하였다. 이송속도는 1500 mm/min으로 설정하였으며, 경로계획오차 한계치는 50 μm로 설정하였다. Fig. 7은 미소블록이 포함된 경우에 대해서 알고리즘 적용 전후의 결과를 비교한 것이다. 경로계획오차를 제한하기 전에 최대경로계획오차는 79.8 μm였으나, 경로계획오차 제한 알고리즘을 적용한 후에는 최대경로계획오차가 한계치인 50 μm 이하인 49.9 μm로 감소하였다. Fig. 7(b)에서 블록간 최대경로계획오차가 경로계획오차 한계치보다 작은 경우에는, 경로계획오차 제한이 적용되지 않는 것을 확인할 수 있다. 알고리즘 적용 전의 이송시간은 7.410 s였으나, 알고리즘 적용 후에는 7.557 s로 이송시간이 증가하였다.
5. 결론
본 논문에서는 코너 블렌딩에서 중첩시간이 감소할 때 경로계획오차를 찾기 위한 알고리즘을 제안하였으며, 이를 이용해 블렌딩에 의한 경로계획오차를 제한하기 위한 보간기를 제작하였다.
제안된 알고리즘의 성능을 검증하기 위하여 블록간 이송속도가 다른 경우와 미소블록이 포함된 경우에 대해서 보간기를 실행하였으며, 제안된 알고리즘에 의해 최대경로계획오차가 설정된 한계치 이하로 제한되는 것을 확인하였다.
Acknowledgments
본 연구는 산업통상자원부의 시스템산업 미래성장동력사업의 일환으로 수행되었다(No. 10053248, 과제명: 탄소섬유복합재(CFRP) 가공시스템 개발).
REFERENCES
-
Wang, J.-B. and Yau, H.-T., “Real-Time NURBS Interpolator: Application to Short Linear Segments,” International Journal of Advanced Manufacturing Technology, Vol. 41, Nos. 11-12, pp. 1169-1185. 2009.
[https://doi.org/10.1007/s00170-008-1564-8]

-
Zhao, H., Zhu, L., and Ding, H., “A Real-Time Look-Ahead Interpolation Methodology with Curvature-Continuous B-Spline Transition Scheme for CNC Machining of Short Line Segments,” International Journal of Machine Tools and Manufacture, Vol. 65, pp. 88-98, 2013.
[https://doi.org/10.1016/j.ijmachtools.2012.10.005]

-
Tsai, M.-C., Cheng, C.-W., and Cheng, M.-Y., “A Real-Time NURBS Surface Interpolator for Precision Three-Axis CNC Machining,” International Journal of Machine Tools and Manufacture, Vol. 43, No. 12, pp. 1217-1227, 2003.
[https://doi.org/10.1016/S0890-6955(03)00154-8]

-
Heng, M. and Erkorkmaz, K., “Design of NURBS Interpolator with Minimal Feed Fluctuation and Continuous Feed Modulation Capability,” International Journal of Machine Tools and Manufacture, Vol. 50, No. 3, pp. 281-293, 2010.
[https://doi.org/10.1016/j.ijmachtools.2009.11.005]

-
Tulsyan, S. and Altintas, Y., “Local Toolpath Smoothing for Five-Axis Machine Tools,” International Journal of Machine Tools and Manufacture, Vol. 96, pp. 15-26. 2015.
[https://doi.org/10.1016/j.ijmachtools.2015.04.014]

-
Tajima, S. and Sencer, B., “Kinematic Corner Smoothing for High Speed Machine Tools,” International Journal of Machine Tools and Manufacture, Vol. 108, pp. 27-43. 2016
[https://doi.org/10.1016/j.ijmachtools.2016.05.009]

-
Sencer, B., Ishizaki, K., and Shamoto, E., “High Speed Cornering Strategy with Confined Contour Error and Vibration Suppression for CNC Machine Tools,” CIRP Annals-Manufacturing Technology, Vol. 64, No. 1, pp 369-372. 2015.
[https://doi.org/10.1016/j.cirp.2015.04.102]

-
Lin. R.-S., “Real-Time Surface Interpolator for 3-D Parametric Surface Machining on 3-Axis Machine Tools,” International Journal of Machine Tools and Manufacture, Vol. 40, No. 10, pp 1513-1526. 2000.
[https://doi.org/10.1016/S0890-6955(00)00002-X]