소형 솔레노이드를 이용한 개폐 구조 설계
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
In this investigation, a locking mechanism was proposed for electronic products that have battery covers. The exterior design of electronic products has been advanced with diversified materials including polymers and metals. Unlike polymers such as polycarbonate, metals are not easily deformed. Therefore, products with a metallic exterior have an added button to release the battery cover, which limits the quality of the exterior design. In this study, a new design without a release button that included a miniature solenoid inside the product was proposed. The Taguchi method was used to maximize the attraction force of the solenoid while, at the same time, minimizing its dimensions.
Keywords:
Solenoid, Design of experiments, TRIZ, Locking mechanism키워드:
솔레노이드, 실험계획법, 트리즈, 개폐 구조1. 서론
최근 스마트폰 등 전자제품의 디자인이 고급화되면서 제품 외관에 다양한 소재가 사용되고 있다. 특히 외부 케이스가 금속 재질인 제품들이 인기를 얻기 시작하였다.
PC (Polycarbonate)등 고분자 재질의 유연성을 이용하여 배터리 커버를 개폐하는 연구1도 있지만 금속 재질은 쉽게 휘어지지 않으므로 탈착용 버튼과 구조를 이용하여 배터리 커버를 구현한 연구2가 있었다. 이 경우, 버튼은 디자인의 고급화에 제약 요소로 작용하게 된다. 그렇기 때문에 금속 케이스를 채택한 많은 제품이 배터리 일체형 디자인을 채택하게 되는데, 배터리를 교체할 수 없다는 다른 측면의 소비자 불만이 발생하게 된다.
디자인 고급화와 더불어 제품의 두께도 얇아지는 추세이다. 얇은 두께를 가지면서 액츄에이터의 기능을 할 수 있는 부품으로 솔레노이드(Solenoid)를 선택하였다.
솔레노이드에 대하여는 가동철심 구조에 대한 연구,3 끌어당기는 힘(Attraction Force)은 전류와 공극부의 영향을 받는다는 연구4,5등이 있다.
현재 판매되는 솔레노이드의 최소 두께는 10 mm로 얇은 제품에 적용하기에는 너무 두껍다. 본 연구에서는 외부에 탈착용 버튼이 없는 배터리 커버 개폐 구조를 제안하였고 이에 사용하기 위한 두께 6 mm의 소형 솔레노이드를 설계하였으며, 솔레노이드 끌어당기는 힘을 극대화하고 설치 공간을 최소화 하였다.
2. 개폐 구조
2.1 구조
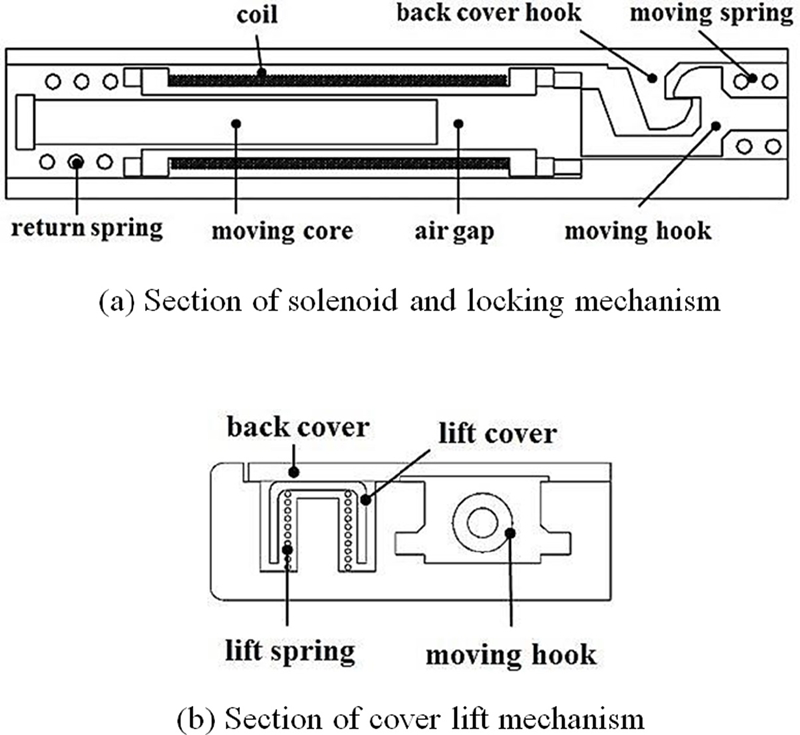
개폐 구조는 배터리 커버를 열고 닫을 수 있는 구조를 말하며 외부 버튼 없이 동작 할 수 있다. 개폐 구조를 Figs. 1(a)와 1(b)에 도시하였다.
Battery cover locking mechanism using solenoid
Fig. 1(a)는 솔레노이드를 구성하는 가동 철심(Moving Core), 공극부(Air Gap), 리턴 스프링(Return Spring), 코일(Coil)과 잠금 기구(Locking Mechanism)를 구성하는 무빙 후크(Moving Hook), 무빙 스프링(Moving Spring)을 보여준다.
Fig. 1(b)는 리프트 기구(Cover Lift Mechanism)를 구성하는 리프트 커버(Lift Cover)와 리프트 스프링(Lift Spring)을 보여준다.
2.2 작동 방법
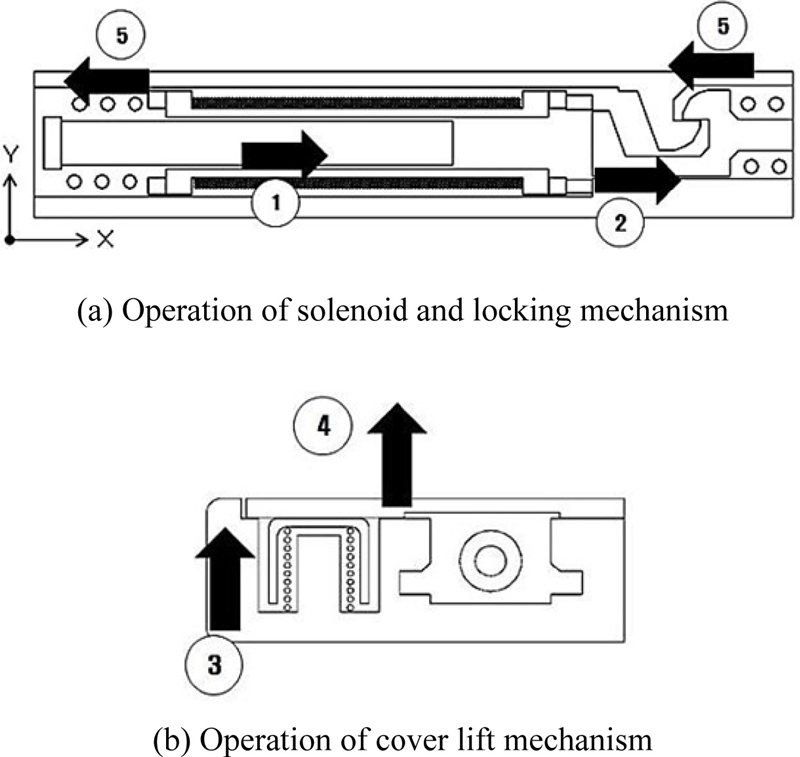
사용자가 개폐 구조의 구동 명령을 내리면 Fig. 2(a)의 코일에 전류가 흐르고 솔레노이드 가동 철심이 공극부가 있는 +X축 방향으로 움직여 무빙 후크가 +X축 방향으로 움직이게 되고 배터리 커버와 체결되어 있던 무빙 후크 걸림량이 줄어들게 된다. 가동 철심이 계속 움직여서 무빙 후크가 커버 후크에서 해제되면 Fig. 2(b)의 리프트 스프링이 리프트 커버를 상승시키고 이 힘에 의해서 배터리 커버는 열리게 된다.
Operation of battery cover locking mechanism using solenoid
배터리 커버가 열린 후 전류가 끊어지게 되면 리턴 스프링과 무빙 스프링의 힘에 의해서 가동 철심과 무빙 후크는 –X축 방향으로 이동하여 원래 자리로 복귀하게 된다.
배터리 커버를 닫으면 커버 후크와 무빙 후크가 다시 체결되어 배터리 커버가 안정적으로 고정된다.
2.3 솔레노이드 설계인자
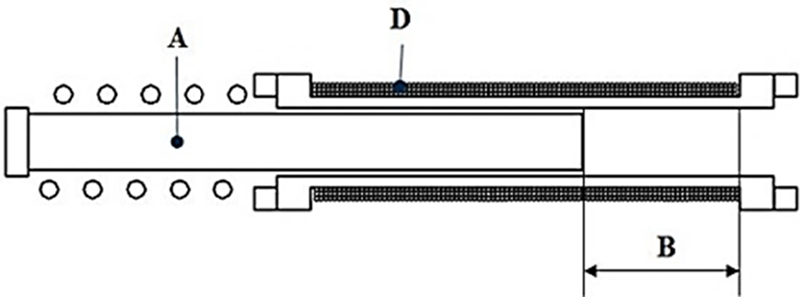
솔레노이드 끌어당기는 힘은 제한된 공간내에서 무빙 후크의 움직임에 중요한 역할을 한다.
끌어당기는 힘에 영향을 주는 설계 인자들을 Fig. 3에 나타내었다. 각 인자들을 2수준으로 설정하여 Table 1에 수록하였다.
Design parameters of the solenoid for optimization
Design parameters in 2 levels
2.4 솔레노이드 끌어당기는 힘 분석
Table 1의 2수준 값들에 대하여 Taguchi 실험계획법6을 수행하였다. L8직교 배열표를 사용하였고 교호작용을 배제하기 위하여 1, 2, 4, 7번 컬럼을 사용하였다. 끌어당기는 힘(F) 측정방법으로 푸시풀 게이지(Push-Pull Gauge)를 사용하였고 총 10회 반복 측정에 대한 평균값을 얻었다.
Test results of L8 orthogonal array for the 4 control factors
Table 2의 결과를 보면 4번 실험(조건: 5.7 g, 12 mm, 5A, 0.22 mm)이 가장 높은 값을, 5번 실험(조건: 3.9 g, 6 mm, 3A, 0.32 mm)이 가장 낮은 값을 갖는 것을 알 수 있다.
Fig. 4는 끌어당기는 힘에 영향을 주는 각 설계인자들의 기여도를 나타낸다. 공극부의 길이, 코일 와이어의 직경, 전류, 가동 철심의 중량 순으로 끌어당기는 힘에 기여를 한다.
Mean value analysis of the design parameters
영향이 큰 설계인자 중 공극부의 길이는 가동 철심의 초기 위치를 결정하며 솔레노이드 크기를 좌우한다. 설치공간의 제약으로 공극부의 길이는 2수준 값으로 확정한다.
코일 와이어 직경은 솔레노이드 두께 6 mm로 검토 했을 때 0.10-0.45 mm범위에서 선택 가능하다. 끌어당기는 힘 극대화를 위한 최적의 코일 와이어 직경 선정이 필요했다. 먼저 끌어당기는 힘에 대한 정량적인 분야에서 검토를 아래와 같이 진행하였다.
3. 코일 와이어 직경의 최적화
3.1 최적화 방법
솔레노이드 끌어당기는 힘 모델의 검증을 위하여 실험을 수행하였다. 검증된 모델을 이용하여 최적의 코일 직경을 도출하고, 이에 가장 근접하는 규격의 코일을 선택하였다.
3.2 끌어당기는 힘 실험
아두이노(Arduino)7를 사용하여 구성한 실험 장치는 Fig. 5와 같다. 가동 철심에 가속도센서를 부착하고 코일에 전류를 흘려서 끌어당기는 힘을 측정하였다. 가속도센서를 통해서 +X축 방향 가속도 값을 총 10회 측정하였다. 평균 가속도 데이터의 적분을 통해 속도 데이터를 얻었다.
Acceleration measuring instrument of solenoid moving core
가속도 센서는 MPU6050 (Invensense社)으로 입력전압 3.3 V, 샘플링레이트 1 kHz, 상한주파수 250 Hz, 분해능 1/16384(LSB/G), 측정 범위 ±2(G) 이다.
3.3 수치 모델
솔레노이드 코일은 저항(Resistor)과 인덕턴스(Inductance)의 직렬 배열로 표현된다. 솔레노이드 전압 방정식은 패러데이 법칙(Faraday’s Law)에 따라 가동 철심의 움직임에 따라 변화하는 자기장에 대해 코일에 유도되는 기전력이 발생함으로 다음과 같이 표현된다.
| (1) |
여기서 I는 전류, R은 저항, N은 코일 감은수, Φ는 자속(Magnetic Flux)이다.
솔레노이드 구조에서 가동 철심의 위치에 따른 자속을 이용하여 자계(Magnetic Field)의 세기를 구하는 공식은 Cheung등9이제안 하였고 수식으로 다음과 같이 표현된다.
| (2) |
여기서 μa는 공기 투자율, μs은 가동 철심 투자율, A는 코일의 축 방향 투영면적, x는 공극부의 길이, l은 가동 철심 길이이다. 위 식을 자속으로 정리하면 다음과 같이 표현된다.
| (3) |
솔레노이드 구조에서 자속은 전류와 공극부의 길이에 영향을 받기 때문에 전미분을 통해 식(1)을 정리하면 다음과 같이 표현된다.
| (4) |
식(4)에 식(3)를 대입하여 정리하면 다음과 같은 솔레노이드 전압 방정식으로 표현된다.
| (5) |
전압 방정식의 양변에 전류(I)를 곱하면 동력 방정식을 구할 수 있다.
| (6) |
식(6)의 기계적 일은 가동 철심의 힘(F)와 속도(V)이므로 다음과 같이 표현된다.
| (7) |
식(7)에서 속도(V)를 양변에서 없애주면 가동 철심의 힘(F)를 구할 수 있다.
| (8) |
1자유도 감쇠 시스템(Spring-Mass-Damper System)에 가동 철심의 힘(F)가 인가된다고 정리하고 식(8)을 대입하여 식(9)과 같이 정리 할 수 있다.
| (9) |
여기서 m은 질량, C는 감쇠계수, K는 스프링 상수이다.
솔레노이드 끌어당기는 힘의 수치 모델을 구하기 위해 식(5)와 식(9)을 이용하여 일차 미분방정식을 구하였고 곽무석10은 아래와 같이 정리하였다.
| (10) |
식(10)에 Table 3의 상수 값을 대입하고 수치 해석 프로그램인 MATLAB으로 가속도, 속도 데이터를 얻을 수 있었다. 고차 미분항 없이 해를 얻을 수 있는 상미분방정식의 수치 해석 방법으로 4th Order Runge-Kutta Method11를 이용하였다.
Constants of optimized solenoid
3.4 수치모델 검증
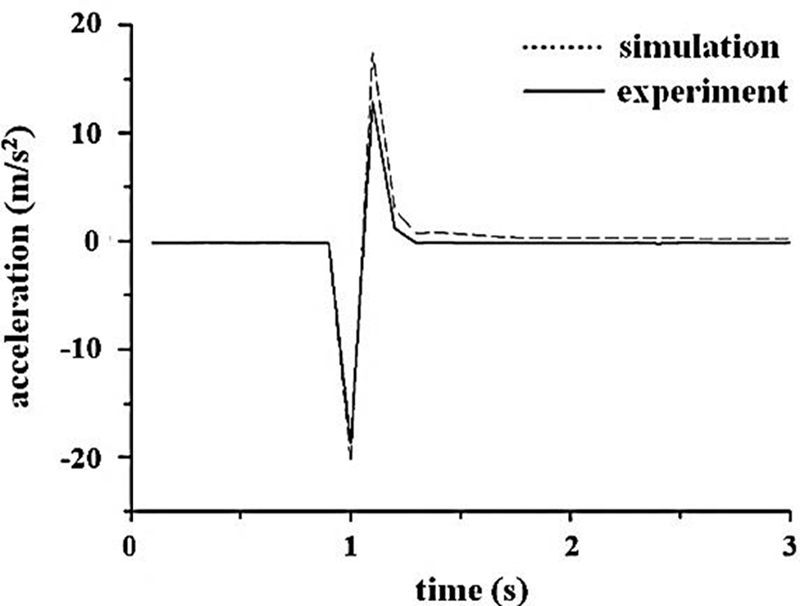
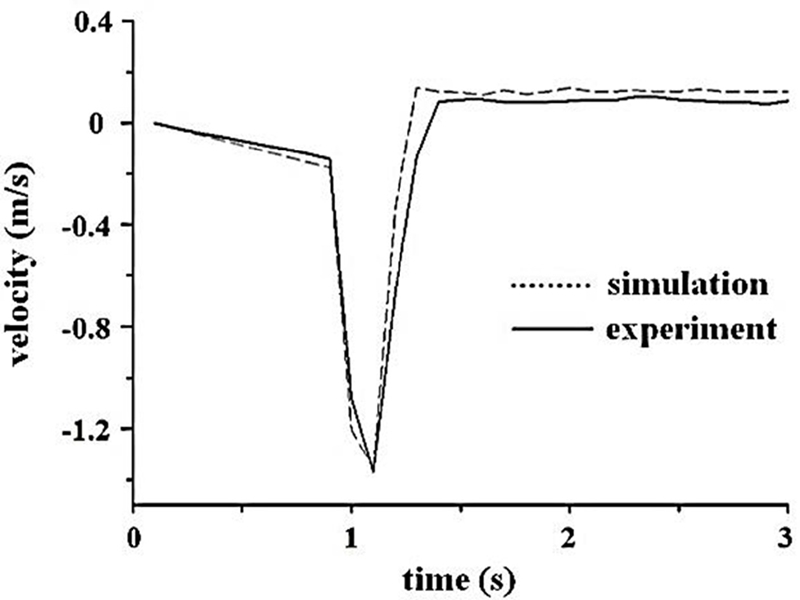
Fig. 5의 실험장비를 통해 얻은 속도, 가속도 값과 식(10) 을 통해 얻은 값을 Figs. 6 과 7 에 나타내었다. Figs. 6과 7의 그래프를 보면 초기 시작 정보(가동 철심과 가속도센서 무게)차이에 따라서 최대값이 약간 상이하게 나오지만 검토 결과 실험 결과와 수치 해석 결과가 대체적으로 일치하여 수치 모델의 신뢰성이 검증 되었다.
Comparison of moving core acceleration: simulation and experiment
Comparison of moving core velocity: simulation and experiment
3.5 코일 와이어 직경 최적화
기존의 솔레노이드 코일에 대한 연구12에 의하면, 코일 와이어 저항(Rcoil)은 코일의 와이어 직경(d), 축방향 권수(N), 반경 방향 권수(M)의 변수들을 통해 다음과 같이 표현된다.
| (11) |
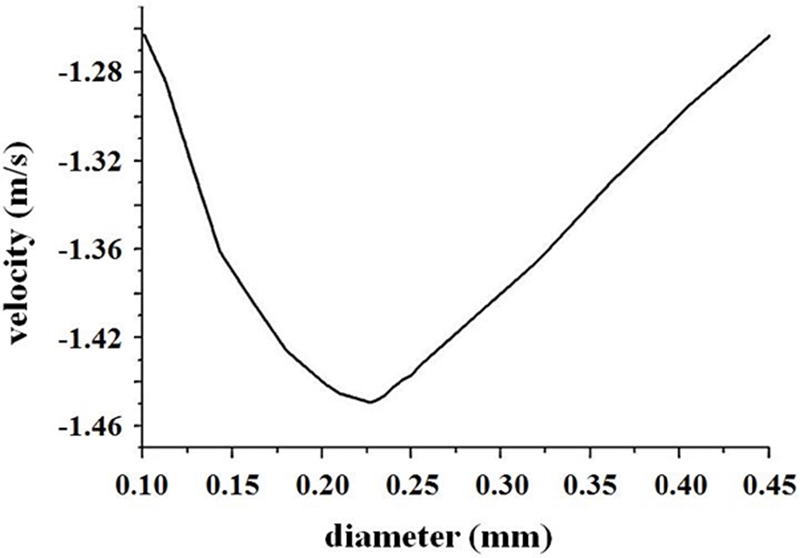
식(11)에 Table 4의 상수값을 대입하였다. 직경(d)은 0.10-0.45 mm 범위를 적용하였고 검증된 수치 모델을 통해 속도 그래프를 구할 수 있다. Fig. 8에서 최대속도를 갖는 직경이 0.22 mm라는 것을 알 수 있다. 그 결과를 가지고 AWG 코일 와이어 규격집13에서 보면 AWG number 31 (0.227 mm)를 선정 할 수 있었다.
Variables and constants of solenoid coil for optimization
Moving core velocity of solenoids with various coil wire diameter
3.6 끌어당기는 힘 검증
Fig. 8의 결과를 반영하여 코일 직경 0.32 mm와 0.22 mm의 끌어당기는 힘을 비교 측정 하였다. 총 10개의 샘플을 제작하여 측정하였고 평균 107 gf, 141 gf으로 확인되었다. 이를 통해 최적 코일 와이어 직경 선정에 따른 끌어당기는 힘이 31% 향상 된 것을 확인 할 수 있었다.
4. 솔레노이드 크기 최소화
끌어당기는 힘의 설계 인자 중 공극부 길이는 솔레노이드 크기와 끌어당기는 힘에 영향을 준다. 현재의 공극부 길이를 유지하면서 솔레노이드 크기를 줄일 수 있는 방법을 TRIZ기법14을 통해 모색하였다.
4.1 TRIZ 모순 해석
TRIZ의 기술적 모순은 다음과 같다.
“솔레노이드 크기를 줄이기 위해서는 가동 철심의 길이를 줄여야 하고 길이가 줄면 리턴 스프링을 설치할 수 없게 되어 복귀력이 소멸된다.”
개선 변수는 가동 철심의 길이로 “움직이는 물체의 부피(7)”이고 상반 변수는 줄어드는 “힘(10)”으로 볼 수 있다. 이 같은 변수들에 관하여 모순 행렬표에 대입하여 Table 5와 같은 문제 해결 원리를 도출 하였다.
TRIZ technical contradiction analysis
4.2 모순 해석을 통한 설계 개선
솔레노이드 크기를 줄이기 위하여, TRIZ의 기술적 모순 해석을 통해 도출된 해결 원리 중 속성 변화(35)의 방법을 적용하였다.
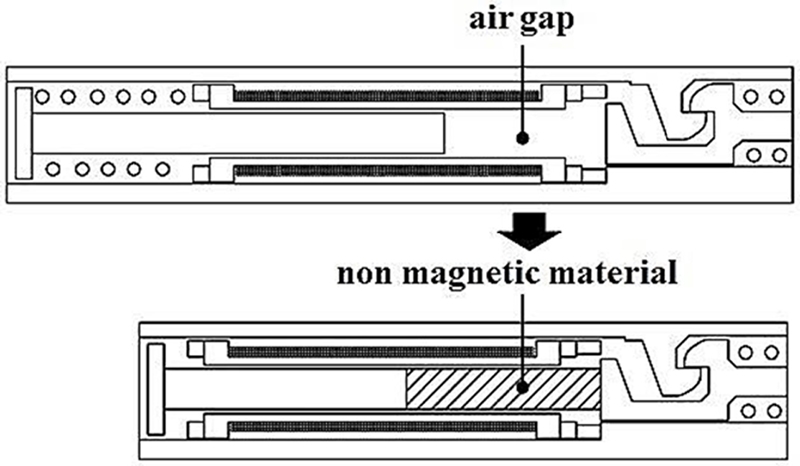
속성변화는 “물리적 상태를 바꾸는 방법”을 의미한다. 이 방법을 적용하여 비어있는 공극부에 비자성체를 삽입하여 가동 철심과 무빙 후크를 하나의 부품으로 제작하였다. 그 결과 리턴 스프링의 기능을 무빙 스프링으로 대체할 수 있어서 리턴 스프링 구간이 필요하지 않아 삭제하였다. 이를 통해 가동 철심의 길이를 기존 설계 대비 8 mm를 줄일 수 있었고, 개선된 설계도면을 Fig. 9 에 나타내었다.
Improvement of battery cover locking mechanism using TRIZ
4.3 개선된 솔레노이드 검증
Fig. 9의 결과를 가지고 기존 설계와 개선 설계의 끌어당기는 힘을 비교 측정 하였다. 총 10개의 샘플을 제작하여 측정하였고 평균 141 gf, 112 gf으로 확인되었다. 이를 통해 솔레노이드 크기 변경에 따른 끌어당기는 힘은 20% 감소 되는 것으로 확인 할 수 있었다. 그 원인으로 공극부가 빈 공간일 때 대비 가동 철심의 가속 구간이 줄어들어 끌어당기는 힘이 줄었다는 것을 알 수 있었다. 그러나 리턴 스프링 삭제로 개폐 동작에 필요한 솔레노이드의 힘이 줄어들어 개폐 구조 동작에는 문제가 없었다.
5. 결론
외부 버튼 없이 배터리 커버를 열고 닫을 수 있는 개폐 구조를 개발하였다. 개폐 구조는 솔레노이드, 잠금 기구, 리프트 기구로 구성 되어있다. 슬림화 추세에 있는 많은 전자제품에 적용하기 위해 두께가 얇은 소형 솔레노이드를 개발하였다. Taguchi 실험계획법으로 주요 설계인자들이 끌어당기는 힘에 미치는 영향을 분석하였다. 실험적으로 검증된 솔레노이드 모델을 기반으로 코일 와이어 직경의 최적화를 수행하여 끌어당기는 힘을 31% 향상시킬 수 있었다. 또한 TRIZ기법을 통해 솔레노이드의 길이를 25% 감소시킬 수 있었다.
REFERENCES
- SAMSUNG Electronics, “Cover Member Biding Device and Portable Terminal with Battery Cover Binding Structure Using the Same,” KOR Patent, 10-2011-0053679, 2011.
- Tang, L., “Battery Cover Latch Mechanism and Portable Electronic Device Using the Same,” US Patent, 20100167114 A1, 2010.
- Vollmer, D. J. and Greame, J. E., “Solenoid Actuator with Electrical Connection Modules,” Automatic Switch Company, US Patent, 4683454 A, 1987.
- Hasel, C.-P., Rauch, F., and Tapper, P., “Solenoid and Actuating Elements with Solenoid,” US Patent, 2010097166 A1, 2010.
- Seo, M., Baek, K., and Cho, S., “Analytical Study on Attraction Force Changes of Armature Driving Solenoid according to Non-Magnetic Material Insertion,” Journal of The Korean Society of Propulsion Engineers, No. 12, pp. 745-751, 2014.
- Yokoyama, Y., “Taguchi Methods: Design of Experiments,” Amer Supplier Inst., 1993.
- Arduino, https://www.arduino.cc, (Accessed 16 OCT 2017)
- TDK InvenSense, “MPU-6050,” https://www.invensense.com/products/motion-tracking/6-axis/mpu-6050, (Accessed 16 OCT 2017)
- Cheung, N. C., Lim, K. W., and Rahman, M. F., “Modelling a Linear and Limited Travel Solenoid,” Proc. of the International Conference Industrial Electronics, Control, and Instrumentation, 1993.
- Kwak, M., “Development of a Car Door Lock in the Upper Weatherstrip Zone for the Reduction of Wind Noise,” M.Sc. Thesis, Korea University, 2016.
-
Hairer, E., Lubich, C., and Roche, M., “The Numerical Solution of Differential-Algebraic Systems by Runge-Kutta Methods,” Lecture Notes in Mathematics, Vol. 1409, pp. 1-137, 1989.
[https://doi.org/10.1137/1033127]
-
Jang, J., Kim, J., and Lee, S., “Parameter Study on the Design of Solenoid to Enhance the Velocity of Coilgun,” Journal of Korean Magnetics Society, Vol. 25, No. 3, pp. 87-91, 2015.
[https://doi.org/10.4283/JKMS.2015.25.3.087]
- ASTM B258-14, “Specification for Standard Nominal Diameters and Cross-Sectional Areas of AWG Sizes of Solid Round Wires Used as Electrical Conductors,” http://www.astm.org/Standards/B258.htm, (Accessed 16 OCT 2017)
- Kang, Y. J., “The Method for Uncoupling Design by Contradiction Matrix of TRIZ and Case Study,” Proc. of 3rd International Conference on Axiomatic Design, p. 7, 2004.