하중 보상 메커니즘을 적용한 3축 모션 플랫폼의 하드웨어 설계
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
This paper was presented at KSPE Spring Conference 2019
Abstract
The motion platform supports the trainee in experiencing a sense of reality in virtual space by performing a motion on the available degrees of freedom for a motion that mimics a specific motion in connection with a virtual reality content or a simulator. The required specification of the motor and driver of motion platform is determined by the target specification for the upward motion of the motion plate. The reason is that the weight of the upper plate always applies gravity in the direction of the downward motion. As a result, the downward motion has an excessive specification compared to the upward motion specification, resulting in an unbalanced motion specification. Additionally, a problem may occur in which a volume increases from the application of a high specification driving unit. In this paper, the motion platform was designed capable of three-axis motion in roll, pitch, and gravity directions using a compression spring to apply a load compensation mechanism. Based on the design results, the specifications of the compression spring for motion platform to satisfy the operating specifications do not excessively move the upward and downward direction derived by the analysis.
Keywords:
Motion platform, Parallel robot, Load compensation, Spring키워드:
모션 플랫폼, 병렬 로봇, 부하 보상, 스프링1. 서론
모션 플랫폼은 가상현실 콘텐츠와 연계하여 각종 상황에 따른 특정 대상물의 움직임을 모방한 적절한 동작을 수행함으로써 체험자로 하여금 가상의 공간에서도 실감을 느낄 수 있게 하는 플랫폼이다. 활용 목적에 따라 정밀성, 모션 출력 사양, 경제성, 공간 효율성 등에 대한 요구 사양을 각기 달리하여 플랫폼을 개발하게 된다. 하지만 원하는 사양 모두를 갖추도록 모션 플랫폼을 개발하는 것은 매우 어려운 일이다. 그래서 보통 모션 플랫폼을 설계하고자 할 때 구동부의 필요 사양은 출력에 해당하는 상부체의 하중을 이겨내며 동작해야 하는 상승 동작에 대한 목표 사양에 초점을 맞추어 결정하게 된다. 이때문에 상승 동작의 출력 사양을 기준으로 하강 동작은 과도한 사양을 가지게 되며, 이에 따른 출력효율에 대한 손실이 발생할 수 있다.
이 문제를 해결하기 위해 스프링과 같이 힘을 축적할 수 있는 부품 등을 활용할 수 있다. 중력에 의한 하중과 같이 일정한 방향으로 작용하는 힘에 대해 이 부품을 활용하여 힘을 축적하고 반대의 방향으로는 힘을 방출할 수 있도록 기구 메커니즘에 적용함으로써 과도한 동작에서는 힘을 축적하여 동작을 완화하고, 부족한 동작에서는 힘을 방출하여 동작을 보상해줄 수 있다.1-3 이러한 메커니즘을 모션 플랫폼에 적용하면 과도한 하강 동작을 완화하고 부족한 상승 동작을 보상하여 서로 비슷한 사양을 가지도록 설계할 수 있다. 또 상승 동작에 대한 목표 사양을 만족하기 위해 필요한 구동기의 출력 사양은 보상되는 힘을 적용하여 기존보다 낮은 사양의 구동기를 선정할 수 있어서 효율적인 설계를 할 수 있다.
본 논문에서는 어느 한 방향으로 과도한 동작 사양을 줄이고 상승과 하강 동작에 대하여 서로 비슷한 사양으로 맞출 수 있도록 압축 스프링을 기반으로 하중의 무게를 보상해줄 수 있는 메커니즘을 적용하고 롤(Roll), 피치(Pitch) 및 중력 방향(z축) 3축 모션이 가능한 플랫폼을 설계하며, 하중 보상을 위해 적용하는 스프링 계수를 시뮬레이션을 통해 도출한다.
2. 3축 모션 플랫폼의 기구 구조 설계
2.1 3축 모션 플랫폼의 메커니즘
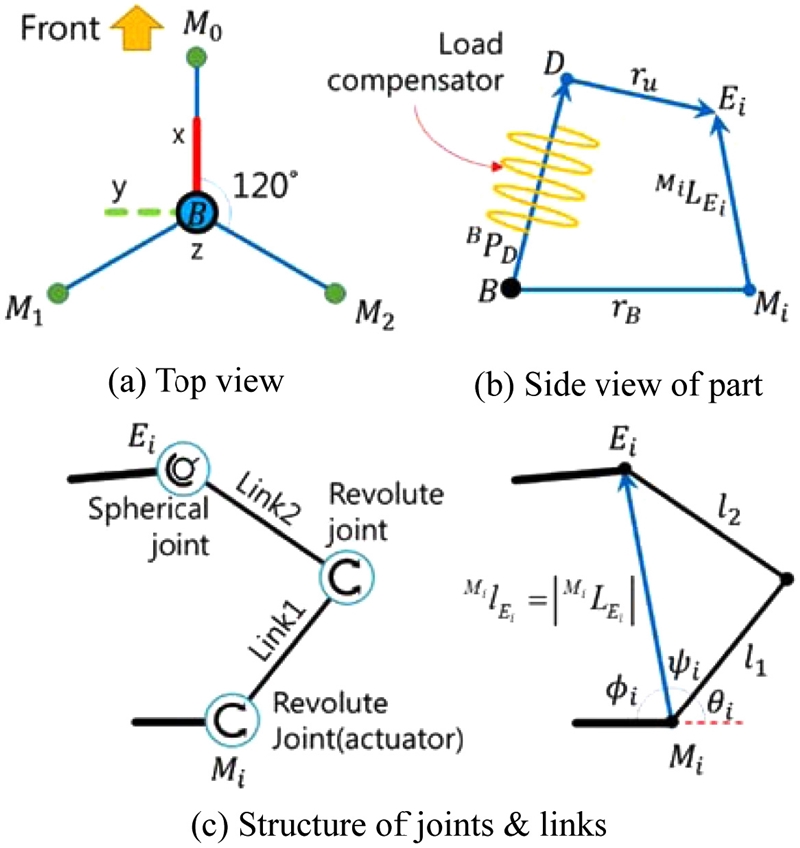
3축 모션 플랫폼의 기본 구조는 하부체와 상부체로 나눌 수 있는데, 하부체는 지면에 고정이 되는 부분을 말하며, 상부체는 구동부 동작에 의하여 모션이 일어나는 부분을 말한다. 상부체는 하부체와 연결된 링크의 동작에 의해 모션이 일어나는데 이 링크의 연결 구조는 Fig. 1(c)와 같이 하부체-회전관절(구동부)-회전관절-구면관절-상부체 구조를 가진다. 이 구조는 하부체와 상부체 사이에 동일한 간격으로 3 방향으로 병렬 배치하는 것으로 전체 메커니즘을 설계한다. 이러한 메커니즘으로 설계하면 상부체의 롤, 피치, z축(중력 방향)으로 3축 모션이 가능하다.4,5
하중 보상 메커니즘은 상승/하강 동작 중 상부체 무게에 의하여 어느 한쪽으로 과도한 사양을 가지지 않고 균형이 잡힌 사양을 가질 수 있어야 한다. 이 메커니즘을 위해 스프링과 압축 실린더를 활용할 수 있다. 압축 실린더의 경우 Stewart Platform과 같이 선형 구동기로 작동하는 모션 플랫폼에 구동기와 비슷한 관절구조로 적용하여 사용하는 경우가 있다.6 그리고 스프링의 경우보다 다양한 모션 플랫폼에 적용할 수 있는데, 각 링크별로 압축 또는 인장 스프링을 적용하는 경우가 많이 있다.7-9 본 논문에는 하중 보상을 위해 압축 스프링을 활용하는데, 이 스프링은 상부체와 하부체의 각 중심점을 잇는 공간(B-D) 사이에 위치한다.10 이 스프링은 상부체의 중력 방향 무게 힘에 의해 압축되는 만큼 힘을 축적하며, 중력 반대 방향의 동작 시 축적된 스프링의 힘을 보상하여 적은 힘으로도 큰 힘을 낼 수 있도록 할 수 있다.
2.2 3축 모션 플랫폼의 역기구학
모션 플랫폼의 상부체가 목표하는 모션을 출력하기 위해서는 역기구학 해석을 통해 목표 모션 값에 대한 각 링크에 배치된 구동부의 값을 구하여야 한다. 먼저 모션 플랫폼 링크의 양 끝단(Mi-Ei) 사이의 기구학을 구하면 다음 식(1)과 같다.
| (1) |
여기서,
α, β: 상부체의 롤, 피치 자세 값, xD, yD, zD: B에 대한 D의 위치 값,
그리고 목표 모션 값을 α, β, zD라 했을 때, 식(1)을 토대로 역기구학을 구하면 다음 식(2)와 같다.
| (2) |
여기서,
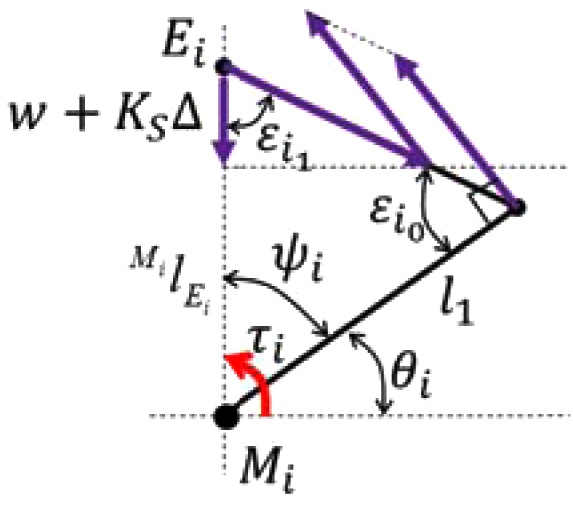
상부체의 무게, 스프링의 힘의 합과 구동부의 토크의 관계식은 Fig. 2를 참고하여 식(3)과 같이 구할 수 있다. 이때 상부체의 모션은 z축 방향만 있으며, 각 구동부의 각도는 모두 같음을 가정한다.
| (3) |
여기서,
Δ : 압축 스프링의 자유길이에 대한 변위
W : 상부체의 무게
3. 3축 모션 플랫폼 설계
3.1 3축 모션 플랫폼 설계
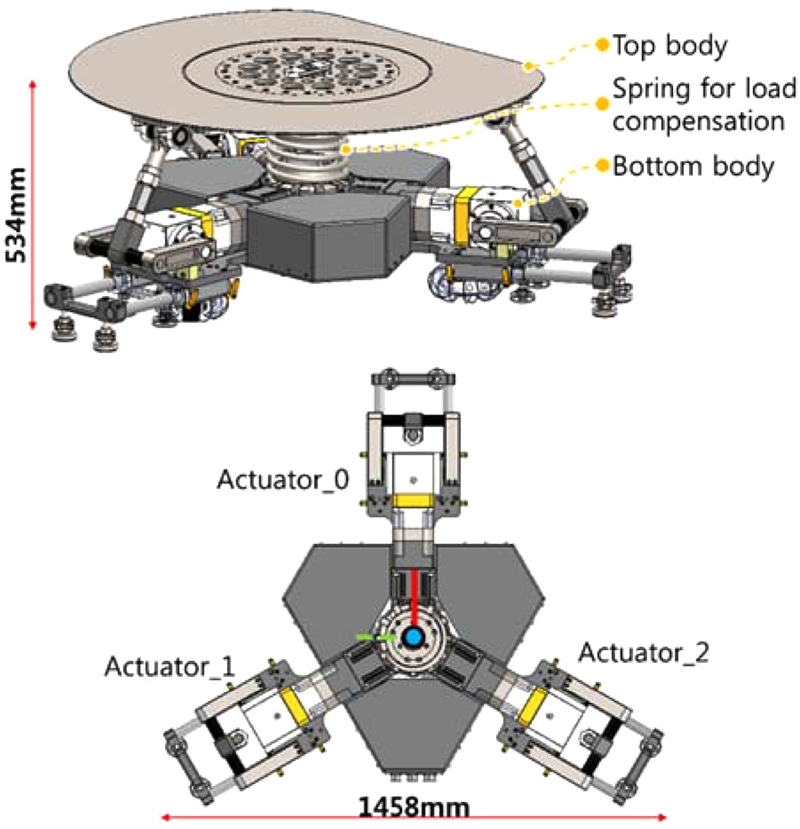
앞서 제시한 3축 모션 플랫폼 메커니즘을 적용하여 기구 설계한 결과와 사양은 Fig. 3 및 Table 1과 같다.
3.2 하중 보상 메커니즘의 설계 적용
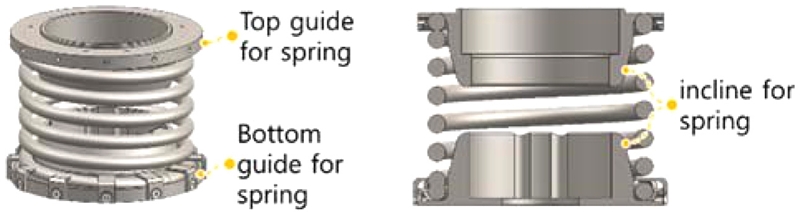
하중 보상을 위한 압축 스프링은 상부체와 하부체 가운데의 사이에 위치한다. 다만, 기존에는 압축 스프링을 적용할 때는 스프링의 선형 동작 이외의 자유도를 구속하고 이탈을 방지하기 위해서 차량용 댐퍼와 같은 선형 실린더 내/외부에 스프링을 끼워 사용한다.2,10 하지만 본 논문에서는 스프링 하중 보상 메커니즘의 단순화를 위해서 선형 실린더 없이 상/하부 가이드를 사용하여 스프링을 구속한다. 모션 플랫폼 하부체는 고정 상태를 유지하지만 상부체는 롤, 피치, 중력 방향으로 3축 모션이 일어난다. 스프링은 상부체의 롤, 피치의 자세 변화 모션이 일어나면 스프링 상/하부가 수평 상태를 벗어나게 되면서 자리를 이탈하는 문제가 생길 수 있다. 그래서 상부/하부 가이드는 롤, 피치 모션에서 기울어지는 만큼의 경사면을 두어 자세가 기울어진 상태에서도 스프링 가이드 역할을 할 수 있도록 Fig. 4와 같이 설계한다.
4. 시뮬레이션을 통한 중력 방향 동작 사양 분석 및 하중 보상을 위한 스프링 사양 선정
4.1 시뮬레이션을 통한 중력 방향 동작 사양 분석
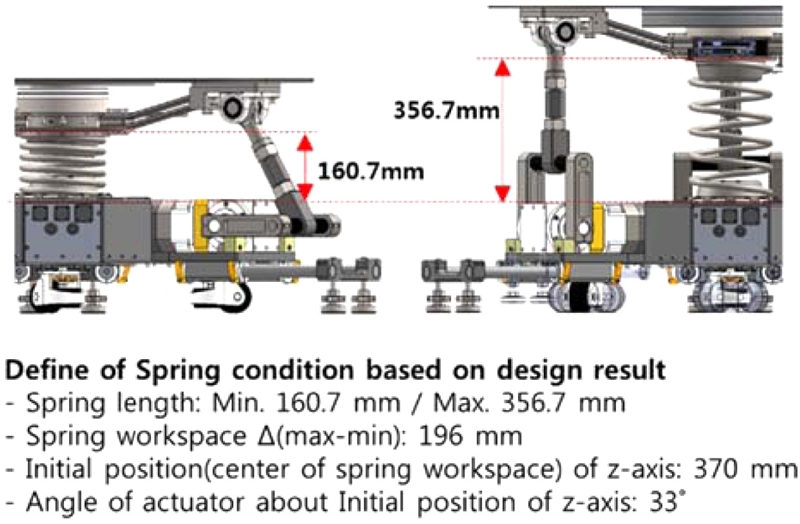
모션 플랫폼의 스프링 사양을 선정함에 있어서 Fig. 5와 같이 설계 결과를 토대로 스프링의 길이 및 변위 조건을 설정한다. 스프링의 자유길이는 356.7, 최저길이 160.7, 가용변위는 196 mm의 값을 가진다. 이 조건을 토대로 스프링 계수를 도출해야 하는데, 스프링 계수가 너무 과하면 상승 동작 사양이 하강 동작의 사양에 비해 과도해지고, 스프링 계수가 너무 약하면 하강 동작 사양이 상승 동작의 사양에 비하여 과도해진다. 그리고 구동부의 동작에 대하여 z축 방향 힘이 가장 약해지는 각도는 스프링 계수에 따라서 달라진다. 그래서 본 논문에서는 스프링 계수 몇가지를 제시하고 각각의 경우에 대하여 시뮬레이션을 통해 상승/하강 동작에 대한 사양을 분석하고 양방향 모션의 1 G의 사양을 만족하는데 가장 적합한 스프링 계수를 선정하고자 한다.
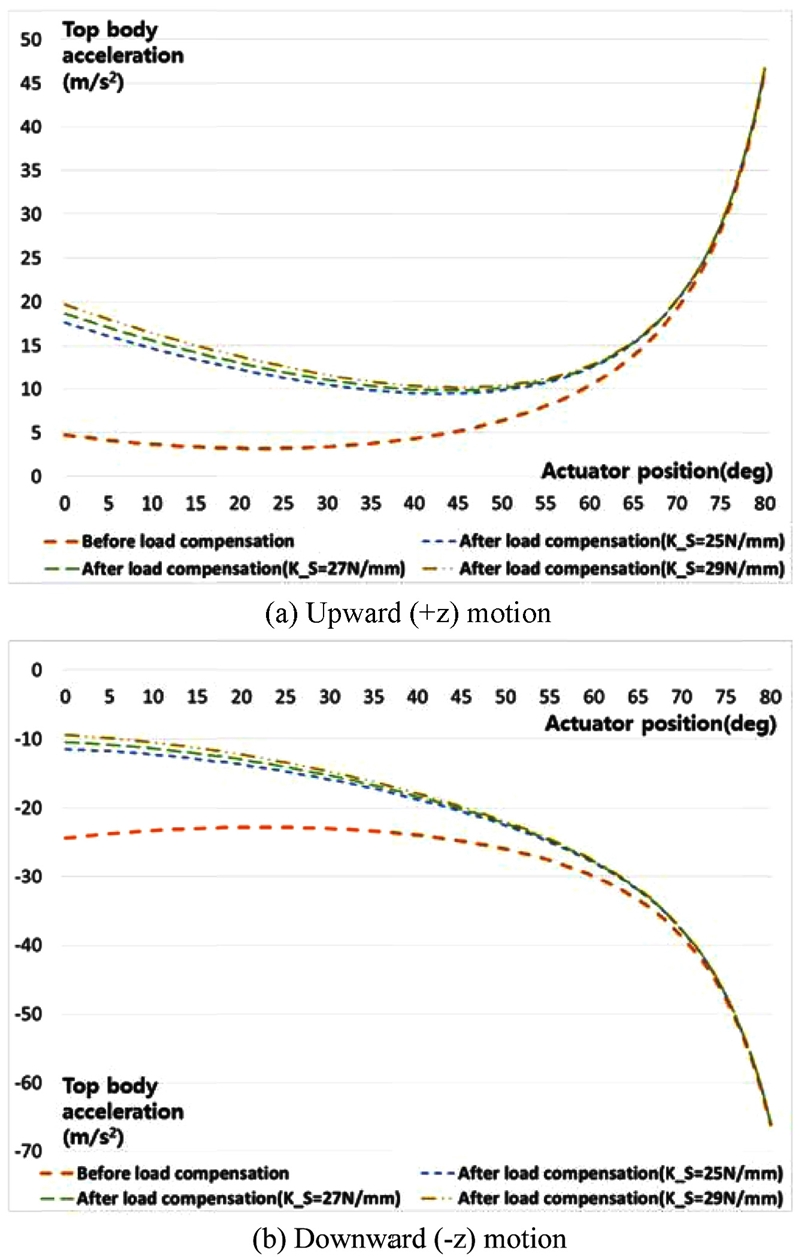
스프링 계수 KS = 25, 27, 29 N/mm를 적용한 경우에 대하여 z축 방향 가속도에 대한 동작 사양을 시뮬레이션 한 결과는 Fig. 6과 같다. 스프링이 없을 경우 하강(-z)과 상승(+z) 방향 절댓값 기준 최소 가속도는 각각 -22.8과 3.19 m/s2의 동작 출력을 낼 수 있다. 그리고 z축 방향 가속도가 3.19 m/s2으로서 가장 약하게 힘이 출력되는 상태의 구동부의 각도는 약 22o이다. 그리고 스프링이 있는 경우에 대하여 -z, +z 방향 절댓값 기준 최소가 되는 가속도 및 구동부의 각도는 Table 2와 같다.
4.2 하중 보상을 위한 스프링 사양 선정
목표 출력 사양을 만족하기 위해 필요한 하중 보상 힘을 토대로 스프링에서 가져야 할 스프링 계수를 도출할 수 있다. 스프링 계수 25 N/mm의 경우 상승 동작 사양이 1 G에 못 미치는 결과를 보였으며, 29 N/mm의 경우 상승 동작 사양이 증가함에 따라 하강 동작 사양이 1 G 미만으로 떨어지는 결과를 보였다. 상부체의 z축 방향 모션에 대하여 상승/하강 동작 사양 모두 1 G 이상을 만족하는 스프링 계수 스프링 계수(KS)는 27 N/mm이다. 이때 -10.4와 9.81 m/s2의 상승/하강 동작의 가속 사양을 가지는 것을 볼 수 있으며, 구동부가 z축 방향에 대하여 가장 약한 힘을 낼 때의 각도는 44o임을 알 수 있다. 이로서 스프링을 통한 하중 보상 메커니즘을 적용하여 중력 방향 상승/하강 동작이 어느 한쪽으로 과도하지 않고 목표 사양을 만족하면서 상승/하강 동작 사양이 서로 비슷한 출력을 낼 수 있는 스프링 계수를 도출할 수 있다.
5. 결론
본 논문에서는 하중 보상 메커니즘을 적용한 모션 플랫폼을 설계하였다. 롤, 피치 및 z축 방향의 3축 모션이 가능한 모션 플랫폼의 기본 메커니즘과 압축 스프링 기반의 하중 보상 메커니즘을 적용한 기구 구조를 설계하였다. 그리고 메커니즘에 대한 역기구학을 도출하였다. 설계된 기구 구조를 토대로 상세 설계를 하였고, 압축 스프링이 상부체의 자세 변화에 따라 이탈되지 않기 위한 스프링 가이드를 상세 설계하였다.
모션 플랫폼 설계 결과를 바탕으로 몇 가지 스프링 계수에 대한 시뮬레이션을 진행하였고, 각 경우에 대해서 z축 방향 가속도에 대한 동작 사양을 분석하였다. 그리고 분석 결과를 토대로 z축 동작에 대하여 목표 사양을 만족하면서 상승/하강 동작 사양이 어느 한쪽으로 과도하지 않고 서로 비슷한 출력을 낼 수 있는 최적의 스프링 계수를 도출하였다.
추후에는 모션 플랫폼에서 가변하는 상부체의 무게를 하중 보상 메커니즘을 이용하여 측정하는 방법에 대하여 연구하도록 하겠다.
NOMENCLATURE
| B : | Center of bottom body |
| D : | Center of top body |
| rB : | Radius of bottom body |
| ru : | Radius of top body |
| θi : | Angle of actuator joint (I = 0, 1, 2) |
| KS : | Spring coefficient |
Acknowledgments
본 연구는 산업통상자원부의 재원으로 산업핵심기술개발사업의 지원을 받아 수행되었습니다(No. 10053028, 재난 재해 대응 특수목적기계 표준화 및 시험평가기술 개발).
References
-
Endo, G., Yamada, H., Yajima, A., Ogata, M., and Hirose, S., “A Passive Weight Compensation Mechanism with a Non-Circular Pulley and a Spring,” Proc. of the IEEE International Conference on Robotics and Automation, pp. 3843-3848, 2010.
[https://doi.org/10.1109/ROBOT.2010.5509797]

-
Lu, Q., Ortega, C., and Ma, O., “Passive Gravity Compensation Mechanisms: Technologies and Applications,” Recent Patents on Engineering, Vol. 5, No. 1, pp. 32-44, 2011.
[https://doi.org/10.2174/1872212111105010032]

-
Altenburger, R., Scherly, D., and Stadler, K. S., “Design of a Passive, Iso-Elastic Upper Limb Exoskeleton for Gravity Compensation,” Robomech Journal, Vol. 3, No. 1, pp. 1-7, 2016.
[https://doi.org/10.1186/s40648-016-0051-5]

- Park, Y., Seo, K. H., Yun, S., Park. S., Jung, M. S., et al., “Inverse Kinematics Analysis of 3DOF Motion Simulator Using SRR-Link,” Proc. of the KSPE Fall Conference, pp. 124-125, 2015.
-
Tetik, H., Kalla, R., Kiper, G., and Bandyopadhyay, S., “Position Kinematics of a 3-RRS Parallel Manipulator,” Romansy 21: Symposium on Robot Design, Dynamics and Control, Vol. 569, pp. 65-72, 2016.
[https://doi.org/10.1007/978-3-319-33714-2_8]

-
Shariatee, M., Akbarzadeh, A., and Nabavi, N., “Design of a Pneumatic Weight Compensation System for the FUM Stewart Robot,” Proc. of the 5th RSI International Conference on Robotics and Mechatronics, pp. 624-629, 2017.
[https://doi.org/10.1109/ICRoM.2017.8466164]

-
Wang, L. and Xi, F., “Smart Devices and Machines for Advanced Manufacturing,” Springer Science & Business Media, 2008.
[https://doi.org/10.1007/978-1-84800-147-3]

-
Laliberté, T., Gosselin, C. M., and Jean, M., “Static Balancing of 3-DOF Planar Parallel Mechanisms,” IEEE/ASME Transactions on Mechatronics, Vol. 4, No. 4, pp. 363-377, 1999.
[https://doi.org/10.1109/3516.809515]

- Leblond, M. and Gosselin, C. M., “Static Balancing of Spatial and Planar Parallel Manipulators with Prismatic Actuators,” Proc. of the ASME Design Engineering Technical Conferences, pp. 13-16, 1998.
- Aminzadeh, M., Mahmoodi, A., and Sabzehparvar, M., “Dynamic Analysis of a 3DoF Motion Platform,” Vol. 1, No. 1, pp. 12-18, 2009.

Senior researcher in the Korea Institute of Robotics and Technology Convergence (KIRO). His research interest is mechanical design, hydraulic systems and machine control
E-mail: idealcreator@kiro.re.kr

Senior researcher in the Korea Institute of Robotics and Technology Convergence (KIRO). His research interests include mobile manipulation, hydraulic systems and exoskeleton systems.
E-mail: hgkim@kiro.re.kr

Principal researcher in the Korea Institute of Robotics and Technology Convergence (KIRO). His research interest is the intelligent system.
E-mail: rockboy@kiro.re.kr

Assistant researcher in the Korea Institute of Robotics and Technology Convergence (KIRO). His research interest is the robot system.
E-mail: psh84@kiro.re.kr

Assistant researcher in the Korea Institute of Robotics and Technology Convergence (KIRO). His research interest is the robot system.
E-mail: ehyojun@kiro.re.kr