유효노치응력법을 이용한 T형 필렛 용접부의 피로수명 분석

1. 서론

선박 및 건설기계와 같은 구조물에서 구조 설계상 허용 기준으로 재료의 항복 강도를 사용하고 있다. 그러나 실제 구조물의 경우 반복 하중으로 인해 항복응력 이하에서도 균열이 발생, 파단되어 인명, 재산 손실을 가져오기도 한다. 이와 같이 재료의 항복응력에 비해 현저하게 작은 하중이 발생함에도 불구하고 반복적인 영향으로 균열 및 파단이 일어나는 현상을 피로파괴라 한다. 따라서 반복적이고 변동적인 하중 상황에 놓여 있는 구조물 또는 제품의 수명 향상을 위해서는 반드시 피로역학적인 개념을 설계 및 제작에 고려하여야만 한다. 그리고 선박이나 건설기계의 제작에 있어서 각 구조물의 결합과 접합 방법으로 금속 간의 용접은 필수적인 방법이지만, 용접 작업은 용접 결함(기공, 혼입, 주조 결함 등)과 용접 시 발생하는 열에 의한 열영향부(HAZ)를 내포하고 있다. 이러한 용접 결함과 열영향부는 금속의 조직 또는 물성을 변화시켜서 피로수명에 큰 영향을 줄 수 있기 때문에 실제 제품에 적용되기 전에 피로수명 평가가 필히 요구된다.¹

용접부의 피로 강도는 금속 조직의 불균일이나 용접 잔류응력, 용접 결함이나 형상 불연속에 의한 응력집중 등이 피로 강도에 영향을 미치는데, 그 중 특히 용접 토우부와 루트부의 형상은 응력집중에 상당히 큰 영향을 미친다.² 현재 선박 및 건설기계와 같은 기계 구조물의 대형화, 복잡화, 경량화에 따라 사용 조건이나 환경이 가혹해짐에 따라 이에 적합한 피로 강도 평가 기법과 구조물의 피로파괴를 방지하기 위한 피로 강도 개선 방법이 요구되고 있다. 용접부의 피로 강도 평가는 실험적 방법과 유한요소해석법이 사용되고 있으며, 유한요소해석법 중 가장 일반적이고 대표적인 방법으로 유효노치응력법이 있다. 유효노치응력법은 핫스팟응력법과는 달리, 용접 구조물에 발생하는 응력집중현상을 가상유효노치를 만들어서 유효노치부에 발생하는 응력으로 해석할 수 있다. 이때, 유효노치응력은 선형 탄성 재료의 동작을 가정하여 얻은 노치의 루트에서의 총 응력으로 정의되고, 노치의 루트부에서의 비선형 재료 거동뿐만 아니라 용접 비드의 형상의 변화를 고려하기 위하여 적절한 노치 반경 등의 형상을 반영한다면, 일관된 결과를 제공한다.^3-5 유효노치응력법을 이용하면 유한요소해석으로부터 용접 구조물의 피로노치계수(K_f)를 계산하여서 용접이 구조물에 미치는 피로수명 감소 영향을 쉽게 계산할 수 있다. 또한, 용접 구조물의 피로수명을 추정하는 방법으로 널리 사용되는 방법은 용접 구조물의 종류마다 다르게 IIW (International Institute of Welding)에서 제시하는 S-N 선도를 이용하여서, 용접 토우부 및 루트부의 피로수명을 추정하는 방법이다.⁶

본 연구의 목적은 굽힘 하중을 받는 굴삭기용 고강도 강재에 대한 T형 필렛 용접부의 피로수명을 피로시험을 수행하여 조사하고, 유효노치응력법을 이용하여서 추정한 피로수명과 비교/검증하는 것이다. 또한, 검증된 유효노치응력법을 사용하여서, T형 필렛 용접부의 토우부 각도가 용접부의 피로수명에 미치는 영향을 조사하고, 최적의 토우부 각도를 결정하는 것이다.

2. 시험 방법

2.1 피로시험편 제작

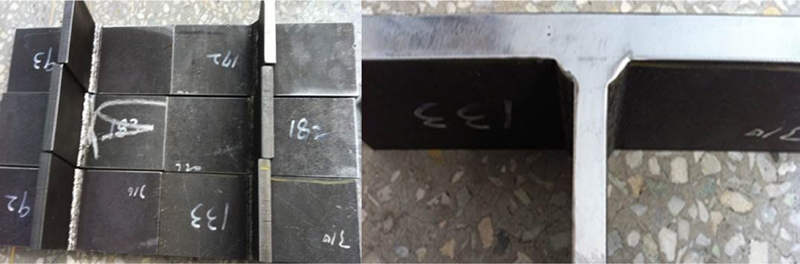
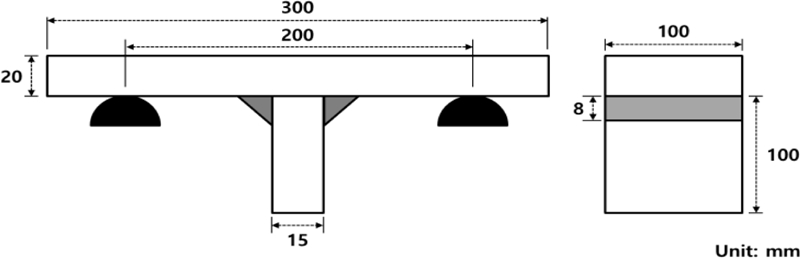
실제 굴삭기에 사용하는 용접구조용 강판 SM490A를 사용하였다. SM490A는 0.2 wt% 이하의 탄소량을 함유하고 있는 용접구조용 압연 강재로 용접이 용이한 특성을 가져 강재를 용접으로 연결할 때 주로 사용한다(Table 1). 피로시험을 위한 T형 용접 구조물은 20 mm 두께의 판재를 이용하여 전류 430 A, 전압 37 V, 용접 속도 300 mm/min의 탄산 가스 아크 용접(CO₂ Gas Arc Welding)을 수행하여서 제작하였으며, ISO 5817의 필렛 용접 규정에 따라 용접을 수행하였다(Table 2).⁷ 이때, 토우부의 각도는 45°로 용접하였다. 토우부의 불균일한 형상으로 토우부에서 발생하는 응력 집중의 크기가 달라지는 것을 방지하고자 표면을 연마하여 최종 피로시험편을 제작하였다(Figs. 1, 2).

Table 1

Chemical compositions (wt%) of SM490A

Table 2

Welding conditions of fillet welding

Fig. 1

T-Type fillet welded joint specimens

Fig. 2

Dimensions of the T-Type fillet welded joint specimen

2.2 피로시험

피로시험은 최대용량 10 ton인 유압식 동적재료시험기(Material Test System, MTS Model 809)를 사용하여 수행하였다. 실험 장비와 지그의 형상을 Fig. 3에 나타내었다. 시험 방법은 실제 굴삭기가 가동될 때, 상하부 프레임에 가장 큰 영향을 주는 굽힘 하중을 반영하기 위해 3점 굽힘 피로실험을 수행하였다. 시험편을 좌우 편향되지 않도록 놓고 받침점 사이 거리의 1/2점(중앙)에서 하중(F)을 가하여 T형 용접 시험편의 치수를 이용하여서 시험편의 표면에 발생하는 굽힘응력(σ_n= (FL/4 × h/2)/(1/12 × b × h³) = F/4 × 200 × 10/(1/12 × 100 × 20³) MPa)을 계산하였다.

Fig. 3

Three-point bending fatigue test machine with a specimen and loading jigs

피로하중 부하 조건으로 가진주파수는 5 Hz의 정현파(Sinusoidal Profile)로 하였고, 응력비(Stress Ratio)는 0.1을 적용하였다. 그리고 21에서 37 kN까지 1 kN 간격으로 하중을 가하였다. 총 18개의 시험편을 사용하여 피로시험을 진행하였고, 시험편에서 완전 파단이 발생할 때까지 시험을 수행하였다. 재료의 피로한도를 2.0 × 10⁶ 사이클로 설정하고, 그 이상의 사이클에서는 런아웃(Run-Out)으로 판단하여 S-N 선도를 분석하였다.

2.3 유효노치응력법

T형 시편 용접부에서 발생하는 응력을 계산하기 위하여 유효노치응력법을 이용하여 가상노치부를 생성하고 이 가상노치부를 생성했을 때, T형 시편에 발생한 최대응력($$ {\overline{\sigma }}_k$$)으로부터 용접부에서 발생하는 응력을 구하였다. 따라서, 가상노치부의 노치 반경(Fictitious Radius)을 선정하기 위하여, Neuber가 제시한 미세조직지원설을 사용하였다. 미세조직지원설은 용접 토우부 및 용접 루트부와 같은 노치부에 발생하는 미세균열은 노치 선단의 응력만 영향을 받는 것이 아닌, 응력집중부 재료의 특정 길이, 면적, 체적을 고려한 평균응력에 의해 영향을 받는다는 가설로 다음의 식(1)로 표현된다.⁸

$\[ {\rho }_f=\rho +s{\rho }^{\mathrm{*}} \]$

(1)

ρ_f는 가상의 노치 반경, ρ는 실제 노치부의 노치 반경(Actual Notch Radius), s는 다축성 계수(Stress Multi-Axiality and Strength Criterion Factor), ρ*는 미세조직 길이(Micro-Structural Length)이다. 다축성 계수의 경우 인장이나 압축 하중의 경우 2-3의 값을 가지며, 그 중 용접부는 2.5의 값을 사용한다. 그리고 미세조직길이는 인장강도 및 항복 강도에 의존하는 다양한 금속 재료의 노치 시험편의 교번피로실험으로부터 결정되는 재료 상수로, 용접부의 조직은 주철의 금속조직과 유사하다고 알려져 있다.⁹ 따라서 본 연구의 경우 용접 토우부 및 용접 루트부에 작용하는 힘은 인장 하중으로 s는 2.5, 주철의 미세조직길이 0.4 mm, 실제 노치 반경은 0으로 가정하고 식(1)로부터 가상의 노치 반경(r)을 1 mm로 결정하였다. 유효노치응력법에서 가상의 노치 반경(r)을 1 mm로 하였을 때, Radaj et al.은 피로노치계수(K_f)와 응력집중계수(K_t)의 값이 일치한다고 보고하였다.¹⁰

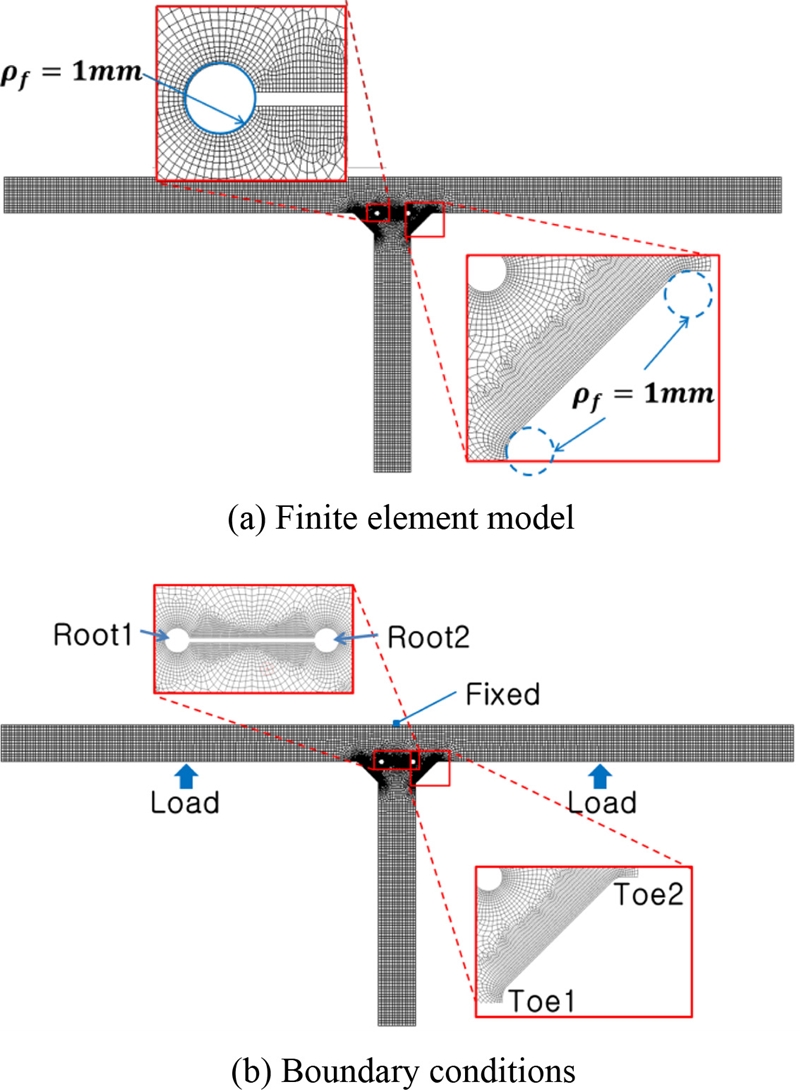
유한요소해석을 이용하여 노치부에서 발생하는 최대응력($$ {\overline{\sigma }}_k$$)을 계산하기 위하여, Fig. 4(a)와 같이 가상의 노치 반경을 반영한 유한요소모델을 생성하였다. 그리고 유한요소모델을 구성하는 격자는 2차원 8절점 평면변형률요소(Plane183)를 사용하였고, 총 Node와 Element 개수는 각각 34,808와 11,044개를 생성하였다. 유한요소해석은 상용 유한요소해석 프로그램인 ANSYS Workbench (Swanson Analysis Corp., USA)를 사용하였다. 유한요소해석 수행을 위하여 Table 3에 있는 SM490A의 재료 물성을 사용하였다. 그리고 경계 조건은 Fig. 4(b)와 같이 3점 굽힘 시험을 모사하기 위 실제 실험 장비의 구동 원리에 따라 액추에이터에 부착된 지그가 시험편에 하중을 가하면 고정된 지그에서 반력이 나타나는 현상을 구현하였다.^5,11,12

Fig. 4

Finite element analysis for the effective notch stress method of T-Type welded joints

Table 3

Mechanical properties of SM490A material

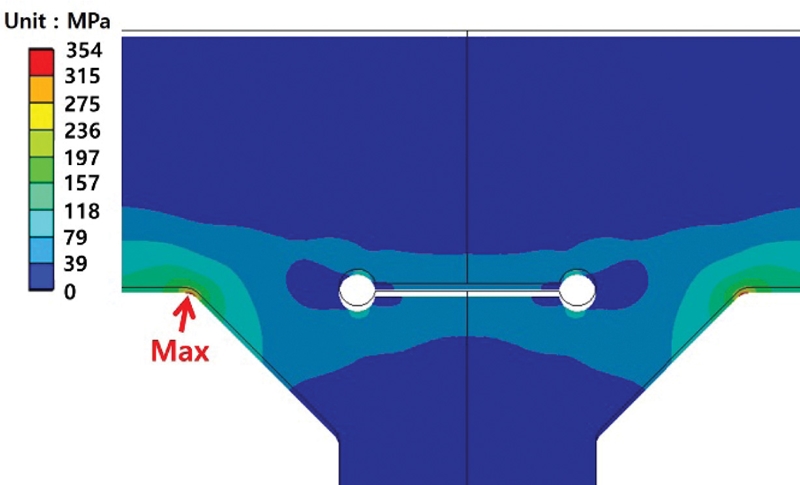
유효노치응력법을 적용하여 발생하중(F = 21 kN)을 가하여서 T형 필렛 용접부의 유한요소해석을 수행하였다. 그 결과 Fig. 5와 같이 용접 토우부에서 유효노치최대응력($$ {\overline{\sigma }}_k$$)이 발생하였다. 또, 이 하중(F = 21 kN)이 가해질 때, T형 시편의 표면에 발생하는 굽힘응력(σ_n = 157.5 MPa)을 계산하였고, 아래 식(2)를 이용하여 응력집중계수(K_t)를 구하였다(Table 4).^11,13

$\[ K_f=K_t=\frac{{\stackrel{-}{\sigma }}_k}{{\sigma }_n} \]$

(2)

Fig. 5

Finite element analysis for the effective notch stress method of T-Type welded joints

Table 4

Calculation of stress concentration factor, Kt

2.4 용접 토우부 최적 각도 설계 방법

용접 토우부의 각도 변화에 따른 피로수명을 조사하여서 최적의 토우부 각도를 선정하기 위하여, 유효노치응력법으로 계산한 유효노치반경을 적용한 유한요소해석 모델을 만들었다(Fig. 5). 용접 토우부 각도의 범위는 최소 15에서 최대 40°로 5°씩 증가시켜 총 6개 토우부 각도를 가지는 모델들로부터 유한요소해석을 진행하였다(Fig. 6).

Fig. 6

Schematic of six different welding toe angles

3. 결과

3.1 피로시험

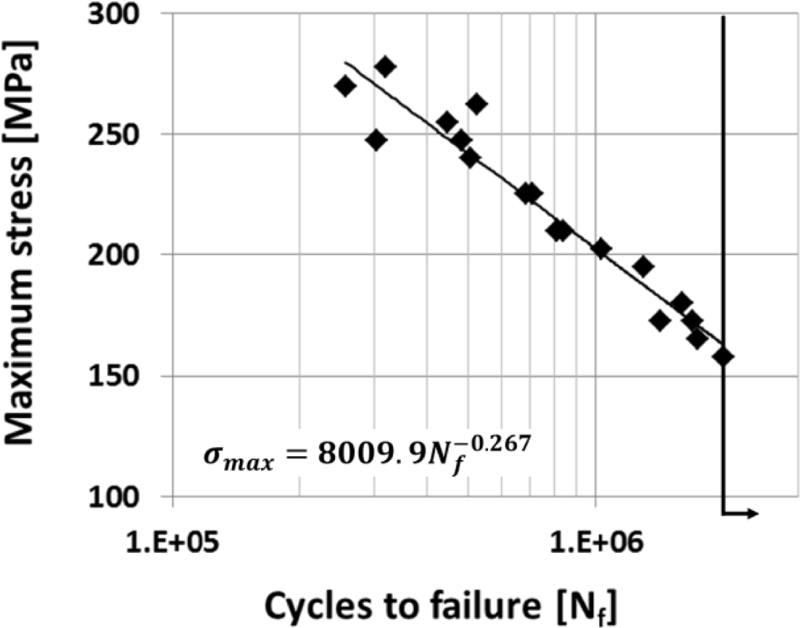
피로시험을 수행한 후 18개의 유효 데이터를 얻었으며, 모든 시험편이 용접 토우부에서 파단이 일어난 것을 확인할 수 있었다(Fig. 7). S-N 선도는 Semi-Log Scale로 나타내었으며(Fig. 8), 가해준 응력은 사인 프로파일의 최댓값으로 정의하였다. 피로한도는 157.5 MPa로 나타났다.

Fig. 7

Fractured T-Type welded joints after fatigue test

Fig. 8

S-N curve in the semi-log scale and its linear fit

3.2 피로시험 결과를 이용한 유효노치응력법 검증

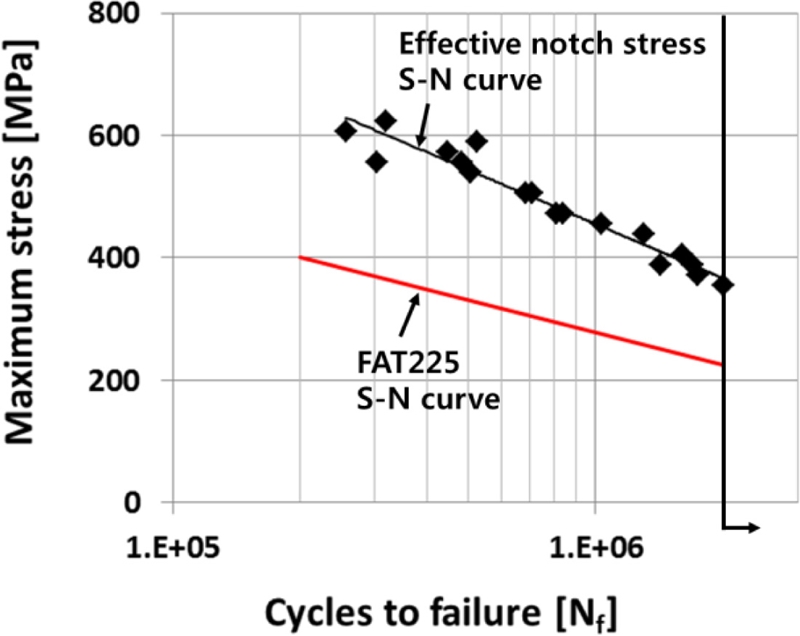
본 연구에서 적용한 유효노치응력법을 검증하기 위하여 Fig. 8의 결과에 피로노치계수(K_f = 2.25)를 곱하여서, T형 필렛 용접부에서 발생하는 유효노치응력($$ {\overline{\sigma }}_k$$)으로 환산한 S-N 선도(Fig. 9)와 IIW에서 십자형 필렛 용접부에 대하여 제시하는 S-N 선도인 FAT225와 서로 비교/분석하였다(Fig. 9). 그 결과 IIW에서 제시하는 FAT-225 S-N 선도부다. 본 연구에서 유효노치응력법을 적용하여서 구한 S-N 선도가 응력 대비 수명이 높은 것을 알 수 있다. 용접부의 특성상 50% 이상의 큰 산포가 발생하는 점을 감안할 때, 본 연구에서 유효노치응력법을 적용하여서 구한 S-N 선도가 FAT225 S-N 선도보다 용접 구조물의 피로수명을 안전하게 예측할 수 있다고 판단할 수 있다.

Fig. 9

Comparison of the effective notch S-N curve and FAT-225 S-N curve

3.3 용접 토우부 최적 각도 설계

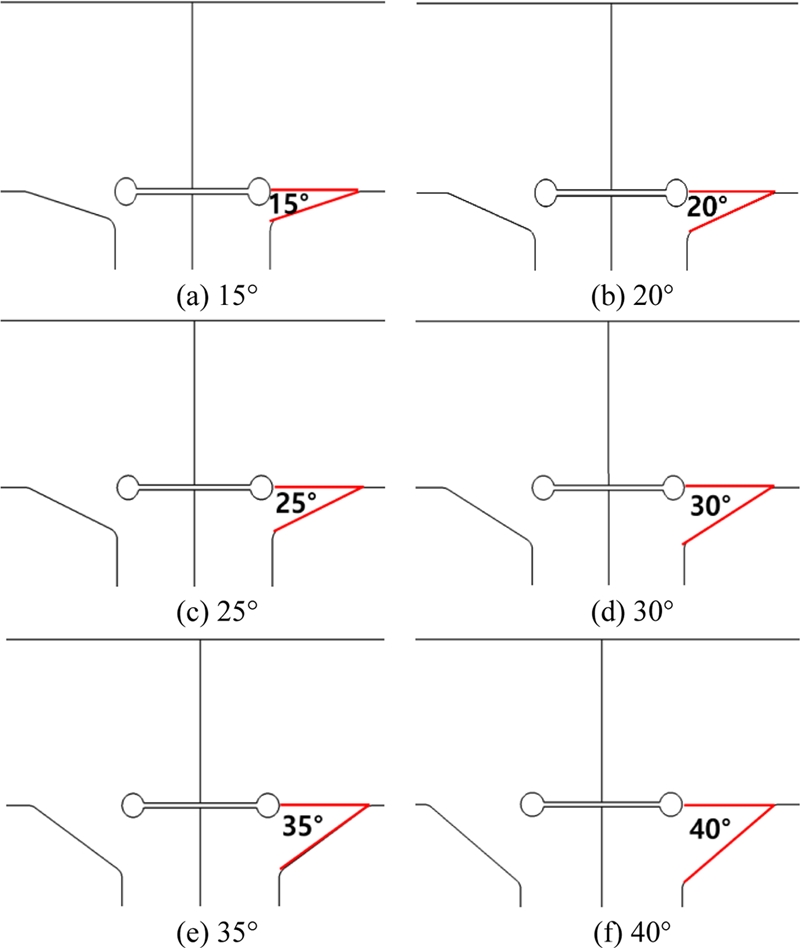
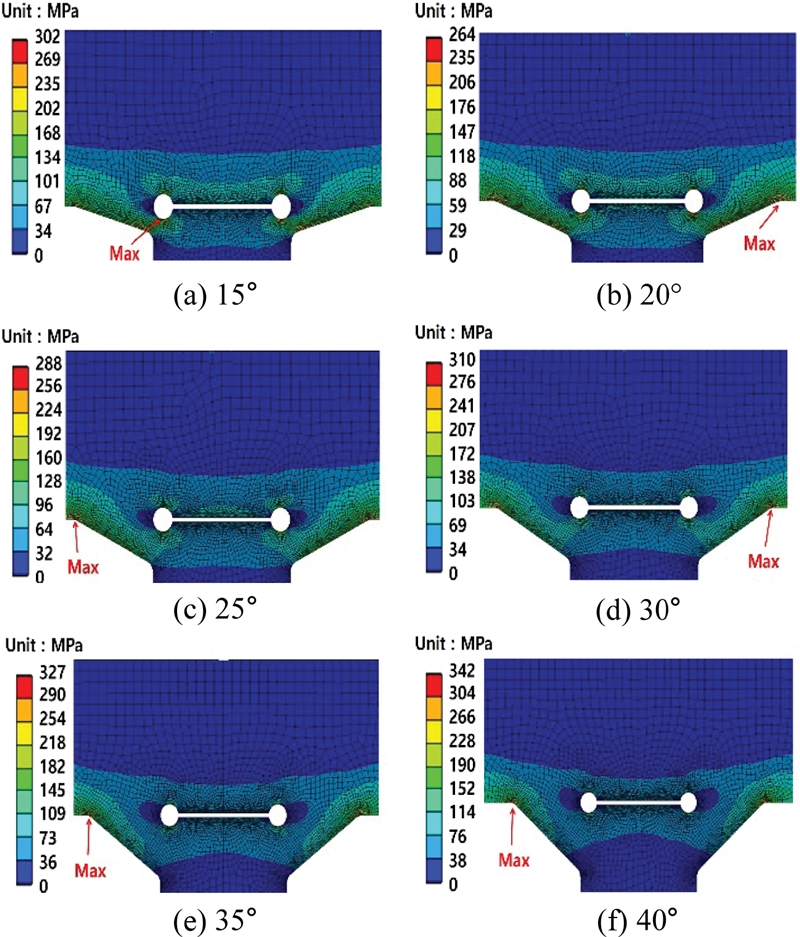
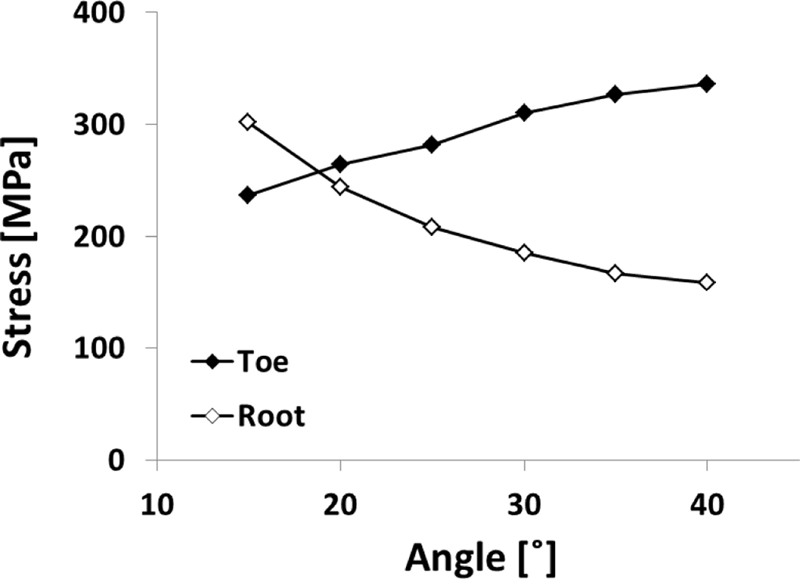
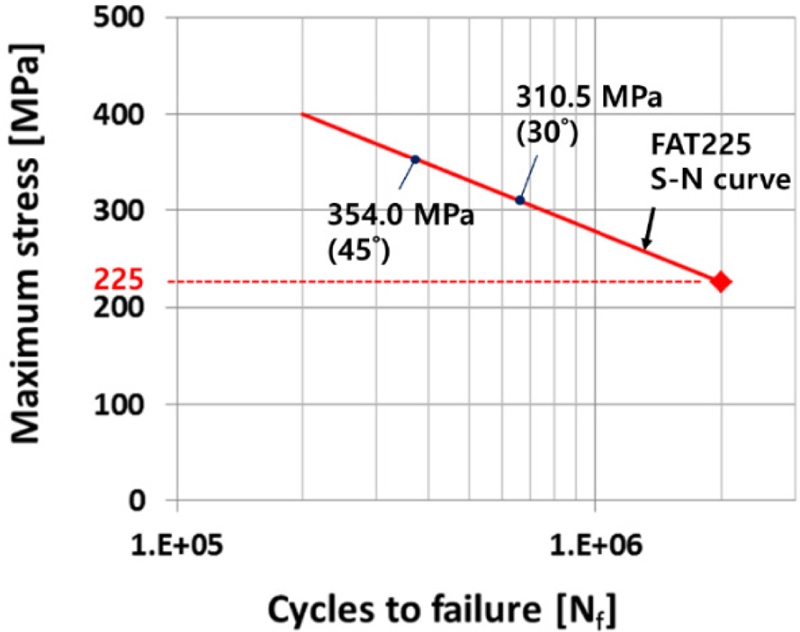
T형 필렛 용접부의 최적의 토우부 각도를 선정하기 위하여 유효노치응력법을 적용하여서 만든 해석 모델을 이용하여서 유한요소해석을 수행하였다. 용접 토우부의 각도가 작아짐에 따라 용접 토우부에서 발생하는 응력은 작아지는 반면에 용접 루트부에서 발생하는 응력은 커지는 것을 확인할 수 있다(Figs. 10, 11). 그리고 용접 루트부의 최대응력이 용접 토우부의 최대응력보다 크게 발생하는 각도는 15°이며, 20°에서 토우부의 최대응력이 루트부보다 커지는 것을 확인할 수 있었다. 용접부에서 피로파괴가 일어날 때, 토우부는 사용자가 균열에 대한 점검을 쉽게 할 수 있지만 루트부에서는 균열에 대한 점검이 쉽지 않다. 따라서 용접 구조물은 용접 토우부에서 균열이 발생하도록 설계되어야 한다. 본 연구의 결과에서 루트부보다 토우부에서 높은 응력이 발생하는 각도는 20에서 40°이다. 하지만 용접 구조물은 기존의 피로수명 자료들과 본 연구의 실험 결과에서 확인할 수 있듯이 동일한 하중에서도 50% 이상의 차이를 가지는 피로수명의 산란 인자(Scattering Factor)도 함께 고려하여야 한다. 50% 이상의 산포를 감안하였을 때, 토우부에서 발생하는 응력이 루트부보다 높은 각도는 30° 이상의 각도임을 알 수 있다. 따라서 산란 인자, 루트부보다 토우부에서 높은 응력 조건, 토우부의 응력 최소화 조건들을 동시에 고려할 때, 토우부의 최적 각도를 30°로 제시할 수 있다. 토우부의 각도가 30°일 때, 토우부에서 발생하는 최대응력(310.5 MPa)은 40°일 때의 최대응력(354.0 MPa)보다 약 14% 감소하였고(Fig. 12), IIW에서 제시하는 FAT-225를 사용할 때 피로수명은 약 30% 향상되었다.

Fig. 10

Maximum principal stress with different toe angles

Fig. 11

Comparison of toe and root stresses with different toe angles

Fig. 12

Comparison of fatigue life with different toe angles

4. 결론

본 연구에서는 굴삭기에 사용되는 강재인 SM490A를 사용하여 T형 필렛 용접 시험편을 제작하고 굽힘 하중에 대한 피로수명을 평가하였다. 그리고 IIW에서 제시하는 용접 구조물에 대한 FAT-225 선도와의 비교를 통하여, 용접 구조물의 피로수명 예측을 위한 유효노치응력법을 검증하였다. 마지막으로 이 유효노치응력법을 사용하여서 T형 필렛 용접 구조물의 토우부 각도 변화에 따른 피로수명의 변화를 조사하였고, 최적의 용접 토우부 각도를 제시하였다.

용접 구조물의 산란 인자, 루트부보다 토우부에서 높은 응력조건, 토우부의 응력 최소화 조건들을 동시에 고려할 때, T형 필렛 용접에서 최적의 용접 토우부 각도를 30°로 제시할 수 있었다. 토우부의 각도가 30°일 때의 최대응력(310.5 MPa)은 40°일 때의 최대응력(354.0 MPa)보다 약 14% 감소하였고, 피로수명은 약 30% 향상되었다. 향후 T형 필렛 용접에서 용접 변수들(전류, 전압, 속도 등)과 용접부, 열영향부, 모재부의 위치에 따른 물성을 반영하여 토우부 각도에 작용하는 영향을 조사하기 위한 연구를 수행할 계획이다.

Acknowledgments

이 과제는 부산대학교 기본연구지원사업(2년)에 의하여 연구되었음.

References

• Stephens, R. I., Fatemi, A., Stephens, R. R., and Fuchs, H. O., “Metal Fatigue in Engineering,” John Wiley & Sons, 2000.
• Kang, S. W., Ha, W. I., Shin, J. S., and Jae, J. S., “A Study on Stress Concentration Factor at Fillet Welded Joint,” Journal of the Society of Naval Architects of Korea, Vol. 33, No. 3, pp. 1-7, 1996.
• Aygül, M., Al-Emrani, M., and Urushadze, S., “Modelling and Fatigue Life Assessment of Orthotropic Bridge Deck Details Using FEM,” International Journal of Fatigue, Vol. 40, pp. 129-142, 2012. [https://doi.org/10.1016/j.ijfatigue.2011.12.015]
• Shahri, M. M. and Sandström, R., “Effective Notch Stress and Critical Distance Method to Estimate the Fatigue Life of T and Overlap Friction Stir Welded Joints,” Engineering Failure Analysis, Vol. 25, pp. 250-260, 2012. [https://doi.org/10.1016/j.engfailanal.2012.05.019]
• Sim, H. B., “Effective Notch Stress Method for Fatigue Evaluation of Welded Joints in a Steel Bridge Deck,” International Journal of Railway, Vol. 5, No. 2, pp. 89-92, 2012. [https://doi.org/10.7782/IJR.2012.5.2.089]
• Hobbacher, A., “Recommendations for Fatigue Design of Welded Joints and Components,” Springer, 2nd Ed., 2016. [https://doi.org/10.1007/978-3-319-23757-2]
• Choy, Y., Kim, Y., and Woo, H., “Effect of Residual Stress on Fatigue Crack Growth Behaviour in Butt Weldment (I) (Experimental Study),” Journal of the Korean Welding Society, Vol. 6, No. 4, pp. 27-34, 1988.
• Neuber, H., “Theory of Notch Stresses: Principles for Exact Stress Calculation,” J. W. Edwards, 1946.
• Radaj, D., “Design and Analysis of Fatigue Resistant Welded Structures,” Abington Publishing, 1990. [https://doi.org/10.1533/9781845698751]
• Radaj, D., Sonsino, C. M., and Fricke, W., “Fatigue Assessment of Welded Joints by Local Approaches,” Woodhead Publishing, 2006. [https://doi.org/10.1201/9781439832806]
• Pradana, M. R., Qian, X., and Swaddiwudhipong, S., “Simplified Effective Notch Stress Calculation for Non-Overlapping Circular Hollow Section K-Joints,” Marine Structures, Vol. 55, pp. 1-16, 2017. [https://doi.org/10.1016/j.marstruc.2017.04.006]
• Rother, K. and Fricke, W., “Effective Notch Stress Approach for Welds Having Low Stress Concentration,” International Journal of Pressure Vessels and Piping, Vol. 147, pp. 12-20, 2016. [https://doi.org/10.1016/j.ijpvp.2016.09.008]
• Topper, T., Wetzel, R., and Morrow, J., “Neuber's Rule Applied to Fatigue of Notched Specimens,” Journal of Materials Science, Vol. 4, No. 1, pp. 200-209, 1969.