Effects of Bearing Locations on the Characteristics of a Spindle System Supported by Tapered Roller Bearings
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
This paper presents the effects of bearing locations on the mechanical characteristics of a multi-stepped spindle system related to bearing fatigue life, natural frequency, and static stiffness. The multi-stepped spindle is supported by a pair of tapered roller bearings (TRBs) and subjected to radial loading. To solve the equilibrium equation of the spindle system which is inherently statically-indeterminate, this study adopts an integrated shaft-bearing model, where the spindle is modelled by the finite shaft elements and the supporting TRBs are modelled by the five degrees-of-freedom TRB model developed by the authors. An iterative computational method is used to estimate the spindle deflection coupled with bearing deflections, and afterwards the bearing stiffness and internal contact loads of rolling elements are computed. The bearing fatigue life based on the ISO standard and the first natural frequency of the spindle system are evaluated with the spindle-bearing model. The influences of bearing locations on the static stiffness and natural frequency of the spindle, and the fatigue life of TRBs are rigorously investigated. The numerical results show the noticeable effects of bearing locations on the spindle system characteristics. The presented results provide a comprehensive assessment to aid for design optimization of spindle-TRB system.
Keywords:
Tapered roller bearing, Spindle, Fatigue life, Natural frequency, Static stiffness키워드:
테이퍼 롤러 베어링, 스핀들, 피로 수명, 주파수, 정적 강성1. Introduction
A spindle-bearing system is a core part of machine tools. The characteristics of a spindle-bearing system greatly influence the machining accuracy and productivity of the machine tool. Therefore, adequate design of a spindle-bearing system is essential to guarantee a high performance of the machine tool.
One of the most important characteristics of spindle-bearing systems is the rigidity, which has a major effect on machining accuracy.1 The spindle-bearing system should be designed to avoid self-excited vibration, or chatter, that can occur during machining.2-4 Because this kind of vibration is closely related with the inherent natural frequencies of spindle-bearing system, high natural frequencies are usually preferable to make the spindle to operate under a broader range of operating speed and excitation frequencies. Nowadays, with the increasing demand for higher productivity, another important characteristic considered in the spindle-bearing system design is the service life, which is mainly determined by the fatigue life of the supporting bearings.5 The above-mentioned characteristics, i.e. spindle rigidity, natural frequency, and service life, are all relevant to the locations of supporting bearings on the spindle. The bearing locations directly affect the amounts of loads applied to the bearings, and inevitably the bearing fatigue lives. The stiffness of a bearing is also a function of the load which is applied on the bearing, and the bearing locations could modify the bearing stiffness, as well as the system natural frequency and rigidity.6 Thus, appropriate placement of the bearing locations is an essential part in the initial design stage of spindle-bearing system.
Traditional spindle-bearing system designs usually considered design objectives such as weight, natural frequency, dynamic stiffness, chatter, and depth of cut.7,8 The associated constraints for the design variables were introduced such as the number and size of bearings, bearing spans, preload, overhang tool length, etc. Lin9 optimized the bearing locations for improving the first natural frequency of a motorized spindle-bearing system using a genetic algorithm. Later, he extended his study to explore optimal locations of bearings and their tolerances simultaneously.10 Cao and Altintas11 designed the optimal bearing spans for avoiding chatter and thus improving the cutting depth of a milling system. Maeda et al.12 proposed an expert spindle design system to find optimal bearing locations for improving chatter stability. Chen and Liu13 investigated the effects of bearing arrangement, the distance between the front and rear bearing sets, and the overhang length of cutter’s free-end, on the spindle natural frequencies. Optimal bearing locations and spindle size for improving the stiffness and natural frequency of a spindle system were studied by Park et al..14 Lin and Tu15 showed that bearing locations are one of the most influential factors on the spindle-bearing system dynamics. In the above studies,9-15 however, the bearing fatigue life was not considered. Indeed, machine tool designs commonly face a struggle of compromise for spindle system characteristics among the rigidity, natural frequency, and bearing life. Hence, understanding the influence of bearing locations on these characteristics is very important.
In this paper, the effects of tapered roller bearing (TRB) locations on the bearing fatigue life, natural frequency, and static stiffness of a spindle-bearing system are investigated. The investigated spindle system consists of a spindle shaft supported by a pair of TRBs in back-to-back arrangement. The spindle is subjected to radial loading. This paper is structured as follows: Section 2 presents the configuration of spindle-bearing system, the calculation methods for bearing stiffness matrix, bearing fatigue life, spindle system deflection and natural frequencies. Section 3 presents the numerical results and discussion. The numerical results of the basic reference rating life of TRBs, and the static stiffness and natural frequencies of the spindle system as a function of TRB locations are reported in detail. Finally, Section 4 concludes the paper.
2. Spindle-Bearing System Model
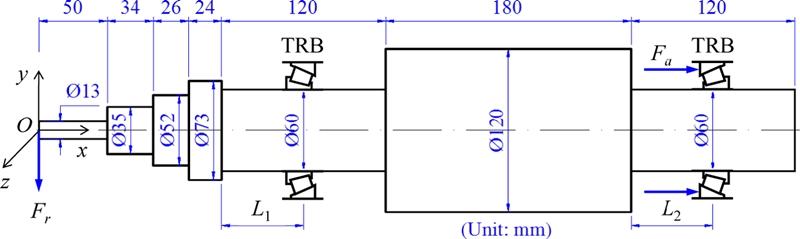
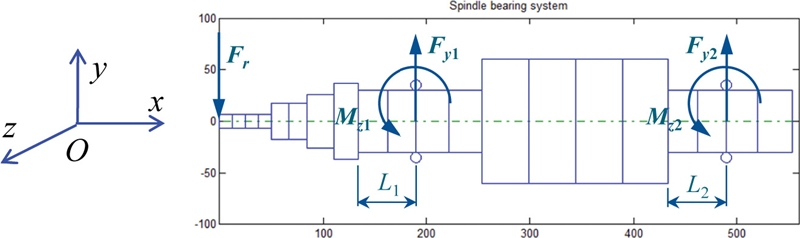
Fig. 1 illustrates the configuration of the investigated spindle system, which is a milling spindle supported by a pair of TRBs in back-to-back arrangement. The external load on the spindle system consists of a radial load Fr placed at the left tip of the shaft. The bearings are preloaded by a constant force method. To determine the characteristics of the spindle-bearing system such as bearing fatigue life, natural frequency, and static stiffness, the loads and stiffness matrices of the supporting bearings are needed. These can be obtained after solving the equilibrium equations of spindle-bearing system. The bearing stiffness model, fatigue life computation, and spindle FE model are briefly addressed in this section.
2.1 TRB Stiffness Model
Fig. 2 presents a five DOF model for a TRB. The inner ring of the TRB is loaded by a load vector {F} and is displaced by a displacement vector {δ}, where:
| (1) |
| (2) |
Free-body diagram and two solving procedures for bearing subject to initial displacements or external loading
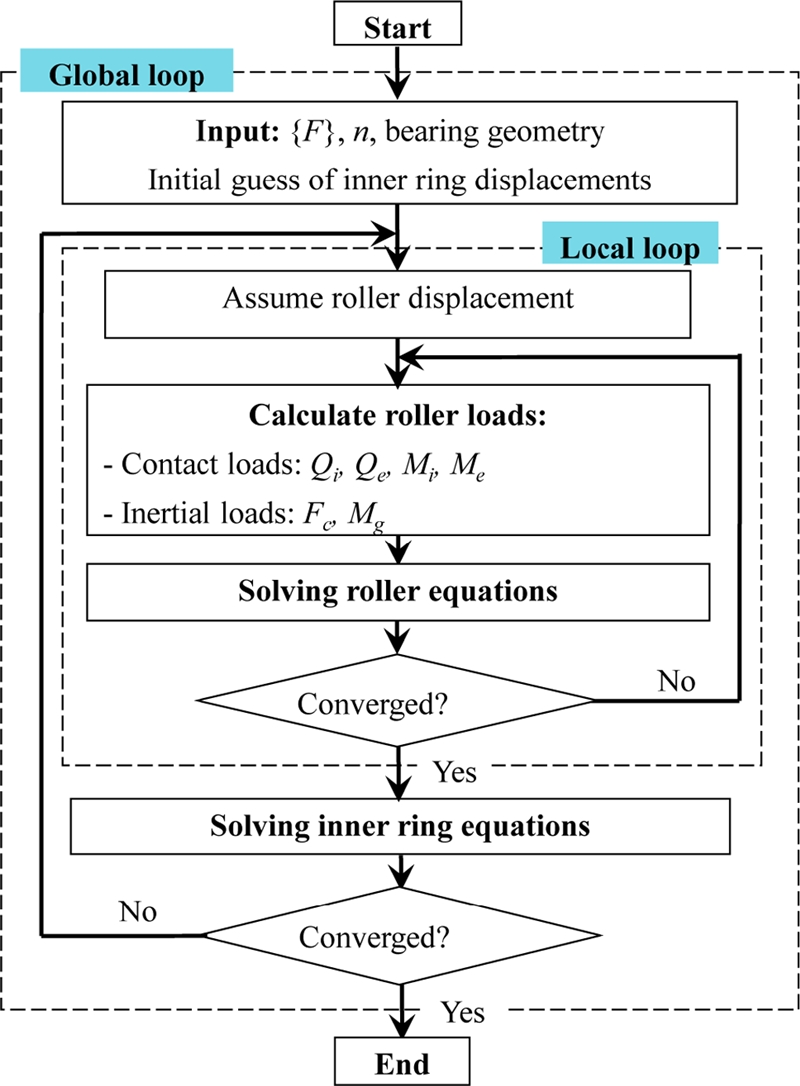
There are two types of computational procedure for the TRB model according to the input and output conditions as shown in Fig. 2. The first computational procedure is related with the stiffness matrix and displacements of the TRB subject to bearing loading. Fig. 3 shows the calculation flowchart of the first procedure. This procedure is based on a two-loop iteration: The global loop for the inner equilibrium and the inner loop for local equilibrium of each roller. The calculation process starts by assuming the initial displacements of the inner ring and rollers. Subsequently, the contact loads between the rollers and raceways are calculated using the slicing method.16 Next, the new displacements of rollers are determined by solving the equilibrium equations of rollers using the Newton-Raphson method. The free-body diagram of a roller with all applied loads is demonstrated in Fig. 2. After the equilibriums of individual rollers are solved, the inner ring equilibrium equation can be solved for the unknown inner ring displacements. At the end of the local or global loop, the convergence should be checked, in which the current displacements of rollers or inner ring are compared to those of the previous iteration. A new iteration is needed if the differences between the current and previous displacements are larger than a given tolerance. Details of the roller loads, roller and inner ring equilibrium equations, and stiffness matrix formulation may be referred from several papers by the authors.16,17
The second computational procedure is such that the displacement vector of inner ring is given a priori, and the applied load and stiffness matrix of the bearing are determined. This procedure may be a simplified version of the first procedure, because only the equilibriums of rollers are needed to solve. Accordingly, the computational procedure is similar to Fig. 2 except excluding the outer loop.
Both the two computation procedures provide the stiffness matrix and roller-race contact loads, which are essential for the estimation of the natural frequency, static stiffness, and bearing fatigue life of the spindle-bearing system. The TRB stiffness matrix is determined by Eq. (3).
| (3) |
which is a [5 × 5] matrix represented as Eq. (4):
| (4) |
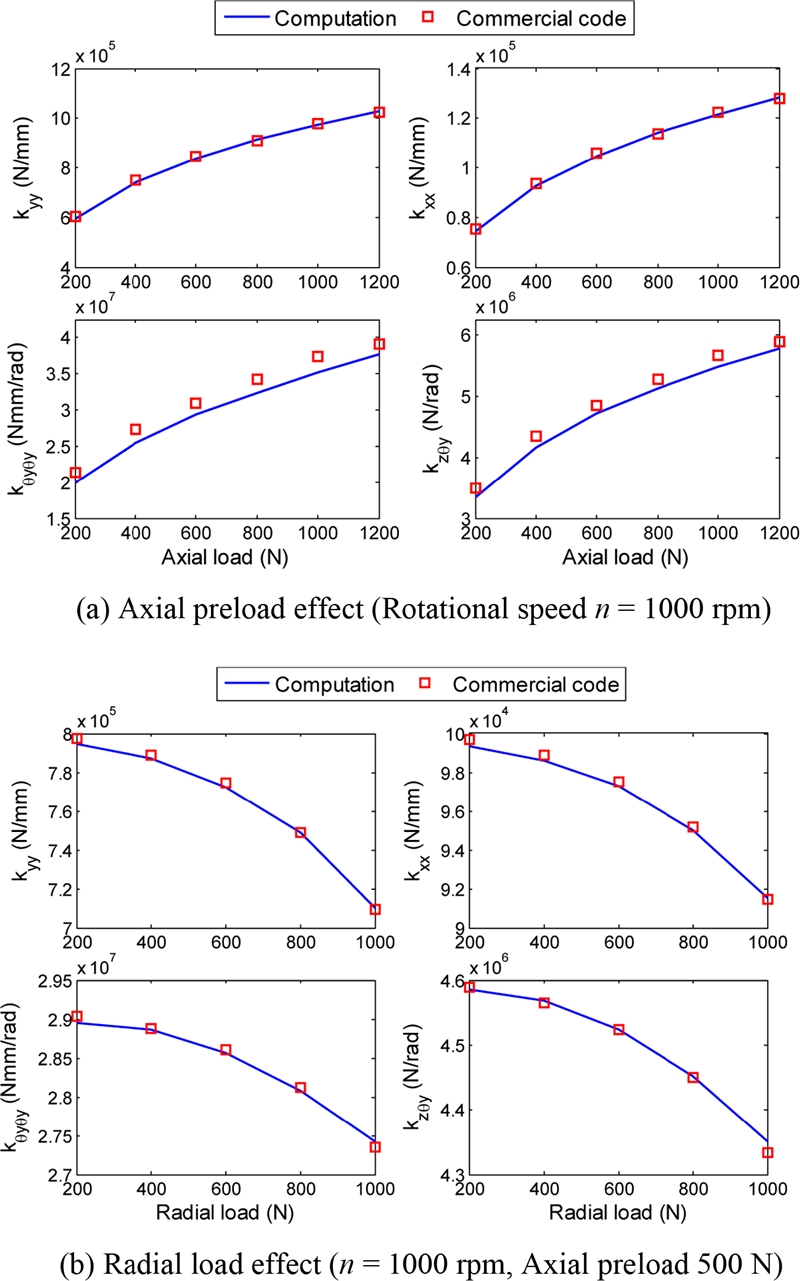
Fig. 4 shows the numerically obtained stiffness of a TRB as a function of axial and radial loads. The bearing geometric data are taken from.16 The computed stiffness values are compared with those determined by a commercial code.18 It can be observed that the calculated results match well with those from the commercial code.
2.2 Bearing Fatigue Life
In this section, the fatigue life of TRB is estimated in terms of reference rating life with roller loads. The reference rating life (L10r) is defined as the number of revolutions (in 106 Revolutions) such that a bearing may survive with a probability of 90%. Determination of L10r is outlined in ISO standard19 and briefly summarized below.
First, the basic dynamic load ratings of inner and outer ring are determined as:
| (5) |
| (6) |
where the subscripts i and e represent the inner and outer races, respectively. λν = 0.83 represents the reduction factor considering the effect of stress concentration and variation of exponent.19 Parameter c depends on the TRB geometry including the roller mean diameter (Da), pitch diameter (dm), and contact angle (α) as Eq. (7):
| (7) |
Cr is the basic dynamic radial load rating of the TRB, which is determined by Eq. (8):19
| (8) |
where bm = 1.1 indicates the contemporary improvement factor of bearing quality. fc = 88.02 denotes a factor representing the accuracy regarding the geometry and material of manufactured bearing components.
Next, the basic load ratings of a slice are calculated as Eqs. (9) and (10):
| (9) |
| (10) |
Considering the TRB with rotating inner ring and stationary outer ring, the dynamic equivalent loads on the k-th slice of inner and outer rings are calculated by Eqs. (11) and (12):
| (11) |
| (12) |
where pikj and pekj indicate the maximum contact pressures at the k-th slice and the j-th roller of inner and outer race (denoted by i and e), which are found by means of contact pressure analysis. In this calculation, the roller and race contact pressure is determined by using a three dimensional elastic contact model.20,21 Z is the total number of rollers in the TRB. Finally, the basic reference rating life of TRB is estimated as follows:
| (13) |
2.3 Spindle Natural Frequency
To determine the natural frequency, the spindle system is modelled using Timoshenko beam elements.22 The shaft is discretized into a number of finite elements and two TRBs are located at nodes as shown in Fig. 5. The shaft internal damping and bearing damping are neglected here. The equation of motion for a shaft element is expressed as follows:
| (14) |
where ms and gs are the [4 × 4] mass and gyroscopic matrices of shaft element, respectively. {ys} and {zs} represent the [4 × 1] displacement vectors in xOy and xOz planes, respectively. The equation of motion for a bearing is represented as Eq. (15):
| (15) |
where denotes the force vector of the bearing. represent [2 × 2] bearing stiffness matrix obtained from the bearing model. Assembling the shaft element and bearing equations gives the equation of motion for the whole spindle system as follows:
| (16) |
The state space form of the system equation of motion is as follows:
| (17) |
where
| (18) |
| (19) |
| (20) |
| (21) |
The eigenvalue problem in association with Eq. (17) can be written as
| (22) |
where α and {h} are the eigenvalue and corresponding eigenvector, respectively. Then the natural frequencies can be obtained from the imaginary parts of the eigenvalues.
2.4 Calculation Process
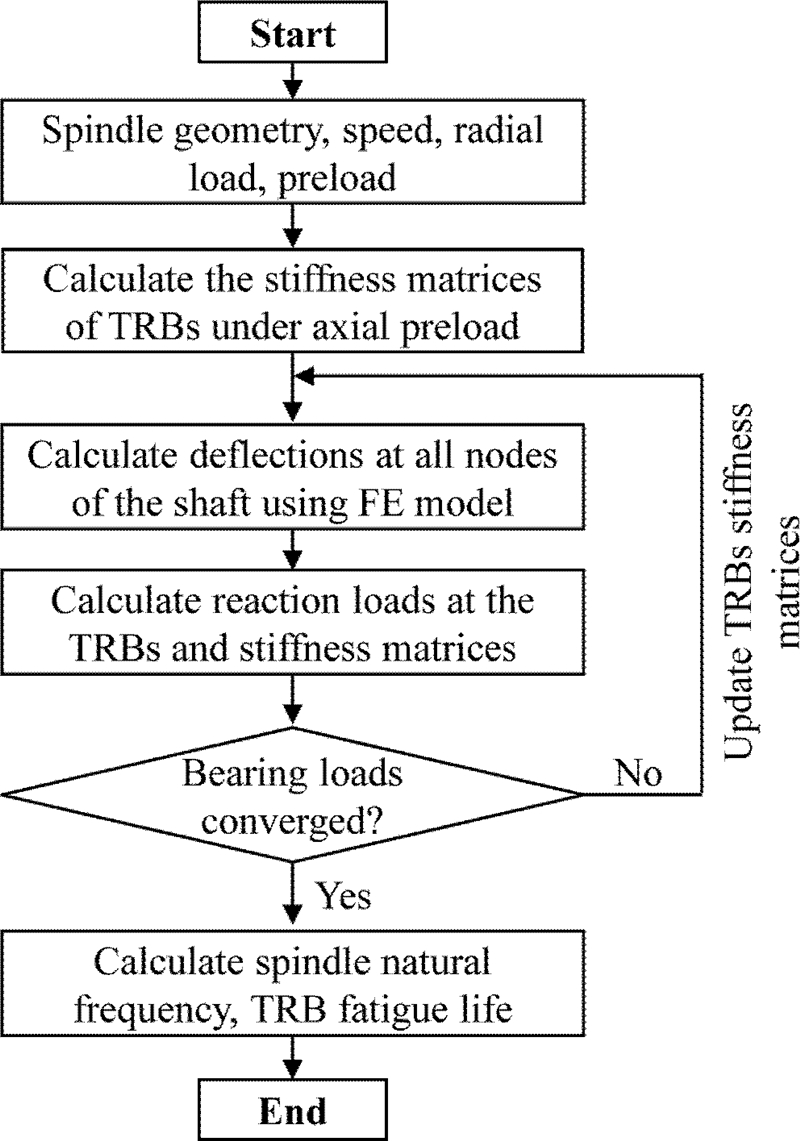
When the spindle shaft is subjected to radial loading, the resulting reaction loads at TRBs commonly include radial, axial and, moment loads. Likewise, the multi-stepped spindle shaft is elastically bent under loading. As a result, the equilibrium equation of the spindle system becomes indeterminate and could not be directly calculated using force equilibrium equations.22,23 Moreover, because the bearing stiffness depends nonlinearly on the applied loads as shown in Fig. 4, the shaft equilibrium cannot be solved separately with assuming a given bearing stiffness. Therefore, the equilibrium equation of spindle system coupled with bearing stiffness and the reaction forces should be solved simultaneously. In order to overcome this problem, an iterative procedure is used in this study as shown in Fig. 6. First, the stiffness matrices of TRBs are calculated under initial axial preload using the first iteration of bearing calculation procedure. Having obtained the bearing stiffness matrices, the combined stiffness matrix of the whole spindle-bearing system [K] can be constructed using the FE model presented in previous section. Then, the displacement vector of all nodes {q} is obtained by using the following static relationship:
| (23) |
where {f} is the load vector of spindle-bearing system. In this study, because only one radial load Fr is applied on the spindle nose as shown in Fig. 1, the load vector {f} contains only one non-zero element Fr at the correspondent node, while the other elements of {f} are all zero. Obtaining the displacement vector {q}, the reaction loads on the TRBs and the TRB stiffness matrices are re-calculated using the next bearing calculation procedure. In the next step, the convergence for the bearing loads is checked. If the differences in the bearing loads between the current and previous steps are higher than a pre-assigned tolerance value, then the bearing stiffness matrices are updated and a new iteration begins. Otherwise, the iterative process is stopped. Finally, the fatigue lives of TRBs and the spindle natural frequency are calculated.
3. Numerical Results and Discussion
This section presents the numerical results and discussion. The radial load on the spindle is Fr = 2,000 N. The preload values of the two TRBs are set to be identical, Fa = 1,500 N. The rotational speed of the spindle-bearing system n is 1000 rpm. The TRB locations are represented by distances L1 and L2 as shown in Fig. 1, which are all varied from 11 to 106 mm. The length of the shaft segments on which TRBs are placed is L = 120 mm. Here, L1 and L2 are slightly smaller than L because the bearings have their own width, requiring some space for assembly.
3.1 Bearing Load
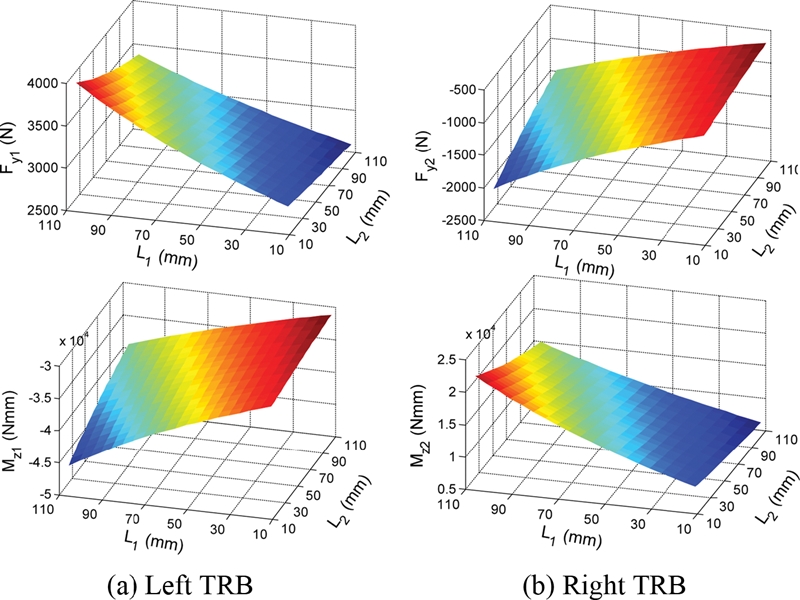
Fig. 7 shows the bearing reaction loads on the shaft, which are also equal to the loads sustained by the bearings but in the opposite directions. The TRBs are all preloaded by the constant force preload method, and the varying loads to each TRB include a radial load and a bending moment as shown in Fig. 7. Fig. 8 shows the radial and moment loads on the shaft determined at TRB locations as a function of bearing location variables, L1 and L2. It is observed that the left TRB endures higher load compared to that of the right TRB. The loads of TRBs all increase with increasing L1, i.e., increasing the distance between the left TRB and the radial loading point. Moreover, the left bearing location (L1) manifests a higher influence on the bearing load variation than the right bearing location (L2). This could be because the left TRB is closer to the loading point than the right one.
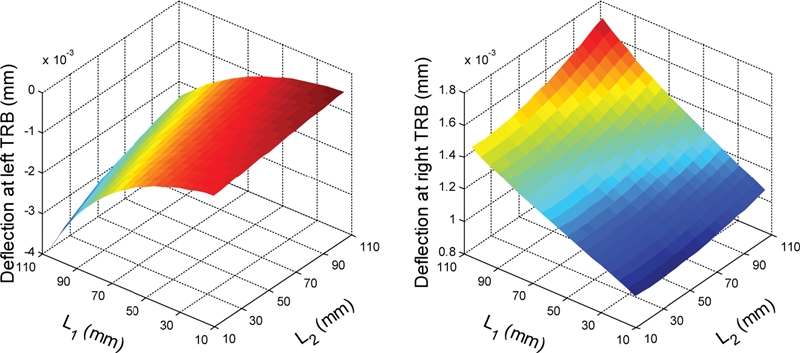
Fig. 9 shows the vertical deflections of TRBs in y direction (See Fig. 7) with varying the TRB locations. The deflections of TRBs vary significantly with changing the TRB locations along the shaft. The relationship between the deflections and TRB locations shows a high degree of nonlinearity. Owing to the above-mentioned changes in the TRB loads and deflections, the TRB fatigue life and shaft deflection are varied accordingly. Moreover, the spindle natural frequency is also influenced by the nonlinear dependence between the bearing loads and stiffness. The behavior of fatigue life, natural frequency and static stiffness as a function of bearing locations will be discussed in the next section.
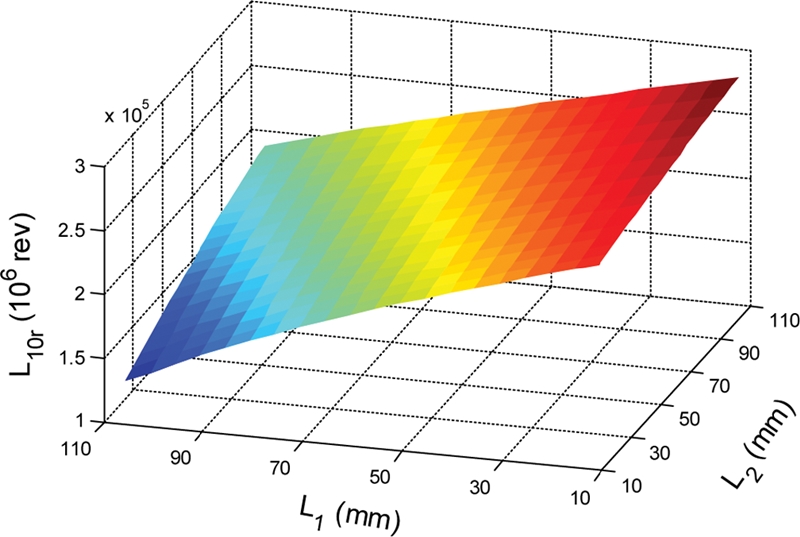
3.2 Bearing Fatigue Life
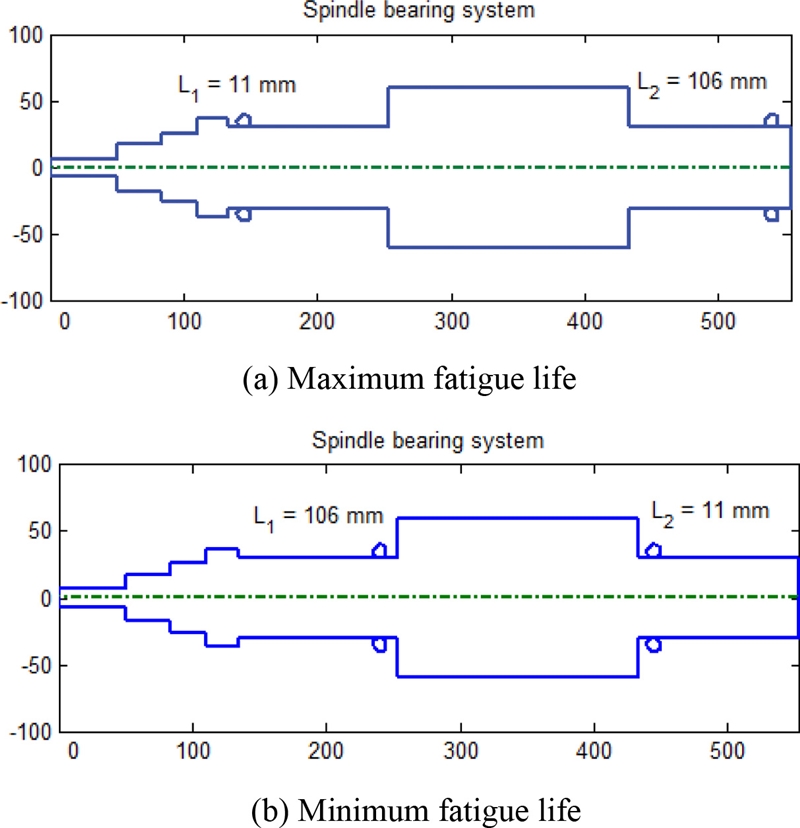
As shown in Fig. 8, the loads on the left TRB are significantly higher than those of the right TRB. Therefore, we consider only fatigue of the left TRB. Fig. 10 indicates that the maximum fatigue life is reached when L1 = 11 mm and L2 = 106 mm. On the other hand, the minimum bearing fatigue life is obtained when L1 = 106 mm and L2 = 11 mm. This demonstrates that the maximum fatigue life is obtained when the distance between the two TRBs is longest as shown in Fig. 11(a). To the contrary, when the distance between two TRBs is minimized, the fatigue life is deteriorated as shown in Fig. 11(b). The behavior of the TRB fatigue life in Fig. 10 can be explained by the correspondent variation of bearing loads already shown in Fig. 8. The bearing fatigue life generally reveals an opposite tendency to the load applied to bearing.
3.3 Natural Frequency of Spindle-Bearing System
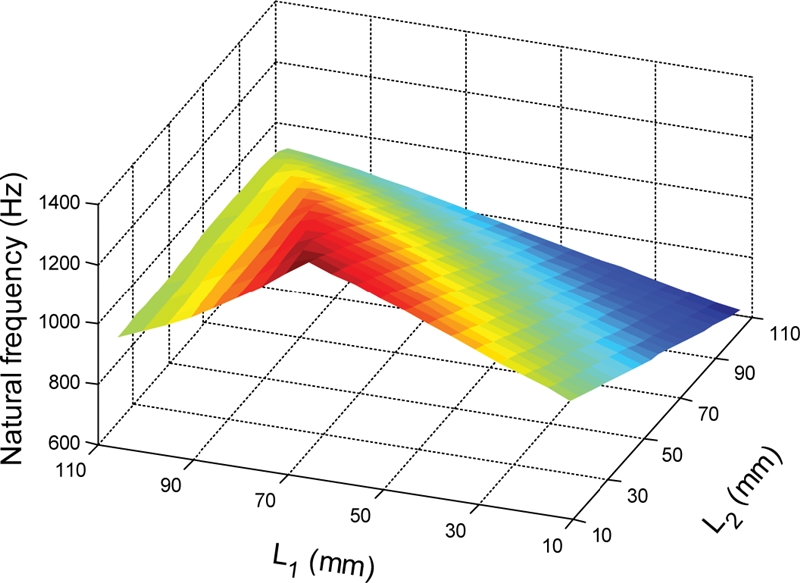
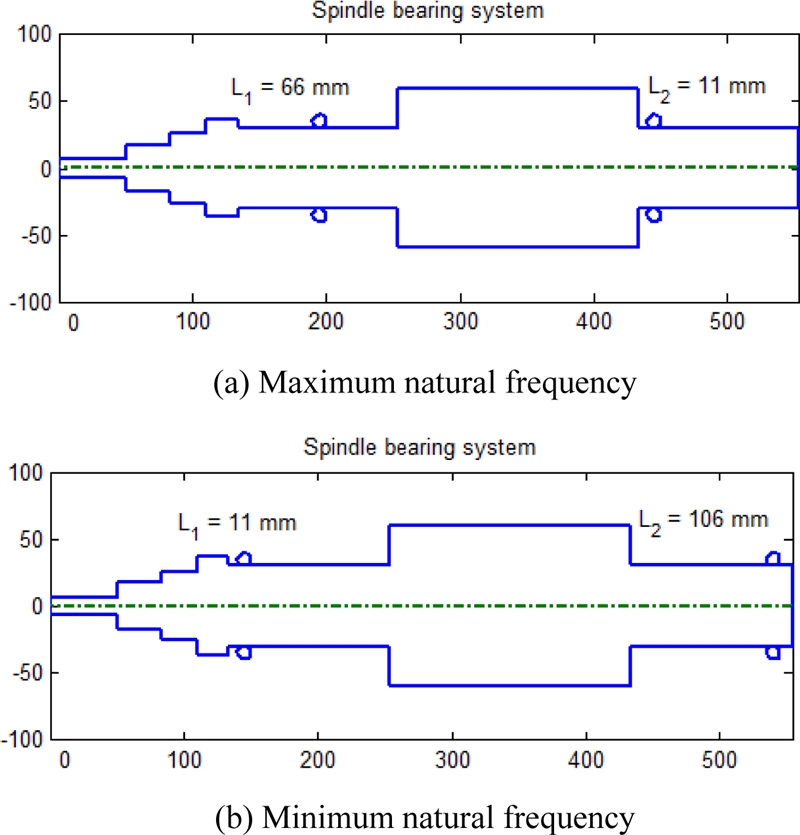
Fig. 12 shows the influence of bearing locations on the natural frequency of spindle system. In this study, we consider only the first natural frequency. Fig. 12 illustrates that the maximum natural frequency is 1,312.7 Hz when L1 = 66 mm and L2 = 11 mm. The minimum natural frequency is 648.44 Hz when L1 = 11 mm and L2 = 106 mm. This result demonstrates that the bearing locations significantly influence the spindle natural frequency. The bearing locations at which the natural frequency becomes minimal and maximal are shown in Fig. 13. It should be noted from Figs. 11(a) and 13(b) that the bearing locations of L1 = 66 mm and L2 = 11 mm maximize the bearing fatigue life but minimize the spindle natural frequency. Hence, the bearing locations should be carefully determined to consider such trade-off between the bearing fatigue life and spindle natural frequency.
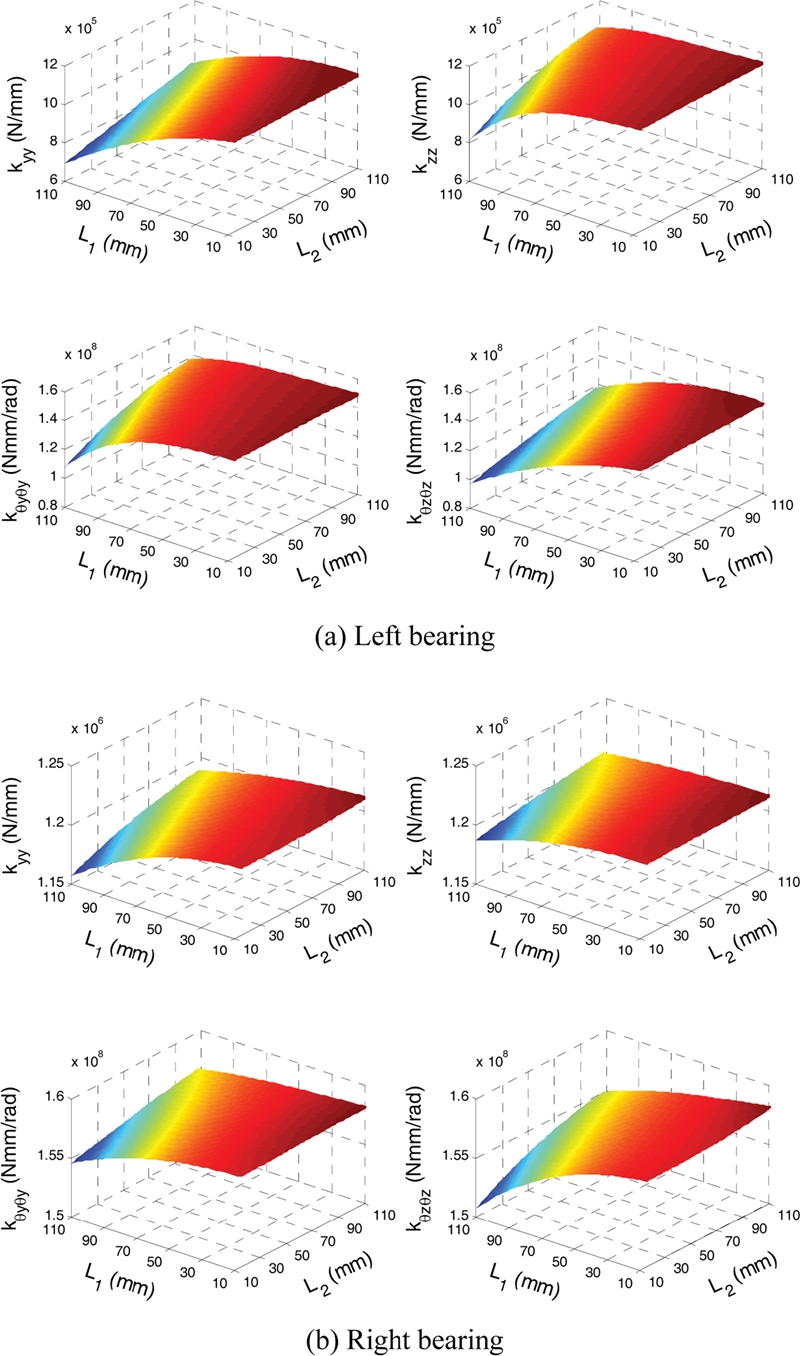
Fig. 14 shows the effects of TRB locations on the stiffnesses of the TRBs. The bearing stiffnesses show a contrary behavior against the external radial load shown earlier in Fig. 8(a). This is because increasing the radial load reduces the number of contacted rollers under loading. The stiffnesses of the left TRB vary significantly with bearing locations; the maximum stiffnesses are increased by more than 31% when compared to the minimum stiffnesses. On the other hand, the stiffnesses of the right TRB have only slight dependency on the bearing locations. Here, the differences between the maximum and minimum stiffnesses are approximately 4.5%. It is also noted that the bearing stiffnesses converge to their maximum values when the distances L2 reaches its upper limit of 106 mm, and L1 reaches its lower limit of 11 mm. Although the bearing stiffnesses become maximum, they could not ensure the highest spindle natural frequency as can be seen in Fig. 12.
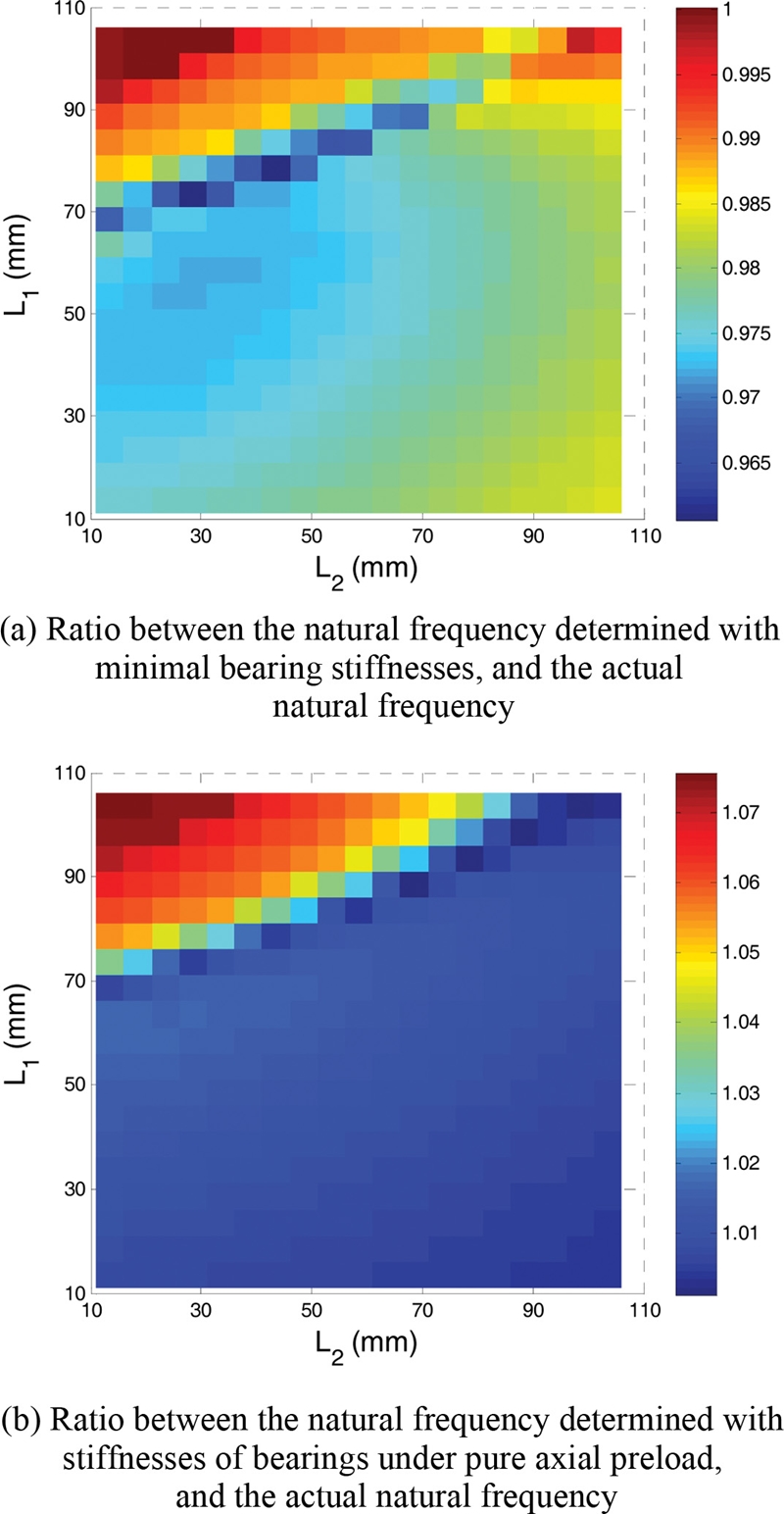
To evaluate the spindle natural frequency change with respect to the TRB stiffnesses variation caused by the bearing locations, Fig. 15 plots the natural frequency ratios that are defined as fi divided by ft, in which fi is the natural frequency determined with invariant bearing stiffnesses, and ft is the natural frequency determined with actual bearing stiffnesses. First, fi is calculated with intentionally excluding the effect of bearing locations on the bearing stiffnesses. Secondly, fi is calculated with the minimum values of bearing stiffnesses, i.e., the stiffnesses under pure axial preload. The resulting frequency ratios are shown in Figs. 15(a) and 15(b). Fig. 15(a) shows that the minimum value of natural frequency ratio is approximately 0.96. This means that the natural frequency estimated with the minimal bearing stiffnesses would be reduced by approximately 4% compared to the current natural frequency. On the other hand, Fig. 15(b) shows that under pure axial preload, we can obtain a maximum increase of the spindle natural frequency by approximately 7.5% compared to the current natural frequency. Through Figs. 14 and 15, changes in bearing locations lead to the subsequent change in the bearing stiffnesses, and therefore the spindle natural frequency.
3.4 Static Stiffness
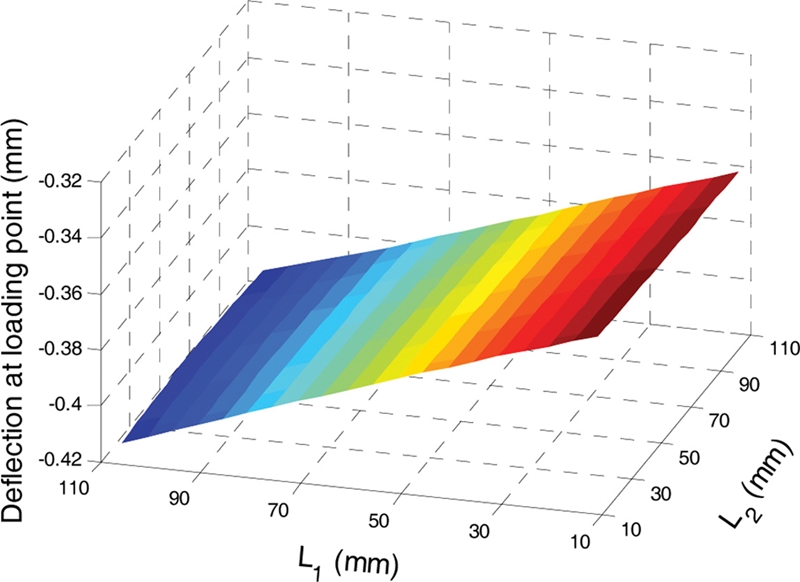
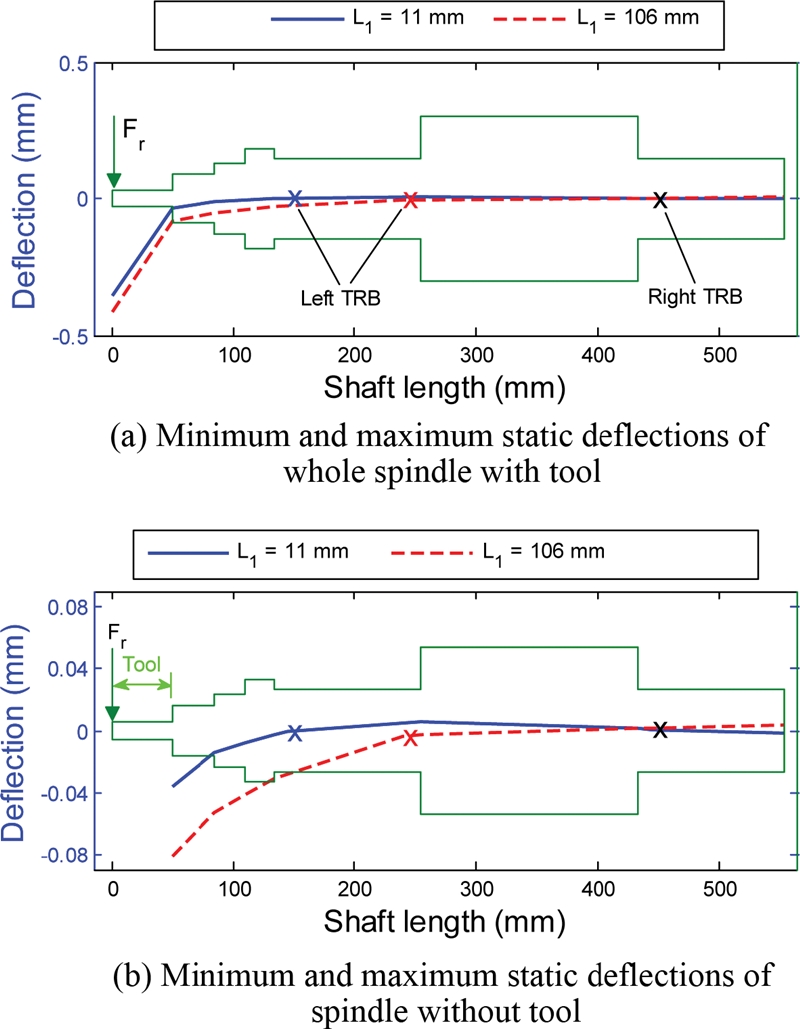
Fig. 16 shows the static deflection of spindle determined at the loading point. Unlike the spindle natural frequency and bearing fatigue life, the deflection at the loading point mainly depends on the location of the left TRB. The effect of the right TRB location on the loading point deflection is very limited. Fig. 17 illustrates the minimum and maximum static deflections of the spindle calculated at L1 = 11 mm and L1 = 106 mm, respectively, while L2 is kept as 11 mm. The deflection shape of the whole spindle, as shown in Fig. 17(a), demonstrates that most of the deflection stems from the elastic cutting tool. In order to view more details of spindle deflection, Fig. 17(b) illustrates the deflections without the tool part. The left TRB location L1 = 11 mm, which leads to the minimal static deflection, does not necessarily guarantee the highest spindle natural frequency.
4. Conclusions
This paper presented the effects of bearing locations on the bearing fatigue life, spindle natural frequency, and static stiffness for a spindle system with TRBs. Variation of TRB locations critically alters the reaction loads acting on the bearings, and eventually most of the characteristics of the spindle and TRBs. The behaviors of stiffness and TRB fatigue life with respect to bearing locations are quite similar to each other, whilst the bearing location effects on the TRB fatigue life and spindle natural frequency are dissimilar to each other. The bearing locations at which static stiffness are maximized are not necessarily best for gaining higher spindle natural frequency. The reported results in this paper provide a basis for the design optimization of spindle-bearing system in consideration of multiple objectives of the spindle static stiffness, natural frequency, and bearing fatigue life.
Acknowledgments
This research was supported by National Research Foundation of Korea (No. NRF-2019R1F1A1063783).
References
-
Li, J., Zhu, Y., Yan, K., Yan, X., Liu, Y., et al., “Research on the Axial Stiffness Softening and Hardening Characteristics of Machine Tool Spindle System,” The International Journal of Advanced Manufacturing Technology, Vol. 99, Nos. 1-4, pp. 951-963, 2018.
[https://doi.org/10.1007/s00170-018-2456-1]

-
Nam, S., Hayasaka, T., Jung, H., and Shamoto, E., “Proposal of Novel Chatter Stability Indices of Spindle Speed Variation based on its Chatter Growth Characteristics,” Precision Engineering, Vol. 62, pp. 121-133, 2020.
[https://doi.org/10.1016/j.precisioneng.2019.11.018]

-
Cao, H., Li, B., and He, Z., “Chatter Stability of Milling with Speed-Varying Dynamics of Spindles,” International Journal of Machine Tools and Manufacture, Vol. 52, No. 1, pp. 50-58, 2012.
[https://doi.org/10.1016/j.ijmachtools.2011.09.004]

-
Wang, C., Zhang, X., Yan, R., Chen, X., and Cao, H., “Multi Harmonic Spindle Speed Variation for Milling Chatter Suppression and Parameters Optimization,” Precision Engineering, Vol. 55, pp. 268-274, 2019.
[https://doi.org/10.1016/j.precisioneng.2018.09.017]

-
Razban, M. and Movahhedy, M. R., “A Speed-Dependent Variable Preload System for High Speed Spindles,” Precision Engineering, Vol. 40, pp. 182-188, 2015.
[https://doi.org/10.1016/j.precisioneng.2014.11.008]

-
Cao, H., Holkup, T., and Altintas, Y., “A Comparative Study on the Dynamics of High Speed Spindles with Respect to Different Preload Mechanisms,” The International Journal of Advanced Manufacturing Technology, Vol. 57, Nos. 9-12, pp. 871-883, 2011.
[https://doi.org/10.1007/s00170-011-3356-9]

-
Taylor, S., Khoo, B., and Walton, D., “Microcomputer Optimisation of Machine Tool Spindle Stiffnesses,” International Journal of Machine Tools and Manufacture, Vol. 30, No. 1, pp. 151-159, 1990.
[https://doi.org/10.1016/0890-6955(90)90049-O]

-
Lee, D. S. and Choi, D. H., “Reduced Weight Design of a Flexible Rotor with Ball Bearing Stiffness Characteristics Varying with Rotational Speed and Load,” Journal of Vibration and Acoustics, Vol. 122, No. 3, pp. 203-208, 2000.
[https://doi.org/10.1115/1.1303066]

-
Lin, C. W., “Optimization of Bearing Locations for Maximizing First Mode Natural Frequency of Motorized Spindle-Bearing Systems Using a Genetic Algorithm,” Applied Mathematics, Vol. 5, No. 14, pp. 2138-2152, 2014.
[https://doi.org/10.4236/am.2014.514208]

-
Lin, C. W., “Simultaneous Optimal Design of Parameters and Tolerance of Bearing Locations for High-Speed Machine Tools Using a Genetic Algorithm and Monte Carlo Simulation Method,” International Journal of Precision Engineering and Manufacturing, Vol. 13, No. 11, pp. 1983-1988, 2012.
[https://doi.org/10.1007/s12541-012-0261-6]

-
Altintas, Y. and Cao, Y., “Virtual Design and Optimization of Machine Tool Spindles,” CIRP Annals, Vol. 54, No. 1, pp. 379-382, 2005.
[https://doi.org/10.1016/S0007-8506(07)60127-9]

-
Maeda, O., Cao, Y., and Altintas, Y., “Expert Spindle Design System,” International Journal of Machine Tools and Manufacture, Vol. 45, Nos. 4-5, pp. 537-548, 2005.
[https://doi.org/10.1016/j.ijmachtools.2004.08.021]

- Chen, X. and Liu, J., “Model-Based Design of Motorized Spindles with Different Bearing Configurations,” Journal of Vibroengineering, Vol. 15, No. 4, pp. 1853-1865, 2013.
-
Park, S. J., Lee, C. M., and Hwang, Y. K., “Lightweight Design of 45,000 r/min Spindle Using Full Factorial Design and Extreme Vertices Design Methods,” Journal of Central South University of Technology, Vol. 18, No. 1, pp. 153-158, 2011.
[https://doi.org/10.1007/s11771-011-0673-y]

-
Lin, C. W. and Tu, J. F., “Model-Based Design of Motorized Spindle Systems to Improve Dynamic Performance at High Speeds,” Journal of Manufacturing Processes, Vol. 9, No. 2, pp. 94-108, 2007.
[https://doi.org/10.1016/S1526-6125(07)70111-1]

-
Tong, V. C. and Hong, S. W., “Study on the Stiffness and Fatigue Life of Tapered Roller Bearings with Roller Diameter Error,” Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology, Vol. 231, No. 2, pp. 176-188, 2017.
[https://doi.org/10.1177/1350650116649889]

-
Tong, V. C. and Hong, S. W., “Characteristics of Tapered Roller Bearing with Geometric Error,” International Journal of Precision Engineering and Manufacturing, Vol. 16, No. 13, pp. 2709-2716, 2015.
[https://doi.org/10.1007/s12541-015-0346-0]

- Schaeffler Technologies AG & Co. KG, “Bearinx®-Online Shaft Calculation,” https://www.schaeffler.de/content.schaeffler.de/en/news_media/media_library/videos/downloadcenter-global-pages/index.jsp?videoid=96642&pvideoid=96643&tab=mediathek-vid&uid=96643&subfilter=app:dc, (Accessed 9 JULY 2020)
- ISO/TS 16281:2008, “Rolling Bearings-Methods for Calculating the Modified Reference Rating Life for Universally Loaded Bearings,” 2008.
-
Tong, V. C. and Hong, S. W., “Characteristics of Tapered Roller Bearings in Relation to Roller Profiles,” Journal of Mechanical Science and Technology, Vol. 29, No. 7, pp. 2913-2919, 2015.
[https://doi.org/10.1007/s12206-015-0622-z]

-
Tong, V. C. and Hong, S. W., “The Effect of Angular Misalignment on the Stiffness Characteristics of Tapered Roller Bearings,” Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 231, No. 4, pp. 712-727, 2017.
[https://doi.org/10.1177/0954406215621098]

-
Tong, V. C., Bae, G. H., and Hong, S. W., “Dynamic Analysis of Spindle Supported by Multiple Bearings of Different Types,” Journal of the Korean Society for Precision Engineering, Vol. 32, No. 2, pp. 117-125, 2015.
[https://doi.org/10.7736/KSPE.2015.32.2.117]

- Hong, S. W., Kang, J. O., and Shin, Y. C., “Dynamic Characteristics of Indeterminate Rotor Systems with Angular Contact Ball Bearings Subject to Axial and Radial Loads,” International Journal of Precision Engineering and Manufacturing, Vol. 3, No. 2, pp. 61-71, 2002.

He is a Postdoc researcher in the Department of Ultra Precision Machines and Systems, Korea Institute of Machinery & Materials. His research interests are spindle bearing modeling and simulation.
E-mail: canhtong@kimm.re.kr

He is a principal researcher in the Department of Ultra Precision Machines and Systems, Korea Institute of Machinery & Materials. His research interests are precision machines and metrology.
E-mail: jooho@kimm.re.kr

He is a professor in the Department of Mechanical System Engineering, Kumoh National Institute of Technology. His research interests are spindle and bearings modeling and analysis, command shaping for positioning systems, and structural vibration analysis for mechanical system.
E-mail: swhong@kumoh.ac.kr