금속 적층 제조 격자 구조물의 압축 변형 거동 및 재구조화에 대한 실험적 분석
Copyright © The Korean Society for Precision Engineering
This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Abstract
We studied compressive behavior of two types of lattice structures having small-scale struts fabricated by utilizing a metal additive manufacturing process. Generally known, the lattice structure has some advantages such as lightweight and high specific mechanical strength, allowing diverse potential applications in the aerospace and mobility industries. In this work, we proposed two types of lattice such as body-centered truss (BCT) and octahedral truss (OCT) that were designed and fabricated for a compression test. From the experimental results, the OCT has much higher strength than the BCT, and all cases showed several buckling modes during the compressive behavior. Furthermore, ‘restructuring’ occurred with BCT, and the compressive force increased overall but fluctuated due to the restructuring by an increase of compression. Through this work, we found out that the BCT has the interesting compressive behaviors, and a repetitive bucking-restructuring was found. In fact, its strength could be increased continuously by the restructuring during compression. In conclusion, the BCT has key-characteristics of lightweight and re-strengthening, which are applicable to various applications in the industry.
Keywords:
Lattice structure, Additive manufacturing, Bucking mode, Compressive test, Restructuring키워드:
격자 구조, 적층 제조, 파단 모드, 압축시험, 재구조화1. 서론
항공, 자동차, 국방, 일반기계 등 다양한 기계 관련 산업분야에서 제품의 경량화를 통한 에너지 효율증대는 중요한 연구 주제이다. 에너지 효율을 향상시키는 방법으로 제품 경량화를 들 수 있으며 경량화 방법으로는 위상최적화(Topology Optimization)와 같은 형상 설계변수의 최적화를 통해 하중이 많이 걸리지 않는 부분을 제거하는 최적화 방식이 일반적으로 적용되고 있다.1 또는 경량화 소재를 적용하거나 구조물 내부에 미세한 격자 구조(Lattice Structure)를 적용하여 강성은 어느정도 유지하면서 경량화를 달성할 수 있다.2 내부 격자 구조를 이용한 방법으로는 샌드위치 패널(Sandwich Panel) 형태로 외부 형상 사이에 다공성 격자 구조를 넣는 방법이 주로 사용되고 있으며 비강성이 높고, 내충격성 등의 다른 부가적인 특성을 구현할 수 있다.3
격자 구조물은 단위셀(Unit Cell)이라고 하는 3차원 구조를 설계공간 안에 반복적으로 배열하고 단위셀 간에 조인트(Joint)와 스트럿(Strut)으로 연결하여 전체적인 내부 격자 구조체를 구성한다. 단위셀은 일반적으로 격자의 반복적 배열이 용이하도록 정육면체 형상을 기본으로 하고 강성에 따라 다양한 모양의 구조를 갖도록 설계한다. 단위셀의 크기가 작을수록 전체적인 기계적 강성이 높으나 내부에 작은 단위셀이 연속적으로 배열된 구조물을 제작하기가 어렵다.4 그러나 최근에 금속 적층 제조(Additive Manufacturing) 공정기술의 발달로 어느 수준까지는 미세하고 복잡한 격자 구조 제작이 가능하여 경량의 고강성 기계 구조물 제작에 활용할 수 있게 되었다.5,6
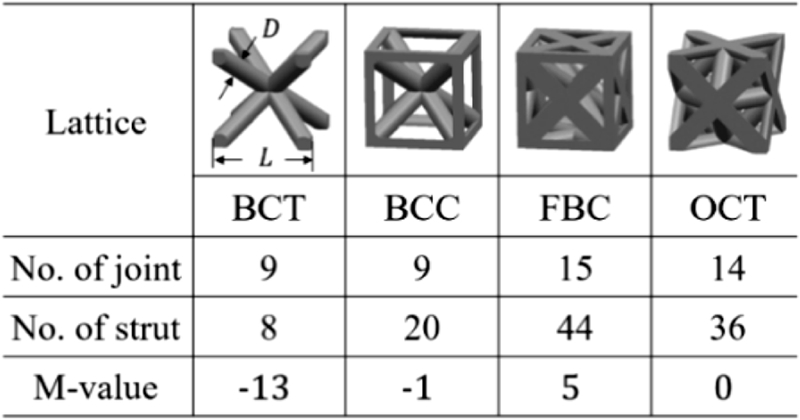
격자 구조를 이용한 경량화 연구사례로는 다음과 같다. Han 등은 샌드위치 코어에 격자 구조를 적용하고 서로 다른 재료를 채워 넣어 비강성을 향상시키는 연구를 진행하였다.7 Cheng 등은 위상최적화 기법을 이용하여 상대밀도(Relative Density) 분포에 따라 격자 구조를 최적화하고 에너지 전달효율 향상 및 강도를 높이는 연구를 진행하였다.8 또한 Daynes 등은 구조해석을 통해 응력 방향을 고려한 최적화 연구를 진행하였다.9 그리고 Kang 등은 위상최적화 상대밀도 분포 기반의 다중 격자 구조를 최적화하였고, SLM (Selective Laser Melting) 공정을 통해 제작하고 굽힘 변형 실험으로 강성을 평가하였다.10 그 외에도 많은 격자 구조를 이용한 다양한 연구가 진행되었다.11-13 그러나 현재까지 연구에서는 격자 구조물의 압축 변형 거동에 대한 연구가 많지 않으며, 지지 구조와 같은 많은 기계 구조물은 압축 거동이 중요한 경우가 많기에 내부 격자 구조 적용 시 압축 변형 거동을 분석하는 것은 중요하다. 내부 격자 구조가 압축에 의해서 변형이나 파손될 경우, 전체 구조물의 강성에도 영향을 주게 된다. 기존 연구에서 내부 격자의 형상을 4가지로 나누고 굽힘 변형에 대한 거동을 분석하였다.10 기존 연구 결과에서 평가한 4가지 격자 형상은 Fig. 1에 나타낸 것과 같으며 스트럿과 조인트가 증가함에 따라 격자의 강도가 증가하였다. 본 연구는 위에서 언급한 4가지 격자에 대해서 기본적인 압축 거동을 비교해보고 그 중에서 가장 효과적인 2가지의 형상에 대해서 실험적으로 자세한 압축 거동을 분석하고자 한다.
2. 압축 시편 설계 및 제작
2.1 내부 격자 형상설계
내부 격자 구조물은 정육면체 형상 안에 격자 구조를 가지는 형태를 기본으로 하였다. 격자의 형상설계는 격자 구조의 반복 배열 특징을 고려하여 3가지 수직축 방향에서 대칭성을 가지도록 설계하였으며 Fig. 1과 같이 기존 연구에서 적용된 BCT (Body-Centered Truss), BCC (Body-Centered Cubic), FBC (Face-Body Cubic), OCT (Octet Truss) 격자 구조를 사용하였다.10,14 단위 격자의 크기는 적층 제조의 제작성을 고려하여 변의 길이(L)가 2 mm인 정육면체를 기반으로 스트럿 직경(D)을 0.3, 0.4, 0.5 mm로 다양하게 설계하였다. 단위 격자 구조의 거동 특성은 식(1)의 Maxwell 안정성 임계지수 M (Maxwell’s Stability Criterion)을 이용하여 굽힘 또는 인장/압축에 유리한 격자의 기초 특성을 정의할 수 있다.16
| (1) |
여기서 b, j는 각각 단위 격자의 스트럿, 조인트 수를 의미한다. Maxwell의 안정성 기준에 따르면 M < 0인 경우, 굽힘 변형이 지배적인 구조이며, M ≥ 0 경우는 인장 또는 압축 변형이 지배적인 격자 구조이다.15
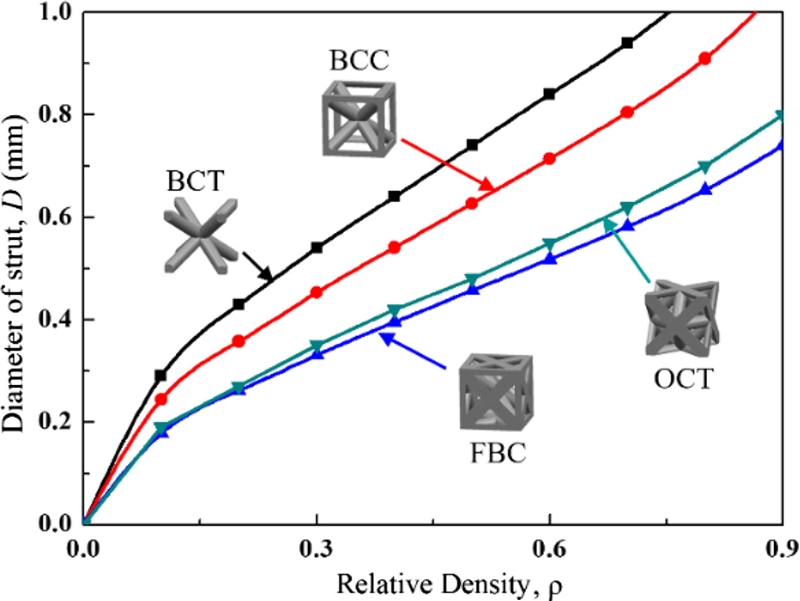
일반적으로 M 값이 작을수록 강성이 약하여 변형량이 크다. 이와 반대로 M 값이 큰 인장변형 지배적 구조는 강성이 높고 변형량이 작은 특성이 있으나 적층 제조에서 제작성이 떨어지는 단점이 있다. 따라서 Fig. 1에 나타낸 4가지 구조에서 BCT와 BCC 구조는 상대적으로 변형이 쉽게 되는 구조이며 제작성이 높고, FBC와 OCT는 높은 강성을 가지지만 제작성때문에 스트럿 직경 변화를 다양하게 할 수 없다. Fig. 2는 스트럿 직경 변화에 따라는 단위 격자의 상대밀도(ρ) 변화에 대하여 비교한 것이다. 상대밀도의 정의는 식(2)에 나타낸 것처럼 단위 격자 체적(Vl)과 완전한 정육면체 체적(Vs= 8 mm3)의 비로 나타내었다.
| (2) |
따라서 본 연구에서는 4가지 격자 구조에서 강성과 제작성에서 차이가 큰 BCT와 OCT 구조를 선정해서 압축 거동에 대해서 실험적으로 분석하였다.
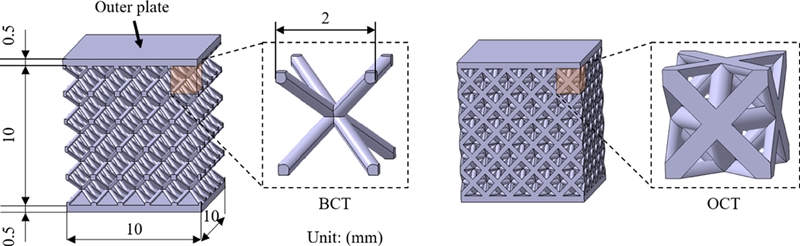
BCT와 OCT 단위 격자 기반의 압축 시편은 Fig. 3과 같이 모델링하였다. 격자 구조의 스트럿 직경은 0.3, 0.4, 0.5 mm로 세종류로 하였고, 단위 격자의 크기는 2 × 2 × 2 mm이다. 격자 간 압축 거동 분석을 위해서 시편의 높이 방향으로 5층으로 격자를 적층하고, 상하부에 0.5 mm 두께의 판재(Outer Plate)를 갖도록 설계하였다.
2.2 압축 시편 제작
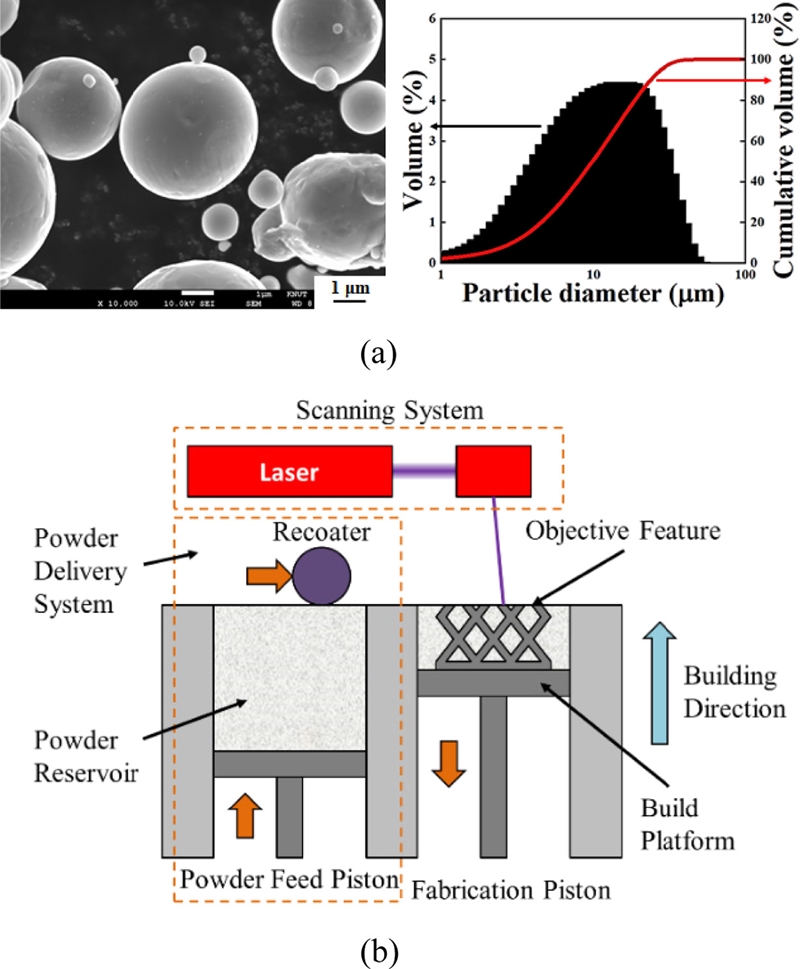
Figs. 4(a)와 4(b)는 사용된 금속분말과 공정 장치에 대한 개략도를 나타낸 것이다. 제작에 사용 분말은 SUS-630 소재이며 평균 입자 크기는 약 12.9 μm이다. 제작 장비는 ProX-300(3D Systems, USA)이며 제작정밀도는 약 0.2 mm, 최대 레이저 출력은 500 W이다. 제작공정은 Fig. 4(b)에 나타낸 것과 같이 플랫폼 위에 금속분말을 약 40 μm씩 적층하고 리코터(Recoater)로 적층된 분말을 고르게 다진 후 제작을 시작한다. 질소가스 분위기에서 레이저로 분말을 용융시켜 한 층을 제작하게 된다. 시편 제작 공정 조건으로 레이저 출력 170 W, 레이저 조사속도 1.6 m/s로 하였다.
설계된 2가지 내부 격자 구조의 기초 제작 결과를 비교해보면 Figs. 5(a)와 5(b)에 나타낸 것과 같이 BCT 구조는 스트럿 직경이 0.3, 0.4, 0.5 mm 모두 제작이 가능하였지만, OCT의 스트럿 직경이 0.3 mm인 경우 제작이 불가능하여 제작이 가능한 0.4, 0.5 mm 2가지만 제작하였다. 이는 OCT의 경우 구조가 복잡하고 수평 방향의 스트럿 구조를 포함하고 있어 스트럿 직경이 작은 경우 제작의 어려움이 있다. 시편은 각 형상마다 3개씩 제작하여 압축시험을 하였다.
3. 압축 실험
3.1 실험 구성 및 방법
내부 격자를 가진 시편의 압축 실험은 Fig. 6에서 표시된 것처럼 재료시험기(RB-310, R&B Co., Korea)에 압축용 펀치(Punch), 시편 고정 장치(Fixture) 등을 설치하였다. 내부 격자 구조의 변형 거동 분석을 위하여 실험은 시편 높이 50%인 5 mm까지 압축하였다. 또한 ASTM E9-89a 실험 규격인 압축속도 0.5 mm/min로 진행하였다.17 실험은 두 종류 형태의 격자 구조에서 스트럿 직경이 다른 5가지 시편을 각각 3개씩 만들어 총 15회 압축 실험을 진행하였다.
3.2 실험 결과
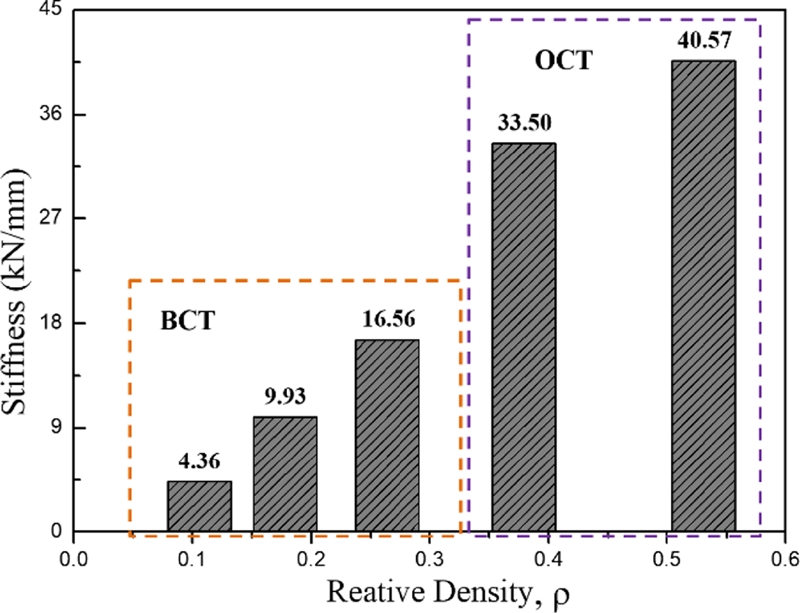
압축 실험에서 각 시편의 기계적 선형강성(Linear Stiffness)은 식(3)과 같이 탄성 거동 구간의 최대하중(Fm)을 변형량(dL)으로 나누어서 계산하였으며 Fig. 7에 격자 구조별 시편의 강성을 비교하였다.
| (3) |
BCT와 OCT구조를 비교하면 같은 스트럿 직경에서 상대밀도가 큰 OCT 구조가 약 2.5-3배 수준으로 강성이 높은 것을 알 수 있다. 또한 BCT의 경우 스트럿 직경이 0.3, 0.4, 0.5로 증가할 때 거의 선형적으로 강성이 약 두 배씩 올라가서 BCT 구조의 경우 스트럿 직경 변화를 이용하여 구조물의 변형량 조절이 가능함을 알 수 있다. Figs. 8(a)부터 8(c)는 스트럿 직경 변화에 따른 BCT 구조의 전체 변경 거동을 나타낸 것이다. 또한 Fig. 8(d)는 스트럿 직경 0.4 mm의 OCT 구조의 변형 거동을 나타낸 것이다. 스트럿 직경이 0.5 mm인 OCT 구조는 높은 강성으로 인해 거의 변형하지 않아 결과정리에서 제외하였다.
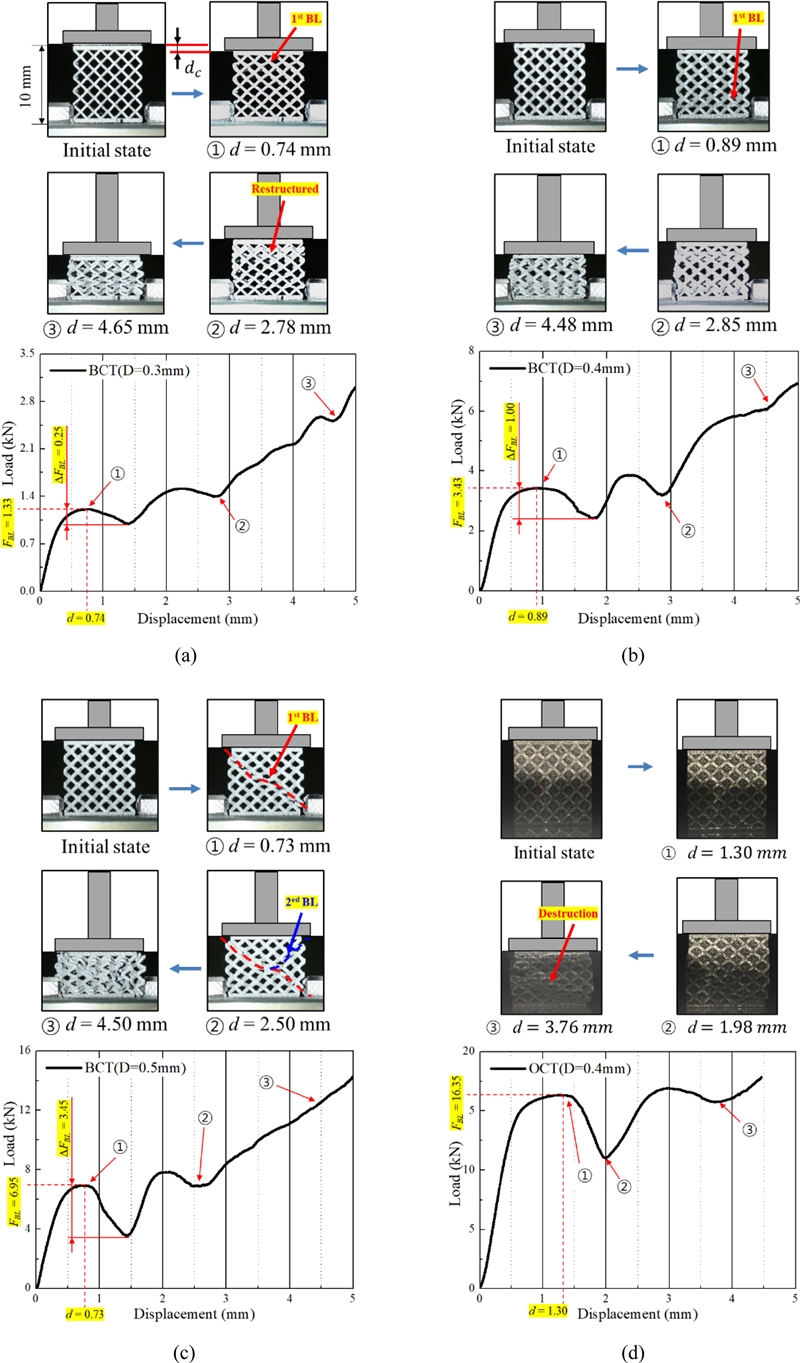
Load-Displacement result of compression test, (a) BCT with strut diameter (D) = 0.3 mm, (b) BCT with D = 0.4 mm, (c) BCT with D = 0.5 mm and (d) OCT with D = 0.4 mm. BL means ‘buckled layer’
내부 격자를 가지는 시편의 압축 실험에서 거동 분석을 해보면 전반적으로 국부적인 파단이 하중이 증가함에 따라 주기적으로 발생하였고 국부적 파단 시 하중이 떨어지고 재구조화(Restructuring)이 되면서 하중이 다시 증가하는 형태로 변형 거동이 발생하였다. 이것은 일반적인 솔리드 상태의 시편의 거동과 차이점이며 국부적 좌굴과 재구조화를 반복적으로 진행하면서 전체적인 강성이 지속적으로 올라가는 형상이다. 특이한 것은 내부 격자의 첫 번째 파단(좌굴)은 모든 시편에서 중앙부에서 발생하였다. 이것은 상하부에 판재 구조로 인해서 가장자리의 격자 변형이 상대적으로 안정되고 중간부로 갈수록 격자 변형이 자유로워 변형이 쉽게 발생하는 것으로 사료된다.
또한, 압축 변형에서 BCT와 OCT 구조에서 모두 배불림 형태로 중앙부의 변형률이 증가하며 변형량은 압축의 수직 평면에서 양방향 동일하게 발생하여 평면 등방성(Planar Isotropy) 가진다고 볼 수 있다. 이것은 내부 격자의 형태가 좌우대칭 구조이기에 나타나는 현상이다.6 앞서 기술한 바와 같이 압축 하중에 의해서 국부적으로 파단이 발생하더라도 전체 구조가 완전히 무너지는 형태가 아니라 재구조화를 통해서 강성을 유지하는 것이 일반적인 솔리드 상태의 시편 거동과 큰 차이가 나는 점이다. 따라서 재구조화가 진행되면서 최대하중 발생 시점은 5 mm 변형 한계까지 발생한다. Figs. 8(a)부터 8(c)에 나타낸 것처럼 변형된 BCT 구조에서 내부 격자가 국부적으로 좌굴층(Buckled Layer, BL)이 발생되고 좌굴층 주변에서 다른 층과 일체화된 재구조화가 발생하여 하중을 계속 지지한다. 내부 격자의 좌굴은 가장 취약한 중간부부터 시작되고 재구조화된 중간층을 기점으로 다시 양쪽으로 이등분화하여 새로운 중간부 좌굴층형 순차적으로 발생시킨다(Fig. 9 참조).
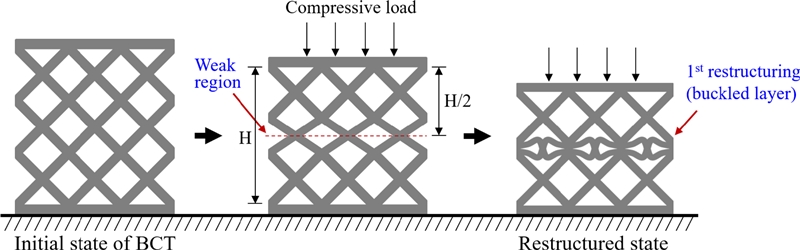
Progress of restructuring by compression, (a) Initial status of lattice structure, (b) Stage of 1-layer buckling and (c) Stage of restructuring
그러나 OCT 구조는 좌굴이 BCT 구조처럼 층을 나눠 일어나지 않고 하나의 일체화된 형체처럼 전단응력(Shear Stress)이 가장 큰 방향인 사선 방향으로 발생했다. 이것은 Fig. 7에 나타낸 것처럼 OCT의 경우 격자의 선형강성이 BCT에 비하여 동일 스트럿 직경 0.4 mm 조건에서 약 3.7배 더 높기에 국부적인 좌굴 보다는 솔리드 형태처럼 시편 전체에 하중이 분산되어 재료 거동을 하기 때문이다.
Figs. 8(a)부터 8(d)에 나타낸 첫번째 좌굴이 발생하기 전의 최대하중과 상대밀도에 대한 관계를 통해서 내부 격자의 강성을 분석하기 위해서 식(4)와 식(5)와 같이 관계식을 제시하였다. 본 연구는 상대밀도가 다른 두 BCT 구조의 격자 한 층의 재구조화 하중과 상대밀도가 관련 있고, x는 그 관련지수를 나타낸다.
| (4) |
| (5) |
여기서 F1, F2, ρ1, ρ2는 해당하는 2개의 격자 구조의 첫 번째 좌굴 발생 직전의 최대 압축 하중(FBL)과 상대밀도이다. Figs. 8(a)부터 8(c)에서 상응하는 재구조화 하중과 상대밀도를 위 식에 도입하여 Figs. 8(a)와 8(b), Figs. 8(b)와 8(c) 그리고 Figs. 8(a)와 8(c)의 관련지수를 계산한 결과: xab = 2.56, xbc = 2.89, xac= 2.70로서 xac를 기준으로 관련지수의 차이는 평균 7% 미만으로 나타났다. 따라서 상대밀도 증가에 따라 내부 격자의 강성이 평균적으로 2.7배 증가됨을 알 수 있다.
4. 결론
본 연구에서는 금속 적층 공정을 통해 내부 격자 구조인 BCT, OCT 구조에서 스트럿 직경을 달리한 형태로 압축 시편을 제작하고 압축 실험을 통해 변형 거동을 분석하였다. 실험 결과 다음과 같은 결론을 얻었다.
첫째, BCT 격자 구조는 중간부가 가장 취약하여 좌굴이 중간부에서 먼저 발생하고 이후 격자 재구조화를 통해서 다시 두번째 좌굴 지점이 발생한다. 따라서 연속적으로 변형과 좌굴이 주기적으로 발생하는 거동을 나타낸다. BCT 구조의 재구조화는 하중이 증가함에 따라 내부 격자가 좌굴되어 무너지지만 전체적으로 재구조화를 통한 강성 증대가 계속 발생되는 현상이다. 따라서 변형에너지 흡수가 용이하여 내충격성을 요구하는 구조물의 설계에 적용이 가능하다. 둘째, OCT의 구조는 구조 특성으로 인해 전단응력이 가장 큰 방향인 압축 하중의 45o 방향에서 좌굴 변형이 발생되었다. 또한 변형 강성도 OCT에 비하여 3배 수준으로 높게 나타나서 압축에 견디는 기계 구조물에 적용이 유리하다. 마지막으로 BCT 격자 구조의 첫 번째 좌굴 발생 직전의 최대하중은 상대밀도와 관련성이 있으며 상대밀도 증가에 따라 내부 격자의 강성이 평균적으로 약 2.7배 증가되는 것으로 나타났다.
본 연구를 통해서 내부 격자를 가지는 구조물의 압축 거동을 이용하여 다양한 기계적 특성을 가지는 형태로 설계가 가능할 것으로 사료된다.
NOMENCLATURE
| M : | Maxwell’s stability criterion |
| b : | Number of struts |
| J : | Number of joints |
| ST : | Stiffness of total structure |
| F : | Load of elastic region |
| dc : | Load displacement of compression test |
| Nclash : | Times of clash enhancement |
| Nlaver : | Number of lattice structure layers |
Acknowledgments
이 연구는 2018년도 산업통상자원부 및 산업기술평가관리원(KEIT) 지원에 의한 연구임(No. 20000201). 또한 부분적으로 과학기술정보통신부와 한국연구재단의 지원을 받아 수행된 연구임(No. NRF-2019R1A5A808320111).
References
-
Marder, M. and Liu, X., “Instability in Lattice Fracture,” Physical Review Letters, Vol. 71, No. 15, pp. 2417-2420, 1993.
[https://doi.org/10.1103/PhysRevLett.71.2417]

-
Schlangen, E. and Garboczi, E. J., “Fracture Simulations of Concrete Using Lattice Models: Computational Aspects,” Engineering Fracture Mechanics, Vol. 57, Nos. 2-3, pp. 319-332, 1997.
[https://doi.org/10.1016/S0013-7944(97)00010-6]

-
Gümrük, R. and Mines, R., “Compressive Behaviour of Stainless Steel Micro-Lattice Structures,” International Journal of Mechanical Sciences, Vol. 68, pp. 125-139, 2013.
[https://doi.org/10.1016/j.ijmecsci.2013.01.006]

-
Bonatti, C. and Mohr, D., “Mechanical Performance of Additively-Manufactured Anisotropic and Isotropic Smooth Shell-Lattice Materials: Simulations & Experiments,” Journal of the Mechanics and Physics of Solids, Vol. 122, pp. 1-26, 2019.
[https://doi.org/10.1016/j.jmps.2018.08.022]

-
Kim, D. I., Lee, H. J., Ahn, D. G., Kim, J. S., and Kang, E. G., “Preliminary Study on Improvement of Surface Characteristics of Stellite21 Deposited Layer by Powder Feeding Type of Direct Energy Deposition Process Using Plasma Electron Beam,” Journal of the Korean Society for Precision Engineering, Vol. 33, No. 11, pp. 951-959, 2016.
[https://doi.org/10.7736/KSPE.2016.33.11.951]

-
Kim, Y., Kim, Y., and Ryu, S., “Elastic and Fracture Property Analyses of Triangular and Square Lattice Spring Models at a Large Deformation Regime,” Journal of Mechanical Science and Technology, Vol. 32, No. 6, pp. 2693-2706, 2018.
[https://doi.org/10.1007/s12206-018-0526-9]

-
Han, B., Zhang, Z. J., Zhang, Q. C., Zhang, Q., Lu, T. J., et al., “Recent Advances in Hybrid Lattice-Cored Sandwiches for Enhanced Multifunctional Performance,” Extreme Mechanics Letters, Vol. 10, pp. 58-69, 2017.
[https://doi.org/10.1016/j.eml.2016.11.009]

-
Cheng, L., Zhang, P., Biyikli, E., Bai, J., Robbins, J., et al., “Efficient Design Optimization of Variable-Density Cellular Structures for Additive Manufacturing: Theory and Experimental Validation,” Rapid Prototyping Journal, Vol. 23, No. 4, pp. 660-677, 2017.
[https://doi.org/10.1108/RPJ-04-2016-0069]

-
Daynes, S., Feih, S., Lu, W. F., and Wei, J., “Optimisation of Functionally Graded Lattice Structures Using Isostatic Lines,” Materials & Design, Vol. 127, pp. 215-223, 2017.
[https://doi.org/10.1016/j.matdes.2017.04.082]

-
Kang, D., Park, S., Son, Y., Yeon, S., Kim, S. H., et al., “Multi-Lattice Inner Structures for High-Strength and Light-Weight in Metal Selective Laser Melting Process,” Materials & Design, Vol. 175, No. 5, Paper No. 107786, 2019.
[https://doi.org/10.1016/j.matdes.2019.107786]

-
Alzahrani, M., Choi, S. K., and Rosen, D. W., “Design of Truss-Like Cellular Structures Using Relative Density Mapping Method,” Materials & Design, Vol. 85, pp. 349-360, 2015.
[https://doi.org/10.1016/j.matdes.2015.06.180]

-
Kim, Y., “Analysis of Bending Fracture Propagation of Laminar Composite Materials Using Quasi-Molecular Dynamics,” KSME International Journal, Vol. 12, No. 6, pp. 1026-1033, 1998.
[https://doi.org/10.1007/BF02942576]

-
Chang, P. S. and Rosen, D. W., “The Size Matching and Scaling Method: A Synthesis Method for the Design of Mesoscale Cellular Structures,” International Journal of Computer Integrated Manufacturing, Vol. 26, No. 10, pp. 907-927, 2013.
[https://doi.org/10.1080/0951192X.2011.650880]

-
Alzahrani, M., Choi, S. K., and Rosen, D. W., “Design of Truss-Like Cellular Structures Using Relative Density Mapping Method,” Materials & Design, Vol. 85, pp. 349-360, 2015.
[https://doi.org/10.1016/j.matdes.2015.06.180]

-
Liu, C., Du, Z., Zhang, W., Zhu, Y., and Guo, X., “Additive Manufacturing-Oriented Design of Graded Lattice Structures through Explicit Topology Optimization,” Journal of Applied Mechanics, Vol. 84, No. 8, Paper No. 081008, 2017.
[https://doi.org/10.1115/1.4036941]

-
Deshpande, V., Ashby, M., and Fleck, N., “Foam Topology: Bending Versus Stretching Dominated Architectures,” Acta Materialia, Vol. 49, No. 6, pp. 1035-1040, 2001.
[https://doi.org/10.1016/S1359-6454(00)00379-7]

-
Amani, Y., Dancette, S., Delroisse, P., Simar, A., and Maire, E., “Compression Behavior of Lattice Structures Produced by Selective Laser Melting: X-Ray Tomography Based Experimental and Finite Element Approaches,” Acta Materialia, Vol. 159, pp. 395-407, 2018.
[https://doi.org/10.1016/j.actamat.2018.08.030]


Master course student at the School of Mechanical Engineering in Pusan National University. His research interest is design of optimized lattice structure with topology optimization.
E-mail: sub6953@pusan.ac.kr

Master course student at the School of Mechanical Engineering in Pusan National University. His research interest is additive manufacturing of lattice structure.
E-mail: jsis001@pusan.ac.kr

Researcher in Korea Institute of Industrial Technology (KITECH). His research interest is design for additive manufacturing.
E-mail: simo@kitech.re.kr

Principal researcher in Korea Institute of Industrial Technology (KITECH). His research interest is additive manufacturing process.
E-mail: sonyong@kitech.re.kr

He is a Professor in the School of Mechanical Engineering at Pusan National University. His research fields are in engineeing for additive manufacturing, and surface treatment.
E-mail: sanghu@pusan.ac.kr