슬러리 공급 조건에 의한 패드 온도 분포의 변화

1. 서론

반도체 칩이 처리할 수 있는 데이터를 증가시키기 위해 높은 집적도가 필요하게 됨에 따라, 미세 선폭 구현을 통한 고집적 반도체가 요구되고 있다. 요구 사양을 달성하기 위해서 최근에는 극자외선 노광 공정이 주목받고 있다. 극자외선 노광 공정은 미세 선폭 구현을 위해 짧은 파장의 광원을 사용하여 해상도를 향상시킨다. 하지만 짧은 파장의 광원은 해상도 향상과 동시에 초점심도의 깊이의 감소를 유발하여 공정 불량을 초래한다. 이와 같은 문제를 해결하기 위해서 화학기계적 평탄화(Chemical Mechanical Planarization, CMP) 공정을 통한 광역적 평탄화를 해결책으로 낮은 초점심도의 조건에서 공정 조건을 만족시킨다.¹

공정에서 요구되는 광역적 평탄화를 위해서는 기존에 주로 다루었던 재료제거율(Material Removal Rate, MRR)에 대한 연구와 함께 연마균일도(With-In Wafer Non-Uniformity, WIWNU)에 대한 연구가 필요하다.^2,3 CMP 공정은 2축 회전하는 패드와 웨이퍼 사이의 마찰력에 의해 온도가 상승한다. H. J. Kim⁴은 공정 온도와 재료제거율 사이의 관계를 제시했다. 온도 상승에 따라 화학 용액인 슬러리와 웨이퍼 화학반응의 변화에 따라 MRR에 차이가 생긴다고 설명한다. 또한 온도의 변화는 패드의 물성을 변화시켜 Preston 지배방정식에서 Preston 상수와 압력의 변화에 의한 MRR 관계를 설명 가능하다.^5,6

즉, MRR은 공정 온도에 비례하여 상승한다. 따라서 웨이퍼 전역의 MRR의 편차인 WIWNU를 향상시키기 위해서 패드 반경 방향으로의 균일한 온도 분포가 필요하다. 하지만 공정이 진행됨에 따라 다양한 원인에 의해 패드 온도 분포에는 편차가 생긴다. 일반적으로 CMP 공정에서 온도 제어를 위해 칠러를 사용하나, 연마율 상승효과를 가질뿐 연마 균일도에 향상을 위한 사용이 어렵다.⁷ 또한 패드 표면에 직접 접촉하는 모듈을 제작해 표면 온도를 제어함으로서 연마균일도 향상시키기 위한 연구가 진행되기도 했다.⁸ 이와 달리 본 연구에서는 패드 온도 분포 편차에 대한 원인뿐만 아니라 냉각 효과를 주는 슬러리의 공급 방식에 따른 온도 제어 방식을 제시한다.

2. 이론적 배경

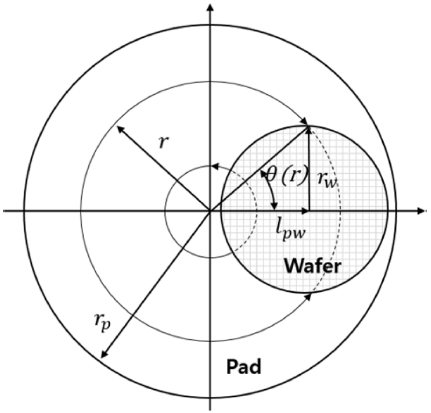
CMP 공정 중에는 Fig. 1과 같이 패드 온도 분포에 편차가 생긴다. 이는 패드 반경 방향으로 공급되는 에너지의 차이에 의해 발생한다. 패드와 웨이퍼의 접촉 계면에서 발생하는 마찰에 의한 마찰에너지가 주된 공급 에너지원이다.⁷ 패드와 웨이퍼의 크기 차이에 의해 반경 방향으로 마찰 거리, 상대속도 그리고 마찰 시간에 따라 공급에너지의 차이가 발생한다. 따라서 본 장에서는 반경 방향으로의 마찰에너지를 식으로 나타내었다. 이론적 모델을 도출하고 적용함에 있어 다음과 같이 가정하였다.

Fig. 1

Temperature distribution with IR camera during process

(1) 주변 환경과의 열전달에 의한 에너지 손실은 무시한다.

(2) CMP 공정은 윤활막의 동압에 의한 영향이 없는 직접 접촉하고 있는 경계윤활(Boundary Lubrication, BL) 모델이다.⁹

(3) 마찰 계수는 가공 시간과 온도의 영향을 받지 않는다.

(4) 리테이너에 의한 연마 패드 온도의 변화는 무시한다.

(5) 공정 중 패드 내의 압력 분포는 동일하다.

2.2 마찰 거리와 시간

패드와 웨이퍼는 2개의 축을 가지는 원 운동을 함으로써 상대 운동을 하게 된다. 따라서 웨이퍼와 패드의 직경, 회전속도에 따라 웨이퍼 위의 미소체적의 운동은 패드 중심과의 거리 r에 대한 함수로 나타난다. 이때 에너지가 공급되는 구간의 길이를 d_H라 하고, Fig. 2로 수식화하면 다음 식(5)와 식(6)과 같다.

$\[ d_H\left(r\right)=2\cdot \text{r}\cdot {\text{cos}}^{-\text{1}}\theta \]$

(5)

$\[ \theta \left(r\right)=\frac{r^2+{l_{pw}}^2-{r_w}^2}{2\cdot r\cdot l_{pw}} \]$

(6)

Fig. 2

Schematic of position between pad and wafer with included angle and radius

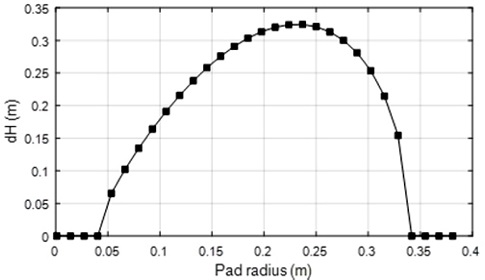
l_pw는 웨이퍼 중심과 패드 중심과의 거리, r_w는 웨이퍼 반지름, θ(r)는 끼인각이다. 식을 통해 패드의 직경 방향으로 에너지 공급 거리 값에 차이가 생김을 알 수 있고, 그 결과는 Fig. 3 그래프와 같은 분포를 가진다.

$\[ t_H\left(r\right)=\frac{2\cdot {\text{cos}}^{-\text{1}}\theta }{w_p} \]$

(7)

Fig. 3

Heating distance graph of pad with diameter of 762 mm (0.762 m) and 300 mm (0.3 m) wafer

식(5)에 패드의 선 속도를 나누어 패드 반경에 따른 마찰에너지 공급 시간을 계산할 수 있다.¹⁰

2.4 공급에너지

2.2장에서 정의한 패드 온도 변화에 대한 식(4)에 마찰 시간 식(7)과 상대속도 식(10)을 대입하여 공급에너지를 구할 수 있다.

$\[ \text{Δ}{E}_{friction}=P\cdot \left\{r\cdot w_p-r_w\cdot w_w\right\}\cdot \frac{2\cdot {\text{cos}}^{-\text{1}}\theta }{w_p} \]$

(11)

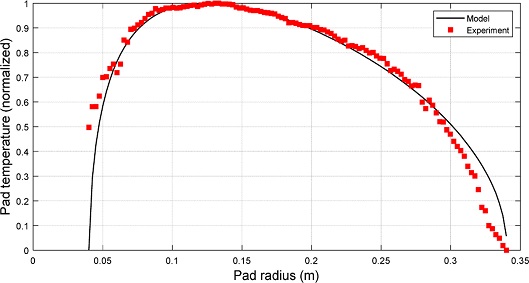
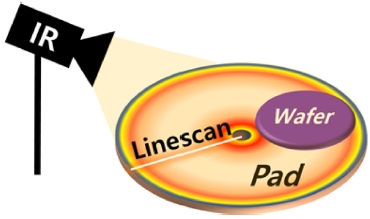
Fig. 4는 제시한 에너지 공급 모델과 실험을 통한 패드 온도 분포를 정규화하여 비교한 결과이다. 실험은 화학적 반응과 슬러리에 의한 에너지 손실을 최소화하기 위해 Table 1의 슬러리 공급 조건을 사용했다. 온도 측정은 FLIR사의 T420 카메라를 사용하여 Fig. 5와 같이 라인주사 방법으로 측정했다. 온도 측정에서의 슬러리의 영향을 최소화하기 위해 슬러리 공급 지역의 이전 공간을 측정했다. 측정 결과 공급되는 에너지와 온도의 분포는 14.3%의 오차로 상당히 일치함을 확인할 수 있고, 결과적으로 가장 많은 에너지가 공급되는 지역의 온도가 가장 높을 것으로 예상된다.

Fig. 4

Graph of energy model and measured values

Table 1

Experimental conditions

Fig. 5

Measuring pad temperature by using IR camera

3. 패드 온도 분포 제어

2장에 따르면 식(11)에서 최댓값을 가지는 지점이 공정 중 가장 높은 온도가 측정될 것을 예상할 수 있다.

Table 1의 조건을 사용하면 약 r = 0.13m에서 가장 많은 에너지를 공급받는다. 이후 실험에서 결과를 이용해 최고온도가 예상되는 지점을 r = 0.13m로 지정하고 실험을 진행한다.

3.1 슬러리 공급 위치에 따른 온도 분포

공정 중에 열 전달에 의한 에너지 손실은 슬러리와 상호 작용이 대부분을 차지한다. 따라서 본 실험에서는 냉각재 역할의 슬러리의 공급 위치를 조정하여 패드 온도 분포를 제어한다.

3.1.1 실험 조건

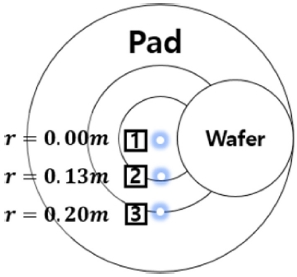
실험은 GnP 테크놀로지의 POLI-762 연마기를 사용했으며 구리 웨이퍼를 연마했다. CMP 소모품인 패드와 슬러리는 KPX사의 4세대 연마 패드와 구리 연마에 사용되는 콜로이달 실리카인 FUJIFILM사의 CLS-9044 슬러리를 사용하였다. 웨이퍼는 ADVANTEC사의 12 in 크기의 1.5 μm의 두께의 구리박막을 가진 평판 웨이퍼를 사용했다. 공정 조건은 Table 2와 같다. 슬러리 공급 위치는 Fig. 5와 같이 3점으로 나눈다.

Table 2

Model conditions

Position 1: Pad Center (r = 0m)
Position 2: Point between Pad Center and Wafer Center (r = 0.13m)
Position 3: Wafer Center (r = 0.2m)

Position 1은 주로 사용되는 슬러리 공급 지점인 패드 중심부 r = 0 m, Position 2는 최고온도가 예상되는 r = 0.13m 지점 그리고 Position 3은 비교를 위해 r = 0.2m로 설정했다. 패드 안정화를 위해 20분 동안 더미 웨이퍼를 연마하였으며 2분간 상온 상태에 패드를 두어 형성된 패드 온도인 30^oC를 초기온도로 설정 후 실험을 진행했다. 연마는 2분간 진행했으며, 설정된 초기온도 형성을 위해 2분간 상온에 두었다. 온도는 FLIR사의 T420 열화상 카메라로 측정했다.

3.1.2 실험 결과

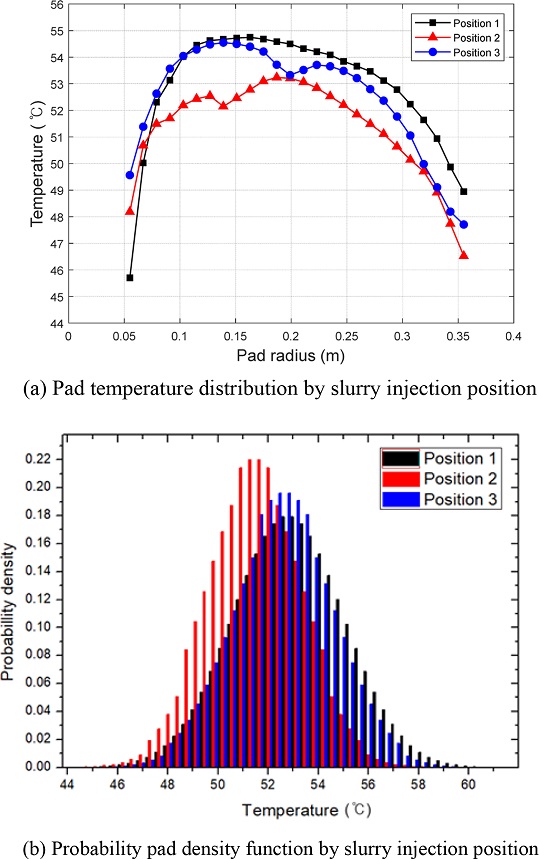
Fig. 6에서 Position 1은 슬러리가 공급되는 웨이퍼의 앞단의 온도가 낮음을 알 수 있고, r = 0.13m 부근에서 최고온도가 나타난다. Position 2는 슬러리가 공급된 r = 0.13m 지점에서 부분적 온도 감소 효과를 확인할 수 있다. Position 3은 부분적 온도 감소 효과는 확인할 수 있으나, 최고온도 지점은 변화시키지 못한다. 또한 Fig. 7의 확률 밀도 함수를 통해 기존 방식인 Position 1의 평균은 52.89이고 편차는 2.218이다. Position 2의 평균은 51.34, 편차는 1.806 그리고 Position 3의 평균 52.50, 편차는 2.027이다. 이를 통해 Position 2의 경우 기존의 방식보다 온도 편차를 18.5% 감소시킴을 확인 가능하다. 즉 결과적으로 Position 2에 슬러리를 공급하면 최고온도 지점을 변화시켜주며 온도 편차를 줄이는 효과를 얻을 수 있다.

Fig. 6

Schematic of slurry injection position

Fig. 7

Comparison of pad temperature by slurry injection position

3.2 공급 유량 비에 따른 온도 분포

3.1장의 실험을 통해 슬러리가 공급되는 위치의 온도가 지역적으로 감소함을 확인했다. 3.2장에서는 기존의 단일 노즐을 사용한 공급이 아닌 다중 노즐을 사용한 슬러리 공급을 통해 앞선 실험에서의 국소적인 온도 감소 문제를 해결하고 편차를 감소시키는 방안을 제시한다.

3.2.1 실험 조건

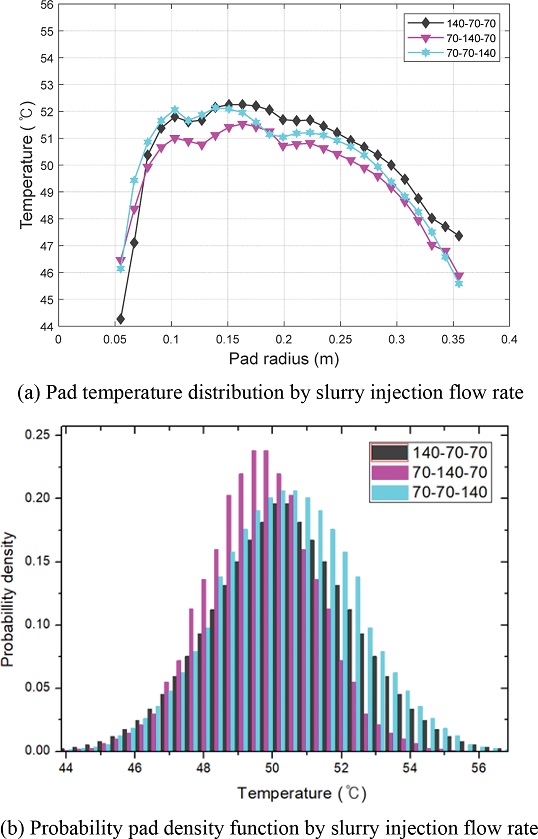
실험은 3.1.1장의 조건과 동일하나 단일 노즐이 아닌 다중 노즐을 사용해 Fig. 5의 Positions 1부터 3의 모든 지점에 슬러리를 공급한다. 지역적으로 공급되는 유량 비를 Table 3과 같이 조절하며 패드 온도 분포에 미치는 영향을 측정했다.

Table 3

Experimental conditions

3.2.2 실험 결과

결과는 Fig. 8(a)와 같이 3.1.2장의 결과처럼 큰 차이를 확인할 수는 없다. 하지만 많은 유량의 슬러리를 공급해준 지역의 온도가 상대적으로 많이 감소한다. 이는 Positions 1부터 3에 슬러리를 동시 공급하여도 유량에 따라 온도 분포 제어에 영향을 줌을 알 수 있는 결과이다. Fig. 8(b)에 의해 3.1.2장의 결과와 유사하게 Position 2에 가장 많은 유량을 공급해줄 때, 편차가 감소하여 확률 밀도 함수의 폭이 줄어듦을 확인할 수 있다. Position 1에 많은 유량을 공급했을 때 평균은 50.38, 편차는 2.025이다. Position 2에 많은 유량을 공급했을 때 평균은 49.74, 편차는 1.670이다. Position 3에 많은 유량을 공급했을 때 평균은 50.20, 편차는 1.928이다. 결과적으로 다중 노즐을 사용하여 Position 2에 많은 유량을 공급해 줄 때 기존 대비 편차가 24.7% 감소되며 패드 온도 분포의 편차가 가장 적게 형성된다.

Fig. 8

Comparison of pad temperature by slurry injection flow rate

Table 4

Experimental conditions

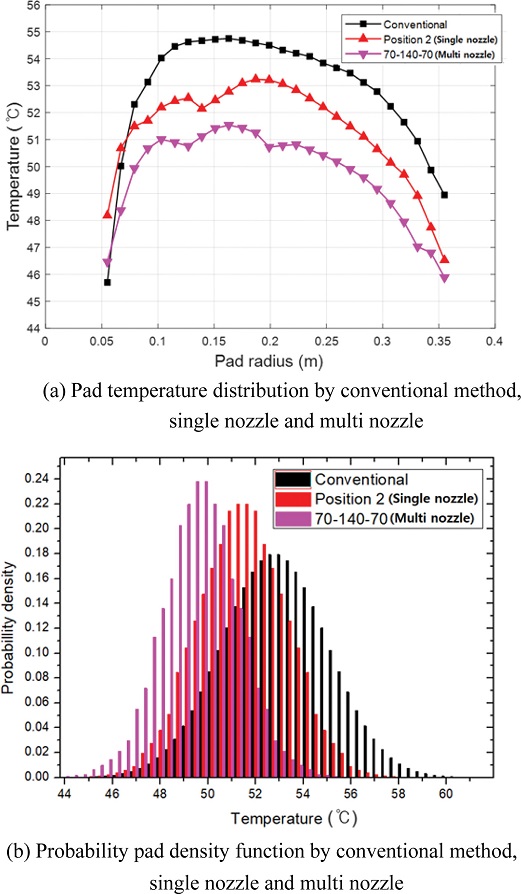
이를 앞선 실험의 결과와 비교해 보면 Fig. 9와 같다. 단일 노즐을 사용할 경우 Position 2에 슬러리를 공급해 주는 것이 패드 온도 제어에 가장 효과적이고, 다중 노즐을 사용할 경우 Position 3에 가장 많은 유량의 슬러리를 공급해주는 것이 가장 효과적임을 알 수 있다.

Fig. 9

Comparison of pad temperature by conventional method, single nozzle and multi nozzle

즉, 패드 온도 편차를 효과적으로 제어하기 위해서는 다중 노즐을 사용하는 것이 바람직하며, 최고온도가 예상되는 지역에 많은 유량의 슬러리를 공급해주면 단일 노즐보다 편차를 감소시킬 수 있다.

3.3 MRR 비교

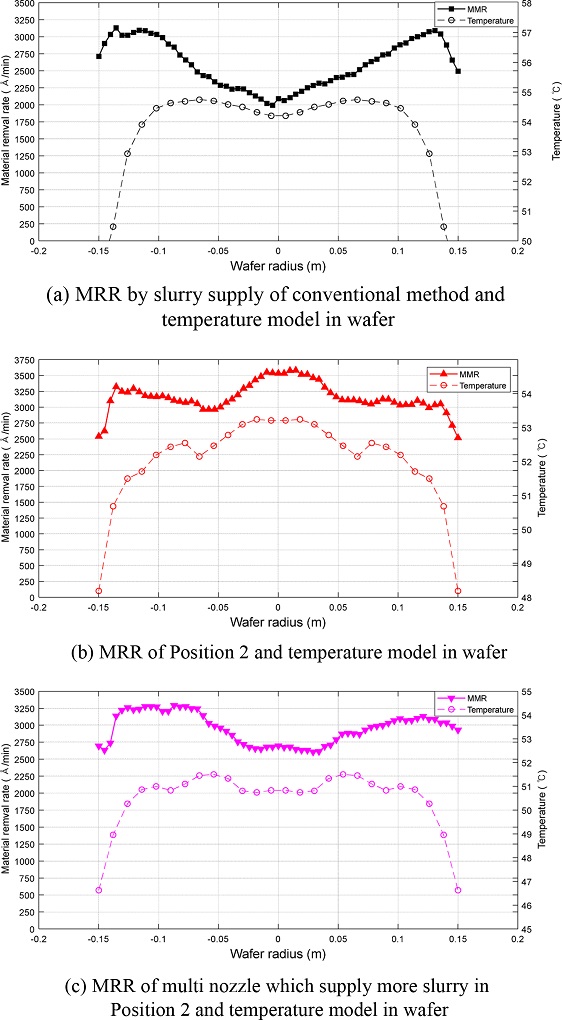
3.2.2장의 결과에 따라 패드 온도 분포 편차의 향상과 MRR의 상관관계를 규명하기 위해 MRR과 비교하면 Fig. 10과 같다. 기존의 공급 방식을 사용한 연마 결과 WIWNU는 13.95%, Position 2에 공급해줄 때 5.79%, 다중 노즐을 사용할 때 7.68%이다. 앞의 결과에 따르면 온도 편차가 적은 다중 노즐에서 가장 적은 WIWNU가 예상되지만 실제로는 단일 노즐에서 가장 낮은 WIWNU를 얻는다.

Fig. 10

Comparison between WIWNU and temperature distribution

이는 WIWNU는 패드 온도가 아닌 연마 표적인 웨이퍼의 온도 분포를 따르기 때문이다. 공정 중 웨이퍼 내의 온도를 예측하기 위해 패드 온도 분포를 웨이퍼 기준으로 수정하는 과정이 필요하다. 측정한 패드 온도 분포 그래프를 웨이퍼 중심을 축으로 360^o 회전시켜 MRR과 비교하면 Fig. 10과 같다. -0.15--0.1, 0.1-0.15의 구간을 1영역, -0.1-0.1의 구간을 2영역이라 하자. 1영역에서는 실제 공정 중 리테이너에 의한 패드 리바운딩 효과에 의해 가장자리에서 연마율이 높게 나타난다.^13,14 2영역에서는 연마 형상이 패드 온도 분포의 형상과 유사함을 유추할 수 있다. 즉, WIWNU 향상을 위해서는 웨이퍼 센터의 온도가 높아야 하고, Position 2에 슬러리를 공급해줌으로 패드의 최고온도 위치를 제어할 수 있다. 따라서 Fig. 10(b)의 결과와 같이 최고온도 지점을 웨이퍼 센터로 제어하면, 기존의 연마 경향과 달리 중심부의 MRR를 상승시켜 WIWNU를 향상시킬 수 있다.

4. 결론

본 연구에서는 공정 중 패드 온도의 편차를 줄이기 위한 제어 방법을 제시하기 위해 에너지적 접근법으로 식(11)과 같이 나타내어 편차 경향을 수식화하였다. 이를 통해 패드의 최고온도 지점을 예상할 수 있으며, 온도 제어 방식의 근거가 된다. 공급되는 에너지는 미소면적에 대한 상대속도, 마찰 시간, 마찰 거리를 고려했으며 실험을 통해 얻은 온도 편차와 비교하여 검증하였다.

실험을 통해 슬러리가 공급되는 지역의 부분적 온도 감소 효과를 확인했고, 이를 이용해 패드의 온도 분포를 제어했다. Table 1의 조건에서 r = 0.13m 부근에서 최고온도가 예상되었고, 예상 지점에 슬러리를 공급해준 결과 기존 대비 편차가 18.5% 감소하였다. 이후 국소적인 온도 감소 문제를 해결하기 위해 다중 노즐을 사용하여 예상 지점에 가장 많은 슬러리를 공급해주었을 때, 편차가 24.7% 감소했다. 이와 같이 기존과 다른 공급 방식을 통해 패드 온도 편차 감소를 위한 제어가 가능하다.

그러나 MRR은 패드 온도 분포와 다른 경향을 보인다. 이는 웨이퍼가 온도 분포의 차이가 생긴 패드 위를 회전하며 연마가 진행되기 때문이다. 패드 온도 분포를 웨이퍼 중심을 축으로 회전시키면 웨이퍼의 온도를 예측할 수 있고, 이는 MRR 경향과 상당히 일치한다(Fig. 10). 따라서 패드의 온도 편차뿐만 아니라 웨이퍼의 회전을 고려한 온도 제어를 통해 더욱 효과적인 WIWNU 향상이 가능할 것이라 판단된다.

Acknowledgments

이 연구는 2020년도 정부(미래창조과학부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. NRF-2019R1A2B5B01070489).

REFERENCES

• Takeno, Y. and Okamoto, K., “New Market Trend in CMP Equipment/Material for the “More than Moore” Era,” Proc. of the International Conference on Electronics Packaging and iMAPS All Asia Conference, pp. 423-425, 2018. [https://doi.org/10.23919/ICEP.2018.8374338]
• Li, Y., “Microelectronic Applications of Chemical Mechanical Planarization,” John Wiley & Sons, pp. 1-24, 2007. [https://doi.org/10.1002/9780470180907]
• Kwon, D., Kim, H., and Jeong, H., “Heat and its Effects to Chemical Mechanical Polishing,” Journal of Materials Processing Technology, Vol. 178, Nos. 1-3, pp. 82-87, 2006. [https://doi.org/10.1016/j.jmatprotec.2005.11.025]
• Kim, H., Kim, H., Jeong, H., Lee, E., and Shin, Y., “Friction and Thermal Phenomena in Chemical Mechanical Polishing,” Journal of Materials Processing Technology, Vol. 130, pp. 334-338, 2002. [https://doi.org/10.1016/S0924-0136(02)00820-8]
• Park, Y., Lee, Y., Lee, H., and Jeong, H., “Effect of Heat according to Wafer Size on the Removal Rate and Profile in CMP Process,” Electronic Materials Letters, Vol. 9, No. 6, pp. 755-758, 2013. [https://doi.org/10.1007/s13391-013-6003-9]
• Kim, H., Pak, B., Jeong, S., Lee, D., and Jeong, H., “Planarization Modeling based on Contact Mode between Pad Asperity and Oxide Pattern during CMP,” Journal of the Korean Society for Precision Engineering, Vol. 36, No. 4, pp. 363-372, 2019. [https://doi.org/10.7736/KSPE.2019.36.4.363]
• Kim, H., Kwon, D., Jeong, H., Lee, E., and Shin, Y., “A Study on the Distribution of Friction Heat Generated by CMP Process,” Journal of the Korean Society for Precision Engineering, Vol. 20, No. 3, pp. 42-49, 2003.
• Matsunaga, T., Uneda, M., Takahashi, Y., Shibuya, K., Nakamura, Y., et al., “Influence into Platen and Polishing Pad Surface Temperature on Removal Rate in Sapphire-Chemical Mechanical Polishing,” Proc. of the International Conference on Planarization/CMP Technology, pp. 1-4, 2015.
• Wu, C., Sampurno, Y., Liao, X., Jiao, Y., Theng, S., et al., “Pad Surface Thermal Management during Copper Chemical Mechanical Planarization,” ECS Journal of Solid State Science and Technology, Vol. 4, No. 7, pp. 206-212, 2015. [https://doi.org/10.1149/2.0101507jss]
• Gwon, D. H., Kim, H. J., Jeong, H. D., Lee, E. S., and Sin, Y. J., “A Study on the Correlation between Temperature and CMP Characteristics,” Journal of the Korean Society for Precision Engineering, Vol. 19, No. 10, pp. 156-162, 2002.
• White, D., Melvin, J., and Boning, D., “Characterization and Modeling of Dynamic Thermal Behavior in CMP,” Journal of the Electrochemical Society, Vol. 150, No. 4, pp. 271-278, 2003. [https://doi.org/10.1149/1.1560642]
• Kim, M. K., Yoon, Y. B., Koh, Y. H., Hong, C. G., and Shin, S. H., “Velocity Measurements of Slurry Flows in CMP Process by Particle Image Velocimetry,” Journal of the Korean Society for Precision Engineering, Vol. 23, No. 5, pp. 59-67, 2006.
• Lee, J. W., Lee, D. S., Jeong, S. H., Kim, H. J., Park, B. J., et al., “Analytical Study of Contact Stress on Wafer Edge in CMP,” Journal of the Korean Society for Precision Engineering, Vol. 35, No. 2, pp. 157-161, 2018. [https://doi.org/10.7736/KSPE.2018.35.2.157]
• Bae, J., Lee, H., Lee, S., Guo, Y., Park, J., et al., “Effect of Retainer Pressure on Removal Profile and Stress Distribution in Oxide CMP,” Proc. of the International Conference on Planarizaiton/CMP Technology, pp. 345-349, 2009.